A New Time-Sensitive Graph Model for Conflict Resolution with Simultaneous Decision-Maker Moves
Abstract
1. Introduction
2. Preliminaries
2.1. Key Concepts in GMCR
2.2. Classical Graph Model for Conflict Resolution
3. Time-Sensitive Graph Model for Conflict Resolution
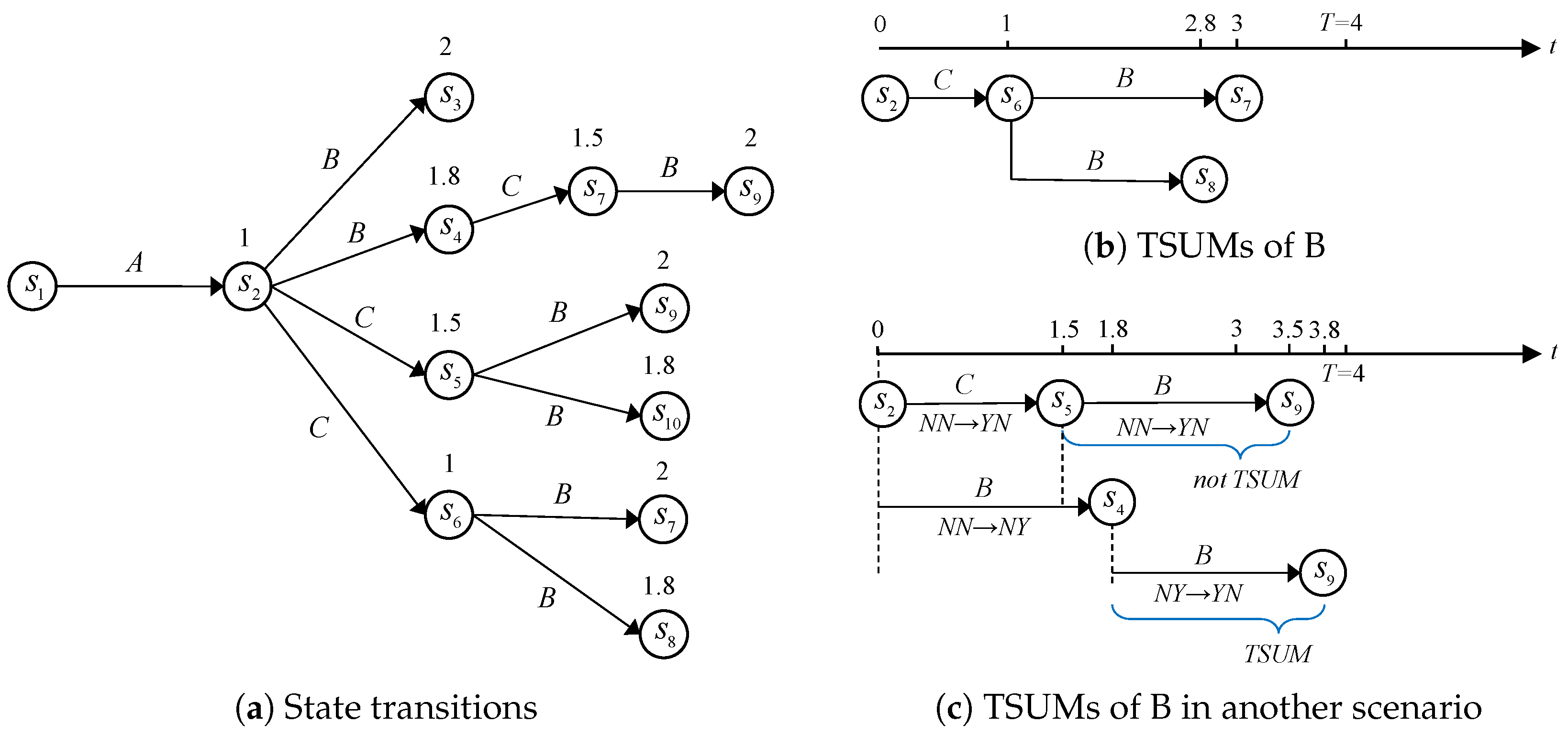
3.1. Structure of Time-Sensitive Graph Model for Conflict Resolution
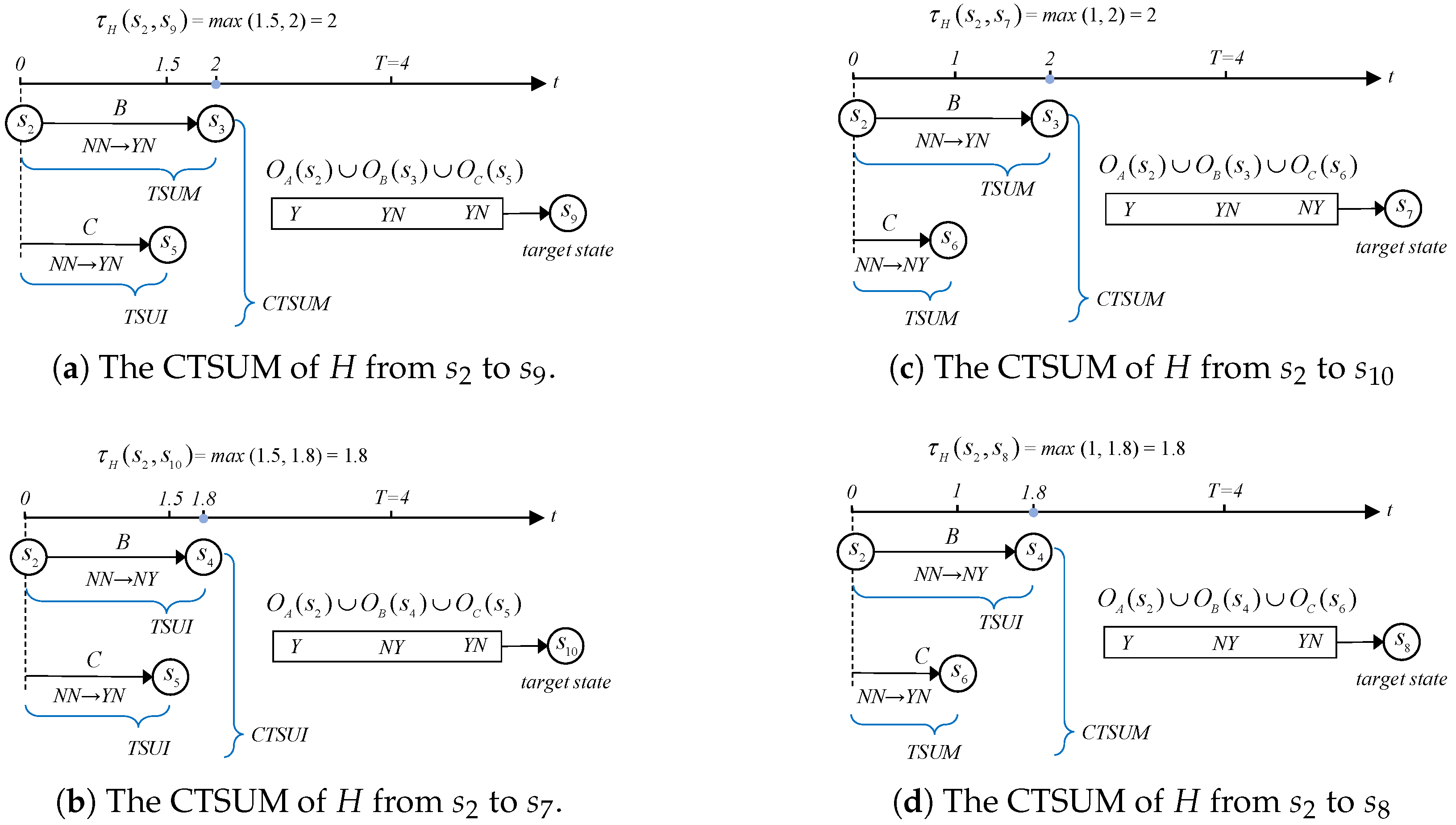
3.2. Unilateral Moves and Unilateral Improvements in TSGMCR
3.3. Stability Analysis of TSGMCR
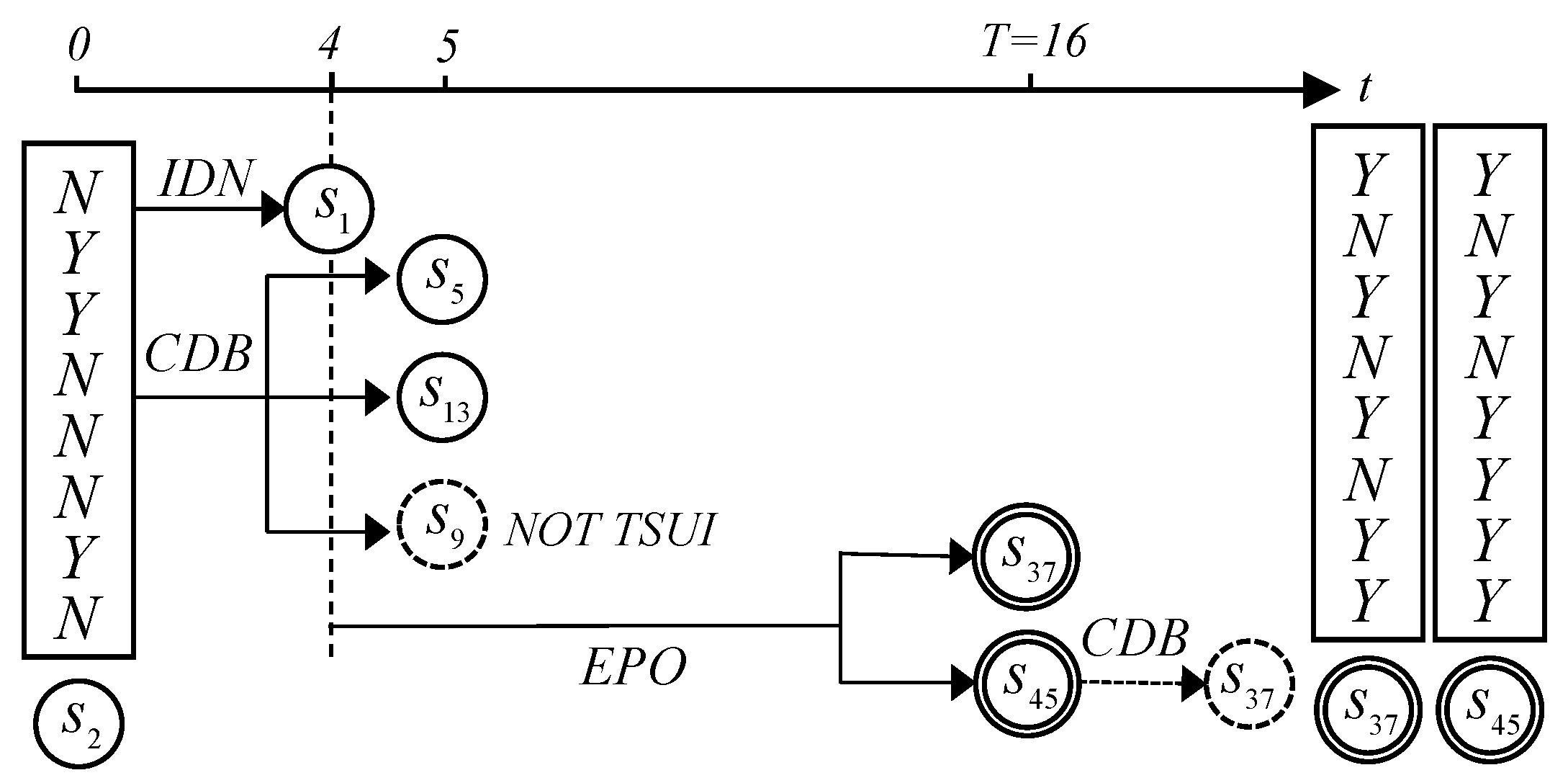
3.4. TSGMCR Analysis of Real-World Conflict Problem Process
3.5. Inter-Relationships Between Key Concepts of TSGMCR and Classic GMCR
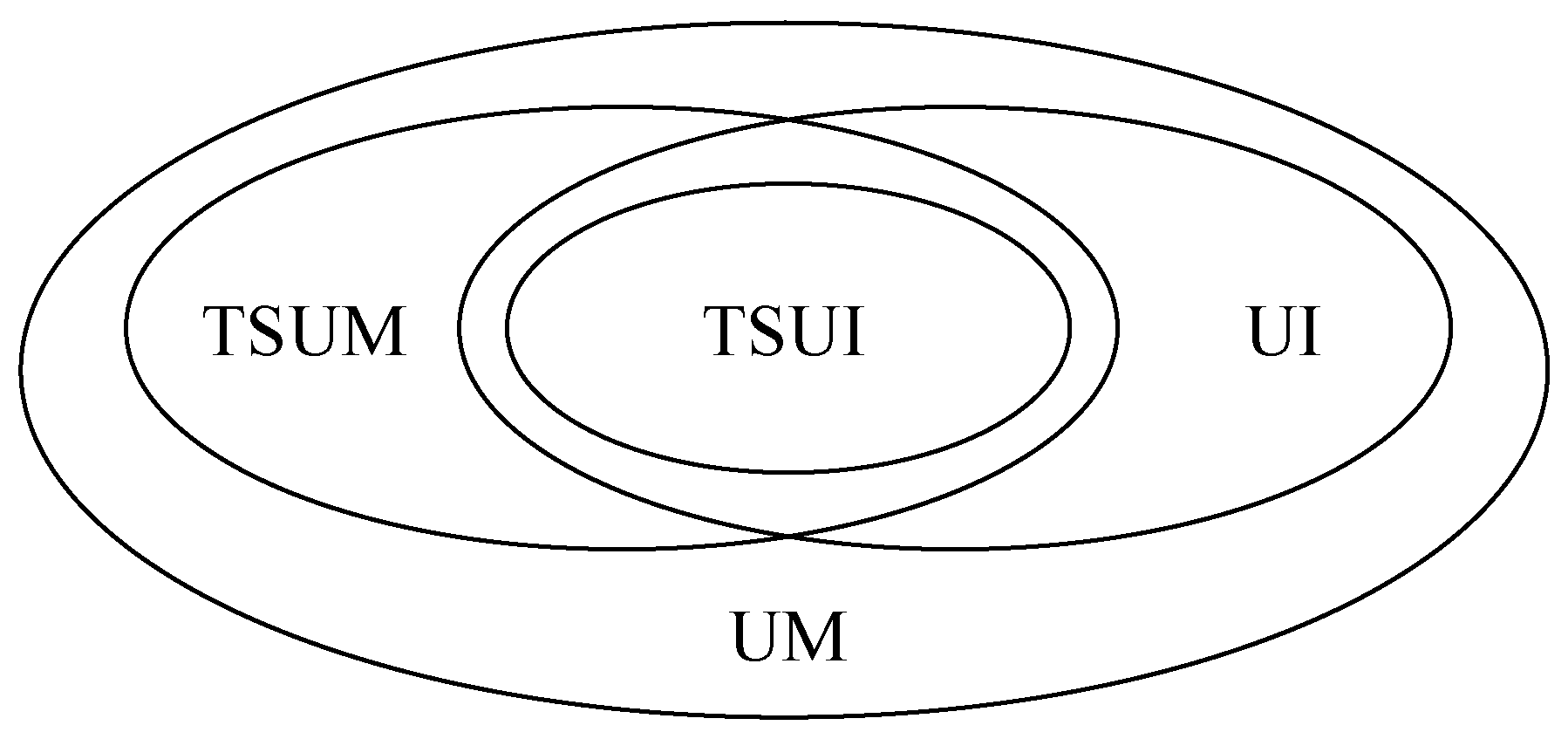
3.5.1. Inter-Relationships Among UMs, UIs, TSUMs, and TSUIs
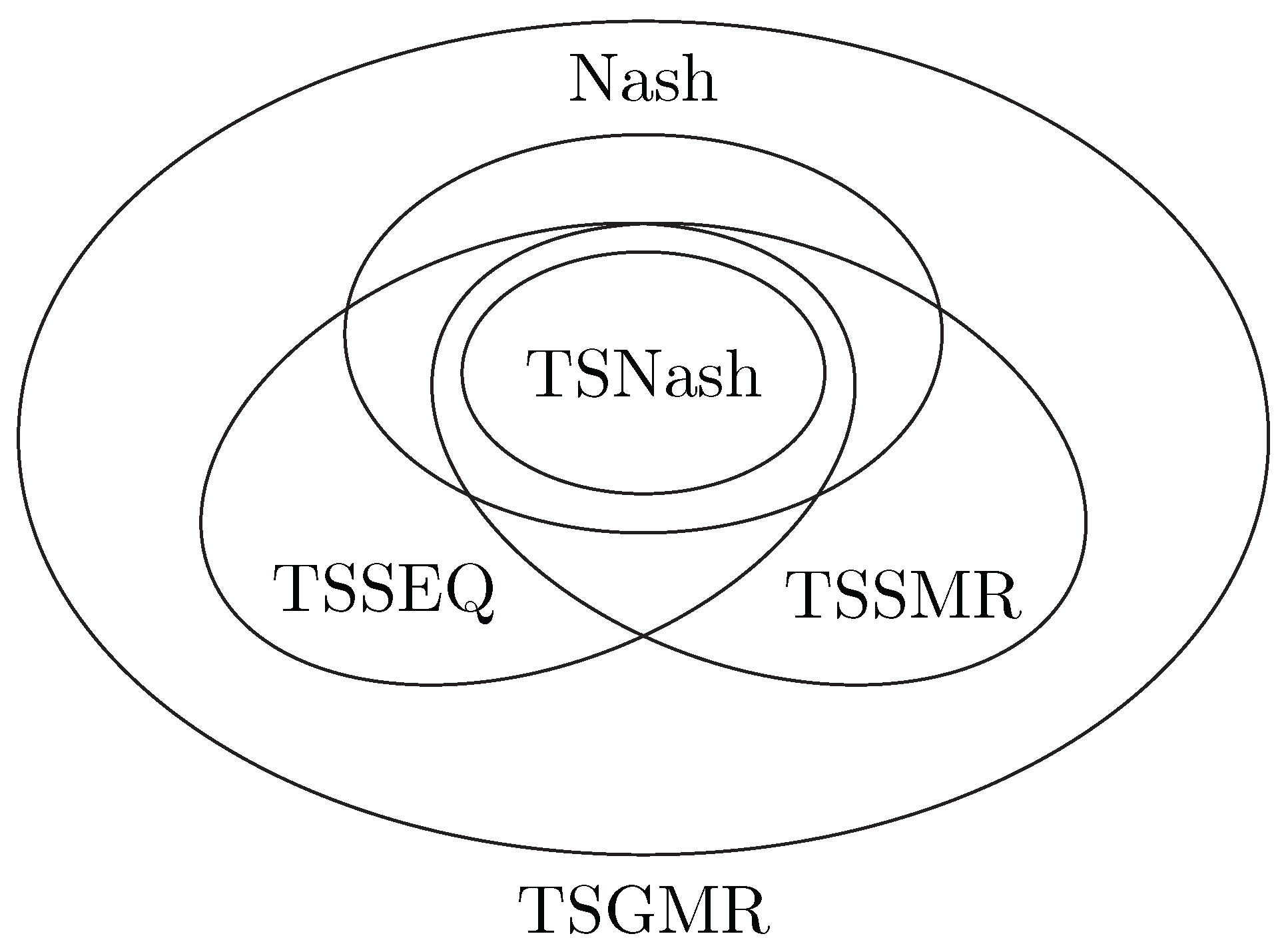
3.5.2. Inter-Relationships Among Time-Sensitive Stabilities
4. Case Studies
4.1. Background of Jakarta–Bandung High-Speed Railway Project Conflict
4.2. Modeling the Jakarta-Bandung HSR Conflict
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, L.; Hipel, K.W.; Kilgour, D.M. Interactive Decision Making: The Graph Model for Conflict Resolution; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Kilgour, D.M.; Hipel, K.W.; Fang, L. The graph model for conflicts. Automatica 1987, 23, 41–55. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, H.; Ke, G.Y. A novel consensus and dissent framework under grey preference based on the graph model for conflict resolution for two decision makers. Group Decis. Negot. 2024, 33, 711–744. [Google Scholar] [CrossRef]
- Li, X.; Xu, H.; Yang, B.; Yu, J. A novel grey-inverse graph model for conflict resolution approach for resolving water resources conflicts in the Poyang Lake Basin, China. J. Clean. Prod. 2023, 415, 137777. [Google Scholar] [CrossRef]
- Liu, P.; Qiu, X.; Pan, Q.; Wu, X. Graph model for conflict resolution with hybrid information based on prospect theory and PROMETHEE method and its application in water resources conflict. Inf. Sci. 2025, 689, 121498. [Google Scholar] [CrossRef]
- Wang, D.; Lai, X.; Dhaarna; Wen, X.; Xu, Y. Matrix representation of the graph model for conflict resolution based on intuitionistic preferences with applications to trans-regional water resource conflicts in the Lancang–Mekong River Basin. Inf. Sci. 2025, 691, 121615. [Google Scholar] [CrossRef]
- Huang, Y.; Ge, B.; Hou, Z.; Li, J.; Jiang, J.; Yang, K. Interactive technology selection in a system-of-systems context using graph model for conflict resolution with improved fuzzy option prioritization. IEEE Trans. Comput. Soc. Syst. 2025, 1–13. [Google Scholar] [CrossRef]
- Liu, P.; Wang, X.; Fu, Y.; Wang, P. Graph model for conflict resolution for mixed-stability combinatorial foresight based on the cmbination of regret theory and VIKOR method. IEEE Trans. Fuzzy Syst. 2024, 32, 6486–6499. [Google Scholar] [CrossRef]
- Wu, N.; Xu, Y.; Wang, H.; Kilgour, D.M. Matrix representation and behavioral analysis in a graph model for conflict resolution with incomplete fuzzy preferences. IEEE Trans. Syst. Man Cybern. 2023, 54, 300–311. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y.; Zhou, S.; Yang, B. Grey preference for analyzing the influence of externality within the graph model for conflict resolution. Expert. Syst. Appl. 2024, 249, 123736. [Google Scholar] [CrossRef]
- Howard, N. Paradoxes of Rationality: Theory of Metagames and Political Behavior; MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Fraser, N.M.; Hipel, K.W. Solving complex conflicts. IEEE Trans. Syst. Man Cybern. 1979, 9, 805–816. [Google Scholar] [CrossRef]
- Kuhn, J.R.D.; Hipel, K.W.; Fraser, N.M. A coalition analysis algorithm with application to the Zimbabwe conflict. IEEE Trans. Syst. Man Cybern. 1983, 13, 338–352. [Google Scholar] [CrossRef]
- Meister, D.B.G.; Hipel, K.W.; De, M. Coalition formation metrics for decision making. In Proceedings of the 1991 IEEE International Conference on Systems, Man, and Cybernetics, Charlottesville, VA, USA, 13–16 October 1991; pp. 2017–2022. [Google Scholar] [CrossRef]
- Hipel, K.W.; Meister, D.B.G. Conflict analysis methodology for modelling coalition in multilateral negotiations. Inf. Decis. Technol. 1994, 19, 85–103. [Google Scholar]
- Kilgour, D.M.; Hipel, K.W.; Fang, L.; Peng, X. Coalition analysis in group decision support. Group Decis. Negot. 2001, 10, 159–175. [Google Scholar] [CrossRef]
- Inohara, T.; Hipel, K.W. Coalition analysis in the graph model for conflict resolution. Syst. Eng. 2008, 11, 343–359. [Google Scholar] [CrossRef]
- Inohara, T.; Hipel, K.W. Interrelationships among noncooperative and coalition stability concepts. J. Syst. Sci. Syst. Eng. 2008, 17, 1–9. [Google Scholar] [CrossRef]
- Zhu, Z.; Kilgour, D.M.; Hipel, K.W. A new approach to coalition analysis within the graph model. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 2231–2241. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, H.; Hipel, K.W.; Fang, L. Mixed coalitional stabilities with full participation of sanctioning opponents within the graph model for conflict resolution. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3911–3925. [Google Scholar] [CrossRef]
- Zhu, Z.; Kilgour, D.M.; Hipel, K.W.; Yu, J. Interrelationships of non-cooperative, classical and pareto coalitional stability definitions. Eur. J. Oper. Res. 2025, 321, 884–894. [Google Scholar] [CrossRef]
- Wang, D.; Huang, J.; Xu, Y.; Wu, N. Water–Energy–Food nexus evaluation using an inverse approach of the graph model for conflict resolution based on incomplete fuzzy preferences. Appl. Soft Comput. 2022, 120, 1568–4946. [Google Scholar] [CrossRef]
- Li, K.W.; Kilgour, D.M.; Hipel, K.W.; Fang, L. Preference uncertainty in the graph model for conflict resolution. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2004, 34, 507–520. [Google Scholar] [CrossRef]
- Hamouda, L.; Kilgour, D.M.; Hipel, K.W. Strength of preference in the graph model for conflict resolution. Group Decis. Negot. 2004, 13, 449–462. [Google Scholar] [CrossRef]
- Xu, H.; Hipel, K.W.; Kilgour, D.M. Preference strength and uncertainty in the graph model for conflict resolution for two decision-makers. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 2907–2912. [Google Scholar] [CrossRef]
- Lu, C.; Xu, H.; Witold, P. Conflict analysis based on a novel three-way decisions graph model for conflict resolution method under hesitant fuzzy environment. Inf. Fusion 2023, 100, 101936. [Google Scholar] [CrossRef]
- Inohara, T. State transition time analysis in the graph model for conflict resolution. Appl. Math. Comput. 2016, 274, 372–382. [Google Scholar] [CrossRef]
- He, S. A time sensitive graph model for conflict resolution with application to international air carbon negotiation. Eur. J. Oper. Res. 2022, 302, 652–670. [Google Scholar] [CrossRef]
- Huang, Y.; Ge, B.; Hou, Z.; Xie, H.; Hipel, K.W.; Yang, K. Inverse Preference Optimization in the Graph Model for Conflict Resolution With Uncertain Cost. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5580–5592. [Google Scholar] [CrossRef]
- Pan, Y. The Politicization of China’s Outbound High-speed railway investment: The case of the Jakarta-Bandung railway. J. Contemp.-Asia-Pac. Stud. 2017, 5, 107–132. [Google Scholar]
- Ecns. cn. Southeast Asia’s First High-Speed Railway Opens in Indonesia. 2023. Available online: https://www.ecns.cn/news/2023-10-18/detail-ihcuappp4690703.shtml (accessed on 11 May 2025).
- Trissia, W. “Risk is not measured, but contested and compromised”: A case study of Jakarta–Bandung high-speed railway. J. Contemp. Asia 2024, 55, 405–429. [Google Scholar] [CrossRef]
- Dialogue Earth. Bungled Jakarta–Bandung High–Speed Rail Line Causes Chaos. 2020. Available online: https://dialogue.earth/en/pollution/bungled-jakarta-bandung-high-speed-rail-line-causes-chaos/ (accessed on 12 May 2025).
- Zhao, D. Study on the technical standards of Jakarta-Bandung high speed railway. China Railw. 2018, 12, 7–14. [Google Scholar]
- Post, The Jakarta. Three Lawsuits to Proceed Against Bandung-Jakarta Train Project. 2022. Available online: https://www.thejakartapost.com/news/2018/07/11/three-lawsuits-to-proceed-against-bandung-jakarta-train-project.html (accessed on 11 May 2025).
- Blow, L.; Browning, M.; Crawford, I. Non-parametric analysis of time-inconsistent preferences. Rev. Econ. Stud. 2021, 88, 2687–2734. [Google Scholar] [CrossRef]
- Rieger, M.O.; Wang, M.; Hens, T. Universal time preference. PLoS ONE 2021, 16, e0245692. [Google Scholar] [CrossRef]
- Ji, J.; Wang, D. Evaluation analysis and strategy selection in urban flood resilience based on EWM-TOPSIS method and graph model. J. Clean. Prod. 2023, 425, 138955. [Google Scholar] [CrossRef]
- Yang, M.; Yang, K.; Che, Y.; Lu, S.; Sun, F.; Chen, Y.; Li, M. Resolving transboundary water conflicts: Dynamic evolutionary analysis using an improved GMCR model. Water Resour. Manag. 2021, 35, 3321–3338. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| N | The set of all decision-makers (DMs) in conflict |
| k | A specific DM in N |
| S | The set of all states in conflict |
| The set of state transitions by DM k | |
| The preference statement of DMs | |
| The truth value of state s under the ith preference statement | |
| The preference score of state s | |
| The Unilateral Move (UM) list of DM k in state s | |
| The Unilateral Improvement (UI) list of DM k in state s | |
| H | A nonempty coalition of |
| The reachable list of coalition H in state s | |
| The UI list of coalition H in state s | |
| t | Time elapsed since the beginning of the conflict |
| T | The deadline of the conflict |
| A specific state at time t | |
| The time required to finish UMs by DM k | |
| The strategy of DM k | |
| The choice of option i controlled by DM k | |
| The Time-Sensitive Unilateral Move (TSUM) list of DM k in state | |
| The Time-Sensitive Unilateral Improvement (TSUI) list of DM k in state | |
| The preference radio of a TSUM from to for DM k | |
| the Time-Sensitive Unilateral Moves of a Coalition (CTSUM) (H) in state (s) | |
| The Time-Sensitive Unilateral Improvements of a Coalition (CTSUM) (H) in state s |
| DMs | Options | States | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | N | Y | Y | Y | Y | Y | Y | Y | Y | Y | |
| B | N | N | Y | N | N | N | Y | N | Y | N | |
| N | N | N | Y | N | N | N | Y | N | Y | ||
| C | N | N | N | N | Y | N | N | N | Y | Y | |
| N | N | N | N | N | Y | Y | Y | N | N | ||
| Dimension | Classical GMCR [1,2] | Inohara [27] | He [28] | This Paper |
|---|---|---|---|---|
| DM’s Move Order in UM | N/A | The DM with the minimum state transition time is prioritized | Each DM is restricted to a single action per round, and the DM with the minimum state transition time is prioritized | The DMs not in state transition processes are eligible |
| DM’s Move Order in UI | N/A | Same as UM requirements | Based on the requirements of UM, prioritizes DM with minimum state transition time and maximum preference ratio | Same as UM requirements, but DMs must select state transitions with the maximum preference ratio |
| Deadline? | No | No | Yes | Yes |
| Time of UM/UI? | No | Yes | Yes | Yes |
| Multi-DM Simultaneous Move? | No | No | No | Yes |
| DMs | States | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B | 2 | 4 | 12 | 13 | 7 | 1 | 9 | 10 | 13 | 9 |
| C | 1 | 7 | 9 | 11 | 16 | 8 | 15 | 5 | 2 | 2 |
| DMs | Options | Time / Months (N to Y) | Time / Months (Y to N) | Descriptions or Sources |
|---|---|---|---|---|
| IDN | 1: Adopt full Chinese technology supply chain | 3 | 6 | See Sources 1,2 |
| 2: Insist on localization adjustments | 8 | 4 | ||
| CN | 3: Strictly implement Chinese standards | 4 | 5 | See Sources 1–3 |
| 4: Compromise on technical adjustments | 6 | 3 | ||
| CDB | 5: Add environmental clauses and prolong approval | 5 | 4 | CDB tends to |
| 6: Suspend loans to pressure | 1 | 1 | control risk 4–6 | |
| EPO | 7: Radical protests | 2 | 1 | See Sources 7 |
| 8: Legal litigation | 12 | 6 |
| States | IDN | CN | CDB | EPO | States | IDN | CN | CDB | EPO | States | IDN | CN | CDB | EPO | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| Y | N | Y | N | N | N | Y | N | Y | N | Y | N | N | N | N | Y | Y | N | Y | N | N | N | Y | Y | |||
| N | Y | Y | N | N | N | Y | N | N | Y | Y | N | N | N | N | Y | N | Y | Y | N | N | N | Y | Y | |||
| Y | N | N | Y | N | N | Y | N | Y | N | N | Y | N | N | N | Y | Y | N | N | Y | N | N | Y | Y | |||
| N | Y | N | Y | N | N | Y | N | N | Y | N | Y | N | N | N | Y | N | Y | N | Y | N | N | Y | Y | |||
| Y | N | Y | N | Y | N | Y | N | Y | N | Y | N | Y | N | N | Y | Y | N | Y | N | Y | N | Y | Y | |||
| N | Y | Y | N | Y | N | Y | N | N | Y | Y | N | Y | N | N | Y | N | Y | Y | N | Y | N | Y | Y | |||
| Y | N | N | Y | Y | N | Y | N | Y | N | N | Y | Y | N | N | Y | Y | N | N | Y | Y | N | Y | Y | |||
| N | Y | N | Y | Y | N | Y | N | N | Y | N | Y | Y | N | N | Y | N | Y | N | Y | Y | N | Y | Y | |||
| Y | N | Y | N | N | Y | Y | N | Y | N | Y | N | N | Y | N | Y | Y | N | Y | N | N | Y | Y | Y | |||
| N | Y | Y | N | N | Y | Y | N | N | Y | Y | N | N | Y | N | Y | N | Y | Y | N | N | Y | Y | Y | |||
| Y | N | N | Y | N | Y | Y | N | Y | N | N | Y | N | Y | N | Y | Y | N | N | Y | N | Y | Y | Y | |||
| N | Y | N | Y | N | Y | Y | N | N | Y | N | Y | N | Y | N | Y | N | Y | N | Y | N | Y | Y | Y | |||
| Y | N | Y | N | Y | Y | Y | N | Y | N | Y | N | Y | Y | N | Y | Y | N | Y | N | Y | Y | Y | Y | |||
| N | Y | Y | N | Y | Y | Y | N | N | Y | Y | N | Y | Y | N | Y | N | Y | Y | N | Y | Y | Y | Y | |||
| Y | N | N | Y | Y | Y | Y | N | Y | N | N | Y | Y | Y | N | Y | Y | N | N | Y | Y | Y | Y | Y | |||
| N | Y | N | Y | Y | Y | Y | N | N | Y | N | Y | Y | Y | N | Y | N | Y | N | Y | Y | Y | Y | Y | |||
| DMs | Preference Statements | Description |
|---|---|---|
| IDN | 1∣(2 & 4) | IDN will adopt Chinese technology or implement localization adjustments with CN’s technical adjustments |
| 1 IF 3 | If CN enforces technical standards, IDN tendsto adopt the full Chinese supply chain | |
| −7 & −8 | IDN will absolutely avoid protests or litigation by environmental groups | |
| −7 & 2 | IDN tends toward localization adjustments when EPO does not choose protests | |
| 2 | IDN hopes to insist on localization adjustments | |
| 5 IF 1 | If IDN adopts Chinese technology, IDN wishes CDB can add environmental clauses | |
| −6 IF (2 & 4) | If localizing adjustments are made and CN compromises technically, IDN wishes CDB does not suspend loans | |
| −5∣−6 | IDN prefers avoiding CDB’s prolonged approval or loan suspension | |
| 2 IF −4 | If CN abandons technical compromise, IDN will accept localization | |
| CN | 1 & 3 | CN will enforce standards and expects IDN to adopt Chinese technology |
| 3∣(4 & 1) | CN will enforce Chinese standards or compromise technically if IDN adopts Chinese technology | |
| 4 IF 2 | If IDN chooses localization, CN wishes to compromise technically | |
| −8 & (−7∣−6) | CN wants to avoid litigation and prevent either protests or CDB loan suspension | |
| −4 IF 5 | If CDB adds environmental clauses, CN rejects technical compromise | |
| −3 IF −1 | If IDN does not adopt Chinese technology, CN will not implement Chinese standards strictly | |
| −7 | CN hopes EPO rejects radical protests | |
| −6 IF (1 & 3) | If CN enforces standards and expects IDN to adopt Chinese technology, CN wishes CDB will not suspend loans | |
| −5 & 3 | CDB will reject adding environmental clauses when CN implements Chinese standards strictly | |
| CDB | 5∣(6 & −7) | CDB will prolong approval or suspend loans if no protests occur |
| 5 IF (3∣4) | If CN enforces standards or compromises, CDB wishes to add environmental clauses | |
| −8 & (−2∣−4) | CDB tends to avoid litigation and ensure IDN avoids localization or CN avoids compromise | |
| 2 & 4 | When CN compromises on technical adjustments, IDN may insist on localization adjustments | |
| −6 IF 1 | If IDN adopts Chinese technology, CDB will not suspend loans | |
| −7∣−8 | CDB prioritizes evading direct actions by environmental groups | |
| 1 & 3 | CN will enforce standards and expects IDN to adopt Chinese technology | |
| EPO | 2 & 4 | When CN compromises on technical adjustments, IDN may insist on localization adjustments |
| 7∣(8 &−1) | EPO will launch protests or litigation if IDN rejects Chinese technology | |
| 7 IF 3 | If CN enforces standards, EPO wishes to protest | |
| 5 | EPO hopes that CDB can add environmental clauses and prolong approval | |
| −1 & −3 & −5 | EPO trends to oppose Chinese technology, enforced standards, and CDB’s prolonged approval | |
| −7 IF 2 | If IDN tends to localization adjustments, EPO does not choose protests | |
| (7 & 8) IF 1 | If IDN adopts full Chinese technology, EPO tends to radical protests and legal litigation | |
| 8 IF 6 | If CDB suspends loans, EPO will switch to litigation | |
| −2∣−4 | CDB wishes to accept either IDN’s localization or CN’s technical compromise |
| IDN | States | ||||||||||||||||
| Scores | 447 | 447 | 443 | 441 | 415 | 415 | 415 | 415 | 411 | 411 | 409 | 409 | 399 | 399 | 399 | 398 | |
| States | |||||||||||||||||
| Scores | 398 | 398 | 397 | 397 | 397 | 396 | 396 | 396 | 391 | 391 | 391 | 391 | 391 | 391 | 390 | 390 | |
| States | |||||||||||||||||
| Scores | 390 | 390 | 390 | 390 | 63 | 63 | 63 | 61 | 31 | 31 | 31 | 31 | 31 | 31 | 29 | 29 | |
| CN | States | ||||||||||||||||
| Scores | 507 | 506 | 479 | 478 | 477 | 476 | 475 | 474 | 473 | 473 | 472 | 472 | 250 | 234 | 222 | 222 | |
| States | |||||||||||||||||
| Scores | 218 | 218 | 218 | 206 | 206 | 202 | 202 | 202 | 179 | 178 | 151 | 151 | 150 | 150 | 147 | 147 | |
| States | |||||||||||||||||
| Scores | 147 | 146 | 146 | 146 | 122 | 106 | 94 | 94 | 90 | 90 | 90 | 78 | 78 | 74 | 74 | 74 | |
| CDB | States | ||||||||||||||||
| Scores | 119 | 118 | 118 | 118 | 115 | 114 | 110 | 110 | 110 | 110 | 108 | 108 | 103 | 102 | 102 | 102 | |
| States | |||||||||||||||||
| Scores | 101 | 100 | 100 | 100 | 99 | 98 | 97 | 96 | 78 | 70 | 67 | 66 | 23 | 22 | 22 | 22 | |
| States | |||||||||||||||||
| Scores | 19 | 18 | 14 | 14 | 14 | 12 | 12 | 7 | 6 | 6 | 5 | 4 | 4 | 4 | 1 | 0 | |
| EPO | States | ||||||||||||||||
| Scores | 494 | 494 | 486 | 486 | 486 | 484 | 478 | 478 | 470 | 470 | 470 | 468 | 239 | 239 | 239 | 239 | |
| States | |||||||||||||||||
| Scores | 235 | 235 | 233 | 233 | 231 | 231 | 231 | 229 | 207 | 207 | 207 | 207 | 203 | 203 | 201 | 201 | |
| States | |||||||||||||||||
| Scores | 199 | 199 | 199 | 197 | 175 | 175 | 143 | 143 | 107 | 107 | 75 | 75 | 43 | 43 | 11 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, X.; Huang, Y.; Ge, B.; Hou, Z.; Zhu, J. A New Time-Sensitive Graph Model for Conflict Resolution with Simultaneous Decision-Maker Moves. Systems 2025, 13, 726. https://doi.org/10.3390/systems13090726
Wang H, Zhang X, Huang Y, Ge B, Hou Z, Zhu J. A New Time-Sensitive Graph Model for Conflict Resolution with Simultaneous Decision-Maker Moves. Systems. 2025; 13(9):726. https://doi.org/10.3390/systems13090726
Chicago/Turabian StyleWang, He, Xinhang Zhang, Yuming Huang, Bingfeng Ge, Zeqiang Hou, and Jianghan Zhu. 2025. "A New Time-Sensitive Graph Model for Conflict Resolution with Simultaneous Decision-Maker Moves" Systems 13, no. 9: 726. https://doi.org/10.3390/systems13090726
APA StyleWang, H., Zhang, X., Huang, Y., Ge, B., Hou, Z., & Zhu, J. (2025). A New Time-Sensitive Graph Model for Conflict Resolution with Simultaneous Decision-Maker Moves. Systems, 13(9), 726. https://doi.org/10.3390/systems13090726






