Supply Chain Design Method for Introducing Floating Offshore Wind Turbines Using Network Optimization Model
Abstract
1. Introduction
2. Proposed Method
2.1. Supply Chain Modeling
2.2. Supply Chain Flow Optimization
2.3. Generating Candidate Supply Chain Proposal
3. Case Studies
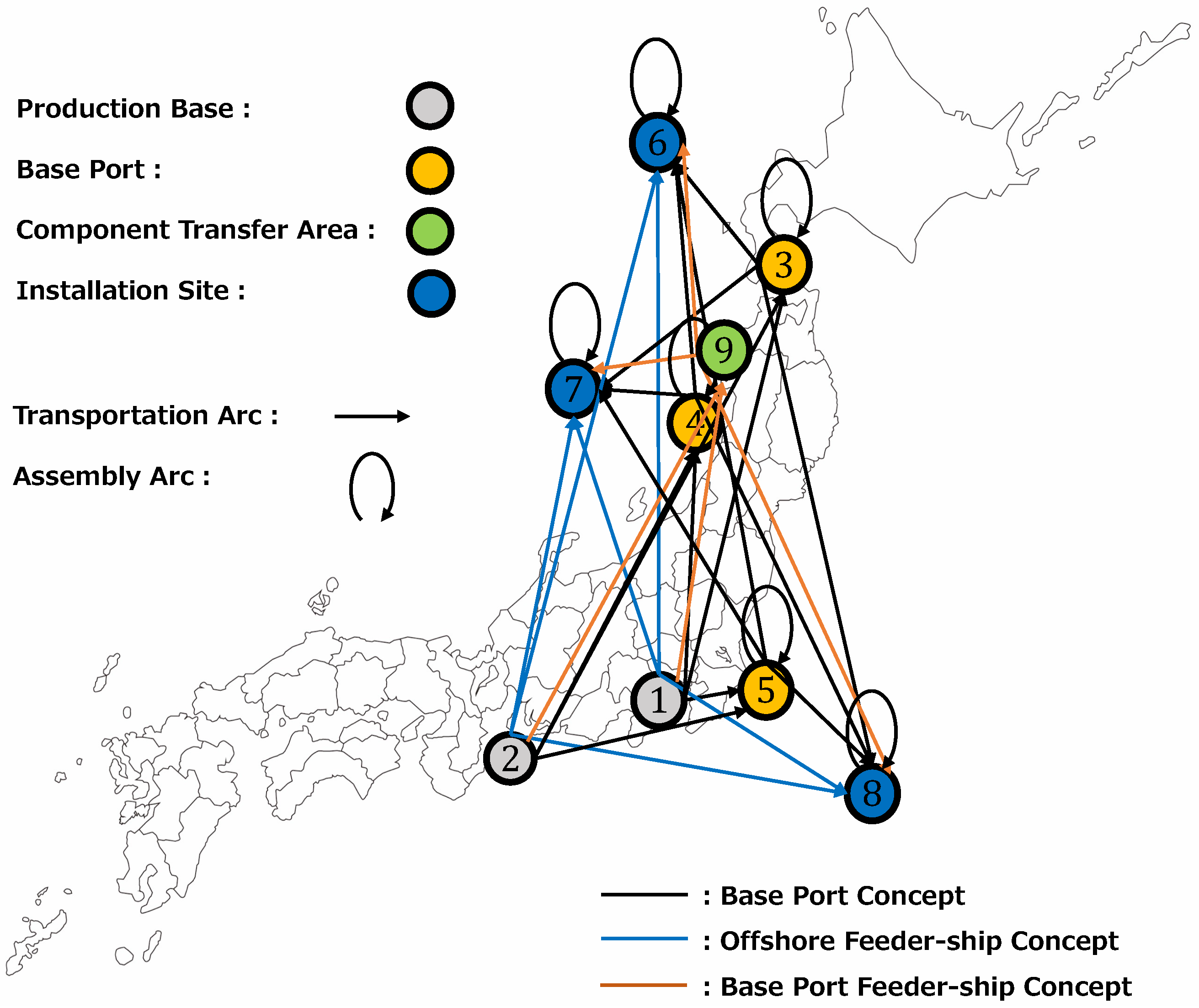
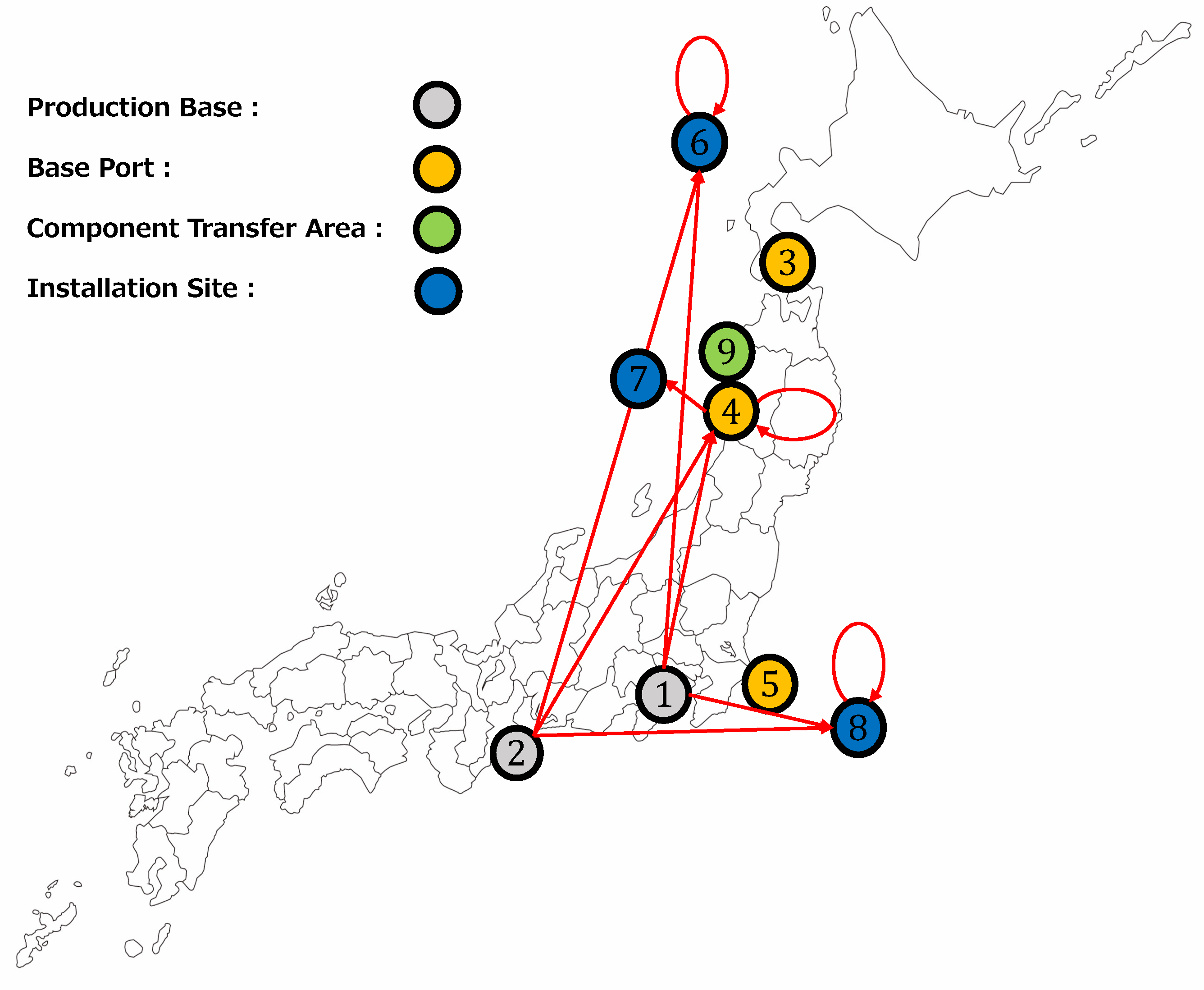
3.1. Case A: Design of Supply Chain Base Plan
3.1.1. Problem Setting
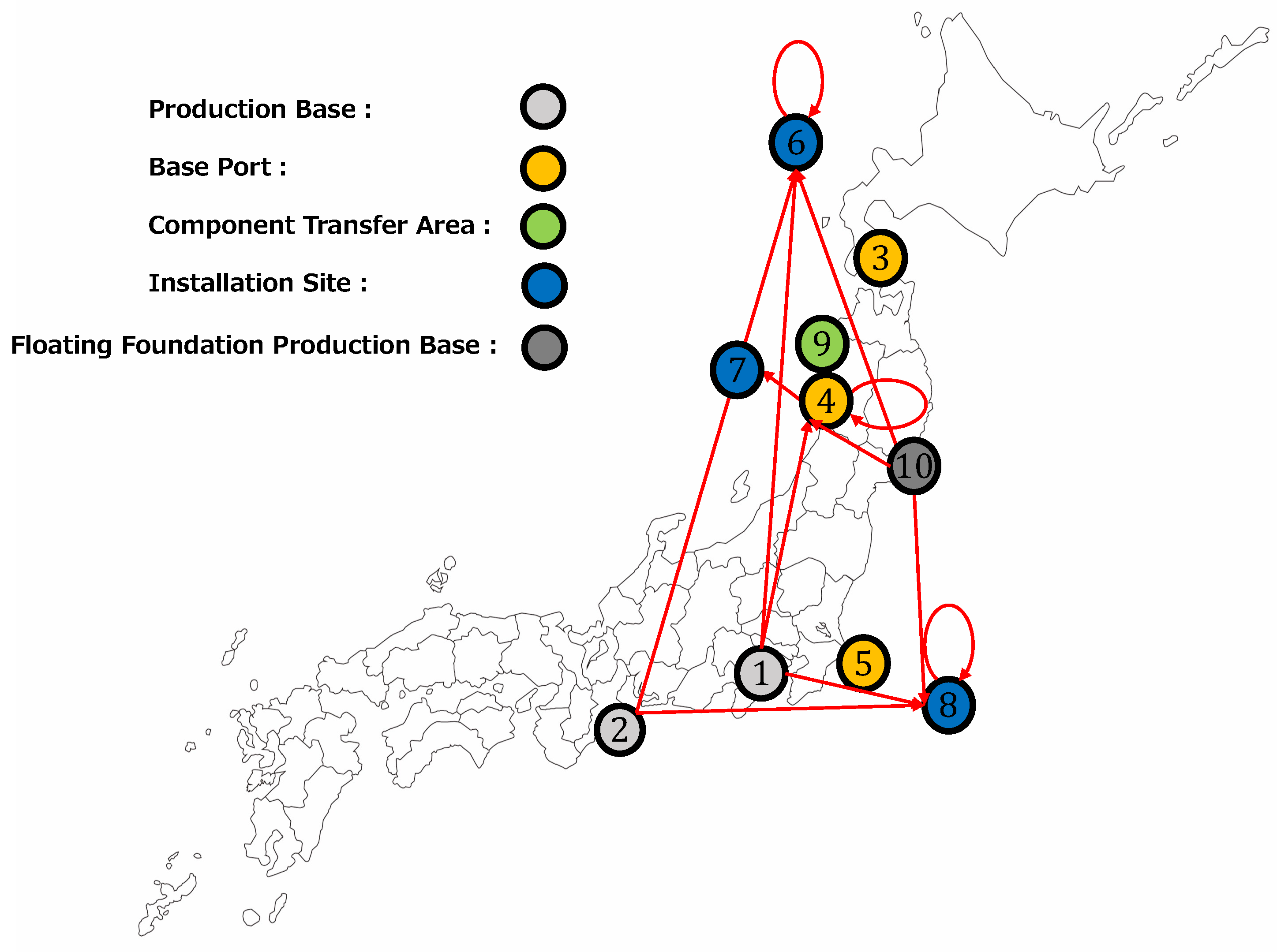
3.1.2. Result
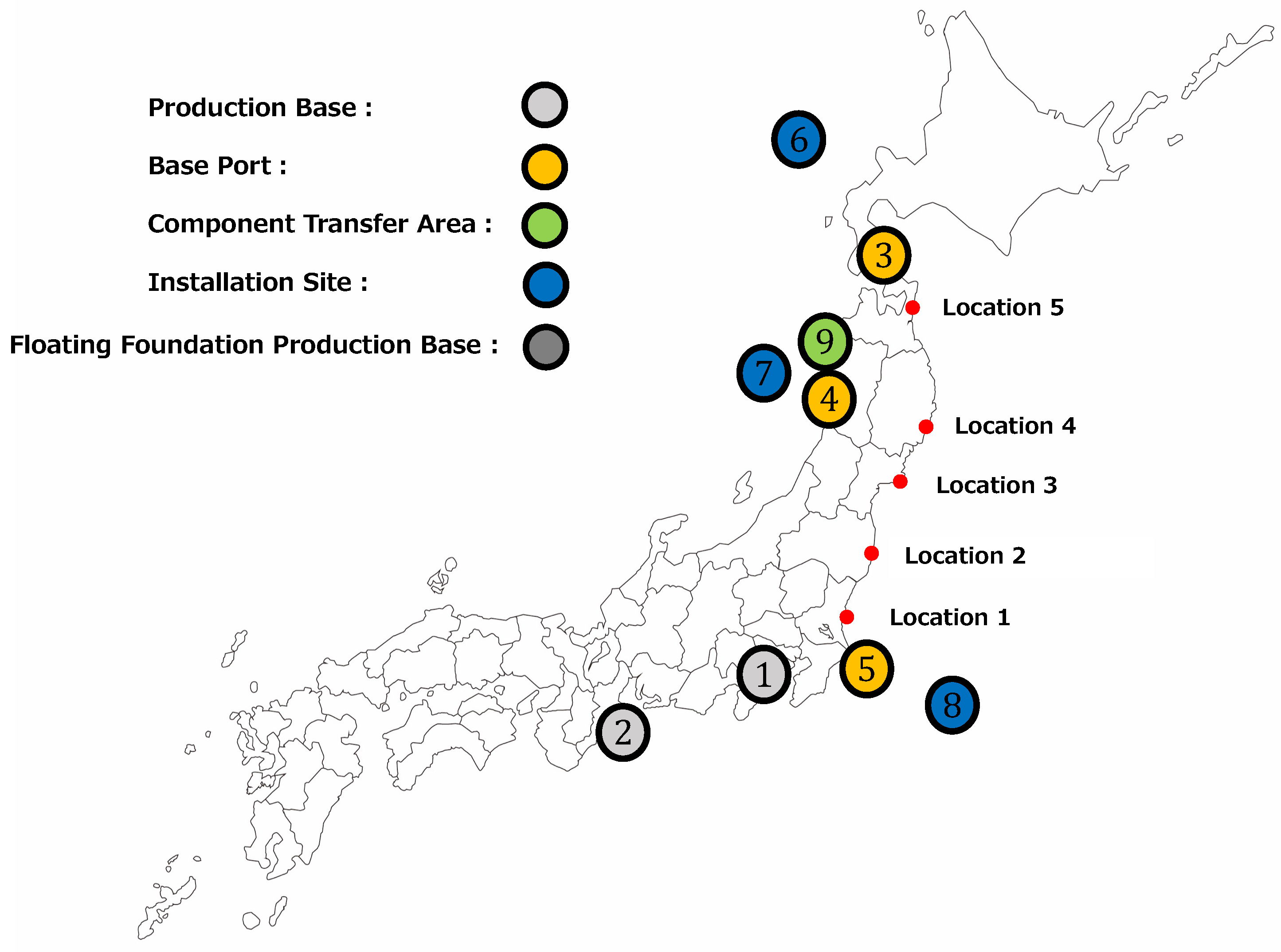
3.2. Case B: Exploring the Optimal Location for Floating Foundation Production Base
3.2.1. Problem Setting
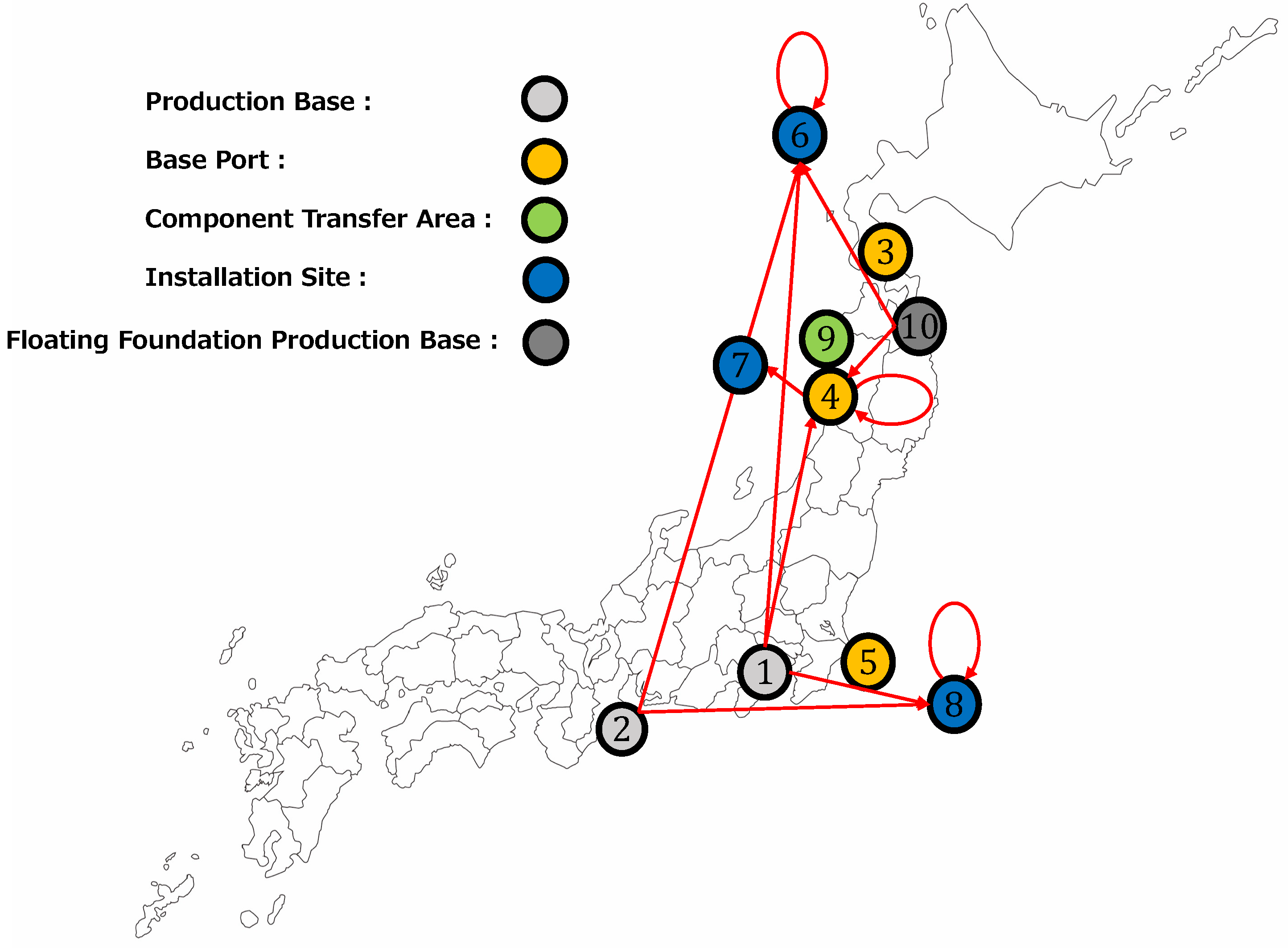
3.2.2. Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahari, M.; Akbari, Y.; Akbari, N.; Jafari, M.; Qezelbigloo, S.; Zahedi, R.; Yousefi, H. Techno-Economic Analysis and Optimization of a Multiple Green Energy Generation System Using Hybrid Wind, Solar, Ocean and Thermoelectric Energy. Energy Syst. 2024. [Google Scholar] [CrossRef]
- Kara, O. Assessment of Economic, Energy, and Exergy Efficiencies Using Wind Measurement Mast Data for Different Wind Turbines. Environ. Sci. Pollut. Res. 2023, 30, 97447–97462. [Google Scholar] [CrossRef] [PubMed]
- Spiru, P.; Simona, P.L. Wind Energy Resource Assessment and Wind Turbine Selection Analysis for Sustainable Energy Production. Sci. Rep. 2024, 14, 10708. [Google Scholar] [CrossRef] [PubMed]
- Rinne, E.; Holttinen, H.; Kiviluoma, J.; Rissanen, S. Effects of Turbine Technology and Land Use on Wind Power Resource Potential. Nat. Energy 2018, 3, 494–500. [Google Scholar] [CrossRef]
- Saeed, M.A.; Ahmed, Z.; Zhang, W. Wind energy potential and economic analysis with a comparison of different methods for determining the optimal distribution parameters. Renew. Energy 2020, 161, 1092–1109. [Google Scholar] [CrossRef]
- Fazelpour, F.; Markarian, E.; Soltani, N. Wind energy potential and economic assessment of four locations in Sistan and Balouchestan province in Iran. Renew. Energy 2017, 109, 646–667. [Google Scholar] [CrossRef]
- Charabi, Y.; Abdul-Wahab, S. Wind Turbine Performance Analysis for Energy Cost Minimization. Renew. Wind Water Solar 2020, 7, 5. [Google Scholar] [CrossRef]
- Akbari, N.; Irawan, C.A.; Jones, D.F.; Menachof, D. A Multi-Criteria Port Suitability Assessment for Developments in the Offshore Wind Industry. Renew. Energy 2017, 102, 118–133. [Google Scholar] [CrossRef]
- Prostean, G.; Badea, A.; Vasar, C.; Octavian, P. Risk Variables in Wind Power Supply Chain. Procedia-Soc. Behav. Sci. 2014, 124, 124–132. [Google Scholar] [CrossRef]
- Sarker, B.R.; Faiz, T.I. Minimizing Transportation and Installation Costs for Turbines in Offshore Wind Farms. Renew. Energy 2017, 101, 667–679. [Google Scholar] [CrossRef]
- Kaiser, M.J.; Snyder, B.F. Modeling Offshore Wind Installation Costs on the U.S. Outer Continental Shelf. Renew. Energy 2013, 50, 676–691. [Google Scholar] [CrossRef]
- Ahn, D.; Shin, S.c.; Kim, S.y.; Kharoufi, H.; Kim, H.c. Comparative Evaluation of Different Offshore Wind Turbine Installation Vessels for Korean West–South Wind Farm. Int. J. Nav. Archit. Ocean. Eng. 2017, 9, 45–54. [Google Scholar] [CrossRef]
- Vis, I.F.; Ursavas, E. Assessment Approaches to Logistics for Offshore Wind Energy Installation. Sustain. Energy Technol. Assess. 2016, 14, 80–91. [Google Scholar] [CrossRef]
- Barlow, E.; Tezcaner Öztürk, D.; Revie, M.; Akartunalı, K.; Day, A.H.; Boulougouris, E. A Mixed-Method Optimisation and Simulation Framework for Supporting Logistical Decisions during Offshore Wind Farm Installations. Eur. J. Oper. Res. 2018, 264, 894–906. [Google Scholar] [CrossRef]
- Faraggiana, E.; Giorgi, G.; Sirigu, M.; Ghigo, A.; Bracco, G.; Mattiazzo, G. A Review of Numerical Modelling and Optimisation of the Floating Support Structure for Offshore Wind Turbines. J. Ocean. Eng. Mar. Energy 2022, 8, 433–456. [Google Scholar] [CrossRef]
- Maienza, C.; Avossa, A.M.; Picozzi, V.; Ricciardelli, F. Feasibility Analysis for Floating Offshore Wind Energy. Int. J. Life Cycle Assess. 2022, 27, 796–812. [Google Scholar] [CrossRef]
- Laura, C.S.; Vicente, D.C. Life-cycle cost analysis of floating offshore wind farms. Renew. Energy 2014, 66, 41–48. [Google Scholar] [CrossRef]
- Myhr, A.; Bjerkseter, C.; Ågotnes, A.; Nygaard, T.A. Levelised cost of energy for offshore floating wind turbines in a life cycle perspective. Renew. Energy 2014, 66, 714–728. [Google Scholar] [CrossRef]
- Hasumi, T.; Yokoi, T.; Haneda, K.; Chujo, T.; Fujiwara, T. Research on Offshore Installation Time Estimation Model for Floating Offshore Wind Farms. J. Jpn. Soc. Nav. Archit. Ocean. Eng. 2023, 38, 127–139. [Google Scholar] [CrossRef]
- Poulsen, T.; Lema, R. Is the supply chain ready for the green transformation? The case of offshore wind logistics. Renew. Sustain. Energy Rev. 2017, 73, 758–771. [Google Scholar] [CrossRef]
- Kruger, T.; Price, S.; Wiedijk, M. Floating Offshore Wind Supply Chain Constraints and Opportunities. In Proceedings of the OTC Offshore Technology Conference, Houston, TX, USA, 6–9 May 2024; p. D021S004R003. Available online: https://onepetro.org/OTCONF/proceedings-pdf/24OTC/2-24OTC/D021S004R003/3403124/otc-35398-ms.pdf (accessed on 1 July 2025.).
- González, M.O.A.; Nascimento, G.; Jones, D.; Akbari, N.; Santiso, A.; Melo, D.; Vasconcelos, R.; Godeiro, M.; Nogueira, L.; Almeida, M.; et al. Logistic Decisions in the Installation of Offshore Wind Farms: A Conceptual Framework. Energies 2024, 17, 6004. [Google Scholar] [CrossRef]
- Díaz, H.; Guedes Soares, C. Approach for Installation and Logistics of a Floating Offshore Wind Farm. J. Mar. Sci. Eng. 2023, 11, 53. [Google Scholar] [CrossRef]
- Ishimatsu, T. Generalized Multi-Commodity Network Flows: Case Studies in Space Logistics and Complex Infrastructure Systems. Doctoral Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Ait-Alla, A.; Oelker, S.; Lewandowski, M.; Freitag, M.; Thoben, K.D. A Study of New Installation Concepts of Offshore Wind Farms by Means of Simulation Model. In Proceedings of the Twenty-Seventh (2017) International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; Volume 27, pp. 607–612. [Google Scholar]
- Bashir, M.B.A. Principle Parameters and Environmental Impacts That Affect the Performance of Wind Turbine: An Overview. Arab. J. Sci. Eng. 2022, 47, 7891–7909. [Google Scholar] [CrossRef] [PubMed]

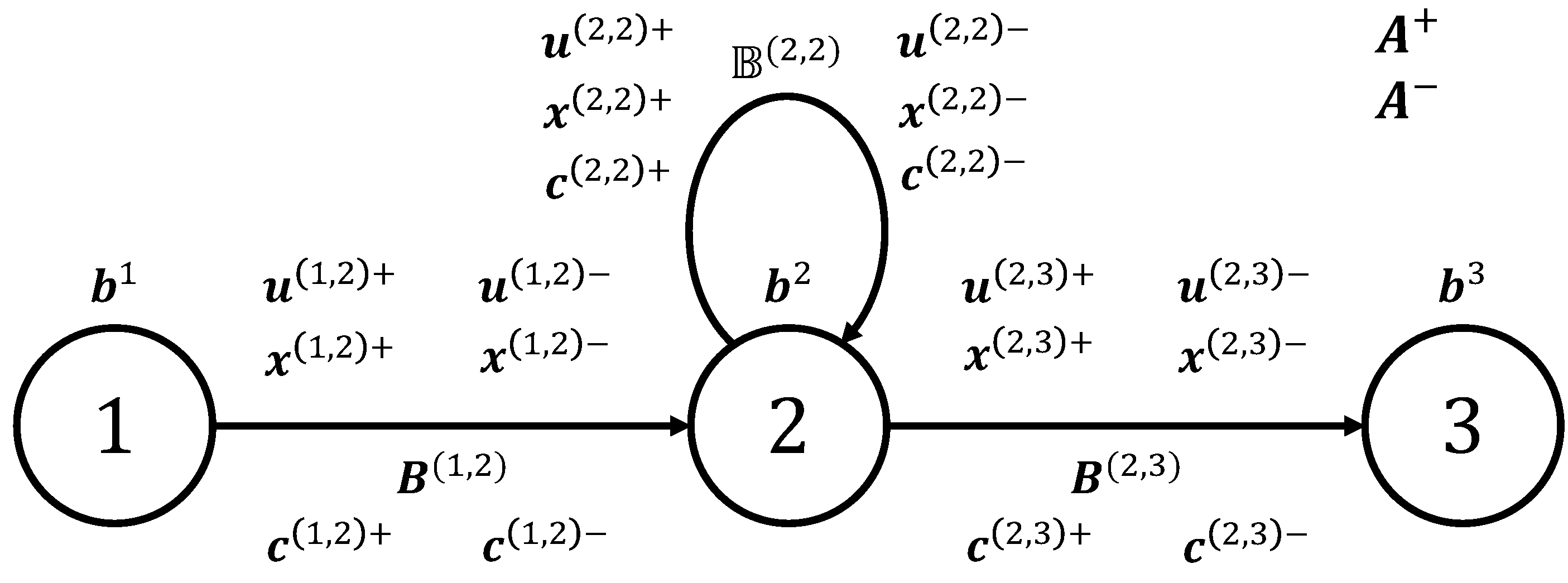


| Node j | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Node i | 1 | 29.4 | 39.0 | 6.0 | 47.4 | 41.4 | 7.8 | 40.8 | ||
| 2 | 40.8 | 50.4 | 15.6 | 57.0 | 49.8 | 14.4 | 48.0 | |||
| 3 | 3.0 | 32.4 | 18.0 | 49.2 | ||||||
| 4 | 3.0 | 28.8 | 2.4 | 69.6 | ||||||
| 5 | 3.0 | 82.2 | 68.4 | 2.4 | ||||||
| 6 | 5.0 | |||||||||
| 7 | 5.0 | |||||||||
| 8 | 5.0 | |||||||||
| 9 | 31.2 | 6.0 | 65.4 | |||||||
| 2, 2 | 6, 6 | 2, 2 | 1, 1 | 0, 0 | |
| 1, 1 | 3, 3 | 1, 1 | 1, 1 | 0, 0 | |
| 0, 0 | 0, 0 | 0, 0 | 1, 1 | 0, 0 | |
| 0, 0 | 0, 0 | 0, 0 | 1, 1 | 0, 0 | |
| 1, 1 | 3, 3 | 1, 1 | 1, 1 | 0, 0 | |
| 2, 2 | 6, 6 | 2, 2 | 1, 1 | 0, 0 | |
| 2, 0 | 6, 0 | 2, 0 | 2, 0 | 0, 2 | |
| 0, 0 | 0, 0 | 0, 0 | 0, 0 | 2, 2 | |
| 2, 9 | 6, 0 | 2, 0 | 2, 1 | 0, 2 | |
| 2, 0 | 6, 0 | 2, 0 | 2, 1 | 0, 2 |
| Node j | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Location 1 | 4.3 | 6.0 | 0.1 | 6.9 | 5.8 | 0.3 | 5.6 | |||
| Location 2 | 3.6 | 5.3 | 0.7 | 6.2 | 5.1 | 0.7 | 4.9 | |||
| Location 3 | 2.8 | 4.5 | 1.6 | 5.4 | 4.3 | 1.8 | 4.1 | |||
| Location 4 | 2.0 | 3.7 | 2.1 | 4.7 | 3.5 | 2.3 | 3.3 | |||
| Location 5 | 0.6 | 2.3 | 3.7 | 3.2 | 2.1 | 3.4 | 1.9 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitsuyuki, T.; Shimozawa, T.; Mizokami, I.; Wanaka, S. Supply Chain Design Method for Introducing Floating Offshore Wind Turbines Using Network Optimization Model. Systems 2025, 13, 598. https://doi.org/10.3390/systems13070598
Mitsuyuki T, Shimozawa T, Mizokami I, Wanaka S. Supply Chain Design Method for Introducing Floating Offshore Wind Turbines Using Network Optimization Model. Systems. 2025; 13(7):598. https://doi.org/10.3390/systems13070598
Chicago/Turabian StyleMitsuyuki, Taiga, Takahiro Shimozawa, Itsuki Mizokami, and Shinnosuke Wanaka. 2025. "Supply Chain Design Method for Introducing Floating Offshore Wind Turbines Using Network Optimization Model" Systems 13, no. 7: 598. https://doi.org/10.3390/systems13070598
APA StyleMitsuyuki, T., Shimozawa, T., Mizokami, I., & Wanaka, S. (2025). Supply Chain Design Method for Introducing Floating Offshore Wind Turbines Using Network Optimization Model. Systems, 13(7), 598. https://doi.org/10.3390/systems13070598






