Evolutionary Game of Medical Knowledge Sharing Among Chinese Hospitals Under Government Regulation
Abstract
1. Introduction
2. Literature Review
2.1. Medical KS Level
2.2. Application of Evolutionary Games in the Medical Area
2.3. The Influence of Government Regulation
3. Problem Description and Model Construction
3.1. Problem Description
- RQ1: What are the ESS choices and preferences of the three parties (general hospitals, community health centers, and government) in the medical KS game under government regulation?
- RQ2: How do critical factors—such as sharing costs, synergistic benefits, government incentives and penalties, and patient evaluations—influence the strategic choices and evolutionary paths of each party?
- RQ3: What is the role of government regulation in this process, and how can regulatory policies be designed to effectively promote sustainable KS among hospitals of different levels?
3.2. Model Assumptions and Construction
3.2.1. Model Assumptions
3.2.2. Model Construction
- Strategy Combination 1: (Sharing, Sharing, Regulating). Both hospitals adopt the “Sharing” strategy and the government adopts the “Regulating” strategy.
- Strategy Combination 2: (Sharing, Not Sharing, Regulating). The general hospital adopts the “Sharing” strategy, the community health service center adopts the “Not Sharing” strategy, and the government adopts the “Regulating” strategy.
- Strategy Combination 3: (Not Sharing, Sharing, Regulating). The general hospital adopts the “Not Sharing” strategy, the community health service center adopts the “Sharing” strategy, and the government adopts the “Regulating” strategy.
- Strategy Combination 4: (Not Sharing, Not Sharing, Regulating). Both hospitals adopt the “Not Sharing” strategy and the government adopts the “Regulating” strategy.
- Strategy Combination 5: (Sharing, Sharing, Not Regulating). Both hospitals adopt the “Sharing” strategy and the government adopts the “Not Regulating” strategy.
- Strategy Combination 6: (Sharing, Not Sharing, Not Regulating). The general hospital adopts the “Sharing” strategy, the community health service center adopts the “Not Sharing” strategy, and the government adopts the “Not Regulating” strategy.
- Strategy Combination 7: (Not Sharing, Sharing, Not Regulating). The general hospital adopts the “Not Sharing” strategy, the community health service center adopts the “Sharing” strategy, and the government adopts the “Not Regulating” strategy.
- Strategy Combination 8: (Not Sharing, Not Sharing, Not Regulating). Both hospitals adopt the “Not Sharing” strategy and the government adopts the “Not Regulating” strategy.
4. Replicator Dynamic Equation
5. Evolutionary Stability Analysis
5.1. Stability Analysis of Subject Strategies
- (1)
- Strategy stability analysis of the general hospital
- (2)
- Strategy stability analysis of the community health service center
- (3)
- Strategy stability analysis of the government
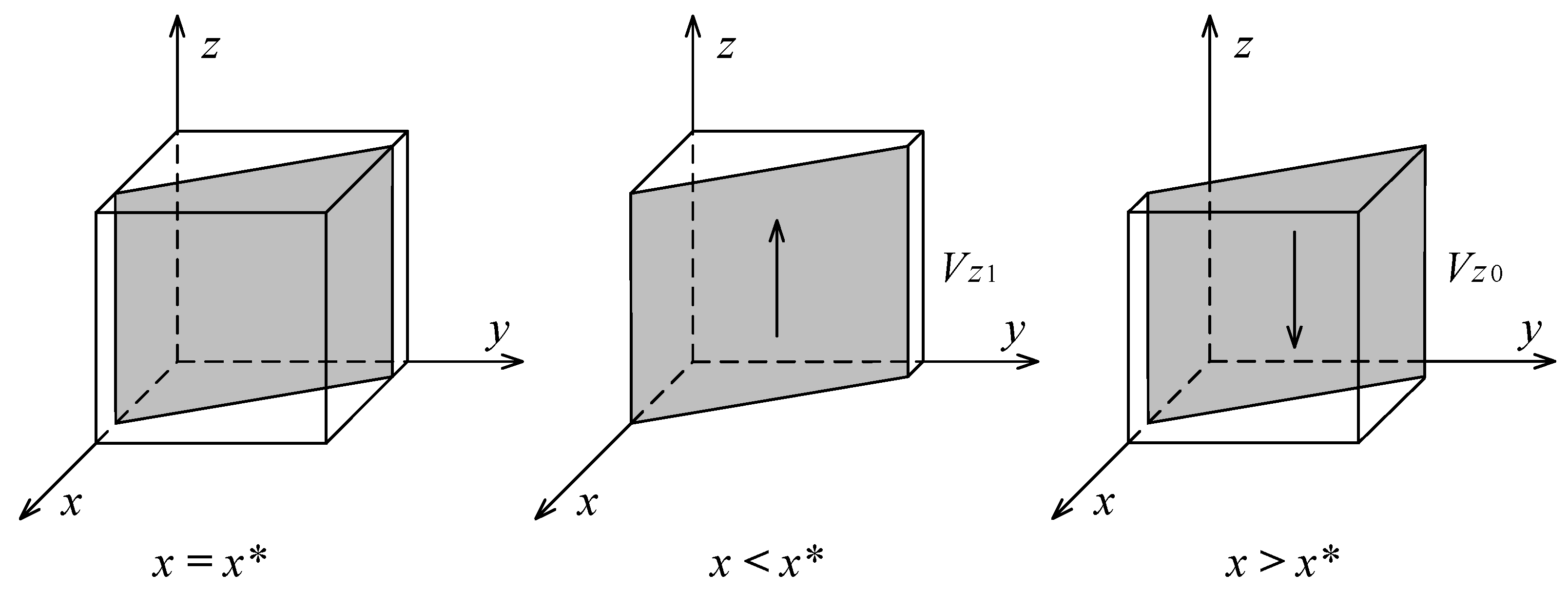
5.2. Stability Analysis of System Equilibrium Points
6. Simulation Experiments Analysis
6.1. Stability Strategy Simulation
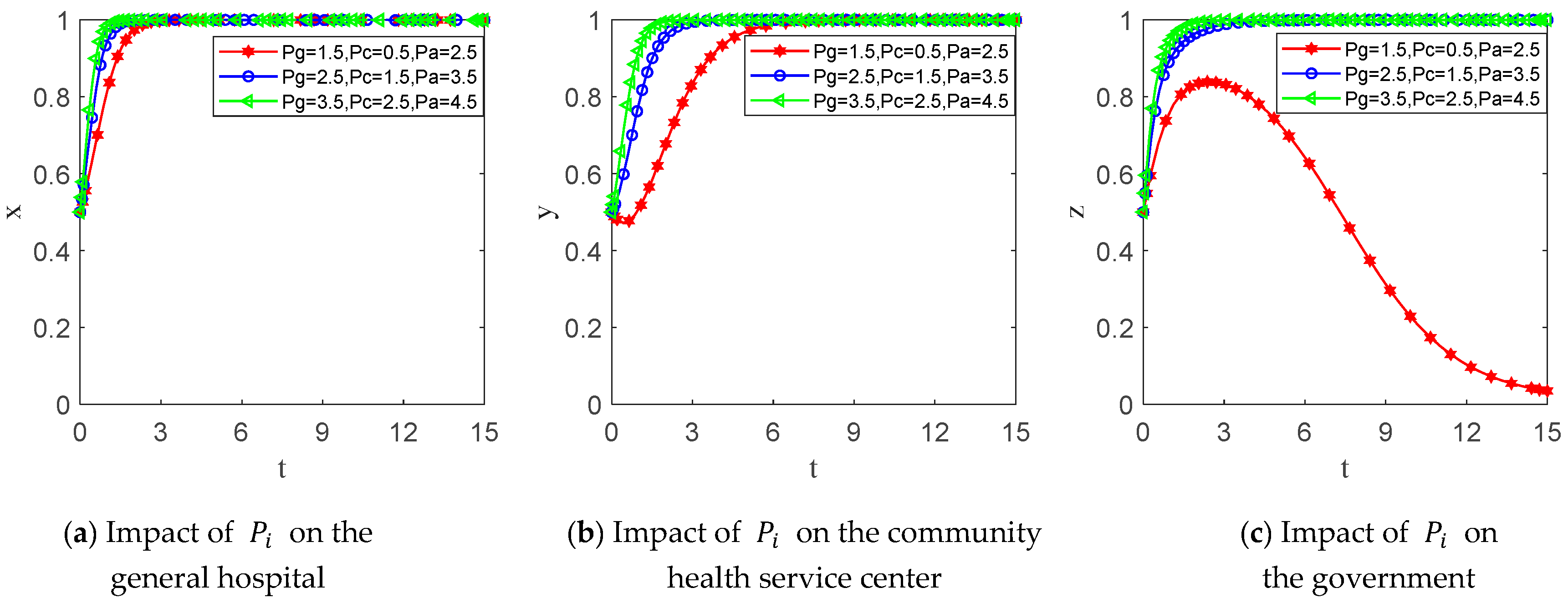
6.2. Parameter Sensitivity Analysis
7. Discussion and Conclusions
7.1. Marginal Contributions
7.2. Main Conclusions and Management Insights
- (1)
- The system’s equilibrium state is determined by the relationship between KS synergistic benefits, government reward benefits and punishment costs, patient evaluation benefits and punishment costs, and sharing costs. The ESS (Sharing, Sharing, Regulating) emerges only when the cumulative benefits from reward and punishment mechanisms exceed the combined input costs borne by both hospitals and the government in the KS process. Crucially, to effectively deter non-sharing, the magnitude of government penalties must be sufficiently large relative to the KS costs incurred by hospitals; our simulations suggest that penalties should be set at a level significantly higher than the perceived cost of sharing to ensure a strong deterrent effect.
- (2)
- The likelihood of KS between general hospitals and community health service centers exhibits a positive correlation with both the reciprocal KS rate and the intensity of government regulation. Conversely, governmental regulatory intervention decreases as inter-institutional KS rates rise. Therefore, policy efforts should promote the establishment of long-term cooperative relationships between general hospitals and community health service centers to facilitate knowledge flow through joint training, resource-sharing platforms, and research projects. In addition, the government needs to dynamically adjust its regulatory intensity, gradually reducing its direct intervention in institutions with high sharing rates and focusing more resources on institutions with low sharing rates, thereby achieving the efficient allocation of regulatory resources.
- (3)
- Increasing government rewards and punishments can help promote KS behaviors among hospitals of different levels, but the promotion effect exhibits diminishing marginal returns. Furthermore, the government’s willingness to regulate is weakened with the increase in rewards due to the associated fiscal burden. Therefore, the government should establish a financially sustainable reward and punishment mechanism. This entails not only providing appropriate rewards (such as financial subsidies, tax breaks, or policy support) to stimulate active KS participation, but also setting penalties (such as reducing fund allocation or restricting project eligibility) at levels significantly exceeding KS costs to constrain speculative behavior. Critically, policymakers must carefully assess the budgetary impact of rewards, especially when extending them to both hospital types simultaneously. Our model indicates that while rewarding both parties enhances cooperation, it substantially increases government expenditure; therefore, reward levels and eligibility criteria must be calibrated against fiscal constraints to ensure long-term viability. Simultaneously, the government should maintain a balance between the reward/punishment intensity and its regulatory commitment to avoid undermining regulatory willingness due to excessive reward costs.
- (4)
- Patient evaluation rewards and punishments have a positive effect on KS among hospitals and government regulation. Therefore, it is necessary to raise patients’ awareness of KS and guide them to actively participate in evaluation and feedback, so as to give full play to the role of patients in the process of KS. The government and hospitals can build convenient feedback channels, strengthen the protection of patients’ privacy, carry out health promotion and education, and link the evaluation results to hospital performance evaluation to enhance patients’ trust and motivation to participate, thus forming a positive interaction among hospitals, patients, and the government, and promoting the continuous improvement in the quality of healthcare services and resource sharing.
7.3. Limitations and Future Research
- (1)
- The current sensitivity analysis employs the optimal equilibrium point as its benchmark, neglecting sensitivity assessments of the other three equilibrium points. Future studies should therefore incorporate sensitivity analyses for all four equilibrium points while investigating their interrelationships.
- (2)
- While the current research focuses on domestic medical data ecosystems, future work could construct transnational research frameworks. By examining diverse data-sharing paradigms and national regulatory architectures, such frameworks could elucidate the coupling mechanisms between cultural traditions, legal systems, and heterogeneous sharing trend levels in shaping data-sharing behaviors.
- (3)
- Current policy discussions involve extrapolations beyond the simulated ranges. Therefore, future research will rigorously explore the specific thresholds triggering behavioral shifts and theoretically derive the detailed quantitative relationships between incentive levels, willingness to regulate, and knowledge-sharing outcomes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Definition |
|---|---|
| General hospital, community health service center and the government | |
| Probability of hospital KS/government regulation | |
| Basic benefits | |
| Direct benefits | |
| Knowledge aggregation benefits | |
| Synergistic benefits of KS | |
| Governmentreward benefits | |
| Governmentpunishment costs | |
| Patient evaluation reward benefits | |
| Patient evaluationpunishment costs | |
| Social and economic benefits of the government | |
| Knowledge sharing/Regulating costs |
Appendix B
Appendix C


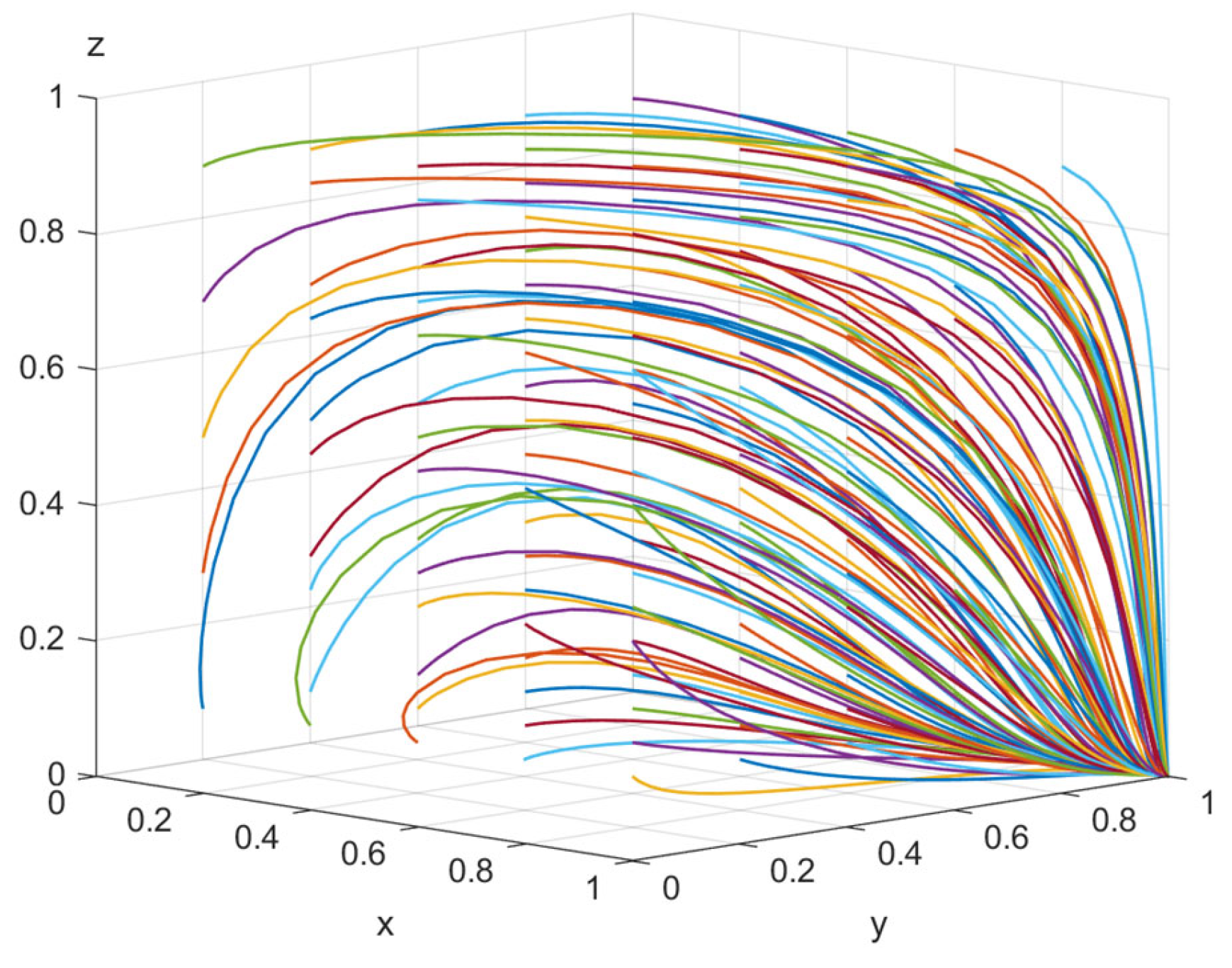

References
- Liang, J.; Li, Y.; Zhang, Z.; Shen, D.; Xu, J.; Yu, G.; Dai, S.; Ge, F.; Lei, J. Evaluating the applications of health information technologies in China during the past 11 years: Consecutive survey data analysis. JMIR Med. Inform. 2020, 8, e17006. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Xie, Z.; Yu, K.; Jiang, B.; Zheng, S.; Pan, X. COVID-19 and healthcare system in China: Challenges and progression for a sustainable future. Glob. Health 2021, 17, 14. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Chen, K. Equity and efficiency of medical and health service system in China. BMC Health Serv. Res. 2023, 23, 33. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Krumholz, H.M.; Yip, W.; Cheng, K.K.; De Maeseneer, J.; Meng, Q.; Mossialos, E.; Li, C.; Lu, J.; Su, M. Quality of primary health care in China: Challenges and recommendations. Lancet 2020, 395, 1802–1812. [Google Scholar] [CrossRef]
- Wang, X.; Nie, X. The uneven distribution of medical resources for severe diseases in China: An analysis of the disparity in inter-city patient mobility. Appl. Geogr. 2024, 165, 103226. [Google Scholar] [CrossRef]
- Wu, C.; Tu, Y.; Li, Z.; Yu, J. An early assessment of the County Medical Community reform in China: A case study of Zhejiang province. J. Chin. Gov. 2021, 6, 463–485. [Google Scholar] [CrossRef]
- Ye, Y.; Evans, R.; Jing, L.; Rizwan, M.; Xuan, Y.; Lu, W. The impact of county medical community reform on the medical service efficiency of county-level public general hospitals in China: A case study of Shanxi Province. Int. J. Environ. Res. Public Health 2022, 19, 13827. [Google Scholar] [CrossRef]
- Roba, D.; Jimma, W.; Diriba, C. Individual, organizational and technological factors affect knowledge sharing practices in Assosa Hospital, Ethiopia. Eur. Acad. Res. 2016, 5, 2286–4822. [Google Scholar]
- Lee, H.S.; Hong, S.A. Factors affecting hospital employees’ knowledge sharing intention and behavior, and innovation behavior. Osong Public Health Res. Perspect. 2014, 5, 148–155. [Google Scholar] [CrossRef]
- Zhu, C.; Zhou, L.; Zhang, X.; Walsh, C.A. Tripartite Evolutionary Game and Simulation Analysis of Healthcare Fraud Supervision under the Government Reward and Punishment Mechanism. Healthcare 2023, 11, 1972. [Google Scholar] [CrossRef]
- Fan, R.; Wang, Y.; Lin, J. Study on multi-agent evolutionary game of emergency management of public health emergencies based on dynamic rewards and punishments. Int. J. Environ. Res. Public Health 2021, 18, 8278. [Google Scholar] [CrossRef] [PubMed]
- Xue, R.; Xiong, L.; Wang, K. An evolutionary game approach for information sharing within medical consortium based on complex network. Comput. Ind. Eng. 2025, 203, 110963. [Google Scholar] [CrossRef]
- Yang, B.; Ye, S.; Bandarchi, M. A new model for investigating the factors influencing the innovation in medical services: The mediating role of attitude toward knowledge sharing. Vine J. Inf. Knowl. Manag. Syst. 2020, 50, 669–690. [Google Scholar] [CrossRef]
- Rubin, G.D.; Ryerson, C.J.; Haramati, L.B.; Sverzellati, N.; Kanne, J.P.; Raoof, S.; Schluger, N.W.; Volpi, A.; Yim, J.-J.; Martin, I.B. The role of chest imaging in patient management during the COVID-19 pandemic: A multinational consensus statement from the Fleischner Society. Radiology 2020, 296, 172–180. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Mardani, A. Empirical analysis of the influencing factors of knowledge sharing in industrial technology innovation strategic alliances. J. Bus. Res. 2023, 157, 113635. [Google Scholar] [CrossRef]
- Zhou, L.; Nunes, M.B. Barriers to knowledge sharing in Chinese healthcare referral services: An emergent theoretical model. Glob. Health Action 2016, 9, 29964. [Google Scholar] [CrossRef]
- Liu, X.; Ai, S. Analysis of Evolutionary Game on Knowledge-Sharing Behavior in IT Outsourcing. Oper. Res. Manag. Sci. 2015, 24, 82. [Google Scholar]
- Yang, S.; Wang, H.; Lin, X. Dynamic decision of health information exchange under different hospital relationships: A differential game approach. J. Ind. Manag.Optim. 2023, 19, 6634–6663. [Google Scholar] [CrossRef]
- Song, L.; Yu, Z.; Fang, J.; He, Q. Evolutionary game theory and simulations based on doctor and patient medical malpractice under government regulation. Sci. Rep. 2023, 13, 18234. [Google Scholar] [CrossRef]
- Nishihata, Y.; Liu, Z.; Nishi, T. Evolutionary-game-theory-based epidemiological model for prediction of infections with application to demand forecasting in pharmaceutical inventory management problems. Appl. Sci. 2023, 13, 11308. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, W.; Song, Z.; Liu, H.; Jiang, T. Evolutionary game of resources integration on rural basic medical institution in family physician signing model. Chin. J. Health Policy 2018, 12, 35–44. [Google Scholar]
- Tian, S.; Chen, Y. Vertical integration of electronic health records in medical consortiums: Dynamic modeling approach based on the evolutionary game theory. JMIR Serious Games 2023, 11, e41528. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yu, C.; Li, C.; Han, J. Cooperation or conflict in doctor-patient relationship? An analysis from the perspective of evolutionary game. IEEE Access 2020, 8, 42898–42908. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zhao, H. Evolutionary Game Analysis of Collaborative Prevention and Control for Public Health Emergencies. Sustainability 2022, 14, 15089. [Google Scholar] [CrossRef]
- Yuan, Y.; Du, L.; Luo, L.; Cui, L. Allocation strategy of medical supplies during a public health emergency: A tripartite evolutionary game perspective. Sci. Rep. 2023, 13, 9571. [Google Scholar] [CrossRef]
- Dong, C.; Liu, J.; Mi, J. Information-driven integrated healthcare: An analysis of the cooperation strategy of county medical community based on multi-subject simulation. Healthcare 2023, 11, 2019. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.; Geng, N. Evolutionary Game Analysis of Medical Information Sharing Based on the Government Regulation. Oper. Res. Manag. Sci. 2020, 29, 23–31. [Google Scholar]
- Dong, Y.; Sun, Z.; Qiu, L. A Tripartite Evolutionary Game Analysis of Enterprise Data Sharing Under Government Regulations. Systems 2025, 13, 151. [Google Scholar] [CrossRef]
- Qi, M.; Ren, J. An overview and visual analysis of research on government regulation in healthcare. Front. Public Health 2023, 11, 1272572. [Google Scholar] [CrossRef]
- Luo, L.; Zhang, S.; Xiang, J. Development of the family doctor service: An evolutionary game theory analysis. Ekon. Istraz. 2023, 36, 2106507. [Google Scholar] [CrossRef]
- Fan, W.; Wang, S.; Gu, X.; Zhou, Z.; Zhao, Y.; Huo, W. Evolutionary game analysis on industrial pollution control of local government in China. J. Environ. Manag. 2021, 298, 113499. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudi, R.; Rasti-Barzoki, M. Sustainable supply chains under government intervention with a real-world case study: An evolutionary game theoretic approach. Comput. Ind. Eng. 2018, 116, 130–143. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, Q.; Tang, J. Evolutionary game analysis of environmental pollution control under the government regulation. Sci. Rep. 2022, 12, 474. [Google Scholar] [CrossRef] [PubMed]
- Zhai, J.; Xu, X.; Xu, J.; Lyu, X. Research on green collaborative innovation mechanism of cloud manufacturing enterprises under government supervision. Math. Probl. Eng. 2021, 2021, 8820791. [Google Scholar] [CrossRef]
- Zhou, Z.; Ruan, L.; Ding, Q. Evolutionary Game Analysis of Cross-organizational Knowledge Sharing Behavior in Enterprise Innovation Network. Oper. Res. Manag. Sci. 2021, 30, 83. [Google Scholar]
- Ayala, N.F.; Paslauski, C.A.; Ghezzi, A.; Frank, A.G. Knowledge sharing dynamics in service suppliers’ involvement for servitization of manufacturing companies. Int. J. Prod. Econ. 2017, 193, 538–553. [Google Scholar] [CrossRef]
- Renqiang, X.; Wende, Z. An empirical study on the impact of platform environmental factors on knowledge sharing in virtual communities. Technol. Soc. 2022, 71, 102094. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Deng, Z.; Chen, X. Knowledge sharing motivations in online health communities: A comparative study of health professionals and normal users. Comput. Hum. Behav. 2017, 75, 797–810. [Google Scholar] [CrossRef]
- Ma, R.; Jiang, L.; Wang, T.; Wang, X.; Ruan, J. How do manufacturing companies and service providers share knowledge in the context of servitization? An evolutionary-game model of complex networks. Int. J. Prod. Res. 2023, 61, 4279–4301. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, B. The Large-Small Group-Based Evolutionary Game on Knowledge Sharing in Uncertain Environment under the Background of Telemedicine Service. Complexity 2020, 2020, 9818417. [Google Scholar] [CrossRef]
- Selten, R. A Note on Evolutionarily Stable Strategies in Asymmetric Animal Conflicts; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Chen, N.; Lv, N.; Chen, Z. Knowledge Sharing among Hospitals of Different Levels: A Complex Network Evolutionary Game Approach. IEEE Access 2025, 13, 41040–41053. [Google Scholar] [CrossRef]
- Xiao, J.; Bao, Y.; Wang, J.; Yu, H.; Ma, Z.; Jing, L. Knowledge sharing in R&D teams: An evolutionary game model. Sustainability 2021, 13, 6664. [Google Scholar] [CrossRef]
- Razak, N.A.; Pangil, F.; Zin, M.L.M.; Yunus, N.A.M.; Asnawi, N.H. Theories of knowledge sharing behavior in business strategy. Procedia Econ. Fin. 2016, 37, 545–553. [Google Scholar] [CrossRef]
- Koh, J.; Kim, Y.-G. Knowledge sharing in virtual communities: An e-business perspective. Expert Syst. Appl. 2004, 26, 155–166. [Google Scholar] [CrossRef]








| General Hospital | Community Health Service Center | Government | |
|---|---|---|---|
| Sharing | Sharing | ||
| Not Sharing | |||
| Not Sharing | Sharing | ||
| Not Sharing | |||
| Equilibrium Point | Conclusion | Condition | |||
|---|---|---|---|---|---|
| – | – | Uncertain | ESS | ) | |
| – | – | Uncertain | ESS | ) | |
| Uncertain | + | Uncertain | Instability | \ | |
| Uncertain | + | Uncertain | Instability | \ | |
| + | Uncertain | Uncertain | Instability | \ | |
| + | Uncertain | Uncertain | Instability | \ | |
| Uncertain | Uncertain | Uncertain | ESS | ||
| Uncertain | Uncertain | Uncertain | ESS |
| Parameters | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | 1.5 | 1 | 1 | 0.5 | 3 | 1.5 | 3 | 10 | 6 | 8 | 1 | 0.5 | 2.5 |
| Scenario 2 | 1.5 | 1 | 1 | 0.5 | 2.5 | 1 | 3 | 9 | 5 | 6 | 1 | 0.5 | 2.5 |
| Scenario 3 | 1.5 | 1.5 | 1 | 0.5 | 2.5 | 1.5 | 2 | 6 | 3 | 5 | 1.5 | 1 | 2.5 |
| Scenario 4 | 1.5 | 1.5 | 1 | 0.5 | 2.5 | 1.5 | 4 | 5 | 4 | 5 | 1.5 | 1 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lv, N.; Chen, N. Evolutionary Game of Medical Knowledge Sharing Among Chinese Hospitals Under Government Regulation. Systems 2025, 13, 454. https://doi.org/10.3390/systems13060454
Zhang L, Lv N, Chen N. Evolutionary Game of Medical Knowledge Sharing Among Chinese Hospitals Under Government Regulation. Systems. 2025; 13(6):454. https://doi.org/10.3390/systems13060454
Chicago/Turabian StyleZhang, Liqin, Na Lv, and Nan Chen. 2025. "Evolutionary Game of Medical Knowledge Sharing Among Chinese Hospitals Under Government Regulation" Systems 13, no. 6: 454. https://doi.org/10.3390/systems13060454
APA StyleZhang, L., Lv, N., & Chen, N. (2025). Evolutionary Game of Medical Knowledge Sharing Among Chinese Hospitals Under Government Regulation. Systems, 13(6), 454. https://doi.org/10.3390/systems13060454






