Hierarchical Control Based on Ramp Metering and Variable Speed Limit for Port Motorway
Abstract
1. Introduction
- A hierarchical traffic control method is proposed, which integrates RM and VSLs, explicitly tailored for port motorways dominated by CVs. The method uses real-time CV data to dynamically optimize traffic flow through a two-layer control structure.
- The proposed method is evaluated using a microscopic simulation platform, which accurately models the specialized maneuvering behavior of container trucks and simulates detailed CV communication and control strategies within a realistic and logistically important section of the Chuanshan Port Motorway in Ningbo.
- The results highlight the potential of advanced coordinated control methods in significantly enhancing the efficiency and sustainability of freight transportation operations.
2. Hierarchical Traffic Control Framework for Port Motorways
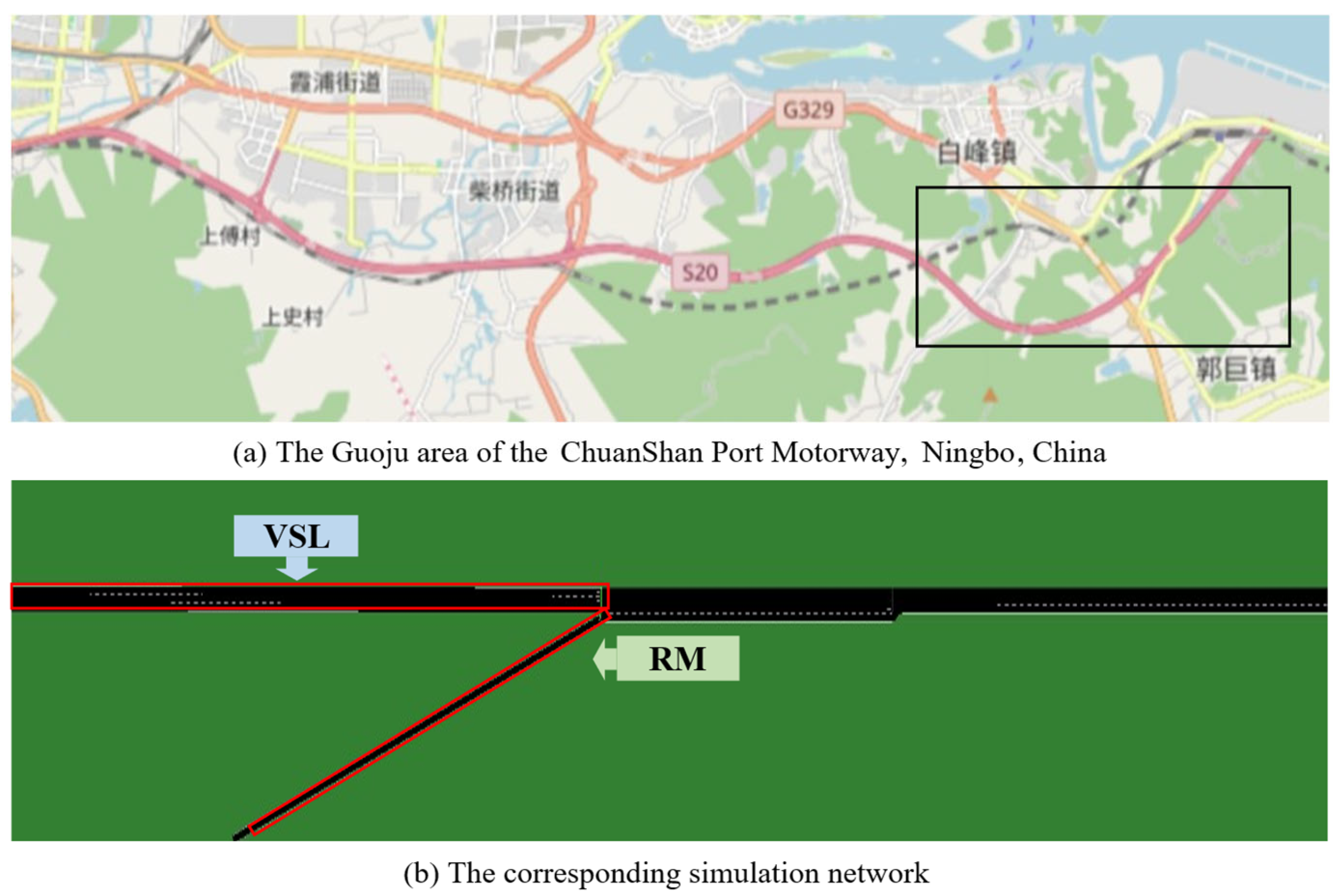
2.1. Research Scenario
2.2. Hierarchical Traffic Control Framework
2.2.1. The Upper-Level Layer
- To ensure that the upstream arrival flow does not exceed its capacity (veh/h), Equation (6) is considered.
- To ensure that the flow does not experience sudden changes, even under VSL control, Equation (7) is introduced. This constraint limits the deviation between the upstream arrival flow at time step and that at the time step within a controlled range, in order to prevent sudden fluctuations that may compromise traffic stability.where represents the flow adjustment bound, defining the maximum allowable variation in upstream arrival flow between two consecutive time steps.
- To ensure that the merging flow does not exceed the actual demand on the on-ramp, Equation (8) limits the released flow to the sum of the demand and the number of vehicles queuing at the on-ramp.
- Since the on-ramp connects to segment 2, Equation (9) is considered to ensure that the merging flow remains within the residual capacity of segment 2, thereby preventing an unrealistic value.where (veh/h) represents the saturation flow of the on-ramp. (veh/km) denotes the maximum density.
2.2.2. The Lower-Level Layer
3. Simulation Implementation and Experimental Evaluation
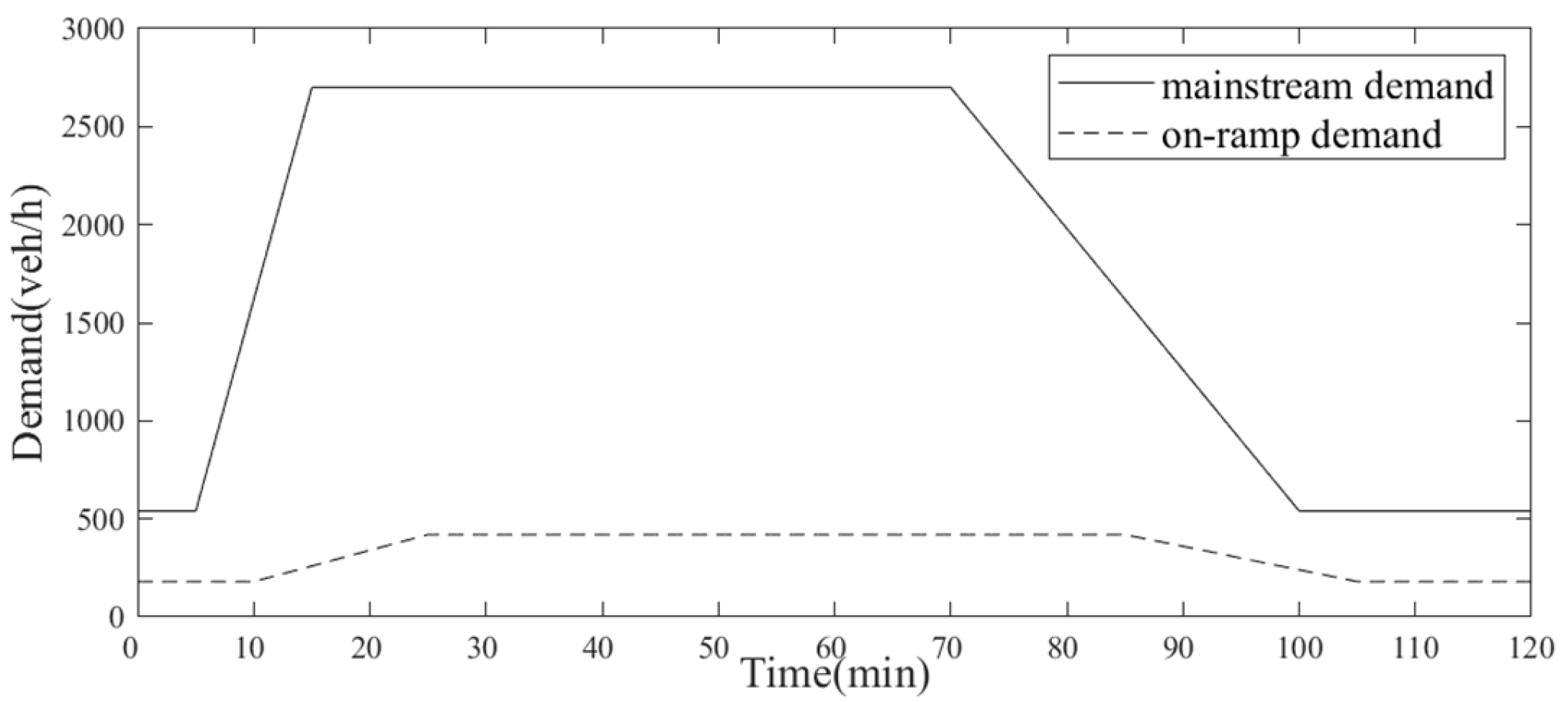
3.1. Simulation Experiment Design
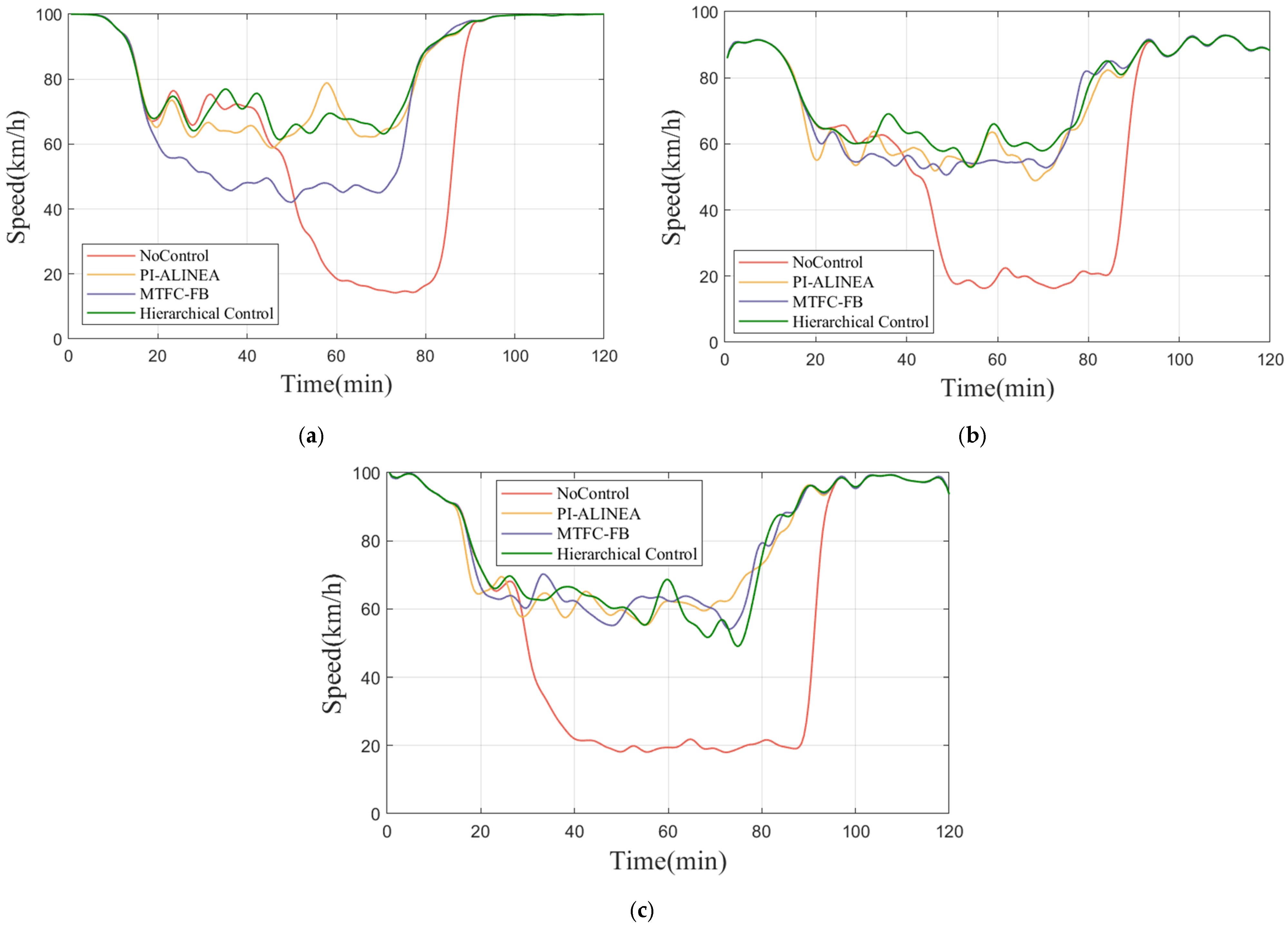
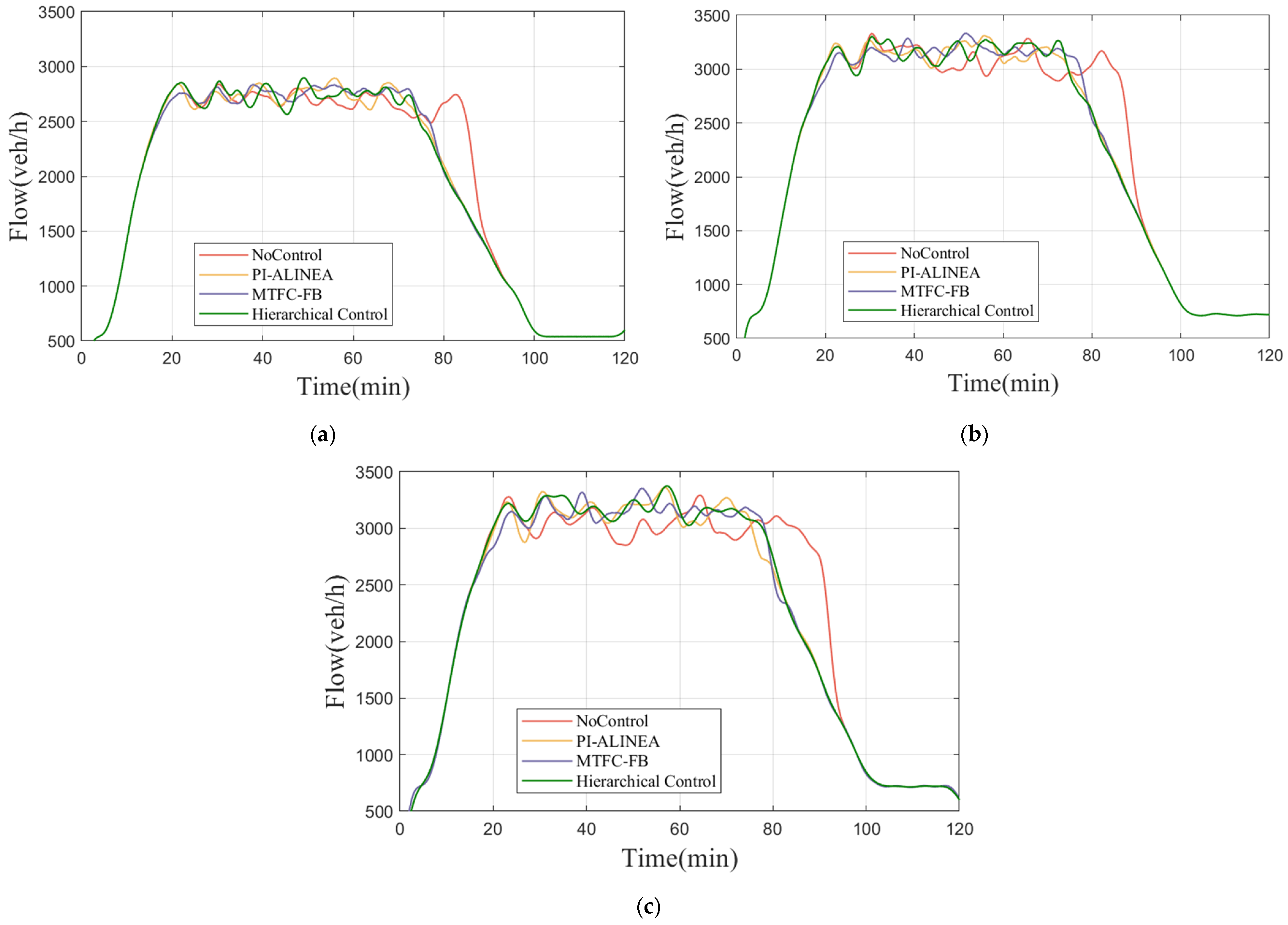
3.2. Density, Speed, and Flow Analysis in Different Scenarios
3.3. Total Time Spent Analysis in Different Scenarios
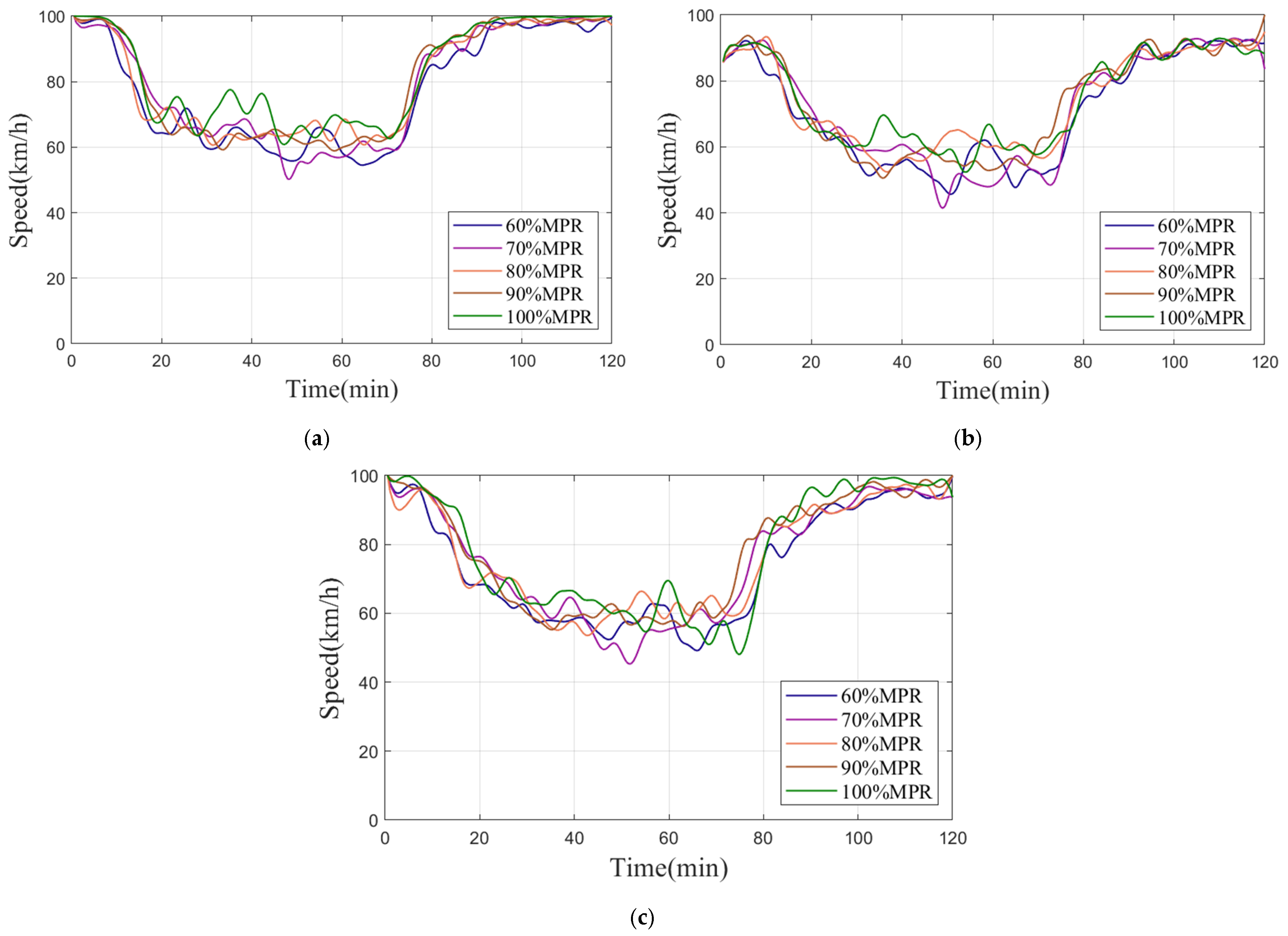
3.4. Stability Analysis of Hierarchical Control in Different Penetration Rates
3.4.1. Density, Speed, and Flow Analysis in Different MPRs
3.4.2. Total Time Spent Analysis in Different MPRs
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Calvert, S.C.; Schakel, W.J.; van Arem, B. Evaluation and modelling of the traffic flow effects of truck platooning. Transp. Res. Part C Emerg. Technol. 2019, 105, 1–22. [Google Scholar] [CrossRef]
- Yang, D.; Kuijpers, A.; Dane, G.; der Sande, T.V. Impacts of large-scale truck platooning on dutch highways. Transp. Res. Procedia 2019, 37, 425–432. [Google Scholar] [CrossRef]
- Carboni, A.; Deflorio, F.; Caballini, C.; Cangelosi, S. Advances in terminal management: Simulation of vehicle traffic in container terminals. Marit. Econ. Logist. 2024. [Google Scholar] [CrossRef]
- Ma, W.; He, Z.; Wang, L.; Abdel-Aty, M.; Yu, C. Active traffic management strategies for expressways based on crash risk prediction of moving vehicle groups. Accid. Anal. Prev. 2021, 163, 106421. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Hadj-Salem, H.; Blosseville, J. ALINEA: A local feedback control law for on-ramp metering. Transp. Res. Rec. 1991, 1320, 58–67. [Google Scholar]
- Faulkner, L.; Dekker, F.; Gyles, D.; Papamichail, I.; Papageorgiou, M. Evaluation of HERO-coordinated ramp metering installation at m1 and m3 freeways in queensland, australia. Transp. Res. Rec. J. Transp. Res. Board 2014, 2470, 13–23. [Google Scholar] [CrossRef]
- Smaragdis, E.; Papageorgiou, M.; Kosmatopoulos, E. A flow-maximizing adaptive local ramp metering strategy. Transp. Res. Part B Methodol. 2004, 38, 251–270. [Google Scholar] [CrossRef]
- Papamichail, I.; Papageorgiou, M. Traffic-responsive linked ramp-metering control. IEEE Trans. Intell. Transp. Syst. 2008, 9, 111–121. [Google Scholar] [CrossRef]
- Wang, Y.; Kosmatopoulos, E.B.; Papageorgiou, M.; Papamichail, I. Local ramp metering in the presence of a distant downstream bottleneck: Theoretical analysis and simulation study. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2024–2039. [Google Scholar] [CrossRef]
- Masher, D.P.; Ross, D.W.; Wong, P.J.; Tuan, P.L.; Zeidler, H.M.; Petracek, S. Guidelines for Design and Operation of Ramp Control Systems; Stanford Research Institute: Menlo Park, CA, USA, 1975. [Google Scholar]
- Ferrara, A.; Sacone, S.; Siri, S.; Vivas, C.; Rubio, F.R. Switched observer-based ramp metering controllers for freeway systems. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 6777–6782. [Google Scholar]
- Frejo, J.R.D.; De Schutter, B. Feed-forward ALINEA: A ramp metering control algorithm for nearby and distant bottlenecks. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2448–2458. [Google Scholar] [CrossRef]
- Wolshon, B.; Ishak, S.; Qi, Y.; Korkut, M.; Sun, X.; Alecsandru, C. Trucker perceptions of lane restriction and differential speed limit policies on freeways. J. Transp. Saf. Secur. 2009, 1, 101–120. [Google Scholar] [CrossRef]
- Chen, J.; Lin, W.; Yang, Z.; Li, J.; Cheng, P. Adaptive ramp metering control for urban freeway using large-scale data. IEEE Trans. Veh. Technol. 2019, 68, 9507–9518. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Y.; Cao, S.; Zhu, L.; Shen, G. A ramp metering method based on congestion status in the urban freeway. IEEE Access 2020, 8, 76823–76831. [Google Scholar] [CrossRef]
- Bellemans, T.; De Schutter, B.; De Moor, B. Model predictive control for ramp metering of motorway traffic: A case study. Control Eng. Pract. 2006, 14, 757–767. [Google Scholar] [CrossRef]
- Gu, C.; Wu, C.; Teo, K.L.; Wu, Y.; Wang, S. A smoothing method for ramp metering. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13358–13371. [Google Scholar] [CrossRef]
- Han, Y.; Ramezani, M.; Hegyi, A.; Yuan, Y.; Hoogendoorn, S. Hierarchical ramp metering in freeways: An aggregated modeling and control approach. Transp. Res. Part C Emerg. Technol. 2020, 110, 1–19. [Google Scholar] [CrossRef]
- Tabadkani Aval, S.S.; Eghbal, N. Feedback-based cooperative ramp metering for highway traffic flow control: A model predictive sliding mode control approach. Int. J. Robust. Nonlinear Control 2020, 30, 8259–8277. [Google Scholar] [CrossRef]
- Gu, C.; Zhou, T.; Wu, C. Deep koopman traffic modeling for freeway ramp metering. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6001–6013. [Google Scholar] [CrossRef]
- Georgantas, A.; Lazarou, M.; Timotheou, S.; Stathaki, T.; Panayiotou, C.G. Highway traffic control with ramp metering utilizing variational autoencoders. IFAC-Pap. 2022, 55, 75–80. [Google Scholar] [CrossRef]
- Lemarchand, A.; Martinez, J.J.; Koenig, D. Hierarchical coordinated freeway on-ramp metering using switching system theory. IFAC Proc. Vol. 2010, 43, 342–349. [Google Scholar] [CrossRef]
- Papamichail, I.; Kotsialos, A.; Margonis, I.; Papageorgiou, M. Coordinated ramp metering for freeway networks—A model-predictive hierarchical control approach. Transp. Res. Part C Emerg. Technol. 2010, 18, 311–331. [Google Scholar] [CrossRef]
- Geroliminis, N.; Srivastava, A.; Michalopoulos, P. A dynamic-zone-based coordinated ramp-metering algorithm with queue constraints for minnesota’s freeways. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1576–1586. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Y. Optimizing coordinated ramp metering: A preemptive hierarchical control approach. Comput-Aided Civ. Infrastruct. Eng. 2013, 28, 22–37. [Google Scholar] [CrossRef]
- Ferrara, A.; Incremona, G.P.; Piacentini, G. A hierarchical MPC and sliding mode based two-level control for freeway traffic systems with partial demand information. Eur. J. Control 2021, 59, 152–164. [Google Scholar] [CrossRef]
- Pasquale, C.; Sacone, S.; Siri, S.; Ferrara, A. Hierarchical centralized/decentralized event-triggered control of multiclass traffic networks. IEEE Trans. Control Syst. Technol. 2021, 29, 1549–1564. [Google Scholar] [CrossRef]
- Xu, P.; Xiao, X.; Yao, S. A review of train passenger safety—Inspiration from passive safety passenger protection technology of automobile. Transp. Saf. Env. 2021, 4, tdab032. [Google Scholar] [CrossRef]
- Obeidat, M.S.; Obeidat, R.M.; Dweiri, F. Unravelling the veil of traffic safety: A comprehensive analysis of factors influencing crash frequency across US states. Transp. Saf. Env. 2024, 6, tdae016. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, H.; Ioannou, P.A. A simple roadway control system for freeway traffic. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M. Local feedback-based mainstream traffic flow control on motorways using variable speed limits. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1261–1276. [Google Scholar] [CrossRef]
- Chen, D.; Ahn, S.; Hegyi, A. Variable speed limit control for steady and oscillatory queues at fixed freeway bottlenecks. Transp. Res. Part B Methodol. 2014, 70, 340–358. [Google Scholar] [CrossRef]
- Martínez, I.; Jin, W. Optimal location problem for variable speed limit application areas. Transp. Res. Part B Methodol. 2020, 138, 221–246. [Google Scholar] [CrossRef]
- Du, S.; Razavi, S. Fault-tolerant control of variable speed limits for freeway work zone using likelihood estimation. Adv. Eng. Inf. 2020, 45, 101133. [Google Scholar] [CrossRef]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M. Integrated feedback ramp metering and mainstream traffic flow control on motorways using variable speed limits. Transp. Res. Part C Emerg. Technol. 2014, 46, 209–221. [Google Scholar] [CrossRef]
- Iordanidou, G.; Papamichail, I.; Roncoli, C.; Papageorgiou, M. Feedback-based integrated motorway traffic flow control with delay balancing. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2319–2329. [Google Scholar] [CrossRef]
- Shaaban, K.; Khan, M.A.; Kim, I.; Hamila, R. Queue discharge at freeway on-ramps using coordinated operation of a ramp meter and an upstream traffic signal. Procedia Comput. Sci. 2020, 170, 347–353. [Google Scholar] [CrossRef]
- Frejo, J.R.D.; De Schutter, B. Logic-based traffic flow control for ramp metering and variable speed limits—Part 1: Controller. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2647–2657. [Google Scholar] [CrossRef]
- Frejo, J.R.D.; De Schutter, B. Logic-based traffic flow control for ramp metering and variable speed limits—Part 2: Simulation and comparison. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2658–2668. [Google Scholar] [CrossRef]
- Liu, S.; Sadowska, A.; Frejo, J.R.D.; Núñez, A.; Camacho, E.F.; Hellendoorn, H.; De Schutter, B. Robust receding horizon parameterized control for multi-class freeway networks: A tractable scenario-based approach. Int. J. Robust. Nonlinear Control 2016, 26, 1211–1245. [Google Scholar] [CrossRef]
- Chiang, Y.; Juang, J. Control of freeway traffic flow in unstable phase by $ h_ {\infty} $ theory. IEEE Trans. Intell. Transp. Syst. 2008, 9, 193–208. [Google Scholar] [CrossRef]
- Van de Weg, G.S.; Hegyi, A.; Hoogendoorn, S.P.; De Schutter, B. Efficient freeway MPC by parameterization of ALINEA and a speed-limited area. IEEE Trans. Intell. Transp. Syst. 2019, 20, 16–29. [Google Scholar] [CrossRef]
- Mittal, A.; Kim, E.; Mahmassani, H.S.; Hong, Z. Predictive dynamic speed limit in a connected environment for a weather affected traffic network: A case study of chicago. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 13–24. [Google Scholar] [CrossRef]
- Silgu, M.A.; Erdagi, I.G.; Goksu, G.; Celikoglu, H.B. Combined control of freeway traffic involving cooperative adaptive cruise controlled and human driven vehicles using feedback control through SUMO. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11011–11025. [Google Scholar] [CrossRef]
- Radac, M.; Lala, T. Hierarchical cognitive control for unknown dynamic systems tracking. Mathematics 2021, 9, 2752. [Google Scholar] [CrossRef]
- Zhu, W.; Hayashibe, M. A hierarchical deep reinforcement learning framework with high efficiency and generalization for fast and safe navigation. IEEE Trans. Ind. Electron. 2022, 70, 4962–4971. [Google Scholar] [CrossRef]
- Zhuo, H.; Yang, Z.; You, Y.; Xu, N.; Liao, L.; Wu, J.; He, J. A hierarchical control method for trajectory tracking of aerial manipulators arms. Actuators 2024, 13, 333. [Google Scholar] [CrossRef]
- Blanch-Fortuna, A.; Zambrano-Prada, D.; López-Santos, O.; Aroudi, A.E.; Vazquez-Seisdedos, L.; Martinez-Salamero, L. Hierarchical control of power distribution in the hybrid energy storage system of an ultrafast charging station for electric vehicles. Energies 2024, 17, 1393. [Google Scholar] [CrossRef]
- Griggs, W.M.; Ordonez-Hurtado, R.H.; Crisostomi, E.; Hausler, F.; Massow, K.; Shorten, R.N. A large-scale SUMO-based emulation platform. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3050–3059. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. Event-driven based reinforcement learning predictive controller design for three-phase NPC converters using online approximators. IEEE Trans. Power Electron. 2024, 40, 4914–4926. [Google Scholar] [CrossRef]
- Chen, X.; Wei, C.; Xin, Z.; Zhao, J.; Xian, J. Ship detection under low-visibility weather interference via an ensemble generative adversarial network. J. Mar. Sci. Eng. 2023, 11, 2065. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508), Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Chen, S.; Piao, L.; Zang, X.; Luo, Q.; Li, J.; Yang, J.; Rong, J. Analyzing differences of highway lane-changing behavior using vehicle trajectory data. Phys. A Stat. Mech. Its Appl. 2023, 624, 128980. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Y.; Zhang, J.; Ran, B. Integrated traffic control for freeway recurrent bottleneck based on deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15522–15535. [Google Scholar] [CrossRef]
- Spiliopoulou, A.D.; Papamichail, I.; Papageorgiou, M. Toll plaza merging traffic control for throughput maximization. J. Transp. Eng. 2010, 136, 67–76. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Kotsialos, A. Freeway ramp metering: An overview. IEEE Trans. Intell. Transp. Syst. 2002, 3, 271–281. [Google Scholar] [CrossRef]
- Feng, J.; Lin, K.; Shi, T.; Wu, Y.; Wang, Y.; Zhang, H.; Tan, H. Cooperative traffic optimization with multi-agent reinforcement learning and evolutionary strategy: Bridging the gap between micro and macro traffic control. Phys. A Stat. Mech. Its Appl. 2024, 647, 129734. [Google Scholar] [CrossRef]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M. Mainstream traffic flow control on freeways using variable speed limits. Transportes 2014, 21, 56–65. [Google Scholar] [CrossRef]
- Carlson, R.C.; Manolis, D.; Papamichail, I.; Papageorgiou, M. Integrated ramp metering and mainstream traffic flow control on freeways using variable speed limits. Procedia—Soc. Behav. Sci. 2012, 48, 1578–1588. [Google Scholar] [CrossRef]




| Vehicle Type | Length (m) | Accelerate (m/s2) | Decelerate (m/s2) | |
|---|---|---|---|---|
| Car | 5.0 | 2.6 | 4.5 | |
| Container Truck | carry TEU | 10.0 | 1.0 | 2.0 |
| carry FEU | 16.0 | 0.3 | 1.0 | |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| (s) | 30 | (veh/km) | 40 |
| (s) | 3 | (veh/km) | 60 |
| (veh/h) | 3400 | (veh/km) | 90 |
| (veh/h) | 2700 | (veh/km) | 255 |
| (veh/h) | 840 | (km/h) | 20 |
| (veh/h) | 600 | 0.4 |
| Scenario | TTT (min) | TWT (min) | TTS (min) |
|---|---|---|---|
| No-Control | 13,966.0 | 0 | 13,966.0 |
| PI-ALINEA | 6870.4 | 656.0 | 7526.4 (−46.1%) |
| MTFC-FB | 7490.2 | 0 | 7490.2 (−46.4%) |
| Hierarchical Control | 6757.6 | 94.0 | 6851.6 (−50.9%) |
| Scenario | TTT (min) | TWT (min) | TTS (min) |
|---|---|---|---|
| 60%MPR | 7250.5 | 230.6 | 7481.1 |
| 70%MPR | 7093.9 | 288.7 | 7382.6 |
| 80%MPR | 6915.3 | 158.5 | 7073.8 |
| 90%MPR | 6885.1 | 127.4 | 7012.5 |
| 100%MPR | 6757.6 | 94.0 | 6851.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, W.; Yang, H.; Li, M.; Wang, Y.; Zhou, Y.; Zheng, P. Hierarchical Control Based on Ramp Metering and Variable Speed Limit for Port Motorway. Systems 2025, 13, 446. https://doi.org/10.3390/systems13060446
Yue W, Yang H, Li M, Wang Y, Zhou Y, Zheng P. Hierarchical Control Based on Ramp Metering and Variable Speed Limit for Port Motorway. Systems. 2025; 13(6):446. https://doi.org/10.3390/systems13060446
Chicago/Turabian StyleYue, Weiqi, Hang Yang, Meng Li, Yibing Wang, Yusheng Zhou, and Pengjun Zheng. 2025. "Hierarchical Control Based on Ramp Metering and Variable Speed Limit for Port Motorway" Systems 13, no. 6: 446. https://doi.org/10.3390/systems13060446
APA StyleYue, W., Yang, H., Li, M., Wang, Y., Zhou, Y., & Zheng, P. (2025). Hierarchical Control Based on Ramp Metering and Variable Speed Limit for Port Motorway. Systems, 13(6), 446. https://doi.org/10.3390/systems13060446






