An Evolutionary Game Analysis of Carbon Trading Mechanisms for Governments, Farmer Professional Cooperatives and Farmers
Abstract
1. Introduction
2. Materials and Methods
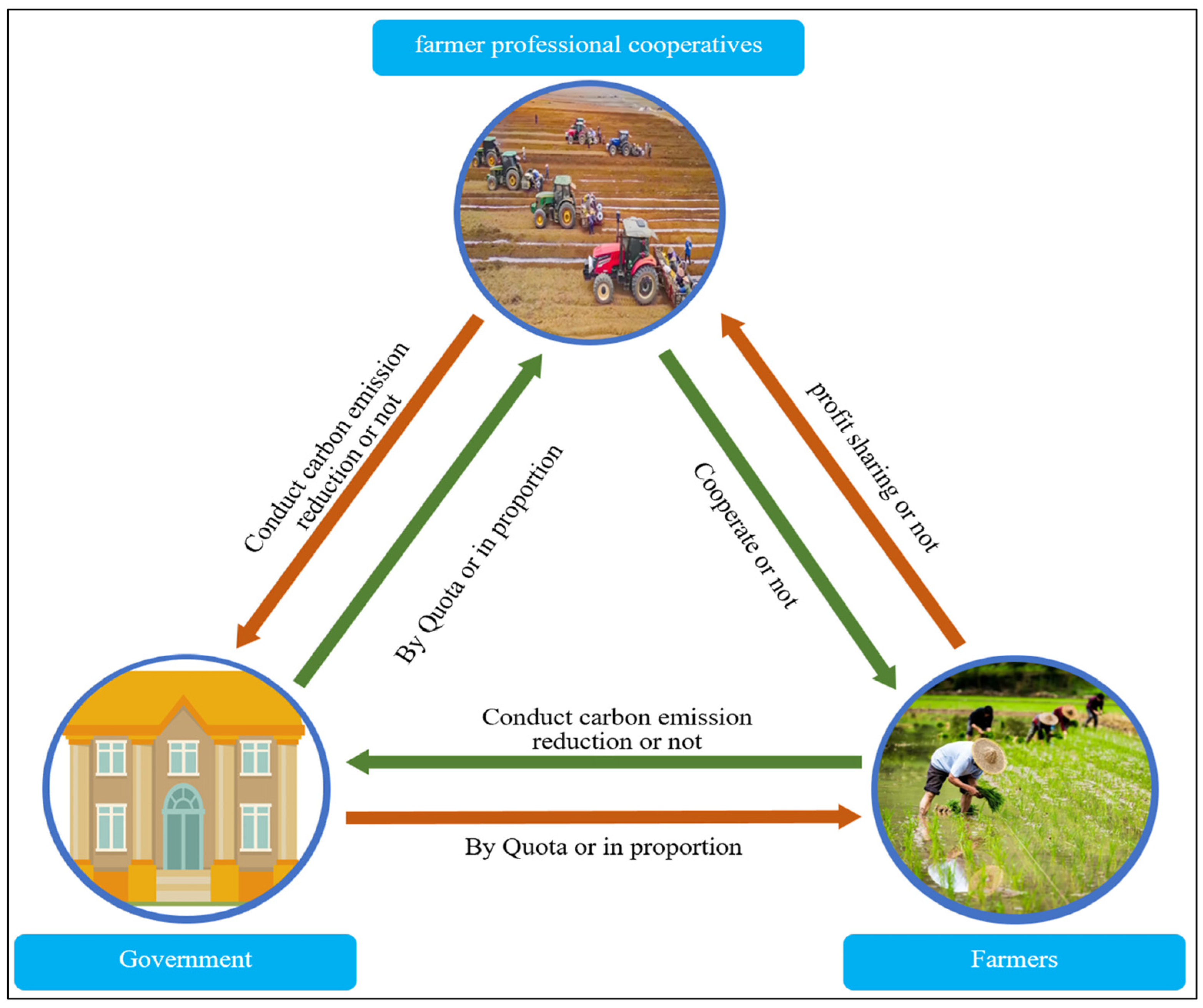
2.1. Problem Description
2.2. Basic Assumptions and Model Parameters
2.3. Model Construction
2.4. Replicative Dynamic Modeling of Subjects
3. Results
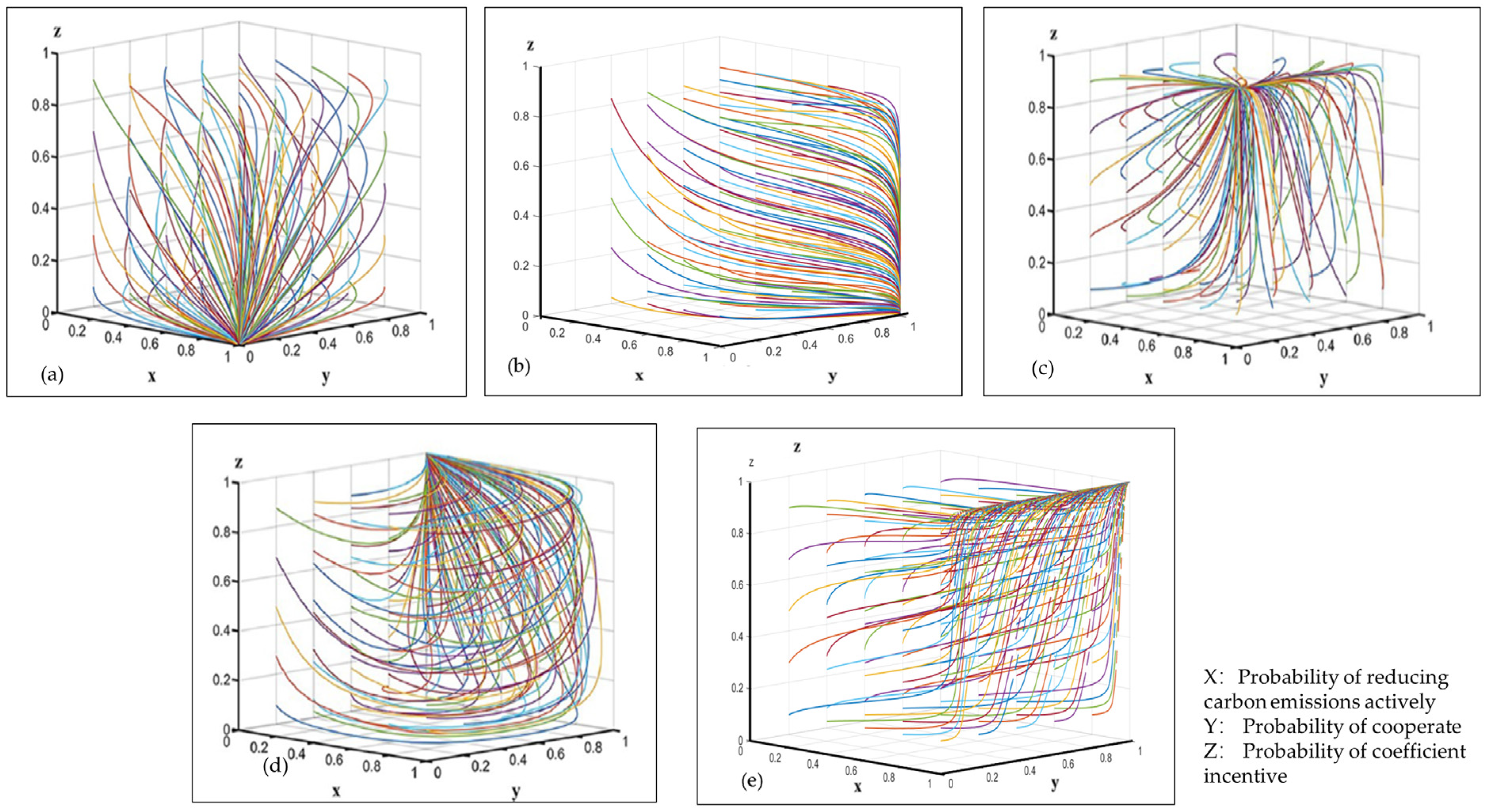
3.1. Equilibrium Points of the Game
3.2. Stability Analysis
4. Numerical Simulation
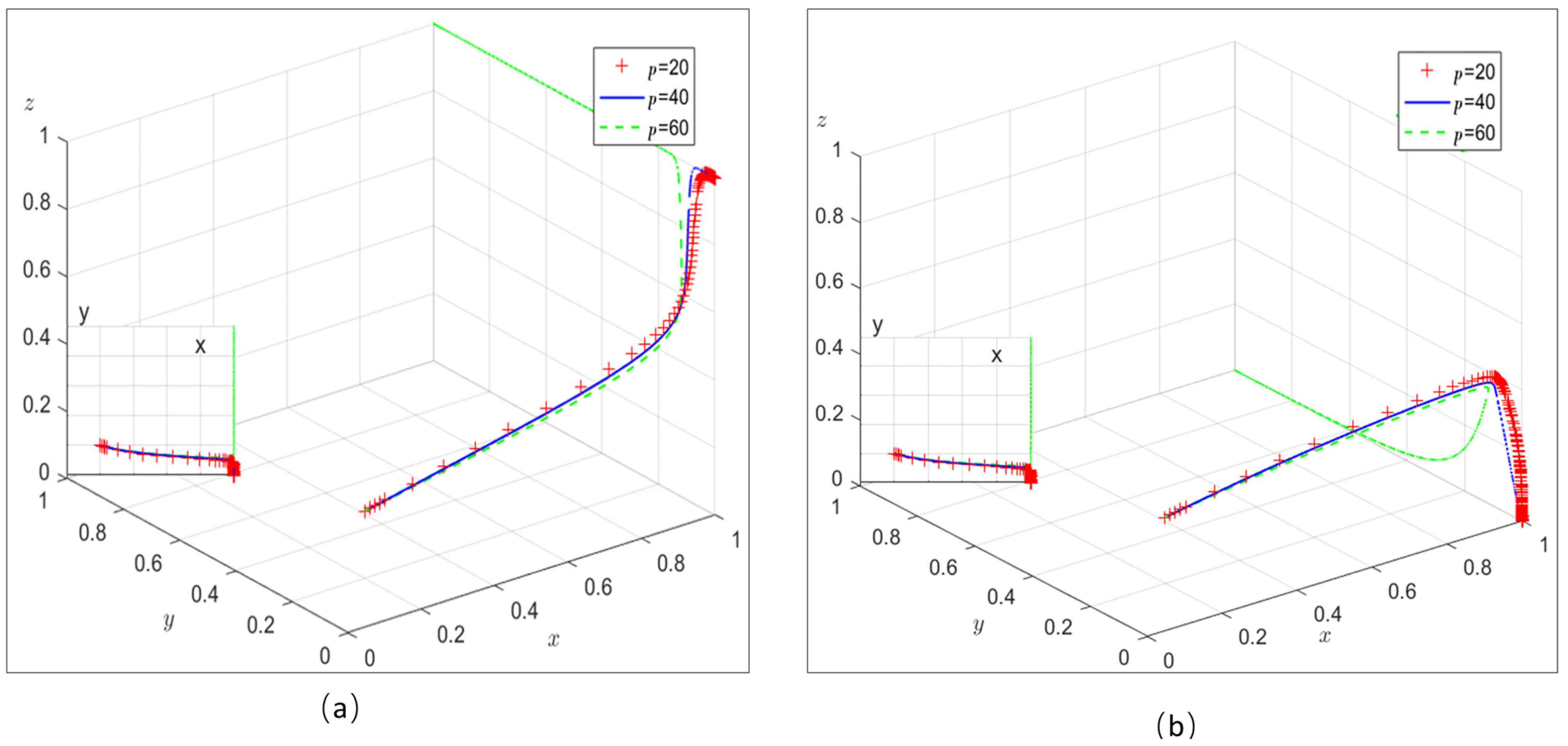
4.1. The Effect of the Carbon Trading Price p on the Evolutionary Outcome
4.2. The Effect of the Reward Coefficient θ on the Evolutionary Outcome
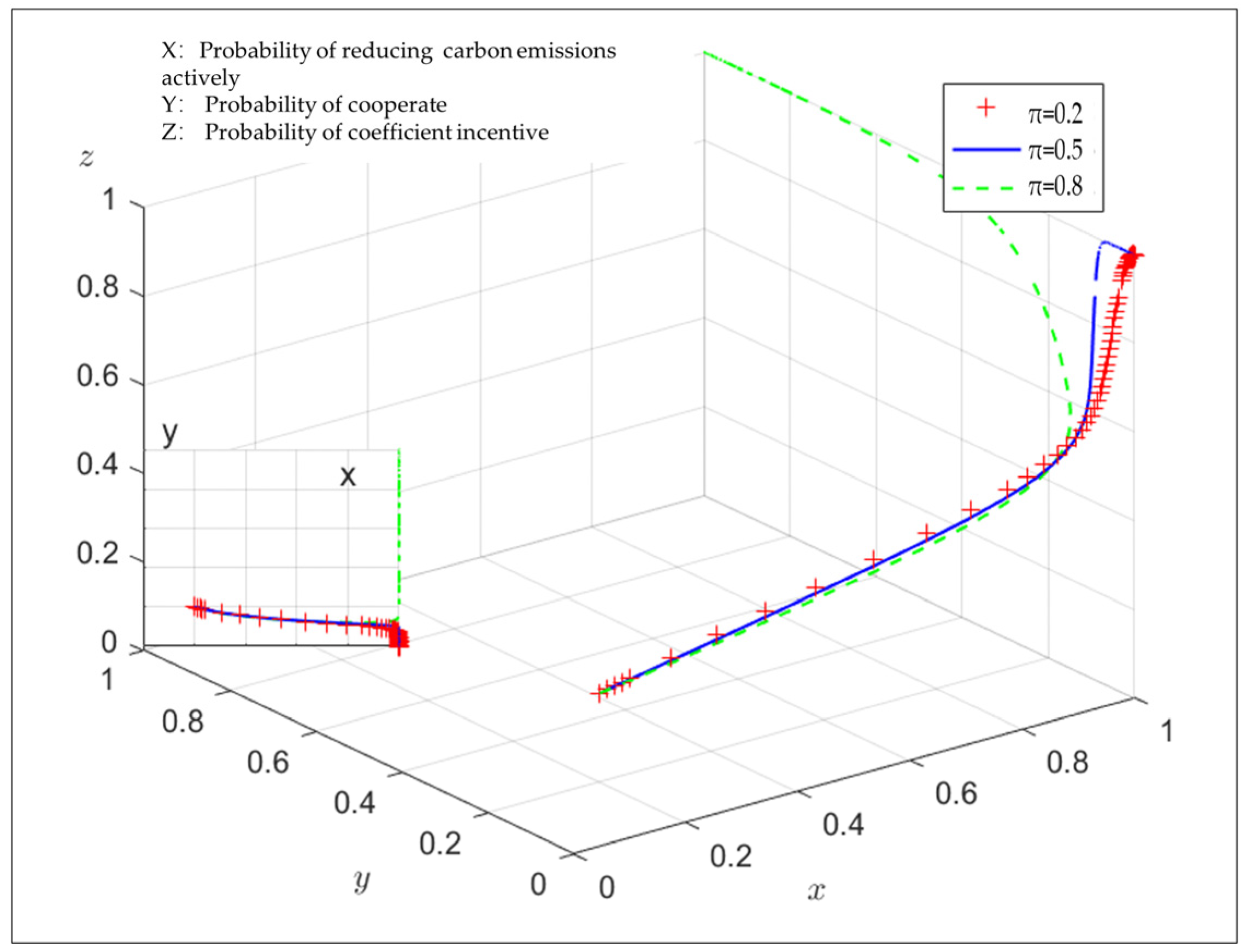
4.3. The Influence of the Income Sharing Ratio π of the Farmer Professional Cooperative on the Evolutionary Results
5. Discussion
5.1. Carbon Price Thresholds and Systemic Feedback
5.2. Revenue Sharing as a Stabilizing Mechanism
5.3. Policy Levers for Systemic Resilience
5.4. Limitations and Future Directions
6. Conclusions and Policy Recommendations
6.1. Conclusions
- The carbon trading mechanism effectively mitigates the negative effect of cost by providing carbon trading income.
- Reasonable regulation of carbon trading prices can promote the participation of farmer professional cooperatives in carbon emission reduction. Carbon prices above 60 CNY/ton enable cooperatives to reduce regional emissions.
- Farmer professional cooperatives play a pivotal role in agricultural carbon emission reduction. By utilizing the advantages of scale economy and technology, they can promote the development of low-carbon agriculture. When the sharing ratio increases from 20% to 80%, farmers gain additional benefits by cooperating with the farmer professional cooperative and adopting emission reduction strategies.
6.2. Policy Implication
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Detailed Replicator Dynamics Derivation
References
- Black, H.; Reed, M.S.; Kendall, H.; Parkhurst, R.; Cannon, N.; Chapman, P.J.; Orman, M.; Phelps, J.; Rudman, H.; Whaley, S.; et al. What Makes an Operational Farm Soil Carbon Code? Insights from a Global Comparison of Existing Soil Carbon Codes Using a Structured Analytical Framework. Carbon Manag. 2022, 13, 554–580. [Google Scholar] [CrossRef]
- De Cara, S.; Vermont, B. Policy Considerations for Mandating Agriculture in a Greenhouse Gas Emissions Trading Scheme: A Comment. Appl. Econ. Perspect. Policy 2011, 33, 661–667. Available online: https://www.jstor.org/stable/41336229 (accessed on 20 March 2024). [CrossRef]
- Zhang, C.C.; Lin, B.Q. Impact of Introducing Chinese Certified Emission Reduction Scheme to the Carbon Market: Promoting Renewable Energy. Renew. Energy 2024, 222, 119887. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Liu, J.Y.; Woodward, R.T. Has Chinese Certified Emission Reduction Trading Reduced Rural Poverty in China? Aust. J. Agric. Resour. Econ. 2023, 67, 438–458. [Google Scholar] [CrossRef]
- Ma, M.L.; Lin, J.; Sexton, R.J. The Transition from Small to Large Farms in Developing Economies: A Welfare Analysis. Am. J. Agric. Econ. 2021, 104, 111–133. [Google Scholar] [CrossRef]
- Liang, Q.; Hendrikse, G.; Huang, Z.; Xu, X.C. Governance Structure of Chinese Farmer Cooperatives: Evidence from Zhejiang Province. Agribusiness 2015, 31, 198–214. [Google Scholar] [CrossRef]
- Ji, C.; Jin, S.Q.; Wang, H.T.; Ye, C.H. Estimating Effects of Cooperative Membership on Farmers’ Safe Production Behaviors: Evidence from Pig Sector in China. Food Policy 2019, 83, 231–245. [Google Scholar] [CrossRef]
- Yu, L.; Chen, C.; Niu, Z.; Gao, Y.; Yang, H.; Xue, Z. Risk Aversion, Cooperative Membership and the Adoption of Green Control Techniques: Evidence from China. J. Clean. Prod. 2021, 279, 123288. [Google Scholar] [CrossRef]
- Sambuo, D. Co-operatology and the Science of Cooperative Societies: A Synthetic Review of Research on Cooperative Evolution. J. Coop. Organ. Manag. 2023, 11, 100190. [Google Scholar] [CrossRef]
- Verhofstadt, E.; Maertens, M. Can Agricultural Cooperatives Reduce Poverty? Heterogeneous Impact of Cooperative Membership on Farmers’ Welfare in Rwanda. Appl. Econ. Perspect. Policy 2015, 37, 86–106. [Google Scholar] [CrossRef]
- Liu, J.Z.; Yang, M.W.; Zhang, Z.Y. Can Rural Cooperatives Reduce Poverty Vulnerability of Smallholder Households? Evidence from Rural Western China. Front. Sustain. Food Syst. 2023, 7, 1222455. [Google Scholar] [CrossRef]
- Zheng, H.; Vatsa, P.; Ma, W.; Rahut, D.B. Does Agricultural Cooperative Membership Influence Off-Farm Work Decisions of Farm Couples? Ann. Public Coop. Econ. 2023, 94, 831–855. [Google Scholar] [CrossRef]
- Das, K.; Mahanta, A. Rural Non-Farm Employment Diversification in India: The Role of Gender, Education, Caste and Land Ownership. Int. J. Soc. Econ. 2023, 50, 741–765. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Shi, K.Y.; Liu, Z.Q.; Qiu, L.; Wang, Y.; Liu, H.; Fu, X.H. The Effect of Technical Training Provided by Agricultural Cooperatives on Farmers’ Adoption of Organic Fertilizers in China: Based on the Mediation Role of Ability and Perception. Int. J. Environ. Res. Public Health 2022, 19, 14277. [Google Scholar] [CrossRef]
- Khan, N.; Ray, R.L.; Kassem, H.S.; Ihtisham, M.; Siddiqui, B.N.; Zhang, S. Can Cooperative Supports and Adoption of Improved Technologies Help Increase Agricultural Income? Evidence from a Recent Study. Land 2022, 11, 361. [Google Scholar] [CrossRef]
- Xin, Y.L.; Xu, Y.Q.; Zheng, Y. A Study on Green Agricultural Production Decision-Making by Agricultural Cooperatives under Government Subsidies. Sustainability 2024, 16, 1219. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, Y.; Wang, W. Risk Assessment of Biological Asset Mortgage Loans of China’s New Agricultural Business Entities. Complexity 2020, 2020, 8865840. [Google Scholar] [CrossRef]
- Zhu, M.L.; Zhu, H. Efficiency of Decisions under Membership Heterogeneity and Government Regulations: Insights from Farmer Cooperatives in China. Econ. Dev. Cult. Change 2020, 68, 1009–1040. [Google Scholar] [CrossRef]
- Mei, L.; Zheng, Y.; Tian, M.; Wu, Y. Driven by the Policy or Bent by the Market? Cracking the Digital Transformation Code of Farmer Cooperatives. Technol. Forecast. Soc. Chang. 2024, 208, 123659. [Google Scholar] [CrossRef]
- Becot, F.A.; Inwood, S.; Contzen, S.; Budge, H.; Reusch, M.; Kroeplin, A. New Insights on the Role of the Farm Household-Farm Operation Interface in Family Farm Persistence and a Call for Future Research. J. Rural Stud. 2024, 112, 103449. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, T. The Effects of Farmer Cooperatives on Agricultural Carbon Emissions Reduction: Evidence from Rural China. J. Clean. Prod. 2024, 450, 141881. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Z.; Ma, W.; Valentinov, V.J. The Effect of Cooperative Membership on Agricultural Technology Adoption in Sichuan, China. China Econ. Rev. 2020, 62, 101334. [Google Scholar] [CrossRef]
- Zhong, Z.; Jiang, W.Y.; Li, Y.H. Bridging the Gap Between Smallholders and Modern Agriculture: Full Insight into China’s Agricultural Cooperatives. J. Rural Stud. 2023, 101, 103037. [Google Scholar] [CrossRef]
- Abate, G.T. Drivers of Agricultural Cooperative Formation and Farmers’ Membership and Patronage Decisions in Ethiopia. J. Coop. Organ. Manag. 2018, 6, 53–63. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, M.; Wang, K.; Wen, F.; Liu, F. The Carbon Emissions Reduction Effect of Green Agricultural Subsidy Policy: A Quasi-Natural Experiment. Sustainability 2024, 16, 5210. [Google Scholar] [CrossRef]
- Yao, J. The Synergistic Effect of the Carbon Emission Trading Scheme on Pollution and Carbon Reduction in China’s Power Industry. Sustainability 2024, 16, 8681. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Zhao, X.; Zhang, L.; Yuan, K. Estimating Effects of Cooperative Membership on Farmers’ Safe Production Behaviors: Evidence from the Rice Sector in China. Environ. Sci. Pollut. Res. 2021, 28, 25400–25418. [Google Scholar] [CrossRef]
- Feng, J.; Yang, D. Optimal Operation of Agricultural Park Considering Carbon-Green Certificate Joint Trading and Demand Response. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024. [Google Scholar] [CrossRef]
- Zheng, Q.; Liu, J.; Sun, H. Economic and Carbon Emission Performance of Green Farming by Marketing Cooperatives. Heliyon 2023, 9, e15913. [Google Scholar] [CrossRef]
- Radov, D.; Klevnas, P.; Skurray, J. Market Mechanisms for Reducing GHG Emissions from Agriculture, Forestry and Land Management. 2007. Available online: https://www.semanticscholar.org/paper/Market-mechanisms-for-reducing-GHG-emissions-from-Radov-Klevnas/cfd84ead4c3864d6d5116bf67a3fca84825cec20 (accessed on 20 May 2024).
- Hou, S.; Chen, M.; Tao, S.; Li, P.; He, Y. Regional Heterogeneity of Agricultural Carbon Emission Reduction Potential in China. Environ. Eng. Res. 2024, 29, 230399. [Google Scholar] [CrossRef]
- Han, F.; Hu, W.; Zheng, J.; Feng, D.; Zhang, X. Estimating Soil Organic Carbon Storage and Distribution in a Catchment of Loess Plateau, China. Geoderma 2010, 154, 261–266. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, Y.; Guo, S. The Evolutionary Game Analysis of Multiple Stakeholders in the Low-Carbon Agricultural Innovation Diffusion. Complexity 2020, 2020, 6309545. [Google Scholar] [CrossRef]
- Luo, J.; Huang, M.; Bai, Y. Promoting Green Development of Agriculture Based on Low-Carbon Policies and Green Preferences: An Evolutionary Game Analysis. Environ. Dev. Sustain. 2024, 26, 6443–6470. [Google Scholar] [CrossRef]
- Dong, J.; Chen, J.; Zhang, Y.; Cong, L.; Dean, D.; Wu, Q. Examining the Value Realization of Ecological Agricultural Products in China: A Tripartite Evolutionary Game Analysis. J. Environ. Manag. 2025, 374, 124134. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Su, Y.; Li, F. The Evolutionary Game Analysis of Low Carbon Production Behaviour of Farmers, Government and Consumers in Food Safety Source Governance. Int. J. Environ. Res. Public Health 2022, 19, 12211. [Google Scholar] [CrossRef]
- Luo, J.; Hu, M.; Huang, M.; Bai, Y. How Does Innovation Consortium Promote Low-Carbon Agricultural Technology Innovation: An Evolutionary Game Analysis. J. Clean. Prod. 2023, 384, 135564. [Google Scholar] [CrossRef]
- Zou, B.; Ju, C.; Bao, F.; Lai, Y.; Xu, C.; Zhu, Y. Exploring an efficient evolutionary game model for the government–Enterprise–Public during the double carbon policy in China. Int. J. Environ. Res. Public Health 2022, 19, 4607. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, J. The relationship among government, enterprise, and public in environmental governance from the perspective of multi-player evolutionary game. Int. J. Environ. Res. Public Health 2019, 16, 3351. [Google Scholar] [CrossRef]
- Zou, C.; Huang, Y.; Hu, S.; Huang, Z. Government participation in low—Carbon technology transfer: An evolutionary game study. Technol. Forecast. Soc. Chang. 2023, 188, 122320. [Google Scholar] [CrossRef]
- Sun, H.; Gao, G.; Li, Z. Evolutionary Game Analysis of Enterprise Carbon Emission Regulation Based on Prospect Theory. Soft Comput. 2022, 26, 13357–13368. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C. Agricultural Manufacturers’ Carbon Abatement Oriented to Government Subsidy and Sales Efforts. Environ. Dev. Sustain. 2024, 26, 4335–4363. [Google Scholar] [CrossRef]
- Weinstein, M.I. Lyapunov Stability of Ground States of Nonlinear Dispersive Evolution Equations. Commun. Pure Appl. Math. 2010, 39, 51–67. [Google Scholar] [CrossRef]
- Cui, B.; Shui, Z.; Yang, S.; Lei, T. Evolutionary Game Analysis of Green Technology Innovation under the Carbon Emission Trading Mechanism. Front. Environ. Sci. 2022, 10, 997724. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Huang, P.F.; Liu, Z.X. Predictive Approach for Sensorless Bimanual Teleoperation under Random Time Delays with Adaptive Fuzzy Control. IEEE Trans. Ind. Electron. 2018, 65, 2439–2448. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Hao, J.Q.; Cao, C.J.; Han, H.S. Evolutionary Game Analysis of Three-Player for Low-Carbon Production Capacity Sharing. Sustainability 2019, 11, 2996. [Google Scholar] [CrossRef]

| Parameters | Instructions |
|---|---|
| C | The cost of the government choosing the incentive policy |
| F1 | The fine to the farmer professional cooperative when the government chooses the quota incentive policy |
| F2 | The fine to the farmers when the government chooses the quota incentive policy |
| I1 | The subsidy to the farmer professional cooperative when the government chooses the quota incentive policy |
| I2 | The subsidy to the farmers when the government chooses the quota incentive policy |
| ε1 | The fine coefficient of the government to the farmer professional cooperative under the coefficient incentive policy |
| ε2 | The fine coefficient of the government to the farmers under the coefficient incentive policy |
| θ1 | The subsidy coefficient of the government to the farmer professional cooperative under the coefficient incentive policy |
| θ2 | The subsidy coefficient of the government to farmers under the coefficient incentive policy |
| e0 | The fixed quota of carbon emissions which is given by the government to the farmer professional cooperative |
| e01 | The fixed quota of carbon emissions which is given by the government to farmers |
| eh | The carbon emission amount of the farmer professional cooperative that does not actively reduce carbon emissions |
| eh1 | The carbon emission amount of the farmers who do not actively reduce carbon emissions |
| ej | The carbon emission amount of the farmer professional cooperative that actively reduces carbon emissions |
| ej1 | The carbon emission amount of the farmers who actively reduce carbon emissions |
| C1 | Research and development funds needed by the farmer professional cooperative to actively reduce carbon emissions |
| C2 | Research and development funds needed by the farmer professional cooperative not to actively reduce carbon emissions |
| C3 | Funds needed for farmers to upgrade their own technologies for carbon emission reduction |
| C4 | Funds needed for farmers to cooperate with the farmer professional cooperative to upgrade their own technologies fpr carbon emission reduction |
| α | The proportion of carbon trading income the farmer professional cooperatives share with farmers |
| p | The CCER trading price |
| γ | The coefficient of the government’s carbon trading fee |
| W | The increasing income of the farmer professional cooperative when the farmers cooperate |
| π | The proportion of the increasing benefits of the farmer professional cooperative shared with the farmers when they cooperate |
| Farmers | Government | |||
|---|---|---|---|---|
| Coefficient Incentive (z) | Quota Incentive (1 − z) | |||
| Farmer professional cooperatives | Reducing carbon emissions actively (x) | Cooperate (y) | ||
| Non-cooperate (1 − y) | ||||
| Reducing carbon emissions inactively (1 − x) | Cooperate (y) | |||
| Non-cooperate (1 − y) | ( | |||
| Equilibrium Points | Eigenvalues |
|---|---|
| E1(0,0,0) | , , |
| E2(1,0,0) | , , |
| E3(1,1,0) | , , |
| E4(1,0,1) | , , |
| E5(0,1,0) | , , |
| E6(0,1,1) | , , |
| E7(0,0,1) | , , |
| E8(1,1,1) | , , |
| Equilibrium Points | Symbol | Stability | Conditions |
|---|---|---|---|
| E1(0,0,0) | (+, N, N) | Saddle/Unstable | Null |
| E2(1,0,0) | (−, −, −) | ESS | condition1: ① ② ③ |
| E3(1,1,0) | (−, −, −) | ESS | condition2: ① ② ③ |
| E4(1,0,1) | (−, −, −) | ESS | condition3: ① ② ③ |
| E5(0,1,0) | (+, N, N) | Unstable | Null |
| E6(0,1,1) | (−, −, −) | ESS | Condition 4: ① ② ③ , |
| E7(0,0,1) | (N, +, N) | Unstable | Null |
| E8(1,1,1) | (−, −, −) | ESS | Condition 5: ① ② ③ |
| Parameter | F1 (CNY) | F2 (CNY) | ε1 (CNY) | ε2 (CNY) | θ1 (CNY) | θ2 (CNY) | e0 (tCO₂e) | e01 (tCO₂e) | eh (tCO₂e) |
|---|---|---|---|---|---|---|---|---|---|
| numerical value | 200 | 50 | 90 | 30 | 15 | 5 | 25 | 10 | 30 |
| Parameter | eh1 (tCO₂e) | ej (tCO₂e) | ej1 (tCO₂e) | C1 (CNY) | C2 (CNY) | C3 (CNY) | C4 (CNY) | A (100%) | W (CNY) |
| numerical value | 15 | 20 | 5 | 200 | 50 | 100 | 20 | 0.5 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Q.; Li, H.; Cannon, N.; Chang, X.; Feng, J. An Evolutionary Game Analysis of Carbon Trading Mechanisms for Governments, Farmer Professional Cooperatives and Farmers. Systems 2025, 13, 413. https://doi.org/10.3390/systems13060413
Chu Q, Li H, Cannon N, Chang X, Feng J. An Evolutionary Game Analysis of Carbon Trading Mechanisms for Governments, Farmer Professional Cooperatives and Farmers. Systems. 2025; 13(6):413. https://doi.org/10.3390/systems13060413
Chicago/Turabian StyleChu, Qianqian, Haoyang Li, Nicola Cannon, Xianmin Chang, and Jian Feng. 2025. "An Evolutionary Game Analysis of Carbon Trading Mechanisms for Governments, Farmer Professional Cooperatives and Farmers" Systems 13, no. 6: 413. https://doi.org/10.3390/systems13060413
APA StyleChu, Q., Li, H., Cannon, N., Chang, X., & Feng, J. (2025). An Evolutionary Game Analysis of Carbon Trading Mechanisms for Governments, Farmer Professional Cooperatives and Farmers. Systems, 13(6), 413. https://doi.org/10.3390/systems13060413






