Emission Reduction Decisions in the Agricultural Supply Chain Considering Dual Fairness Concerns
Abstract
1. Introduction
2. Mathematical Model
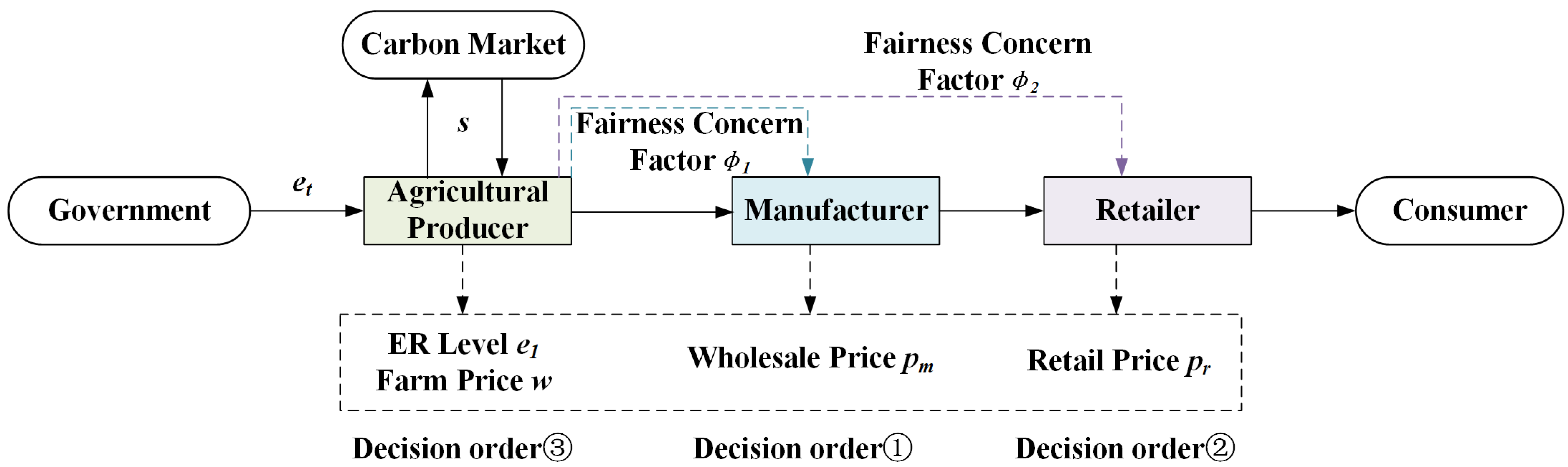
2.1. Problem Description
- (1)
- The manufacturer first sets the wholesale price;
- (2)
- The retailer then determines the optimal retail price based on the wholesale price;
- (3)
- Finally, the agricultural producer decides the ER level and the farmgate price based on the preceding decisions of the manufacturer and retailer.
2.2. Centralized Model ()
2.3. Decentralized Model Without Fairness Concerns ()
2.4. Decentralized Model with Fairness Concerns ()
3. Model Analysis
3.1. Profits
3.2. ER Level and Market Demand
3.3. Fairness Concern Intensity
4. Numerical Experiments
4.1. Main Results
- (1)
- Comparison of ER levels and profits under centralized vs. decentralized models
- (2)
- Differential impact of fairness concerns on the participants’ profits
- (3)
- Impact of ER costs and carbon quotas on ER levels and profits
4.2. Sensitivity Analysis
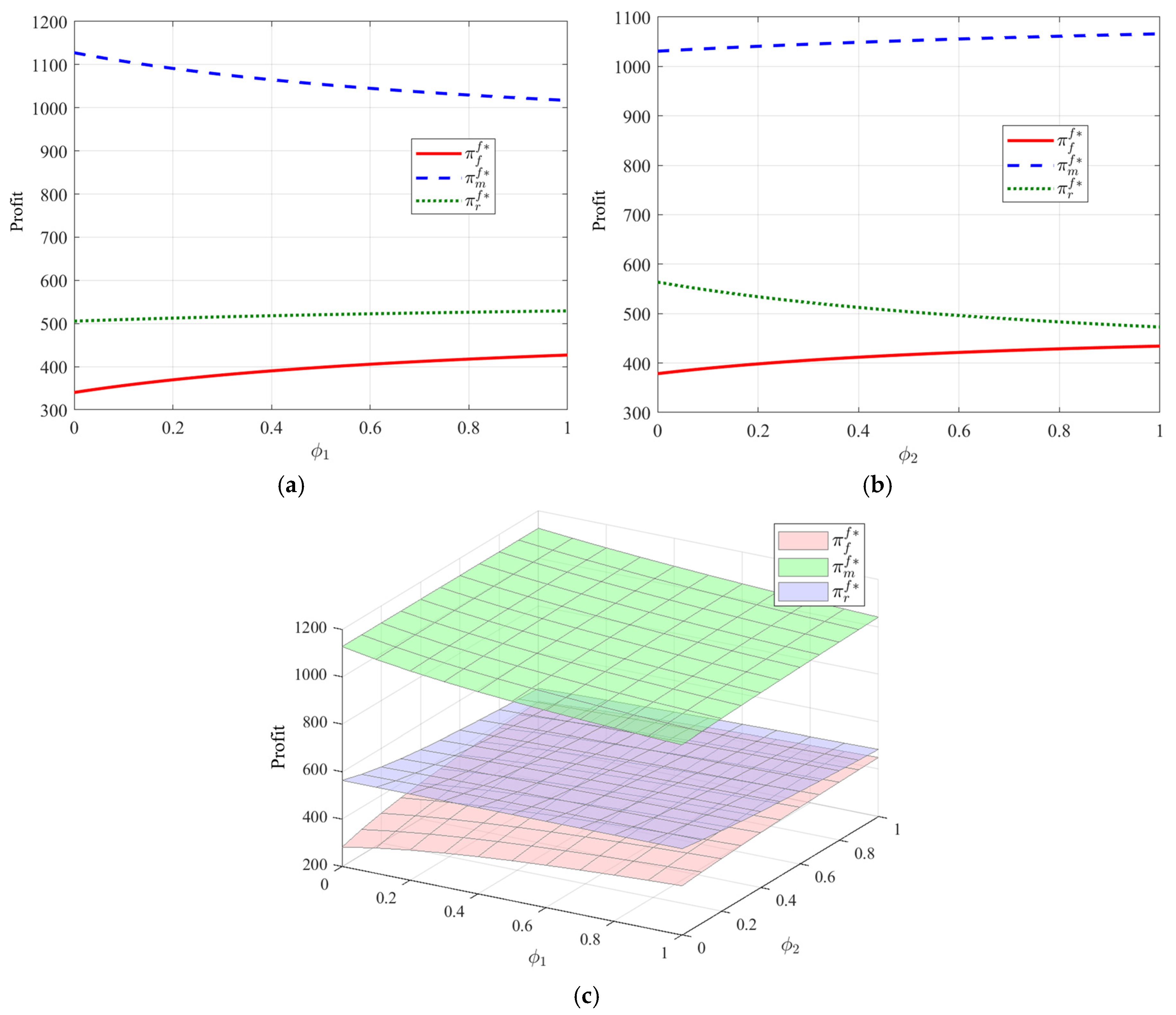
- (1)
- Impact of fairness concerns on participants’ profits
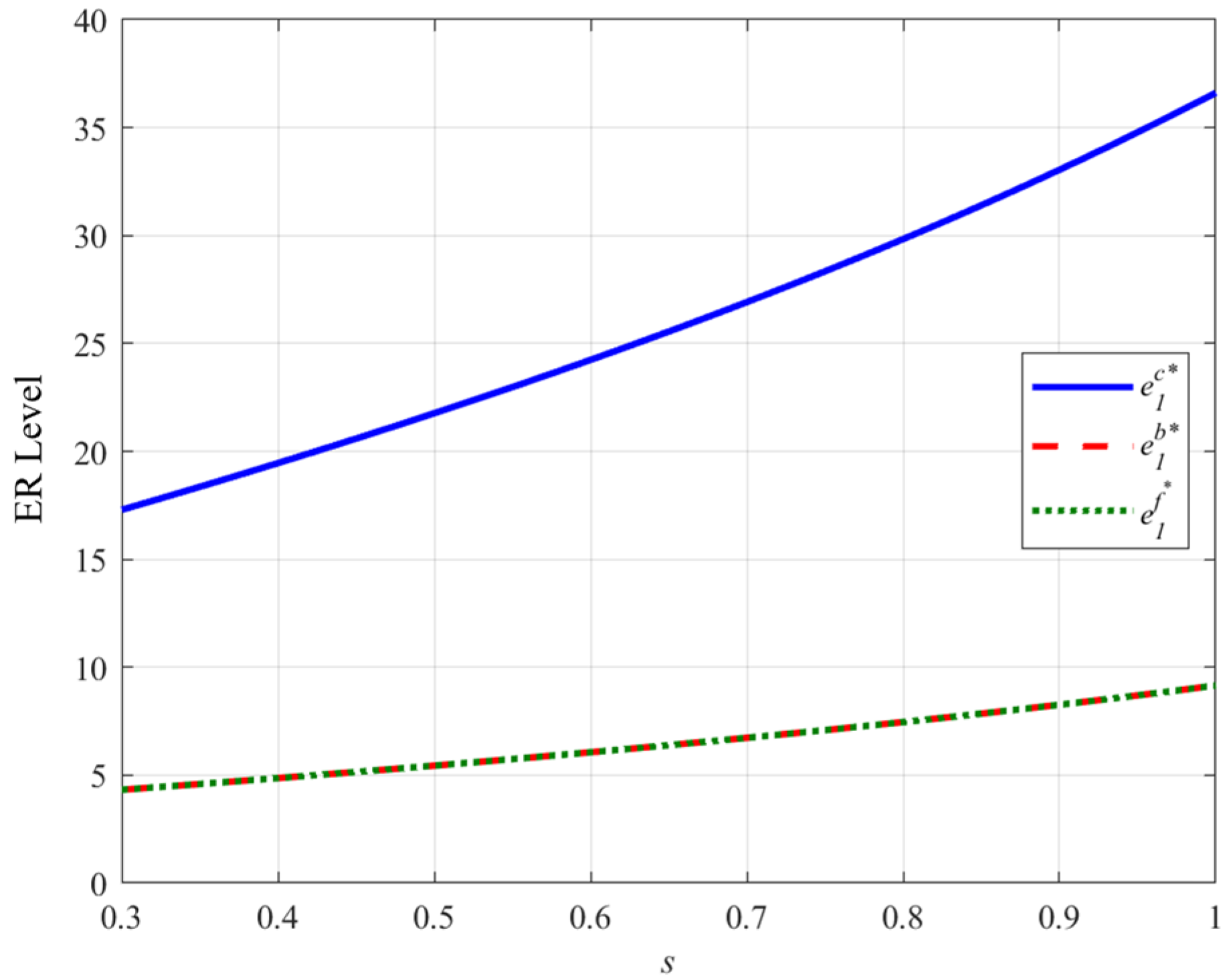
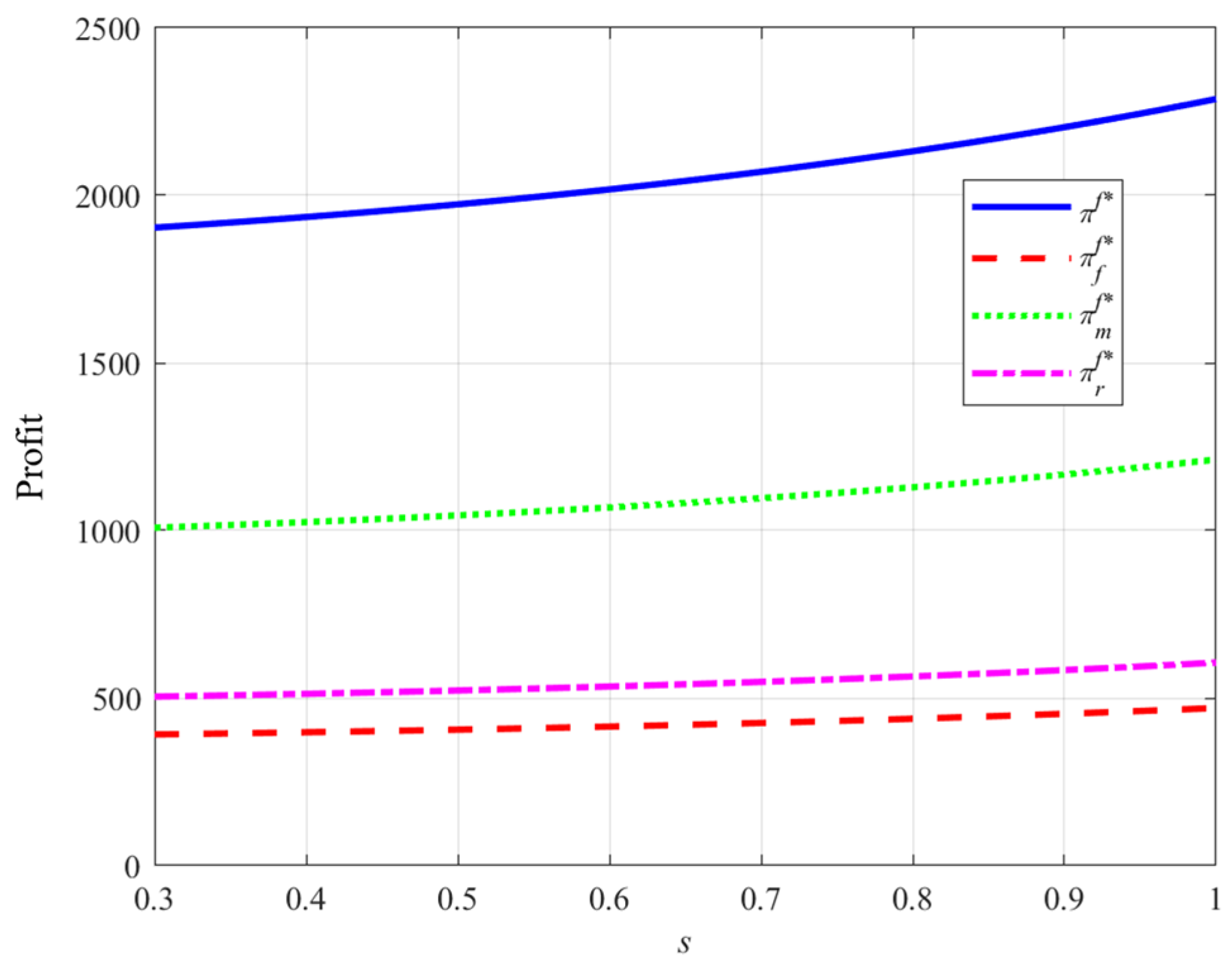
- (2)
- Impact of carbon trading prices on the ER levels and profits
5. Managerial Implications
- (1)
- Promoting centralized decision-making to improve efficiency
- (2)
- Addressing fairness issues to stabilize profit distribution
- (3)
- Enhancing ER level and market demand
- (4)
- Strategic response to the intensity of fairness concern
- (5)
- Policy and industry recommendations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FAO | Food and Agriculture Organization |
| ER | Emission Reduction |
Appendix A. Proofs
- 1.
- Centralized Model Solution
- 2.
- Decentralized Model Solution without Fairness Concerns
- (1)
- Third Stage: Agricultural Producer Decides Farmgate Price and ER Level
- Substitute Equations (1) and (7) into Equation (2) to obtain the agricultural producer’s profit function:
- (2)
- Second Stage: Retailer Decides Unit Profit
- (3)
- First Stage: Manufacturer Decides Unit Profit
- 3.
- Decentralized Model Solution with Fairness Concerns
- (1)
- Third Stage: Agricultural Producer Decides Farmgate Price and ER Level
- (2)
- Second Stage: Retailer Decides Unit Profit
- (3)
- First Stage: Manufacturer Decides Unit Profit
- 4.
- Proof of Proposition 1
- 5.
- Proof of Adjusting Farmgate Price
- 6.
- Proof of Proposition 2
- 7.
- Proof of Proposition 3
- Since , and , by observation, we can see that and .
- 8.
- Proof of Proposition 4
- 9.
- Proof of Proposition 5
- 10.
- Impact of Emission Reduction Cost Coefficient
- (i)
- Centralized model
- (ii)
- Decentralized model without fairness concerns
- (iii)
- Decentralized model with fairness concerns
- 11.
- Impact of Government-Provided Free Carbon Allowances
- (i)
- Centralized model
- (ii)
- Decentralized model without fairness concerns
- (iii)
- Decentralized model with fairness concerns
References
- Costa, C.; Wollenberg, E.; Benitez, M.; Newman, R.; Gardner, N.; Bellone, F. Roadmap for Achieving Net-Zero Emissions in Global Food Systems by 2050. Sci. Rep. 2022, 12, 15064. [Google Scholar] [CrossRef]
- FAO Greenhouse Gas Emissions from Agrifood Systems: Global, Regional and Country Trends, 2000–2020; FAO: Rome, Italy, 2022.
- Wang, H.; Fan, X.; Guo, J.; Zhao, Q.; Dai, Z. Towards Sustainable Beef: The Role of Altruistic Preference in the Value Chain Transformation. Food Policy 2024, 127, 102687. [Google Scholar] [CrossRef]
- Bolotova, Y.V. Competition Issues in the U.S. Beef Industry. Appl. Econ. Perspect. Policy 2022, 44, 1340–1358. [Google Scholar] [CrossRef]
- Fischer, B.L.; Outlaw, J.L.; Anderson, D.P. The U.S. Beef Supply Chain: Issues and Challenges Proceedings of a Workshop on Cattle Markets; Agricultural and Food Policy Center, Texas A&M University: Kansas City, MO, USA, 2021. [Google Scholar]
- Pannell, D.J.; Crawford, M. Challenges in Making Soil-Carbon Sequestration a Worthwhile Policy. Farm Policy J. 2022, FPJ1901. [Google Scholar]
- Buck, H.J.; Palumbo-Compton, A. Soil Carbon Sequestration as a Climate Strategy: What Do Farmers Think? Biogeochemistry 2022, 161, 59–70. [Google Scholar] [CrossRef]
- Thamo, T.; Pannell, D.J. Challenges in Developing Effective Policy for Soil Carbon Sequestration: Perspectives on Additionality, Leakage, and Permanence. Clim. Policy 2016, 16, 973–992. [Google Scholar] [CrossRef]
- Wreford, A.; Ignaciuk, A.; Gruère, G. Overcoming Barriers to the Adoption of Climate-Friendly Practices in Agriculture; OECD: Paris, France, 2017. [Google Scholar]
- Li, X.; Jensen, K.L.; Clark, C.D.; Lambert, D.M. Consumer Willingness to Pay for Beef Grown Using Climate Friendly Production Practices. Food Policy 2016, 64, 93–106. [Google Scholar] [CrossRef]
- Katare, B.; Yim, H.; Byrne, A.; Wang, H.H.; Wetzstein, M. Consumer Willingness to Pay for Environmentally Sustainable Meat and a Plant-Based Meat Substitute. Appl. Econ. Perspect. Policy 2023, 45, 145–163. [Google Scholar] [CrossRef]
- USDA ERS. Food Dollar Series. Available online: https://www.ers.usda.gov/data-products/food-dollar-series/ (accessed on 5 April 2023).
- Wang, H.; Fan, X.; Zhao, Q.; Cui, P. Emissions Reduction Strategy in a Three-Stage Agrifood Value Chain: A Dynamic Differential Game Approach. PLoS ONE 2023, 18, e0294472. [Google Scholar] [CrossRef]
- Leahy, S.; Clark, H.; Reisinger, A. Challenges and Prospects for Agricultural Greenhouse Gas Mitigation Pathways Consistent with the Paris Agreement. Front. Sustain. Food Syst. 2020, 4, 69. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, M.; Chen, X.; Xu, X. Co-Op Advertising and Emission Reduction Cost Sharing Contracts and Coordination in Low-Carbon Supply Chain Based on Fairness Concerns. J. Clean. Prod. 2016, 133, 402–413. [Google Scholar] [CrossRef]
- Barling, D.; Samoggia, A.; Olafsdottir, G. Dynamics of Food Value Chains: Resilience, Fairness and Sustainability. Agriculture 2022, 12, 720. [Google Scholar] [CrossRef]
- Duffy, R.; Fearne, A.; Hornibrook, S. Measuring Distributive and Procedural Justice: An Exploratory Investigation of the Fairness of Retailer-Supplier Relationships in the Uk Food Industry. Br. Food J. 2003, 105, 682–694. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, T.; Qiu, Y. Price and Carbon Emission Reduction Decisions and Revenue-Sharing Contract Considering Fairness Concerns. J. Clean. Prod. 2018, 190, 303–314. [Google Scholar] [CrossRef]
- Zhang, L.; Xue, B.; Liu, X. Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies. Sustainability 2018, 10, 1209. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Cheng, T.C.E.; Zhou, R.; Gao, J. Decision and Coordination of E-Commerce Closed-Loop Supply Chains with Fairness Concern. Transp. Res. Part E. Logist. Transp. Rev. 2023, 173, 103092. [Google Scholar] [CrossRef]
- Sharma, A.; Dwivedi, G.; Singh, A. Game-Theoretic Analysis of a Two-Echelon Supply Chain with Option Contract under Fairness Concerns. Comput. Ind. Eng. 2019, 137, 106096. [Google Scholar] [CrossRef]
- Pan, K.; Cui, Z.; Xing, A.; Lu, Q. Impact of Fairness Concern on Retailer-Dominated Supply Chain. Comput. Ind. Eng. 2020, 139, 106209. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Shen, L. Study on the Decision-Making and Coordination of an e-Commerce Supply Chain with Manufacturer Fairness Concerns. Int. J. Prod. Res. 2019, 57, 2788–2808. [Google Scholar] [CrossRef]
- Wang, Y.; Su, M.; Shen, L.; Tang, R. Decision-Making of Closed-Loop Supply Chain under Corporate Social Responsibility and Fairness Concerns. J. Clean. Prod. 2021, 284, 125373. [Google Scholar] [CrossRef]
- Yoshihara, R.; Matsubayashi, N. Channel Coordination between Manufacturers and Competing Retailers with Fairness Concerns. Eur. J. Oper. Res. 2021, 290, 546–555. [Google Scholar] [CrossRef]
- Xue, C.; Wu, Y.D.; Zhu, W.; Zhao, X.; Chen, J. Mitigating Behavioral Supply Risk under Dual Sourcing: Evidence from an Order Allocation Game. Prod. Oper. Manag. 2022, 31, 1788–1801. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, X.; Shen, Z. Risk Mitigation Benefit from Backup Suppliers in the Presence of the Horizontal Fairness Concern. Decis. Sci. 2015, 46, 663–696. [Google Scholar] [CrossRef]
- Zhao, D.; Zhang, X.; Ren, T.; Fu, H. Optimal Pricing Strategies in a Product and Service Supply Chain with Extended Warranty Service Competition Considering Retailer Fairness Concern. Math. Probl. Eng. 2019, 2019, 8657463. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Shi, T.; Jiao, W. Green Product Design with Competition and Fairness Concerns in the Circular Economy Era. Int. J. Prod. Res. 2020, 58, 165–179. [Google Scholar] [CrossRef]
- Xiao, Q.; Chen, L.; Xie, M.; Wang, C. Optimal Contract Design in Sustainable Supply Chain: Interactive Impacts of Fairness Concern and Overconfidence. J. Oper. Res. Soc. 2021, 72, 1505–1524. [Google Scholar] [CrossRef]
- Li, G.; Reimann, M.; Zhang, W. When Remanufacturing Meets Product Quality Improvement: The Impact of Production Cost. Eur. J. Oper. Res. 2018, 271, 913–925. [Google Scholar] [CrossRef]
- Zhang, Y.; Rao, X.; Wang, H.H. Organization, Technology and Management Innovations through Acquisition in China’s Pork Value Chains: The Case of the Smithfield Acquisition by Shuanghui. Food Policy 2019, 83, 337–345. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, R.; Shen, L.; Jin, M. Decisions and Coordination of Green E-Commerce Supply Chain Considering Green Manufacturer’s Fairness Concerns. Int. J. Prod. Res. 2020, 58, 7471–7489. [Google Scholar] [CrossRef]
- Toktaş-Palut, P. An Integrated Contract for Coordinating a Three-Stage Green Forward and Reverse Supply Chain under Fairness Concerns. J. Clean. Prod. 2021, 279, 123735. [Google Scholar] [CrossRef]
- Cooper, G.S.; Rich, K.M.; Shankar, B.; Rana, V.; Ratna, N.N.; Kadiyala, S.; Alam, M.J.; Nadagouda, S.B. Identifying ‘Win-Win-Win’ Futures from Inequitable Value Chain Trade-Offs: A System Dynamics Approach. Agric. Syst. 2021, 190, 103096. [Google Scholar] [CrossRef] [PubMed]
- Hoang, V.; Nguyen, A.; Hubbard, C.; Nguyen, K.-D. Exploring the Governance and Fairness in the Milk Value Chain: A Case Study in Vietnam. Agriculture 2021, 11, 884. [Google Scholar] [CrossRef]
- Gudbrandsdottir, I.Y.; Olafsdottir, G.; Oddsson, G.V.; Stefansson, H.; Bogason, S.G. Operationalization of Interorganizational Fairness in Food Systems: From a Social Construct to Quantitative Indicators. Agriculture 2021, 11, 36. [Google Scholar] [CrossRef]
- Kang, K.; Wang, M.; Luan, X. Decision-Making and Coordination with Government Subsidies and Fairness Concerns in the Poverty Alleviation Supply Chain. Comput. Ind. Eng. 2021, 152, 107058. [Google Scholar] [CrossRef]
- FAO. Managing Risks to Build Climate-Smart and Resilient Agrifood Value Chains: The Role of Climate Services; FAO: Rome, Italy, 2022. [Google Scholar]
- Puri, M. How Access to Energy Can Influence Food Losses. Available online: https://www.fao.org/fsnforum/resources/reports-and-briefs/how-access-energy-can-influence-food-losses (accessed on 18 August 2023).
- Neven, D. Developing Sustainable Food Value Chains: Guiding Principles; FAO: Rome, Italy, 2014. [Google Scholar]
- FAO; UNDP. Toolkit for Value Chain Analysis and Market Development Integrating Climate Resilience and Gender Responsiveness; FAO: Rome, Italy; UNDP: New York, NY, USA, 2020. [Google Scholar]
- Zhang, L.; Zhou, H.; Liu, Y.; Lu, R. Optimal Environmental Quality and Price with Consumer Environmental Awareness and Retailer’s Fairness Concerns in Supply Chain. J. Clean. Prod. 2019, 213, 1063–1079. [Google Scholar] [CrossRef]
- Liu, J.; Ke, H.; Tian, G. Impact of Emission Reduction Investments on Decisions and Profits in a Supply Chain with Two Competitive Manufacturers. Comput. Ind. Eng. 2020, 149, 106784. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Shen, L.; Dong, W. Impacts of Altruistic Preference and Reward-Penalty Mechanism on Decisions of E-Commerce Closed-Loop Supply Chain. J. Clean. Prod. 2021, 315, 128132. [Google Scholar] [CrossRef]
- Swami, S.; Shah, J. Channel Coordination in Green Supply Chain Management. J. Oper. Res. Soc. 2013, 64, 336–351. [Google Scholar] [CrossRef]
- Yang, D.; Xiao, T. Pricing and Green Level Decisions of a Green Supply Chain with Governmental Interventions under Fuzzy Uncertainties. J. Clean. Prod. 2017, 149, 1174–1187. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Jin, M.; Mao, J. Decisions and Coordination of Retailer-Led Low-Carbon Supply Chain under Altruistic Preference. Eur. J. Oper. Res. 2021, 293, 910–925. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating Fairness into Game Theory and Economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Liu, J.; Ke, H.; Zhang, R.; Duan, K. Who Exhibits Fairness Concern Is Better for Supply Chain Stability and the Environment. J. Clean. Prod. 2023, 386, 135645. [Google Scholar] [CrossRef]


| Notations | Definitions |
|---|---|
| Decision Variables | |
| Manufacturer’s unit profit (the manufacturer’s decision variable) | |
| Farmgate price (the agricultural producer’s decision variable) | |
| ER level (the agricultural producer’s decision variable) | |
| Retailer’s unit profit (the retailer’s decision variable) | |
| Dependent variables | |
| Wholesale price | |
| Retail price | |
| Market demand | |
| Agricultural producer’s profits | |
| Manufacturer’s profits | |
| Retailer’s profits | |
| Agricultural supply chain’s profits | |
| Fairness concern utility for the agricultural producer | |
| Parameters | |
| Initial market size | |
| Demand coefficients for retail prices | |
| Consumer’s sensitivity to emission reduction | |
| Unit production cost | |
| Unit carbon trading price | |
| Cost coefficient of emission reduction | |
| Initial carbon emissions per unit of product produced | |
| Free carbon quotas allocated by the government to the agricultural producer | |
| Fairness concern coefficient of the agricultural producer towards the manufacturer | |
| Fairness concern coefficient of the agricultural producer towards the retailer | |
| Equitable payoff proportion of the agricultural producer to the manufacturer | |
| Equitable payoff proportion of the agricultural producer to the retailer |
| Centralized Model | Decentralized Model Without Fairness Concerns | Decentralized Model with Fairness Concerns | |
|---|---|---|---|
| Manufacturer’s unit profit | — | ||
| Retailer’s unit profit | — | ||
| Farmgate price | — | see Appendix A | |
| Wholesale price | — | see Appendix A | |
| Retail price | |||
| ER Level | |||
| Market demand | |||
| Agricultural producer’s profit | — | see Appendix A | |
| Manufacturer’s profit | — | ||
| Retailer’s profit | — | ||
| Supply chain’s profit |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, Q.; Cui, H.; Guo, J.; Zhang, Q. Emission Reduction Decisions in the Agricultural Supply Chain Considering Dual Fairness Concerns. Systems 2025, 13, 313. https://doi.org/10.3390/systems13050313
Wang H, Zhao Q, Cui H, Guo J, Zhang Q. Emission Reduction Decisions in the Agricultural Supply Chain Considering Dual Fairness Concerns. Systems. 2025; 13(5):313. https://doi.org/10.3390/systems13050313
Chicago/Turabian StyleWang, Huanhuan, Qilan Zhao, Hanxing Cui, Junjie Guo, and Qiuxia Zhang. 2025. "Emission Reduction Decisions in the Agricultural Supply Chain Considering Dual Fairness Concerns" Systems 13, no. 5: 313. https://doi.org/10.3390/systems13050313
APA StyleWang, H., Zhao, Q., Cui, H., Guo, J., & Zhang, Q. (2025). Emission Reduction Decisions in the Agricultural Supply Chain Considering Dual Fairness Concerns. Systems, 13(5), 313. https://doi.org/10.3390/systems13050313






