Optimizing Security of Radio Frequency Identification Systems in Assistive Devices: A Novel Unidirectional Systolic Design for Dickson-Based Field Multiplier

Abstract

The emergence of the Internet of Things (IoT) technologies has greatly enhanced the lives of individuals with disabilities by leveraging radio frequency identification (RFID) systems to improve autonomy and access to essential services. However, these advancements also pose significant security risks, particularly through side-channel attacks that exploit weaknesses in the design and operation of RFID tags and readers, potentially jeopardizing sensitive information. To combat these threats, several solutions have been proposed, including advanced cryptographic protocols built on cryptographic algorithms such as elliptic curve cryptography. While these protocols offer strong protection and help minimize data leakage, they often require substantial computational resources, making them impractical for low-cost RFID tags. Therefore, it is essential to focus on the efficient implementation of cryptographic algorithms, which are fundamental to most encryption systems. Cryptographic algorithms primarily depend on various finite field operations, including field multiplication, field inversion, and field division. Among these operations, field multiplication is especially crucial, as it forms the foundation for executing other field operations, making it vital for the overall performance and security of the cryptographic framework. The method of implementing field multiplication operation significantly influences the system’s resilience against side-channel attacks; for instance, implementation using unidirectional systolic array structures can provide enhanced error detection capabilities, improving resistance to side-channel attacks compared to traditional bidirectional multipliers. Therefore, this research aims to develop a novel unidirectional systolic array structure for the Dickson basis multiplier, which is anticipated to achieve lower space and power consumption, facilitating the efficient and secure implementation of computationally intensive cryptographic algorithms in RFID systems with limited resources. This advancement is crucial as RFID technology becomes increasingly integrated into various IoT applications for individuals with disabilities, including secure identification and access control.

1. Introduction

The integration of RFID technology into assistive applications has garnered significant attention in recent years, particularly as part of the broader IoT landscape. RFID systems have been recognized for their potential to enhance the autonomy of individuals with disabilities, facilitating improved access to essential services and support systems [1,2]. For instance, RFID technology can be employed in various assistive devices, such as smart canes for the visually impaired, which not only aid in navigation but also provide auditory feedback about the environment and nearby obstacles [1]. In addition to smart canes, RFID technology is applied in other assistive devices, such as wearable health monitors for individuals with chronic illnesses [3]. These devices can track vital signs and send data to caregivers or medical professionals, ensuring timely interventions when necessary. Furthermore, RFID tags can be attached to mobility aids, such as wheelchairs, to provide real-time location tracking, helping caregivers monitor their users’ movements and ensuring their safety [4].

RFID systems can effectively monitor the habits and activities of elderly individuals or those with disabilities, tracking the use of food, beverages, and medications to provide timely reminders and alerts that significantly improve users’ adherence to health regimens. Studies have shown that RFID systems achieve high specificity (0.9) and sensitivity (1) when monitoring user behavior, indicating their reliability in home environments [5]. Additionally, RFID technology facilitates automatic support and monitoring systems, enabling disabled individuals to live independently while ensuring timely assistance is available when needed. This is particularly relevant for people with chronic health conditions or cognitive impairments. By integrating RFID with the IoT, these systems can gather and analyse data to promote a safer living environment, thereby reducing reliance on family members and fostering greater social inclusion [6].

Another significant application of RFID is in assistive communication devices for individuals with speech impairments [7]. By using RFID-enabled tags, users can communicate their needs or thoughts by simply scanning the appropriate tag, which can trigger pre-recorded messages or alerts. Additionally, RFID technology can support individuals with autism by helping them navigate social scenarios through wearable devices that provide contextual information and cues [8].

RFID also plays a crucial role in improving urban accessibility for individuals with disabilities. By utilizing radio frequency technologies, researchers have proposed methods to analyze movement accessibility in cities, ensuring that urban spaces are designed to be more inclusive [9]. Additionally, RFID can aid in indoor navigation, providing sensory guidance for individuals with cognitive disabilities during daily tasks or in emergencies [10]. This application addresses the need for reliable indoor location services in environments like hospitals and public buildings.

One of the key advantages of RFID in assistive applications is its ability to enable the real-time tracking and monitoring of users [11]. This capability is particularly beneficial for elderly individuals or those with cognitive impairments, as it allows caregivers to monitor their activities and ensure their safety without being intrusive. Studies have shown that RFID-based systems can effectively track daily activities and provide alerts in case of unusual behavior, thereby enhancing the quality of care provided to these individuals. Moreover, RFID technology can facilitate communication between assistive devices and other smart systems within a user’s environment [12]. For example, RFID-enabled devices can interact with home automation systems to adjust lighting or temperature based on the user’s preferences or needs, promoting a more comfortable living environment. This interconnectedness is crucial for fostering independence among users, as it allows them to control their surroundings more effectively.

Despite the advantages provided by RFID systems, the advancement of this technology introduces significant security challenges that impact disabled individuals utilizing assistive devices. One major concern is eavesdropping, where unauthorized readers can intercept communications between RFID tags and readers, risking the compromise of disabled individuals’ sensitive information, such as personal identification and health-related data [13]. This vulnerability underscores the urgent need for comprehensive security measures to ensure the privacy and integrity of disabled users. Replay attacks pose another risk, allowing attackers to record and later replay valid communication between an RFID tag and reader to gain unauthorized access to assistive devices or sensitive information [14]. Cloning is also a concern, as attackers can capture data from an RFID tag, enabling them to create a duplicate tag and impersonate the original user, potentially leading to unauthorized access to services designed for individuals with disabilities [15]. Furthermore, denial-of-service (DoS) attacks can disrupt the normal functioning of RFID systems used in assistive devices by overwhelming them with requests or jamming communication signals, leaving users without essential support [16]. Man-in-the-middle attacks complicate matters further, as attackers can intercept and alter communication between the RFID tag and reader, leading to unauthorized access or data manipulation that could endanger the safety of disabled individuals relying on these technologies [17].

Among these threats, side-channel attacks have emerged as particularly concerning due to their ability to exploit vulnerabilities inherent in the physical design and operation of RFID systems [18,19]. Side-channel attacks target the physical implementation of RFID tags and readers, leveraging the information gained from the system’s physical characteristics to compromise sensitive information. For example, timing analysis allows attackers to infer sensitive information based on variations in the response times of the RFID system. Physical tampering involves manipulating the RFID tags themselves, enabling attackers to extract sensitive data or alter the functionality of the device. Such tactics not only threaten user privacy by exposing personal information but also severely limit the overall effectiveness of assistive technologies designed to improve the quality of life for individuals with disabilities.

Notably, side-channel attacks can undermine the security of devices like the RFID cane, which assists visually impaired users in navigating their surroundings. This device not only helps users determine their location but also communicates information via Bluetooth or ZigBee, enabling them to store destination names as audible messages. While the RFID cane significantly enhances navigation and fosters independence for visually impaired users, it simultaneously exposes them to a range of threats that can undermine its effectiveness and safety. These threats can enable malicious actors to gain unauthorized access to critical location data. Such vulnerabilities are particularly concerning in scenarios where reliable navigation is paramount, as compromised data could lead to dangerous situations or disorientation.

As RFID technologies increasingly integrate into the daily lives of disabled individuals, ensuring their security against multifaceted attacks is paramount for maintaining user trust and promoting safe independent living [20,21,22,23,24,25]. Significant strides have been made to enhance the security of RFID systems through various specialized solutions [26,27]. Among the most advanced methods currently employed, elliptic curve cryptography (ECC) stands out for its robust security features, offering strong protection with smaller key sizes. However, ECC often proves impractical for low-cost RFID tags due to its demanding computational requirements [25]. In response, lightweight protocols have emerged, specifically designed for resource-constrained environments. While these protocols aim to reduce computational overhead, they remain susceptible to impersonation and data interception, raising concerns about their efficacy in securing sensitive applications [28,29]. To address these vulnerabilities, several methods have been proposed, including the use of masking techniques to obscure sensitive data, the introduction of noise to disrupt power analysis, and the implementation of hardware countermeasures to protect against physical tampering. Recent developments, including group authentication strategies that align with established protocols and innovative approaches using permutation matrix encryption, aim to strike a balance between security and efficiency for cost-sensitive RFID systems [30]. However, many of these solutions assume secure communication channels between servers and readers, which might not be viable in mobile RFID applications.

To implement efficient cryptographic protocols that resist side-channel attacks, it is crucial to focus on the implementation of cryptographic algorithms to minimize data leakage, as they are central to most cryptographic protocols. The implementation of cryptographic algorithms, such as elliptic curve cryptography (ECC), mainly relies on several finite field operations, including field multiplication, field inversion, and field division [31,32,33,34,35,36,37,38,39,40,41,42]. Among these operations, field multiplication is particularly fundamental, serving as the backbone for other field operations that are essential for the performance and security of cryptographic algorithms. However, while leveraging the properties of finite fields enhances data security, the complexity involved in executing these operations can pose significant challenges, particularly for low-cost RFID devices that are often resource-constrained. These devices must navigate the delicate balance between maintaining robust security measures and accommodating the limitations of their hardware capabilities. The method used to implement finite field operations greatly impacts the resilience of RFID systems against side-channel attacks [43,44,45]. For instance, the bidirectional structure of systolic multipliers, commonly used in many implementations, often proves inadequate for developing multipliers with effective error-detection capabilities that improve resistance to side-channel attacks [45]. These multipliers must be resilient against various side-channel threats, particularly in elliptic curve cryptosystems, where the stakes for data security are particularly high. In contrast, a unidirectional systolic array structure presents a promising alternative, as it can be specifically designed to incorporate error detection mechanisms that bolster resistance to side-channel attacks [45]. Therefore, this research paper will focus on creating a novel unidirectional systolic array structure based on the Dickson basis multiplier, which is expected to demonstrate lower space and power usage compared to traditional methods. By addressing the challenges associated with data leakage and side-channel vulnerabilities, this study aims to produce efficient modular multipliers that facilitate the implementation of secure yet computationally intensive cryptographic algorithms like ECC. This advancement is particularly important as RFID technology continues to be integrated into several IoT applications for disabled people, from secure identification to access control and beyond.

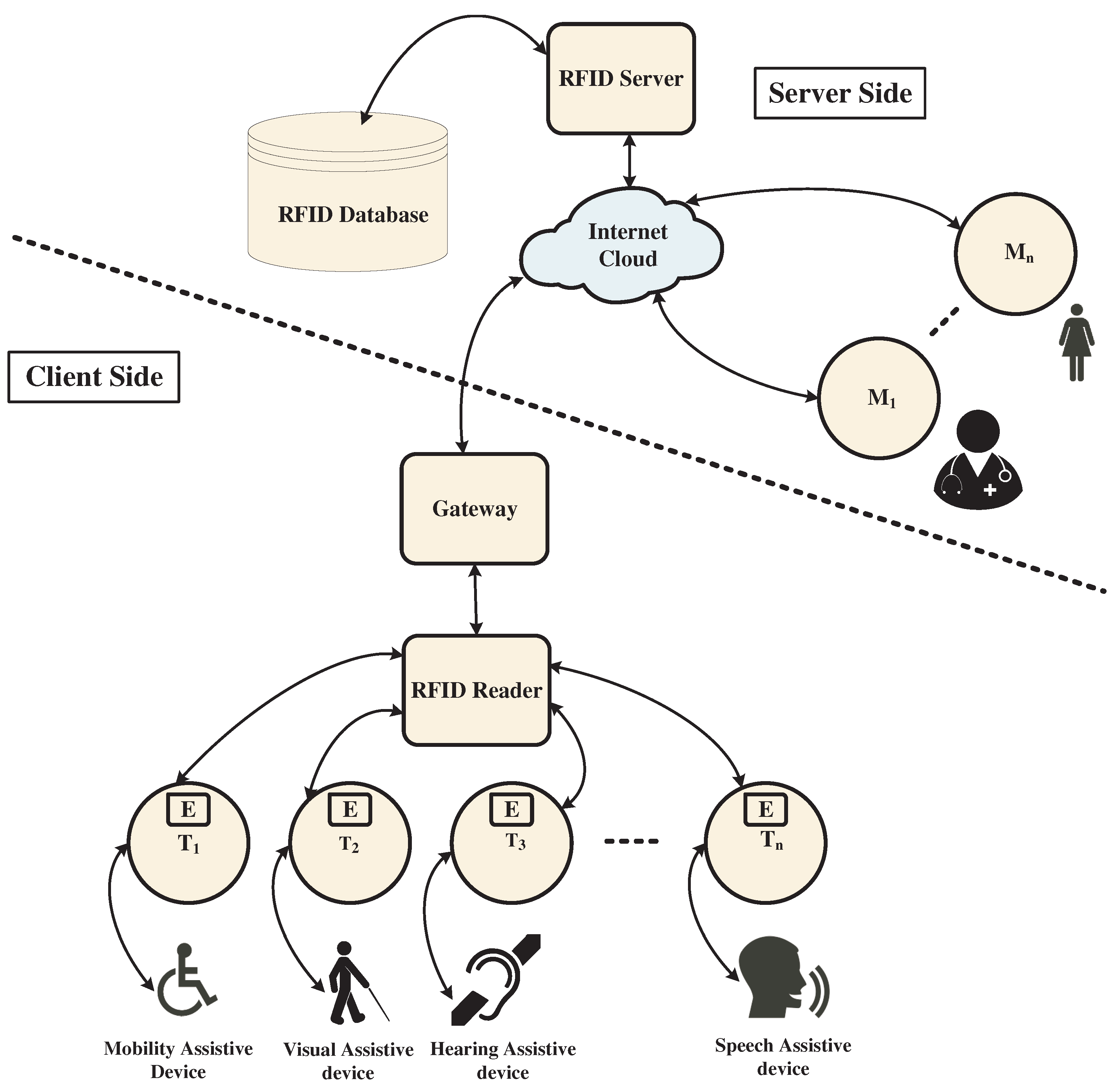
2. RFID-Based IoT-Assistive System

Figure 1 illustrates a client–server model specifically designed for an RFID-based IoT telehealth system aimed at assisting individuals with disabilities, which may include hearing loss, blindness, limited mobility, or speech impairments. On the client side, individuals with disabilities are assumed to be located in various settings, such as remote clinics, emergency transport services, or in-home care situations. On the server side, healthcare professionals and caregivers connect to the RFID server using Internet-enabled mobile devices $(M_1,M_2,\cdots ,M_n)$. RFID tags $(T_1,T_2,\cdots ,T_n)$ facilitate communication and sensing between these individuals and the RFID reader, subsequently relaying data through a gateway G. This gateway plays a vital role in securely transmitting and receiving information from the Internet cloud and serves as a hardware root-of-trust (HRoT) with fog computing capabilities.

The square blocks on the RFID tags signify the implementation of the ECC encryption algorithm, which effectively safeguards the data stored within these tags through advanced cryptographic techniques. By employing ECC, the RFID system ensures that the information exchanged between tags and readers is encrypted, thus protecting sensitive data from unauthorized access and maintaining user privacy. Furthermore, the proposed compact unidirectional systolic multiplier structure, which constitutes the core operation in ECC, plays a pivotal role in enhancing the implementation of the ECC encryption algorithm on resource-constrained tags. This approach improves error detection capabilities and hence significantly enhances resistance to side-channel attacks, thereby strengthening the overall security framework of the system. Such resilience is essential in thwarting potential exploits that could compromise user data, especially in environments where physical security cannot be guaranteed. Consequently, the remainder of this paper will focus on the methodology utilized to extract the intended unidirectional and compact systolic multiplier. This investigation is critical for facilitating the implementation of secure, yet computationally intensive, ECC encryption algorithms within the RFID system, ensuring both efficiency and robust security.

It is crucial to consider the impact of deploying the encryption module on RFID tags in terms of data generation, compatibility with existing hardware or commercial off-the-shelf (COTS) devices, and cost implications for large-scale implementations. Integrating ECC into RFID tags may lead to a slight increase in generated data due to encryption overhead. However, the system effectively manages this through efficient data management techniques. At the sensor level, strategies such as data filtering, prioritization algorithms, and event-triggered transmission focus on essential information, ensuring that only significant data—like critical changes in vital signs—are transmitted [46]. Meanwhile, at the gateway level, aggregation techniques summarize data from multiple sensors, allowing devices like smart wheelchairs to efficiently track speed, direction, and obstacles while sending only relevant information to the cloud. This minimizes bandwidth usage while enhancing system responsiveness and user-friendliness [47,48].

Importantly, the incorporation of ECC does not compromise compatibility with existing hardware and COTS devices. Although encryption may increase data volume, the system’s management techniques keep overall data within acceptable limits for standard processing capabilities, ensuring data manageability and interoperability [47,48,49]. For instance, a user’s smart door lock can receive encrypted data from an RFID-enabled mobility aid, enhancing secure access control and navigation safety for individuals. In terms of financial considerations, while implementing ECC may introduce initial hardware costs, these should be viewed in the context of large-scale deployments [50]. The upfront investment may be higher, but the benefits—such as improved data security and privacy—are especially valuable for vulnerable populations. Additionally, the efficiency of the gateway in managing data can significantly reduce the need for costly processing power in the cloud as the system scales, thus mitigating the overall cost impact [47,48].

3. Literature Review

The efficiency of finite field multiplication is significantly influenced by the choice of base representations for elements in GF($2^m$). Various representations, including polynomial basis (PB), normal basis (NB), dual basis (DB), and redundant basis (RB), each provide distinct advantages tailored to different applications [43,44,45]. Among various representations, the normal basis (NB) offers several compelling advantages, particularly in cryptographic applications. One of the primary strengths of normal bases is their exceptional efficiency in squaring operations. This efficiency arises from the ability to perform squaring through simple cyclic shifts, which require minimal computational resources and time. Such operations are crucial in cryptographic protocols, where squaring is frequently utilized, making normal bases particularly advantageous for high-speed computations. In addition to their efficiency in squaring, normal bases provide a degree of uniformity in element representation. This uniformity contributes to a more regular pattern in arithmetic operations, enabling predictable performance that simplifies hardware optimization. Such predictability is essential in designing efficient digital circuits, where consistent timing and resource usage are key considerations. In contrast, other bases, like polynomial basis (PB), can introduce variability in operational complexity, complicating the design and optimization processes for hardware applications [51,52,53,54,55].

Despite their strengths, normal bases do have limitations, particularly concerning element multiplication. The multiplication process in a normal basis can be more complex than in other representations. This added complexity can hinder the overall performance, especially in applications that require frequent multiplications. To overcome these challenges, specialized forms of normal basis, such as optimal normal basis (ONB) and Gaussian normal basis (GNB), have been developed. These variations aim to improve the multiplication efficiency while retaining the advantageous properties of normal bases.

In light of the limitations associated with normal bases, the Dickson basis presents a strong alternative for constructing efficient finite field multipliers. The space complexity of Dickson-based multipliers is generally comparable to that of ONB multipliers, making this approach particularly suitable for environments with limited resources. Researchers, including Hasan and Negre [43], have explored lightweight Dickson polynomials—such as binomials and trinomials—to enhance multiplier performance. Chiou et al. [44] have also made significant contributions by developing high-throughput bidirectional systolic array multipliers that utilize the Dickson basis, demonstrating its practical applications in cryptography. However, the bidirectional structure often found in existing designs, such as those by Chiou [44], presents challenges when integrating effective error-detection mechanisms. These mechanisms are vital for protecting against side-channel attacks, which can exploit weaknesses in elliptic curve cryptography. This challenge highlights the necessity for robust architectures that can seamlessly incorporate security features without compromising performance. In contrast, the authors of [45] proposed a unidirectional systolic array structure for the Dickson basis multiplier, allowing for the integration of robust error-detection mechanisms, but its quadratic area complexity makes it unsuitable for use in compact, ultra-low power devices like RFID tags.

The selection of irreducible polynomials is crucial to the performance of finite field multipliers, serving as the foundation for the arithmetic operations involved. This choice can significantly impact the overall efficiency [51,52,53,54,55]. While irreducible trinomials and pentanomials are often preferred for their operational advantages, generic polynomial-based multipliers remain relevant across various applications due to their versatility. Additionally, all irreducible polynomials, though less commonly employed, can still provide valuable benefits in specific contexts, facilitating the design of efficient multipliers [56,57,58]. This diversity in polynomial selection contributes to the adaptability and effectiveness of finite field multiplication in different technological environments.

The methods of implementation can lead to a variety of multiplier architectures, each with distinct characteristics. For example, bit-serial multipliers are characterized by their compact size and significant power savings, although they require multiple clock cycles to complete a single multiplication operation [32,59,60]. Conversely, bit-parallel multipliers can deliver results in a single clock cycle, but they typically incur higher hardware costs and power consumption [34,35,38,61,62,63,64,65,66]. In the realm of very large-scale integration (VLSI), systolic and semi-systolic array designs are increasingly preferred due to their modularity and capability for concurrent processing. These designs lend themselves well to high-speed operations and can efficiently utilize available hardware resources.

Numerous researchers have focused on optimizing systolic and semi-systolic multipliers for binary extension fields GF($2^m$). For instance, innovative error-detecting semi-systolic array multipliers have been introduced by scholars like Lee and Chiou [32,67], while Huang et al. [33] have concentrated on enhancing time and space efficiency in their designs. Additionally, the work of Choi and Lee [35] on systolic array architectures, which enables simultaneous multiplication and squaring operations, has significantly enhanced the performance of modular exponentiation while minimizing hardware overhead. Their integration of least-significant-bit-(LSB)-first multiplication techniques further contributes to operational efficiency.

Recent advancements in multiplier architectures have focused on enhancing efficiency and speed, particularly for cryptographic applications that demand rapid computations. Chiou et al. [44] introduced a semi-systolic array multiplier that significantly reduces time complexity, making it highly effective for fast multiplication tasks. Building on this, Lee [68,69] developed semi-systolic Montgomery modular multipliers that leverage dual levels of systolic computation to improve area efficiency and minimize latency—critical factors for VLSI designs. This dual-level approach facilitates efficient parallel processing and pipelining, greatly boosting the performance of modular multiplication. Additionally, Mathe and Boppana [70] proposed a versatile multiplier architecture capable of handling both parallel and serial inputs, optimizing the performance across different operand types. Ibrahim [42] contributed by designing one-dimensional bit-serial and bit-parallel systolic array structures specifically for computations in GF($2^m$), which enhance resource utilization and are particularly suited for tasks like error correction codes and cryptography. Pillutla and Boppana [53] further advanced the field by introducing a polynomial basis systolic multiplier targeting specific field sizes, reflecting a trend toward specialized architectures. Lee’s use of a Toeplitz matrix–vector representation has simplified the complexity of Montgomery-based bit-parallel multipliers, resulting in more efficient designs [64]. Sarmadi’s two-dimensional parallel systolic multiplier [65], based on the Montgomery algorithm, achieved a high performance while minimizing space requirements, allowing for the simultaneous processing of multiple operations and improving throughput. Mathe [66] enhanced this by implementing interleaving multiplication techniques in a two-dimensional parallel systolic multiplier structure, effectively balancing high performance with optimized resource management. Together, these innovations represent a concerted effort to develop adaptable multiplier architectures that meet the changing demands of modern cryptography while improving overall performance and resource efficiency in hardware implementations.

3.1. Paper Contribution

This paper introduces a novel unidirectional systolic array structure for the Dickson basis multiplier, aiming to achieve reduced space and power consumption compared to traditional unidirectional and bidirectional designs. The unidirectional nature of our architecture simplifies modifications, allowing for the integration of robust error-detection mechanisms that enhance resistance against side-channel attacks — an essential feature for supporting secure elliptic curve cryptography across various technological domains. As the need for secure communications grows in our increasingly digital landscape, these advancements are critical for ensuring the confidentiality and integrity of sensitive information. Unlike previous research, which often relied on ad hoc methods that overlooked the optimization of key performance factors such as latency, throughput, and power consumption, our approach focuses on the careful selection of scheduling and projection functions to create an architecture tailored to the specific needs of the target application. This mathematical framework enables a systematic analysis of the multiplier structure, leading to refined performance characteristics.

The proposed multiplier structure significantly boasts lower area complexity compared to existing two-dimensional designs, with a linear complexity $\mathcal{O}\left(m\right)$ as opposed to the quadratic complexity $\mathcal{O}\left(m^2\right)$ seen in many known architectures. This reduction results in considerable savings in physical space and energy consumption, making the construction more efficient and cost-effective. Notably, the performance of our multiplier remains competitive, maintaining comparable temporal delays as two-dimensional constructions to ensure rapid computation. Furthermore, the modular design and local connectivity of the processing elements (PEs) enhance its suitability for VLSI implementation by minimizing wire delays and improving data transmission efficiency. The significant space and power savings provided by our multiplier structure make it an attractive solution for compact RFID systems with limited resources, effectively addressing the challenges of resource-constrained environments while enabling the integration of advanced functionalities without compromising performance or energy efficiency. Such advancements are vital as RFID technology becomes more deeply integrated into a variety of IoT applications aimed at enhancing the lives of individuals with disabilities. This integration plays a crucial role in enabling secure identification and access control, which are essential for promoting independence and accessibility. By implementing robust and efficient cryptographic algorithms within these systems, we can ensure that sensitive information remains protected while providing disabled users with the necessary tools to navigate their environments safely and securely. As the demand for inclusive technology continues to grow, the development of such secure solutions will be instrumental in fostering an environment where individuals with disabilities can fully participate in society.

3.2. Paper Organization

The remainder of this paper is structured as follows. In Section 4, we provide a concise overview of the Dickson basis, highlighting its significance and application in multiplier design. Section 5 offers an in-depth analysis of the dependency graphs (DGs) related to the described Dickson-based multiplier. This section explores the complex relationships and interdependencies among various operations within the multiplier methodology, clarifying how these components interact and influence overall performance. By examining the DG, we uncover valuable insights into data flow and identify the critical paths that impact execution efficiency. Section 6 details the architecture and implementation of the proposed systolic Dickson basis multiplier, discussing its innovative features and expected performance benefits. In Section 7, we conduct a comparative analysis of the performance metrics for various multipliers, including Dickson basis multipliers. This analysis evaluates their efficiency and suitability specifically for RFID-based IoT applications aimed at assisting disabled individuals. Finally, Section 8 presents a summary of our findings and outlines potential directions for future research.

4. Dickson Basis Multiplier in GF(${\mathbf{2}}^{\mathit{m}}$)

Let R be a ring and b be an element of R ($b\in R$). The $h^{th}$ Dickson polynomial of the ${(l+1)}^{th}$ kind, denoted as $D_{h,l}(\alpha ,b)$, is significant in algebra and number theory. It is defined by the following equation [43,44,45]:

$$D_{h,l}(\alpha ,b)=\sum _{i=1}^{\lfloor {\displaystyle \frac{h}{2}}\rfloor }{\displaystyle \frac{h-li}{h-i}}\left({\displaystyle \genfrac{}{}{0pt}{}{h-i}{i}}\right){(-b)}^i{\alpha }^{h-2i}$$

(1)

Here, $\lfloor {\displaystyle \frac{h}{2}}\rfloor$ indicates the floor function applied to ${\displaystyle \frac{h}{2}}$, while $\left({\displaystyle \genfrac{}{}{0pt}{}{h-i}{i}}\right)$ signifies the number of ways to select i combinations from $h-i$ distinct items. To simplify matters, we will consider the $h^{th}$ Dickson polynomial of the first kind (where $l=0$), which is defined as follows:

$$D_h(\alpha ,b)=\sum _{i=1}^{\lfloor {\displaystyle \frac{h}{2}}\rfloor }{\displaystyle \frac{h}{h-i}}\left({\displaystyle \genfrac{}{}{0pt}{}{h-i}{i}}\right){(-b)}^i{\alpha }^{h-2i}$$

(2)

where $D_0(\alpha ,b)=2$ and $D_1(\alpha ,b)=\alpha$ for the cases when $h=0$ and $h=1$, respectively. Building upon the equations provided, the Dickson polynomials can be computed recursively using the following relationships:

$$D_i(\alpha ,b)=\left\{\begin{array}{cc}2\hfill & \mathrm{if}i=0,\hfill \\ \alpha \hfill & \mathrm{if}i=1,\hfill \\ \alpha D_{i-1}(\alpha ,b)-b{D}_{i-2}(\alpha ,b)\hfill & \mathrm{if}i\ge 2\hfill \end{array}\right.$$

(3)

Within the finite field $GF\left(2\right)$, we focus on the $h^{th}$ Dickson polynomial where $b=1$, specifically denoted as $D_h(\alpha ,1)$. Let ${\theta }_i=D_i(\alpha ,1)$ for each integer i. The Dickson basis formed by an irreducible polynomial G of degree m in $GF\left(2\right)$ can be defined in the following manner: $\Theta =\{{\theta }_1,{\theta }_2,...,{\theta }_m\}$. For instance, we have ${\theta }_1=\alpha$, ${\theta }_2={\alpha }^2$, and ${\theta }_3={\alpha }^3+\alpha$, illustrating the structure of the basis elements. Consequently, an element $X\in GF\left(2^m\right)$ can be expressed as $X=x_1{\theta }_1+x_2{\theta }_2+·+x_m{\theta }_m$, where $x_i\in GF\left(2\right)$ for $1\le i\le m$. By leveraging the inherent properties of GF($2^m$), we can reformulate Equation (3) to more effectively highlight these characteristics. This reformulation can be expressed in the following way:

$${\theta }_i=\left\{\begin{array}{cc}0\hfill & \mathrm{if}i=0,\hfill \\ \alpha \hfill & \mathrm{if}i=1,\hfill \\ \alpha {\theta }_{i-1}+{\theta }_{i-2}\hfill & \mathrm{if}i\ge 2\hfill \end{array}\right.$$

(4)

An irreducible polynomial G is termed a Dickson binomial when expressed as a two-term polynomial of the form $G={\theta }_m+1$, which is significant for its simplicity and efficiency in cryptographic applications. It is classified as a Dickson trinomial if it takes the form $G={\theta }_m+{\theta }_s+1$, where $1\le s\le {\displaystyle \frac{m}{2}}$, allowing for more complex interactions that enhance security. Both Dickson binomials and trinomials are widely used to achieve the goals of lightweight cryptography, which aims to optimize the performance while ensuring security, especially in resource-constrained environments. This research will specifically focus on the application of Dickson binomials in lightweight cryptographic systems.

Dickson Basis Multiplication Process: Let the Dickson basis be represented, as mentioned before, as $\Theta =\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_m\}$, and consider the irreducible binomial defined by $G={\theta }_m+1$ for the purpose of generating various elements. The elements $X,Y,Z$ in the finite field GF($2^m$) can be expressed in terms of the basis as follows: $X=x_1{\theta }_1+x_2{\theta }_2+\cdots +x_m{\theta }_m$, $Y=y_1{\theta }_1+y_2{\theta }_2+\cdots +y_m{\theta }_m$, $Z=z_1{\theta }_1+z_2{\theta }_2+\cdots +z_m{\theta }_m$, where $x_i,y_i,z_i$ are elements belonging to $GF\left(2\right)$ for $1\le i\le m$. Furthermore, the element Z is defined as the product of X and Y computed under modulo G, which can be represented as $Z=X\times YmodG$. This formulation is crucial for various applications in the context of lightweight cryptography.

According to the findings presented in [43,45], when the irreducible binomial $G={\theta }_m+1$ is utilized for generating elements, it can be established that the relationship ${\theta }_{m+i}={\theta }_i+{\theta }_{m-i}$ holds true for all integers $i\ge 0$. Consequently, the product Z can be calculated using this relationship as follows:

$$Z=XY=\underbrace{\sum _{i,j=1}^m{x}_i{y}_j{\theta }_{i+j}}+\underbrace{\sum _{i,j=1}^m{x}_i{y}_j{\theta }_{|i-j|}}$$

(5)

Equation (5) can be reformulated in matrix form, which is essential for the accurate design of a unidirectional systolic multiplier. The product Z is derived from three distinct matrix–vector products [43,45], specifically denoted as $Z_1$, $Z_2$, and $Z_3$, as demonstrated in Equation (6).

$$\begin{array}{c}Z=\underset{Z1}{\underbrace{\left[\begin{array}{ccccc}{x}_m& x_{m-1}& x_{m-2}& \cdots & x_1\\ x_1& x_m& x_{m-1}& \cdots & x_2\\ x_2& x_1& x_m& \cdots & x_3\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{m-1}& x_{m-2}& x_{m-3}& \cdots & x_m\end{array}\right]\times \left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ ⋮\\ y_m\end{array}\right]}}\\ +\underset{Z2}{\underbrace{\left[\begin{array}{ccccc}0& x_1& x_2& \cdots & x_{m-1}\\ 0& 0& x_1& \cdots & x_{m-2}\\ 0& 0& 0& \cdots & x_{m-3}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 0\end{array}\right]\times \left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ ⋮\\ y_m\end{array}\right]}}\\ +\underset{Z3}{\underbrace{\left[\begin{array}{ccccc}{x}_{m-1}& 0& x_{m-1}& \cdots & x_2\\ x_{m-2}& x_{m-1}& 0& \cdots & x_3\\ x_{m-3}& x_{m-2}& x_{m-1}& \cdots & x_4\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& x_1& x_2& \cdots & x_{m-1}\end{array}\right]\times \left[\begin{array}{c}{y}_m\\ y_{m-1}\\ y_{m-2}\\ ⋮\\ y_1\end{array}\right]}}\end{array}$$

(6)

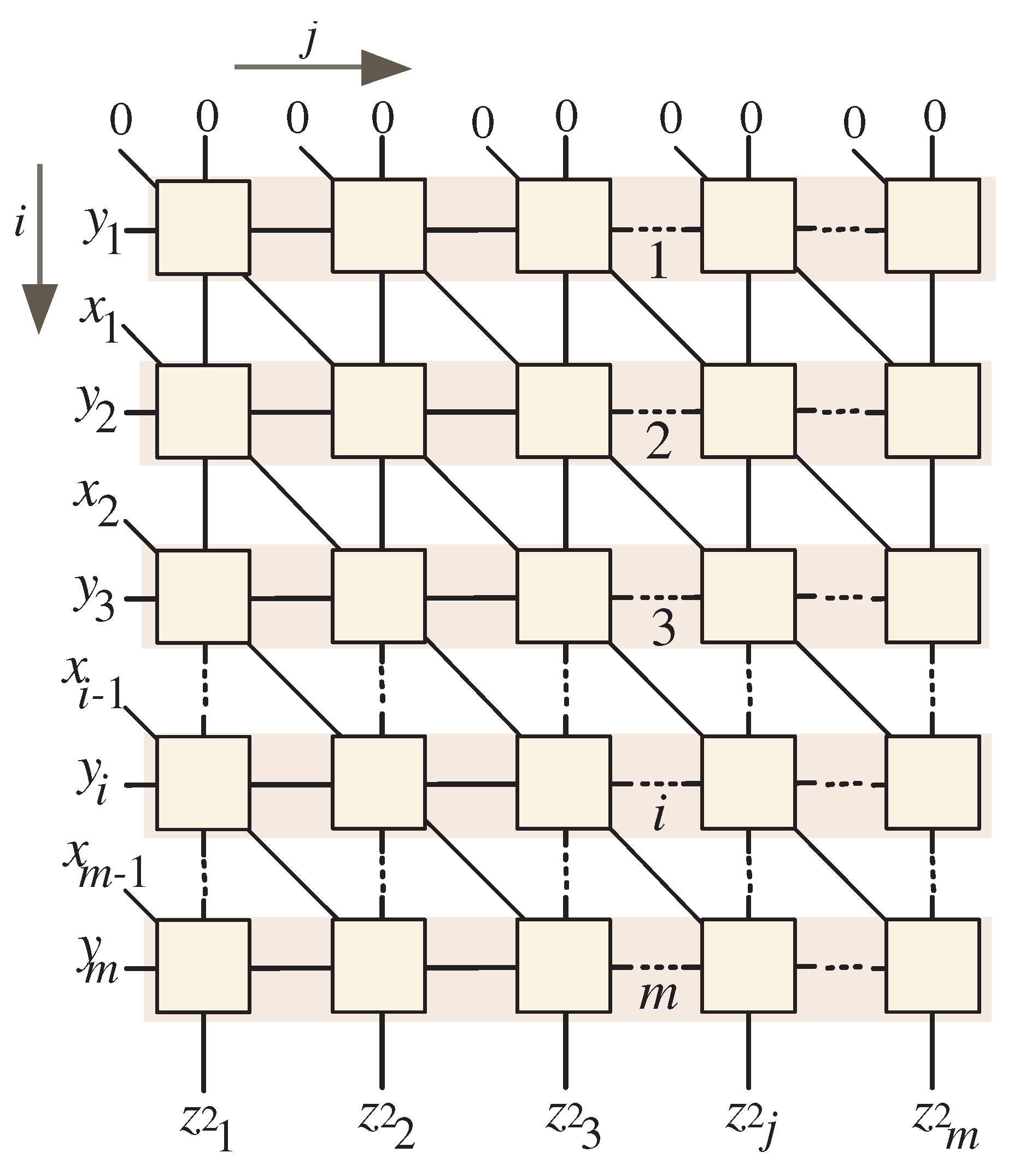
5. Constructing Dependency Graphs

To gain clearer insight into the computational dependencies and patterns described in Equation (6), we can utilize dependency graphs (DGs) for representation. It is important to note that the three matrix–vector products $Z1$, $Z2$, and $Z3$ in Equation (6) share the same computational framework but differ in the sequence of input elements provided to the computing unit. To illustrate this distinction, we will create a DG for each matrix–vector product.

Figure 2 depicts DG for the matrix–vector product $Z1$. In this figure, the inputs of the DG are arranged in specific orientations to enhance the computation process. Below is a detailed explanation of the input directions and their associated signals:

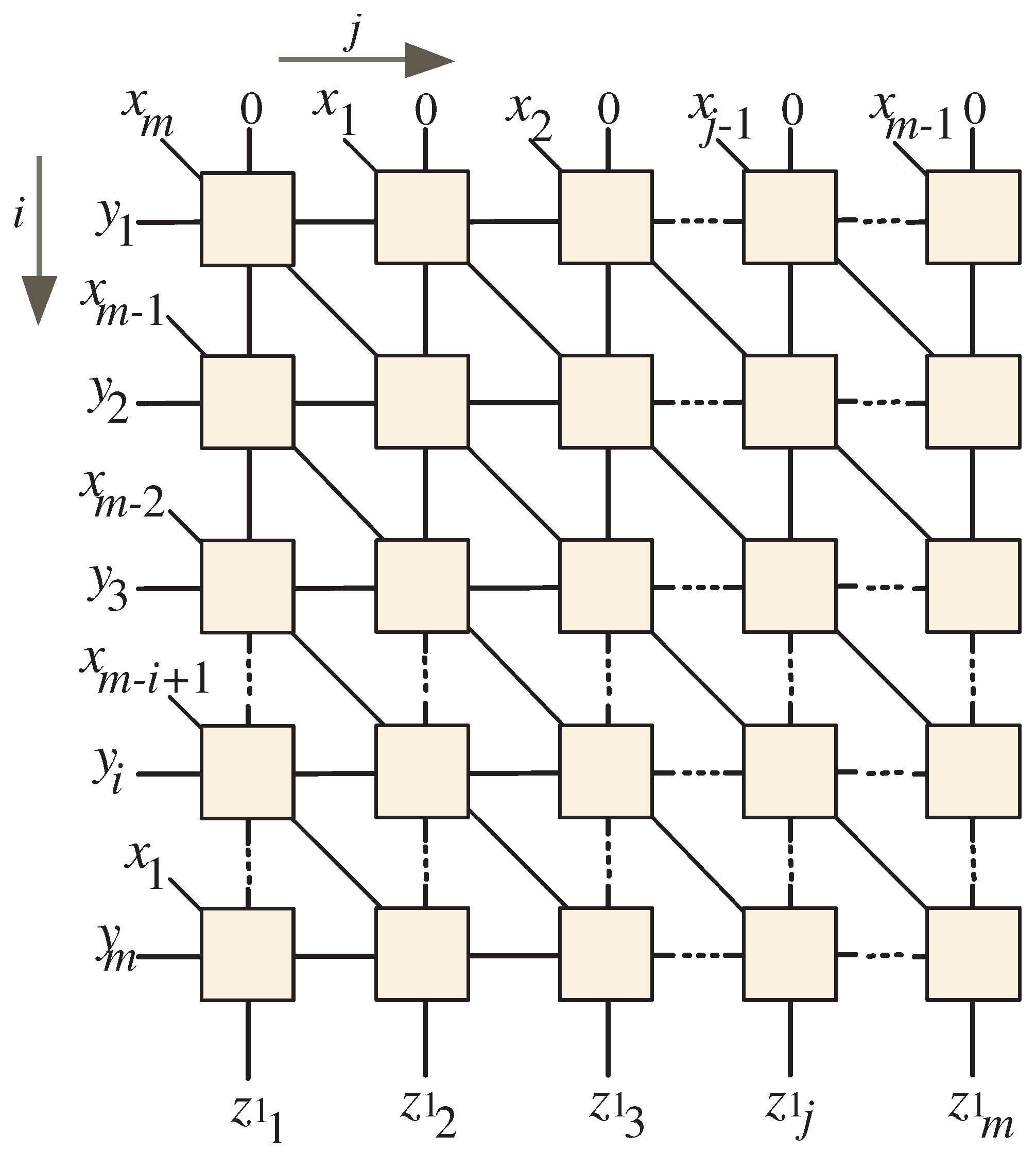
• Horizontal flow: This flow is specifically assigned to the input signals $y_i$, where $1\le i\le m$. These signals are strategically introduced into the dependency graph (DG) from the left side, ensuring a clear pathway for processing them effectively.
• Top input entry: The top section of the DG serves as the initial input location for the zero values of the $Z1$ signals ($z{1}_j$, for $1\le j\le m$). In Section 6, we will provide a detailed explanation of how to properly set up $Z1$ by clearing the flip-flops that control its output, thus preparing the system for accurate computation from the outset.
• Diagonal connectors: The diagonal connectors depicted at the left edges of the input nodes are utilized to incorporate the input signals $x_{j-1}$ and $x_{m-i+1}$, where $2\le j\le m$ and $1\le i\le m$. This design choice facilitates the effective integration of these signals into the computation, enhancing the overall functionality of the DG.

In the context of the DG, the temporary partial results related to matrix–vector product $Z1$ are computed at each node, allowing for a step-by-step accumulation of data. These partial results are subsequently transmitted to the nodes located in the next row of the graph, ensuring that each computation builds upon the previous one. This operation continues iteratively until the final row at the base of the DG is attained, effectively capturing all necessary calculations. At the base of the DG, the resultant output bits of $Z1$ are generated, representing the culmination of the entire computation process.

In a similar manner, the inputs of the DG illustrated in Figure 3 are organized in specific orientations to optimize the computational process of matrix–vector product $Z2$. By structuring the inputs thoughtfully, we can enhance the efficiency of data handling. Let us examine the input orientations and their associated signals in detail:

• Horizontal flow: This orientation is also designated for the input signals $y_i$, where $1\le i\le m$. These signals are introduced into the DG from the left side.
• Top input entry: The upper section of the DG serves as the access point for the initial zero values of the $Z2$ signals ($z{2}_j$, for $1\le j\le m$). In Section 6, we will detail how to internally initialize $Z2$ by clearing the flip-flops associated with its output at the beginning of the computation.
• Diagonal connectors: The diagonal lines illustrated at the left edges of the input nodes are utilized to incorporate the initial zero inputs of the signal $x_{j-1}$ and signal $x_{i-1}$, where $2\le j\le m$ and $1\le i\le m$.

Within the DG, the temporary partial results related to the output bits of the matrix–vector product $Z2$ are computed at each node. These partial results are then transmitted to the nodes in the next row, ensuring that each computation builds upon the previous one. This iterative process continues until the final row at the base of the DG is reached, effectively capturing all necessary calculations. At the base of the DG, the resulting output bits for $Z2$ are generated.

In a comparable fashion, the inputs of the dependency graph (DG) shown in Figure 4 are structured in specific orientations to optimize the computational workflow for the matrix–vector product $Z3$. By strategically arranging the inputs, we can significantly improve the efficiency of processing. Let us explore the input orientations and their corresponding signals in more detail:

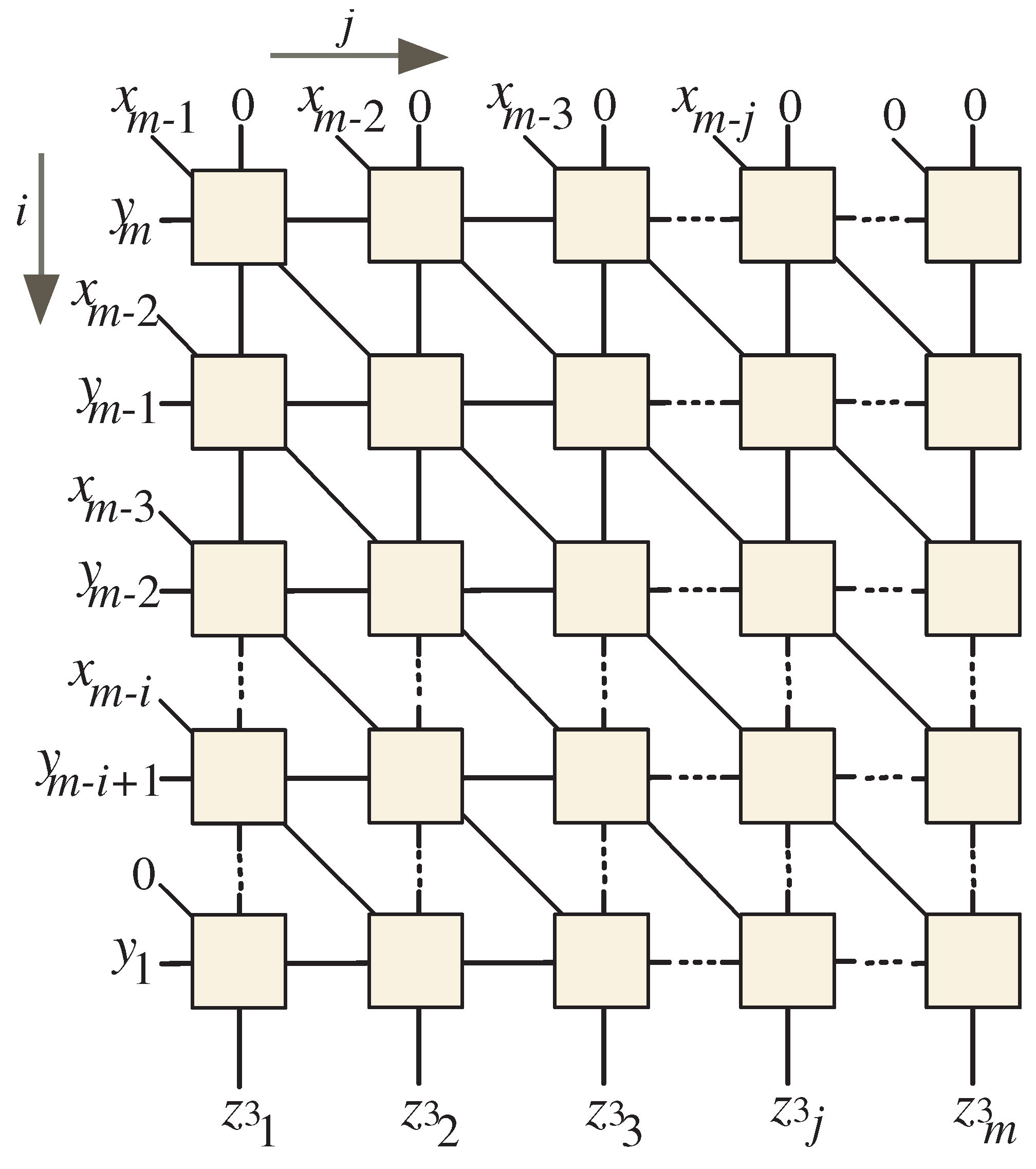
• Horizontal flow: This flow is designated for the input signals $y_{m-i+1}$, where $1\le i\le m$. These signals come from the left side of the DG, facilitating a seamless progression of data.
• Top input entry: The top section of the DG functions as the entry point for the initial zero values of the $Z3$ signals ($z{3}_j$, for $1\le j\le m$). In Section 6, we will explain how to set up $Z3$ by clearing the flip-flops that control its outputs at the start of the computation. This step ensures that the system initializes correctly, paving the way for accurate calculations.
• Diagonal connectors: The diagonal connectors illustrated at the left edges of the input nodes are employed to input the coefficients of the signals $x_{m-j}$ and $x_{m-i}$, where $1\le i,j\le m$. It is essential to highlight that the coefficient input $x_m$ is consistently set to zero, which is vital for maintaining calculation accuracy.

Throughout the DG, the temporary partial results associated with the output bits of the variable $Z3$ are calculated at each node. These results are then passed on to the subsequent nodes in the next row, ensuring that each computation relies on the results from the prior step. This iterative mechanism persists until the final row at the base of the DG is reached, effectively capturing all necessary computations. At the base of the DG, the output bits corresponding to variable $Z3$ are produced.

The overall product Z is achieved by combining the resulting output bits from the products $Z1$, $Z2$, and $Z3$. This combination is essential for combining the contributions from each product to form the overall result. To carry out this operation, two-input XOR gates are employed, which effectively handle the binary addition.

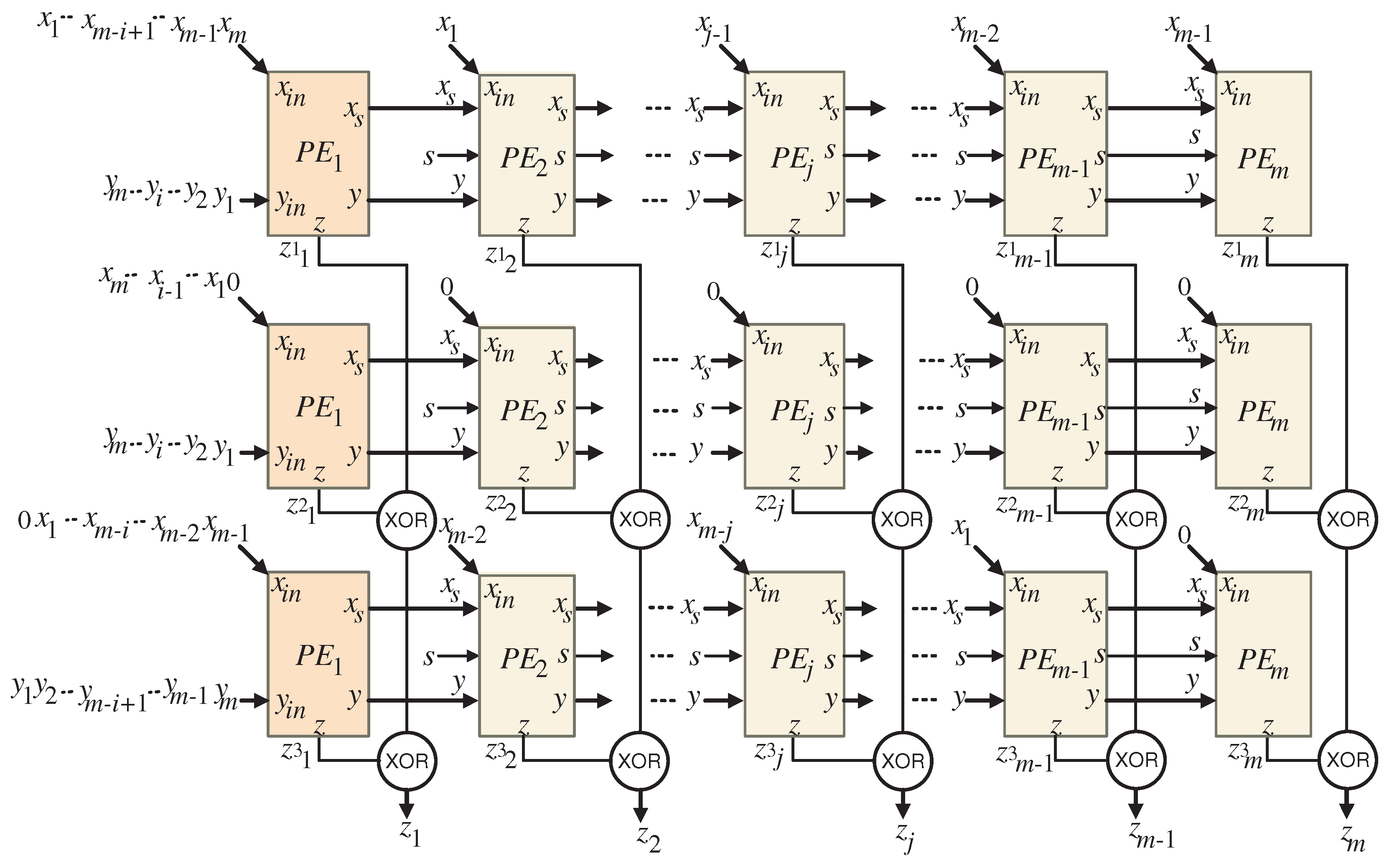
6. Unidirectional Dickson-Based Systolic Multiplier Structure Construction

In this section, we employ the method outlined in [71,72,73] to develop the unidirectional systolic multiplier design. This methodology involves scheduling and node projection techniques, which are applied to the DGs to develop an efficient parallel multiplier structure based on the chosen Dickson basis multiplication technique. We will apply this methodology to the DGs shown in Figure 2, Figure 3 and Figure 4. As we notice the DGs have exactly the same structure but with feeding input coefficients in a different order. Therefore, the applied methodology will result in the same systolic array structure for the three matrix–vector products of $Z1,Z2,Z3$.

6.1. Scheduling Function

Let us take a closer look at the data points (nodes) represented in DG illustrated in Figure 2. Each data point is denoted as $\mathbf{Q}(i,j)=\left[ij\right]$, where i and j correspond to specific indices that reflect the operations within the multiplier algorithm. To establish the order in which each node should be executed, we employ a scheduling vector denoted as $\mathbf{\Psi }=\left[{\psi }_0{\psi }_1\right]$. This vector serves as a tool for organizing the execution sequence. Additionally, we utilize a scheduling function, represented by $\mathrm{\Pi }\left(\mathbf{Q}\right)$, which plays a crucial role in determining how the points in the DG are processed. The definition of this scheduling function is as follows:

$$\mathrm{\Pi }\left(\mathbf{Q}\right)=\mathbf{\Psi }\mathbf{p}-\rho =i{\psi }_0+j{\psi }_1-\rho$$

(7)

where $\mathbf{Q}$ signifies the position vector $\left[ij\right]$, and $\rho$ is a scalar value that is essential for the scheduling mechanism. The inclusion of $\rho$ ensures that all nodes in the DG are allocated positive time values, which is critical for establishing a valid execution sequence. By assigning $\rho \equiv 0$, we create a reference point that guarantees that each node in the DG illustrated in Figure 2 receives a positive time value. This strategy not only avoids the assignment of negative time values but also streamlines the scheduling of operations, ultimately improving the algorithm’s efficiency and effectiveness.

The scheduling vector $\mathbf{\Psi }=\left[{\psi }_0{\psi }_1\right]$ is subject to certain constraints that govern the execution order of the nodes. One crucial constraint dictates that nodes located at $\mathbf{Q}=\left[ij\right]$ must be executed only after the nodes at $\mathbf{Q}=[i-1j]$ have been completed. This ensures a proper flow of operations and prevents any potential conflicts in the execution sequence. This requirement can be formalized as the following inequality:

$$\mathrm{\Pi }(\mathbf{Q}=[ij\left]\right)>\mathrm{\Pi }(\mathbf{Q}=[i-1j\left]\right)$$

(8)

When considering the coordinate values of $\mathbf{\Psi }$, this inequality can be formulated as:

$$\begin{array}{ccc}i{\psi }_0+j{\psi }_1& >& (i-1){\psi }_0+j{\psi }_1\hfill \\ \hfill {\psi }_0& >& 0\hfill \end{array}$$

(9)

The above constraint imposed on the scheduling vector $\mathbf{\Psi }$ guarantees that the time value allocated to a node at $\mathbf{Q}=\left[ij\right]$ exceeds that of the node at $\mathbf{Q}=[i-1j]$. By adhering to this constraint, we can achieve the required execution order of the nodes in the DG. This ensures that operations dependent on prior computations are executed in the correct sequence, thereby maintaining the integrity and efficiency of the overall algorithm.

Furthermore, there is a timing requirement that stipulates that the operations assigned to the nodes at $\mathbf{Q}=[ij+1]$ must be carried out only after the operations at $\mathbf{Q}=[i-1j]$ have been completed. This constraint is critical for maintaining the correct flow of computations, as it ensures that any dependencies associated with these nodes are respected. Mathematically, this can be expressed as:

$$\mathrm{\Pi }(\mathbf{Q}=[ij+1\left]\right)>\mathrm{\Pi }(\mathbf{Q}=[i-1j\left]\right)$$

(10)

When we formulate the relationships in terms of the coordinate values of $\mathbf{\Psi }$, we derive the following equations.

$$\begin{array}{ccc}i{\psi }_0+j{\psi }_1+{\psi }_1& >& i{\psi }_0-{\psi }_0+j{\psi }_1\hfill \\ \hfill {\psi }_1& >& -{\psi }_0\hfill \end{array}$$

(11)

This inequality establishes a timing boundary on the scheduling vector $\mathbf{\Psi }$. It ensures that the time assigned to a node at $\mathbf{Q}=[ij+1]$ exceeds the time assigned to the node at $\mathbf{Q}=[i-1j]$. This stipulation is critical for maintaining the correct order of operations within the DG. By adhering to this guideline, we can uphold the necessary dependencies, allowing computations to be executed in the proper sequence.

By analyzing the inequalities (9) and (11), we can identify appropriate scheduling vectors. The feasible choice for an effective scheduling vector, which delivers the optimal design in the context of resource-limited RFID designs, is:

$$\begin{array}{ccc}\mathbf{\Psi }& =\hfill & \hfill \left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(12)

By employing the scheduling function on the DGs presented in Figure 2, Figure 3 and Figure 4, we derive the same scheduling vector discussed earlier (Equation (12)). The timing of the nodes after this scheduling vector is applied is illustrated in Figure 5, Figure 6 and Figure 7. A detailed observation of these figures indicates that the output signals $z{1}_j$, $z{2}_j$, and $z{3}_j$ (for $1\le j\le m$) are generated at the same time after the m clock cycles.

6.2. Projection Function

Based on the findings of Gebali [71], the projection function is fundamental in the process of converting a large set of DG nodes, represented as $\mathbf{Q}(i,j)$, into a single processing element denoted as $\overline{\mathbf{Q}}$. This transformation is critical for simplifying the complexity of the system. By interconnecting these processing elements, one can effectively create a systolic or semi-systolic array. The mathematical formulation of the projection function can be articulated as follows:

$$\overline{\mathbf{Q}}=\mathbf{Y}\mathbf{Q}$$

(13)

In this equation, the projection matrix is denoted by $\mathbf{Y}$. A critical step in deriving this matrix involves identifying its null space, which is referred to as $\mathbf{\Omega }$. Understanding the properties of this null space is essential for ensuring that the projection matrix functions as intended. As highlighted in [71], it is necessary to impose a specific constraint on the projection vector $\mathbf{\Omega }$ to maintain both the accuracy and effectiveness of the projection process. This constraint can be articulated as follows:

$$\mathbf{\Psi }\mathbf{\Omega }\ne \mathbf{0}$$

(14)

This constraint plays a vital role in ensuring that each processing element carries out its specific tasks at different times. This method of time separation allows for effective multiplexing, which in turn optimizes resource usage and significantly improves overall system performance.

In light of the condition specified in Equation (14) and the provided scheduling vector $\mathbf{\Psi }=\left[10\right]$, along with the necessity for a bit-parallel systolic structure, we can identify the appropriate projection vector that meets these requirements. The formulation of this projection vector can be represented as follows:

$$\begin{array}{ccc}\mathbf{\Omega }& =\hfill & \hfill \left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(15)

This designated projection vector ensures compliance with the condition described in Equation (14) for both the scheduling vector $\mathbf{\Psi }$ and the projection vector $\mathbf{\Omega }$. As a result, it plays a crucial role in facilitating the creation of a unidirectional bit-parallel systolic structure that possesses the desired attributes. This alignment between the vectors is essential for achieving optimal performance in the system.

The projection matrix, denoted by $\mathbf{Y}$, can be established by recognizing that $\mathbf{\Omega }$ serves as the null space for $\mathbf{Y}$. This relationship is crucial as it allows us to articulate the projection matrix in the following manner:

$$\begin{array}{ccc}\mathbf{Y}& =\hfill & \hfill \left[\begin{array}{cc}0& 1\end{array}\right]\end{array}$$

(16)

This matrix serves to demonstrate how the original group of DG nodes is converted into a single processing element. By establishing this mapping, we can efficiently streamline the processing tasks, ensuring that multiple nodes are effectively represented within one computational unit. This transformation is essential for optimizing performance and resource allocation in the system.

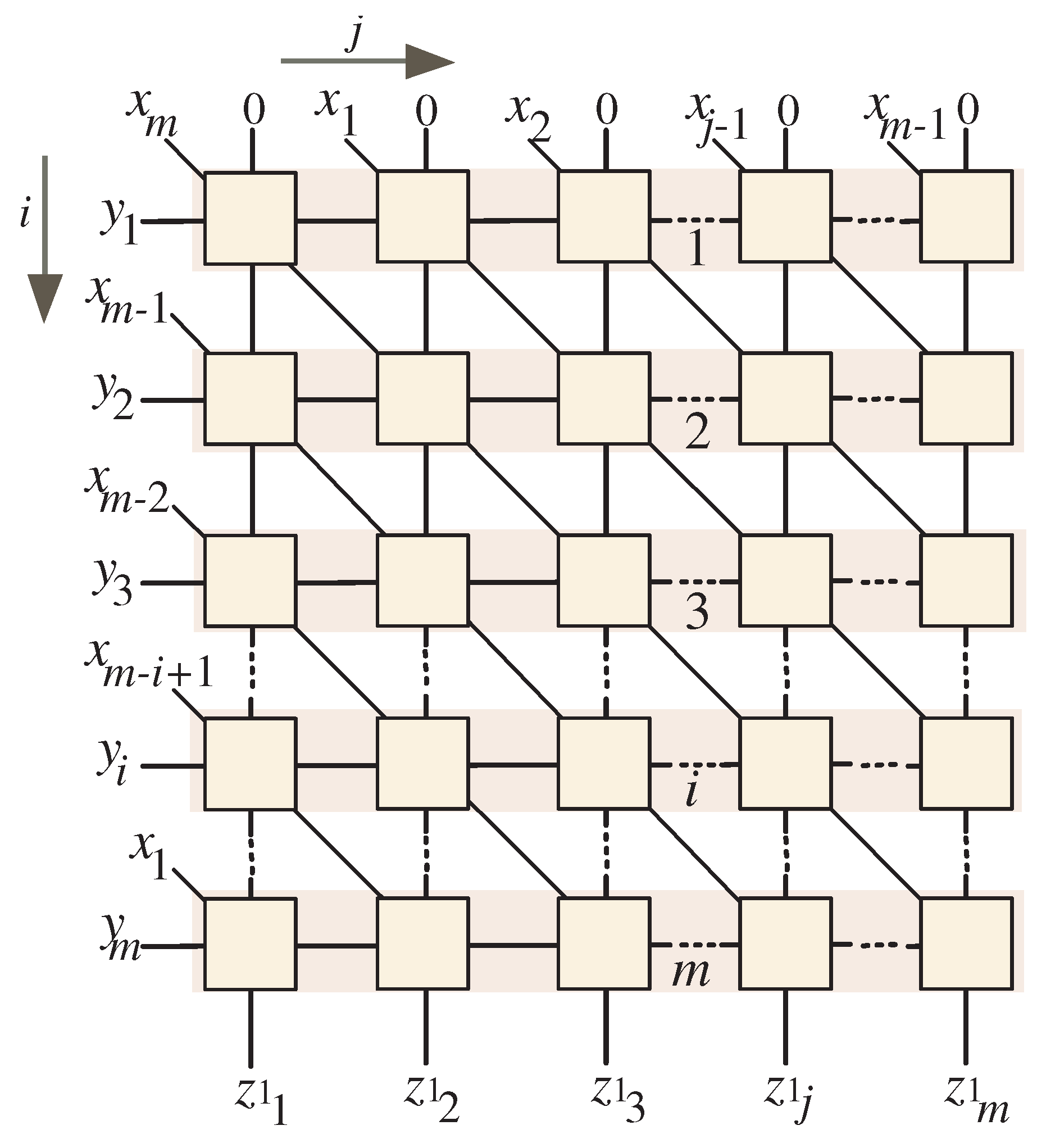
6.3. Extracting the Unidirectional Systolic Multiplier Design

The functions $\mathrm{\Pi }\left(\mathbf{Q}\right)$ and $\overline{\mathbf{Q}}\left(\mathbf{Q}\right)$ associated with each node $\mathbf{Q}(i,j)$ in the dependency graphs illustrated in Figure 2, Figure 3 and Figure 4 can be constructed by integrating the vectors $\mathbf{\Psi }=\left[10\right]$ and $\mathbf{Y}=\left[01\right]$ into the Equations (7) and (13). This integration facilitates a systematic representation of the computational relationships and scheduling requirements of the nodes. The resulting functions, $\mathrm{\Pi }\left(\mathbf{p}\right)$ and $\overline{\mathbf{Q}}\left(\mathbf{Q}\right)$, play a vital role in optimizing the overall performance of the system, ensuring that each operation is executed in the correct sequence. These functions can subsequently be defined as follows:

$$\begin{array}{c}\hfill \mathrm{\Pi }\left(\mathbf{Q}\right)=i\\ \hfill \overline{\mathbf{Q}}\left(\mathbf{Q}\right)=j\end{array}$$

(17)

By applying the derived functions $\mathrm{\Pi }\left(\mathbf{Q}\right)=i$ and $\overline{\mathbf{Q}}\left(\mathbf{p}\right)=j$ to the nodes represented in the DGs of Figure 2, Figure 3 and Figure 4, we can successfully create a unidirectional bit-parallel systolic multiplier configuration. This design is particularly advantageous for executing high-performance multiplication operations. As shown in Figure 8, the structure consists of three unidirectional one-dimensional systolic arrays, each working in conjunction to enhance processing speed. Within each array, m processing elements (PEs) are arranged in a linear configuration, allowing for streamlined data flow and efficient computation. This arrangement not only optimizes resource utilization but also significantly boosts the overall performance of the multiplication process.

The top systolic array is dedicated to calculating the output bits of the matrix–vector product $Z1$. As illustrated in Figure 9, the combinational logic schematic for the standard processing element (${\mathrm{PE}}_j$) is designed to perform essential calculations, generating bits based on its input. This PE’s combinational logic includes AND gate, XOR gate, with square boxes representing latches and triangles indicating tri-state buffers. The first processing element (${\mathrm{PE}}_1$), illustrated in Figure 10, retains the structural characteristics of the standard processing element (${\mathrm{PE}}_j$) but omits the tri-state buffers, reflecting its distinct operational requirements. Specifically, ${\mathrm{PE}}_1$ does not necessitate a selection mechanism between the input signals routed to the $x_{in}$ port and the intermediate signals allocated to the $x_s$ port. This design choice effectively streamlines the architecture of ${\mathrm{PE}}_1$ by eliminating the tri-state buffers, thereby enhancing its operational efficiency. This adjustment not only results in a more efficient systolic array but also significantly reduces the area overhead while enhancing overall performance by removing unnecessary computations and simplifying the logic structure, thus improving the speed and reliability of the system.

The central systolic array, as shown in Figure 8, is specifically designed to calculate the output bits of the matrix–vector product $Z2$. In this array, each PE performs designated tasks to generate these bits based on the incoming data it receives from neighbor elements. This arrangement ensures efficient data processing and flow throughout the system. Notably, both the standard processing element (${\mathrm{PE}}_j$) and the first processing element (${\mathrm{PE}}_1$) exhibit an identical structural design to the PEs utilized in the top systolic array. This structural consistency is clearly illustrated in Figure 9 and Figure 10, respectively, highlighting the uniformity in design, which facilitates easier integration and optimization within the overall architecture.

The lowermost systolic array, as shown in Figure 8, is specifically tasked with calculating the output bits of the matrix–vector product $Z3$. Every PE within this array executes specific calculations to produce these bits based on the incoming data it receives from adjacent elements. Importantly, both ${\mathrm{PE}}_j$ and ${\mathrm{PE}}_1$ share the same structural design as those in the top and central systolic arrays, ensuring compatibility and efficiency. This similarity in design is clearly illustrated in Figure 9 and Figure 10, respectively, highlighting a uniform architecture that facilitates seamless integration and significantly enhances the overall efficiency of the entire system. By maintaining this consistent structure across the various arrays, we can effectively optimize the performance and streamline the processing tasks involved, leading to improved computational speed and reliability.

In Figure 8, it is clearly indicated that the initial bits for the products $Z1$, $Z2$, and $Z3$ are all initialized to zero. This important observation creates a valuable opportunity for optimization, particularly concerning area and delay complexities within the system. By strategically clearing the $D_z$ flip-flops, dedicated in Figure 9 and Figure 10, at the appropriate times during operation, we can enhance the overall efficiency. When these flip-flops are cleared, the required zero values can be directly provided to the input of the XOR gate. This streamlined approach not only simplifies the logic design but also removes the necessity for additional circuitry to compute those values, thereby significantly improving both the performance and reliability of the entire computational architecture.

The offered unidirectional linear and parallel systolic multiplier introduces a substantial enhancement over conventional two-dimensional parallel systolic designs, especially when considering its area complexity. Unlike traditional two-dimensional architectures, which typically exhibit a quadratic area complexity $\mathcal{O}\left(m^2\right)$, the novel multiplier achieves a more favorable linear area complexity $\mathcal{O}\left(m\right)$. This significant improvement leads to a much more efficient utilization of available resources, which is essential for optimizing overall hardware performance. When this new design is compared to the Montgomery and Dickson two-dimensional parallel systolic structures referenced in [44,45,68,69], it becomes evident that the proposed multiplier excels in terms of space efficiency. The reduction in area complexity not only enhances the effective usage of hardware but also establishes the proposed structure as a superior option in terms of area efficiency. Furthermore, when evaluated against parallel multipliers that utilize traditional field multiplication techniques, such as those mentioned in [33,34,44,65,66,74,75], the new multiplier shows significant advantages in area performance. Detailed findings and performance metrics that highlight these advancements will be presented in the results section, effectively demonstrating the recommended multiplier’s superiority in both area and energy efficiency.

The configuration of the newly designed unidirectional parallel systolic multiplier, depicted in Figure 8, utilizes a systematic approach for input signal allocation and processing. Initially, input signals $x_{j-1}$, 0, and $x_{m-j}$, where $1\le j\le m$, are assigned to ${\mathrm{PE}}_j$ across the top, central, and bottom systolic arrays, respectively. This careful assignment ensures that each PE receives the specific inputs necessary for its computations, allowing for optimal performance throughout the multiplication process. Sequentially, input signals $x_{m-i+1}$ (for $1\le i\le m$) are fed into the first PE of the top systolic array, while signals $x_{i-1}$ are directed to the first PE in the central systolic array. Similarly, the first PE (${\mathrm{PE}}_1$) in the bottom systolic array receives input signals $x_{m-i}$. This sequential feeding of inputs is crucial for maintaining the flow of data and ensuring that each PE can perform its calculations in a timely manner. Additionally, input signals $y_i$ (for $1\le i\le m$) are sequentially fed to the first PE (${\mathrm{PE}}_1$) of both the top and central systolic arrays, passing through all regular PEs. In the bottom systolic array, input signals $y_{m-i+1}$ (for $1\le i\le m$) follow the same path through ${\mathrm{PE}}_1$ and all subsequent standard PEs (${\mathrm{PE}}_j$), further reinforcing the structured flow of data.

After m clock cycles, the resulting coefficient bits—denoted as $z{1}_j$, $z{2}_j$, and $z{3}_j$ (for $1\le j\le m$)—are made available concurrently at the outputs of all PEs. This parallel output mechanism allows for efficient retrieval of results from each systolic array, significantly reducing the time required to obtain the final output. Finally, at clock cycle m, the final product bits $z_j$ (for $1\le j\le m$) are calculated by adding the corresponding bits of $z{1}_j$, $z{2}_j$, and $z{3}_j$ using 2-input XOR gates. This addition process effectively consolidates the outputs into the final product representation, ensuring that the multiplication results are both accurate and efficiently generated.

The functioning of the analyzed unidirectional bit-parallel systolic multiplier configuration can be detailed in the following steps, which outline the specific processes and interactions that contribute to its efficient performance in multiplication tasks.

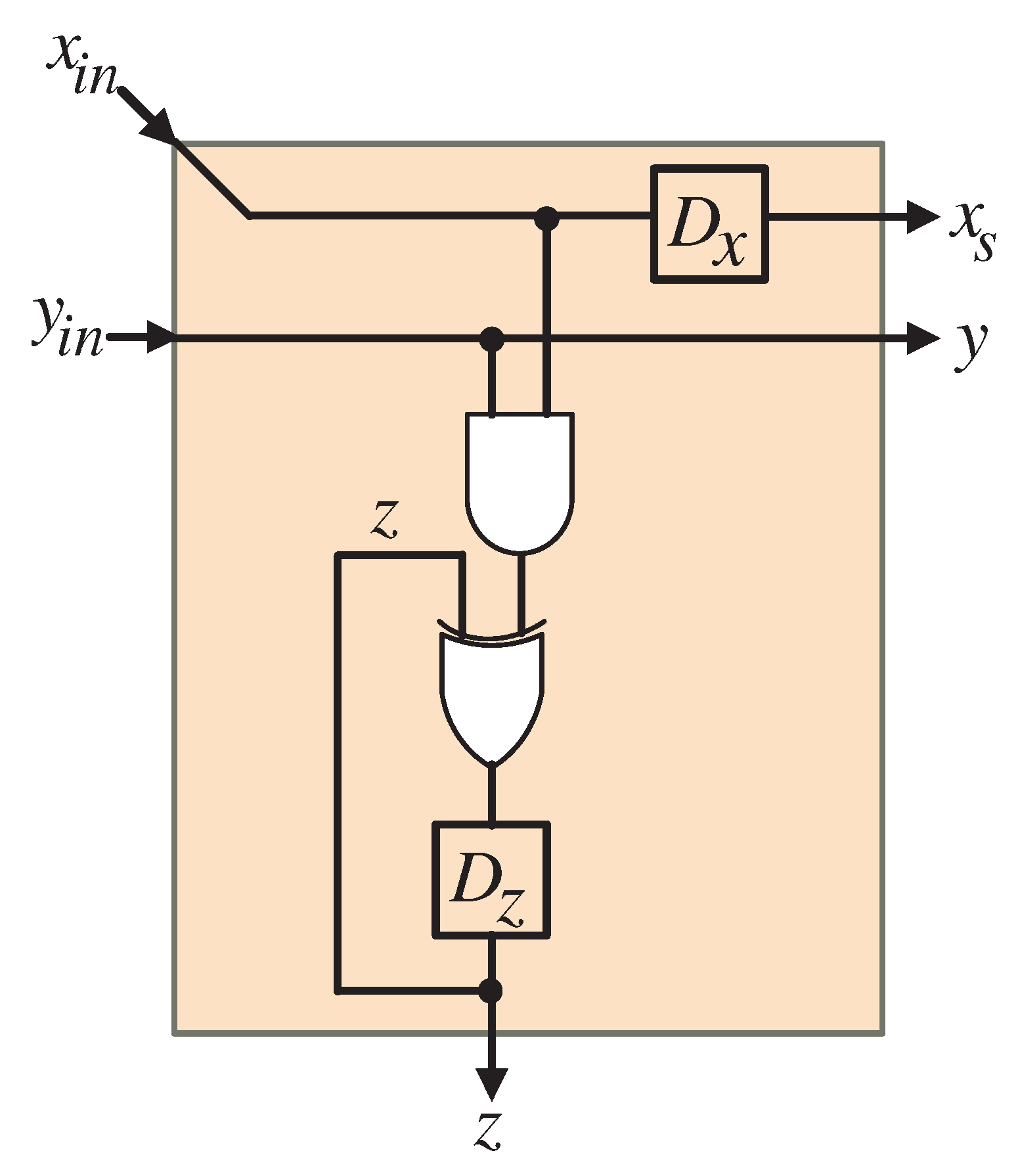
• Setup: In the first clock cycle, the latches $D_z$ illustrated in Figure 9 and Figure 10 are cleared, resulting in the coefficient bits z being initialized to zero. This crucial step eliminates any previous data, preparing the system for fresh computations. Simultaneously, the control signal s is enabled ($s=1$), which facilitates the flow of input signals assigned to the port $x_{in}$—specifically $x_{j-1}$, 0, and $x_{m-j}$, for $1\le j\le m$—through the top tri-state buffer shown in Figure 9. This ensures that the signals are accurately routed to their respective PEs. Additionally, during this clock period, the initial bits of the signals $x_{m-i+1}$, $x_{i-1}$, and $x_{m-i}$ (for $1\le i\le m$) are introduced to the appropriate first PE (PE1) in each systolic array via the port $x_{in}$ depicted in Figure 10, initiating the computation process.
• Processing: From the second clock cycle onward, continuing through clock cycle m, the control signal s is turned off ($s=0$). This change allows the temporary signals $x_s$ to be processed through the standard PEs (${\mathrm{PE}}_j$), enabling the calculation of values assigned to the z port of the systolic arrays. During these clock cycles, it is essential for the remaining bits of the signals $x_{m-i+1}$, $x_{i-1}$, and $x_{m-i}$ (for $1\le i\le m$) to be fed sequentially into the appropriate first PE (${\mathrm{PE}}_1$) of the upper, central, and bottom systolic arrays through port $x_{in}$. This structured input ensures a continuous and efficient flow of data throughout the system.
• Final Output: At the conclusion of the operation, specifically during clock cycle m, the output bits of the product Z, denoted as $z_j$ (for $1\le j\le m$), are generated at the outputs of the final row of XOR gates illustrated in Figure 8. This concurrent generation of outputs marks the successful completion of the multiplication process, allowing for immediate access to the results.

7. Results Overview and Analysis

This section focuses on a comparative analysis of the explored unidirectional systolic multiplier against several prominent systolic and semi-systolic multiplier configurations from the literature [44,45,68,69,74]. The analysis is organized into two subsections. The first subsection examines the resource utilization and processing time of the offered design architecture in relation to those of competing architectures. By thoroughly analyzing these complexities, we aim to provide insights into resource utilization and performance speed. In the second subsection, we will confirm our complexity analysis through real implementation. By deploying the recommended design in an actual setting, we can assess its true performance and compare it to the anticipated complexities. This implementation will guarantee that our analysis accurately captures the behavior of the multiplier in real-world applications.

7.1. Complexity Analysis

Following a detailed analysis of the unidirectional systolic construction illustrated in Figure 8, it becomes clear that the design encompasses a total of $3m$ PEs, each of which plays a crucial role in the overall functionality of the system. Within these PEs, there is a variety of logic components, specifically $3m$ AND gates, $3m$ XOR gates, 0 multiplexers (MUXes), and $6m$ latches. These components work together in synergy to execute the necessary computations required within each PE.

To obtain the final result bits, which are represented as $z_j$, an additional group of $2m$ XOR gates is utilized specifically for this purpose. These gates are tasked with adding the corresponding bits from $z{1}_j$, $z{2}_j$, and $z{3}_j$, where $1\le j\le m$, thereby facilitating the accumulation of results. Consequently, the overall quantity of XOR gates required in the architecture sums to $5m$. This total comprehensively accounts for both the XOR gates present within the PEs and the extra gates utilized for the bit addition operations.

In order to evaluate the efficiency of the suggested multiplier with respect to speed, it is essential to determine the critical path delay (CPD). The critical path is defined as the most extended route within the circuit that dictates the total delay experienced during operation. In this particular instance, the critical path comprised two two-input XOR gates, which contribute a delay represented as $2T_X$.

Examining the functionality of the multiplier configuration, it is important to highlight that the suggested multiplier achieves its ultimate results in an m clock periods. This indicates that the complete computation, starting at the beginning of the multiplication to the delivery of the output bits, occurs within m clock cycles. Such information is essential for assessing both the efficiency and speed of the multiplier, enabling a thorough evaluation of its performance in real-world scenarios.

Table 1. Investigation of space and time complexities in suggested and competing multipliers.

Design	AND	XOR	MUX	Latch	Latency	CPD	Area	Time
							Complexity	Complexity
Chiou [44]	$m^2$	$3m^2+2m$	0	$3m^2+4m$	$m+1$	$T_A+3T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Chiou [45]	$m^2$	$m^2+m$	0	$3m^2$	$m+2$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Lee [68]	$m^2+m$	$m^2+2m$	0	$1.6m^2+4m$	$(m+7)/2$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Lee [69]	$m^2+m$	$m^2+(7m+1)/2$	0	$2.1m^2+6.5m$	$(m+7)/2$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Chiou [74]	$m^2$	$m^2+m$	m	$2m^2+3m$	$m+1$	$T_A+T_X+T_M$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Proposed	$\mathbf{3}\mathit{m}$	$\mathbf{5}\mathit{m}$	$\mathbf{0}$	$\mathbf{6}\mathit{m}$	$\mathit{m}$	$\mathbf{2}{\mathit{T}}_{\mathit{X}}$	$\mathcal{O}\left(\mathit{m}\right)$	$\mathcal{O}\left(\mathit{m}\right)$

offers an in-depth analysis that contrasts the suggested unidirectional parallel systolic multiplier with various established parallel systolic and semi-systolic multiplier designs [44,45,68,69,74]. This examination focuses on three pivotal criteria: the utilization of components such as gates, multiplexers (MUXs), and latches; the associated latency for each multiplier design; and the critical path delay (CPD), which influences overall performance.

The findings indicate a notable difference in space complexity between the proposed configuration and the existing designs. Specifically, the multiplier layouts referenced in the literature exhibit a space complexity of $\mathcal{O}\left(m^2\right)$, suggesting that their component requirements increase quadratically as the input size m grows. Conversely, the unidirectional systolic multiplier demonstrates a more favorable linear space complexity of $\mathcal{O}\left(m\right)$, highlighting a significant reduction in resource consumption. This efficiency is particularly relevant for RFID-Based IoT applications for disabled people, where constraints on both resource availability and physical space are common challenges. Moreover, the analysis shows that all designs under consideration share the same time complexity of $\mathcal{O}\left(m\right)$. This consistency indicates that the proposed systolic multiplier can deliver computational efficiency on par with existing designs while consuming far fewer resources. Such a balance between performance and resource utilization makes the proposed arrangement an attractive solution for practical applications, especially in scenarios where efficient resource management is crucial.

The explored systolic multiplier configuration presents a range of benefits that enhance its applicability for RFID-based IoT applications for disabled people. One of the primary advantages is its compact design, which minimizes the area requirements and optimizes the use of existing hardware resources. This efficient use of space not only contributes to a smaller physical footprint but also positively influences critical performance metrics. As a result of this space efficiency, both the area–delay product (ADP) and the power–delay product (PDP) of the multiplier are improved. These enhancements lead to a superior overall performance and increased energy efficiency, making the proposed layout a compelling choice for applications where resource constraints and power consumption are significant considerations.

The advantages of the proposed multiplier configuration are reinforced by the real implementation results showcased in

Table 2. Evaluating the efficiency of different multiplier configurations for $m=283$.

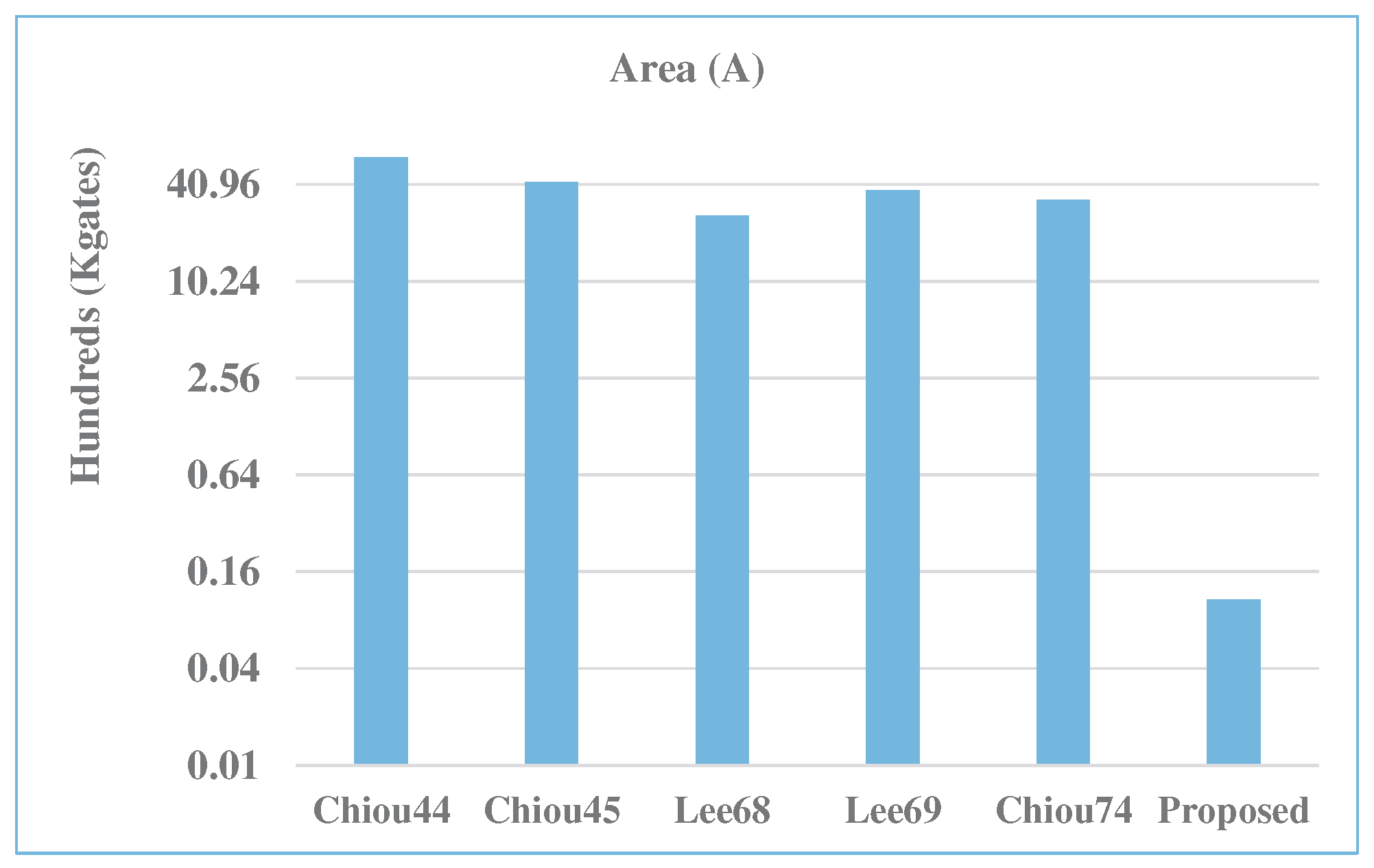
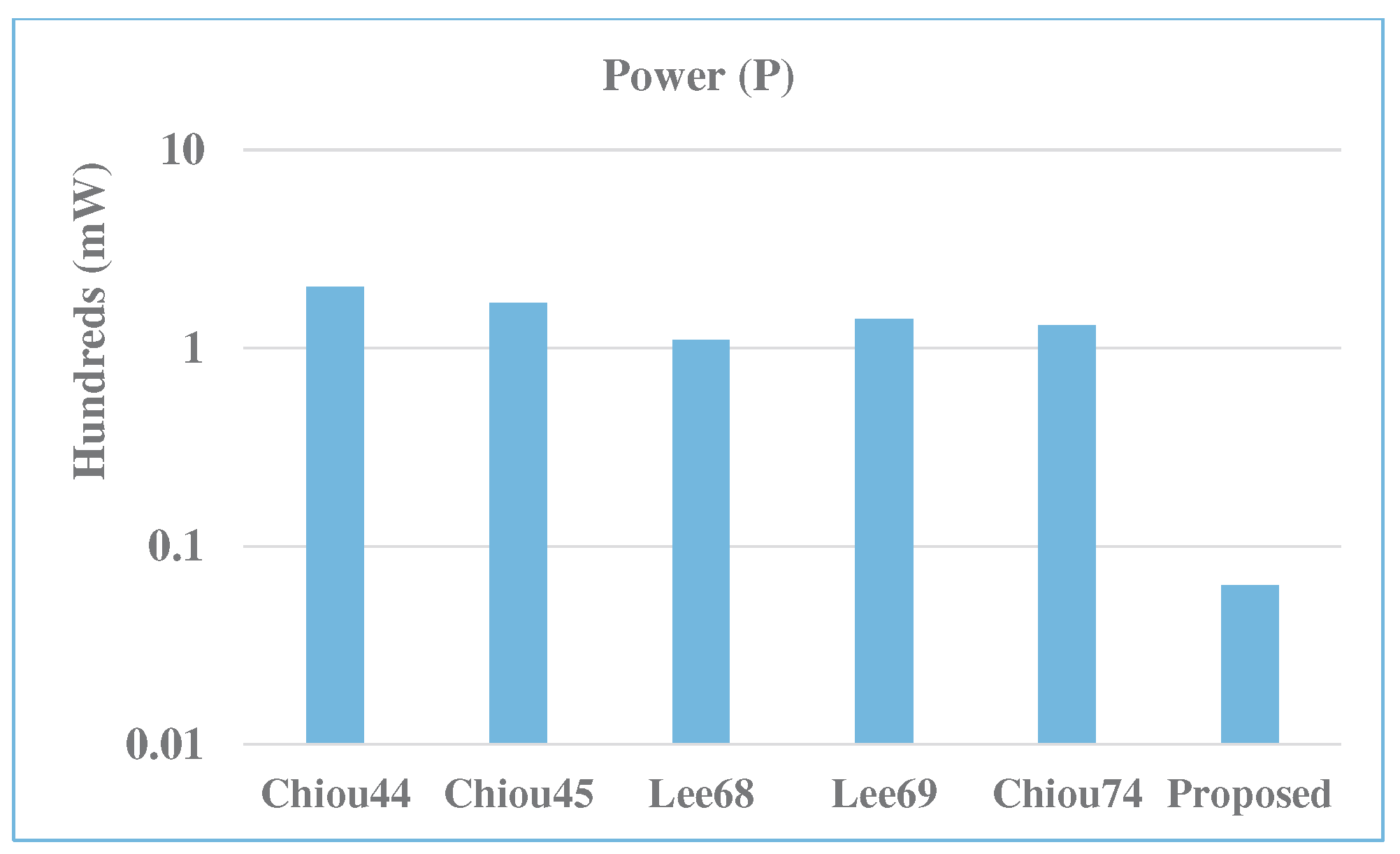
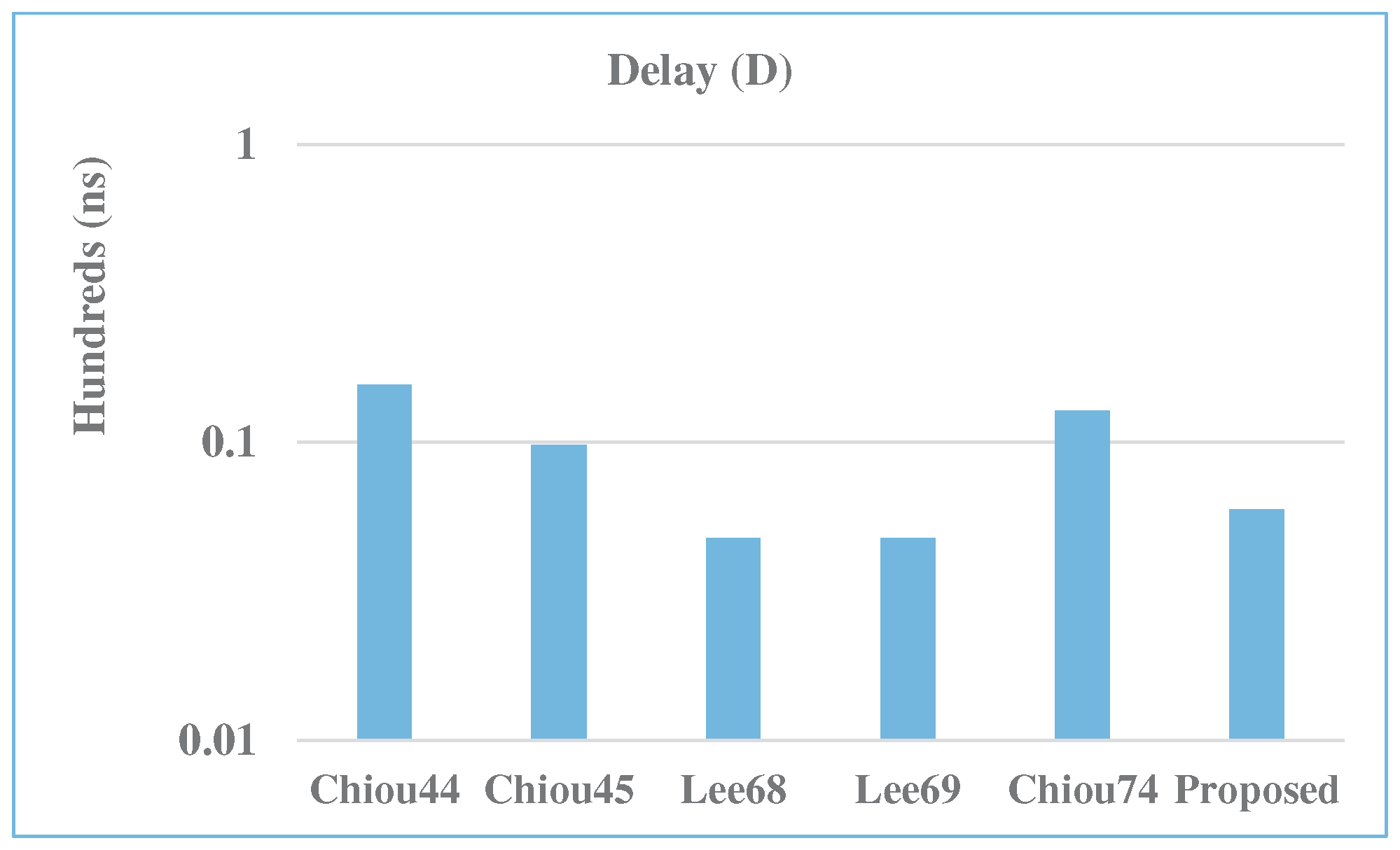
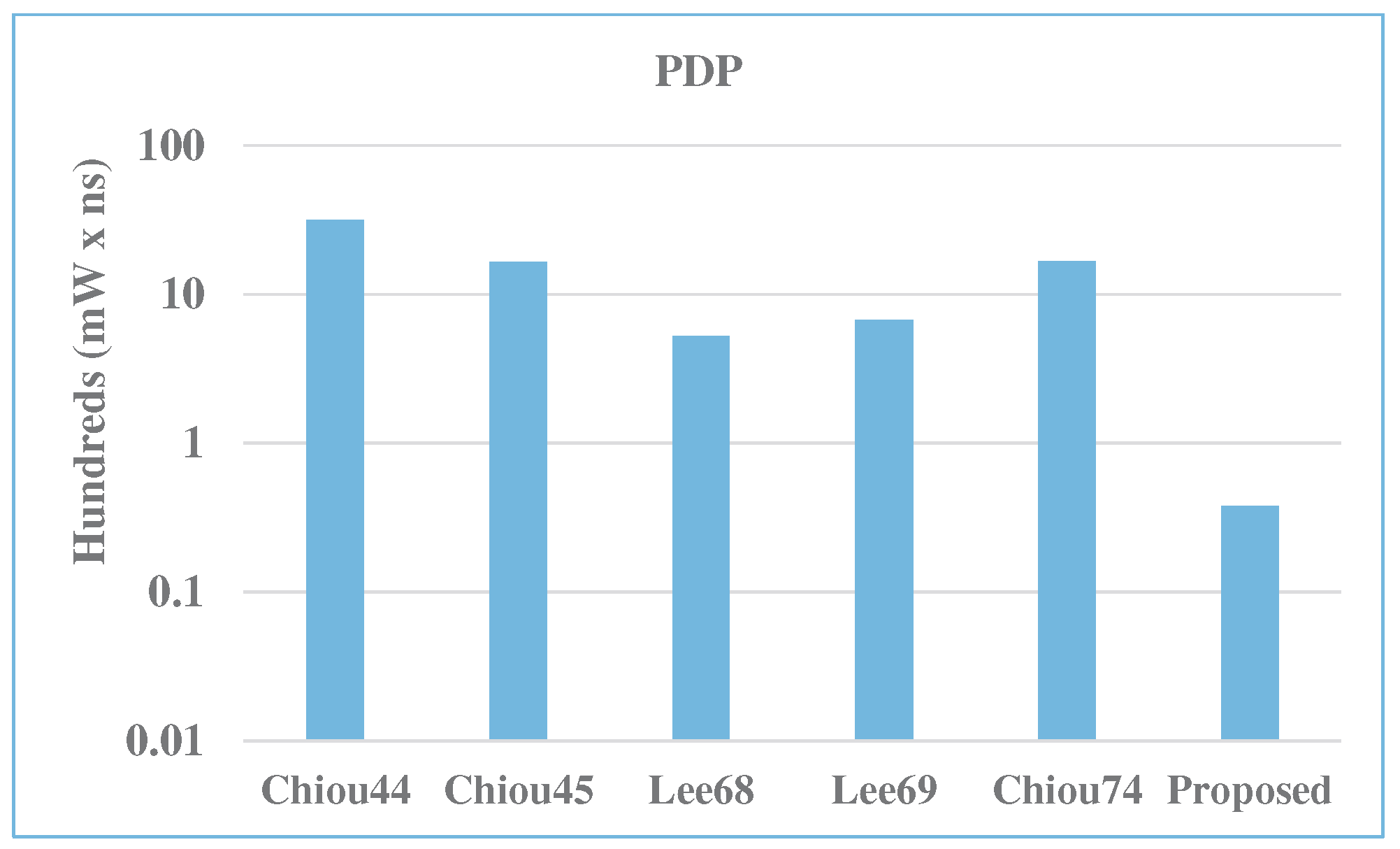
Multiplier	m	A	D	P	ADP	PDP	A Saving	P Saving	ADP Saving	PDP Saving
		[Kgates]	[ns]	[mW]			(%)	(%)	(%)	(%)
Chiou [44]	283	6082.6	15.6	202.3	95,117.0	3162.7	99.8	96.9	99.9	98.8
Chiou [45]	283	4276.3	9.8	169.7	41,720.3	1655.3	99.7	96.2	99.8	97.7
Lee  [68]	283	2631.2	4.8	109.5	12,562.2	522.6	99.6	94.2	99.5	92.8
Lee [69]	283	3771.2	4.8	140.4	18,005.1	670.3	99.7	95.5	99.6	94.3
Chiou [74]	283	3273.6	12.8	130.6	41,904.4	1671.4	99.7	95.1	99.8	97.7
Proposed	283	10.7	5.9	6.4	63.8	37.9	-	-	-	-

. These findings substantiate the assertions related to reduced space complexity and enhancements in both the area–delay product (ADP) and power–delay product (PDP). By achieving lower resource utilization without sacrificing performance, the proposed layout delivers significant tangible benefits. This is particularly relevant for RFID-based IoT applications for disabled individuals, where considerations such as power consumption, efficient area utilization, and overall operational efficiency are paramount.

7.2. Implementation Findings

The introduced systolic multiplier design was rigorously evaluated in comparison with existing systolic and semi-systolic multiplier implementations [44,45,68,69,74] through a thorough approach. The modeling and implementation of the various multiplier setups were accomplished using the VHDL programming language, which facilitates precise hardware description. For synthesis, the process utilized the Synopsis Design Compiler along with the Nangate library (15 nm, 0.8 V), renowned for providing accurate estimations of area, delay, and power consumption at a granular level.

In order to verify that the designs met functional specifications, an extensive validation process was carried out using ModelSim’s simulation tools. This phase included the development of elaborate testbenches tailored to assess a wide range of operational scenarios, thereby confirming the reliability of outputs under different conditions. The rigorous nature of this verification was essential in identifying potential issues early on, ensuring that only designs that passed all functional tests proceeded to the synthesis stage, thereby optimizing the overall development workflow.

The synthesis phase is essential for converting the VHDL code of each multiplier design into a gate-level netlist, a task efficiently handled by the Synopsys Design Compiler. This critical process translates high-level design specifications into a format ready for physical implementation, ensuring that the designs can be effectively realized in hardware. The resulting gate-level netlists provide a detailed representation of the logical structure, facilitating further optimization and analysis in the subsequent stages of the design flow. This compiler leveraged the Nangate library, which supplies critical technology-specific parameters, including gate dimensions, interconnect delays, and power attributes, essential for achieving the accurate and efficient synthesis tailored to the specific technology node. During this phase, the design compiler optimized the netlist according to predefined constraints such as area and power requirements, ensuring that the final implementation not only met performance targets but also adhered to design specifications. This optimization process is crucial for enhancing the overall functionality and reliability of the multiplier layouts.

Once the synthesis is completed, key performance metrics—namely area, delay, and power consumption—are extracted from the synthesized netlists. Analyzing these metrics provides valuable insights into the efficiency of each design, enabling a robust comparison that highlight the strengths and weaknesses of the various multiplier configurations in real-world applications.

The synthesized results for the recommended unidirectional systolic multiplier design, alongside existing configurations [44,45,68,69,74], are detailed in Table 2 for a field size of $m=283$. This table encapsulates critical performance metrics, including area, delay, power consumption, area–delay product (ADP), and power–delay product (PDP), all derived from the synthesis outputs. Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 illustrate bar charts on a logarithmic scale that compare the performance metrics of area, power consumption, delay, ADP, and PDP for the suggested unidirectional multiplier design alongside existing competitive designs. These charts effectively showcase the advantages and limitations of the new design, providing valuable insights into its performance across different criteria.

A thorough analysis of the data presented in Table 2 and Figure 11 and Figure 12 reveals that the recommended unidirectional systolic multiplier demonstrates remarkable improvements in both space efficiency and power usage when compared to existing designs. Specifically, the reduction in space utilization is striking, ranging from 99.6% to 99.8%, which highlights a dramatic decrease in the hardware resources required. Furthermore, power consumption improvements are equally impressive, with reductions between 94.2% and 96.9%. These results underscore a significant enhancement in energy efficiency, making the proposed design particularly advantageous for applications where resource constraints are a critical consideration.

An important observation regarding the proposed design is that it demonstrates a marginally higher delay when compared to several existing configurations, as shown in Figure 13. This increased delay is largely attributed to the moderately larger latency and elevated CPD observed in the proposed layout. The CPD, which indicates the longest delay path within the multiplier circuit, plays a crucial role in determining overall performance. However, despite this minor increase in delay, the proposed design maintains a level of computational efficiency that is comparable to other options in terms of time complexity. This characteristic ensures its suitability for a wide range of practical applications, where performance requirements are balanced with other design considerations.

From Table 2 and Figure 14 and Figure 15, we observed that the suggested unidirectional systolic multiplier arrangement demonstrates significant advantages in terms of the ADP and PDP, two critical design parameters that reflect the trade-offs between area, delay, and power consumption. Notably, the proposed design achieves impressive reductions in ADP, ranging from 99.5% to 99.9% across the compared designs. This indicates not only a substantial enhancement in overall performance but also improved resource utilization. In addition, the PDP improvements are striking, with reductions ranging from 92.8% to 98.8%. These figures underscore the energy efficiency benefits of the proposed configuration. Given these results, the unidirectional bit-parallel systolic multiplier emerges as an ideal choice for deployment in resource-constrained RFID-based IoT applications for individuals with disabilities, where the efficient use of resources is paramount.

Based on the previous analysis, the proposed multiplier design effectively combines significant space and power savings with a delay comparable to competing designs, ensuring efficient computation and responsiveness in time-sensitive applications. Furthermore, it achieves substantial reductions in both the ADP and PDP, indicating enhanced overall performance and efficiency. These improved metrics reflect effective hardware utilization and greater energy efficiency, making the design particularly well suited for resource-constrained RFID tags that require optimized performance and extended battery life.

Considering these factors, the introduced unidirectional bit-parallel systolic multiplier is an excellent choice for cryptographic protocols in RFID tags with limited resources, as it optimizes the space and power consumption while delivering efficient performance, making it particularly suitable for RFID-based IoT applications aimed at assisting disabled individuals. Importantly, the introduced unidirectional systolic structure can be easily reconfigured to incorporate error detection capabilities, thereby enhancing its resistance to side-channel attacks. This enhances the functionality and security of devices such as smart mobility aids and health monitoring systems, ensuring that sensitive data remain secure without compromising battery life. The compact nature of the design allows for integration into small, user-friendly RFID tags, facilitating seamless interactions and enabling features like real-time location tracking and personalized assistance services. By improving the performance of RFID tags, the proposed multiplier not only reinforces secure communications but also significantly enhances the quality of life for disabled individuals, contributing to greater independence and empowerment through advanced assistive technologies.

8. Key Findings and Conclusions

This study concentrates on the creation of an innovative and high-performing unidirectional systolic array configuration for Dickson-basis multiplication within the binary extension field. The methodology involves deriving a DG for the chosen multiplier. By implementing appropriate scheduling and node projection functions for each node in the DG, we successfully construct a practical unidirectional bit-parallel systolic multiplier. This cutting-edge design facilitates rapid and efficient multiplication operations using the Dickson method. One of the primary benefits of this unidirectional systolic arrangement is its notably reduced space complexity. Unlike earlier parallel designs that exhibit quadratic space requirements, this new layout achieves linear space complexity, representing a significant enhancement in resource efficiency, particularly for VLSI applications. The complexity analysis indicates that this multiplier occupies a considerably smaller area, further confirming its efficiency and feasibility for implementation. To assess the performance of the proposed design, we synthesized both this new layout and previously developed multiplier architectures using the ASIC CMOS library. The synthesis results highlighted significant reductions in area and power, while key metrics such as power–delay product and area–delay product showed notable improvements, reinforcing the efficiency of the proposed architecture. Consequently, the findings support the conclusion that this multiplier framework is well suited for cryptographic protocols in RFID tags with limited resources, effectively optimizing both space and power consumption. It also allows for enhanced error detection capabilities, improving the functionality of devices such as smart mobility aids and health monitoring systems for individuals with disabilities. Looking ahead, the design can be adapted to include error detection features, further increasing its resilience against side-channel attacks.