Exploring the Evolutionary Traits of Post-Disaster Reconstruction Under the Background of Sustainable Development
Abstract
1. Introduction
2. The Literature Review
2.1. PDR Models
2.2. PDR Composition
2.3. Conceptualizing Sustainable PDR
2.4. The Position of This Paper
3. Evolutionary Model of PDR
3.1. Model Assumptions
3.2. Model Construction
3.3. Model Analysis
3.3.1. Evolutionary Stability Analysis
3.3.2. Evolutionary Pathway Analysis
4. Numerical Simulations
4.1. Simulations on Evolutionary Stability
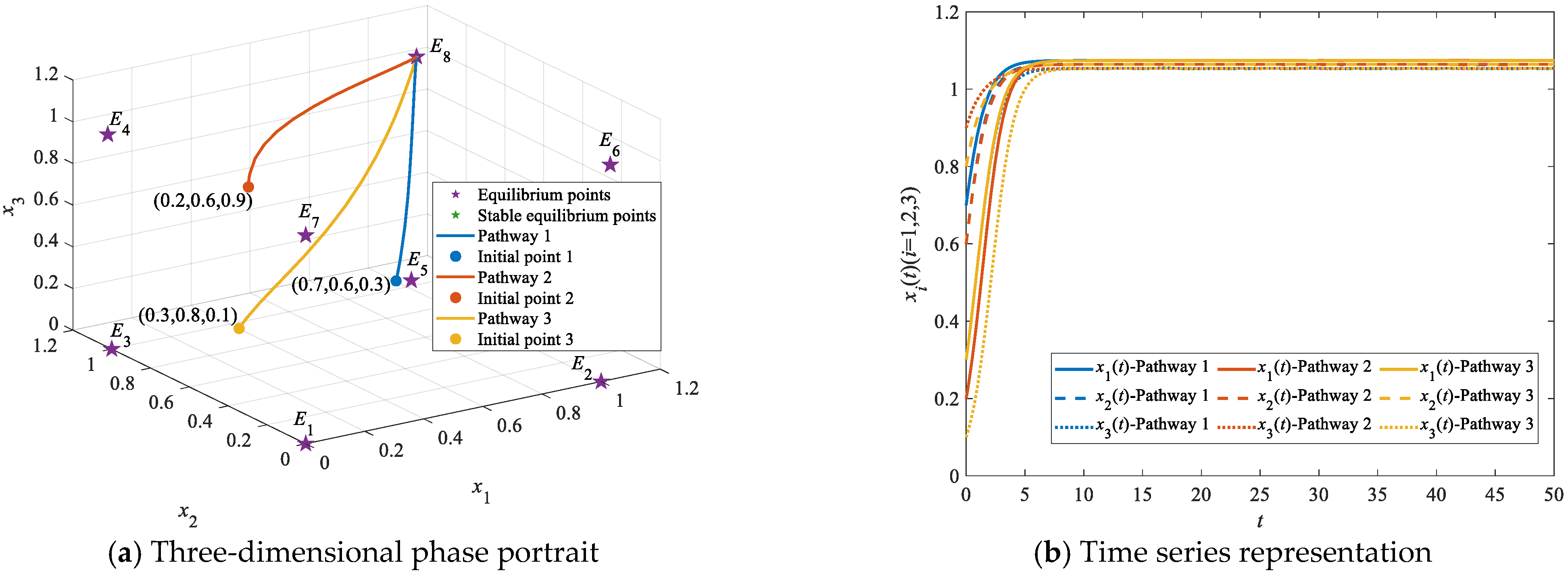
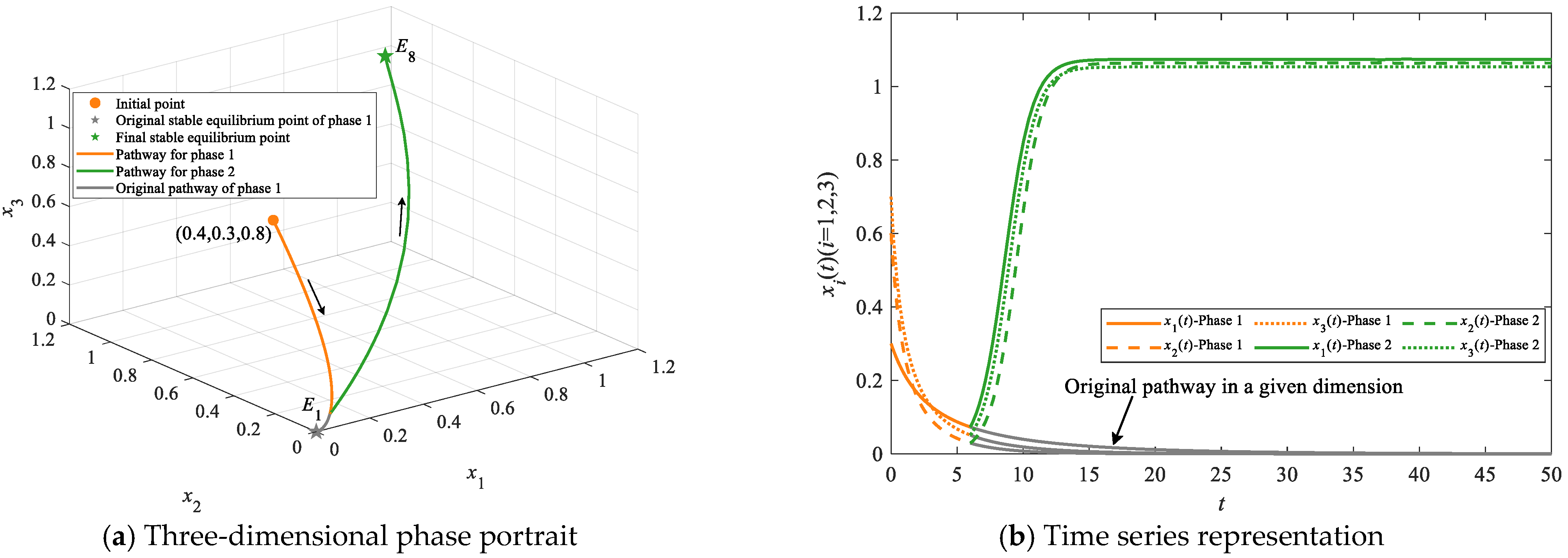
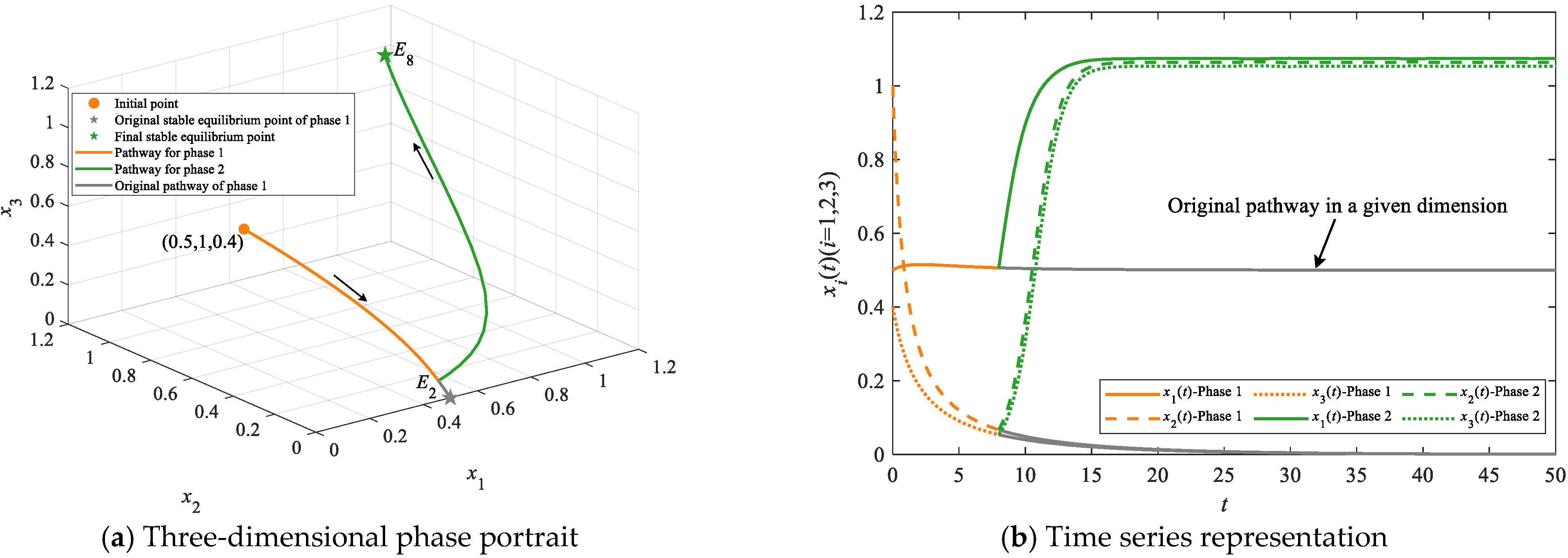
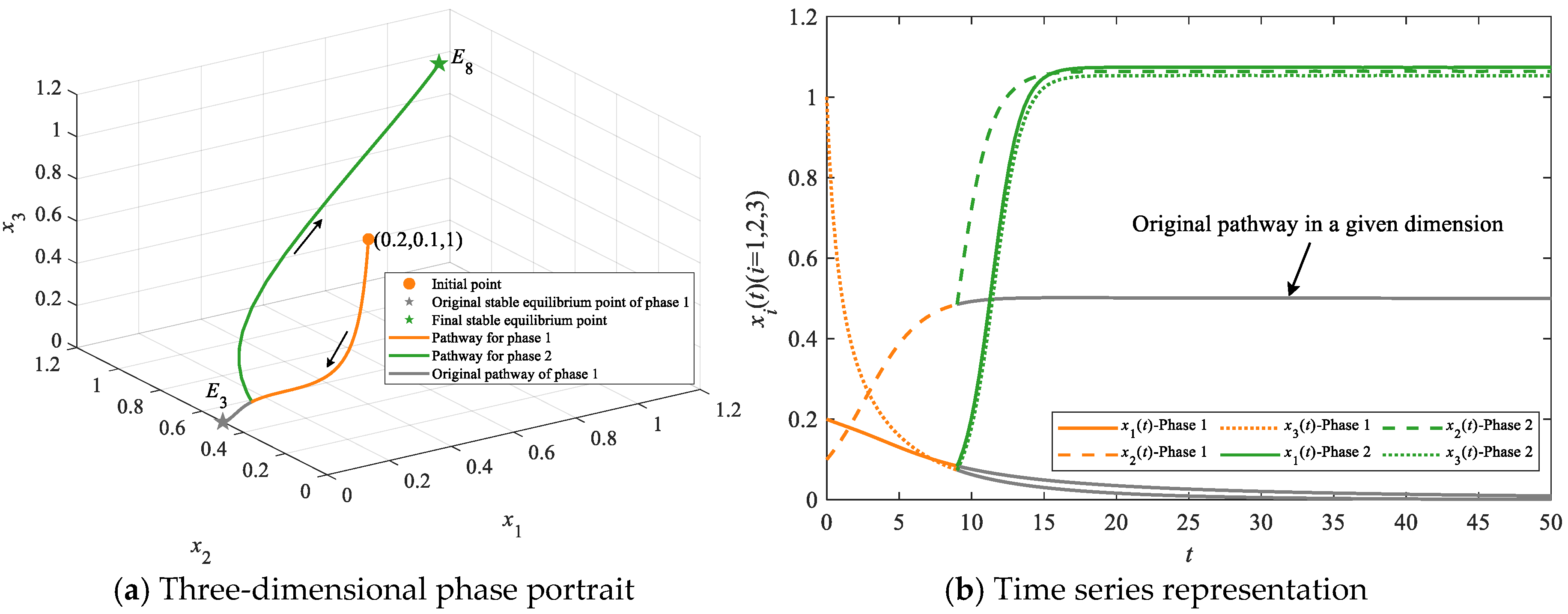
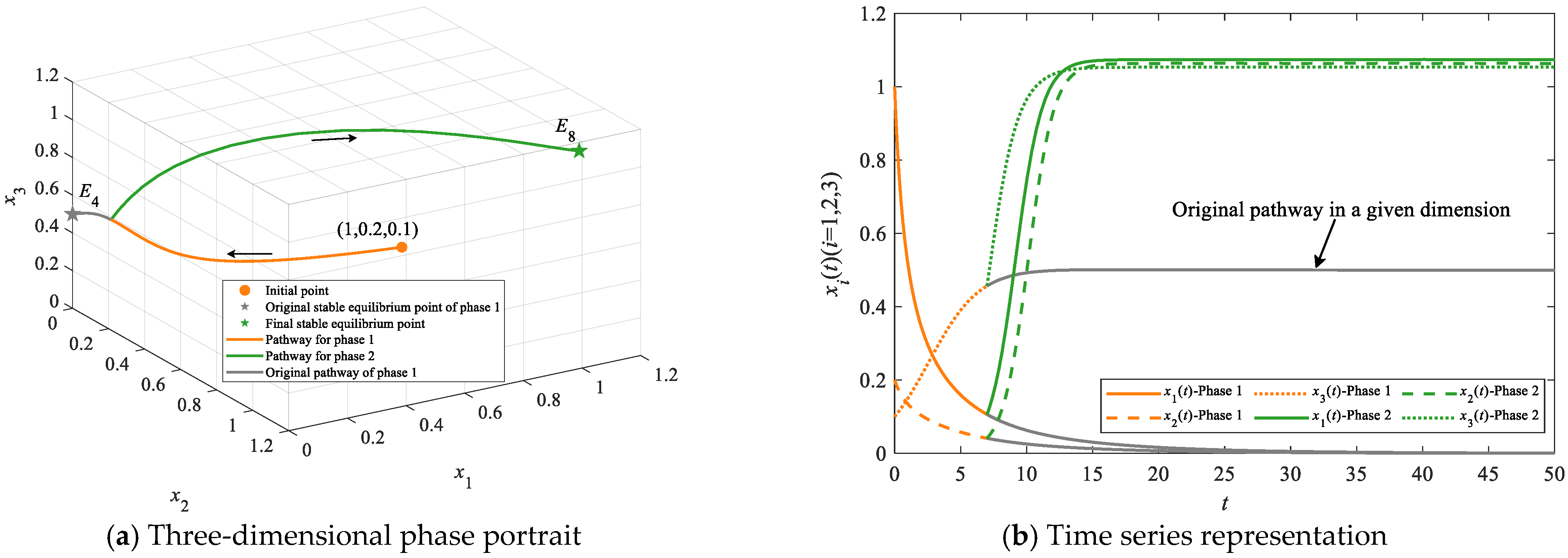
4.2. Simulations on Evolutionary Pathways
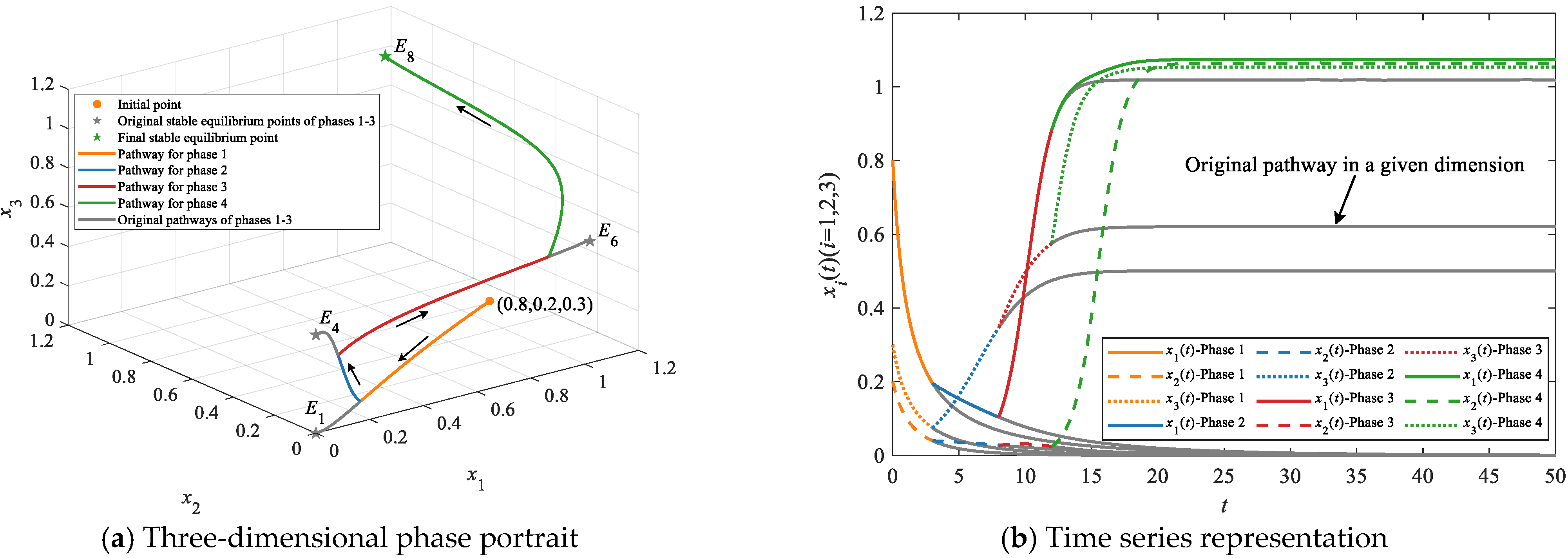
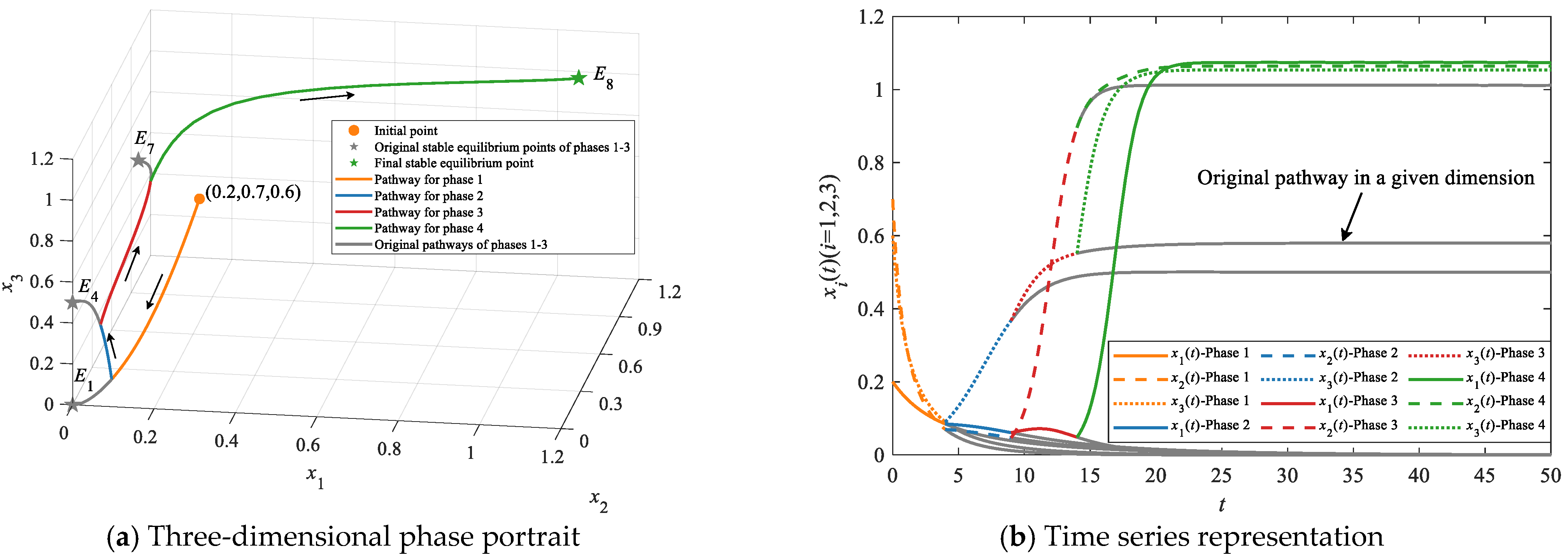
4.2.1. Simulations on Stepwise Evolutionary Pathways
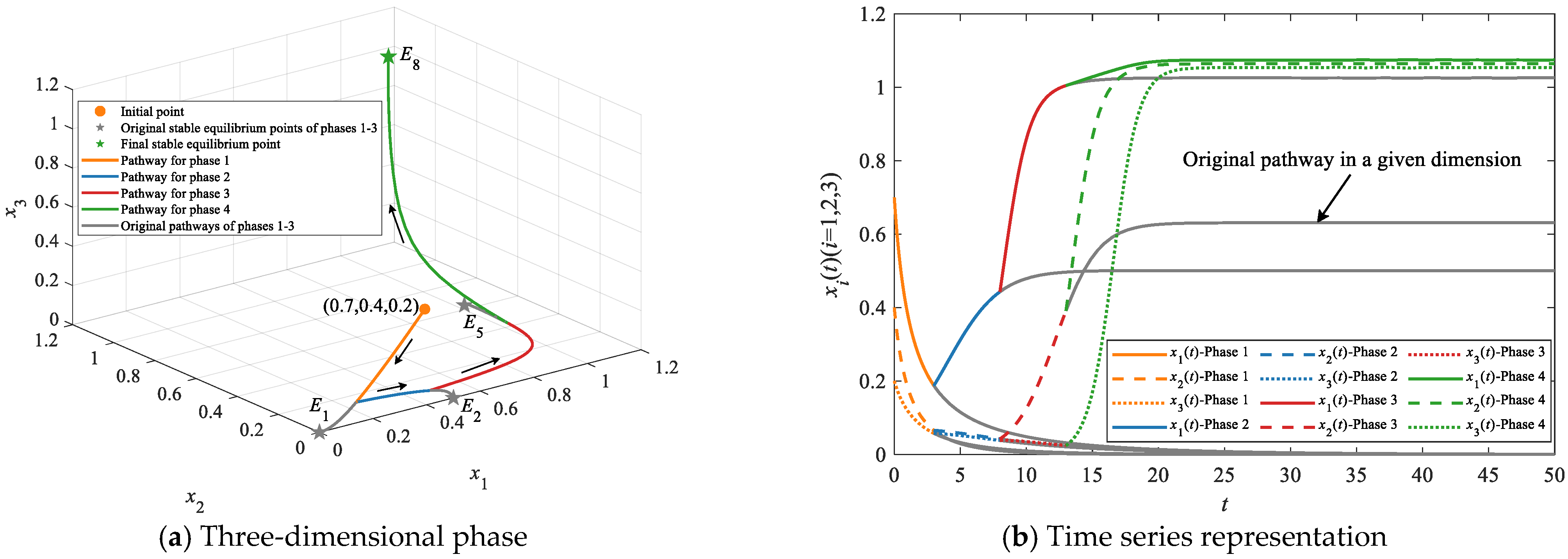
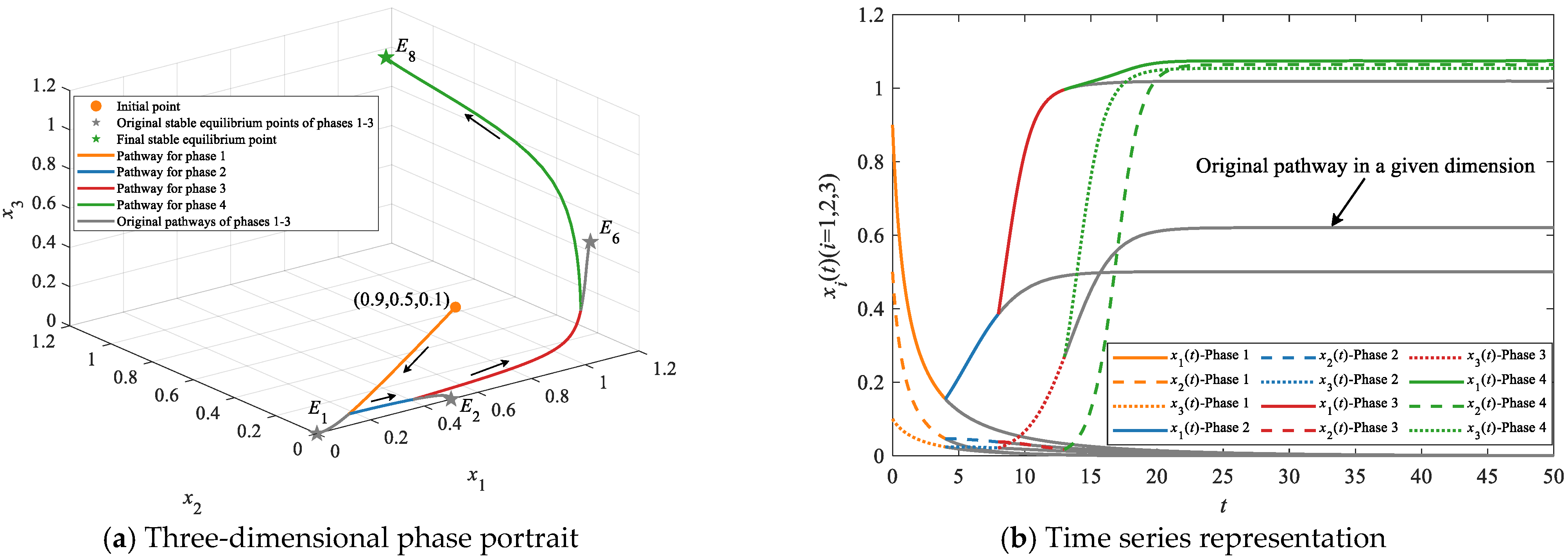
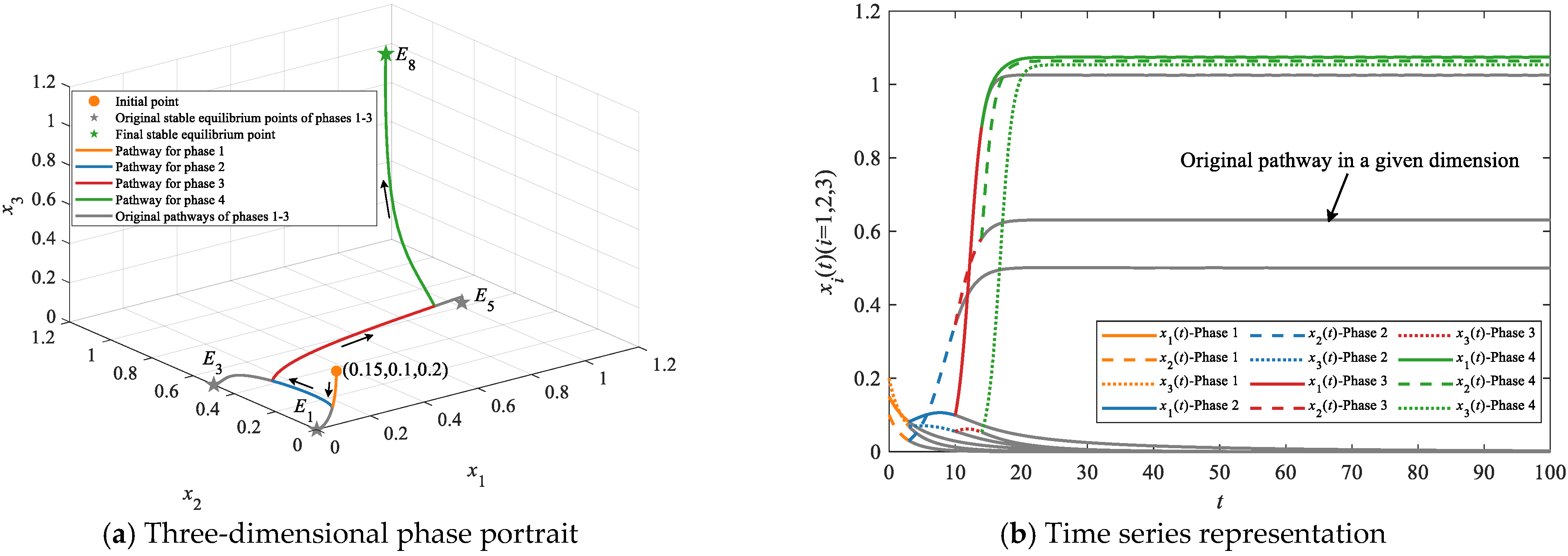
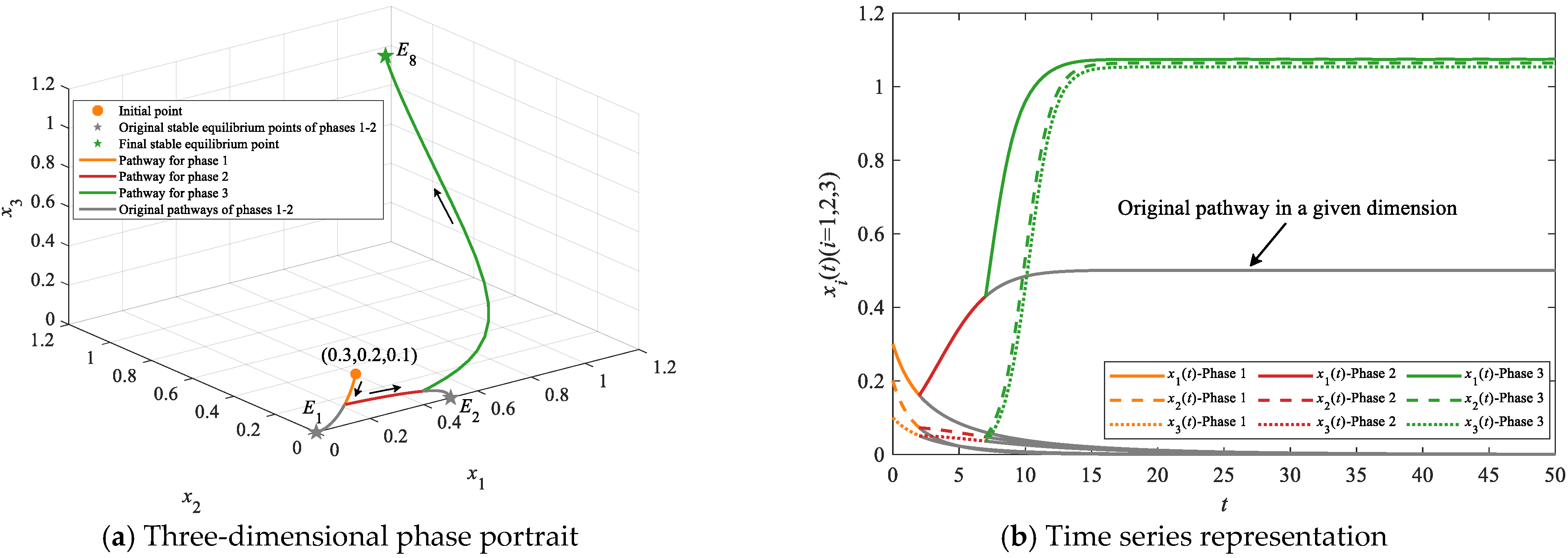
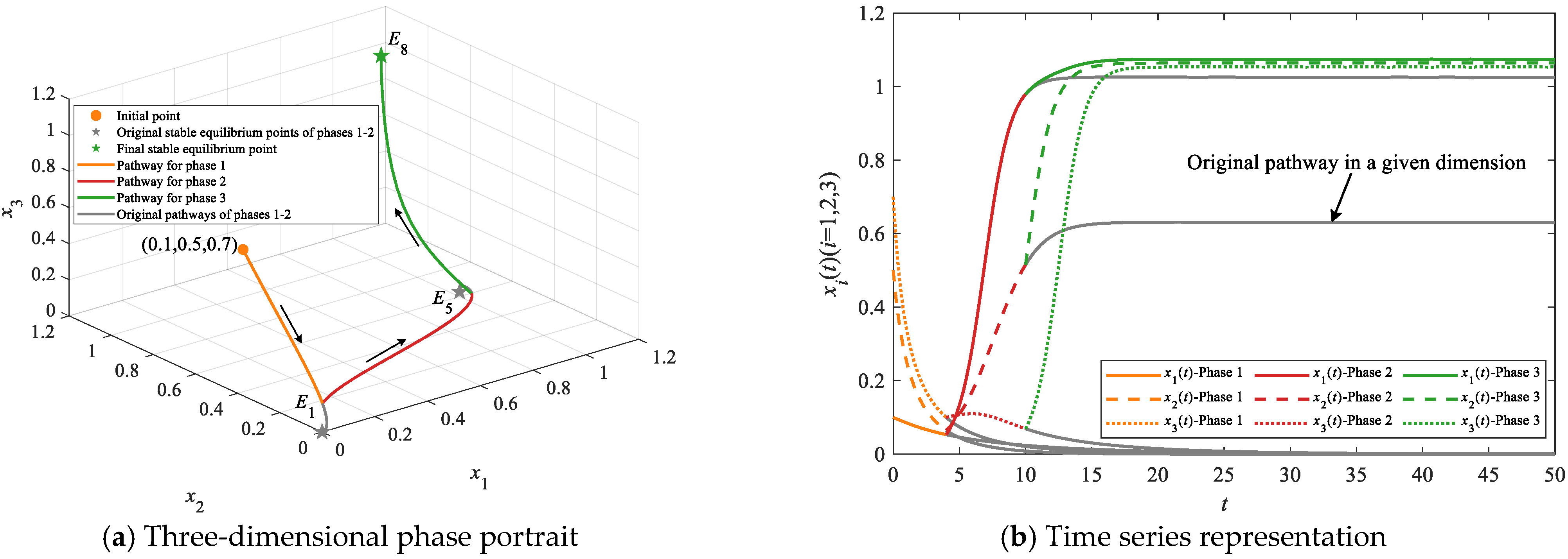
4.2.2. Simulations on Leapfrogging Evolutionary Pathways
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hosseini, S.M.A.; Farahzadi, L.; Pons, O. Assessing the sustainability index of different post-disaster temporary housing unit configuration types. J. Build. Eng. 2021, 42, 102806. [Google Scholar] [CrossRef]
- Pomponi, F.; Moghayedi, A.; Alshawawreh, L.; D’Amico, B.; Windapo, A. Sustainability of post-disaster and post-conflict sheltering in Africa: What matters? Sustain. Prod. Consum. 2019, 20, 140–150. [Google Scholar] [CrossRef]
- Opabola, E.A.; Galasso, C.; Rossetto, T.; Meilianda, E.; Idris, Y.; Nurdin, S. Investing in disaster preparedness and effective recovery of school physical infrastructure. Int. J. Disaster Risk Reduct. 2023, 90, 103623. [Google Scholar] [CrossRef]
- Mushtaha, A.W.; Alaloul, W.S. Sustainability factors influencing post-disaster reconstruction projects: Critical review and bibliometric analysis. Sustain. Futures 2025, 10, 100930. [Google Scholar] [CrossRef]
- Hendriks, E.; Opdyke, A. The influence of technical assistance and funding on perceptions of post-disaster housing safety after the 2015 Gorkha earthquakes in Nepal. Int. J. Disaster Risk Reduct. 2022, 73, 102906. [Google Scholar] [CrossRef]
- Opabola, E.A.; Galasso, C. A probabilistic framework for post-disaster recovery modeling of buildings and electric power networks in developing countries. Reliab. Eng. Syst. Saf. 2024, 242, 109679. [Google Scholar] [CrossRef]
- Matsushita, T.; Ghezelloo, Y.; Maly, E.; Kondo, T.; Meyer, M.; Newman, G. Placemaking mediating dilemmas by addressing the gaps in post-disaster recovery process: Long-term citizen-driven place-nurturing in New Orleans after hurricane Katrina. Int. J. Disaster Risk Reduct. 2024, 106, 104457. [Google Scholar] [CrossRef]
- Asgary, A.; Naeemi, P.; Ganguli, N.; Tofighi, M.; Attarian, K.; Fioretto, T. Road to resettlement: Understanding post-disaster relocation and resettlement challenges and complexities through a serious Game. Int. J. Disaster Risk Sci. 2024, 15, 521–535. [Google Scholar] [CrossRef]
- Hadlos, A.; Opdyke, A.; Hadigheh, S.A.; Gato, C. Pathways of multi-hazard post-disaster housing reconstruction among Ivatan Indigenous households. J. Build. Eng. 2024, 91, 109636. [Google Scholar] [CrossRef]
- Kobayashi, A.; Kobayashi, T.; Maeda, M.; Hidaka, T.; Mizuki, R. Factors ensuring healthy work environments for municipal office workers in the disaster area after the Fukushima Daiichi nuclear power plant accident: A qualitative analysis. Int. J. Disaster Risk Reduct. 2025, 116, 105125. [Google Scholar] [CrossRef]
- Ngulube, N.K.; Tatano, H.; Samaddar, S. Factors impacting participatory post-disaster relocation and housing reconstruction: The case of Tsholotsho District, Zimbabwe. Int. J. Disaster Risk Sci. 2024, 15, 58–72. [Google Scholar] [CrossRef]
- Sospeter, N.G.; Rwelamila, P.D.; Gimbi, J.J. A conceptual framework for managing post-disaster reconstruction projects in emerging economies: The case of Angola. Built Environ. Proj. Asset Manag. 2022, 12, 205–222. [Google Scholar] [CrossRef]
- Deng, H.; Li, H.; Xu, L.; Khudhair, A.; Song, H.; Gao, Y. Real-time bridge disaster management: Enabling technology and application framework. Autom. Constr. 2025, 174, 106150. [Google Scholar] [CrossRef]
- Xue, J.; Park, S.; Mondal, W.U.; Reia, S.M.; Yao, T.; Ukkusuri, S.V. An agent-based model of post-disaster recovery in multilayer socio-physical networks. Sustain. Cities Soc. 2024, 115, 105863. [Google Scholar] [CrossRef]
- Sharif, S.V.; Moshfegh, P.H.; Kashani, H. Simulation modeling of operation and coordination of agencies involved in post-disaster response and recovery. Reliab. Eng. Syst. Saf. 2023, 235, 109219. [Google Scholar] [CrossRef]
- Daşbaşı, T.; Daşbaşı, B. Fractional-order model of the post-disaster period: Study on the earthquakes in Türkiye. Math. Model. Numer. Simul. Appl. 2025, 5, 117–142. [Google Scholar] [CrossRef]
- Ghaffarian, S.; Roy, D.; Filatova, T.; Kerle, N. Agent-based modelling of post-disaster recovery with remote sensing data. Int. J. Disaster Risk Reduct. 2021, 60, 102285. [Google Scholar] [CrossRef]
- Wei, M.; Xu, J. Assessing road network resilience in disaster areas from a complex network perspective: A real-life case study from China. Int. J. Disaster Risk Reduct. 2024, 100, 104167. [Google Scholar] [CrossRef]
- Haken, H. Synergetics. Phys. Bull. 1977, 28, 412. [Google Scholar] [CrossRef]
- Sina, D.; Chang-Richards, A.Y.; Wilkinson, S.; Potangaroa, R. What does the future hold for relocated communities post-disaster? Factors affecting livelihood resilience. Int. J. Disaster Risk Reduct. 2019, 34, 173–183. [Google Scholar] [CrossRef]
- Liu, K.; Chang-Richards, A.; Costello, S.B.; L’Hermitte, C.; Li, N. What factors influence building material supply for post-disaster reconstruction and recovery? A systematic review applying systems thinking. Int. J. Disaster Risk Reduct. 2024, 114, 104981. [Google Scholar] [CrossRef]
- Mushtaha, A.W.; Alaloul, W.S.; Baarimah, A.O.; Musarat, M.A.; Alzubi, K.M.; Khan, A.M. A decision-making framework for prioritizing reconstruction projects in post-disaster recovery. Results Eng. 2025, 25, 103693. [Google Scholar] [CrossRef]
- Okunola, O.H.; Werners, S.E. A multi-dimensional framework for assessing disaster recovery pathways: Lessons and experiences from Germany and Nigeria. Int. J. Disaster Risk Reduct. 2024, 112, 104777. [Google Scholar] [CrossRef]
- Wang, C.; Wu, J.; Guo, E.; Wang, Y. The TransIRIO model: Capturing the economic ripple effect of different economic behaviours in post-disaster emergency-recovery-reconstruction. Int. J. Disaster Risk Reduct. 2024, 110, 104634. [Google Scholar] [CrossRef]
- Lagap, U.; Ghaffarian, S. Digital post-disaster risk management twinning: A review and improved conceptual framework. Int. J. Disaster Risk Reduct. 2024, 110, 104629. [Google Scholar] [CrossRef]
- Davidson, C.H.; Johnson, C.; Lizarralde, G.; Dikmen, N.; Sliwinski, A. Truths and myths about community participation in post-disaster housing projects. Habitat Int. 2007, 31, 100–115. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z.; Wang, T.; Lin, Z.; Fang, D. Post-disaster recovery planning for infrastructure systems based on residents’ needs: A hypernetwork approach. Int. J. Disaster Risk Reduct. 2025, 118, 105258. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, J. Low-carbon reconstruction: A meta-synthesis approach for the sustainable development of a post-disaster community. Syst. Res. Behav. Sci. 2016, 33, 173–187. [Google Scholar] [CrossRef]
- Lazarević, M.P. Elements of mathematical phenomenology of self-organization nonlinear dynamical systems: Synergetics and fractional calculus approach. Int. J. Non-Linear Mech. 2015, 73, 31–42. [Google Scholar] [CrossRef]
- Kabir, K.A.; Tanimoto, J. The role of pairwise nonlinear evolutionary dynamics in the rock–paper–scissors game with noise. Appl. Math. Comput. 2021, 394, 125767. [Google Scholar] [CrossRef]
- Chen, X.; Kwan, M.P.; Li, Q.; Chen, J. A model for evacuation risk assessment with consideration of pre-and post-disaster factors. Comput. Environ. Urban Syst. 2012, 36, 207–217. [Google Scholar] [CrossRef]
- Xiao, Y.; Tian, K.; Yuan, M.; Ouyang, Y.; Huang, H. Examining the complex relationships between socioeconomic development and the improvement of ecological environment in post-disaster reconstruction: The case of Wenchuan earthquake disaster area in Western China. J. Clean. Prod. 2022, 337, 130581. [Google Scholar] [CrossRef]
- Moghri, A.; Khalili, A. Investigating the influential post-disaster factors in determining the optimal location of shelters: A case study, Sarpol-e Zahab, Kermanshah province, Iran. Front. Archit. Res. 2022, 11, 846–864. [Google Scholar] [CrossRef]
- Ngulube, N.K.; Tatano, H.; Samaddar, S. Community insights: Citizen participation in Kamaishi Unosumai decade-long recovery from the Great East Japan Earthquake. Int. J. Disaster Risk Sci. 2023, 14, 886–897. [Google Scholar] [CrossRef]
- Okunola, O.H. Stakeholder engagement in disaster recovery: Insights into roles and power dynamics from the Ahr Valley, Germany. Int. J. Disaster Risk Reduct. 2024, 114, 104960. [Google Scholar] [CrossRef]
- Khan, M.T.I.; Anwar, S.; Sarkodie, S.A.; Yaseen, M.R.; Nadeem, A.M.; Ali, Q. Comprehensive disaster resilience index: Pathway towards risk-informed sustainable development. J. Clean. Prod. 2022, 366, 132937. [Google Scholar] [CrossRef]
- Yuan, M.; Xiao, Y.; Yang, Y.; Liu, C. Coupling coordination analysis of the economy-ecology-society complex systems in China’s Wenchuan earthquake disaster area. Ecol. Indic. 2023, 156, 111145. [Google Scholar] [CrossRef]
- Sartori, S.; Latrônico, F.; Campos, L. Sustainability and sustainable development: A taxonomy in the field of literature. Ambiente Soc. 2014, 17, 01–22. [Google Scholar] [CrossRef]
- Olawumi, T.O.; Chan, D.W. A scientometric review of global research on sustainability and sustainable development. J. Clean. Prod. 2018, 183, 231–250. [Google Scholar] [CrossRef]
- Ruggerio, C.A. Sustainability and sustainable development: A review of principles and definitions. Sci. Total Environ. 2021, 786, 147481. [Google Scholar] [CrossRef]
- Dresner, S. The Principles of Sustainability, 2nd ed; Routledge: London, UK, 2012; pp. 1–224. ISBN 978-1-84407-496-9. [Google Scholar]
- Keeble, B.R. The Brundtland report: ‘Our common future’. Med. War 1988, 4, 17–25. [Google Scholar] [CrossRef]
- Tuazon, D.; Corder, G.D.; McLellan, B.C. Sustainable development: A review of theoretical contributions. Int. J. Sustain. Future Hum. Secur. 2013, 1, 40–48. [Google Scholar] [CrossRef]
- Parris, T.M.; Kates, R.W. Characterizing and measuring sustainable development. Annu. Rev. Environ. Resour. 2003, 28, 559–586. [Google Scholar] [CrossRef]
- Ben-Eli, M.U. Sustainability: Definition and five core principles, a systems perspective. Sustain. Sci. 2018, 13, 1337–1343. [Google Scholar] [CrossRef]
- Paul, B.D. A history of the concept of sustainable development: Literature review. Ann. Univ. Oradea Econ. Sci. Ser. 2008, 17, 576–580. [Google Scholar]
- Mishra, M.; Desul, S.; Santos, C.A.G.; Mishra, S.K.; Kamal, A.H.M.; Goswami, S.; Kalumba, A.M.; Biswal, R.; da Silva, R.M.; dos Santos, C.A.C.; et al. A bibliometric analysis of sustainable development goals (SDGs): A review of progress, challenges, and opportunities. Environ. Dev. Sustain. 2024, 26, 11101–11143. [Google Scholar] [CrossRef] [PubMed]
- Giovannoni, E.; Fabietti, G. What is sustainability? A review of the concept and its applications. In Integrated Reporting: Concepts and Cases That Redefine Corporate Accountability; Busco, C., Frigo, M., Riccaboni, A., Quattrone, P., Eds.; Springer: Cham, Switzerland, 2013; pp. 21–40. ISBN 978-3-319-02167-6. [Google Scholar]
- Johri, A.; Joshi, P.; Kumar, S.; Joshi, G. Metaverse for sustainable development in a bibliometric analysis and systematic literature review. J. Clean. Prod. 2024, 435, 140610. [Google Scholar] [CrossRef]
- Zhao, J.; Gu, Y.; Xie, X.; Yu, D. Actor-critic-disturbance reinforcement learning algorithm-based fast finite-time stability of multiagent systems. Inf. Sci. 2025, 699, 121802. [Google Scholar] [CrossRef]
- Chen, G.; Xia, J.; Park, J.H.; Shen, H.; Zhuang, G. Robust sampled-data control for switched complex dynamical networks with actuators saturation. IEEE Trans. Cybern. 2021, 52, 10909–10923. [Google Scholar] [CrossRef]
- Barnett, W.P.; Carroll, G.R. Competition and mutualism among early telephone companies. Adm. Sci. Q. 1987, 32, 400–421. [Google Scholar] [CrossRef]
- Bertsimas, D.; King, A. Logistic regression: From art to science. Stat. Sci. 2017, 32, 367–384. [Google Scholar] [CrossRef]
- Jie, J.; Yang, Y.; Zhang, P. The construction method of chaotic system model based on state variables and uncertain variables and its application in image encryption. Appl. Math. Model. 2025, 144, 116097. [Google Scholar] [CrossRef]
- Anilkumar, S.; Banerji, H. An inquiry into success factors for post-disaster housing reconstruction projects: A case of Kerala, South India. Int. J. Disaster Risk Sci. 2021, 12, 24–39. [Google Scholar] [CrossRef]
- McCaughey, J.W.; Daly, P.; Mundir, I.; Mahdi, S.; Patt, A. Socio-economic consequences of post-disaster reconstruction in hazard-exposed areas. Nat. Sustain. 2018, 1, 38–43. [Google Scholar] [CrossRef]
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288. [Google Scholar] [CrossRef]

| Papers | PDR Models | PDR Composition | |||
|---|---|---|---|---|---|
| Conceptual Models | Complex Systems Models | Local or Qualitative Exploration | Global and Quantitative Exploration | ||
| Non-Synergetics-Based | Synergetics-Based | ||||
| [6,12,13,22,23,24,25] | ✓ | ||||
| [14,16,17,18,27,28] | ✓ | ||||
| [3,6,33,34,35] | ✓ | ||||
| This paper | ✓ | ✓ | |||
| Evolutionary Pathway Types | Initial Stable Point | Intermediate Stable Point | Ideal Stable Point | Pathways | Intervention Stages Required |
|---|---|---|---|---|---|
| Stepwise evolutionary pathways | E1 | E2, E5/E6; E3, E5/E7; E4, E6/E7; | E8 | E1→E2→E5→E8, E1→E2→E6→E8, E1→E3→E5→E8, E1→E3→E7→E8, E1→E4→E6→E8 and E1→E4→E7→E8 | At least three |
| E2 | E5/E6 | E8 | E2→E5→E8 and E2→E6→E8 | At least two | |
| E3 | E5/E7 | E8 | E3→E5→E8 and E3→E7→E8 | ||
| E4 | E6/E7 | E8 | E4→E7→E8 and E4→E6→E8 | ||
| E5/E6/E7 | None | E8 | E5→E8, E6→E8 and E7→E8 | At least one | |
| Leapfrogging evolutionary pathways | E1 | E2/E3/E4/E5/E6/E7 | E8 | E1→E2→E8, E1→E3→E8, E1→E4→E8, E1→E5→E8, E1→E6→E8 and E1→E7→E8 | At least two |
| E1 | None | E8 | E1→E8 | At least one | |
| E2/E3/E4 | None | E8 | E2→E8, E3→E8 and E4→E8 |
| Parameters (10−1) | Effective Equilibrium Points | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α1 | α2 | α3 | β11 | β12 | β13 | β21 | β22 | β23 | β31 | β32 | β33 | Stable | Unstable |
| −1 | −3 | −2 | 10 | −0.3 | −0.4 | 4 | 10 | −0.2 | 3 | 0.2 | 10 | E1 | None |
| 5 | 1 | 1 | 10 | −0.3 | −0.4 | 4 | 10 | 0.2 | 4 | 0.2 | 10 | E2 | E1, E3, E4, E7 |
| 2 | 5 | 1 | 10 | 4.5 | 0.3 | −0.3 | 10 | −0.2 | 0.3 | 4 | 10 | E3 | E1, E2, E4, E6 |
| 1 | 1 | 5 | 10 | 0.3 | 4 | 4 | 10 | 0.4 | −0.4 | −0.2 | 10 | E4 | E1, E2, E3, E5 |
| 10 | 6 | 2 | 10 | −0.3 | −0.4 | −0.3 | 10 | −0.2 | 3 | 0.2 | 10 | E5 | E1, E2, E3, E4, E7 |
| 10 | 2 | 6 | 10 | −0.3 | −0.4 | 4 | 10 | 0.2 | −0.2 | −0.3 | 10 | E6 | E1, E2, E3, E4, E7 |
| 2 | 10 | 6 | 10 | 4.5 | −0.2 | −0.3 | 10 | −0.2 | 3 | 0.2 | 10 | E7 | E1, E2, E3, E4, E6 |
| 10 | 10 | 10 | 10 | −0.4 | −0.3 | −0.4 | 10 | −0.2 | −0.3 | −0.2 | 10 | E8 | Ei(i = 1, 2, …, 7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Zhu, J.; Bao, J. Exploring the Evolutionary Traits of Post-Disaster Reconstruction Under the Background of Sustainable Development. Systems 2025, 13, 1063. https://doi.org/10.3390/systems13121063
Song Z, Zhu J, Bao J. Exploring the Evolutionary Traits of Post-Disaster Reconstruction Under the Background of Sustainable Development. Systems. 2025; 13(12):1063. https://doi.org/10.3390/systems13121063
Chicago/Turabian StyleSong, Zhiting, Jianhua Zhu, and Jingwen Bao. 2025. "Exploring the Evolutionary Traits of Post-Disaster Reconstruction Under the Background of Sustainable Development" Systems 13, no. 12: 1063. https://doi.org/10.3390/systems13121063
APA StyleSong, Z., Zhu, J., & Bao, J. (2025). Exploring the Evolutionary Traits of Post-Disaster Reconstruction Under the Background of Sustainable Development. Systems, 13(12), 1063. https://doi.org/10.3390/systems13121063






