System-Level Evaluation of Autonomous Vehicle Lane Deployment Strategies Under Mixed Traffic Flow
Abstract
1. Introduction
1.1. Literature Review
1.2. Objectives and Contributions
2. Model Formulation
2.1. Network Description
2.2. Assumptions
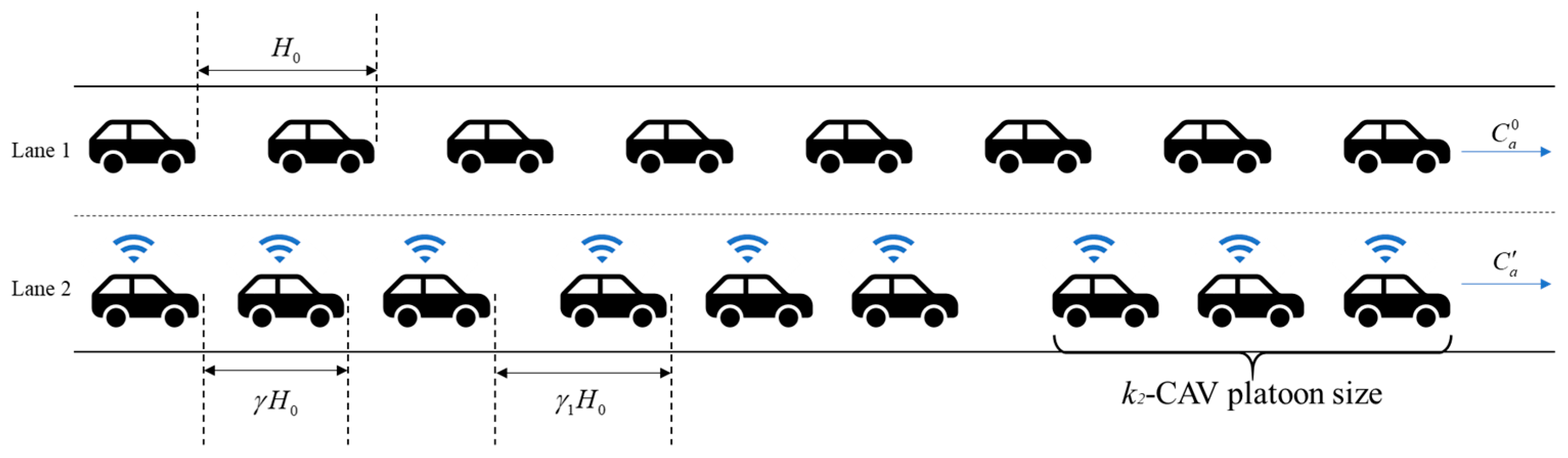
2.3. Travel Time Function of Mixed-Flow Environment
2.4. Travel Costs for HV and CAV Users
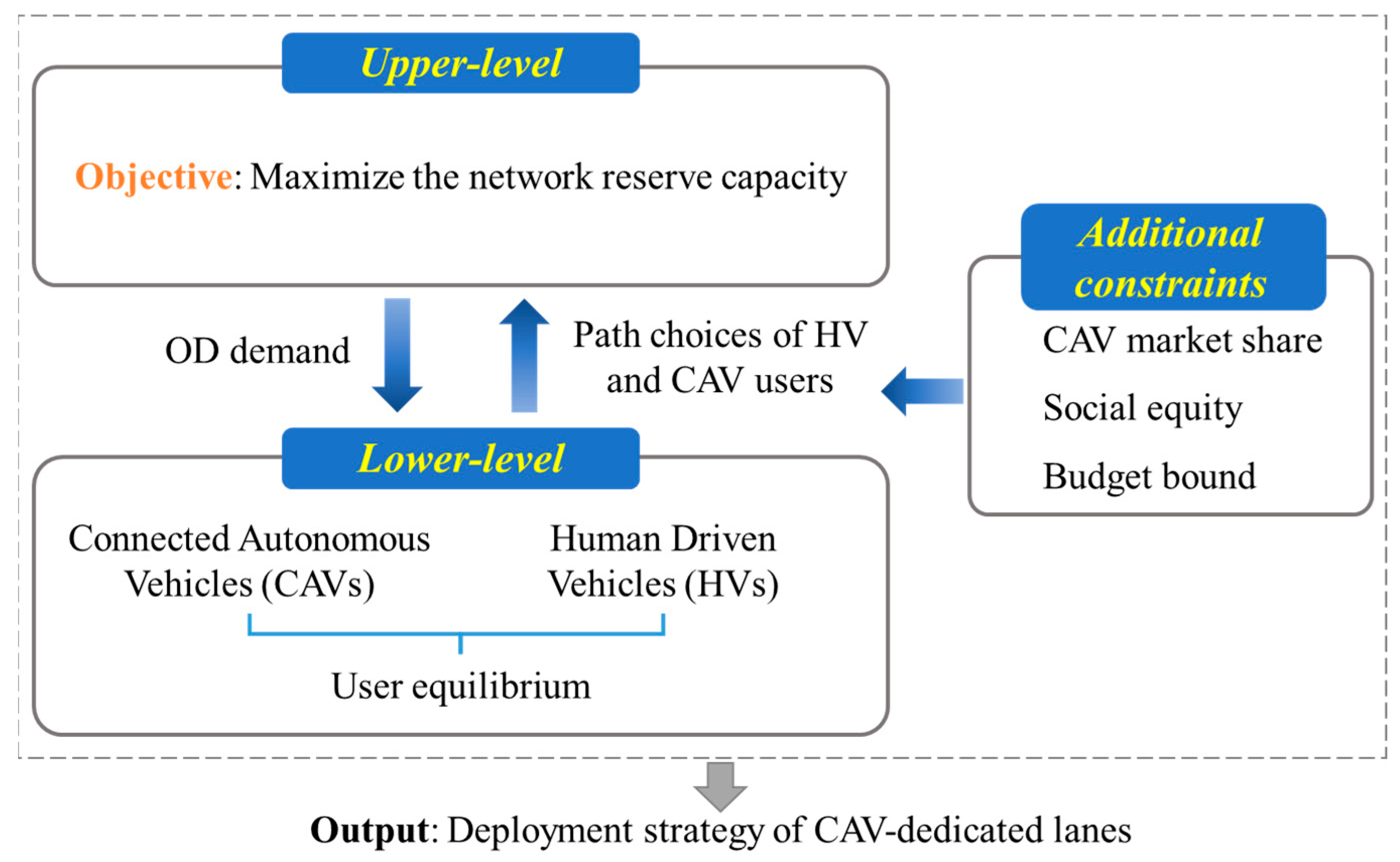
3. Bi-Level Programming with Deployment Constraints
3.1. Mixed-Flow Reserve Capacity Model
3.2. Practical Constraints for CAV-Dedicated Lane Deployment
3.2.1. CAV Market Penetration Ratio
3.2.2. Social Equity
3.2.3. Budget Bound
3.3. Bi-Level Optimization Model for CAV-Dedicated Lane-Deployment Strategy
4. Solution Technique
4.1. Linearization of the UE Principle
4.2. Linearization of Link Travel Time
5. Numerical Experiments
5.1. Experimental Setup and Parameters
5.2. Optimal Deployment Strategy
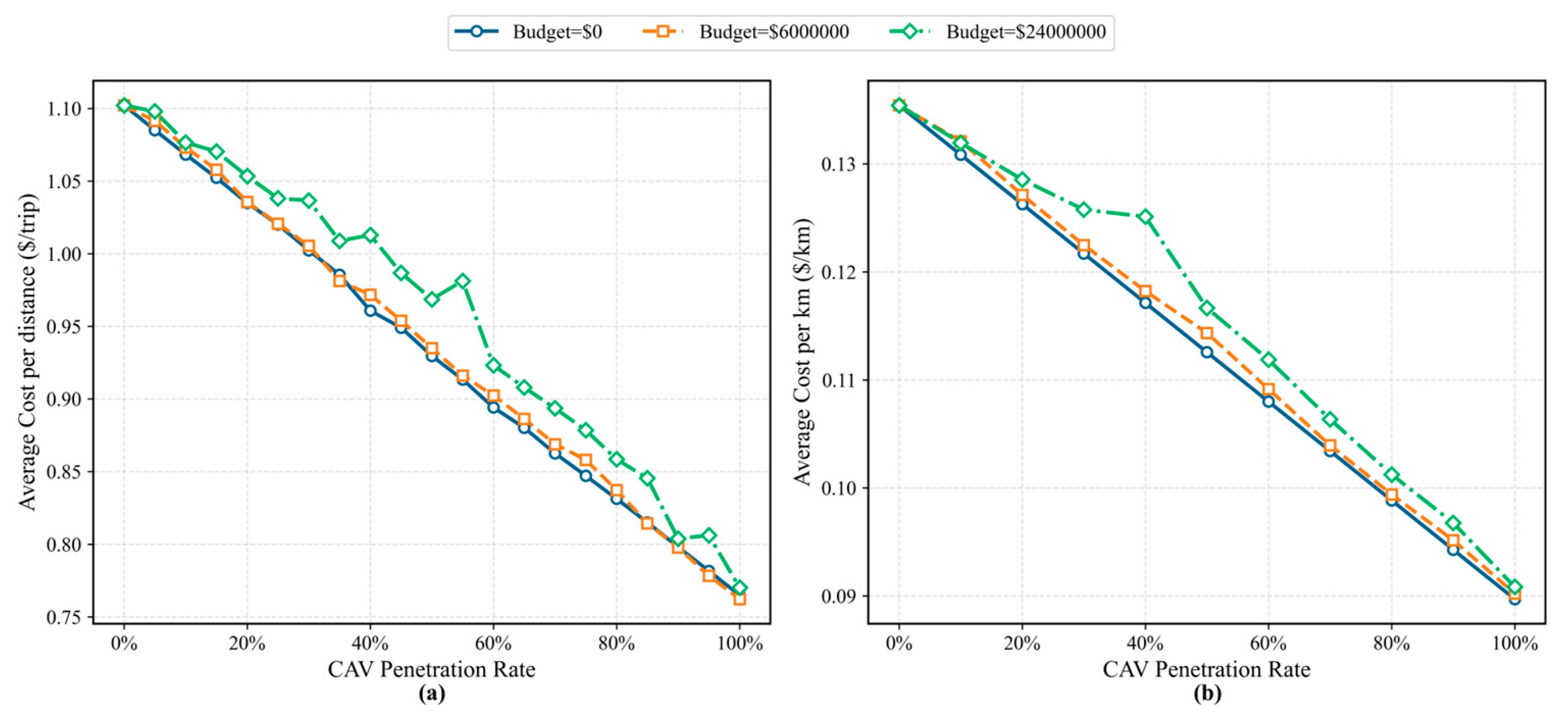
5.3. Sensitivity Analysis
5.3.1. Impact of Budget Constraint
5.3.2. Impact of Equity Constraints
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HV | Human-driven Vehicle |
| CAV | Connected Autonomous Vehicle |
| OD | Origin–Destination |
| VOT | Value of Time |
| UE | User Equilibrium |
| MPR | CAV Market Penetration Rate |
| MINLP | Mixed-Integer Nonlinear Programming |
| MILP | Mixed-Integer Linear Programming |
| PLA | Piecewise Linear Approximation |
Appendix A
| Sets: | |
|---|---|
| Set of regular links, | |
| Set of CAV-dedicated candidate links, | |
| Set of all links, , | |
| N | Set of road nodes, |
| R | Set of origin zones, |
| S | Set of destination zones, |
| M | Set of travel modes, M = [human-driven vehicle (HV), connected autonomous vehicle (CAV)], |
| Set of paths between OD pair (r, s), | |
| Parameters: | |
| The parallel link of regular link | |
| Lane capacity of link with pure HV flow (veh/h) | |
| Lane capacity of link in a mixed HVs and CAVs environment (veh/h) | |
| Length of link (km) | |
| Number of lanes on link | |
| Free-flow travel time of link (km/h) | |
| Fuel cost of vehicle per unit kilometer ($/km) | |
| Value of travel time for mode m users ($/h) | |
| Unit construction cost of CAV-dedicated lane in per kilometer ($/km) | |
| Maximum budget for total CAV-dedicated lane construction cost | |
| Equity degree of impacts on HV users under the deployment of CAV-dedicated lanes | |
| Market share of CAV in the network | |
| Spacing between an HV and another HV | |
| Spacing coefficient between a CAV and another CAV in the platoon | |
| Spacing coefficient for a CAV platoon following an HV | |
| Spacing coefficient for an HV following a CAV platoon | |
| Number of HVs between two CAV platoons | |
| CAV platoon size (the number of CAVs per platoon) | |
| A sufficiently large number | |
| Variables: | |
| A continuous variable indicating the toll of driving on CAV-dedicated link for HVs per unit kilometer ($/km) | |
| Average vehicle headway | |
| A binary decision variable indicating link is deployed with CAV-dedicated lane, and 0 otherwise, | |
| An auxiliary binary variable indicating path takes flow, and 0 otherwise | |
| A binary decision variable indicating path uses link , and 0 otherwise | |
| CAV proportion in the traffic flow of link | |
| Travel demand of mode m between OD pair (r, s) | |
| Total travel demand between OD pair (r, s), | |
| Travel cost on path k of mode m between OD pair (r, s) | |
| The shortest travel cost of mode m between OD pair (r, s) | |
| Flow of mode m on path k between OD pair (r, s) | |
| Total flow on link | |
| Flow of mode m on link | |
| Travel time on link | |
References
- Arman, M.A.; Tampère, C.M. Lane-level trajectory reconstruction based on data-fusion. Transp. Res. Part C Emerg. Technol. 2022, 145, 103906. [Google Scholar] [CrossRef]
- Wang, J.; Peeta, S.; He, X. Multiclass traffic assignment model for mixed traffic flow of human-driven vehicles and connected and autonomous vehicles. Transp. Res. Part B Methodol. 2019, 126, 139–168. [Google Scholar] [CrossRef]
- Fan, B.; Su, Z.; Chen, Y.; Wu, Y.; Xu, C.; Quek, T.Q.S. Ubiquitous control over heterogeneous vehicles: A digital twin empowered edge AI approach. IEEE Wirel. Commun. 2022, 30, 166–173. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Y.; Wu, Y.; Xiu, Y.; Fu, X.; Zhang, K. The Effects of Autonomous Vehicles on Traffic Efficiency and Energy Consumption. Systems 2023, 11, 347. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Levin, M.W. Optimal policy for integrating Autonomous Vehicles into the auto market. Transp. Res. Part C Emerg. Technol. 2022, 143, 103821. [Google Scholar] [CrossRef]
- Wang, J.; Lu, L.; Peeta, S.; He, Z. Optimal toll design problems under mixed traffic flow of human-driven vehicles and connected and autonomous vehicles. Transp. Res. Part C Emerg. Technol. 2021, 125, 102952. [Google Scholar] [CrossRef]
- Jia, Y.; Qu, D.; Song, H.; Wang, T.; Zhao, Z. Car-following characteristics and model of connected autonomous vehicles based on safe potential field. Phys. A Stat. Mech. Its Appl. 2022, 586, 126502. [Google Scholar] [CrossRef]
- Levin, M.W.; Boyles, S.D. A multiclass cell transmission model for shared human and autonomous vehicle roads. Transp. Res. Part C Emerg. Technol. 2016, 62, 103–116. [Google Scholar] [CrossRef]
- Xiong, B.-K.; Jiang, R.; Li, X. Managing merging from a CAV lane to a human-driven vehicle lane considering the uncertainty of human driving. Transp. Res. Part C Emerg. Technol. 2022, 142, 103775. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Z.; Chen, Y.; Yang, P.; Chen, B. An advanced control strategy for connected autonomous vehicles based on Micro simulation models at multiple intersections. Phys. A Stat. Mech. Its Appl. 2023, 623, 128836. [Google Scholar] [CrossRef]
- Mohajerpoor, R.; Ramezani, M. Mixed flow of autonomous and human-driven vehicles: Analytical headway modeling and optimal lane management. Transp. Res. Part C Emerg. Technol. 2019, 109, 194–210. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, S.; Zhu, F.; Wu, Y.; Yao, Z. A mixed capacity analysis and lane management model considering platoon size and intensity of CAVs. Phys. A Stat. Mech. Its Appl. 2023, 615, 128557. [Google Scholar] [CrossRef]
- Rosca, M.A.; Oprea, F.C.; Dragu, V.; Dinu, O.M.; Costea, I.; Burciu, S. Evaluating the Impact of Automated Vehicle Penetration on Intersection Traffic Flow: A Microsimulation-Based Approach. Systems 2025, 13, 751. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.; Cheng, Q.; Yin, R.; Wang, M. Estimation of urban network capacity with second-best constraints for multimodal transport systems. Transp. Res. Part B Methodol. 2021, 152, 276–294. [Google Scholar] [CrossRef]
- Xu, X.; Chen, A.; Jansuwan, S.; Yang, C.; Ryu, S. Transportation network redundancy: Complementary measures and computational methods. Transp. Res. Part B Methodol. 2018, 114, 68–85. [Google Scholar] [CrossRef]
- Zhou, W.; Weng, J.; Li, T.; Fan, B.; Bian, Y. Modeling the road network capacity in a mixed HV and CAV environment. Phys. A Stat. Mech. Its Appl. 2024, 636, 129526. [Google Scholar] [CrossRef]
- Rad, S.R.; Farah, H.; Taale, H.; van Arem, B.; Hoogendoorn, S.P. Design and operation of dedicated lanes for connected and automated vehicles on motorways: A conceptual framework and research agenda. Transp. Res. Part C Emerg. Technol. 2020, 117, 102664. [Google Scholar]
- Lee, S.; Oh, C.; Hong, S. Exploring lane change safety issues for manually driven vehicles in vehicle platooning environments. IET Intell. Transp. Syst. 2018, 12, 1142–1147. [Google Scholar] [CrossRef]
- Van Arem, B.; Van Driel, C.J.; Visser, R. The impact of cooperative adaptive cruise control on traffic-flow characteristics. IEEE Trans. Intell. Transp. Syst. 2006, 7, 429–436. [Google Scholar] [CrossRef]
- Laan, Z.V.; Sadabadi, K.F. Operational performance of a congested corridor with lanes dedicated to autonomous vehicle traffic. Int. J. Transp. Sci. Technol. 2017, 6, 42–52. [Google Scholar] [CrossRef]
- Rahman, M.S.; Abdel-Aty, M. Longitudinal safety evaluation of connected vehicles’ platooning on expressways. Accid. Anal. Prev. 2018, 117, 381–391. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, M.; van Arem, B. Traffic Flow Impacts of Converting an HOV Lane Into a Dedicated CACC Lane on a Freeway Corridor. IEEE Intell. Transp. Syst. Mag. 2020, 12, 60–73. [Google Scholar] [CrossRef]
- Wang, T.; Li, Y.; Jia, B.; Long, J. An autonomous vehicle exclusive lane design problem under the mixed autonomy traffic environment: Model formulation and large-scale algorithm design. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103534. [Google Scholar] [CrossRef]
- Seilabi, S.E.; Pourgholamali, M.; Miralinaghi, M.; Homem de Almeida Correia, G.; He, X.; Labi, S. Optimizing dedicated lanes and tolling schemes for connected and autonomous vehicles to address bottleneck congestion considering morning commuter departure choices. J. Intell. Transp. Syst. 2024, 1–18. [Google Scholar] [CrossRef]
- Chen, Z.; He, F.; Zhang, L.; Yin, Y. Optimal deployment of autonomous vehicle lanes with endogenous market penetration. Transp. Res. Part C Emerg. Technol. 2016, 72, 143–156. [Google Scholar] [CrossRef]
- Madadi, B.; Van Nes, R.; Snelder, M.; Van Arem, B. Optimizing Road Networks for Automated Vehicles with Dedicated Links, Dedicated Lanes, and Mixed-Traffic Subnetworks. J. Adv. Transp. 2021, 2021, 8853583. [Google Scholar] [CrossRef]
- Chen, Z.; He, F.; Yin, Y.; Du, Y. Optimal design of autonomous vehicle zones in transportation networks. Transp. Res. Part B Methodol. 2017, 99, 44–61. [Google Scholar] [CrossRef]
- Zhu, D.; Xie, T.; Liu, Y.; Zou, B.; Rujeerapaiboon, N. Optimal deployment of an equitable CAV platoonable corridor on road networks with mixed traffic flow. Transp. Res. Part C Emerg. Technol. 2023, 157, 104399. [Google Scholar] [CrossRef]
- SAE International. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Walker, F.; Forster, Y.; Hergeth, S.; Kraus, J.; Payre, W.; Wintersberger, P.; Martens, M. Trust in automated vehicles: Constructs, psychological processes, and assessment. Front. Psychol. 2023, 14, 1279271. [Google Scholar] [CrossRef] [PubMed]
- Ngoduy, D.; Nguyen, C.H.; Lee, S.; Zheng, Z.; Lo, H.K. A dynamic system optimal dedicated lane design for connected and autonomous vehicles in a heterogeneous urban transport network. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103562. [Google Scholar] [CrossRef]
- He, S.; Ding, F.; Lu, C.; Qi, Y. Impact of connected and autonomous vehicle dedicated lane on the freeway traffic efficiency. Eur. Transp. Res. Rev. 2022, 14, 1–14. [Google Scholar] [CrossRef]
- Bureau of Public Roads. Traffic Assignment Manual for Application with a Large, High Speed Computer; US Department of Commerce; US Bureau of Public Roads; Office of Planning; Urban Planning Division: Washington, DC, USA, 1964.
- Chen, D.; Ahn, S.; Chitturi, M.; Noyce, D.A. Towards vehicle automation: Roadway capacity formulation for traffic mixed with regular and automated vehicles. Transp. Res. Part B Methodol. 2017, 100, 196–221. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Z.; He, Y.; Song, Z. Network user equilibrium problems with infrastructure-enabled autonomy. Transp. Res. Part B Methodol. 2021, 154, 207–241. [Google Scholar] [CrossRef]
- Yang, H.; Bell, M.G.; Meng, Q. Modeling the capacity and level of service of urban transportation networks. Transp. Res. Part B Methodol. 2000, 34, 255–275. [Google Scholar] [CrossRef]
- Litman, T. Evaluating Transportation Equity; Victoria Transport Policy Institute: Victoria, BC, Canada, 2017. [Google Scholar]
- Behbahani, H.; Nazari, S.; Kang, M.J.; Litman, T. A conceptual framework to formulate transportation network design problem considering social equity criteria. Transp. Res. Part A Policy Pract. 2019, 125, 171–183. [Google Scholar] [CrossRef]
- Feng, T.; Zhang, J. Multicriteria evaluation on accessibility—Based transportation equity in road network design problem. J. Adv. Transp. 2014, 48, 526–541. [Google Scholar] [CrossRef]
- Patriksson, M. The Traffic Assignment Problem: Models and Methods; Courier Dover Publications: Garden City, NY, USA, 2015. [Google Scholar]
- Noruzoliaee, M.; Zou, B.; Liu, Y. Roads in transition: Integrated modeling of a manufacturer-traveler-infrastructure system in a mixed autonomous/human driving environment. Transp. Res. Part C Emerg. Technol. 2018, 90, 307–333. [Google Scholar] [CrossRef]
- Xu, M.; Wu, T.; Tan, Z. Electric vehicle fleet size for carsharing services considering on-demand charging strategy and battery degradation. Transp. Res. Part C Emerg. Technol. 2021, 127, 103146. [Google Scholar] [CrossRef]
- Guéret, C.; Prins, C.; Sevaux, M. Applications of Optimisation with Xpress-MP; Dash Optimization Ltd.: Blisworth, UK, 2002. [Google Scholar]



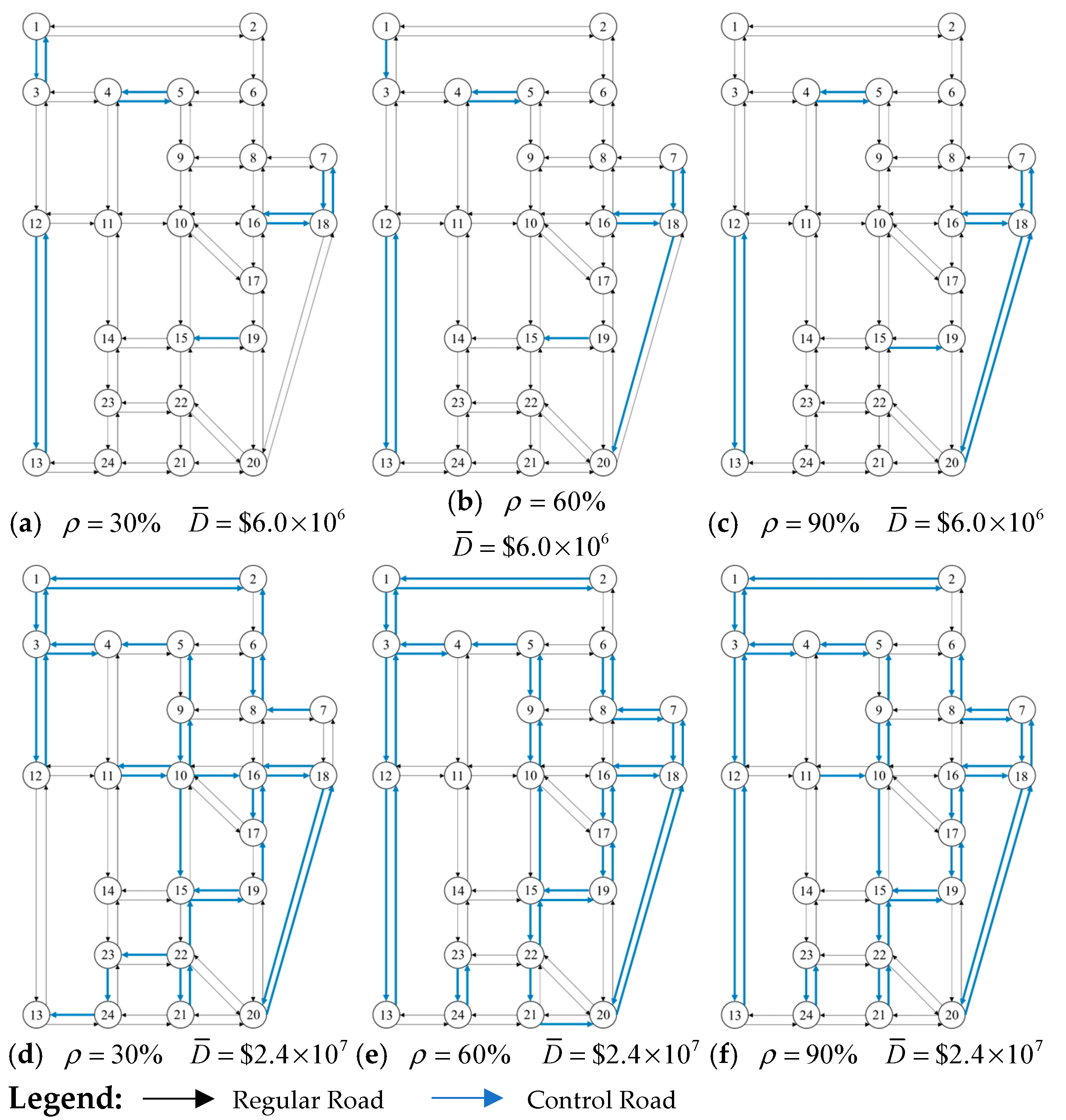
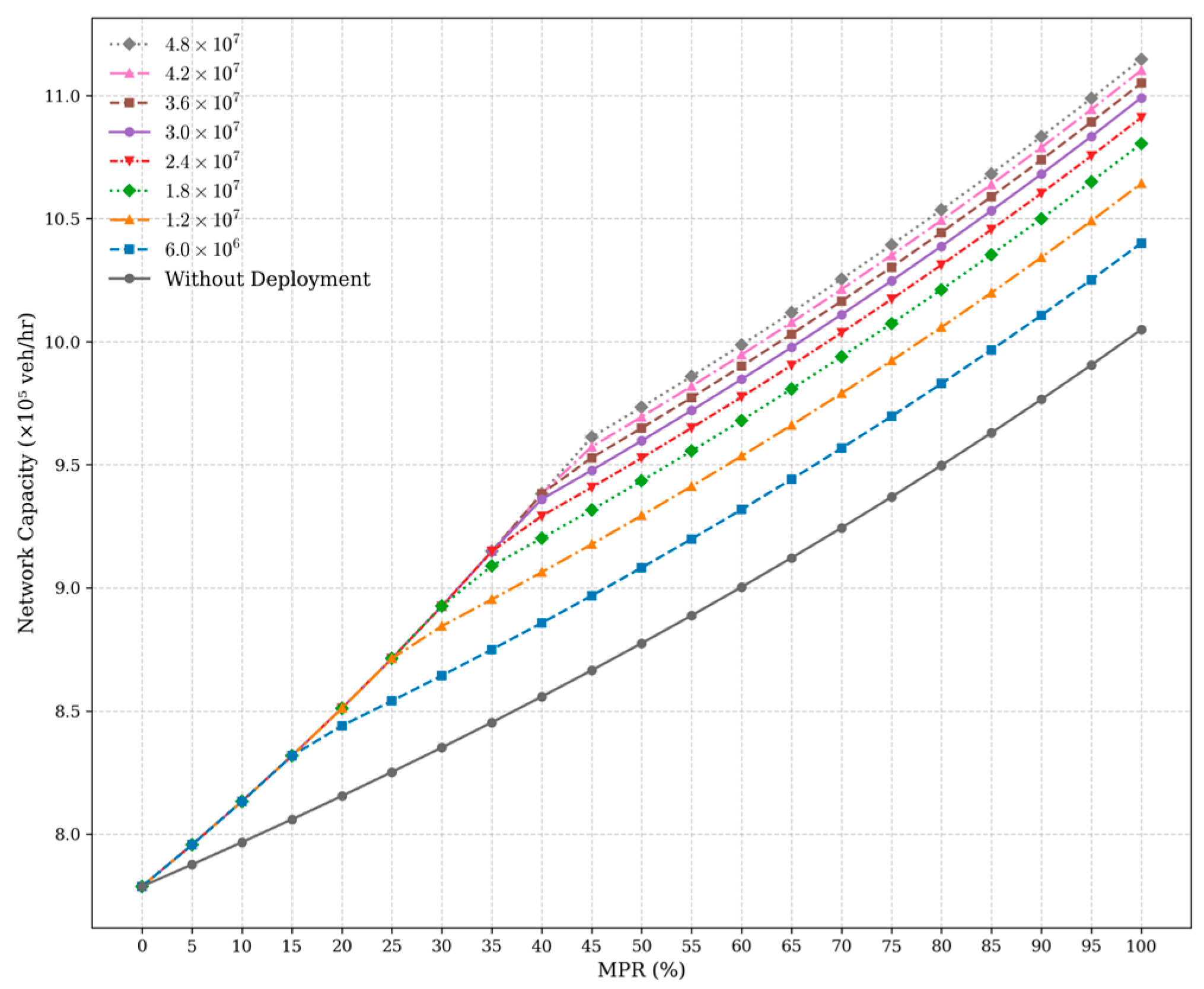
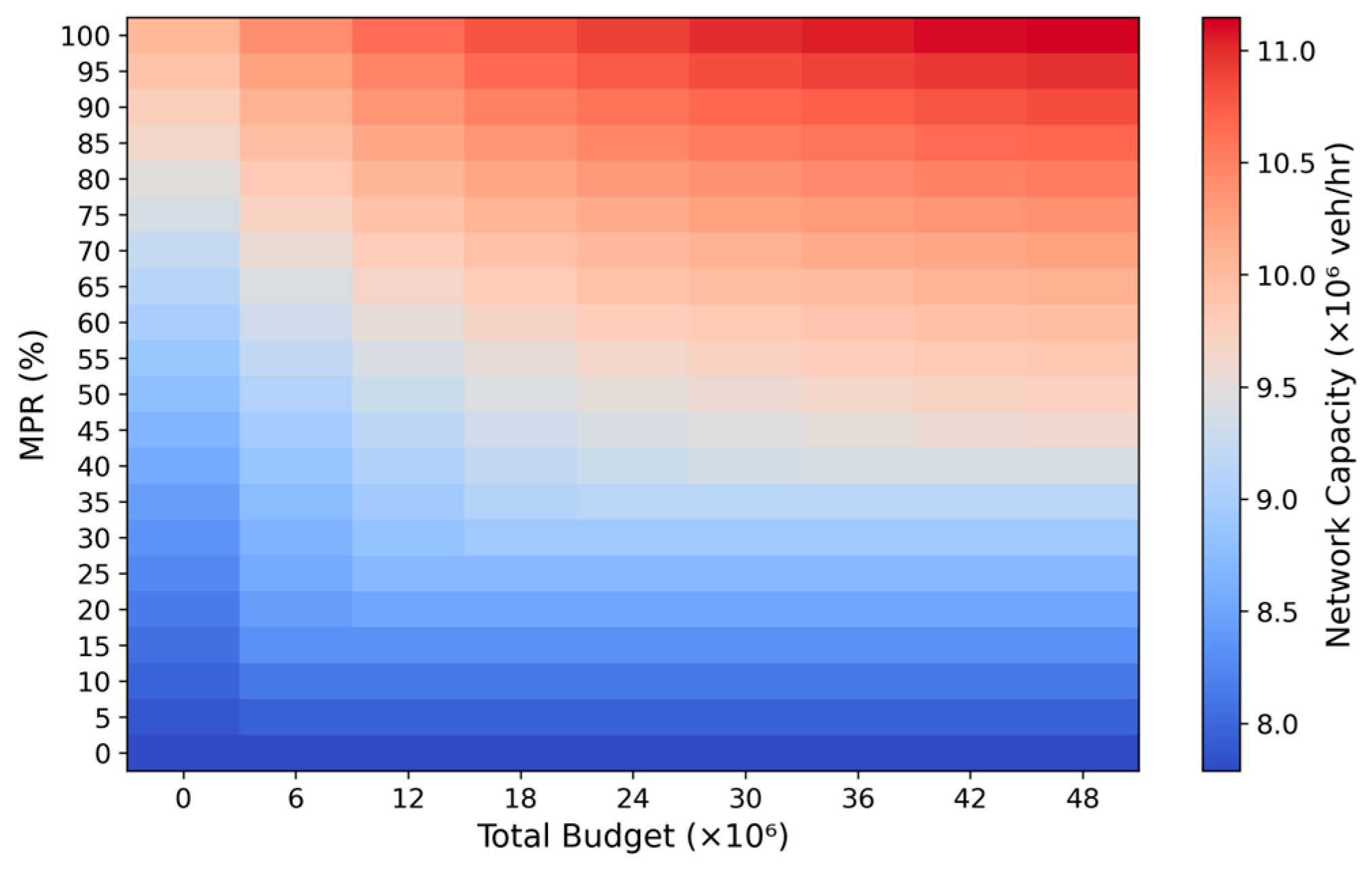

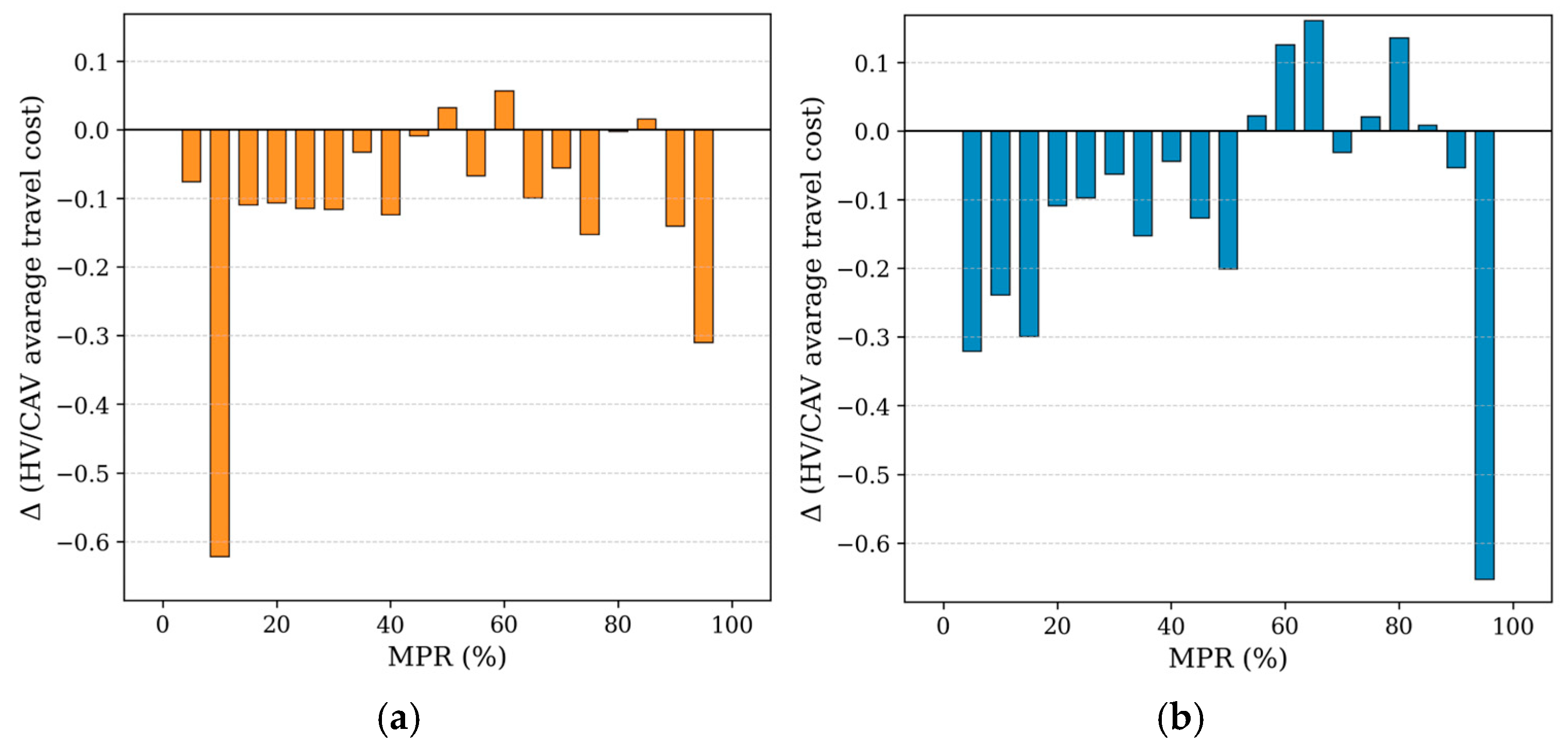
| Case | Network Capacity (veh/h) | Total Travel Cost ($) | Average Travel Cost ($/Trip) | HV’s Average Travel Cost ($/Trip) | CAV’s Average Travel Cost ($/Trip) |
|---|---|---|---|---|---|
| Base | 778,787 | 858,343.3 | 1.102 | \ | 1.102 |
| (a) | 864,367 | 869,124.4 | 1.005 | 1.107 | 0.768 |
| (b) | 931,818 | 840,903.0 | 0.902 | 1.237 | 0.679 |
| (c) | 1,010,687 | 806,244.3 | 0.798 | 1.412 | 0.729 |
| (d) | 892,543 | 925,244.3 | 1.037 | 1.118 | 0.847 |
| (e) | 977,518 | 902,505.7 | 0.923 | 1.142 | 0.778 |
| (f) | 1,060,254 | 852,288.5 | 0.804 | 1.294 | 0.749 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, W.; Wang, W.; Jin, K. System-Level Evaluation of Autonomous Vehicle Lane Deployment Strategies Under Mixed Traffic Flow. Systems 2025, 13, 958. https://doi.org/10.3390/systems13110958
Long W, Wang W, Jin K. System-Level Evaluation of Autonomous Vehicle Lane Deployment Strategies Under Mixed Traffic Flow. Systems. 2025; 13(11):958. https://doi.org/10.3390/systems13110958
Chicago/Turabian StyleLong, Weiyi, Wei Wang, and Kun Jin. 2025. "System-Level Evaluation of Autonomous Vehicle Lane Deployment Strategies Under Mixed Traffic Flow" Systems 13, no. 11: 958. https://doi.org/10.3390/systems13110958
APA StyleLong, W., Wang, W., & Jin, K. (2025). System-Level Evaluation of Autonomous Vehicle Lane Deployment Strategies Under Mixed Traffic Flow. Systems, 13(11), 958. https://doi.org/10.3390/systems13110958





