Probabilistic Models for Military Kill Chains

Abstract

Military kill chains are the sequence of events, tasks, or functions that must occur to successfully accomplish a mission. As the Department of Defense moves towards Combined Joint All-Domain Command and Control, which will require the coordination of multiple networked assets with the ability to share data and information, kill chains must evolve into kill webs with multiple paths to achieve a successful mission outcome. Mathematical frameworks for kill webs provide the basis for addressing the complexity of this system-of-systems analysis. A mathematical framework for kill chains and kill webs would provide a military decision maker a structure for assessing several key aspects to mission planning including the probability of success, alternative chains, and parts of the chain that are likely to fail. However, to the best of our knowledge, a generalized and flexible mathematical formulation for kill chains in military operations does not exist. This study proposes four probabilistic models for kill chains that can later be adapted to kill webs. For each of the proposed models, events in the kill chain are modeled as Bernoulli random variables. This extensible modeling scaffold allows flexibility in constructing the probability of success for each event and is compatible with Monte Carlo simulations and hierarchical Bayesian formulations. The probabilistic models can be used to calculate the probability of a successful kill chain and to perform uncertainty quantification. The models are demonstrated on the Find–Fix–Track–Target–Engage–Assess kill chain. In addition to the mathematical framework, the MIMIK (Mission Illustration and Modeling Interface for Kill webs) software package has been developed and publicly released to support the design and analysis of kill webs.

1. Introduction

Military kill chains are the sequence of events, tasks, or functions that must occur to successfully accomplish a mission. The traditional example of a kill chain is the successful employment of a weapon against a target, but kill chains can be used for any mission where the outcomes is based on a sequence of events, for example, a cyber attack to exfiltrate information from an information system or the successful collection of information from a aerial reconnaissance mission. The term kill chain implies that this is a linear sequence of events that must be accomplished. However, the United States Department of Defense (DoD) is moving toward Combined Joint All-Domain Command and Control (CJADC2), which will require the coordination of multiple networked assets with the ability to share data and information [1]. This complex system of systems will require the evolution of the kill chain to a kill web with multiple paths to completing the mission [2]. 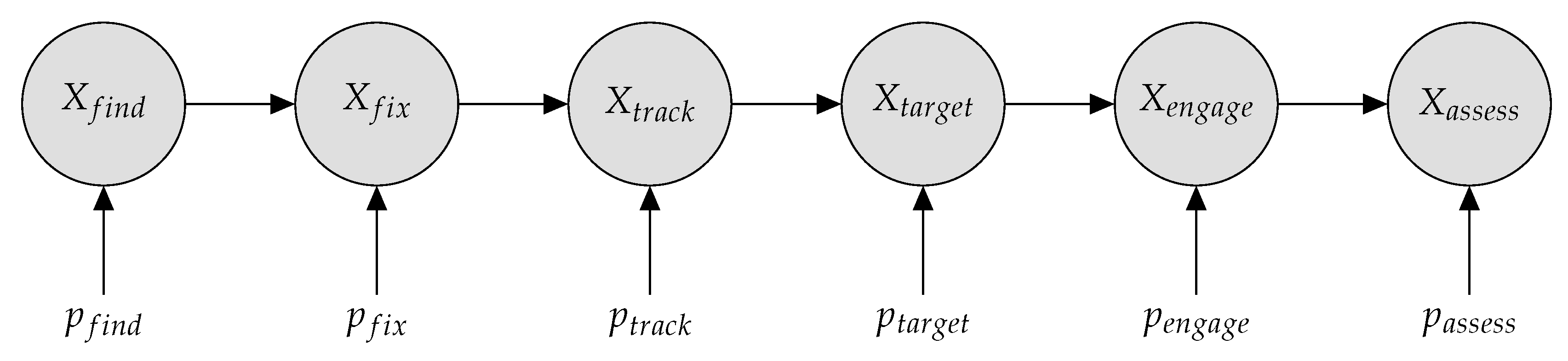Figure 1 displays an example of a common kill chain, the Find–Fix–Track–Target–Engage–Assess model (F2T2EA) [3,4], and a kill web with multiple paths. Further complicating matters is the addition of artificial intelligence into the kill web, which may have the ability to make autonomous decisions using probabilistic models [5]. Mathematical models for the kill web will be required to perform analysis and optimize decision-making. However, mathematical models for the kill chain need to be developed before moving to the more complex kill web.

Mission engineering applies systems engineering concepts to designing, planning, and analyzing a mission and is becoming more integrated in DoD operations [6,7,8]. Critical components of mission engineering are defining the mission architecture and performing mission engineering analysis. The mission architecture is composed of mission engineering threads, a series of activities that must be completed to have a successful mission. These threads are equivalent to kill chains, and the mission architecture is equivalent to kill webs. Traditional mission engineering approaches rely heavily on model-based systems engineering tools, such as the Systems Modeling Language (SysML), and digital engineering for modeling the mission engineering threads and the mission architecture [9,10]. The mathematical framework proposed in this work is intended to provide a mathematical foundation for kill chains that can be used alongside or integrated into tools like SysML to support mission engineering. More specifically, the proposed mathematical framework is composed of a set of customizable models that provide the user with the capability to simulate mission outcomes, assess failure points in the kill chain, and calculate the uncertainty around the mission outcomes. Further, the presented work provides the foundation for future work that will expand to more complex kill webs, perform resilience analysis, and optimize mission components.

Traditional methods for modeling the kill chain generally rely on a single mathematical framework for the entire chain. For example, Farrell and Wilkening use statistical methods and saddlepoint analysis to estimate the probability that the kill chain will be completed in the required time [11]. While this approach is sound, it only addresses a single aspect of the kill chain. Wang et al. utilize optimization to find optimal decisions and prospect theory to incorporate the preferences of decision makers [12]. Kewei et al. use multi-objective decision-making, such as the ant colony evolutionary algorithm, to improve decision-making in the kill web [13]. Jiang et al. model the resilience of kill webs using a system-of-systems approach [14]. There are models for military decision-making beyond the kill chain. The most common is the iterative concept of the Observe, Orient, Decide, and Act (OODA) loop (Figure 2) [15,16]. Johnson et al. demonstrate how the OODA loop can be mapped to the kill chain [5]. While these models provide military decision makers with some tools for analyzing kill chains, each approach is specific to a particular aspect of mission modeling. We strive to build a unified mathematical framework to assist decision makers with multiple aspects of mission planning, including visualizing the kill chain, assessing weak points, calculating the probability of success, and performing uncertainty quantification.

Another derivation of the typical kill chain is the cyber kill chain. Created by Lockheed Martin in 2011, this kill chain is a specific framework that analyzes malicious threat actors within the cyber space [17]. Tasks within the cyber kill chain include Reconnaissance, Weaponization, Delivery, Exploitation, Installation, Command and Control (C2), and Actions on Objectives. Previous research focused on exploring the technical aspects of the cyber kill chain as well as providing critiques on its design [18,19]. From this research, two distinctions emerge between the standard kill chain and the cyber kill chain. The first being that kill chains are created by mission planners, while cyber kill chains serve as an analytical model for cybersecurity specialists. That is, a cyber kill chain is an extensive, theoretical mission framework that malicious actors could use. Additionally, not every cyber-attacker would use each task in its own mission, compared to a standard kill chain in which each task must be executed sequentially and successfully for the whole kill chain to succeed. More recent research on cyber kill chains has begun to explore how AI can be incorporated into the analysis of each task, with the expectation that AI will be used by threat actors to execute that same task [20].

Reliability engineering centers on estimating the probability that a system will fail within a specified time period and under specified conditions [21,22]. Fault tree analysis (FTA) is an analytical tool that leverages block diagrams to estimate the reliability of a system [23,24]. There are clear ties between mission engineering and reliability engineering. However, reliability engineering is a more narrow practice that usually focuses on a specific system with a specific objective, i.e., estimating the probability of failures, while mission engineering is broader in scope and focuses on the integration of systems of systems [25]. Similarly, modeling kill chains is closely related to FTA, but prior work has demonstrated the limitations of directly applying FTA to kill chains [26]. The concepts of reliability engineering and FTA should be integrated into parts of mission engineering and kill chain analysis where applicable. In particular, methods for estimating the failure rates of systems could be utilized to estimate the parameters of the models proposed in this work.

This study outlines a general and flexible mathematical formulation for kill chains. The core concept is that each step in the kill chain is modeled as a random variable where the outcome is either that the event was successful or that the event was unsuccessful. If the event was successful, the chain can progress to the next event. If the event was unsuccessful, the chain ends and is considered unsuccessful. More specifically, each event is modeled as a Bernoulli random variable with a probability of success. The objective of the probabilistic model is to estimate the probability that the kill chain was successful, which implies that every event in the chain was successful. The probabilistic formulation also allows for more advanced analysis, such as calculating the variance of the chain being successful and the average number of successful events in the chain. The proposed mathematical framework is general enough to model a wide range of kill chains and brings together concepts from Markov models, stochastic processes, Bayesian modeling, and Monte Carlo simulations.

The probabilistic models are demonstrated on an F2T2EA kill chain. This is a common kill chain paradigm composed of six steps: (1) find the adversary, (2) fix the location of the adversary, (3) track the adversary, (4) target the adversary, (5) engage the adversary with a weapon, and (6) assess the damage done to the adversary. In addition to the proposed mathematical framework, we have developed and publicly released the MIMIK (Mission Illustration and Metric Interface for Kill webs) software package 1, which uses the proposed mathematical framework as the underlying model. MIMIK has the ability to load, manipulate, and visualize kill webs. It also has the ability to perform Monte Carlo simulations and calculate metrics. The use case in Section 3 uses MIMIK to produce the numerical experiments. These experiments are used to validate the mathematical models, demonstrate their capability, and illustrate the usefullness of MIMIK.

2. Methods

This section outlines the probabilistic kill chain models. Figure 3 displays the relationship between the models. The most general model, as the base model from which all other models are derived, is the Bernoulli process model. This model assumes a conditional relationship between the sequence of events and known success probabilities. This model only requires the success probability for each event to be known.

In practice, estimating these probabilities could be difficult, and the impact of incorrectly estimating the success probability could be detrimental to the analysis of the kill chain. A sensitivity analysis can be performed to determine the correlation between the success probability of an event and the estimated success of the kill chain. The success probabilities could be estimated through expert knowledge, simulations, or data collected from tests and operations. We elaborate on possible techniques for modeling these quantities in Section 4. The mathematical formulation proposed in this work has been designed to be adaptable and updatable over time. For example, the hyperparameters in the hierarchical Bayesian formulation could be refined using a Bayesian update with the most recent operational data. Furthermore, collected data could be compared to the current distributions associated with an event and used to determine if the event follows the assumed distribution, for example, using a statistical test to determine if an event’s probability of success estimated from test data follows a beta distribution.

The Bernoulli process model is a good starting point when modeling a new kill chain due to its simplicity and the relatively few number of parameters. The Markov chain model assumes that each event is a state and is particularly suited for quickly estimating the probability of success using the steady-state distribution. The conditional beta-Bernoulli process model assumes a beta prior on the success probabilities. This model provides a more complex way of generating the success probabilities but still provides closed-form solutions for estimating the probability of success of the kill chain and the variance. The Hierarchical Bayesian Model is a generalization of the conditional beta-Bernoulli process model where the prior on the success probabilities can have any structure. This model provides a practitioner the most flexibility in modeling the success probabilities but requires Monte Carlo simulations for estimating the probability of success of the kill chain.

2.1. Bernoulli Process Model

Let $X\sim \mathrm{Bern}\left(p\right)$ be a Bernoulli random variable with a success probability p. For a Bernoulli random variable, $\mathbb{P}(X=1)=p$ and $\mathbb{P}(X=0)=1-p=q$. The probability mass function for a Bernoulli random variable is

$$f(x;p)=p^x{(1-p)}^{1-x}\mathrm{for}x\in \{0,1\}.$$

(1)

The kill chain is modeled as a sequence of binary events with either a success outcome ($X=1$) or an unsuccessful outcome ($X=0$). Let $S_M=\{X_1,X_2,\dots ,X_M\}$ be a sequence of M Bernoulli random variables, and let $S_M=1$ represent the scenario where every event in $S_M$ is successful, i.e., ${\{X_m=1\}}_{m=1}^M$. If each $X_m$ is independent given p and the sequence of random variables is interchangeable, then $S_M$ can be modeled as a binomial distribution. The binomial distribution models the number of successful outcomes of N independent trials. This does not align with the concept of a kill chain. First, the events must take place in order; therefore, events in $S_M$ are not interchangeable. Second, in order for a kill chain to be considered successful, all events in the chain must be successful. Third, the success of the events in the kill chain are not independent; i.e., the current event can only have a successful outcome if all previous events also have a successful outcome. Therefore, a more complex probabilistic model of a kill chain that incorporates these properties is needed. Furthermore, we need to model the joint probability of all the events in the sequence, and, in particular, we need to estimate the probability that every event in the sequence is successful.

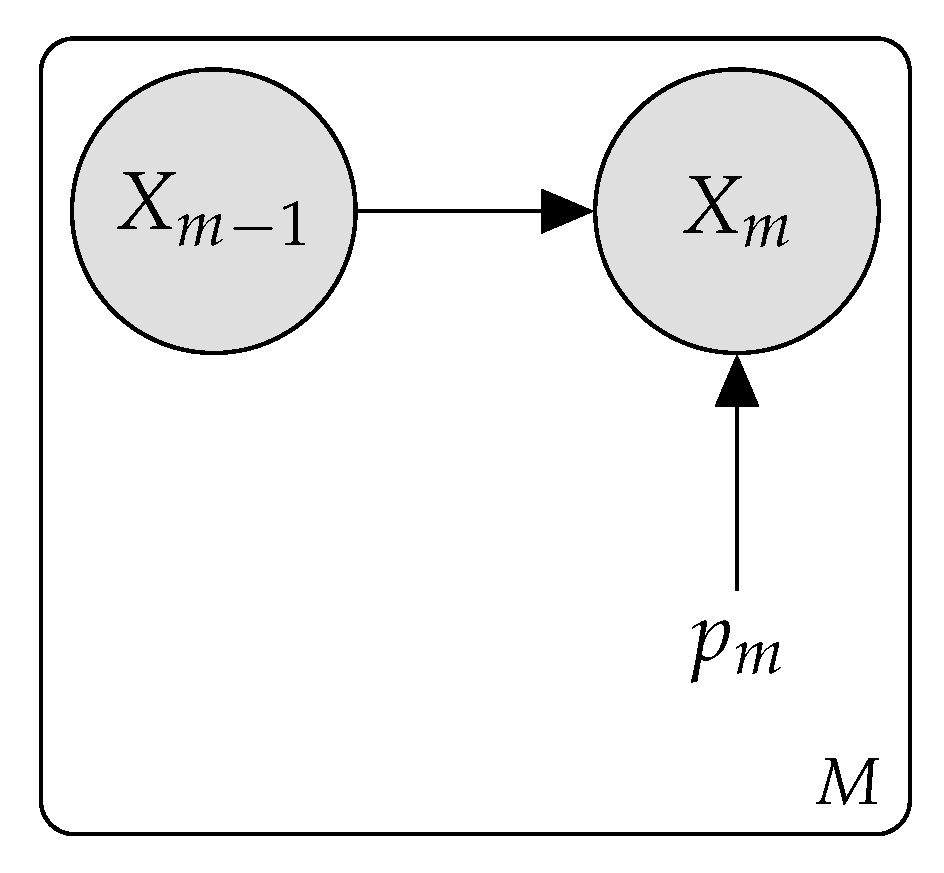
For a general probabilistic kill chain model, we assume that the events are not independent but conditional on the previous event being successful, where

$$\mathbb{P}(X_m=1|X_{m-1})=\left\{\begin{array}{cc}{p}_m\hfill & \mathrm{if}{X}_{m-1}=1\hfill \\ 0\hfill & \mathrm{if}{X}_{m-1}=0\hfill \end{array}\right.$$

(2)

and

$$\mathbb{P}(X_m=0|X_{m-1})=\left\{\begin{array}{cc}1-p_m\hfill & \mathrm{if}{X}_{m-1}=1\hfill \\ 1\hfill & \mathrm{if}{X}_{m-1}=0.\hfill \end{array}\right.$$

(3)

A graphical model for the general kill chain is displayed in Figure 4.

In general, the joint probability of random variables can be written as the product of conditional probabilities, where

$$\mathbb{P}(X_1,\dots ,X_M)=\mathbb{P}\left(X_M\right|X_1,\dots ,X_{M-1})\mathbb{P}\left(X_{M-1}\right|X_1,\dots ,X_{m-2})\dots \mathbb{P}\left(X_1\right).$$

(4)

As formulated in Figure 4, the events follow the Markov property, where

$$\mathbb{P}\left(X_m\right|X_1,\dots ,X_{m-1})=\mathbb{P}\left(X_m\right|X_{m-1})\forall m.$$

(5)

Therefore, the joint probability for the general kill chain model is

$$\mathbb{P}\left(S_M\right)=\mathbb{P}\left(X_1\right)\prod _{m=2}^M\mathbb{P}\left(X_m\right|X_{m-1}).$$

(6)

The probability of $S_M=1$ is

$$\begin{array}{cc}\hfill \mathbb{P}(S_M=1)& =\mathbb{P}(X_1=1,\dots ,X_M=1)\hfill \\ \hfill & =\mathbb{P}(X_1=1)\prod _{m=2}^M\mathbb{P}(X_m=1|X_{m-1}=1).\hfill \end{array}$$

(7)

Due to the conditional dependence of the sequence of events, $\mathbb{P}(X_1=1,\dots ,X_M=1)=\mathbb{P}(X_M=1)$. Therefore, $\mathbb{P}(S_M=1)=\mathbb{P}(X_M=1)$.

If $p_m$ is known and stationary for $m=1,\dots ,M$, then

$$\mathbb{P}(X_M=1)=\prod _{m=1}^M{p}_m.$$

(8)

If $p_m=p\forall m$, then

$$\mathbb{P}(X_M=1)=p^M.$$

(9)

2.2. Markov Chain Model

The kill chain can also be modeled as a Markov chain. In this formulation, let $X_m$ represent the state of the Markov chain at time m. Assume there are $I+2$ states in the Markov chain, and let $\mathbb{P}(X_m=j|X_{m-1}=i)=p_{ij}$ be the transition probability from state i to j at time m. Let $i=0$ be an absorbing failure state, and let $i=I+1$ be an absorbing success state. The initial state probability is defined as $\mathbb{P}(X_1=i)=p_i$. Let p and P be the initial distribution array and the transition matrix, respectively. This kill chain based on the Markov model is defined as follows:

• $0<p_{i-1,i}<1$ for $0<i\le I$,
• $0<p_{i,0}<1$ for $0<i\le I$,
• $p_{i,i+1}+p_{i,0}=1$ for $0<i\le I$,
• $p_{0,0}=1$,
• $p_{I+1,I+1}=1$,
• All other transition probabilities are 0,
• $p_1=1$, and $p_j=0\forall j\ne 1$.

The Markov model is displayed in Figure 5. The Markov model formulation for the kill chain allows the success probability (and failure probability) to be estimated by finding the steady-state distribution $\pi ={\mathbf{p}}^{\top }{\mathbf{P}}^{\infty }$.

2.3. Conditional Beta-Bernoulli Process Model

In general, a beta-Bernoulli process models a sequence of Bernoulli random variables with a prior distribution on $p\sim \mathrm{Beta}(\alpha ,\beta )$[27]. The standard beta-Bernoulli process cannot be used for the probabilistic kill chain model due to the conditional dependence between $X_j$ and $X_i$. Therefore, a conditional beta-Bernoulli process is proposed, where a prior distribution is defined for $p\sim \mathrm{Beta}(\alpha ,\beta )$ in the general kill chain model shown in Figure 4. Initially, assume that $\alpha$ and $\beta$ are stationary over $m=1,\dots ,M$. This assumption can be relaxed so that the prior on the success probability is specific to each event in the kill chain. The graphical model is shown in Figure 6.

As previously stated, one of the primary objectives for the kill chain analysis is to estimate $\mathbb{P}(X_M=1)$. To derive the relevant quantities for the conditional beta-Bernoulli process, let us start with as simple two-step kill chain $M=2$. The joint distribution of $X_1$ and $p_1$ is

$$\mathbb{P}(X_1=x,p_1)=\mathbb{P}(X_1=x|p_1)\mathbb{P}\left(p\right).$$

(10)

The conditional distribution of $X_1$ given $p_1$ is the Bernoulli distribution, where

$$\mathbb{P}(X_1=x|p_1)=p^x{(1-p_1)}^{1-x}.$$

(11)

The marginal distribution of $X_1$ is

$$\begin{array}{cc}\hfill \mathbb{P}(X_1=x)& =\mathbb{E}\left[\mathbb{P}(X_1=x|p_1)\right]\hfill \\ \hfill & ={\int }_0^1{p}_1^x{(1-p_1)}^{1-x}{\displaystyle \frac{1}{\mathrm{B}(\alpha ,\beta )}}{p}_1^{\alpha -1}{(1-p_1)}^{\beta -1}d{p}_1\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathrm{B}(\alpha ,\beta )}}{\int }_0^1{p}_1^{x+\alpha -1}{(1-p_1)}^{1-x+\beta -1}d{p}_1\hfill \\ \hfill & ={\displaystyle \frac{\mathrm{B}(\alpha +x,1-x+\beta )}{\mathrm{B}(\alpha ,\beta )}}\hfill \\ \hfill & ={\displaystyle \frac{{\alpha }^x{\beta }^{1-x}}{\alpha +\beta }}\hfill \end{array}$$

(12)

For the final step, first understand that $\mathsf{\Gamma }(a+j)=a^{\left[j\right]}\mathsf{\Gamma }\left(a\right)$, where $a^{\left[j\right]}=a(a+1)\dots (a+(j-1))$. Also, $a^{\left[0\right]}=1$ and $a^{\left[1\right]}=a$. When j is the random variable X, $a^{\left[x\right]}=a^x$. The last step then can be derived from the definition of the beta function, where

$$\mathrm{B}(\alpha ,\beta )={\displaystyle \frac{\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}{\mathsf{\Gamma }(\alpha +\beta )}}.$$

(13)

The expectation and variance of $X_1$ are

$$\begin{array}{cc}\hfill \mathbb{E}\left[X_1\right]& =\mathbb{E}\left[\mathbb{E}\left[X_1\right|p_1]\right]\hfill \\ \hfill & =\mathbb{E}\left[p_1\right]\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{\alpha +\beta }}.\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill \mathrm{Var}\left[X_1\right]& =\mathbb{E}\left[X_1^2\right]-\mathbb{E}{\left[X_1\right]}^2\hfill \\ \hfill & =\mathbb{E}\left[\mathbb{E}\left[X_1^2\right|p_1]\right]-\mathbb{E}{\left[\mathbb{E}\left[X_1\right|p_1]\right]}^2\hfill \\ \hfill & =\mathbb{E}\left[p_1\right]-\mathbb{E}{\left[p_1\right]}^2\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{\alpha +\beta }}-{\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^2\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{\alpha +\beta }}\left(1-{\displaystyle \frac{\alpha }{\alpha +\beta }}\right)\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{\alpha +\beta }}{\displaystyle \frac{\beta }{\alpha +\beta }}\hfill \\ \hfill & ={\displaystyle \frac{\alpha \beta }{{(\alpha +\beta )}^2}}.\hfill \end{array}$$

(15)

Before deriving the joint distribution of $X_1$ and $X_2$, we state the conditional distribution of $X_2$ as

$$\mathbb{P}(X_2=x_2|X_1=1,p_2)=p_2^{x_2}{(1-p_2)}^{1-x_2}.$$

(16)

For completeness, $\mathbb{P}(X_2=1|X_1=0,p_2)=0$ and $\mathbb{P}(X_2=0|X_1=0,p_2)=1$.

There are four combinations for the joint probability of $X_1$ and $X_2$. The first is $X_1=0$ and $X_2=0$

$$\mathbb{P}(X_1=0,X_2=0)=\mathbb{P}(X_1=0)\ast \mathbb{P}(X_2=0|X_1=0).$$

(17)

$$\mathbb{P}(X_2=0|X_1=0)=1$$

(18)

Therefore,

$$\begin{array}{cc}\hfill \mathbb{P}(X_1=0,X_2=0)& =\mathbb{P}(X_1=0)\hfill \\ \hfill & ={\displaystyle \frac{\beta }{\alpha +\beta }}\hfill \end{array}$$

(19)

   The second is $X_1=0$ and $X_2=1$, with

$$\mathbb{P}(X_1=0,X_2=1)=\mathbb{P}(X_1=0)\ast \mathbb{P}(X_2=1|X_1=0).$$

(20)

$$\mathbb{P}(X_2=1|X_1=0)=0$$

(21)

Therefore,

$$\mathbb{P}(X_1=0,X_2=1)=0.$$

(22)

   The third is $X_1=1$ and $X_2=0$, with

$$\begin{array}{cc}\hfill \mathbb{P}(X_1=1,X_2=0)& =\mathbb{P}(X_1=1)\ast \mathbb{P}(X_2=0|X_1=1)\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{\alpha +\beta }}\left(1-{\displaystyle \frac{\alpha }{\alpha +\beta }}\right)\hfill \\ \hfill & ={\displaystyle \frac{\alpha \beta }{{(\alpha +\beta )}^2}}\hfill \end{array}$$

(23)

   The fourth is $X_1=1$ and $X_2=1$, with

$$\begin{array}{cc}\hfill \mathbb{P}(X_1=1,X_2=1)& =\mathbb{P}(X_1=1)\ast \mathbb{P}(X_2=1|X_1=1)\hfill \\ \hfill & ={\displaystyle \frac{\alpha }{\alpha +\beta }}\ast {\displaystyle \frac{\alpha }{\alpha +\beta }}\hfill \\ \hfill & ={\displaystyle \frac{{\alpha }^2}{{(\alpha +\beta )}^2}}.\hfill \end{array}$$

(24)

The joint distribution is disjoint, so a closed-form solution for the marginal of $\mathbb{P}(X_2=x_2)$ does not exist. However,

$$\mathbb{P}(X_2=x_2)=\sum _{X_1}\mathbb{P}(X_1=x_1,X_2=x_2)$$

(25)

so

$$\begin{array}{cc}\hfill \mathbb{P}(X_2=0)& =\mathbb{P}(X_1=0,X_2=0)+\mathbb{P}(X_1=1,X_2=0)\hfill \\ \hfill & ={\displaystyle \frac{\beta }{\alpha +\beta }}+{\displaystyle \frac{\alpha \beta }{{(\alpha +\beta )}^2}},\hfill \end{array}$$

(26)

and

$$\begin{array}{cc}\hfill \mathbb{P}(X_2=1)& =\mathbb{P}(X_1=0,X_2=1)+\mathbb{P}(X_1=1,X_2=1)\hfill \\ \hfill & =0+{\displaystyle \frac{{\alpha }^2}{{(\alpha +\beta )}^2}}\hfill \\ \hfill & ={\displaystyle \frac{{\alpha }^2}{{(\alpha +\beta )}^2}}.\hfill \end{array}$$

(27)

The above can be generalized to estimate the marginal probability for each possible outcome for a sequence of length m. Due to the conditional dependence of the sequence, $X_k=1$ implies that $X_j=1\forall j<m$. Under the conditional beta-Bernoulli model,

$$\mathbb{P}(X_m=1)={\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^m,$$

(28)

and

$$\mathbb{P}(X_m=0)=1-{\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^m.$$

(29)

Therefore,

$$\mathbb{P}(X_M=1)={\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^M,$$

(30)

and

$$\mathbb{P}(X_M=0)=1-{\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^M.$$

(31)

The expectation for the marginals is $\mathbb{E}\left[X_m\right]=\mathbb{P}(X_m=1)$ and $\mathbb{E}\left[X_M\right]=\mathbb{P}(X_M=1)$. The variance for each is

$$\mathrm{Var}\left[X_m\right]={\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^m-{\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^{2m},$$

(32)

and

$$\mathrm{Var}\left[X_M\right]={\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^M-{\left({\displaystyle \frac{\alpha }{\alpha +\beta }}\right)}^{2M}.$$

(33)

The model can be generalized further to assume that the success probability is not stationary $p_m\sim \mathrm{Beta}({\alpha }_m,{\beta }_m)$, with

$$\mathbb{P}(X_M=1)=\prod _{m=1}^M{\displaystyle \frac{{\alpha }_m}{{\alpha }_m+{\beta }_m}}$$

(34)

and

$$\mathbb{P}(X_M=0)=1-\prod _{m=1}^M{\displaystyle \frac{{\alpha }_m}{{\alpha }_m+{\beta }_m}}.$$

(35)

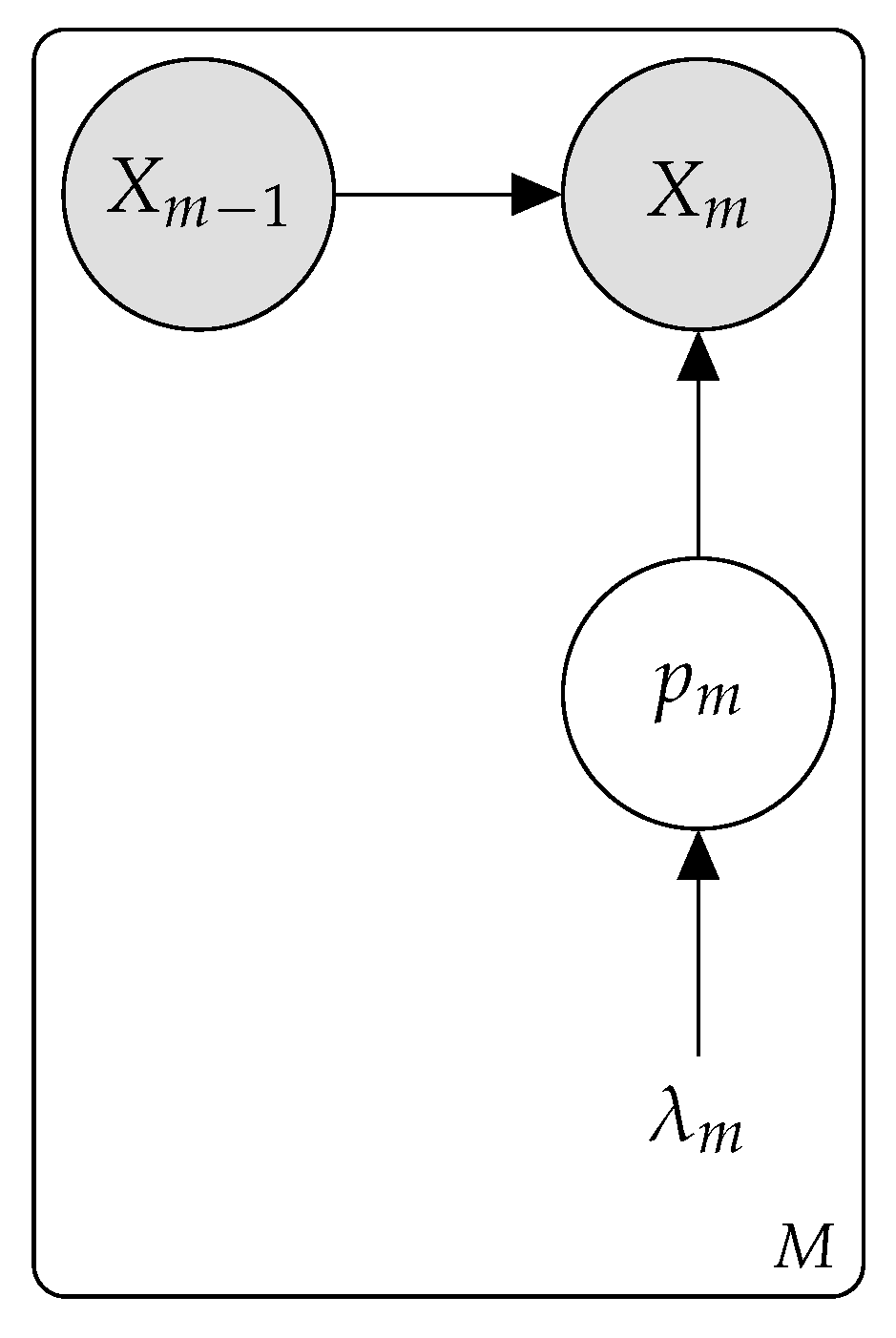
2.4. Hierarchical Bayesian Model

The conditional beta-Bernoulli process for the kill chain assumes that the prior on p follows a Beta distribution at each event. The hierarchical Bayesian formulation of the kill chain allows for the prior to be generalized to any type of distribution, including multi-level hierarchical distributions. Let ${\mathcal{P}}_m\left(p_m\right|{\lambda }_m)$ be the generic prior on $p_m$ where ${\lambda }_m$ is the set of hyperparameters. Figure 7 displays the graphical model for the hierarchical Bayesian kill chain.

The hierarchical Bayesian formulation provides the designer the ability to customize the distribution that defines the success probability, including a fixed distribution over all events (the most simple version) and hierarchical Bayesian models (as complex as needed). For example, assume that the model parameters also have a prior distribution where $\lambda \sim {\mathcal{P}}_m\left({\lambda }_m\right|{\psi }_m)$. Then, the graphical model could be expanded as shown in Figure 8.

Due to the complexity of the proposed model and the variability that is possible when designing the hierarchical structure for the success probability, closed-form solutions for the quantities of interest, such as $\mathbb{P}(X_M=1)$ and the variance of success, can not be determined, and a Monte Carlo simulation is used to estimate distributions of the results [28,29].

3. Numerical Experiments

This section outlines the use of the proposed probabilistic kill chain models on a common military use case.

3.1. F2T2EA Kill Chain

Find, Fix, Track, Target, Engage, and Assess (F2T2EA) is a common paradigm for a kill chain used throughout the military [3,4]. The F2T2EA kill chain is defined by the following steps:

• Find—Identify the target.
• Fix—Locate the target.
• Track—Monitor the target’s location over time.
• Target—Select the appropriate weapon system.
• Engage—Use the weapon on the target.
• Assess—Evaluate the effectiveness of the weapon on the target.

3.2. Bernoulli Process Model Experiment

The F2T2EA kill chain can be mapped into the proposed probabilistic model by assuming that each step is an event modeled by the random variable $X_m$. The challenge then becomes correctly modeling or estimating the success probability $p_m$ for each event in the kill chain. All aspects of the event being successful need to be incorporated into the estimation of $p_m$, including the fact that the event was completed within the required time frame. Figure 9 displays the graphical model for the F2T2EA kill chain.

For demonstration of the quantities derived in Section 2.1, assume that the success probabilities are $p_{find}=p_{fix}=p_{track}=0.9$ and $p_{target}=p_{engage}=p_{assess}=0.8$. Then, using Equation (8), the success of the kill chain is estimated to be 0.373. This is validated through a Monte Carlo simulation with 1000 replications. The distribution of each event being successful is displayed in Figure 10. Using the estimated probability of success, the variance of $X_{assess}$ can be calculated, where

$$\begin{array}{cc}\hfill \mathrm{Var}\left[X_{assess}\right]& =\mathbb{P}(X_{assess}=1)\ast (1-\mathbb{P}(X_{assess}=1)\hfill \\ \hfill & =0.234.\hfill \end{array}$$

(36)

3.3. Markov Chain Model Experiment

The F2T2EA kill chain can also be modeled using the Markov chain. For this formulation, the transition probabilities are $p_{find,fix}=p_{fix,track}=p_{track,target}=0.9$ and $p_{target,engage}=p_{engage,assess}=p_{assess,success}=0.8$. The $I+1$ success state is designated as $success$. Figure 11 displays the Markov chain. The probability that the kill chain is successful can be calculated by finding the steady-state distribution using $\pi ={\mathbf{p}}^{\top }{\mathbf{P}}^{\infty }$. In practice this is calculated by raising the transition matrix to a power much greater than I. For the presented kill chain model, the success probability is 0.373, which matches the result from the previous section, as expected.

3.4. Conditional Beta-Bernoulli Process Model Experiment

The F2T2EA kill chain is modeled as a conditional beta-Bernoulli process with ${\alpha }_m=10$ $\forall m\in M$ and ${\beta }_m=1\forall m\in M$. The expected value of $p_m$ is 0.901. This model will produce different results than the prior demonstrations and represents the case where information about the prior distribution of the success probability is available.

Using Equations (30) and (32), the success probability of the kill chain and the variance are calculated as $\mathbb{P}[X_{assess}=1]=0.564$ and $\mathrm{Var}\left[X_{assess}\right]=0.246$. A Monte Carlo simulation with $N=10,000$ is performed to confirm these results. In this demonstration, N was increased due to the complexity of the model. The proportion of successfully completed kill chains is 0.564, and the estimated variance is 0.246. Figure 12 displays the distribution of successful events, and Figure 13 displays the success probabilities drawn from the prior beta distribution.

3.5. Hierarchical Bayesian Model Experiment

Figure 14 displays a graphical model for the hierarchical Bayesian formulation of the F2T2EA kill chain. Each event is modeled as follows:

• Find: $p_{find}\sim \mathrm{Beta}({\alpha }_{find},{\beta }_{find})$ and ${\beta }_{find}\sim \mathrm{Lognormal}(\mu ,{\sigma }^2)$,
• Fix: $p_{fix}$ is fixed,
• Track: $p_{find}\sim \mathrm{Beta}({\alpha }_{track},{\beta }_{track})$ and ${\alpha }_{track}\sim \mathrm{Gamma}(k,\theta )$,
• Target: $p_{target}=1$ (the target event is always successful),
• Engage: $p_{find}\sim \mathrm{Beta}({\alpha }_{engage},{\beta }_{engage})$, and
• Assess: $p_{assess}$ is fixed.

The parameters for the hierarchical Bayesian demonstration are selected to be close to the parameters used in the prior examples and are listed below:

• $\mu =10$,
• ${\sigma }^2=5$,
• ${\alpha }_{find}=100$,
• $p_{fix}=0.9$,
• $k=10$,
• $\theta =1$,
• ${\beta }_{track}=11$,
• ${\alpha }_{engage}=9$,
• ${\beta }_{engage}=2$,
• $p_{assess}=0.95$.

A Monte Carlo simulation is performed with $N=10,000$. The proportion of successful kill chains is 0.247, and the variance is 0.186. Figure 15 displays the distribution of successful events.

4. Discussion

This paper presents a unified mathematical formulation for kill chains in the form of four probabilistic models. The base model is a conditional Bernoulli process that assumes that each step in the kill chain is represented by a binary random variable and conditioned on the prior event being successfully executed. The three other models are derived from this basic principle, representing various levels of complexity. This allows the practitioner to select models based on prior knowledge and data. The ability to calculate the probability that the kill chain is successful and the variance is demonstrated on the F2T2EA kill chain.

The Markov chain model is essentially the same as the conditional Bernoulli process model. The stationary distribution of the Markov chain can be easily calculated to estimate the probability of success or failure. However, the probability of success using the conditional Bernoulli process is just as easy to calculate. The variance in the probability of success can also be easily calculated under the conditional Bernoulli process model. All the models presented in this study assume discrete time and do not consider the time between events. The Markov chain model may be able to expanded to these situations where it is necessary to consider the time between events.

The extensions of the conditional Bernoulli process model, the conditional beta-Bernoulli process and the hierarchical Bayesian model, offer more fidelity but require greater insight into the underlying processes generating the probability of success for each event. The simple conditional Bernoulli process model only requires an estimate of the success probability for each event. A single point estimate may not reflect the real-world system. The conditional beta-Bernoulli process allows for a prior distribution on the probability of success of each event. This requires that the beta prior distribution be estimated, most likely from data. This model also assumes that the prior distribution for each event is a beta distribution. The beta prior can offer several advantages, including being a better reflection of the real-world system, the ability to provide robust estimates for the probability of success if data collection is scarce, and the ability to incorporate prior knowledge through the selection of hyperparameters. The hierarchical Bayesian models offers the most flexibility of the four models but requires the greatest number of modeling decisions. The probability of success for each event is modeled separately and can be as complex or simple as required (or the data will allow).

The probability of success for an event can be defined in several ways, and, in practice, the mission context will have a significant impact on this quantity. In the proposed formulation, the probability of success incorporates all relevant mission contexts such as the time to complete the event and the operational space. In future work, we plan to expand the capabilities of the proposed framework to include the mission context. For example, the time to complete a task can be modeled as a random variable and incorporated into the objective function. The mission environment can be incorporated into the model using Bayesian networks; e.g., the probability of success of an event could be conditioned on a variable representing the weather. The proposed method provides the foundation for these types of models to be developed in the future.

The success probabilities for each event can be estimated through a number of methods. The first and most straightforward is to make strong assumptions about each event and select a success probability from prior knowledge. This strategy provides the most variance around the estimate and is essentially testing the connection between an event and the success of the chain. Another method is to estimate these probabilities from data. Data is collected on systems through a number of means. Most military systems are rigorously tested before deployment, and these test results could be used in modeling the success probability of each event. Furthermore, data from operations could be collected and used to update the success probabilities for each event. We envision that the kill chain model can be refined over time. A decision maker should start with the general Bernoulli process model and add complexity as the systems are tested or deployed.

The proposed set of models rely on two strong assumptions: The first is that each event is modeled as a binary random variable. The second is that each event occurs at a standard time epoch and that time is not a factor. In our future work, we plan to increase the complexity of our models by having the possibility of multiple outcomes for each event. We also plan to incorporate a temporal component either through multi-objective optimization or by incorporating time into the state space, as is performed in semi-Markov processes [30].

5. Conclusions

This paper presents a mathematical formulation for analyzing kill chains, which provides various levels of operational utility. By modeling each event in the kill chain as a probabilistic process, ranging from simple Bernoulli sequences to more complex hierarchical Bayesian frameworks, these models enable mission planners and analysts to quantify the likelihood of success, identify weak links, and assess mission risk in a structured and data-driven way. In addition, we have developed the MIMIK software for the analysis of kill webs, which was used to produce the results for the F2T2EA kill chain use case.

The ability to model complex military missions mathematically has direct implications for operational decision-making. For example, planners can simulate different scenarios with varying levels of uncertainty, assess the impact of success probabilities for various elements of the chain, and prioritize investments in new capabilities such as sensors or weapon systems based on this sensitivity analysis. The ability to incorporate prior knowledge, through beta or hierarchical priors, allows for adaptive modeling that evolves with data collected in formal test and evaluation activities, military exercises, or even operational data.

This paper provides a framework for transitioning from linear kill chains to more complex kill webs. As the Department of Defense advances toward CJADC2, it will need the ability to model interdependent, multi-path engagements. The models introduced here can be extended to such architectures, providing a scalable approach for analyzing mission outcomes across distributed systems of systems. Follow-up work will focus on expanding these models to kill webs, where there are multiple paths to successfully completing the kill chain. We believe that the same underlying framework for modeling the success of each event should be used. A critical challenge when multiple paths are involved is finding the optimal path. We plan to test graph-theoretic methods as well as reinforcement learning approaches. Future work should also address methods for estimating the probability of success and modeling these parameters for each event.