Coordinated Development of Urban Transportation Structure Optimization and Energy Conservation, and Emission Reduction Under the Low-Carbon Background in Lanzhou, China
Abstract
1. Introduction
2. Study Area and Methodology
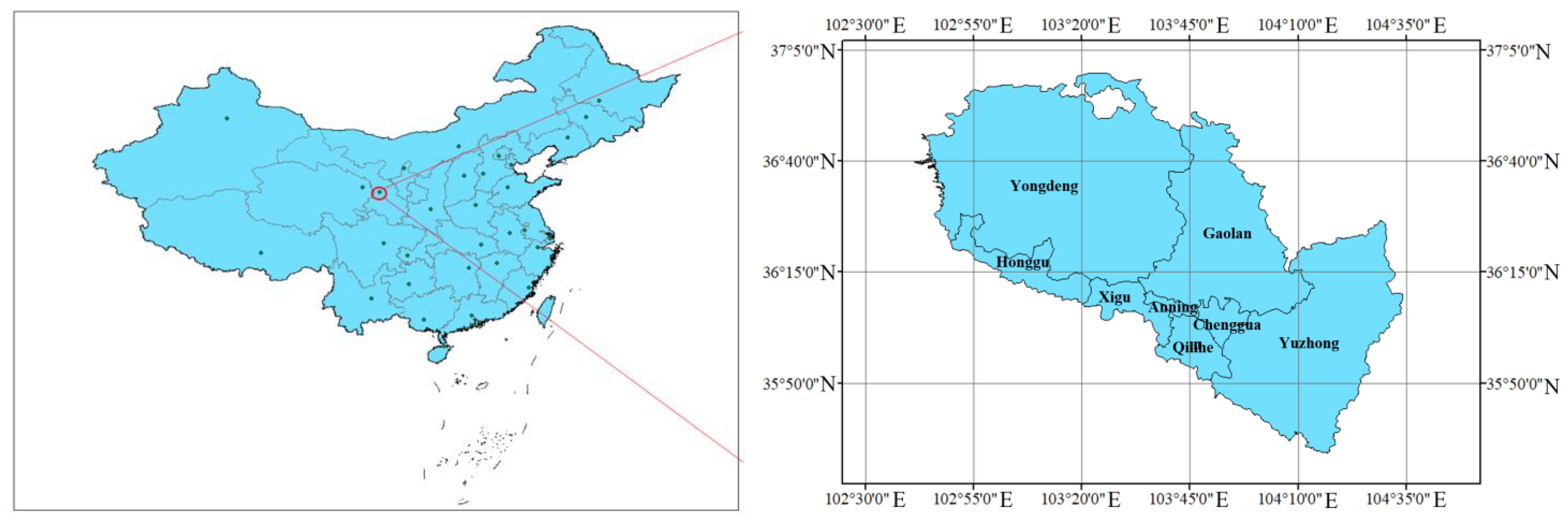
2.1. Study Area
2.2. Computational Principles of the Prediction Model
2.3. Construction of the Structural Optimization Model
- (1)
- Carbon Emissions. This objective quantifies the carbon emissions from urban transportation [16].
- (2)
- Energy Consumption. This objective addresses the energy demands of urban transportation [16].
- (3)
- External Costs. This economic cost objective includes costs due to road congestion, noise, air pollution, and traffic accidents [12].
- (4)
- Roadway Occupancy Area, reflects the efficiency of the city’s roadway network in traffic trip objectives [12].
- (5)
- Transportation Financial Assistance. This economic objective pertains to financial support for transportation [17].
- (6)
- Travel Costs, includes both economic and time costs [12].
- (1)
- Transportation Demand Constraints [16].
- (2)
- Road Network Capacity Constraints [16].
2.4. Coordination Evaluation Model
3. Data and Optimization Results
3.1. Predictive Modeling
3.2. Structural Optimization Model
- Separate System. The assumption that the urban transportation system in Lanzhou functions as a separate entity isolates the analysis from external influences such as transit vehicles from other regions or demographic changes. This allows for a more controlled study of the urban transportation system itself but may overlook interactions with neighboring systems or broader demographic trends that could impact demand and efficiency.
- Modes and Energy Sources. By limiting the model to four primary modes of transportation (buses, taxi, metro, and private cars) and four energy sources (gasoline, diesel, natural gas, and electricity), the model simplifies the complexities of urban transport energy consumption and supply. This makes modeling more manageable but may limit the scope of potential innovations or changes in newer transportation technologies or alternative fuels.
- Constraints. Focusing on five specific constraints (travel demand, energy consumption, transport supply, accessibility, and environmental pollution) helps to streamline the objectives and makes the model practically applicable to real-world scenarios. However, this approach might neglect other potential factors such as economic impacts, social equity, or urban planning changes.
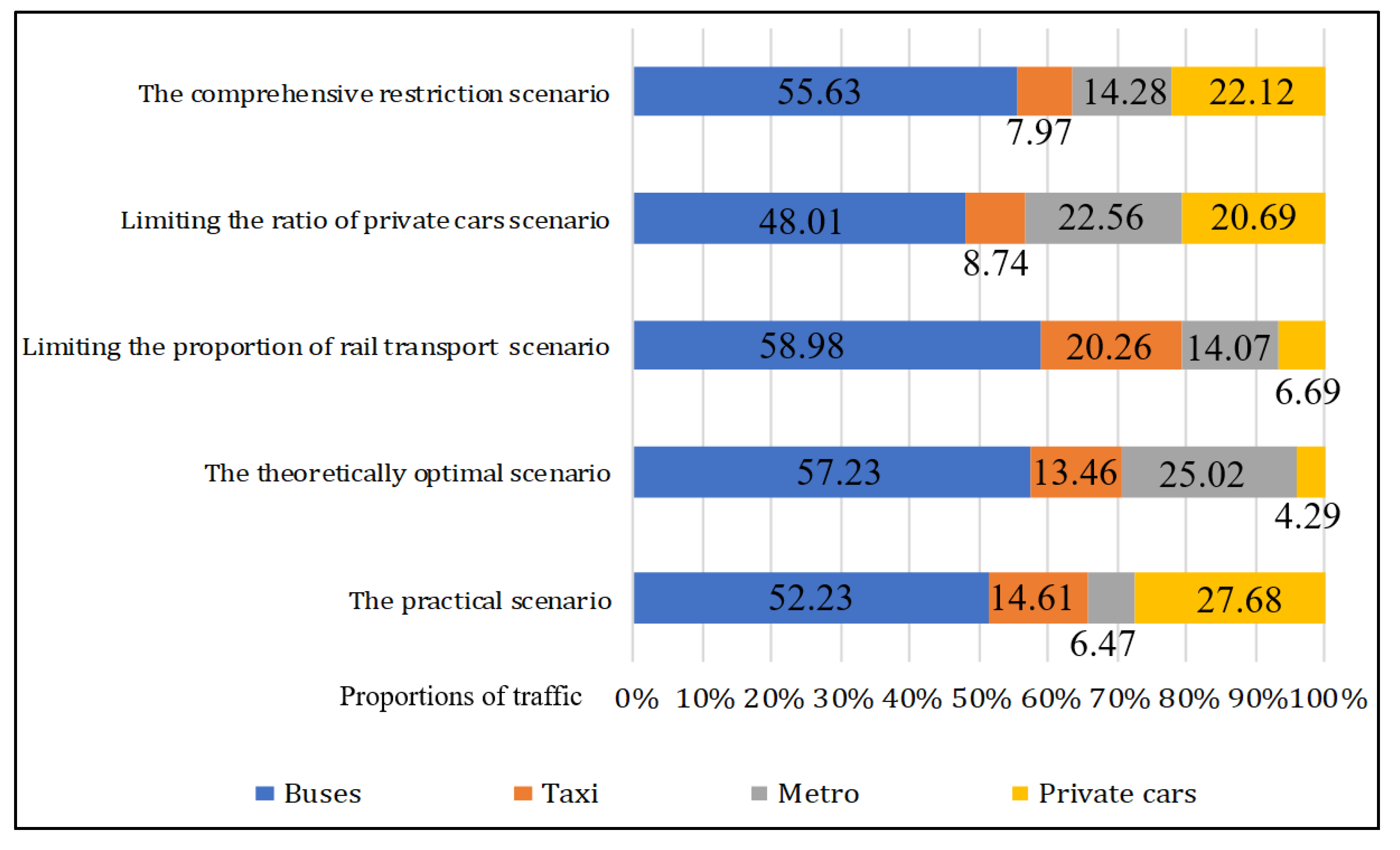
3.3. Optimization Results
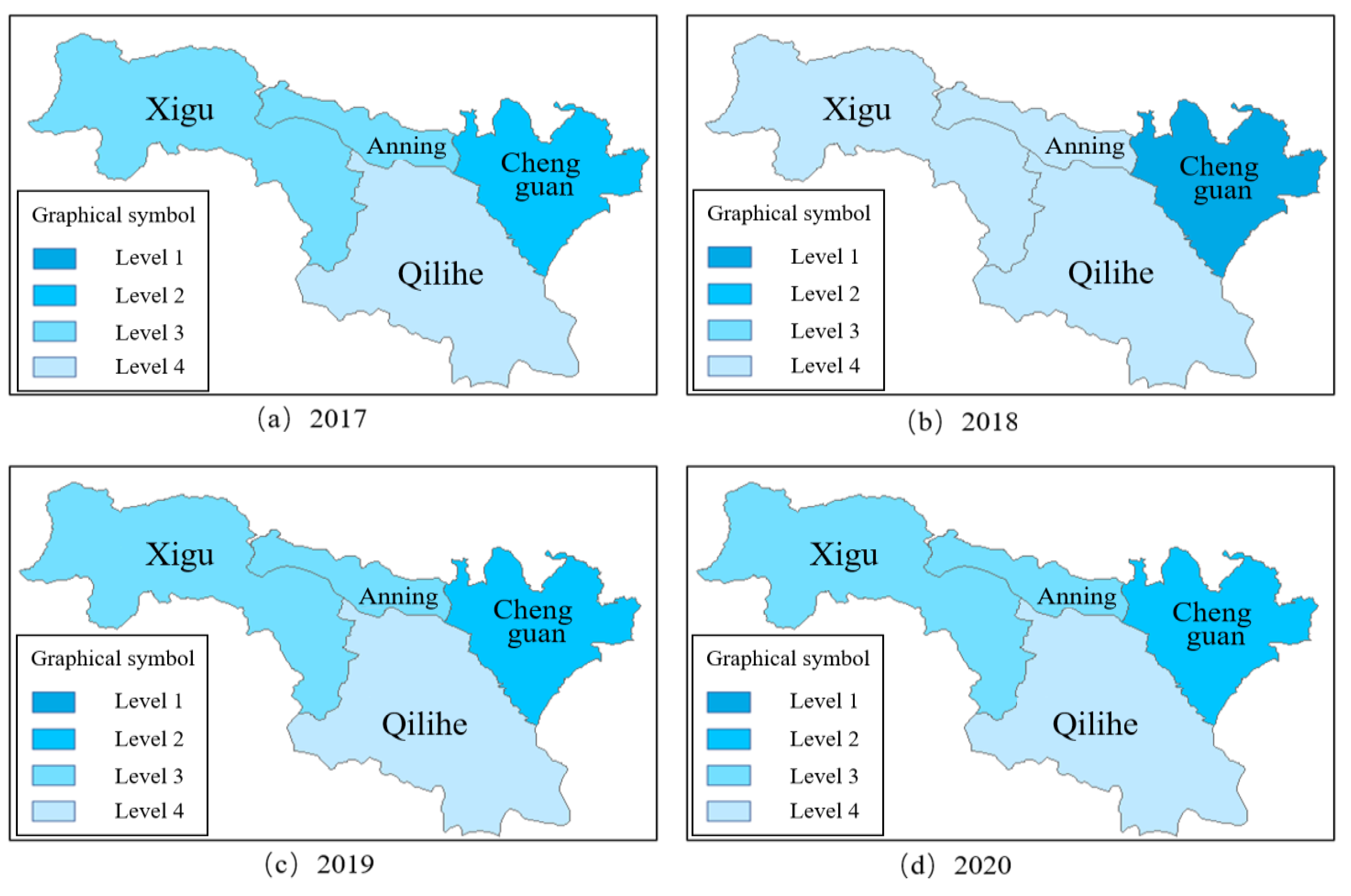
3.4. Evaluation of Harmonization
4. Analysis of Carbon Emission Projection Results
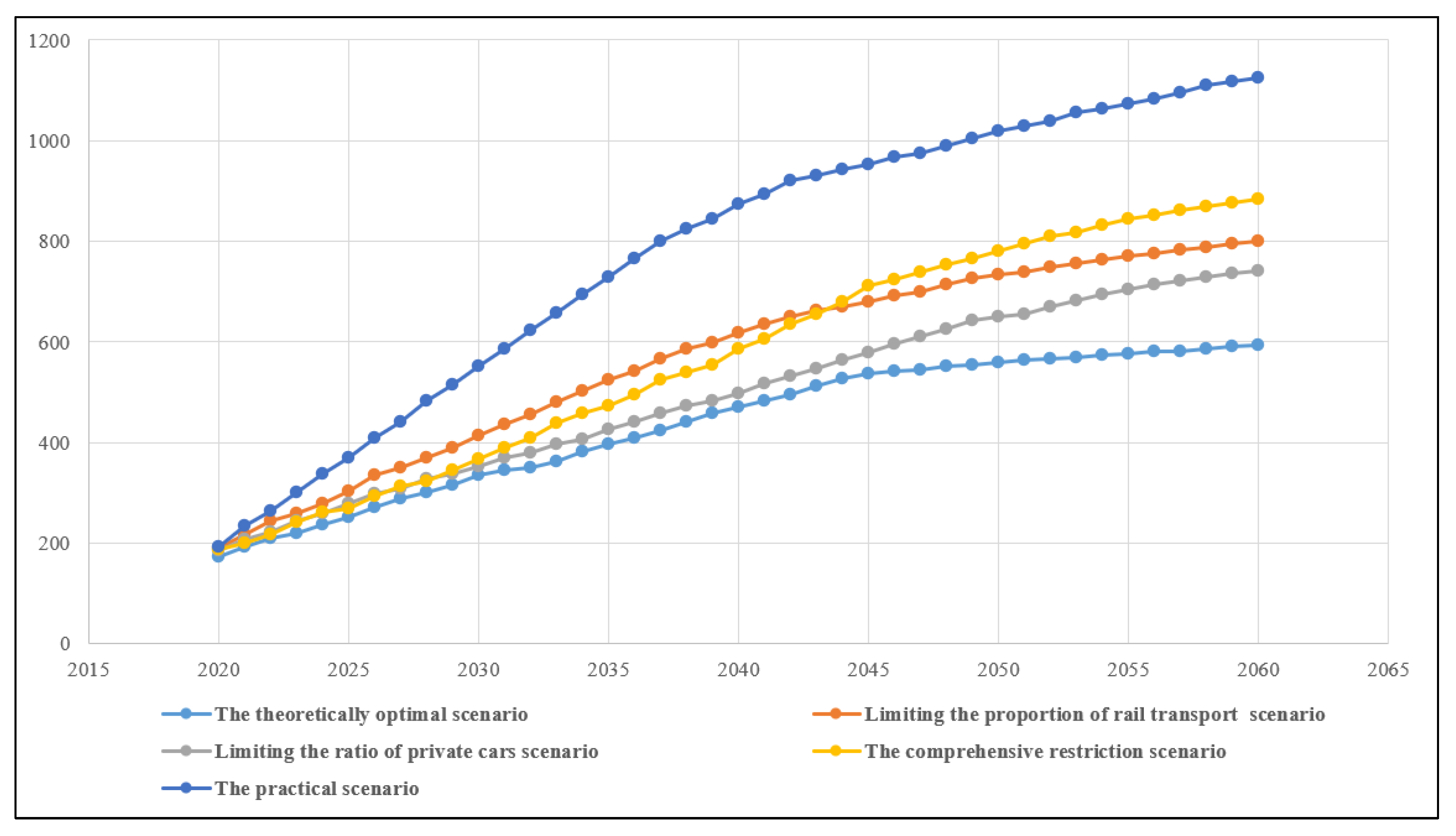
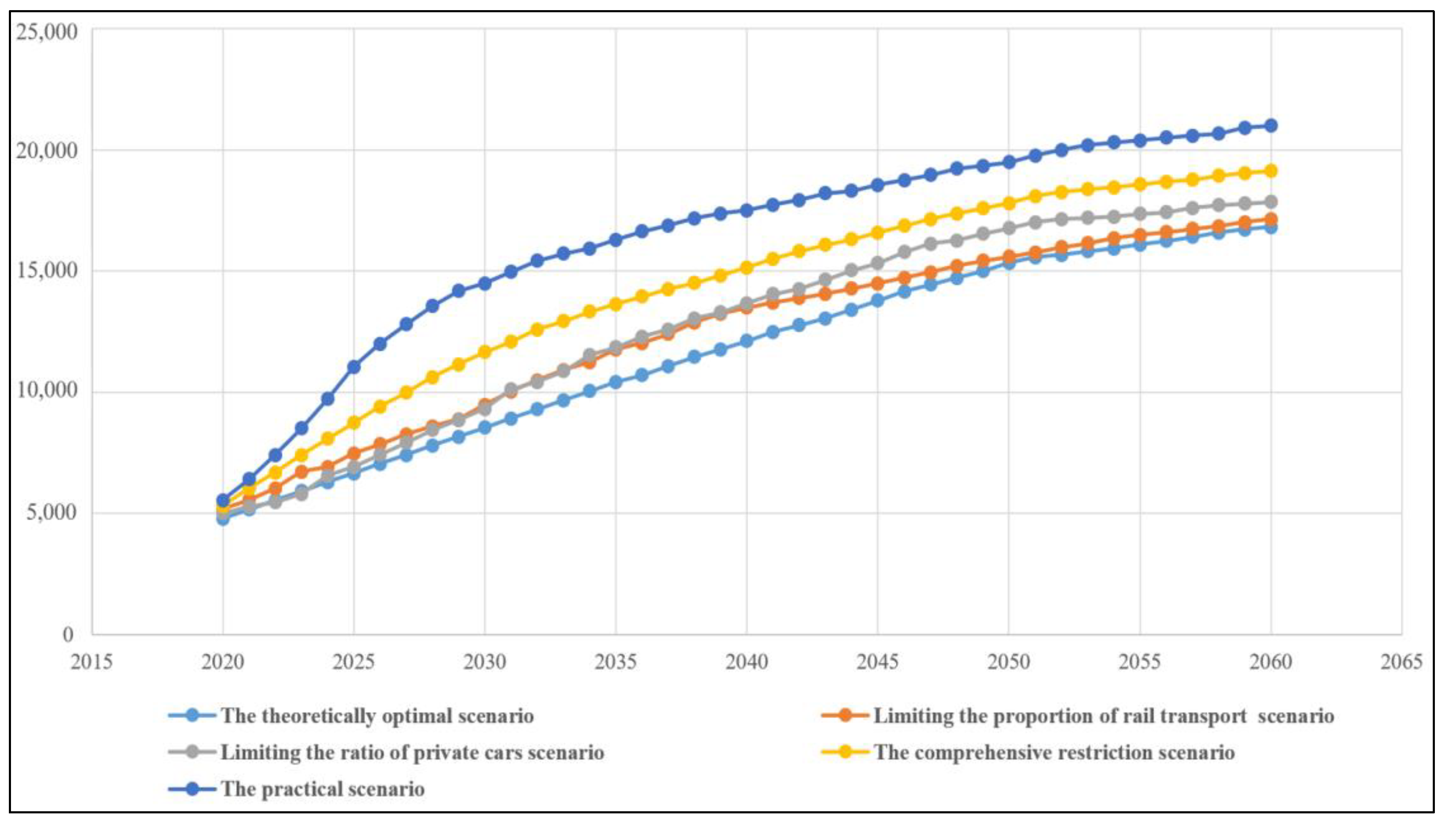
4.1. Projected Results
4.2. Comprehensive Analysis
5. Conclusions
- (1)
- The optimization of the transportation structure can only reduce the growth rate of carbon emissions in the single domain of urban transportation; it cannot bring the growth rate to zero or achieve “carbon peaking”. This finding aligns with the principle that achieving “carbon peaking” and “carbon neutrality” in large regions requires coordinated efforts across all industries and sectors. This also indicates that the carbon emission estimation method employed in this study is reasonable and effective.
- (2)
- In the context of urban transportation systems, rail transit plays a more significant role in energy conservation and emission reduction. Even in scenarios where private car usage accounts for a higher proportion of trips, ensuring the efficiency and convenience of rail transit can help maintain the overall carbon emissions of the urban transportation system at relatively low levels.
- (3)
- The proportion of private car trips should not necessarily be minimized without consideration. On one hand, private cars offer irreplaceable advantages such as flexibility in travel time, spacious and comfortable riding conditions, and strong privacy. On the other hand, the production, manufacturing, and sales of small vehicles are also integral components of the socio-economic system. Given these considerations, both from the perspective of transportation planning and socio-economic analysis, maintaining a necessary proportion of private car usage is essential. Based on scenario-based predictions of energy consumption and emissions, while lowering the minimum proportion of private car usage may lead to increased energy consumption and emissions, it also ensures better system coordination. Achieving green transportation does not equate to simply compromising transportation needs for low-carbon solutions. Instead, it requires minimizing energy consumption and emissions while meeting transportation demands. This represents the true sustainable development concept for green transportation.
- (4)
- The predictive analysis of energy consumption and emissions across various scenarios demonstrates that the comprehensive restriction scenario yields superior coordination with elevated values for both metrics. This indicates that the scenario represents the most balanced and rational approach, closely aligning with the principles of sustainable transportation development. Moreover, the green transportation coordination evaluation model formulated in this study has proven to be both reasonable and effective, further validating its utility in guiding policy and planning decisions.
- (5)
- Although this study has yielded a relatively optimized transportation structure, there remains room for further improvement due to the limitations of the optimization model’s solving algorithms and the constraints of multi-objective programming in mathematics. The current transportation structure can still be optimized to better balance urban traffic energy consumption, carbon emission impacts, and residents’ travel demand.
- (6)
- Furthermore, while the development of urban rail transit has been shown to effectively alleviate the issue of excessive carbon emissions from urban traffic, questions remain about the potential balance between the development of metro systems and ground transportation. Should surface transportation give way to metro development in the process of urban construction? These questions remain unresolved and represent directions for future, in-depth research.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.J.; Zhang, X.W.; Shen, Y. Technology-driven carbon reduction: Analyzing the impact of digital technology on China’s carbon emission and its mechanism. Technol. Forecast. Soc. Chang. 2024, 200, 123124. [Google Scholar] [CrossRef]
- Stockholm Environment Institute. Long-Range Energy Alternatives Planning System User Guide; Stockholm Environment Institute: Stockholm, Sweden, 2018. [Google Scholar]
- Wang, P.; Wang, C.; Hu, Y. Analysis of energy consumption in Hunan Province (China) using a LMDI method based LEAP model. In Proceedings of the International Conference on Applied Energy, Cardiff, UK, 21–24 August 2018. [Google Scholar]
- Li, Y.; Bao, L.; Li, W.; Deng, H. Inventory and Policy Reduction Potential of Greenhouse Gas and Pollutant Emissions of Road Transportation Industry in China. Sustainability 2016, 8, 1218. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Jiang, P.; Liu, L.; Xu, X.; Xu, Y. Sectoral peak CO2 emission measurements and a long-term alternative CO2 mitigation roadmap: A case study of Yunnan, China. J. Clean. Prod. 2024, 247, 119171. [Google Scholar] [CrossRef]
- Huo, T.; Cao, R.; Du, H.; Zhang, J.; Cai, W.; Liu, B. Nonlinear influence of urbanization on China’s urban residential building carbon emissions: New evidence from panel threshold model. Sci. Total Environ. 2021, 772, 145058. [Google Scholar] [CrossRef]
- Lin, D.; Zhang, L.; Chen, C.; Lin, Y.; Wang, J.; Qiu, R.; Hu, X. Understanding driving patterns of carbon emissions from the transportation sector in China: Evidence from an analysis of panel models. Clean Technol. Environ. Policy 2019, 21, 1307–1322. [Google Scholar] [CrossRef]
- Zhao, R.D.; Fang, C.L.; Liu, H.M.; Liu, X. Evaluating urban ecosystem resilience using the DPSIR framework and the ENA model: A case study of 35 cities in China. Sustain. Cities Soc. 2021, 72, 102997. [Google Scholar] [CrossRef]
- Alnour, M.; Awan, A.; Hossain, M.E. Towards a green transportation system in Mexico: The role of renewable energy and transport public- private partnership to curb emissions. J. Clean. Prod. 2024, 442, 140984. [Google Scholar] [CrossRef]
- Jarosław, W.; Aleksandra, B.; Ewa, Z.; Wojciech, S. Sustainable cities and communities assessment using the DARIA-TOPSIS method. Sustain. Cities Soc. 2022, 83, 103926. [Google Scholar]
- Wang, Q.; Li, S.Q.; Li, R.R. Evaluating water resource sustainability in Beijing, China: Combining PSR model and matter-element extension method. J. Clean. Prod. 2019, 206, 171–179. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W.; Sun, W.; Jiao, Y.; He, Y.; Li, D.; Gong, J. Tapping into the potential CO2 emission reduction of a crude oil transportation system from carbon footprint perspective. J. Clean. Prod. 2023, 413, 137409. [Google Scholar] [CrossRef]
- Zhang, L.; Long, R.; Li, W.; Wei, J. Potential for reducing carbon emissions from urban traffic based on the carbon emission satisfaction: Case study in Shanghai. J. Transp. Geogr. 2020, 85, 102733. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Peng, J.; Li, F.; Zhu, L.; Zhao, H.; Shi, R. Can China achieve its 2030 and 2060 CO2 commitments? Scenario analysis based on the integration of LEAP model with LMDI decomposition. Sci. Total Environ. 2023, 888, 164151. [Google Scholar] [CrossRef] [PubMed]
- Mancini, S.; Pezzella, F.; Pisacane, O. A path-based solution approach for the Green Vehicle Routing Problem. Comput. Oper. Res. 2019, 103, 109–122. [Google Scholar]
- Maxim, M.; Lyudmila, D. Economic and Information Support of Technological Integration with the use of “Green” Traffic Flows. Transp. Res. Procedia 2022, 61, 715–718. [Google Scholar]
- Jia, Z.Y.; Yin, J.W.; Cao, Z.P.; Wei, N.; Jiang, Z.; Zhang, Y.; Wu, L.; Zhang, Q.; Mao, H. Large-scale deployment of intelligent transportation to help achieve low-carbon and clean sustainable transportation. Sci. Total Environ. 2024, 949, 174724. [Google Scholar] [CrossRef]
- Duan, H.Y.; Hou, C.H.; Yang, W.; Song, J. Towards lower CO2 emissions in iron and steel production: Life cycle energy demand-LEAP based multi -stage and multi-technique simulation. Sustain. Prod. Consum. 2022, 32, 270–281. [Google Scholar] [CrossRef]
- Ren, H.B.; Wu, Q.; He, W.G.; Wang, W.; Luo, X.; Li, Q.; Jiang, Z. Research on regional low-carbon development path based on LEAP model. Taking the Lin-gang Special Area as an example. Energy Rep. 2022, 8 (Suppl. 15), 327–335. [Google Scholar] [CrossRef]
- El-Sayed, A.H.A.; Khalil, A.; Yehia, M. Modeling alternative scenarios for Egypt 2050 energy mix based on LEAP analysis. Energy 2023, 266, 126615. [Google Scholar] [CrossRef]
- Azam, M.; Othman, J.; Begum, R.A.; Abdullah, S.M.S.; Nor, N.G.M. Energy consumption and emission projection for the road transport sector in Malaysia: An application of the LEAP model. Environ. Dev. Sustain. 2016, 18, 1027–1047. [Google Scholar] [CrossRef]
- Shahid, M.; Ullah, K.; Imran, K.; Mahmood, A.; Arentsen, M. LEAP simulated economic evaluation of sustainable scenarios to fulfill the regional electricity demand in Pakistan. Sustain. Energy Technol. Assess. 2021, 46, 101292. [Google Scholar] [CrossRef]
- Wang, J.J.; Li, Y.; Zhang, Y. Research on Carbon Emissions of Road Traffic in Chengdu City Based on a LEAP Model. Sustainability 2022, 14, 6525. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Huang, L.; Liu, J.; Zhou, Y.; Chen, M.; Hu, J. Carbon dioxide mitigation co-benefit analysis of energy-related measures in the Air Pollution Prevention and Control Action Plan in the Jing-Jin-Ji region of China. Resour. Conserv. Recycl. X 2019, 1, 100006. [Google Scholar] [CrossRef]
- Kalayarsan, M.; Murali, M. Optimization of process parameters in EDM using Taguchi method with grey relational analysis and TOPSIS for ceramic composites. Int. J. Eng. Res. Afr. 2016, 22, 83–93. [Google Scholar] [CrossRef]
- Hernández, K.D.; Fajardo, O.A. Estimation of industrial emissions in a Latin American megacity under power matrix scenarios projected to the year 2050 implementing the LEAP model. J. Clean. Prod. 2021, 303, 126921. [Google Scholar] [CrossRef]
- Bai, C.Q.; Chen, Z.J.; Wang, D.P. Transportation carbon emission reduction potential and mitigation strategy in China. Sci. Total Environ. 2023, 837, 162074. [Google Scholar] [CrossRef]



| Gray Relative Proximity | 0.4–0.45 | 0.45–0.5 | 0.5–0.55 | 0.55–0.6 | 0.6–0.65 |
|---|---|---|---|---|---|
| Coordination level | 1 | 2 | 3 | 4 | 5 |
| Coordination | Uncoordinated | - | - | - | Coordinated |
| Hidden Meaning | Unit | Buses | Taxi | Metro | Private Car | |
|---|---|---|---|---|---|---|
| P0 | Total passenger traffic | 10,000 people | 5799.36 | |||
| L | Average annual distance traveled per mode of travel | kilometers/person | 8.1 | 7 | 11 | 8.5 |
| ε | Emission factors for nitrogen dioxide for all modes of travel | g/(person-km) | 19.8 | 140 | 7.5 | 116.9 |
| e | Energy consumption factor | MJ/(person-km) | 0.714 | 2.85 | 0.322 | 2.795 |
| N | Average passenger load factor for all modes of travel | people/vehicle | 40 | 2.5 | 1400 | 1.5 |
| v | Average speed in congested conditions | km/h | 13.8 | 21 | -- | 21 |
| t | Average delay | h/day | 0.3 | 0.25 | 0 | 0.4 |
| k | Average fuel consumption | km/L | 3.2 | 11.1 | -- | 12 |
| p | Fuel price | CNY/L | 5.7 | -- | -- | -- |
| σ | Average noise pollution costs | CNY/vehicle | 24.03 | -- | -- | -- |
| Q | External costs per vehicle accident | CNY/vehicle | 148.96 | 77.78 | -- | 1.73 |
| s | Per capita dynamic road area | m2 | 6 | 6 | -- | 6 |
| o | Subsidies for public transport operations | CNY/person | 3.5 | -- | 0.5 | -- |
| U | Average economic cost | CNY/person | 1.25 | 15 | 2 | 10 |
| R | Resident population | 10,000 people | 334 | |||
| γ | Average resident travel rate | trips/person/day | 1.89 | |||
| s0 | Road area per capita | m2 | 22.77 | |||
| h | Average time cost | h | 0.578 | 0.483 | 0.633 | 0.558 |
| ω | Hourly wage per capita | CNY/h | 18.9 | |||
| Level I Activity | Secondary Activity Level | Share (%) | Energy Intensity | |
|---|---|---|---|---|
| Lanzhou Transportation | Buses (51.23%) | diesel fuel | 45.92 | 0.0085 (L/person-kilometer) |
| electricity | 54.08 | 0.0188 (degrees/person-kilometer) | ||
| Taxi (14.61%) | diesel | 44.48 | 0.0280 (L/person-kilometer) | |
| petroleum | 44.48 | 0.0400 (m³/person-kilometer) | ||
| electricity | 11.04 | 0.0528 (degrees/person-kilometer) | ||
| Metro (6.47%) | electricity | 100 | 0.0018 (degrees/person-kilometer) | |
| Private cars (27.68%) | diesel | 98.99 | 0.0567 (L/person-kilometer) | |
| electricity | 1.01 | 0.0933 (degrees/person-kilometer) |
| Indicator Name | Numerical Value | Information Entropy (Physics) | Information Utility Value | Weights |
|---|---|---|---|---|
| Intersection crossing distance (m) | 24.6 | 0.774 | 0.226 | 0.032 |
| Average spacing of crossing facilities (m) | 286 | 0.786 | 0.214 | 0.03 |
| Vehicle speed limit on slow-moving roads (km/h) | 60 | 0.764 | 0.236 | 0.033 |
| Average daytime equivalent sound level of road traffic noise/dB | 68.9 | 0.725 | 0.275 | 0.039 |
| Urban transport energy consumption/tons of coal equivalent | / | 0.404 | 0.596 | 0.084 |
| Carbon emissions from urban transport/tons | / | 0.684 | 0.316 | 0.044 |
| Urban transport emissions/tonne | / | 0.582 | 0.418 | 0.059 |
| Public transportation trip-sharing ratio (%) | 67.8 | 0.665 | 0.335 | 0.047 |
| Density of slow road network (km/sq km) | 8.13 | 0.704 | 0.296 | 0.042 |
| Percentage of walking path area (%) | 29.78 | 0.626 | 0.374 | 0.052 |
| Percentage of bicycle path area (%) | 15 | 0.723 | 0.277 | 0.039 |
| Population density (persons/km2) | 7156 | 0.614 | 0.386 | 0.054 |
| Regional GDP (billions, CNY) | 2877.5 | 0.633 | 0.367 | 0.052 |
| GDP per capita (CNY) | 66,500 | 0.756 | 0.244 | 0.034 |
| POI density (pcs/km2) | 54.16 | 0.745 | 0.255 | 0.036 |
| Baseline Scenario | Theoretical Optimal Scenario | Limiting Rail Transit Scenarios | Restrictions on Private Car Scenarios | Combined Constraints Scenarios | |
|---|---|---|---|---|---|
| Gray relative proximity | 0.394044 | 0.490292 | 0.397761 | 0.444961 | 0.457292 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Qian, Y.; Zeng, J.; Wei, X.; Yang, M. Coordinated Development of Urban Transportation Structure Optimization and Energy Conservation, and Emission Reduction Under the Low-Carbon Background in Lanzhou, China. Systems 2025, 13, 34. https://doi.org/10.3390/systems13010034
Shi Z, Qian Y, Zeng J, Wei X, Yang M. Coordinated Development of Urban Transportation Structure Optimization and Energy Conservation, and Emission Reduction Under the Low-Carbon Background in Lanzhou, China. Systems. 2025; 13(1):34. https://doi.org/10.3390/systems13010034
Chicago/Turabian StyleShi, Zheming, Yongsheng Qian, Junwei Zeng, Xu Wei, and Minan Yang. 2025. "Coordinated Development of Urban Transportation Structure Optimization and Energy Conservation, and Emission Reduction Under the Low-Carbon Background in Lanzhou, China" Systems 13, no. 1: 34. https://doi.org/10.3390/systems13010034
APA StyleShi, Z., Qian, Y., Zeng, J., Wei, X., & Yang, M. (2025). Coordinated Development of Urban Transportation Structure Optimization and Energy Conservation, and Emission Reduction Under the Low-Carbon Background in Lanzhou, China. Systems, 13(1), 34. https://doi.org/10.3390/systems13010034






