Abstract
Efficient inventory management, including optimal safety-stock levels, is crucial for operational continuity and cost-effectiveness in various industries. This study seeks the optimal inventory management strategy to minimize costs and determine ideal safety-stock levels. It compares five approaches: the company’s (STAR) current “number of days” method, two alternative models from the literature (the theory of constraints (TOC) replenishment model and the service-level approach), and two newly developed hybrid methodologies (the TOC replenishment model with ABC–XYZ classification and the service-level approach with ABC–XYZ classification). The analysis focused on financial performance, considering inventory holding and shortage costs. Monthly production plans were established and fixed as constant based on predetermined optimum month-end inventory levels derived from each method. Through simulation, actual month-end inventory levels were assessed, comparing total inventory costs (TICs). While unit holding costs (UHCs) were documented in financial records in the company, unit shortage costs (USCs) were not; thus, USCs were examined in three scenarios. The results show that the second proposed hybrid model consistently outperformed the other four methods, including the company’s current approach, significantly reducing TIC. The analysis emphasizes the importance of demand variation in setting safety stocks and demonstrates the second hybrid methodology’s effectiveness in optimizing safety-stock strategies and improving overall inventory management efficiency.
1. Introduction
Inventory management plays a crucial role in the success of any supply chain system. It involves managing the process flow of goods from suppliers to manufacturers, and from manufacturers to distributors and retailers, while minimizing inventory costs and ensuring customer satisfaction. One of the most common methods used in industry for setting inventory levels is the number-of-days method, where a predicted number of days for each stock keeping unit is determined, and inventory levels are set accordingly [1]. However, there are several other methods that have been proposed in the literature, and the study aims to compare the effectiveness of the existing method with two alternative methods in the literature—Theory of constraints (TOC) replenishment model and service-level approach—and two proposed hybrid models—the integration of TOC replenishment model with ABC–XYZ matrix approach and the service-level approach with ABC–XYZ matrix approach.
ABC–XYZ analysis approach is an integration of two analyses, ABC analysis and XYZ analysis. The ABC classification provides inventory categorization and management at different levels and approaches in line with their value to the company [2]. XYZ analysis categorizes stocks based on the predictability and regularity of demand for specific material groups [3]. ABC–XYZ analysis approach is studied as a part of two developed/proposed hybrid approaches.
In Goldratt’s theory of constraints (TOC) replenishment method, instead of relying on a specific formula, it is advised to set the safety stock at 50% of the average demand during both the lead time and replenishment period. This approach eliminates the need for safety factors or determining probability distributions [4]. The TOC replenishment model and its combination with ABC–XYZ analysis were investigated in this study as two alternative approaches for inventory management.
Among the safety-stock-setting research area, especially concerning methods related to service levels, much research is dedicated to finding ways to determine safety stocks in different situations and with various demand patterns [1]. Brown proposed a technique that considers the variability in demand during lead time along with a safety margin to decide the appropriate level of safety stock [5]. Similarly, Ballou and Srivastava demonstrated that when both demand and lead time are uncertain, understanding the standard deviation of demand during lead time becomes crucial [6]. These methods involve setting a desired service level and then computing the necessary safety stock using assumed demand distribution characteristics [1]. The service-level approach and its combination with ABC–XYZ analysis approach were included in the study with the aim of finding the best safety-stock-setting methodology. The aim of the inclusion of the hybrid methodologies was to see whether there would be an increase in efficiency for service levels or inventory costs.
This study aimed to find out the best-performing inventory policy while setting appropriate safety stocks to secure low inventory costs and desired service level for the five products, which had different demand patterns and different values. The five methods in the study had different input parameters, and the research aimed to observe the efficiency of the different parameters’ usage as an input in the models, especially the most differentiated parameter, demand variation.
The results of this study have important implications for supply chain managers and practitioners. By evaluating the effectiveness of different inventory policies, we can provide guidance for better inventory management and cost control. Furthermore, our investigation of safety-stock setting for the number-of-days method provides a valuable contribution to the literature, as this method is widely used in industry but has not been extensively studied [1]. This research aims to bridge this gap by critically examining the number-of-days method within an academic framework. This study also brings a new perspective regarding the usage of hybrid methods with a proposal of two developed approaches to empower the existing safety-stock methods in the literature. Overall, this study provides a comprehensive evaluation of the hybrid usage of inventory management policies and also cost effects on inventory management and contributes to the development of best practices for supply chain management.
2. Literature Review
This section includes the literature of related research, which is categorized into five topics: safety-stock-setting literature, ABC–XYZ analysis approach, number-of-days method, TOC replenishment method and service-level approach for inventory management.
2.1. Safety-Stock-Setting Literature
Collier (1982) investigated the relationship between the degree of component part standardization and aggregate safety-stock inventory levels. The paper concludes with a discussion of the managerial tradeoffs between aggregate safety-stock levels, service level and the degree of component part commonality. A simulation experiment strongly validates the effectiveness of this relationship in a variable operating environment. He claimed that these relationships can be used to forecast service, inventory level and cost standards when there are changes in the commonality of component parts, and also showed three examples to guide practitioners while using this to maintain or improve service levels, reduce or control costs, and set aggregate inventory standards [7].
Eppen and Martin (1988) examined the problem of determining safety-stock levels when both period demand and lead time are random variables. They considered two scenarios: one where the parameters of demand and lead time distributions are known, and another where these parameters are unknown and must be estimated. For the known parameters scenario, the standard procedure from the literature was shown through examples to sometimes produce inaccurate results. The authors presented a correct procedure to address this issue. In cases where parameters are unknown, the authors assumed the use of a simple exponential smoothing model to estimate period demand, and that historical data can be used to create a discrete distribution of lead times. They provided a correct procedure for establishing safety stocks with these inputs for two widely used demand models, noting that the approach can be easily adapted to other demand models [8].
Gallego (1988) studied scheduling multiple items in a single facility, aiming to minimize long-term costs of holding, backorders, and setups where demands follow Brownian Motion, and item-specific drifts, linear time-weighted holding and backlogging costs are considered, with items produced at constant rates and setup times and costs being specific to each item but not dependent on order. He developed a cost-effective schedule in three steps: a target cyclic schedule based on expected demands using Economic Lot Scheduling Problem, a control policy that keeps inventories close to the target schedule—addressed as a linear-quadratic control problem—and safety stocks to hedge against randomness while adhering to the target schedule and recovery policy [9].
Kelle and Silver (1990) examined an inventory control system using continuous review, reorder point, and order quantity methods. The required amount of safety stock is influenced by factors such as the average value and variability of replenishment lead times. They assumed that the random lead times follow Weibull distributions, allowing for the development of analytical expressions to reduce the expected value and variability of total demand until the first critical delivery from a vendor. In the study, an expression is derived for the reorder point that ensures a given probability of no stockout before the first delivery and lower bounds on the order quantity are provided to ensure that the probability of a stockout before any subsequent deliveries (second, third, etc.) is negligible. They presented that the analytical and tabular results of the study can be used to estimate the benefits of order splitting, such as reduced carrying costs and/or increased service levels [10].
Groenevelt et al. (1991) investigated the economic lot size problem for an unreliable manufacturing facility with a constant failure rate and generally random repair times. Due to these stochastic interruptions, safety stocks are necessary to maintain required service levels. The authors developed bounds on the feasible service levels and analyzed how various system parameters affected this range. They introduced an easy-to-implement production control policy, showing that under this policy, safety-stock dynamics can be fully characterized by a renewal process similar to a single-server queuing system’s workload process. This analogy helped derive exact and approximate safety-stock holding costs. The study provided operational insights through model experimentation and integrates the results into a broader management framework for resource allocation to reduce machine failure rates and a trade-off between investing in better maintenance and the savings in safety stocks and repair costs [11].
Molinder (1997) conducted a simulation study on a Material Requirements Planning (MRP) system under the influence of stochastic demand and lead times. The study aimed to assess the impact of three main factors: variability in lead times, variability in demand, and the ratio between stockout costs and inventory holding costs. Using simulated annealing, the study optimized lot sizes, safety stocks, and lead times. The research compared the effectiveness of using safety stocks versus safety lead times as buffering techniques against uncertainties in lead times and demand. Three different product structures were simulated and optimized using simulated annealing. Key findings showed that higher levels of lead time and demand variability significantly influenced the optimal levels of safety lead times and safety stocks. When the stockout cost/inventory holding cost ratio was low, safety stocks were generally preferred. As this ratio increased, there was a tendency to favor safety lead times, especially under higher demand variability [12].
Cheung and Hausman (1997) developed an analytical model to jointly consider preventive maintenance and safety-stock strategies in a production environment facing random machine breakdowns. They studied these two strategies separately. They aimed to create a unified framework that illustrated the trade-off between investing in preventive maintenance and safety stocks. They provided optimality conditions to determine when one or both strategies should be implemented to minimize costs. The analysis includes cases with deterministic and exponential repair time distributions, along with numerical examples to demonstrate the determination of optimal strategies for preventive maintenance and safety stocks. The article also examines optimality conditions under general failure distributions with increasing failure rates and different repair time assumptions. For deterministic repair times, an efficient method to find the optimal solution is provided. For exponentially distributed repair times, a first-order optimality condition is used to determine the optimal maintenance interval, from which the optimal safety stock is derived [13].
Hsu and Wang (1998) proposed a possibility linear programming model to manage production planning issues in assemble-to-order (ATO) environments where there is demand uncertainty. They defined the general two strategies of ATO environment as regulation of the forecasts and safety-stock setting. Additionally, the number of key machine decisions is stated as one of the strategies to reduce capital waste. They proposed an analytical model for the related managerial decision-making process. Zimmermann’s fuzzy programming method was used to find a satisfactory compromise. They proved that the proposed possibilistic model is competent in dealing with ambiguous and uncertain data to solve decision-making problems in ATO practices [14].
Tsou (2008) studied a two-step decision-making process for a multi-objective inventory planning problem that involved balancing conflicting decisions to meet customer demands at minimal cost while maintaining service levels. He studied a two-stage framework using multi-objective particle swarm optimization (MOPSO) to generate non-dominated solutions and the TOPSIS method to rank them based on decision-makers’ preferences. By varying the weights of criteria such as cost, stock-out frequency, and stock-out number, managers can determine optimal order sizes and safety stocks to fit different situations. The study shows that MOPSO performs well in solving multi-objective optimization problem (MOOP) through the information-sharing mechanism among the particles [15].
Taleizadeh et al. (2011) examined a multi-buyer multi-vendor supply chain with several products, limited buyer capacity, and vendor warehouse constraints. Product demand was stochastic and uniformly distributed. Lead-time varied with order quantity and vendor production rate. Shortages were partially backordered, and orders were placed in pre-defined packet multiples with service rate constraints for buyers. The study aimed to minimize supply chain costs while setting the reorder points, safety stocks, and the ordering quantities. The problem was modeled as an integer nonlinear programming problem and solved using a harmony search algorithm, with a genetic algorithm used for validation and performance comparison. The results indicated that the proposed harmony search (HS) algorithm perform better in terms of total supply chain costs, as well as buyers’ and vendors’ costs. They also performed sensitivity analysis to point out how parameter changes impacted these costs [16].
2.2. ABC–XYZ Analysis Approach
The ABC–XYZ analysis approach is an integration of two analyses, ABC analysis and XYZ analysis. ABC classification provides inventory categorization and management at different levels and approaches in line with their value to the company. Stock-keeping units are split into groups due to the Pareto principle, which is based on the traditional Pareto Rule, a small number of items that account for the majority of the outcomes, which is also defined as 20% of the items contributing to 80% of the results. ABC analysis, aligned with the Pareto rule, creates three product groups: Group A typically includes around 20% of products that generate 80% of the total value; Group B contains products contributing approximately 15%; and Group C comprises products that contribute about 5%. This distribution is flexible, with group definitions tailored to the specific requirements of the enterprise [2]. XYZ analysis categorizes stocks based on the predictability and regularity of demand for specific material groups. The analysis divides materials into three groups: X Group has a consistent demand with minimal periodic fluctuations, leading to high forecasting accuracy. Y Group has moderate demand fluctuations, resulting in moderate forecasting accuracy. Z Group exhibits irregular demand patterns, making forecasting less accurate [3]. ABC–XYZ analysis approach is studied as a part of two developed/proposed hybrid approaches.
Gupta et al. (2007) focused on inventory control principles, specifically employing ABC classification based on cost criterion and VED classification based on criticality, in which “V” is for vital items without which a hospital cannot function, “E” for essential items without which an institution can function but may affect the quality of the services, and “D” stands for desirable items, the unavailability of which will not interfere with functioning. Using the ABC–VED matrix, they categorized products into three groups. Category I consisted of 68 drugs (AV + BV + CV + AE + AD), Category II had 159 drugs (BE + CE + BD), and Category III contained 98 drugs (CD). The management of Category I drugs was overseen by top management, leading to more stringent control over annual expenses. Meanwhile, Category II drugs were managed at the middle management level, and Category III drugs were handled at a lower managerial level, ensuring efficient allocation of resources across different product categories [17].
Chen et al. (2008) studied a different approach of ABC analysis for inventory management. The general approach was to classify products considering one criterion, their annual usage value. They applied multi-criteria ABC analysis considering criteria like obsolescence, repairability, criticality, and lead time in addition to annual usage value [18].
ER et al. (2011) combined ABC analysis and fuzzy classification in their research in the pharmaceutical industry, with a claim that in the related industry, other criteria should be considered—like the degree of the effects of the product’s unavailability on patients. These other criteria are typically evaluated based on human observations and experiences, which can be challenging to quantify. So, they solved this issue by combining ABC analysis with fuzzy classification to consider all the important criteria in the pharmaceutical industry [19].
Reiter et al. (2011) applied ABC–XYZ analysis on products for classification, but using a nontraditional way. They used demand forecasts instead of actual sales as an input for the classification. They classified products using an ABC–XYZ matrix of AX, BX, CX, AY, BY, CY, AZ, BZ, and CZ [20].
In Rusănescu’s study (2014), the emphasis was on ABC analysis and the utilization of a multi-criteria approach. The research introduced a classification system that relied on various factors including delivery time, criticality of stock shortage for an item, obsolescence rate, scarcity, substitutability, order size, and other significant criteria that collectively offer a comprehensive framework for managing inventory effectively [21].
Kampf et al. (2016) focused on ABC analysis with the aim of utilizing the effect of cost savings in the automotive industry. They aimed to guide companies to reduce their costs estimated in their inventories by the prioritization of inventories with ABC analysis [22].
Zenkova and Kabanova (2018) modified ABC–XYZ analysis by excluding outliers. They claimed that an extraordinary value can be just for one time, so if a value is an outlier, it should be excluded from the inputs of the analysis. To define whether a value is an outlier, they conducted hypothesis testing. They finalized their analysis after modifying the data without outliers [23].
Li and Rim (2019) focused on a multicriteria ABC inventory classification problem using stochastic multicriteria acceptability analysis as a new procedure. This approach takes into account all potential preferences among the criteria used for evaluation. They determined preference-specific intervals for each criterion and used these to create a decision-making framework that considered various distribution functions of these intervals. By doing so, they developed holistic acceptability indices to effectively classify different stock-keeping units based on their characteristics [24].
Milkova (2019) studied on ABC analysis for inventory classification in MS Excel by an empirical and graphical method. Depending on the level of importance of the inventories due to the groups obtained from the analysis, different approaches for their management are recommended [25].
Abdolazimi et al. (2020) conducted research focusing on enhancing inventory grouping through ABC analysis. They proposed a biobjective mathematical model aimed at optimizing inventory grouping by maximizing total net profits in both central stock and different wards. The model also aimed to optimize service levels while simultaneously optimizing the quantity of inventory groups and the allocation of items. To solve the model efficiently, they employed two exact methods—linear programming metric (LP-metric) and e-constraint—and two meta-heuristic methods—nondominated sorting genetic algorithm (NSGA-II) and multiobjective particle swarm optimization (MOPSO)—catering to both small- and large-scale scenarios. Comparative analysis using statistical methods alongside analytical hierarchy process (AHP) and one of the multiple-criteria decision-making “VIKOR” techniques revealed the e-constraint method’s superiority among exact methods and MOPSO among meta-heuristic methods in terms of efficiency. Finally, they utilized the proposed model in two separate scenarios, each consisting of numerical instances, to illustrate its practical application and effectiveness [26].
Asana et al. (2020) conducted a study focusing on goods classification and determining safety-stock levels for inventory control. They utilized the ABC analysis method to classify goods and employed the min max analysis method to determine safety-stock quantities based on historical sales data. The study incorporated limitation safety-stock amounts derived from the results of the min max method. The testing of the proposed method involved comparing costs before and after its implementation to evaluate its effectiveness [27].
2.3. Number-of-Days Method
A commonly used method to calculate safety stocks in industry is number of days times average demand per day, where number of days is an estimated parameter representing a safety time margin when replenishing stock-on-hand. This approach will henceforth be referred to as the number-of-days method.
Despite its common industrial usage, the number-of-days method remains sparsely discussed in the academic literature. Existing references are few and predominantly descriptive, primarily disseminated through popular science or less scholarly journals. Moreover, these publications exhibit an aged chronology [1].
2.4. TOC Replenishment Method
The theory of constraints (TOC) is a management philosophy introduced by Eliyahu M. Goldratt, asserting that every system has at least one constraint [28]. While initially applied to manufacturing, TOC has evolved into a comprehensive management theory. It serves as a powerful methodology for systemic problem structuring and problem-solving, offering solutions that combine intuitive insights with analytical rigor. This philosophy is now utilized in various functional areas of companies, including production-flow management, marketing, services, and project management, as well as a tool for logical reasoning [29].
Goldratt’s TOC replenishment method is used in the make-to-availability (MTA) methodology, which aims to guarantee the availability of a finished product at a certain warehouse. In the TOC replenishment model, the suggestion is to set the safety stock at 50% of the average demand during both the lead time and replenishment period. The safety stock is set at 50% of the demand regardless of the distribution of the demand. This methodology not only enhances inventory performance but also places a strong emphasis on availability by offering guidance for planning, execution, and control processes. Its effectiveness has been demonstrated through various case studies, including the successful implementation of milk-run replenishment presented at the TOCICO Conference 2013, which resulted with reduced monthly stock levels and increased inventory turnover [4].
Lee and Rim reviewed safety-stock-setting models including a TOC and DDMRP (demand-driven materials requirement planning) replenishment model, which was based on the TOC and developed a new safety-stock formula. They compared the classical DDMRP model, traditional safety-stock model (service-level approach) and their proposed model as an adjusted DDMRP model. The models only differed in their safety-stock calculations [4].
2.5. Service Level Approach
Schmidt et al. (2012) analyzed established mathematical methods for calculating safety stock in which there was a targeted service level as a safety factor input. These methods—in total, nine safety-stock-setting approaches—were described with their specifics and then with the help of an extensive simulation study. The performances of the methods were then mapped regarding the resulting service and safety-stock level against the background of different articles with variant logistical behaviors. The simulation study results showed that due to the variance of the lead time and demand, different safety-stock calculations serve different efficiency levels [30].
Cheng et al. (2015) aimed to compare solutions from the cycle service level model and the fill-rate model in both objective and decision spaces to underscore their differences. Both methods were evaluated under “reorder point lot size inventory models”, and both included the same safety-stock formula with a safety factor, standard deviation of the demand and lead time. The results, evaluated using quality measures and graphical illustrations, indicate that control policies derived from both models are predominantly non-dominated in the objective space. The fill-rate model, in particular, tends to produce control policies with higher service levels [31].
Thomopoulos (2015) published a book about demand forecasting and inventory control and also presented a section about setting strategic safety stocks. He defined two common different methods, service level and percent fill, with two different demand characteristics: standard normal-distributed and truncated normal-distributed demands. Although the most commonly known distribution is standard normal distribution, the demand distribution characteristic needs to be clearly defined in order to choose the most appropriate approach. He also highlighted the demand variation importance on safety-stock levels by comparing the coefficient of variation of the demand (COV) and safety-stock levels where there is a negative correlation between the two [32].
Rădăşanu (2016) published an article about service-level approach and defined the characteristics of safety-stock and inventory management and service-level approaches and their relationship. He stated that companies set a score as high as 95% as a service level target and also presented a different service-level-setting approach like ABC analysis. He stated that ABC classification can also guide companies in their service-level-targeting process instead of having one constant service-level target. He also stated different safety-stock calculations with and without service-level safety factors [33].
Brunaud et al. (2018) developed four different safety-stock calculation methods under two different inventory policies. They developed proportional, piecewise, explicit and guaranteed safety-stock models. They compared the performance of models with two criteria as the service level achieved with the model and the standard deviation of the demand [34].
Lee and Rim (2019) researched an alternative safety-stock calculation method for a demand-driven material requirement planning (DDMRP) process. They presented classical service-level approach calculation and TOC replenishment model calculation and classical DDMRP replenishment model and then proposed a different DDMRP model with some adjustments to avoid inconsistencies. And then, they calculated the performance of the three models with two criteria, average inventory level and shortage rate. Their simulations resulted in the proposed model significantly outperforming the traditional safety-stock model and classical DDMRP replenishment model [3].
Jonsson and Mattsson (2019) studied a benchmark of safety-stock methods, the number-of-days method—which is common in practice and rare in the literature—and the demand–fill-rate method, which is a type of service-level approach in safety-stock setting. They proceed the investigation for eight items in eight different companies, which had different dynamics like demands, order frequencies, unit costs and lead times. They defined five categories for order frequency and cost and compared the performance of two methods in each category of items by average order line fill rate. The study shows that the number-of-days method mostly performs better than the demand–fill-rate method. They stated that this is because of the characteristics of demand data, the length of the lead time and the coefficient of demand variation [4].
Paul et al. (2020) developed an automated safety-stock calculation method using PYTHON software based on the simple service-level approach and then analyzed impacts of this new model on wastage in construction in terms of cost and time with a questionnaire survey, and the results showed that the biggest impact in terms of cost and time came from inadequate planning and scheduling [35].
Gonçalves et al. (2020) published a literature review about safety-stock determination models and presented their calculations and methodologies step by step in the literature. They stated that the simplest approach to determine safety-stock level is a fixed targeted service-level approach, where a safety factor (for targeted service level), standard deviation of demand and lead time are considered in the scope. They also presented different safety-stock calculations in terms of a service-level approach, where demand and lead time are independent variables, and also another formula that considers forecasting error as a variable [36].
Ghadimi et al. (2020) investigated the joint optimization of production capacity and safety stocks in supply chains using the guaranteed service approach (GSA) in which a service level is targeted while setting safety stocks. The problem was modeled as a mixed-integer nonlinear program (MINLP) and addressed for both general acyclic and spanning tree network structures. For general acyclic supply chains, a Lagrangian decomposition method was used, while for spanning tree networks, a Lagrangian relaxation heuristic was applied. Computational experiments showed that the Lagrangian decomposition method achieved near-optimal solutions within 0.1% accuracy for all instances, outperforming a state-of-the-art solver for larger instances. The Lagrangian relaxation heuristic also found optimal or near-optimal solutions efficiently in spanning tree networks. The joint optimization of capacity and safety stocks led to significant cost savings [37].
Lestari and Handayati (2022) performed a case study in a company to improve inventory costs by applying demand forecasting and an EOQ model in inventory optimization. They compared different forecasting techniques in terms of forecasting accuracy and chose the best-performing one to proceed with the process to provide outputs for inventory management. Then, with these outputs, the EOQ inventory model was applied, and the existing inventory model and EOQ model were compared in terms of inventory costs. And the study showed that the EOQ model including a service-level approach safety-stock model resulted in lower inventory costs than the existing inventory model [38].
Tadayonrad and Ndiaye (2023) studied a new key performance indicator (KPI) like supply-chain reliability and developed a new inventory model with this new KPI. The simple service-level approach in their safety-stock calculation was the base model, and they developed this model with forecasted supply reliability factors. In the evaluation step, they made a financial benchmark of the basic model and the developed one, and it resulted in lower inventory costs (excess inventory cost + shortage cost) [39].
3. Materials and Methods
The current inventory management strategy employed by the company “STAR” utilizes the “number of days” method. This method calculates the safety-stock margin by multiplying the daily demand by the number of days required to replenish the stock-on-hand. In the company’s context, this safety-stock margin corresponds to the lead time for each product, as outlined in Table 1.

Table 1.
Lead time of the products under research.
However, this method does not consider other factors that affect inventory levels, such as lead time and demand variability. To address the limitations of the existing method, two proposed hybrid inventory-management approaches are suggested. The characteristics of the existing model and the proposed models are shown in Table 2.

Table 2.
The models under evaluation.
The ABC classification categorizes products based on their value and importance. Products are categorized as A, B, or C based on their relative value to the company [2]. In this study, the value of the products was determined by their annual sales value %, which is given in Equation (1).
Assuming that the total demand during a lead time Lt > 0 is normally distributed with mean μLt and standard deviation σd√Lt, the most simple approach for dimensioning safety stocks for a fixed-target service level is set as below in Equation (2), as is also shown in Table 2 [36].
The XYZ classification categorizes products based on their demand variability [2]. Products were categorized as X, Y or Z based on their predictability in terms of sales forecast. And the predictability parameter was determined as the COV of actual sales for the previous twelve months.
The combination of two classifications is called the ABC–XYZ matrix approach in the literature. The characteristic for each group is shown in Table 3 [2].

Table 3.
ABC–XYZ characteristics [2].
Due to the products’ positions in the matrix, different inventory management tactics are proposed in the literature, which are shown in Table 4, and the calculation for each class is shown in Table 5. For the inventory levels, the lead time was used as a reference to calculate DOHABC-XYZ.

Table 4.
ABC–XYZ inventory management approach [2].

Table 5.
Additional days on hand for each product due to ABC–XYZ inventory-management approach.
The ABC–XYZ matrix provides 9 different categories for stock-keeping units: AX, AY, AZ, BX, BY, BZ, CX, CY, and CZ. For AX, BX, CX, and AY, the proposal is low-inventory, since the risk of stockout is low. The recommendation for AZ, BY, and BZ is average safety-stock levels, and for CY and CZ, it is high safety-stock levels, since there is high stockout risk, and these products’ values are low [2]. The classification limits are not specifically determined in the literature; every company can determine their own limits due to their dynamics and their products’ nature. And in this study, the classification limits were determined as below in Table 6.

Table 6.
ABC–XYZ classification criteria limits.
The dataset with annual sales value % and COV for each product is listed in Table 7.

Table 7.
Collected dataset for each product.
Due to the limits, every product’s category and the determined DOHABC-XYZ using the formulas in Table 5 and the lead time of the products given in Table 1 is shown in Table 8.

Table 8.
ABC–XYZ classification of the products with proposed safety-stock days.
Product 1 falls into category A and category Y. This means that it has high value to the company and moderate demand variability. The safety-stock level recommendation for this product is to keep an additional 4 days of inventory in stock.
Product 2 falls into category B and category X. This means that it has moderate value to the company and low demand variability. The safety-stock level recommendation for this product is to keep an additional 5 days of inventory in stock.
Product 3 falls into category C and category Z. This means that it has low value to the company and high demand variability. The safety-stock level recommendation for this product is to keep an additional 6 days of inventory in stock.
Product 4 falls into category A and category Z. This means that it has high value to the company and high demand variability. The safety-stock level recommendation for this product is to keep an additional 5 days of inventory in stock.
Product 5 falls into category C and category X. This means that it has low value to the company and low demand variability. The safety-stock level recommendation for this product is to keep an additional 3.75 days of inventory in stock.
The number-of-days method—the existing methodology—as the first method only refers to an estimated number of days on hand as safety stock, and estimated days are assumed as the lead times of each product in the company.
Alternative approaches from the literature—as the second and third methods—are the TOC replenishment model and service-level approach, which have their own safety-stock formulae that are shown in Table 2.
The first proposed hybrid approach—as the fourth method—combines the TOC replenishment model and the ABC–XYZ matrix approach. The TOC replenishment model has its own safety-stock formula, considering lead time and the demand together (which is shown in Table 2), while the ABC–XYZ matrix is used to adjust the safety-stock level according to the additional safety-stock days, which is determined as in Table 8.
The second proposed hybrid approach—as the fifth method—combines the service-level approach and ABC–XYZ matrix approach (which is shown in Table 2). The service-level approach is used to determine the safety-stock level, while the ABC–XYZ matrix is used to adjust the safety-stock level according to the additional safety-stock days, which is determined as in Table 8.
4. Results
The methods’ efficiency levels were evaluated with their financial performance. The financial performance criterion was total inventory cost at the end of every month. Total inventory cost (TIC) was calculated as the total holding cost plus the total shortage cost, as given in Equations (3)–(5).
where TIC is total inventory cost, THC is total holding cost, TSC is total shortage cost, I is inventory level at month-end, UHC is unit holding cost, and USC is unit shortage cost.
In most companies, there is no unit shortage cost consideration in the industry. On the other hand, unit holding cost is mostly specified as a cost item in finance. Also, there is nothing specific found in the literature for unit shortage cost calculation; so, four scenarios are studied, as shown in Table 9, assuming the shortage cost as 500%, 1000%, 1500% and 2000% of the holding cost. The company’s target was to reach a minimum 99% service level; since there is high competition in the market, stockout was not desired. The shortage cost was assumed to be minimum five times of the inventory holding cost.

Table 9.
Unit shortage cost (USC) scenarios.
For all methods, we simulated the models with the actual sales and reached actual month-end inventories, where we also see shortages in the inventory; this is presented as TIC first scenario, TIC second scenario, and TIC third scenario in the study.
To reach the actual month-end inventory levels, firstly, the optimal month-end inventory was calculated according to the methods’ formulas, which are shown in Table 2, and then monthly optimal production volume was calculated in order to reach the optimal month-end inventory, and finally, the model was simulated with the actual sales volumes and the optimal production volumes.
The models’ financial benchmark is listed in Table 10 for all the scenarios.

Table 10.
The results.
The results graph is presented in Figure 1. As seen in Figure 1, among all scenarios, the second hybrid model outperformed all other methods in terms of inventory costs.
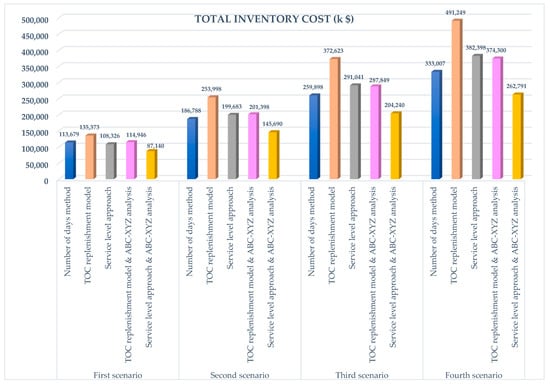
Figure 1.
Comparison graph of the safety-stock methodologies.
5. Discussion
The results obtained from the simulation of different inventory-management methodologies across various scenarios are summarized as below:
- The TOC replenishment model and its combination with the ABC–XYZ analysis approach consistently resulted in the highest total inventory costs across all scenarios. The number-of-days method ranked third in terms of the total inventory costs. The service level approach showed a noticeable reduction in total inventory costs compared to these three methods. The second proposed hybrid methodology demonstrated the lowest total inventory costs among all methodologies and scenarios.
- In the first scenario, where the USC was 500% of the UHC, for the TIC for all products, the second hybrid approach had 30% lower costs than the existing methodology, 55% lower costs than the TOC replenishment model, 24% lower costs than the service-level approach, and 32% lower costs than the first hybrid approach.
- In the second scenario, where the USC was 1000% of UHC, for the TIC for all products, the second hybrid approach had 28% lower costs than the existing methodology, 74% lower costs than the TOC replenishment model, 37% lower costs than the service-level approach, and 38% lower costs than the first hybrid approach.
- In the third scenario, where the USC was 1500% of UHC, for the TIC for all products, the second hybrid approach had 27% lower costs than the existing methodology, 82% lower costs than the TOC replenishment model, 42% lower costs than the service-level approach, and 41% lower costs than the first hybrid approach.
- In the fourth scenario, where the USC was 2000% of UHC, for the TIC for all products, the second hybrid approach had 27% lower costs than the existing methodology, 87% lower costs than the TOC replenishment model, 46% lower costs than the service-level approach, and 42% lower costs than the first hybrid approach.
In the comparison of the methods’ efficiency in terms of total inventory cost, for all types of products, the second hybrid approach resulted in lower costs in real-life scenarios in which product 1 has a forecast accuracy (FCA) of 89%, product 2 of 90%, product 3 of 77%, product 4 of 89% and product 5 of 82%. In these scenarios, just the unit shortage cost formula is different, as shown in Table 9.
For the effectiveness of the hybrid methodologies, the observations are listed as below:
- Combining TOC with ABC–XYZ analysis improves cost compared to the pure TOC replenishment model; in all four scenarios, the combination provides lower inventory costs compared with the pure model in the literature.
- The hybrid method of service-level approach and ABC–XYZ analysis approach provides lower inventory costs compared with the pure service-level approach application in all scenarios.
These summaries provide a clear comparison of the performance of each inventory management methodology, focusing on safety-stock calculation across different scenarios, enabling informed decision-making regarding the adoption of the most suitable approach.
6. Conclusions
Across different scenarios, all methodologies exhibited variations in inventory levels, indicating sensitivity to changes in demand or other factors. The second proposed hybrid methodology consistently maintained lower inventory costs across scenarios, suggesting a more robust performance under varying conditions.
Utilizing a simulation with actual sales data, the existing methodology—number-of-days method—primarily focused on lead time and demand. However, despite its simplicity, it did not give the best performance among the five methods. Additionally, the studied TOC replenishment model resulted in higher inventory costs, and the service-level approach resulted in lower inventory costs.
Introducing additional parameters in the first proposed hybrid approach, such as annual sales volume percentage and COV alongside lead time and demand, led to noticeable reductions in total inventory costs compared to the single TOC replenishment model application across all scenarios, suggesting improved cost-effectiveness.
Similar to the first proposed method, the second proposed hybrid approach expanded the parameter scope to include demand variation besides lead time, annual sales volume percentage and COV. This comprehensive consideration of factors resulted in further reductions in total inventory costs compared to the other four methods across all scenarios, indicating enhanced cost reduction.
Given that the best performer is the combination of a service-level approach and ABC–XYZ analysis, the second is the pure service level method, demand variation—as the only common differentiated parameter in these two methods—plays a big role in setting safety stocks, considering the reality that demand is not forecasted accurately.
In summary, both proposed hybrid inventory management methodologies show promise in reducing inventory costs and optimizing inventory levels compared to the applications of their pure method versions. And the second proposed hybrid methodology appears to offer the most significant improvements across various scenarios among all five methods. Organizations seeking to optimize their inventory management should consider adopting hybrid methodologies; particularly, those integrating service-level approaches offer a balanced solution, minimizing costs, especially under varying demand conditions. However, further analysis and testing may be necessary to validate these findings and determine the most suitable methodology for implementation. And further research should be conducted in order to show the effects of forecast accuracy on supply chain costs.
Author Contributions
Conceptualization, S.D.K., Z.C. and S.B.; Methodology, S.D.K. and S.B.; Formal analysis, S.D.K.; Investigation, S.D.K.; Data curation, S.D.K.; Writing—original draft, S.D.K.; Writing—review and editing, S.D.K., Z.C. and S.B.; Supervision, Z.C. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets presented in this article are not readily available because it is obtained from a third party and not permitted for sharing as an open access.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jonsson, P.; Mattsson, S.A. An inherent differentiation and system level assessment approach to inventory management: A safety stock method comparison. Int. J. Logist. Manag. 2019, 30, 663–680. [Google Scholar] [CrossRef]
- Stojanović, M.; Regodić, D. The significance of the integrated multicriteria ABC-XYZ method for the inventory management process. Acta Polytech. Hung. 2017, 14, 29–48. [Google Scholar] [CrossRef]
- Nowotyńska, I. An application of xyz analysis in company stock management. Mod. Manag. Rev. 2013, 18, 77–86. [Google Scholar] [CrossRef]
- Lee, C.J.; Rim, S.C. A mathematical safety stock model for DDMRP inventory replenishment. Math. Probl. Eng. 2019, 2019, 6496309. [Google Scholar] [CrossRef]
- Brown, R. Materials Managements Systems; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Ballou, R.H.; Srivastava, S.K. Chapter 9 inventory policy decisions. In Business Logistics/Supply Chain Management, 5th ed.; Pearson Education: Noida, India, 2004; pp. 336–433. [Google Scholar]
- Collier, D.A. Aggregate safety stock levels and component part commonality. Manag. Sci. 1982, 28, 1296–1303. [Google Scholar] [CrossRef]
- Eppen, G.D.; Martin, R.K. Determining safety stock in the presence of stochastic lead time and demand. Manag. Sci. 1988, 34, 1380–1390. [Google Scholar] [CrossRef]
- Gallego, G. Scheduling the production of several items with random demands in a single facility. Manag. Sci. 1990, 36, 1579–1592. [Google Scholar] [CrossRef]
- Kelle, P.; Silver, E.A. Safety stock reduction by order splitting. Nav. Res. Logist. (NRL) 1990, 37, 725–743. [Google Scholar] [CrossRef]
- Groenevelt, H.; Pintelon, L.; Seidmann, A. Production batching with machine breakdowns and safety stocks. Oper. Res. 1992, 40, 959–971. [Google Scholar] [CrossRef]
- Molinder, A. Joint optimization of lot-sizes, safety stocks and safety lead times in an MRP system. Int. J. Prod. Res. 1997, 35, 983–994. [Google Scholar] [CrossRef]
- Cheung, K.L.; Hausman, W.H. Joint determination of preventive maintenance and safety stocks in an unreliable production environment. Nav. Res. Logist. (NRL) 1997, 44, 257–272. [Google Scholar] [CrossRef]
- Hsu, H.M.; Wang, W.P. Possibilistic programming in production planning of assemble-to-order environments. Fuzzy Sets Syst. 2001, 119, 59–70. [Google Scholar] [CrossRef]
- Tsou, C.S. Multi-objective inventory planning using MOPSO and TOPSIS. Expert Syst. Appl. 2008, 35, 136–142. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Niaki, S.T.A.; Barzinpour, F. Multiple-buyer multiple-vendor multi-product multi-constraint supply chain problem with stochastic demand and variable lead-time: A harmony search algorithm. Appl. Math. Comput. 2011, 217, 9234–9253. [Google Scholar] [CrossRef]
- Gupta, R.K.G.R.; Gupta, K.K.; Jain, B.R.; Garg, R.K. ABC and VED analysis in medical stores inventory control. Med. J. Armed Forces India 2007, 63, 325–327. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, K.W.; Liu, S.F. A comparative study on multicriteria ABC analysis in inventory management. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 3280–3285. [Google Scholar] [CrossRef]
- Er, M.; Laili, E.N.; Renny, P.K. Classification of Hospital Pharmaceutical Drug Inventory Items by Combining ABC Analysis and Fuzzy Classification. In Proceedings of the International Conference on Advanced Computer Science and Information System (ICACSIS 2011), Jakarta, Indonesia, 17–18 December 2011; pp. 978–979. [Google Scholar]
- Reiter, B.; Heger, J.; Meinecke, C.; Bergmann, J. Integration of Demand Forecasts in ABC-XYZ Analysis: Practical Investigation at an Industrial Company. Int. J. Product. Perform. Manag. 2012, 61, 445–451. [Google Scholar] [CrossRef]
- Rusanescu, M. ABC analysis, model for classifying inventory. Hidraulica 2014, 17. Available online: https://hidraulica.fluidas.ro/2014/nr2/17-20.pdf (accessed on 12 July 2024).
- Kampf, R.; Lorincová, S.; Hitka, M.; Caha, Z. The application of ABC analysis to inventories in the automatic industry utilizing the cost saving effect. NAŠE MORE: Znan. Časopis Za More I Pomor. 2016, 63, 120–125. [Google Scholar] [CrossRef]
- Zenkova, Z.; Kabanova, T. The ABC-XYZ analysis modified for data with outliers. In Proceedings of the 2018 4th International Conference on Logistics Operations Management, (GOL), Le Havre, France, 10–12 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Z.; Wu, X.; Liu, F.; Fu, Y.; Chen, K. Multicriteria ABC inventory classification using acceptability analysis. Int. Trans. Oper. Res. 2019, 26, 2494–2507. [Google Scholar] [CrossRef]
- Milkova, T. Various Methods For ABC Analysis Of Inventory in Ms Excel with Examples. J. Comput. 2019, 13, 183–196. [Google Scholar] [CrossRef]
- Abdolazimi, O.; Esfandarani, M.S.; Shishebori, D. Design of a supply chain network for determining the optimal number of items at the inventory groups based on ABC analysis: A comparison of exact and meta-heuristic methods. Neural Comput. Appl. 2021, 33, 6641–6656. [Google Scholar] [CrossRef]
- Asana, I.M.D.P.; Radhitya, M.L.; Widiartha, K.K.; Santika, P.P.; Wiguna, I.K.A.G. Inventory control using ABC and min-max analysis on retail management information system. J. Phys. Conf. Ser. IOP Publ. 2020, 1469, 012097. [Google Scholar] [CrossRef]
- Goldratt, E.M. Theory of Constraints; Croton-on-Hudson: North River, NY, USA, 1990.
- Tulasi, C.L.; Rao, A.R. Review on theory of constraints. Int. J. Adv. Eng. Technol. 2012, 3, 334–344. [Google Scholar]
- Schmidt, M.; Hartmann, W.; Nyhuis, P. Simulation based comparison of safety-stock calculation methods. CIRP Ann. 2012, 61, 403–406. [Google Scholar] [CrossRef]
- Cheng, L.; Tsou, C.S.; Yang, D.Y. Cost-service tradeoff analysis of reorder-point-lot-size inventory models. J. Manuf. Syst. 2015, 37, 217–226. [Google Scholar] [CrossRef]
- Thomopoulos, N.T. Demand Forecasting for Inventory Control; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–10. [Google Scholar]
- Radasanu, A.C. Inventory management, service level and safety stock. J. Public Adm. Financ. Law 2016, 145–153. Available online: https://www.jopafl.com/uploads/issue9/INVENTORY_MANAGEMENT_SEVICE_LEVEL_AND_SAFETY_STOCK.pdf (accessed on 12 July 2024).
- Brunaud, B.; Laínez-Aguirre, J.M.; Pinto, J.M.; Grossmann, I.E. Inventory policies and safety stock optimization for supply chain planning. AIChE J. 2019, 65, 99–112. [Google Scholar] [CrossRef]
- Paul, B.; Tondihal, S.; Das, B.B. Safety stock in inventory management and wastage analysis at construction sites. In Recent Trends in Civil Engineering: Select Proceedings of TMSF 2019; Springer: Singapore, 2021; pp. 509–517. [Google Scholar] [CrossRef]
- Gonçalves, J.N.; Carvalho, M.S.; Cortez, P. Operations research models and methods for safety stock determination: A review. Oper. Res. Perspect. 2020, 7, 100164. [Google Scholar] [CrossRef]
- Ghadimi, F.; Aouam, T.; Vanhoucke, M. Optimizing production capacity and safety stocks in general acyclic supply chains. Comput. Oper. Res. 2020, 120, 104938. [Google Scholar] [CrossRef]
- Lestari, N.F.; Handayati, Y. Analysis of Inventory Management in Order to Reduce Overstock (Case Study of TVF Footwear). Int. J. Curr. Sci. Res. Rev. 2022, 5, 3670–3680. [Google Scholar] [CrossRef]
- Tadayonrad, Y.; Ndiaye, A.B. A new key performance indicator model for demand forecasting in inventory management considering supply chain reliability and seasonality. Supply Chain Anal. 2023, 3, 100026. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).