1. Introduction
Global growth is anticipated to be 3.1 percent in 2024 and 3.2 percent in 2025, higher than the previous forecast due to resilience in the United States and other economies but still below the historical average, influenced by high central bank rates, reduced fiscal support, and low productivity growth. Inflation is expected to decrease in most regions, reaching 5.8 percent in 2024 and 4.4 percent in 2025, with a downward revision for 2025 [
1]. Despite the acute and chronic instability factors impacting the global economy, it has consistently demonstrated a growth-oriented structure under all conditions. The data indicate that the global economy has exhibited an increasing trend for several decades. Over the past ten years, there has been an approximate 65% increase in GDP despite the pandemic. According to data from the first quarter of 2013, the U.S. GDP was approximately USD 16,648.18 billion, and by the third quarter of 2023, it was calculated to be roughly USD 27,610.13 billion [
2]. This increase in economic growth is expected to continue as the population increases because a growing population means expanding human needs. Like the global economy, the world population has also seen an approximate 6% increase over the last decade. The human population, which was 316.038 million in 2013, rose to 335.979 million in 2023 [
2].
Since the earliest existence of humans, their needs have continually evolved and developed. The best explanation of human needs was introduced in 1943 through a study by Maslow, which later evolved into the well-known Hierarchy of Needs (Maslow, 1943). Maslow’s Hierarchy of Needs likens human needs to a pyramid. Upon satisfying the most fundamental layer of physiological needs and reaching satiation, people immediately desire to fulfill the needs of the next layer in the pyramid, striving to achieve satisfaction at that level. Furniture is one such need. As an essential element for sustaining life immediately after the basic need for shelter, the demand for furniture continues to increase day by day [
3].
The furniture industry has evolved from the past to the present, adapting to the times and growing by shaping itself according to human needs [
4]. The industry’s growth is due to its wide range of products. Furniture in the industry is generally categorized into various types, such as commercial furniture, bedroom furniture, dining room sets, office furniture, and kitchen furniture [
5]. Furniture diversity is present in every aspect of human life, and this variety has enabled the industry to capture a significant market share. Numerous studies have been conducted concerning the market size of the furniture.
The global furniture industry was valued at approximately USD 678.55 billion in 2022. It is expected to reach around USD 728 billion by 2028. The compound annual growth rate (CAGR) for the furniture sector is projected to be 1.19% from 2023 to 2038 [
6]. Another study indicates that the global furniture industry is expected to experience a growth rate of 3.8% by 2031 [
7]. Furthermore, a different study calculated the size of the global furniture market in 2022 at USD 630.55 billion, expected to reach approximately USD 1 trillion by 2032. The global furniture market is anticipated to grow at a CAGR of 5.3% during the period of 2023 to 2032 [
8]. These studies suggest that the furniture sector will expand in response to human needs and that demand for this sector will significantly increase in the coming years. Companies that can adapt to the changing dynamics of the furniture market are likely to gain a competitive advantage in today’s market conditions and secure long-term sustainability. Therefore, making demand forecasts for future periods based on consumer needs will be crucial to gaining competitive advantages for companies in this competitive environment.
In light of the aforementioned economic facts and industrial dynamics, the importance of demand forecasting performance is increasingly recognized. Today, the dimension of competition in all sectors has evolved from competition among firms to competition within supply chains. An effective demand forecasting process yields positive outcomes in planning and implementing all macro-, meso-, and micro-level operational activities related to the supply chain. Consequently, demand forecasting activities have become a critically important issue for all organizations involved in any supply chain.
Demand forecasting generally involves analyzing past data to make inferences about the future. The period and length of past demand data used as input in analyses are critical for accurate predictions of future demand. Empirical studies have shown that no demand forecasting method is 100% accurate [
9]. Forecasting methods are divided into qualitative and quantitative types. If past demand data are not available, qualitative forecasting methods are used. However, when sufficient historical demand data reflecting demand characteristics are available, quantitative methods are commonly employed [
10]. Many factors influence demand forecasting, including the product’s lead time, planned advertising and marketing activities, planned discounts, economic conditions, and competitor activities [
11]. Managing the collective impact of all these factors and minimizing the margin of error in demand forecasting are primary goals. Therefore, following the completion of demand forecasting analyses, it is essential to incorporate demand forecasting performance metrics into the calculations. The output from these performance metrics provides critical information on the suitability of the demand forecast and the methods used, making this phase an indispensable part of demand forecasting studies.
2. Literature Review
When conducting demand forecasting for a product, product family, or market, selecting methods used during the forecasting phase is as crucial as the output of this phase. Additionally, if the study is scientific, it should address a research question that fills a gap in the existing literature. For this reason, scientific studies conducted in previous years have been reviewed in the focus areas of demand forecasting and the wood furniture sector. This approach ensures that the research not only leverages established methodologies but also contributes to filling theoretical and practical gaps in the field.
In past academic studies, demand forecasting has been observed to be used in almost every sector, in various combinations and individually. Below, these scholarly studies are listed and summarized based on their contributions to the field.
Koehler et al. (2001) compared four models including the traditional Holt–Winters method and its underlying three different models. This comparison sought to determine which model would perform better with each parameter in place. The article contributes to the field by providing a framework for forecasting models that include trends and multiplicative seasonality and by addressing issues of model selection and prediction interval estimation [
12].
Tso and Yau (2007) conducted a comparative analysis of three forecasting models to predict electricity consumption in Hong Kong. The models used were Regression Analysis, Decision Tree, and Neural Networks, with the Root Mean Square Error (RMSE) employed to compare the models. The study found all models usable based on their RMSE values, but the Decision Tree and Neural Network models yielded better results. The article contributes to the literature by comparing three different modeling techniques (Regression Analysis, Decision Trees, and Neural Networks) for predicting electricity consumption [
13].
In other recent academic studies, demand forecasting has been widely employed across various sectors and in diverse applications. Bilişik (2011) focused on the retail industry, addressing a demand forecasting problem for revenue management. The study compared the Support Vector Machine (SVM) and Multiple Regression Analysis techniques, evaluating them through metrics such as Mean Absolute Deviation (MAD), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and the correlation coefficient. Results indicated that SVM provided superior outcomes. This research contributes to the literature by introducing a novel approach that integrates statistical learning techniques and nonlinear programming to optimize revenue in retail, enhancing the body of knowledge on dynamic pricing and revenue management [
14].
Sudheer and Suseelatha (2015) implemented a hybrid approach to predict electrical load 24 h ahead, utilizing the Haar wavelet transform as a preprocessing tool to separate the original load series into deterministic and fluctuating series. They modeled seasonal oscillations and trend factors in the deterministic component using the Triple Exponential Smoothing (TES) method. In contrast, the Weighted Nearest Neighbors (WNNs) technique handled the fluctuating component’s faster dynamics. Their methodology, demonstrated using load data from the California and Spain energy markets for 2000 and 2002, showed improved accuracy over the Holt–Winters additive seasonal model, the WNN model alone, and direct use of Haar wavelet with WNN. Their work enriches the research area by proposing a hybrid method for Short-Term Load Forecasting (STLF), integrating wavelet transformation with TES and WNN models, and offering theoretical insights into these techniques [
15].
Tratar and Strmčnik (2016) studied short- and long-term heat load forecasting within Slovenia’s largest regional heating network, employing Multiple Regression Analysis and the Holt–Winters method for comparison. The Multiple Regression Analysis was particularly effective for short-term forecasting, while the Holt–Winters method excelled in the long-term scenario. Their comparative analysis of these two methods contributes valuable insights into the field of heat load forecasting [
16].
Michinaka et al. (2016) conducted a comparative analysis using Naïve, ETS, and ARIMA methods for predicting the prices of Japanese logs. They utilized RMSE, MAE, and MAPE to compare the outcomes of these methods. The forecasting was performed over both 12-month and 6-month periods, with confidence intervals of 80% and 95%. In most cases, ARIMA yielded the best results. The article contributes insights into predicting Japanese log prices, emphasizing the importance of combining forecasting methods to improve accuracy and highlighting data stationarity’s significance in prediction-based modeling [
17].
Puah et al. (2016) modeled monthly and seasonal rainfall series and utilized the Additive Holt–Winters method at nine stations within the Langat River Basin. The performance of these models was assessed using metrics such as Mean Absolute Deviation (MAD), Mean Squared Error (MSE), Mean Absolute Percentage Error (MAPE), and the correlation coefficient. It was found that the accuracy of the seasonal rainfall models generally surpassed that of the monthly models. The article contributes to the field by employing the Additive Holt–Winters method to model rainfall series in Malaysia’s Langat River Basin and examining these rainfall models [
18].
Sugiarto et al. (2016), without specifying product and sector details in their study, comparatively used Additive and Multiplicative Holt–Winters methods for monthly sales forecasting. The performance of the models was evaluated using metrics such as Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Mean Squared Error (MSE). The error rates of both models were found to be similar, and their usability was determined. The article contributes to the field by advocating the implementation of the Holt–Winters method in ERP systems for sales forecasting, focusing on eliminating seasonal patterns and selecting appropriate error measures to enhance forecasting accuracy [
19].
Dantas et al. (2017) conducted demand forecasting in the air transport industry. Their study compared data from fourteen countries using various methods, including SARIMA, Holt–Winters, ETS and Bapped.BLD, MBB.ETS, Seasonal Naive, and Bagging Holt–Winters, with comparisons based on Symmetric Mean Absolute Percentage Error (sMAPE). The best results were obtained using the Bagging Holt–Winters hybrid method. The article provides a valuable forecasting tool for the air industry, which is easy to implement and readily parallelizable, thereby making a significant contribution to the literature [
20].
In their study, Oruç and Çelik Eroğlu (2017) forecasted 20 months of natural gas energy data in the province of Isparta. The forecasting model utilized Grey Estimation, Box–Jenkins, and Exponential Smoothing Methods, considering seasonal variations for comparative analysis. Error metrics such as RMSE, MSE, MAE-MAD, and MAPE were employed in the comparisons. The results indicated that Grey Estimation provided the best outcomes, while Box–Jenkins yielded the least accurate forecasts. The article contributes to the field by providing a natural gas demand forecast for Isparta, a province where natural gas infrastructure investments are ongoing and energy demand is increasing [
21].
Rahman and Ahmar (2017) employed ARIMA, Additive Holt–Winters, and Multiplicative Holt–Winters models to forecast total primary energy consumption in the USA. MAE, RSS, MSE, and RMS values were calculated to compare these models. A comparative analysis was conducted. The R software was used for model analysis. The study found that the Additive Holt–Winters model provided the best results. The article contributes to the field by offering insights into the suitability of ARIMA and Holt–Winters models for predicting primary energy consumption data in the USA based on the analysis of different criteria and comparisons with previous studies [
22].
Demir et al. (2018) focused on forecasting the monthly gold reserves of the Central Bank of the Republic of Türkiye using Artificial Neural Networks (ANNs) and Holt–Winters methods. The results were compared using R2, RMSE, and MAPE values, showing that the ANN model performed the best. The study contributes to the field of financial forecasting by demonstrating the superiority of ANNs in modeling nonlinear data, particularly in the context of gold reserves, over classical statistical methods [
23].
In their study, Tüzmen and Yıldız (2018) conducted a comparative analysis of Türkiye’s unemployment rates using Additive and Multiplicative Holt–Winters methods. The objective was to identify the most accurate forecasting model using error metrics, and the Additive-Seasonal Holt–Winters method yielded the best results. The study predicts that unemployment rates in Türkiye will continue to rise. The article contributes to the research field by providing a comparative analysis of Holt–Winters forecasting methods for predicting unemployment rates in Türkiye [
24].
Taşdemir and Hızıroğlu (2019) investigated the financial performance of a small- to medium-sized enterprise (SME) producer of wooden products. The forecasting models used were Winters’ Multiplicative Model and Multiple Regression Analysis. The performance of these forecasting methods was evaluated using the Mean Absolute Percentage Error (MAPE), with Multiple Regression Analysis showing the best performance with a score of 7.61. The article aims to explore the impact of increasing inventory vulnerability on the financial performance of a value-added wooden products manufacturer, contributing to the intersection of three research streams: Lean Inventory Management, Supply Lot Sizing, and Demand Forecasting [
25].
Ventura et al. (2019) utilized Holt–Winters and Artificial Neural Network (ANN) methods to forecast pollution levels of particulate matter PM2.5 across three different areas (rural, industrial, and urban). The models were compared using the Root Mean Squared Error (RMSE) as an error metric. The best forecasting results for the industrial area were obtained with the Holt–Winters method, while the ANN model provided the best predictions for urban and rural areas. The study contributes to the research area by comparing two air quality forecasting models, Holt–Winters and ANN, for predicting PM2.5 concentrations in different settings, including rural, industrial, and urban areas [
26].
Phumchusri and Ungtrakul (2020) studied daily demand forecasting using data from a hotel in Thailand. They compared various forecasting methods, including Holt–Winters, Box–Jenkins, Box–Cox, ARMA, a trend and multi-seasonal model (BATS), trigonometric BATS, Artificial Neural Networks (ANNs), and Support Vector Machines (SVMs). The results showed that the ANN model provided the best predictions with a Mean Absolute Percentage Error (MAPE) of 8.96%. The article contributes to the literature by addressing the challenges of accurate daily demand forecasting in hotel revenue management, emphasizing its critical importance [
27].
Karakurt et al. (2020) focused on the problem of coal consumption forecasting in BRICS-T countries using Regression Analysis. The developed models were tested for statistical accuracy and forecasting performance using various statistical approaches. The results indicate that the models have strong applicability potential. The article enriches the existing knowledge on energy consumption forecasting by providing statistical models that estimate coal consumption in BRICS-T countries using regression analysis, thereby making a significant contribution to the literature [
28].
Tabar et al. (2021) investigated demand forecasting for residential property prices in the Karşıyaka neighborhood of Central Tokat using ANN and Multiple Regression Analysis. The results indicated better outcomes with ANN; however, Multiple Regression Analysis was chosen for its greater ease of intervention in the model. The article contributes to the current literature by discussing the accuracy and performance of ANN, even with small sample sizes, and its preference among many researchers, thus enhancing the existing body of knowledge [
29].
Saadat et al. (2021) aimed to analyze and forecast the production of major minerals. For this purpose, they employed parametric models, including the Box–Jenkins (BJ) Methodology, an Auto-Regressive Errors Regression Model (ARAR), and the Holt–Winters (HW) method. In non-parametric models, they used Univariate Singular Spectrum Analysis (SSA) and Multivariate SSA (MSSA) modeling approaches. The data were divided into training and testing sets to determine the most suitable model for forecasting. Accuracy measures such as Root Mean Squared Error (RMSE), Mean Absolute Percentage Error, and Theil’s U statistic were utilized. For gas and coal, the HW model was deemed suitable for forecasting. The Automatic Regression Integrated Moving Average (Box–Jenkins ARIMA) and MSSA provided more accurate forecasts for gypsum and oil. The article contributes to the research field by analyzing and forecasting the production of key minerals in Pakistan, particularly gas, oil, gypsum, and coal [
30].
Pliszczuk et al. (2021) conducted a demand forecasting study using past sales data of a company in the furniture sector based on a Long Short-Term Memory (LSTM) network in machine learning. The performance of the forecast was measured using the Mean Squared Error (MSE) with a value of 3197.75. The article contributes to the research area by developing an algorithm based on the LSTM network using past sales data of a furniture sector company to predict sales in the supply chain [
31].
Gorna et al. (2022) utilized ARIMA and SARIMA models to evaluate predictions of prices for various wood types (M2 ZE, M2, S2AP, and S4). The forecasting models employed quarterly data from 2018 to 2022 to predict the upcoming three quarters (2022 Q3, 2022 Q4, and 2023 Q1). The article contributed to the literature by applying time series methods such as ARIMA and SARIMA for the prediction of wood prices, which is crucial for the optimization of forest management [
32].
Mohammed et al. (2022) developed a new forecasting method for short-term demand prediction. This new model combines a simple moving average with Gregory–Newton interpolation curve fitting. The proposed method separately addressed datasets containing trends and seasonality. The article contributes to the field by providing a detailed methodology for integrating the moving average with the Gregory–Newton method for short-term demand forecasting, especially for data containing trends and seasonality [
33].
Arslan and Ertuğrul (2022) conducted a demand forecasting study for electricity market price prediction using the R statistical package with Multiple Regression and ANN models and the ARIMA method with the Ewrews package. The study ranked the ANN, Multiple Regression Analysis, and ARIMA models, respectively. The article contributes to the research field by analyzing market settlement prices in the Türkiye Electricity Market and comparing the performance of commonly used statistical forecasting methods in the literature [
34].
Deniz and Topal (2022) evaluated the durability of thirteen different tuff samples from nine quarries in Cappadocia using Factor Analysis, Multiple Regression Analysis, and Analytical Hierarchy Process (AHP) methods. The results indicated that the performance of the AHP and Multiple Regression Analysis methods provided better outcomes than Factor Analysis. This study contributes to the existing knowledge of the physical and mechanical properties of tuffs, thereby aiding the overall characterization of rocks and durability assessments [
35].
Kozuch et al. (2023) compared RBF and MLP artificial neural networks (ANNs) with the Prophet procedure and traditional models (i.e., ARIMA, ETS, BATS, and TBATS) for predicting timber prices in Poland. Using quarterly time series data of net nominal prices for roundwood (W0) from 2005 to 2021, MLP networks demonstrated superior performance in predicting price changes and levels, fitting minimum and maximum values more accurately than traditional models. While the ETS model provided the best predictions for red alder, BATS and TBATS models excelled for birch timber prices. Among popular roundwood types in Poland, ANNs, particularly MLP models, yielded the best predictions for Scots pine, Norway spruce, and oak. The article highlights the advantages of employing ANN methodology in primary timber markets, offering practical, low-labor solutions for market participants and emphasizing the superiority of MLP networks by comparing various predictive models [
36].
Dong et al. (2023) conducted a demand forecasting study for the tourism sector. The proposed model for this forecasting comprises three parts: the first part develops the demand time series, the second part enhances feature recognition in neural networks through a directed attention mechanism, and the third part generates the tourism demand forecast results. The model aids in identifying the seasonality and non-linearity characteristics in tourism demand data. The study contributes to the literature by addressing the non-stationary nature of tourism demand and the spatiotemporal relationships of the data [
37].
Phumchusri and Suwatanapongched (2023) worked on forecasting the daily room demand of a hotel in Thailand. The forecasting employed methods such as the same day of the previous year, Holt–Winters, Seasonal Autoregressive Integrated Moving Average (SARIMA), and Box–Jenkins Box–Cox transformation with trigonometric ARMA models. The accuracy was evaluated using Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Median Absolute Percentage Error (MdAPE). The evaluation showed that SARIMA provided the best results. The article contributes to the research field by demonstrating the benefits of data transformation and smoothing techniques in enhancing the accuracy of hotel room demand forecasting models [
38].
Cui et al. (2023) focused on electricity demand forecasting. Due to anomalies in the data related to the COVID-19 period, a variable associated with COVID-19 was initially designed and included in the Multiple Regression model. After mitigating the impact of COVID-19, an efficient deep learning algorithm, free from seasonal influences, was developed. The article contributes to the research field by proposing a framework that explains the impact of COVID-19 on electricity demand and produces accurate demand forecasts [
39].
Kim (2023) aimed to develop a machine learning-supported hybrid input model for automobile demand forecasting. To achieve the research objective, the study analyzed the forecasting performance of a machine learning algorithm based on hybrid micro/firm-level (internal) and macro-level (external) factors. The work contributes to the field by exploring the synergistic interaction between business processes and new analytical techniques, particularly in the context of demand forecasting in the automobile industry [
40].
Viverit et al. (2023) studied daily hotel demand forecasting. Despite challenges posed by the COVID-19 period, they developed a robust forecasting model. The model clusters historical reservation curves using a machine learning algorithm that employs an autoregressive method, generating daily occupancy forecasts up to eight weeks in advance. This model was tested with data from three different hotels. The article contributes to the research area by presenting a new approach to hotel demand forecasting, utilizing machine learning and cluster analysis techniques, and providing insights to enhance forecast accuracy and interpretability [
41].
Swaminathan and Venkitasubramoney (2023) conducted a comprehensive review of demand forecasting studies within the fashion industry, recognizing it as a complex problem that has been addressed using various forecasting methodologies. The study categorizes and examines these methods within the article, offering an extensive review of forecasting techniques in the fashion industry. It highlights advancements in artificial intelligence and machine learning and suggests future directions for research, significantly contributing to the field [
42].
İfraz et al. (2023) focused on forecasting spare part demand for bus fleets. The study employed regression-based methods, rule-based methods, tree-based methods, and Artificial Neural Networks (ANNs). Eight years of data were used for the analysis. Among the tested methods, Support Vector Regression (regression-based), Decision Table (rule-based), and MP5 (tree-based) provided the best results. However, when compared across all methods, ANN yielded the best performance. The article contributes to the field of maintenance and repair within the context of bus fleets, particularly in spare part demand forecasting [
43].
Şahin et al. (2023) used Multiple Linear Regression (MLR) and ANN models to study the surface parameters and environmental factors affecting the energy production of a photovoltaic (PV) solar energy plant in Iğdır. In comparing the models, Mean Squared Error (MSE) was examined, with results indicating that ANNs outperformed MLR in capturing the complex models of solar plant efficiency. The article contributes to the field by researching the surface parameters and environmental factors impacting a PV solar plant’s energy production and providing a novel contribution to predicting plant efficiency, which had not been explored in previous studies [
44].
Özbayrak et al. (2023) tackled the challenging problem of predicting the buckling load in transversely reinforced cantilever beams in structural engineering using Multiple Linear Regression Analysis and Multi-Expression Genetic Programming prediction models with the aid of the ANSYS software package. Eight models were created to solve the problem, and they were compared using metrics such as MAE, MSE, RMSE, R2, NSE, W1, and PI values. Model 1 exhibited the best performance. The article addresses the difficulty of predicting the buckling load in transversely reinforced cantilever beams, a significant issue in structural engineering, thus making a valuable contribution to the field [
45].
González Grandón et al. (2024) presented a hybrid approach that combines classical statistics and machine learning algorithms to forecast electricity demand in Ukraine on an hourly, daily, and annual basis. Metrics such as RMSE, MAPE, MAE, and MASE were used to compare the forecast results. The best-performing model was developed by integrating Multiple Regression models with a residual forecasting LSTM hybrid model. The article contributes to the field by analyzing the fundamental structure of the time series of electricity consumption in Ukraine across different time scales, enhancing the understanding of its demand patterns [
46].
The review of studies in the literature reveals that demand forecasting methods are employed across various industries, including energy, retail, air transportation, banking, tourism, automotive, and fashion. Specific topics covered in these studies range from forecasting energy consumption and production, sales data, precipitation data, unemployment rates, and pollution levels to automotive demand. The review shows that quantitative methods are more commonly used in these studies. These quantitative methods appear in the literature as standalone approaches, integrated with one or more other methods, or compared against other methods in the same study. In evaluating the performance of these demand forecasting methods, error metrics such as Mean Absolute Deviation (MAD), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and Median Absolute Percentage Error (MdAPE) are utilized. This broad application of forecasting techniques highlights the importance of developing accurate and reliable forecasting models to support decision-making processes in diverse sectors.
Despite the substantial growth and economic importance of the U.S. furniture industry, existing literature predominantly focuses on general market trends, consumer behavior, and production efficiencies, with limited attention given to the integration and comparative analysis of advanced forecasting models. Literature review results of this study reveal a notable gap: no existing studies have concurrently applied and compared the effectiveness of Multiple Linear Regression (MLR) and Holt–Winters forecasting methods specifically within the U.S. furniture market. This oversight is significant given the dynamic nature of the furniture industry, which is influenced by economic cycles, changing consumer preferences, and external disruptions such as the recent global pandemic. Effective forecasting models are crucial for manufacturers and retailers in this sector to anticipate market demands accurately and align their strategies accordingly. Thus, our study addressed this critical gap by implementing these two robust forecasting methods and evaluating their predictive accuracy and practical applicability to the U.S. furniture industry. In this way, we aimed to provide a foundational framework supporting top management’s strategic decision making and enhancing operational efficiencies in response to market demands. Therefore, this study focused on a demand forecasting analysis for the next 36 months based on retail sales data from 2019 to 2023 and data collected on nine factors potentially influencing the demand for the product range in question in the U.S. Furniture Industry. Therefore, the study’s objective was to determine the future demand trajectory in the U.S. furniture industry using historical retail sales data and quantitative forecasting methods and document the expected changes in the furniture sector market size and demand dynamics. The study aimed to make novel contributions to the target research streams by achieving the abovementioned objective. The expected contributions of the study can be itemized as follows:
The study introduced a detailed forecasting approach for retail furniture sales in the U.S. market, employing both Multiple Linear Regression (MLR) and Holt–Winters methods and comparing their efficacy using the Mean Absolute Percentage Error (MAPE) metric. This offered a robust analysis of predictive performance in a growing market sector.
The study integrated broad economic indicators and industry-specific drivers to enhance the accuracy of the sale forecasts by identifying and utilizing a range of factors, including furniture imports, consumer sentiment, housing starts, etc.
The research acknowledged and quantified the impact of significant external events such as the COVID-19 pandemic, providing insights into how such factors can affect industry dynamics, which is crucial for strategic planning and response strategies in retail sectors.
By employing sophisticated statistical techniques and software for model optimization and validation, the study contributed to the methodological rigor of the demand forecasting literature and offered a template for future research in similar sectors.
To logically report the motivations behind the study, state-of-the-art, systematic methodology employed, findings, and conclusive remarks, the manuscript begins with
Section 1, “Introduction”, which sets the stage for the study by outlining the research objectives and the significance of forecasting in the furniture retail sector. It also highlights the unique contributions of this work to the existing literature.
Section 2, “Materials and Methods”, details the methodologies employed, including Multiple Linear Regression (MLR) and Holt–Winters forecasting models, and explains the data collection and model validation processes.
Section 3, “Results”, presents a comparative analysis of the forecasting methods used, evaluating their effectiveness through the Mean Absolute Percentage Error (MAPE) and other metrics.
Section 4, “Discussion”, interprets the results, discussing their implications for strategic decision-making and addressing external factors that impact model performance. Finally,
Section 5, “Conclusions”, synthesizes the findings, confirms the achievement of the study’s objectives, and underscores the contribution of this work to forecasting practices in the furniture industry while suggesting avenues for future research.
3. Materials and Methods
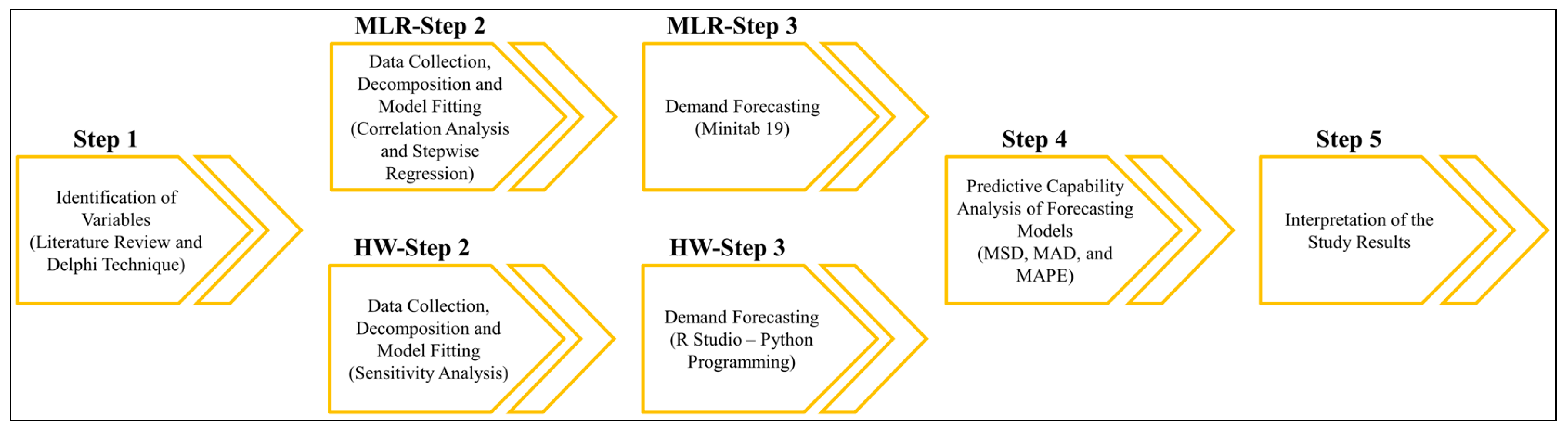
Figure 1 illustrates the phased systematic approach used in the study, highlighting the steps for both Multiple Linear Regression (MLR) and Holt–Winters (HW) forecasting models. In Step 1, relevant independent variables are determined through a literature review and the Delphi technique. Step 2 involves correlation analysis and stepwise regression to identify significant variables for MLR and sensitivity analysis to identify the optimum smoothing constant for the HW model. As the last activity of Step 2, MLR and HW models are constructed using Minitab 19 software and R-Studio Version 2023.06.1+524 (Python programming), respectively. In the following step, predictive capability analysis of forecasting models is run using forecasting error metrics such as MSD, MAD, and MAPE. In the last step of the study, the study results are interpreted to synthesize insights and conclusions from the forecasting models.
Demand forecasting is one of businesses’ most significant tools to guide their future planning. Errors in demand forecasting can adversely affect a business’s operational performance, making it crucial to minimize errors in the forecasting process. Within this study, retail sales of furniture and home furnishings stores in the U.S. for the months of the last 30 years are obtained from the latest releases of the U.S. Census Bureau, and the data for the previous 60 months are used as the dependent variable in forecasting models [
47]. The independent variable is denoted by “Retail Furniture Sales” in the following study sections. Two forecasting models based on Multiple Linear Regression analysis and Holt–Winters methodologies are developed to forecast the demand for the next 36 months. The forecasting horizon is limited to 36 months to avoid the risk of extrapolation lacking explanatory power by predicting far too much into the future. The time-phased distribution of the data is illustrated in the run chart given in
Figure 2.
Generally, a long enough period to capture the entire business cycle is recommended to account for seasonal variations and economic fluctuations. This typically involves 5–10 years of historical data for many industries. This length allows for the inclusion of various economic conditions, such as growth phases and recessions, providing a robust dataset for predictive modeling [
48]. In this study, extending the data period further back could compromise the applicability of the findings to current market dynamics, particularly in light of the significant social, industrial, and economic changes that have occurred in recent years. These include advancements in e-commerce and changes in consumer behavior due to technological developments, socio-economic shifts, and the COVID-19 pandemic. Furthermore, shorter periods might be more appropriate in sectors experiencing rapid technological change or evolving consumer behaviors, such as the furniture retail industry influenced by e-commerce and sustainability trends. This approach ensures that the models reflect recent market dynamics and consumer preferences, which could differ from those more than a decade ago [
49]. For the furniture industry, considering a 5-year period may strike a balance between capturing relevant economic trends and reflecting the current dynamics of the industry, such as the impact of the COVID-19 pandemic on consumer purchasing behaviors and supply chain disruptions [
50].
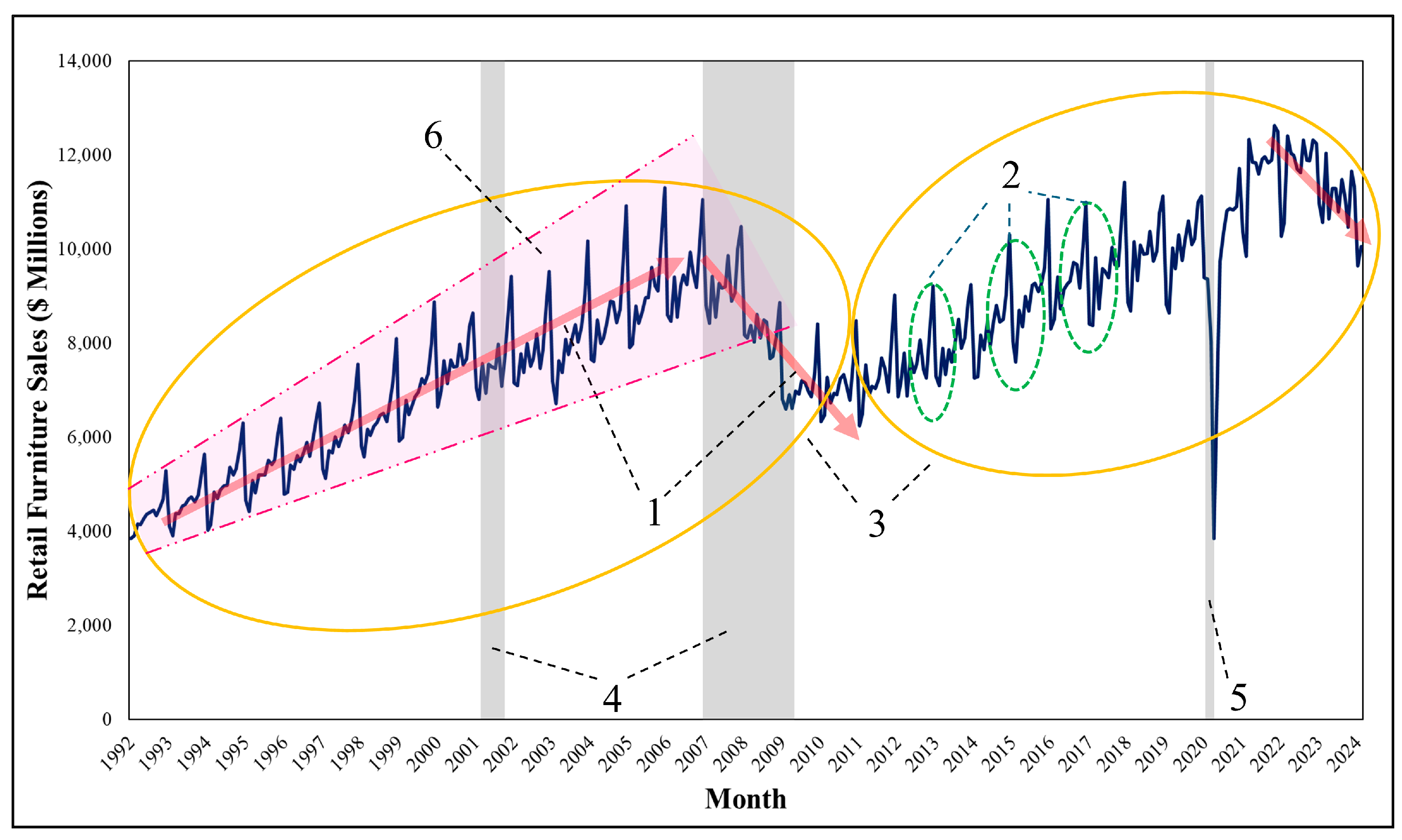
Close examination of the data for the independent variable revealed some significant characteristics of the retail sales data, involving specific trends, cyclicality, seasonality, and a COVID-19 pandemic-driven sudden dipping reaction followed by a fast recovery period. Understanding the underlying patterns in sales data through such a diagnostic procedure aids in selecting the most appropriate forecasting techniques, therefore improving the accuracy and reliability of demand forecasting, which is crucial for decision makers in the furniture industry to better prepare for future demands and market dynamics.
As observed in the graph shown in
Figure 2, marked as Area 1, retail furniture sales exhibit periodic increasing and decreasing trends. The combination of these two trend components creates a relatively premature sign of cyclicality occurring over the first 17 years and the last 15 years of the data span, as shown in yellow circles and marked as 3. The end of the first cycle coincides with a two-year decreasing trend primarily caused by the U.S. recession period from 2008 to 2010. Additionally, the region marked as 2 demonstrates an unmistakable pattern of seasonality across the months of the year in retail furniture sales. Further observing the time-phased data distribution, one could also interpret that the second cycle is closing to an end. Next, the grey areas marked with number 4 in
Figure 2 indicate the other major economic recessions experienced in the United States. The impact of the first of these economic recessions started to be felt across industries in February 2001. The other one influenced the U.S. economy from December 2007 to June 2009. During this period, the U.S. faced a significant increase in unemployment. This economic crisis in the U.S. spread to other developed economies worldwide, especially the EU countries, through strong financial linkages [
51]. The grey area marked with number 5 in
Figure 2 represents the COVID-19 pandemic, which started in China and affected the entire world. Moreover, to incorporate the external factors regarding the current status of the economy and politics in the study, five economic variables were included in the dependent variables set used to construct a Multiple Linear Regression model. Finally, the area marked with number 6 in
Figure 2 shows that the Furniture Retail Sales data depict pronounced seasonality that expands as the upward trend continues. In accordance with Hyndman and Athanasopoulos (2018), this study opted for a multiplicative decomposition method as the demand data exhibited seasonality that scales with the magnitude of the sales figures. This pattern is commonly observed in the retail sector, where peak periods like holidays lead to sales volumes that are not merely additive but scale multiplicatively with the trends in consumer spending [
48].
Within the scope of forecasting, particularly when utilizing advanced machine learning models, the phenomenon known as “hallucination” can occur. This term refers to the model’s tendency to generate predictions that are not grounded in the actual data patterns but are instead artifacts of overfitting to noise or rare events in the training dataset [
52,
53]. Essentially, when a model encounters rare or highly specific information that it has not been adequately trained on, it may produce highly improbable or unrealistic forecasts.
For instance, in the domain of retail sales forecasting, if the model encounters an atypical spike or drop in sales data that was influenced by an isolated event (e.g., a one-time promotional campaign or an unprecedented external shock like a pandemic), it might “hallucinate” this event’s recurrence in its future predictions. This can lead to distorted forecast outputs, making it crucial to implement robust validation and anomaly detection mechanisms to mitigate such risks [
54].
In this study, the risk of hallucination was minimized by ensuring that the training dataset was comprehensive and representative of typical market conditions. Additionally, a variety of relevant variables and thorough cross-validation were used to ensure that the models’ predictions remained realistic and actionable. Multiple Regression Analysis and the Holt–Winters method were selected to forecast retail sales values in the U.S. furniture sector. Initially, with the assistance of three academics and three industry experts, independent variables were determined for the Multiple Regression Analysis. Specifically, we conducted three rounds of Delphi surveys involving six experts from both academia and industry. The criteria for expert selection were based on their extensive experience in market analysis and forecasting methods. A consensus was achieved when an over 75% agreement was reached on the relevance of the selected variables. Within the scope of the study, the dependent variable identified for regression analysis was Furniture Retail Sales [
47]. The nine independent variables were Furniture Imports, Consumer Price Index, Consumer Sentiment Index, Housing Starts, Credit Card Interest Rates, Population, Producer Price Index, Disposable Income, and Pandemic Effect. Multiplicative Decomposition was applied to data sets that were not seasonally adjusted to calculate the seasonality index, and all datasets were seasonally adjusted before being fed into the forecasting models.
Stepwise regression was employed to determine which independent variables should be retained in the Multiple Regression Analysis. Minitab 19 was utilized during this process. The alpha coefficient set for use in stepwise regression was 0.25. The most significant model resulting from this process included the Furniture Imports [
47], Consumer Sentiment Index [
2], Housing Starts [
2], U.S. Population [
2], Producer Price Index [
2], and Pandemic Effect variables. These variables are listed in
Table 1. The correlation matrix formed by these determined variables is provided below in
Table 2.
In Multiple Regression Analysis, the correlation between independent variables indicates the presence of multicollinearity. Multicollinearity occurs when two or more independent variables are highly correlated. This correlation can cause several problems, such as increased variance of the coefficient estimates, reduced precision, difficulties in interpretation, and inflated standard errors. Therefore, each independent variable’s Variance Inflation Factor (VIF) was calculated using a stepwise regression procedure with an inclusion/exclusion alpha level of 0.25 to diagnose and address multicollinearity. The resulting VIF values were checked.
3.1. Multiple Regression Analysis
For a focused study aiming to forecast Monthly Retail Sales for Furniture and Home Furnishing Stores, a Multiple Regression model was developed using a stepwise regression procedure with an inclusion/exclusion alpha level of 0.25. This approach effectively managed the complexity introduced by the nine independent variables under consideration and selected the most significant predictors among a broader set of variables.
Initially, a research question of
“Could on-hand independent variables be used to forecast furniture demand?” was defined to accurately target sales figure prediction, followed by robust data collection and cleaning to ensure data integrity [
55,
56]. Exploratory Data Analysis (EDA) was performed to understand the relationships and distribution among the variables, ensuring the detection and handling of any outliers [
57]. The stepwise regression method was particularly beneficial in this context. It allowed for systematically selecting and eliminating variables based on their statistical significance, minimizing issues like multicollinearity and enhancing the model’s interpretability [
58].
Model specification was carefully crafted considering the dynamics of the furniture sector. After specifying the model, it was estimated using sophisticated statistical software, followed by comprehensive diagnostics to check for any assumption violations, such as homoscedasticity and normality of residuals [
59,
60]. Model validation was carried out using cross-validation techniques to confirm the accuracy and generalizability of the forecast model. The results were then meticulously interpreted, following established reporting standards [
61], and sensitivity analyses were conducted to ascertain the stability of the findings under different scenarios [
62] and only the output of the best-performing model was presented in the findings section of the study. This structured approach ensured that the regression model was robust and provided actionable insights into predicting monthly sales for retail furniture sales effectively. Model specification was carefully constructed considering the interdependencies among the nine independent variables. Following the specification, the model was estimated using Minitab 19 software, and rigorous diagnostic tests were applied to check for violations of regression assumptions, such as homoscedasticity, normality, and independence of errors [
59,
60]. The validity of the regression model was further verified through validation techniques, and the interpretation of the results was aligned with established reporting guidelines [
61]. The mathematical formulation of the Multiple Regression Model is shown in Equation (1).
where
Y represents the dependent variable, which in this context is the future demand for retail furniture sales.
β0 is the intercept of the model.
βj are the coefficients for each independent variable
x1,
x2,…,
xn, representing factors influencing furniture demand, such as Consumer Price Index, Housing Starts, etc.
denotes the error term, accounting for the variation in furniture demand not explained by the model.
3.2. Multiplicative Decomposition Technique
Employing the multiplicative decomposition technique provides a robust method for analyzing and decomposing time series data, especially when seasonal variations are pronounced. The methodology for applying this technique in an academic article can be outlined as follows: (1) data preparation [
48], (2) decomposition process [
63], (3) component estimation [
64], (4) model assessment [
65], and (5) output reporting. During the second phase of the technique, a multiplicative decomposition procedure was followed since it is a more common occurrence in real-life scenarios than the data components having an additive nature. The decomposition procedure aided in determining components of the time series data set associated with trend, cyclical, seasonal, and random variations. The mathematical model for the multiplicative decomposition model is given in Equation (2). In the third phase of the study, the prediction data sets for each independent variable were calculated, which was consequently used to forecast the future data points for the dependent variable.
where,
Xt,
Tt,
Ct,
St, and
Et represent, respectively, the observed value, trend, cyclical, seasonal, and random movement components of the time series at period
t.
3.3. Holt–Winters Method
The Holt–Winters methodology is an exponential smoothing approach that enables direct analysis of the seasonal influence in the data. The method’s formulation comprises three distinct equations, namely the trend, level, and seasonal equations, with seasonal equations presenting a differentiation factor. The seasonal equation can be either additive or multiplicative. In the context of planned analysis, it is recommended to employ the Multiplicative Seasonal technique when the seasonal impact in the data manifests a consistent rise or fall with the trend and the Additive Seasonal technique when the seasonal influence displays an irregular trend of increase or decrease.
Multiplicative Seasonal Holt–Winters Method
The subsequent formulas were utilized to apply the Multiplicative Seasonal Holt–Winters methodology.
The third equation, the forecast equation, comprises level, trend, and seasonality. The fourth, fifth, and sixth equations calculate these components. The Holt–Winters forecasting model was constructed and run in R-studio using Python programming. Pandas, Statsmodels, and Numpy Python libraries were used to build statistical models and run numerical computations.
Parameter optimization for the Holt–Winters method was conducted using the
statsmodels library in Python. The optimization process involved minimizing the Mean Absolute Percentage Error (MAPE) through iterative adjustments of the smoothing parameters (alpha, beta, gamma) using optimization algorithms such as Broyden–Fletcher–Goldfarb–Shanno (BFGS) or Limited-memory Broyden–Fletcher–Goldfarb–Shanno with Box constraints (L-BFGS-B). Initial parameter values for level, trend, and seasonality were estimated heuristically by the library and refined through the optimization process until convergence, which was determined by the stabilization of the loss function (MAPE). To validate the optimized parameters, we employed in-sample evaluation metrics, including Mean Absolute Percentage Error (MAPE), Root Mean Squared Error (RMSE), and R-squared, ensuring the parameters provided the best fit for the historical data. The complete Python code and the detailed pseudocode for the optimization and forecasting procedures were provided in
Appendix A to facilitate replication and transparency.
After forecasting the future demand for the upcoming 36 months using Multiple Regression Analysis and the Holt–Winters method, it is imperative to assess the predictive capability of the models and choose the best-performing forecasting technique. This decision was made by scrutinizing the MAPE value emanating from the forecast error measures.
3.4. Measuring Forecasting Error and Assessing the Forecasting Performance of the Models
Every demand forecast has a random component. A suitable forecasting method should capture the systematic component of demand, not the random one. The random component manifests itself as forecast errors, which can contain valuable information. If the observed errors remain within the bounds of past forecast errors, companies can continue using their already-in-use forecasting methods. However, finding errors that significantly exceed past forecasts may indicate that the current forecasting method is no longer suitable or that there has been a fundamental change in demand characteristics. Furthermore, if a company’s forecasts consistently overestimate or underestimate demand, this could be another signal that the forecasting method needs to be revised. These insights highlight the importance of continuously monitoring forecast performance and being ready to adjust forecasting methods as required. This proactive approach ensures that the forecasting process remains robust and aligned with the actual demand patterns, supporting more effective and strategic decision making within the company.
As previously defined, the forecast error for period
t is given by
et and is calculated as shown in Equation (7),
Here, Dt represents the actual observed value at time t, and Ft represents the forecasted value at time t. This equation essentially measures the discrepancy between what was observed and predicted by the forecasting model.
Several standard error metrics are used to analyze demand forecasting performance by measuring forecast errors. In this study, the Mean Squared Deviation (MSD), Mean Absolute Deviation (MAD), and Mean Absolute Percentage Error (MAPE) are utilized as error metrics, and they are calculated as shown in Equations (8), (9), and (10), respectively.
4. Results
Demand forecasting analysis for the Furniture Retail Sales for the next 36 months was conducted using historical retail sales data from 2019 to 2023. Multiple Regression Analysis and Holt–Winters methods were employed to predict future monthly demand for 2024, 2025, and 2026.
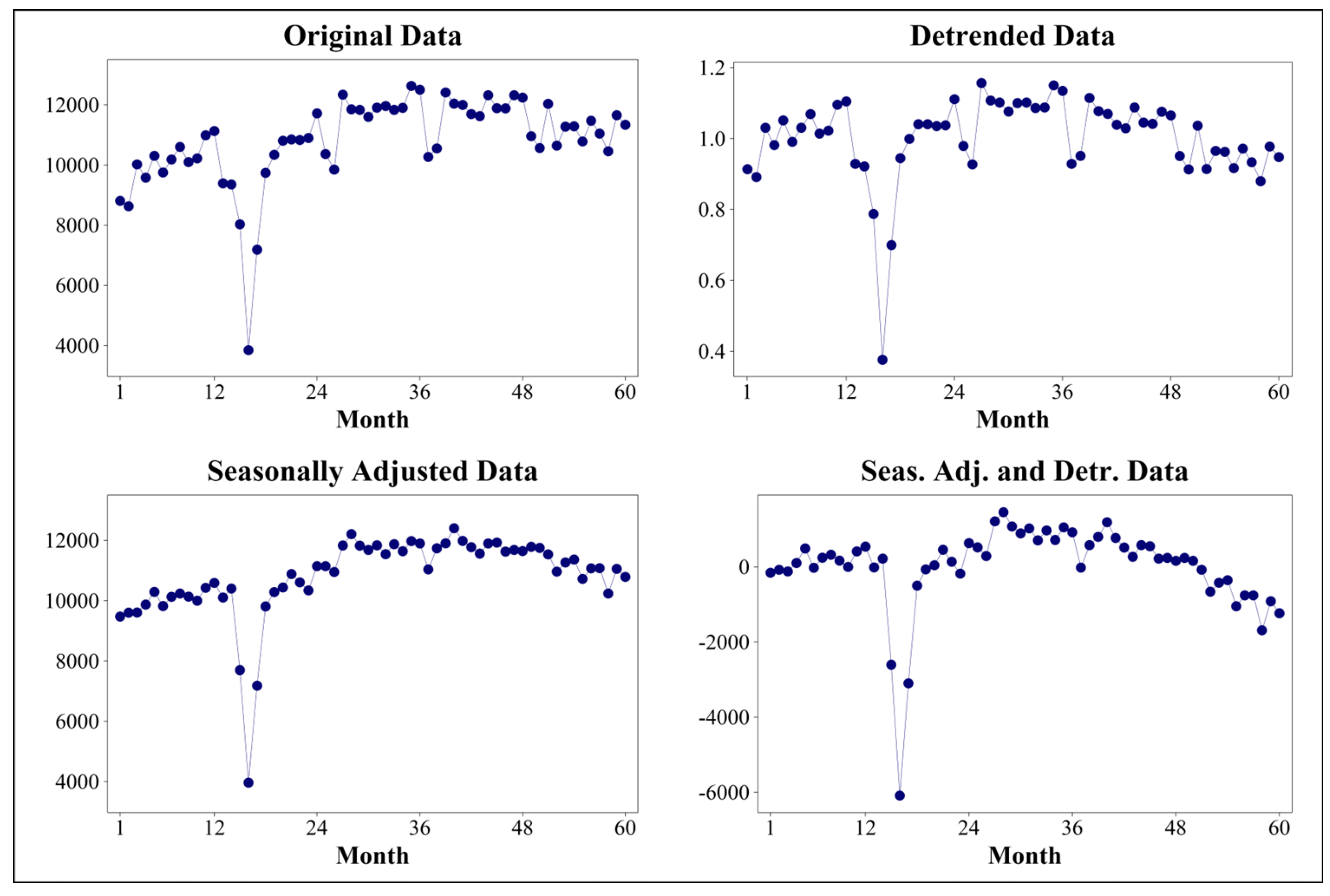
Seasonal indexes for the months of the year were obtained by applying a multiplicative decomposition procedure to the Retail Furniture Sales data, effectively capturing the trend and seasonal components. The seasonally adjusted data and seasonal factors are presented in
Figure 3 and
Table 3, respectively. This approach ensured that variations due to seasonal fluctuations were accounted for, allowing for a more accurate representation of the data’s underlying trend and cyclical components.
When the outcomes of the component analysis illustrated in
Figure 4 were evaluated, original data showed a noticeable dip around months 14 to 18, which aligns with the COVID-19 pandemic period, followed by a rapid recovery. Seasonal peaks and troughs could also be observed. The detrended data showed the sales data after removing the overall trend component. Here, the seasonal effects became more apparent. The data still exhibited significant variations during the pandemic, and regular seasonal peaks and troughs were visible. Removal of the seasonal component left the overall trend and irregular components. The data showed a steady upward trend with an apparent dip during the pandemic, followed by a strong recovery. Seasonally adjusted and detrended data presented the residuals, representing the data after removing the trend and seasonal components. This reveals the irregular component (random fluctuations), highlighting anomalies such as the significant negative deviation during the pandemic period (months 14 to 18).
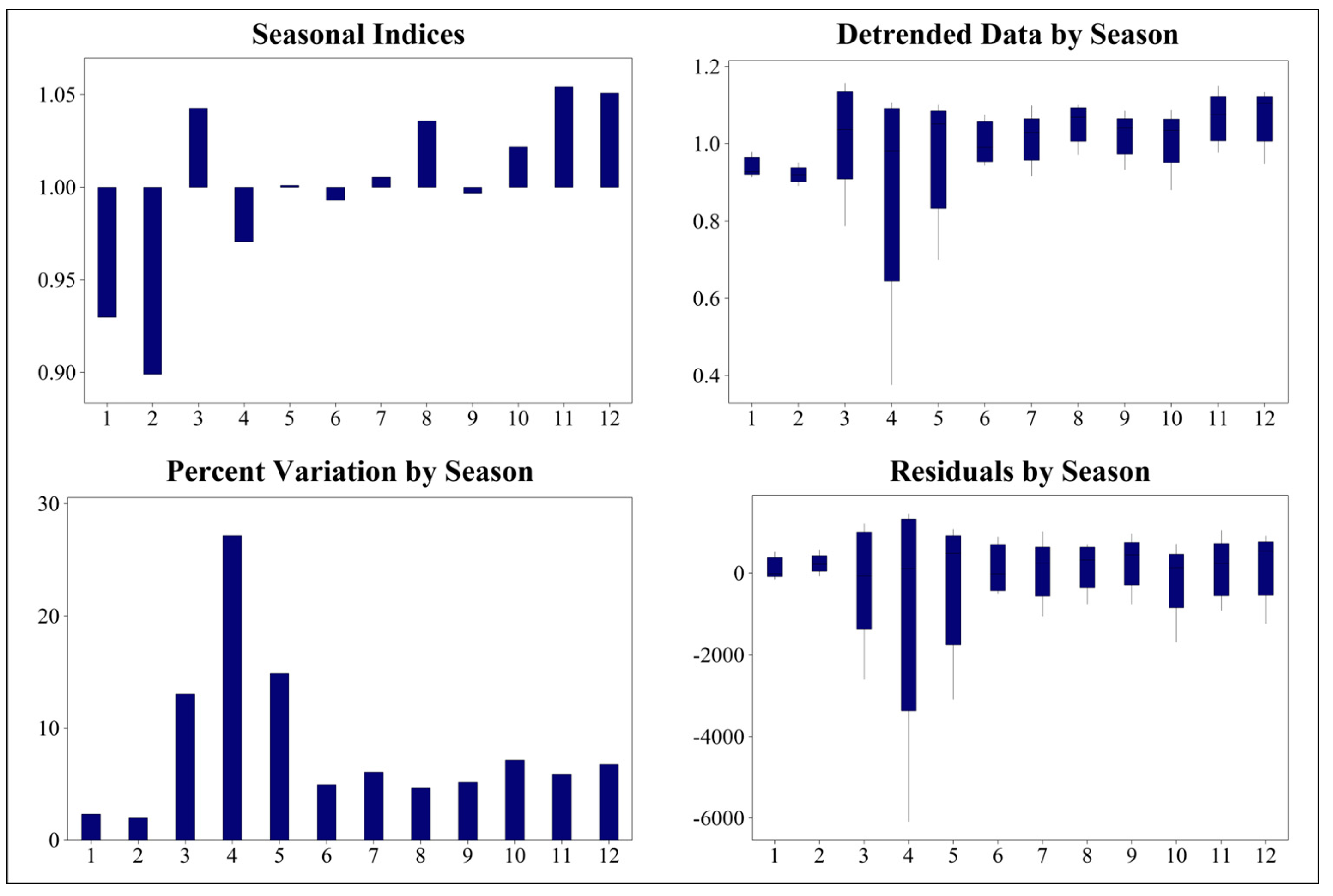
A detailed seasonality analysis, as shown in
Figure 5, was also carried out as part of the decomposition step; the top left graph of the figure shows the seasonal indices for each month. The indices represent the ratio of monthly sales to overall average sales. The indices for March (1.043), November (1.054), and December (1.051) are above one, indicating higher-than-average sales during these months, whereas January (0.930), February (0.899) and April (0.971) had indices below one, indicating lower-than-average sales during these months. The top right graph displays each month’s detrended data (after removing the trend component), highlighting seasonal patterns. March showed significant positive deviations, while April and May exhibited the most considerable negative deviations, with April being the most affected. Most months showed consistent patterns in detrended data except for outliers during the COVID-19 pandemic period. The bottom left bar chart of
Figure 5 depicts the percentage variation for each month compared to the overall annual average. March exhibited the highest variation (~32%), indicating it was the most volatile month. Moreover, November and December also showed significant variations (around 10–15%). February and August had the least variations, indicating stable sales. Furthermore, the bottom right graph presented residuals after removing trend and seasonal components. As one would expect, given the above explanations, March showed a substantial positive residual, while April and May had significant negative residuals. Residuals were generally consistent except for notable outliers during the pandemic period.
The constructed stepwise regression model consisted of two regression equations with five continuous independent variables alongside the pandemic effect categorical variable, as presented in
Table 4. The model calculated the monthly impact of the COVID-19 pandemic on monthly retail furniture sales to be USD 527 million, as can be interpreted from the regression equations.
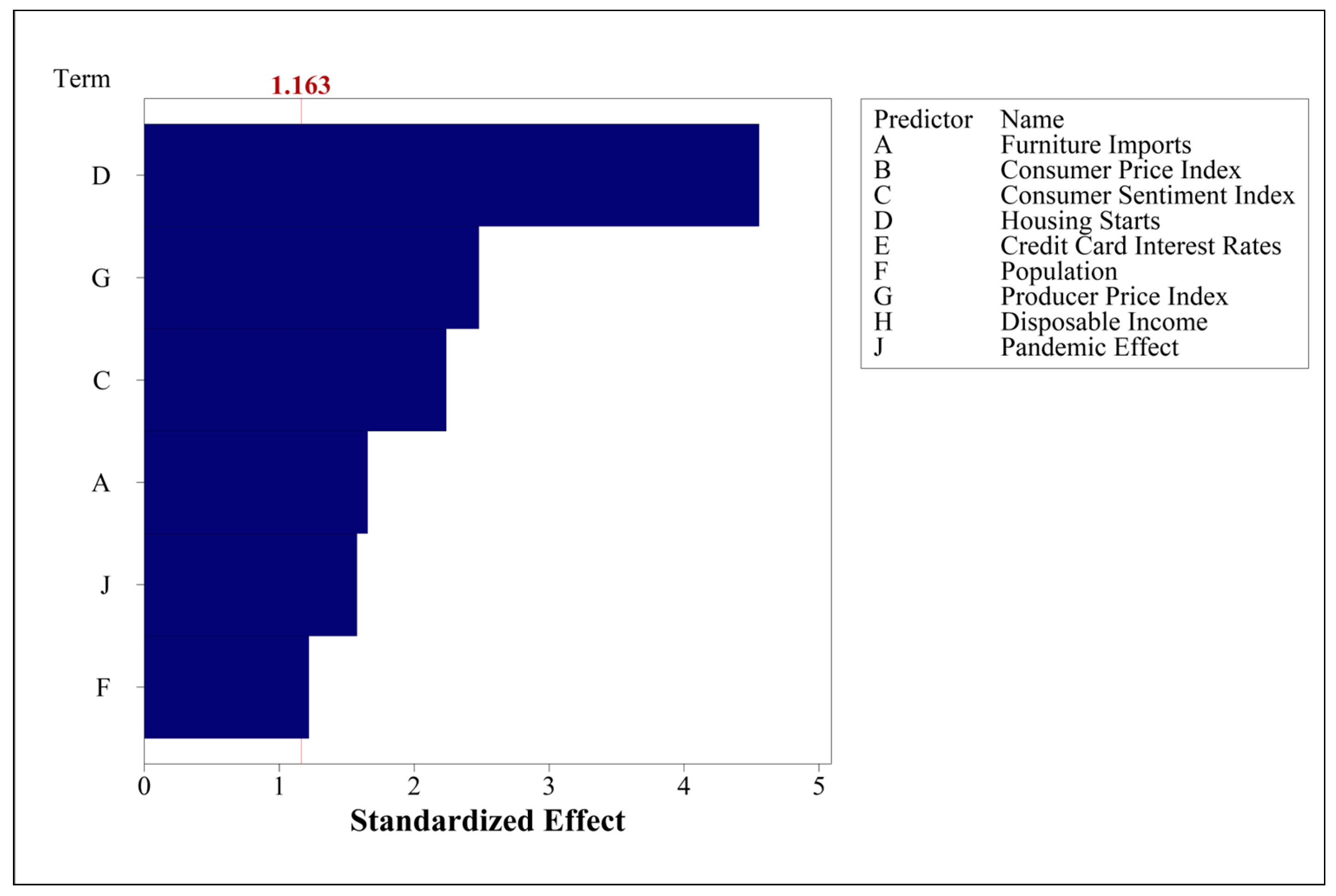
Figure 6 displays the Pareto chart of the standardized effects for the independent variables. According to the predetermined α coefficient for the stepwise regression method, the independent variables of Furniture Imports, Consumer Sentiment Index, Housing Starts, Producer Price Index, and Pandemic Effect were incorporated into the model.
As shown in
Table 5, the R-squared value of the model obtained using stepwise regression was 76.73%, while the adjusted R-squared value was 74.09%, indicating an acceptable level of explanatory capability. High VIF (Variance Inflation Factor) values of the Producer Price Index and Population variables could explain the observed R-squared values of the regression model.
The data for the independent variables spanning the forecasting horizon were generated through multiplicative decomposition, and the forecasted values for each independent variable are presented in
Table 6.
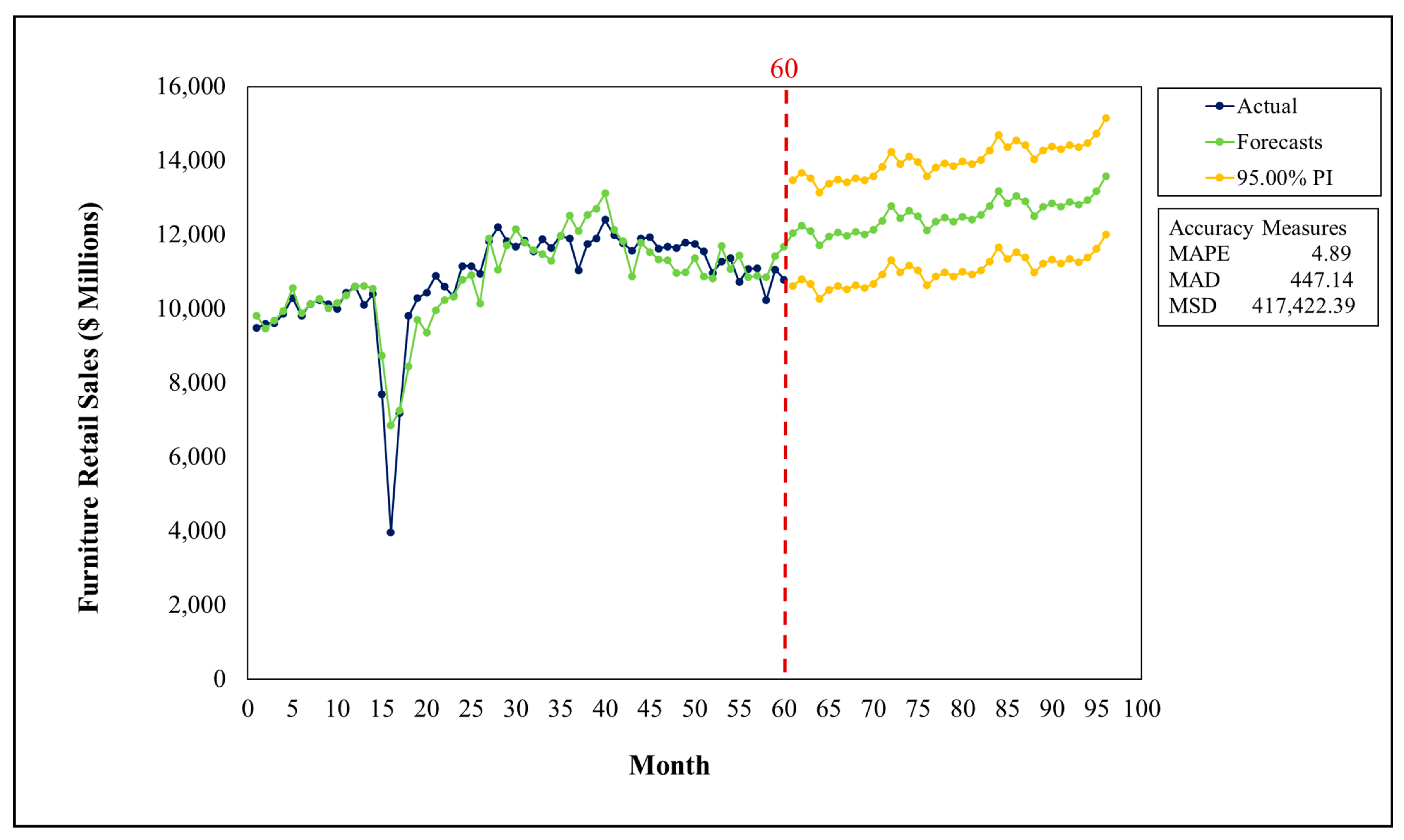
Forecasted values of each independent variable were fed into the developed Multiple Regression Model to forecast the retail furniture sales for the next 36 months. Forecast results and 95% prediction intervals obtained at the end of the Multiple Regression Analysis are presented in
Table 7, and the graph depicting the historical demand data and forecasting horizon is shown in
Figure 7.
As can be seen in
Figure 7, forecast results reflected strong seasonality and a slightly positive trend. Such time-phased distribution of the forecasted data aligned well with the cyclical characteristics of the historical data shown in
Figure 1, which had signs of an ending cycle depicted by a decreasing trend. Additionally, in the forecast generated by the Multiple Regression Analysis, a two-month-long decreasing trend was observed from February to the end of April, followed by a constantly increasing trend peaking at the end of each year. Within the forecasting horizon, for every forecasted year, the lowest forecasted sales value was observed for April, while the highest predicted value was recorded for December. The lowest forecasted demand was projected to be in April 2024, with a value of USD 11,710 million, whereas the highest demand was predicted to occur in December 2026, with a value of USD 13,577 million. The average forecasted annual demand values for 2024, 2025, and 2026 were USD 12,122.50 million, USD 12,522.67 million, and USD 12,922.17 million, respectively.
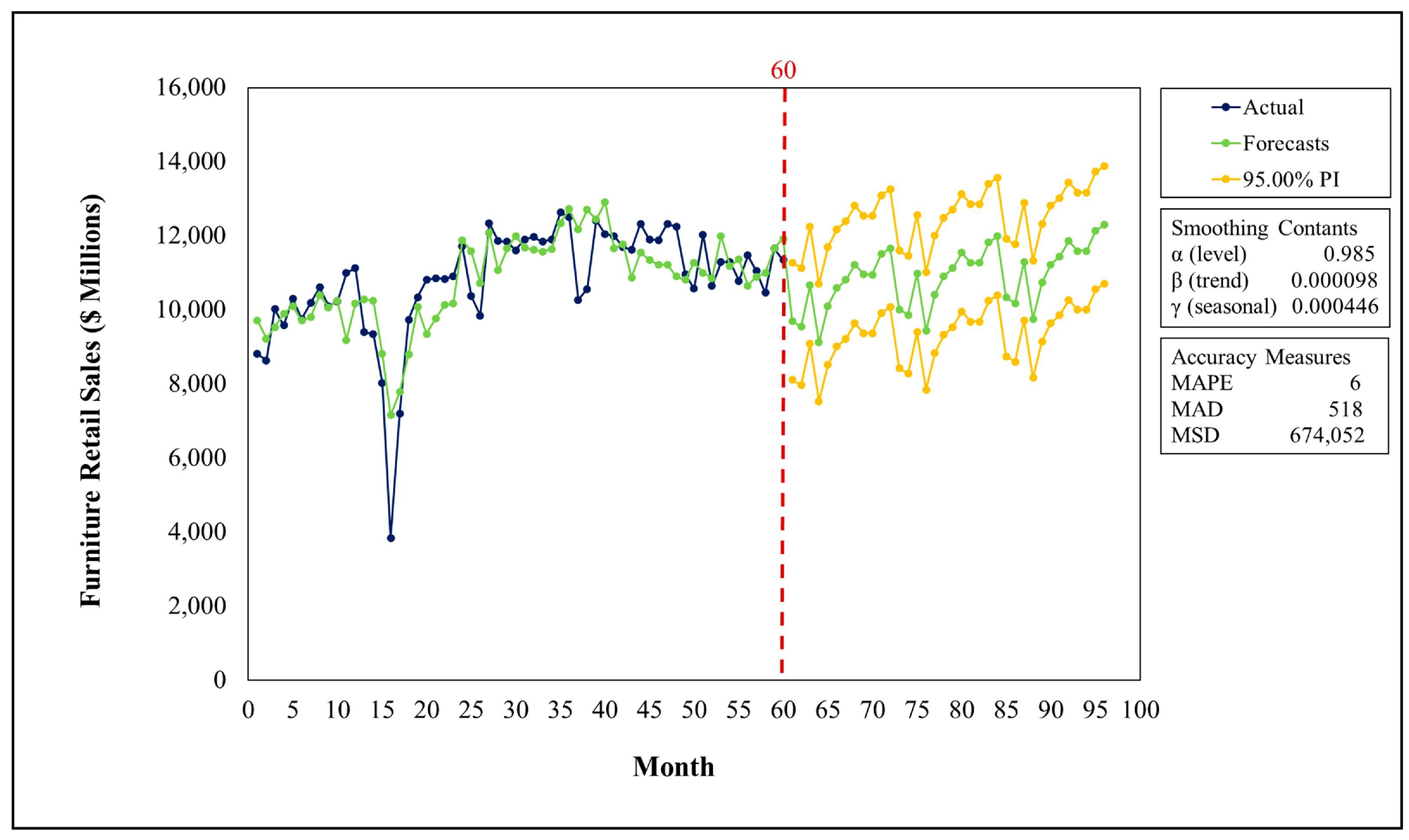
The Holt–Winters method was the second forecasting model used to explore the future of Retail Furniture Sales. The optimization procedure of level, trend, and seasonality coefficients using Python programming resulted in α, β*, and γ* values of 0.985, 0.000098, and 0.000446, respectively. Forecast results and 95% prediction intervals obtained through the Holt–Winters model are presented in
Table 7, and the graph depicting the historical demand data and forecasting horizon is shown in
Figure 8. In
Table 7, monthly peaks and troughs in each year was highlighted by using color shading. Although the terms with the lowest and the highest forecasted demand did not change, the results of the Holt–Winters model yielded a slightly more conservative outcome compared to those of the Multiple Regression Model. The lowest forecasted demand was projected to be in April 2024, with a value of USD 9118 million, whereas the highest demand was predicted to occur in December 2026, with a value of USD 12,298 million. Based on the Holt–Winters model results, the average forecasted annual demand values for 2024, 2025, and 2026 were USD 10,885.83 million, USD 12,522.67 million, and USD 11,202.75 million, respectively. Holt–Winters forecast results showed a similar pattern to the results of the Multiple Regression Model. Two models being complementary to each other could be seen as proof of the validity of the models. The results of this study also validated the assertion made by various market research report outcomes on the future of the furniture industry as detailed in the
Section 1, characterized by a steadily increasing population, predicting a corresponding rise in the demand for furniture.
The predictive capability of two forecasting models was evaluated utilizing three error metrics, namely Mean Squared Deviation (MSD), Mean Absolute Deviation (MAD), and Mean Absolute Percentage Error (MAPE). These metrics indicated that both methods exhibit a high level of capability. The Multiple Regression Model yielded lower values of MAD, MSD, and MAPE. The Multiple Linear Regression Model had MSD, MAD, and MAPE values of 417,422.39, 447.14, and 4.89%, respectively, whereas the Holt–Winters Model had MSD, MAD, and MAPE values of 674,052, 518, and 6%. Since forecasting models with MAPE values below 10% are considered to have an outstanding performance, the forecast results of both models could be used for strategic decision making. However, proceeding with the better performing model is recommended.
5. Discussion
This study focused on forecasting retail furniture sales in the U.S. furniture industry. The outcomes indicated that the forecasting model developed using Multiple Regression Analysis outperformed the Holt–Winters method. When examining relevant literature, Tasdemir and Hiziroglu (2019) conducted a comparative study utilizing Multiple Regression and Winters’ techniques on the inventory management cost analysis of a wood-based panels manufacturer. The developed MLR model in their research incorporated five explanatory independent variables and achieved a MAPE value of 7.61% [
25]. Tabar et al. (2021) explored a demand forecasting study for housing prices, comparing Artificial Neural Networks (ANNs) and Multiple Regression Analysis. In their research, seven independent variables were added to enhance the explanatory power of the Multiple Regression model, resulting in a computed 1-MAPE value of 95.06%. Although ANN exhibited superior forecasting performance, the model derived from Multiple Regression Analysis was recommended. This preference was due to the greater flexibility in adjusting the model in Multiple Regression Analysis, which enhanced the acceptability of the results [
29]. Compared to previous research studies, this study’s findings reported another MLR model with high predictive capability. MLR model flexibility could be the main reason they were outperforming more complex algorithms more often than expected.
The literature consistently demonstrated that the Holt–Winters method is frequently used for forecasting in the presence of seasonal components, providing valuable results supporting decision making. Tratar and Strmčnik (2016) studied short- and long-term heat load forecasting, utilizing the Holt–Winters method for long-term predictions and calculating a MAPE value of 2.54 for the Monthly Holt–Winters (MHW) model, indicating its superior performance [
16]. Puah et al. (2016) applied the Additive Holt–Winters method for monthly and seasonal precipitation forecasting across nine different stations, documenting that the seasonal precipitation forecasting models generally yielded better results with MAPE values ranging from 0.29 to 4.07 [
18]. Sugiarto et al. (2016) conducted a comparative study of the Additive and Multiplicative Holt–Winters methods for sales forecasting, finding that both models produced MAPE values of 4% for the data type in question, thereby confirming the usability of both models [
19]. Rahman and Ahmar (2017) compared ARIMA, Additive, and Multiplicative Holt–Winters methods for forecasting primary energy load consumption, determining that the Additive Holt–Winters model, with a MAD value of 420.99, was more suitable for the characteristics of their dataset [
22]. These examples illustrate that additive and multiplicative Holt–Winters methods are robust tools for forecasting across various applications and datasets with seasonal fluctuations. The model developed in this study for another dataset with an expected seasonality also had high predictive capability with a MAPE value smaller than 10%, proving the Holt–Winters method resilient enough for widespread applicability.
Contradictory to data characteristics observed in this study, Pliszczuk et al. (2021) conducted a study on sales forecasting in the furniture sector, observing that the data used did not contain seasonality and conducted a time-series demand forecasting based on Long Short-Term Memory (LSTM) networks in machine learning [
31].
Additionally, numerous studies have been conducted on the furniture market size by various market research entities, and the results of these studies predict that the furniture market will continue to grow over time. In a study conducted in January 2023, the global furniture market was expected to expand at a compound annual growth rate (CAGR) of 1.19% between 2023 and 2028, reaching USD 728,624.81 million [
6]. In contrast, our study forecasted a CAGR of 8.24% for U.S. furniture retail sales using the Holt–Winters method, with average retail sales expected to reach USD 10,885.83 million during the 2024–2026 forecast period. The MLR method predicted a CAGR of 4.05%, with average retail sales reaching USD 12,522.28 million. Another research company, Allied Market, projected a global furniture market growth rate of 3.8% from 2022 to 2031, which was complementary to the MLR analyses conducted in this study [
7]. In another market research, the global commercial furniture market was expected to reach a market volume of USD 88,267 million with a CAGR of 2.9% during the forecast period from 2024 to 2031, indicating a slower growth in the commercial furniture market [
66]. The results of the aforementioned market research were more conservative when compared to the findings of this study. On the other hand, Precedence Research’s study on the global furniture market size for 2024–2032 predicted that the worldwide furniture market will reach USD 1051.77 billion with a CAGR of 5.3% throughout the forecast horizon [
8]. Similar to our study, the global furniture market studies conducted by Fortune Business Insights and Grand View Research for 2023–2030 calculated CAGR rates of 5.36% and 5.9%, respectively [
67,
68]. When compared to these various sector and market reports, this study’s Holt–Winters forecast model (8.24% CAGR) yielded more optimistic results, while the forecasting method with better predictive capability, MLR (4.05% CAGR), produced results closer to the CAGR documented in these sector reports.
In Mordor Intelligence’s study on the size of the U.S. furniture market, the CAGR calculated for 2024–2029 was over 3% [
69]. This study’s recommended MLR model outputs were observed to be parallel. Both studies observed the significant impact of the COVID-19 pandemic on the sector. Finally, in the North America Furniture Market Sector Analysis Report for 2024–2030 conducted by Stellar Market Research, a CAGR of 8.4% was calculated [
70]. This research result was observed to be parallel with the 8.24% CAGR obtained from the forecast using the Holt–Winters method. Therefore, it can be concluded that the forecasting capabilities of the models created within this study could be deemed decently satisfactory, both from the MAPE values and from the similarities observed between the forecasted demand values and the findings in numerous sector and market research reports.
Overall, the study outcomes could be better understood when evaluated within the context of scientific, managerial, and practical implications. As for the scientific implications, this study provided insights into the efficacy, accuracy, and applicability of the Multiple Regression Analysis and Holt–Winters methods within the context of the retail sales of the furniture industry. Additionally, it facilitated an understanding of market trends and dynamics, contributing to the broader academic discussion on these forecasting techniques’ suitability and performance in sector-specific applications. Within the managerial implications, the conducted forecasting work offers guidance for long-term strategic planning in businesses, enhancing decision-making processes with data-driven insights. This supports more efficient and effective business operations, allowing for companies to optimize resource management and operational processes such as inventory control and production planning. Furthermore, the practical outcomes of this study could guide companies in inventory management, production planning, and marketing strategies. Effective forecasting facilitates better stock management and resource allocation, improving operational outcomes. Moreover, the study’s forecasting efforts provide a basis for scenario-based risk assessment and strategic planning, helping businesses anticipate future challenges and opportunities, thereby enabling strategic adjustments to mitigate risks and capitalize on potential market developments.
Like any scientific inquiry, this study faced several limitations that warrant discussion. A primary constraint involved the subjective nature of the selection procedure for the independent variables used in the Multiple Linear Regression (MLR) model. These variables were identified through a combination of a literature review and the Delphi Method. While these methods are robust in harnessing expert opinion and existing research, they are inherently subject to subjective biases stemming from personal assessments of experts. This subjectivity could potentially influence the selection and weighting of variables. Although more objective statistical methods such as factor analysis or machine learning algorithms for feature selection could provide a less biased approach, the flexibility of the MLR model was deemed suitable for exploring complex interactions within our dataset. Furthermore, the timeframe selected for the historical sales data, spanning from 2019 to 2023, coincides with the unprecedented global disruption caused by the COVID-19 pandemic. This period introduced significant volatility into the data, complicating the task of forecasting with historical accuracy. While the MLR model incorporated the pandemic effect as a special cause variation, adjusting for its impact, the Holt–Winters method does not include parameters specifically designed to handle such anomalies. This limitation resulted in broader prediction intervals and relatively larger forecast errors for the Holt–Winters forecasts. Future studies could explore the integration of external variables that directly measure pandemic-related impacts or employ hybrid models that blend machine learning techniques with time-series forecasting to enhance resilience against such outliers. Additionally, the ability of both models to predict under rapidly changing economic conditions may be limited. The absence of parameters to adjust for sudden market shifts in the Holt–Winters model and the reliance on pre-pandemic data in setting baseline levels in MLR might affect the applicability of the results in post-pandemic market conditions. This highlights the need for continuous model recalibration and validation as new data become available.
Acknowledging these limitations is crucial for interpreting the findings of this study. These limitations and challenges suggest areas for future research that could transcend industries. Future studies might incorporate artificial intelligence-supported methods alongside or in combination with existing approaches to create hybrid, more robust models, thereby enhancing model performance. Such advancements could lead to more precise forecasting tools that are less susceptible to the limitations observed in traditional statistical methods and could adapt to significant economic disruptions and leverage more objective methods for variable selection.