Abstract
This work presents two mixed-integer programming models that intend to minimize the costs of the picking and storage operation through better planning and organization of the places occupied by the products in the warehouse. A large customer that stores frozen goods in a Portuguese cold chain logistics company was selected for the analysis of the allocation of the products in the warehouse and of the corresponding outbound movements. Data with 8525 movements that occurred during 2021 were collected for 228 different product references. For this case study, the products that had a picking place in the initial scenario now have pallets with all the goods in the reserve area, and vice versa. The mathematical models were permitted to obtain savings for the logistics operator costs of around 30.9%. The proposed models can, in the future, be applied in other warehouse scenarios to companies in completely different sectors of activity.
1. Introduction
This work addresses the optimization of the picking and storage operations in a Portuguese company that provides logistics, transport, and storage services for goods under controlled temperature. This is an extended paper of the conference paper [1], which highlighted the cold chain logistics, the environment of the temperature-controlled warehouse, and the consequent possible types of outbound movements. This new paper focuses more on the optimization problem of the picking operations and considers applications for any general warehouse, not only temperature-controlled ones. The contribution of this paper is the presentation of novel mathematical models that can reduce warehouse costs and reflect the actual conditions and requirements of the logistic operations usually performed in companies.
When customer orders are being prepared to leave the warehouse, it is necessary to move boxes and pallets differently according to the way products are stored in the warehouse. Order picking is the retrieval of stock keeping units (SKUs) from the warehouse to satisfy customer orders [2].
Improving warehouse operations and reducing the costs is of critical importance for the companies. To improve a warehouse’s efficiency, integrating picking systems and warehouse optimization should be the focus of researchers [3]. It is estimated that the highest concentration of annual costs of warehouse operations correspond to picking (55%) and storage (20%) operations [4,5,6]. Warehouse design and product allocation can have an impact on the operation costs. The travel time required to retrieve products from storage in response to customer requests depends on the storage location assignment of the products.
1.1. The Storage Location Assignment Problem
The storage location assignment problem (SLAP) concerns the allocation of products into a storage space and the optimization of the material handling costs or the storage space utilization [7]. This is a complex issue that depends on many parameters such as the number of spaces available, the quantity of products, the number of rack levels in the warehouse, and the resources to move, among other things. The storage allocation of products can have different objectives and can be solved with different methodologies [8]. The objectives can address the warehouse space utilization or the time for order preparation and picking operations, considering restrictions such as the available storage capacity, order picking resource capacities, and dispatching policies [7].
The assignment of a location in the warehouse for a product can be fixed, can be chosen randomly, or can be the nearest available location. Random assignment is the most used, and, although it does not optimize the travel distances, it uses the picking area more evenly and can reduce congestion [3]. On the other hand, defining a fixed location dedicated to each SKU can speed up the picking times of high-demand products because operators are familiarized with their location, but it does not optimize space because it requires holding up the locations in the warehouse even when products are out-of-stock.
Storage location assignment policies can also be based on the ABC classes of the Pareto rule, on volume or demand, or on similarity groups [3]. By performing an ABC analysis, products are classified by the degree of importance in relation to value, consumption rate, or frequency of use. Volume-based storage policies assign the most requested SKUs close to the pick-up/drop-off point (P/D). Products in the same similarity group (items that are usually ordered together or have similar functions) can be allocated adjacently [9].
Strategies based on classes or volume obtain a smaller number of trips and perform better than the random assignment strategy [2].
In [3], the four intuitive reasons for locating SKUs nearby in the warehouse are referred to as follows: complementarity (ordered together); compatibility (they work together); popularity (high rotation rate); and size (weight/volume). The strategies for assigning nearby locations for products that are frequently ordered together are proposed in the literature for the food industry [10]. The product structure is used in [11] to find strategies that reduce the order picking times. However, as noted in [12], the performance of a particular storage type greatly depends on the routing method implemented for the order picking.
As suggested in [13], the warehouse design can contemplate a forward area for efficient order picking and a separate reserve area for storage. The decision of which products and quantities are assigned to the forward area and which are assigned to the reserve area is called the forward-reserve allocation problem (FRP). This problem is addressed in [14] by exploring the trade-off between the order picking costs and the internal replenishment. As discussed in [15], assigning a product to the forward area will reduce the labor effort involved in the order picking, but may require concurrent replenishments from the reserve area. A larger quantity of a product allocated to the forward area would reduce this number of replenishments, but the forward area is usually constrained by its limited storage capacity.
To address the warehouse design and storage allocation of products, mixed-integer programming (MIP) models have been used. The decisions about the location and quantity of the products considering the minimization of the total travel times of the picking movements and the maximization of the average storage usage are discussed in [16] with an MIP model. In [17], an MIP model discusses the trade-offs between different warehouse costs, such as picking and other operations, to obtain an optimal design for the FRP where the products are stored in a reserve area and in a forward area.
In [9], a mathematical programming model for a variant of SLAP is developed considering the objectives of minimizing the total travel distance and maximizing the use of the storage capacity. The model is decomposed into subproblems according to the storage dimensions, which are solved sequentially and produce an assignment of the products that is efficient in terms of warehouse utilization and also reduces the operating costs. A mathematical integer programming model that is performed in two stages, where the storage location assignment problem is solved first with a class-based storage policy, and the batching and routing problems are considered in the second stage, is developed in [18] for the automotive industry.
1.2. Storage Allocation in Temperature-Controlled Warehouses
Temperature-controlled warehouses (TCW) are no exception to the need for optimizing the available space and the picking costs. Because of the temperature requirements, the space is usually more constrained, and the need for special equipment makes the holding costs higher in these types of warehouses. The picking operations must fulfill all food quality and safety protocols. A TCW is evaluated regarding criteria such as the implementation of the quality and safety requirements, location of the facility, required equipment to hold the goods, tracking of temperature, humidity and lighting, operational flows, costs, and manpower, among others [19].
In [20], the storage assignment of items in pallet racks of a refrigerated warehouse in Turkey is studied with a mathematical model. By using the consumption patterns to find associations of goods, the storage assignment policies are defined.
An increase in the level of attractiveness and rivalry between competitors associated with the cold logistics sector is expected given that, according to the consultant Grand View Research, the growth expectations for the cold logistics sector will reach 14.8% between the year 2021 and 2028 [21]. The entry of new operators and investors in the market can compromise the performance and constitute a threat to organizations with more traditional facilities and with scarce technological investment. On the other hand, in the current context in which electrical energy, the main resource for creating cold, undergoes high price increases, it is imperative for organizations in the sector to focus on aspects that can be controlled and converge towards cost reduction in their internal logistics operations and a respective increase in efficiency. Mathematical models that optimize costs can contribute to this goal.
Furthermore, in the contemporary era, companies have been increasingly attentive to the environmental and economic impacts of warehouse management. The considerable amount of energy required for heating, cooling, and lighting as well as material handling equipment in warehouses represents approximately of the overall logistical costs [22]. A reduction in the handling costs will result in a reduction in handling and, thus, a saving in the energy used by the resources employed. Consequently, the reduction of warehouses’ energy consumption would result in a significant environmental benefit.
This work presents two different mixed-integer programming models for a variant of the FRP that aims at studying a possible minimization of the costs for the logistics operator with the picking and storage operation and the respective optimization of the places occupied by the products. The results obtained in a case study with frozen food products are presented, and the possible savings for the company are discussed.
The next section presents the methodology followed during the work, and Section 3 explains the underlying concepts of the types of warehouse movements considered in this work. The models are formulated in Section 4, and their results are discussed in Section 5. Finally, the last section concludes the paper.
2. Materials and Methods
The outbound movements from the warehouse were analysed to identify potential changes in the company’s operation. Two mathematical models were formulated using mixed-integer linear programming. The models intend to minimize the costs of the picking and storage operation through a better planning and organization of the places occupied by the products in the warehouse. The models can accommodate only one type of outbound movement, or two different types of movements simultaneously. These mathematical models were implemented in the AMPL, a mathematical programming language, and solved with the Gurobi solver. A large customer that stores a variety of frozen goods in this Portuguese logistics company was selected for the analysis of the allocation of the products in the warehouse and of the corresponding outbound movements. Data with 8525 movements that occurred during 2021 were collected for 228 different product references belonging to this customer.
3. Warehouse Outbound Movements and Product Allocation
The studied warehouse has certain products that have a place on the floor of the warehouse for picking (forward area), with the remaining quantity stored at height on a rack in a reserve area. It also has other products in which the pallets are stored entirely at height on the rack in the reserve area. These forms of allocation of the products in the warehouse originate three possible types of outbound movements:
- PRES (Product in Reserve Area)—It corresponds to the movement of lowering a pallet to the ground and removing the number of boxes necessary to satisfy a certain request/order (List-Pick). After removing the required amount, the pallet is lifted back to its original storage location. For products that have PRES-type movements; that is, where the storage place is defined as a reserve area, there is no allocation of a picking place (place on the floor);
- PHOM (Whole Pallet Order Movement)—It consists of a direct pallet being removed from the storage location; that is, with the entire amount of product it currently has, to serve a merchandise order (Pallet-Pick). This quantity can be the same, which the pallet had when it initially entered the warehouse, or the quantity that remained after removing some items to serve another order (through PRES-type movements);
- PPIC (Product Picking)—It consists of collecting stored products, in order to gather the right product, in the correct quantity according to the order in preparation (List-Pick). Products that have PPIC-type movements have a designated picking place on the warehouse floor.
PRES- and PHOM-type movements are concerned with products allocated in a reserve area, while PPIC-type movements are concerned with products allocated to the forward area.
Considering the compatibility and incompatibility of these types of movements, it is possible that, at a certain moment in time, a product only has one type of movement, or it has a combination of the PRES+PHOM types of movements, or it has a combination of the PPIC+PHOM types of movements. It is not possible for a product in storage to simultaneously have the PRES and PPIC types of movements. There are some records with both the PRES and PPIC types of movements for the same product, but it means that, meanwhile, there was a change in the type of storage of that product. Figure 1 shows the percentage of products with each possible combination of movements.
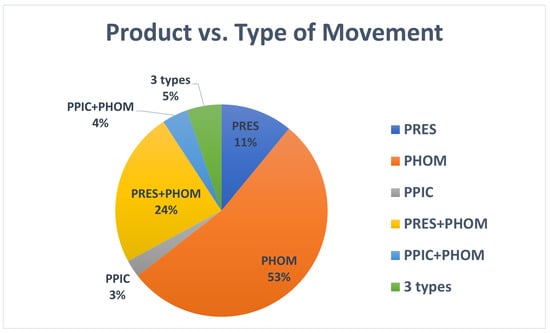
Figure 1.
Percentage of products with each combination of types of movement. Data based on the amount of moved goods during 2021.
As can be seen in Table 1, PHOM is the most common type of outbound movement in this warehouse (74% of all movements). The PHOM type is the most economical type of movement, and it was reported by 86% of the products in the sample.

Table 1.
Number of movements in the warehouse in 2021 and their corresponding products.
During 2021, there was a daily average of 34 outgoing movements of goods for this customer, and around 2541 boxes handled daily.
Each location on the warehouse floor, in the picking area, represents a higher cost for the logistics operator, which must therefore be optimized. If there was a low number of times that picking movements were carried out during the year (2021) for a given product, it may indicate that there is no need for a picking place for the product in question, and it may be worth replacing it with another product: one with a high number of PRES movements, and also a high number of boxes requested. The greater the number of PRES-type movements carried out in the year, the greater the need to create a picking place for this product.
4. Mathematical Models
Two mathematical models were developed, based on the mixed-integer programming method, for a possible minimization of the costs with the picking and storage operation. The difference between the two models is that, while Model 1 is intended for products considering only the predominant type of outgoing movement, Model 2 is intended for products that have two different types of movements simultaneously.
In each model, the set of products is considered. The parameters are identical in both models and include the total number of movements during 2021 for each product, , which is broken down into three parts: , namely, the number of movements of the PRES, PHOM, or PPIC type, respectively, for product i in 2021. The parameter is the maximum number of places available in the picking zone, and parameter is the maximum number of products allowed to change the type of movement. The parameters represent the fixed costs, and represent the variable costs of each type of movement out of the warehouse (PRES, PHOM, PPIC), respectively.
The estimates for the fixed-cost parameters were made based on the cost of space in the warehouse, considering an average annual cost of EUR 120 for storing a pallet on a rack in a reserve area, and a cost 12 times higher for a pallet in a picking area. The fixed cost associated with a PRES-type movement was considered 4 times higher than that for a PHOM-type movement. The variable costs were estimated based on the time needed to carry out each outbound movement, the associated productivity (PRES: 150 boxes handled/hour and PPIC: 200 boxes handled/hour), and the cost per operator (EUR 9.65/h).
Three sets of decision variables are defined for each product i: represent the number of movements of the types PRES, PHOM, PPIC, respectively; are binary variables that state the type of movement for product i; and the binary variables , exclusive to Model 1, flag if there is a change in the type of movement of product i. All the parameters and variables are summarized in Table 2.

Table 2.
Parameters and decision variables of the mathematical models.
MODEL 1
MODEL 2
In both models, the objective function (1) is the same, and it minimizes the total operating costs of picking and storage. Constraints (2) and (12) ensure that the total number of movements of each product is preserved. In Model 1, Constraints (3) and (4) force the choice of only one type of movement for each product. Constraint (5) forces variables to be zero when a product changes its type of movement (), and the previous number of movements of that type was not zero. The same constraint grants that variables have the same value as the previous number of movements of that type when a product does not change its type of movement (). Constraint (6) limits the maximum number of products that can change the type of movement, and (7) limits the number of movements of the PHOM type to the warehouse current capacity.
In Model 2, products are allowed to have more than one type of movement, but there are restrictions on the oscillation between the maximum and minimum number of movements: (13) and (14). The warehouse capacity for picking places is considered in (15) as a direct exchange between products with a picking place (if a product leaves a picking place free, another product must occupy the place).
Model 1 was presented previously in [1], but had some limitations in use, namely, it assumed only one type of movement per product, which produced limited results. In fact, during the course of the company’s operations in 2021, only of the products exhibited a single type of movement. A third of the goods moved in this warehouse were subject to multiple types of movement for the same product, and Model 1 was unable to accommodate them. Therefore, a new model had to be developed to address this practical requirement. This paper presents the new and improved model (Model 2), which has the following two new features: it allows products to have more than one type of movement and balances the number of movements of different types, also considering the limited capacity for picking places in the warehouse.
5. Results
The mathematical models were implemented in AMPL, and the results were obtained using the Gurobi solver. The values of the parameters were based on the information provided by the logistics operator, and the products of the selected customer that had potential for the optimization of their warehouse allocation and, consequently, their type of outbound movements.
According to the analysis of movements by type carried out, only 19 products have the potential for optimization through possible changes in the way they are stored and moved when preparing orders. Note that 122 of the 228 products reported PHOM movements exclusively and, since this is the most economical type of movement, these products do not have the potential to improve. Products with a picking place on the warehouse floor that have a high number of boxes going out in orders with numerous PPIC movements are also considered already optimized. Therefore, the products with a high number of PRES movements and handled boxes compared to the average, and the products that have a picking place with reduced PPIC movements were selected for analysis. This resulted in 19 products to be optimized with Model 1. For Model 2, only the 15 products that had a combination of more than one type of movement were considered.
Regarding Model 1, the obtained results are summarized in Table 3. Note that with the current allocation of the products in the warehouse ( = 0), the total costs with the storage and preparation of orders for the 19 products under analysis, in the year 2021, was EUR 15,510.43. Allowing for changes ( > 0), these costs can be decreased. Savings of 30.9% (EUR 4799) from the 2021 scenario could be obtained using = 0.3, where the model recommends to swap the allocation of five products. By increasing further, either the same optimal solution was obtained, or solutions that were not feasible in practice.

Table 3.
Results obtained with Model 1 for 19 products.
In turn, the results obtained in Model 2 did not decrease as much the costs for the alpha values tested (Table 4 and Figure 2). Model 2 pointed out five products, which had a place in a reserve area in the initial scenario, to be transferred to a picking place. However, considering that this model excluded products that had only one type of product, it was necessary to reassess the products that had exclusively PRES-type movements. As the PHOM movement is the most productive and economical, the results of Model 2 show that it does not interfere with the change in the method of preparing product orders, and this type of movement does not cease to occur.

Table 4.
Results obtained with Model 2 for 15 products.
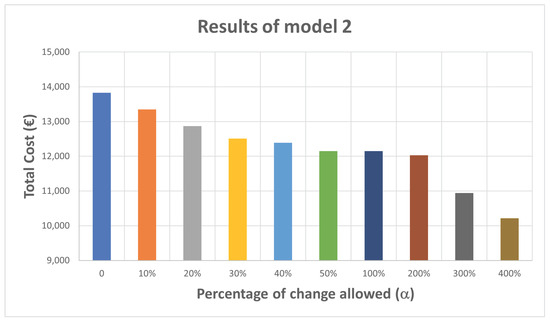
Figure 2.
Results obtained with Model 2 for different values of and the corresponding cost reduction.
The new warehouse allocation of the products includes changing 12 of the 19 products; that is, six products (meat patties, shrimp patties, chicken patties, meat croquettes, chicken pie, custard tarts) that in the initial scenario had a place on the warehouse floor in the picking area, now have all their merchandise on a rack in the reserve area and vice versa. Considering the highest total cost value obtained, it is possible to conclude from the results of both models that the logistics operator could change the allocation of certain products and obtain savings of up to 30.9% compared to the initial scenario of 2021.
The implementation of sustainable strategies that aim to minimize the cost of energy consumption represents an environmental challenge in warehouse management [22]. By optimizing handling operations, and thus saving energy used by the resources employed, models such as these can also contribute to increasing the sustainability of warehouse operations and reducing their environmental impact.
6. Conclusions
The construction and application of mathematical models in AMPL and the Gurobi software explored the possible storage configuration and correspondent picking method of products in a temperature-controlled warehouse for minimizing the total costs.
The obtained results allowed for the creation of a new configuration for the 19 frozen food products under analysis. The new configuration contemplates the alteration of 12 of the 19 products in the analysis, in which 6 of the products that had a picking place in the initial scenario and were covered by movements of the PPIC type now have pallets with all the goods in a reserve area and with PRES-type output movements, and vice versa. Compared to the initial scenario, it was possible to obtain savings for the logistics operator costs of around 30.9%.
The results of the new model presented in this paper (Model 2) seem to have a lower percentage of savings for the company (26.1%) than the results of the Model 1 presented in [1] (30.9%). However, Model 2 presented in this paper is more appropriate for the company since it reflects the actual conditions and requirements of the logistic operations performed in the company. It is also more versatile, as it can also be used in other warehouse scenarios in different sectors of activity.
The proposed models can, in the future, be applied in other warehouse scenarios to companies in completely different sectors of activity.
Further avenues for investigation may be identified through the integration of other controllable variables within these optimization models, such as a warehouse’s energy costs, layout, picking process, and physical inventory.
Author Contributions
Conceptualization, C.L. and A.O.; methodology, C.L.; software, A.O.; validation, C.L.; formal analysis, C.L. and A.O.; investigation, A.O.; resources, A.O.; data curation, A.O.; writing—original draft preparation, A.O.; writing—review and editing, C.L.; visualization, A.O.; supervision, C.L.; project administration, C.L.; funding acquisition, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financed by Portuguese national funds through FCT-Fundação para a Ciência e Tecnologia, under the project UIDB/05422/2020. And The APC was funded by Portuguese national funds through FCT-Fundação para a Ciência e Tecnologia, under the project UIDP/05422/2020.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data is contained within the article
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMPL | A Mathematical Programming Language |
| FRP | Forward-Reserve Allocation Problem |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MIP | Mixed-Integer Programming |
| P/D | Pick-up/Drop-Off Point |
| PHOM | Whole Pallet Order Movement |
| PPIC | Product Picking |
| PRES | Product in Reserve Area |
| SKU | Stock Keeping Unit |
| SLAP | Storage Location Assignment Problem |
| TCW | Temperature-Controlled Warehouse |
| WMS | Warehouse Management System |
References
- Oliveira, A.; Lopes, C. Outbound Movements in a Temperature-Controlled Warehouse. In Flexible Automation and Intelligent Manufacturing: Establishing Bridges for More Sustainable Manufacturing Systems; FAIM 2023. Lecture Notes in Mechanical Engineering; Silva, F., Ferreira, L., Sá, J., Pereira, M., Pinto, C., Eds.; Springer: Cham, Switzerland, 2024; pp. 1074–1081. [Google Scholar]
- Petersen, C.G.; Aase, G. A comparison of picking, storage, and routing policies in manual order picking. Int. J. Prod. Econ. 2004, 92, 11–19. [Google Scholar] [CrossRef]
- Pinto, A.R.F.; Nagano, M.S.; Boz, E. A classification approach to order picking systems and policies: Integrating automation and optimization for future research. Results Control Optim. 2023, 12, 100281. [Google Scholar] [CrossRef]
- Bartholdi, J.; Hackman, S. Warehouse and Distribution Science: Release 0.98.1; Supply Chain and Logistics Institute: Hong Kong, China, 2019. [Google Scholar]
- Tompkins, J.; White, J.; Bozer, Y.; Frazelle, E.; Tanchoco, J. Facilities Planning, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- de Koster, R.; Le-Duc, T.; Roodbergen, K. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Reyes, J.; Solano-Charris, E.; Montoya-Torres, J. The storage location assignment problem: A literature review. Int. J. Ind. Eng. Comput. 2019, 10, 199–224. [Google Scholar] [CrossRef]
- Medrano-Zarazúa, L.; Saucedo-Martínez, J.A.; Bolaños-Zuñiga, J. Storage Location Assignment Problem in a Warehouse: A Literature Review. In Computer Science and Engineering in Health Services; Marmolejo-Saucedo, J.A., Rodríguez-Aguilar, R., Vasant, P., Litvinchev, I., Retana-Blanco, B.M., Eds.; Springer: Cham, Switzerland, 2024; pp. 15–37. [Google Scholar]
- Viveros, P.; González, K.; Mena, R.; Kristjanpoller, F.; Robledo, J. Slotting Optimization Model for a Warehouse with Divisible First-Level Accommodation Locations. Appl. Sci. 2021, 11, 936. [Google Scholar] [CrossRef]
- Bindi, F.; Manzini, R.; Pareschi, A.; Regattieri, A. Similarity-based storage allocation rules in an order picking system: An application to the food service industry. Int. J. Logist. Res. App. 2009, 12, 233–247. [Google Scholar] [CrossRef]
- Brynzér, H.; Johansson, M. Storage location assignment: Using the product structure to reduce order picking times. Int. J. Prod. Econ. 1996, 46–47, 595–603. [Google Scholar] [CrossRef]
- Goran Dukic, V.C.; Opetuk, T. Order-picking Methods and Technologies for Greener Warehousing. Strojarstvo 2010, 52, 23–31. [Google Scholar]
- Frazelle, E. Supply Chain Strategy: The Logistics of Supply Chain Management; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Gu, J.; Goetschalckx, M.; McGinnis, L. Solving the forward-reserve allocation problem in warehouse order picking systems. J. Oper. Res. Soc. 2010, 61, 1013–1021. [Google Scholar] [CrossRef]
- van den Berg, J.P.; Sharp, G.P.; Gademann, A.; Pochet, Y. Forward-reserve allocation in a warehouse with unit-load replenishments. Eur. J. Oper. Res. 1998, 111, 98–113. [Google Scholar] [CrossRef]
- Öztürkoğlu, O. A bi-objective mathematical model for product allocation in block stacking warehouses. Int. Trans. Oper. Res. 2020, 27, 2184–2210. [Google Scholar] [CrossRef]
- Geraldes, C.; Carvalho, S.; Pereira, G. Warehouse design and product assignment and allocation: A mathematical programming model. In European Simulation and Modelling Conference-ESM’2012; FOM University of Applied Sciences: Essen, Germany, 2012. [Google Scholar]
- Ene, S.; Öztürk, N. Storage location assignment and order picking optimization in the automotive industry. Int. J. Adv. Manuf. Technol. 2012, 60, 787–797. [Google Scholar] [CrossRef]
- Yuen, S. Temperature controlled warehouse and cold chain business in Hong Kong: A literature review. Asia Pac. J. Adv. Bus. Soc. Stud. 2017, 3, 8–18. [Google Scholar]
- Yener, F.; Yazgan, H. Optimal warehouse design: Literature review and case study application. Comput. Ind. Eng. 2019, 129, 1–13. [Google Scholar] [CrossRef]
- Interempresas. Cold Storage Will Be Smarter, Greener and Grow at Rates of 14% Per Year. iAlimentar-Informação profissional para a indústria alimentar portuguesa. 2021. Available online: https://www.ialimentar.pt/Artigos/375713-Armazenamento-a-frio-sera-mais-inteligente-ecologico-e-crescera-a-taxas-de-14-por-ciento.html (accessed on 27 March 2024). (In Portuguese).
- Carli, R.; Dotoli, M.; Digiesi, S.; Facchini, F.; Mossa, G. Sustainable Scheduling of Material Handling Activities in Labor-Intensive Warehouses: A Decision and Control Model. Sustainability 2020, 12, 3111. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).