Labor Mobility Networks and Green Total Factor Productivity

Abstract

Population migration continues to reshape the spatial pattern of China’s population and regional economic development. During this internal migration process, production and consumption patterns often change, ultimately leading to changes in green total factor productivity. This paper, based on the Chinese population census data and 1% sampling survey data from 2005 to 2015, utilizes social network analysis methods to measure the labor mobility network indicators of 284 prefecture-level cities. Further, this paper analyzes the impact and mechanisms of regional network status on green total factor productivity using a panel fixed effects model. We find that as network density increases, the interpersonal connections between regions become closer, and the network exhibits a clear pattern of “concentrated inflows” and “dispersed outflows”, with the trend of forming strong alliances becoming increasingly apparent. Regions positioned centrally either in terms of network in-degree or out-degree exhibit higher green total factor productivity. Among these, the labor mobility network plays a crucial role in enhancing green total factor productivity through the channel of technology diffusion effects, which improve investment efficiency via knowledge exchange and material capital accumulation. The promotive effect of labor network status on green total factor productivity is more pronounced in the eastern regions, where talent quality is higher, and in areas with fewer restrictions from the household registration system.

1. Introduction

The rapid development of the Chinese economy since 1978 has relied on the optimized allocation of production factors, especially the most dynamic factor of production, labor, in the optimization of allocation between urban and rural areas, regions, and industries [1]. As shown in Figure 1, since 1996, China’s urbanization process has accelerated significantly, with an average annual growth rate exceeding 1 percentage point, and the urbanization rate of China’s permanent population reached 63.89% in 2020. The urbanization process in China is far from over, and a large number of population migrations will continue to exist for a considerable period of time in the future. According to the United Nations Department of Economic and Social Affairs, China is projected to add 300 million people to its cities by 2050. Large-scale interregional population mobility is mainly attributed to the initial development strategy of prioritizing economic growth in the eastern coastal areas during the early stages of reform and opening-up, which led to a concentrated demand for labor, as well as the gradual relaxation of population mobility policies, especially household registration policies. Due to the gradual decline in China’s natural population growth rate, population migration has become an important driving force for changes in population size and structure in various regions, and it is currently reshaping China’s population spatial pattern and regional economic development pattern.

Population mobility has generated substantial achievements for socio-economic growth in China, typically driven by energy-intensive heavy industries and infrastructure development, which have resulted in significant energy consumption and severe environmental issues. However, for a developing country, it is more crucial to measure GTFP in terms of efficiency and structure, rather than the total amount of energy consumption or environmental pollution. Although various studies have reported differing specific estimates, there is a consensus that China’s GTFP has shown a steady upward trend since the year 2000 [2]. This paper investigates whether the macro-level evolutionary trend of increasing GTFP and labor mobility in China since 2000 is coincidental or inherently connected.

Using data from China’s population censuses and 1% population sample surveys from 2005 to 2015, this study examines how a city’s position in the labor mobility network affects its GTFP. Specifically, it first constructs a city-level labor mobility network based on urban migration information and calculates network centrality measures for in-degree and out-degree, following the approach of Feng and Serletis [3]. Next, a panel fixed effects model is used to empirically test the impact of regional network status on GTFP. Furthermore, the paper dissects two mechanisms driving the relationship between labor mobility network centrality and city GTFP: “resource allocation effects” and “technology diffusion effects”. Results indicate that during the sample period, as the intensity of China’s labor mobility network increased, the interpersonal connections between regions grew closer, and the network exhibited a pattern of “concentrated inflows” and “dispersed outflows”, with a trend toward forming stronger alliances. Regions that are central in terms of network in-degree or out-degree exhibit higher GTFP. The labor mobility network enhances GTFP primarily through technology diffusion effects, which improve investment efficiency by facilitating knowledge exchange and increasing material capital.

The main objective of this paper is to evaluate the role and mechanisms of the spatial structure of labor mobility on GTFP. By addressing gaps in the existing literature, this study provides valuable insights for both the academic community and government agencies. Relative to existing research, the primary contributions of this paper are: First, it expands the field of study on labor mobility’s impact on the environment and global warming, an increasingly scrutinized area given the sharp increase in international migration to the United States during the last century. While previous studies mainly examined the impact of international migration on the natural environment in the United States, the effect of labor mobility on the environment is gaining attention without a unified perspective. For instance, studies by Squalli [4] and Price and Feldmeyer [5] indicate that international migrants do not cause more air pollution in the U.S. However, Muradian [6] suggests that the environmental impact of U.S. immigration could be either positive or negative. Compared to literature focused on international migrants, less research exists on the environmental impacts of domestic migration, especially considering the hundreds of millions of urban internal migrants in China over recent decades, which significantly affect China’s carbon emissions. Studies like Qin and Liao [7] show that domestic labor mobility affects the spatial distribution of populations and related activities, thereby potentially reducing or increasing carbon emissions. This paper also explores the mechanisms through which trust, resources, and information embedded in the labor mobility network affect GTFP. There has been limited discussion on the intrinsic mechanisms by which labor outflows affect GTFP, and no clear conclusions have been formed. Thus, this paper meticulously verifies or excludes different mechanisms, making its findings more reliable and of greater policy significance.

Second, this paper contributes to the research on factors influencing GTFP, particularly revealing factors influencing China’s GTFP growth in recent years. These studies mainly focus on discussing the impact of economic, resource, and ecological factors on a country’s green economic development, with a prominent research direction exploring the effects of economic size, structure, technological advancement, and innovation on green economic development [8,9,10]. Compared to the conventional approach that considers GTFP a function of scale, technology, and structure, this paper expands the theoretical framework by incorporating characteristics of the labor mobility network as a significant factor affecting GTFP, distinguishing between different directions of labor inflow and outflow to facilitate a comprehensive analysis, which is of substantial practical significance for further deepening reforms of the household registration system, rational allocation of labor resources, and promoting sustained and healthy economic development.

Third, this paper also contributes to the study of measuring the spatial structure characteristics of labor mobility. Existing research primarily employs fractal theory and ESDA methods, hotspot analysis [11] and spatial regression [12], Moran’s I [13], and geographically weighted regression models [14] to depict the patterns of population mobility at the provincial, city, and county levels [15]. However, these indicators only reflect aspects of labor mobility between two regions and do not adhere to the conventional statistical assumption of “independence of variables”. The Social Network Analysis (SNA) approach studies social phenomena and structures from the perspective of relationships [16], and the labor mobility network constructed through this method provides a more comprehensive reflection of a region’s relative position and network characteristics within China’s labor mobility network. Especially with the development of information technology, traditional geographical spatial structures are being reshaped by complex network relationships, where labor relations between any two regions are indirectly affected by the relationships in other parts of the network. However, due to data limitations, current research using social network methods on labor mobility patterns often focuses on inter-provincial or specific regional mobility, with fewer studies examining the national labor mobility network from a city-level perspective. A more comprehensive depiction of a region’s position in the labor mobility network is crucial for accurately measuring its network status and empirically analyzing its impact on GTFP.

The remainder of this paper is organized as follows: Section two reviews the related literature on the mechanism of how characteristics of labor mobility networks impact GTFP and proposes research hypotheses. Section three constructs the labor mobility network to analyze the overall pattern of labor mobility and briefly describes typical facts about the relationship between network characteristics and GTFP. Section three also details sample selection and research design and introduces the measurement of other significant variables. Section four analyzes the empirical results, conducts robustness tests, and performs heterogeneity analysis. Section five presents the main conclusions and policy recommendations of this study.

2. Theoretical Explanation

Considering the intricate nature of labor mobility relationships, this paper will comprehensively examine the influence of a city’s position in China’s labor mobility network on its GTFP. The topology of networks fundamentally depends on the characteristics of the nodes within the network, which are the ultimate outcome of interactions in social network relationships, making it a crucial topic of research in social network analysis [17,18]. Network centrality is a key variable for measuring the importance of nodes in a network. Generally, network centrality is used to assess the degree to which actors in a network act as hubs and control access to resources [19,20], directly reflecting a node’s control capability and centrality within the network. Specifically, in the context of labor mobility networks explored in this paper, high centrality implies that a region occupies a central position in labor mobility, engaging in exchanges with numerous other regions. This indicates that the region could serve as a hub for external personnel exchanges with other regions, thus exerting significant control over the entire labor mobility network.

Labor mobility relationships can alter micro-level efficiency and macro-level configuration effects through various pathways, thereby impacting GTFP. Firstly, resource allocation effects. The resource allocation effect posits that regions with high centrality can enhance capital utilization efficiency through cooperative behavior and information transmission, guiding capital to flow from low-efficiency, high-pollution industries to high-efficiency, low-pollution industries, thereby promoting industrial upgrading, optimizing energy structure, and improving GTFP. Interactions in long-term relationships embedded in labor mobility between cities can foster trust and cooperation, facilitating the exchange and transmission of implicit information or making joint decisions in a more timely and effective manner, thereby increasing the likelihood of cooperation [21]. Information can be transmitted through social networks. This information is more likely to be used to guide decision-making. Existing research has shown that two companies with social relationships share valuable information related to investment opportunities, leading to higher similarity in investment decisions between the two companies. When executives face limited information and noise, executives in central positions in social networks are more likely to make investment decisions with informational content, improving investment efficiency [22]. Similarly, cities in central positions in labor mobility networks can cooperate with and transmit information to more regions, thus making more informed investment decisions and improving capital utilization efficiency.

Secondly, technology diffusion effects. Previous studies on labor mobility have assumed that capital supply remains fixed or at least independent of migrant populations in the short term. However, these assumptions are difficult to uphold in reality, as the movement of people generates potential capital inflows. Immigration promotes connections between host countries and their home countries, reducing transaction and information costs, and thereby encouraging foreign direct investment between the two countries [23]. Common nationality between immigrants and their home country firms serves as a channel for knowledge and trust, attracting capital investment (Hernandez, 2014). In the context of China, labor mobility strengthens connections between inflow and outflow areas, promoting the cross-regional flow of capital factors and increasing the input of material capital. Additionally, continuous learning and exchange through rational and effective division of labor and cooperation between migrant workers and locals facilitate the efficient operation of knowledge flow, information flow, and technology flow. Therefore, whether it is knowledge exchange or the increase in material capital, both contribute to technological progress. The agglomeration of human capital brought about by labor inflow may not directly improve the technological level of the recipient area, but the exchange and interaction between labor can promote the diffusion and dissemination of technology, thereby effectively driving the improvement of the informatization level of inflow and outflow areas.

Based on the above analysis, this paper proposes the following research hypothesis: Holding other conditions constant, the higher the centrality of a city in the labor mobility relationship network, the higher its GTFP.

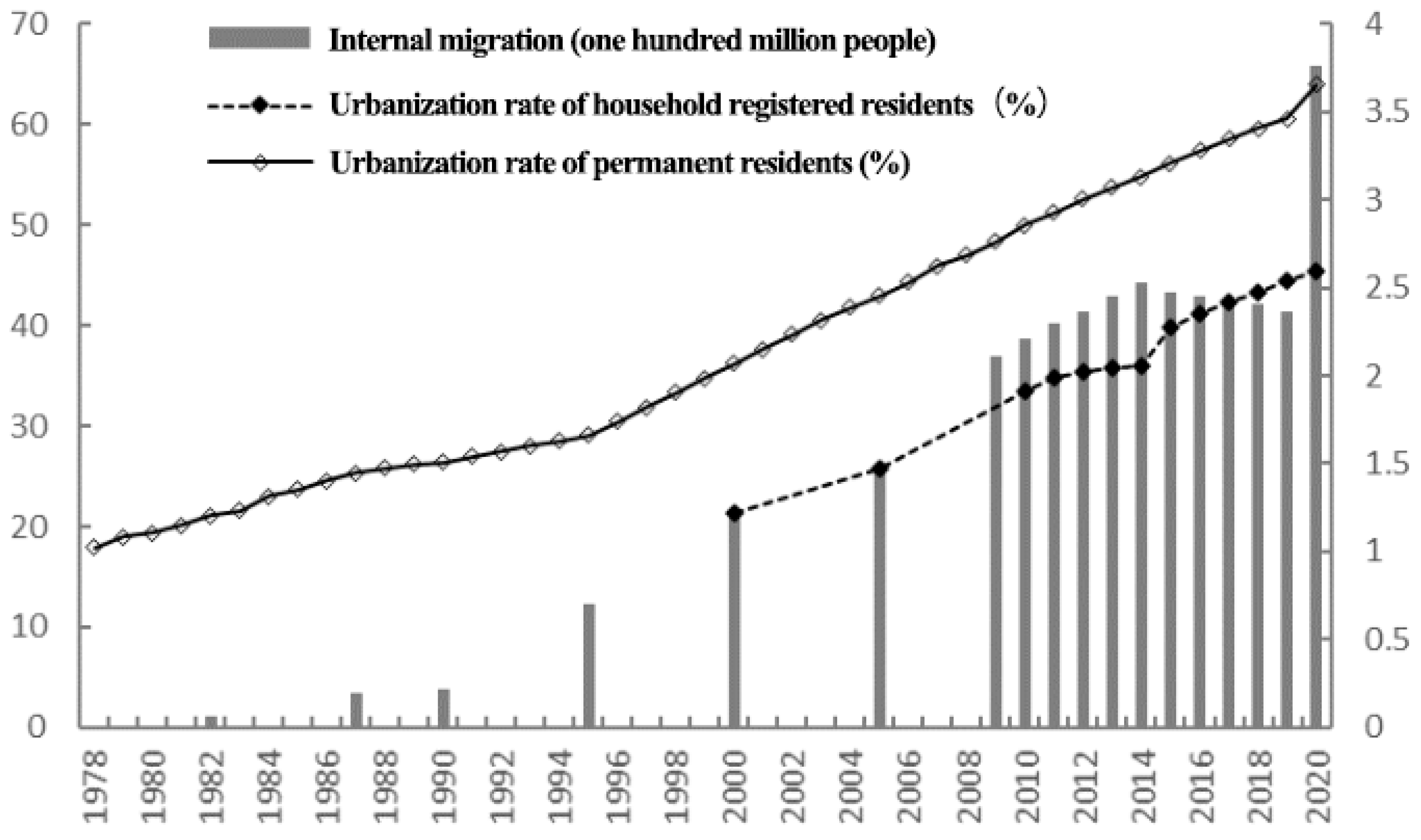
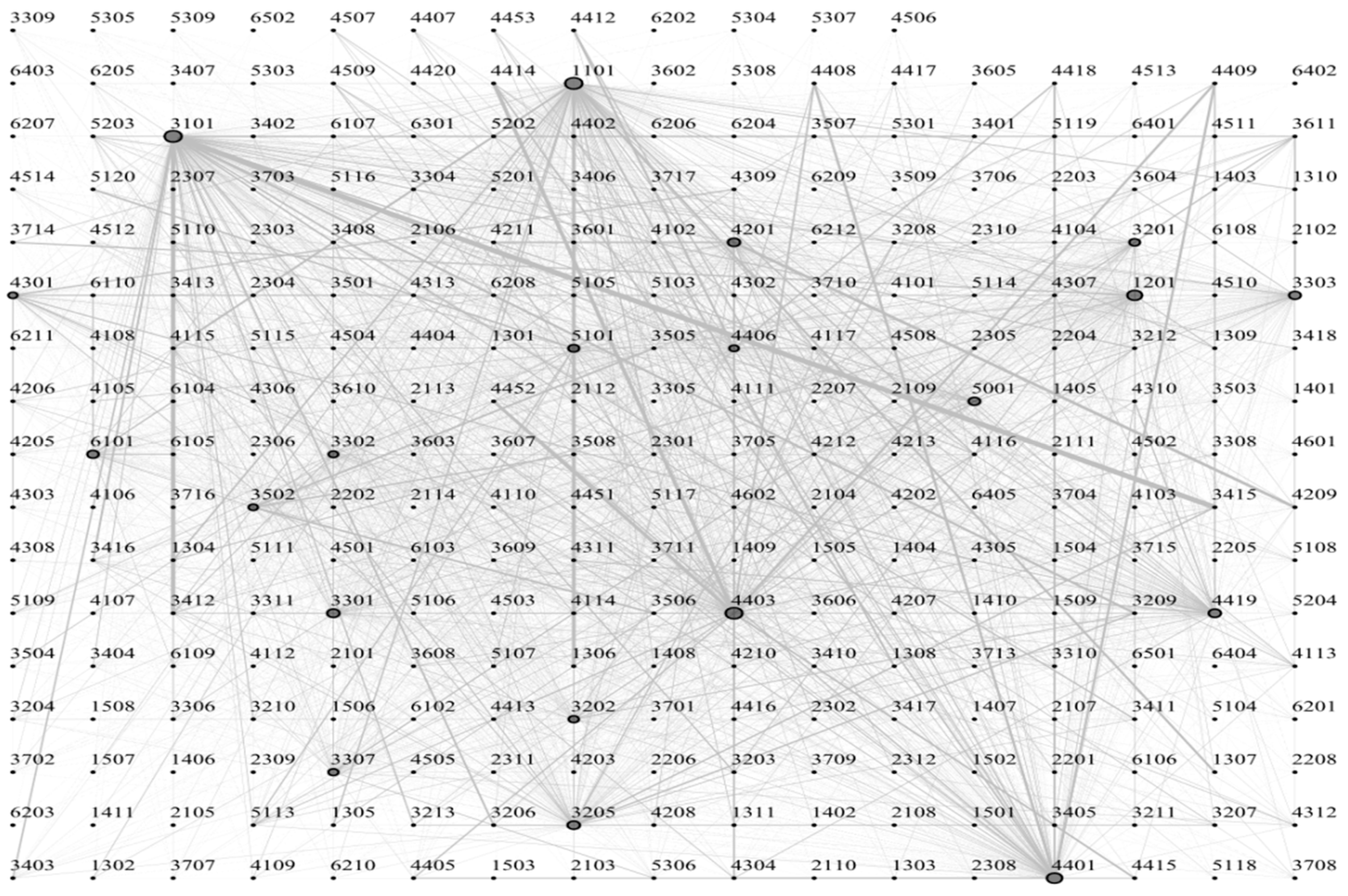
3. Measurement and Analysis of Labor Flow Network

3.1. Construction of Labor Flow Network and Indicators’ Measurement

From a topological perspective, China’s domestic labor flow system is an extremely complex network, not just a simple collection of prefecture-level cities but also intricate connections between cities. This study mainly uses the 2005 1% population sample survey data, the 2010 population census data, and the 2015 1% sample survey data to construct labor inflow and outflow data between different prefecture-level cities. The number of migrants is usually defined as the number of people who change their place of residence or work. The key criterion for determining whether an individual is a migrant is the separation of residency and household registration (the separation of residency and household registration in China refers to a system where each individual holds a household registration, typically tied to their birthplace or their parents’ registered residence, but they may work or live in other cities. In the household registration system, known as “hukou” in Chinese, individuals require administrative permission when migrating from one city to another. Consequently, internal migration between cities in China is still somewhat constrained). To construct the labor flow network between prefecture-level cities, this study focuses on the floating population aged 18–60. Therefore, in this study, we define individuals aged 18–60 who have left their registered residence for more than six months as the floating population. Based on the registered residence and the current residence at the time of the survey, we determine whether they are intercity migrants. For intercity migrants, it indicates that their original registered residence and destination city are different. With the development of urbanization in China, the scope of population mobility is gradually shifting from “interprovincial migration” to “intra-provincial migration”, with an increasing proportion of intercity mobility. Therefore, in this chapter, we use prefecture-level cities as the regional division basis in the baseline regression. Despite certain limitations, this study considers the use of city-level labor flow data as an appropriate approach.

Building upon the labor mobility data mentioned above, this study constructs a network adjacency matrix to measure the labor flow network characteristics of different prefecture-level cities. From the perspective of social network analysis, each prefecture-level city $i$ represents a node in the labor flow network, and if there is labor flow between regions, there exists an edge between the corresponding nodes. To meet the requirements of the measurement methods for network characteristics, this study constructs a directed weighted labor flow network matrix: the directed weighted labor flow network for year $t$ is represented by a $N\times N$ adjacency matrix $A_t$ (with rows representing the labor outflow regions and columns representing the labor inflow regions), where t represents the year. The element $a_{ij}$ in the matrix $A_t$, represents the intensity of labor flow from city $i$ to another $j$. For the sake of analysis accuracy and to prevent relatively weak correlation relationships from affecting the overall distribution of the network, it is necessary to set thresholds for elements in the network matrix. This paper sets the mean of each row in the network matrix as the threshold. If the population flow from region i to region j exceeds a certain threshold in year t, $a_{ij}=1$; Otherwise, it is set to 0. To comprehensively examine the relationship between the labor flow network and green total factor productivity, considering data availability and comparability, this study aims to describe the overall structural features of the labor mobility network among 284 prefecture-level cities in China by using a range of network statistical indicators.

3.2. Characteristics of Labor Flow Network

3.2.1. Overall Network Level Characteristics subsection

This paper employs network edge indicators to characterize the scale of the network; utilizes density, diameter, average path length, and average degree indicators to reflect the network’s connectivity level; employs clustering coefficients to characterize network clustering effects; and measures network connectivity features through reciprocity and assortativity [24].

This paper employs the R programming language to depict the labor flow network structures for the years 2005 and 2015 (see Figure 2 and Figure 3). A link between two regions indicates a trade relationship greater than or equal to the threshold, with thicker lines indicating a higher volume of labor flow between the regions. The results in

Table 1. Statistical characteristics of urban labor mobility network from 2005 to 2015.

	2005	2010	2015
Links	12,043	14,353	15,763
Network diameter	4	5	3
Network density	0.1498	0.1786	0.1961
Reciprocity	0.2729	0.3032	0.4254
Average path length	1.9883	1.8945	1.8205
Clustering	0.4232	0.4395	0.4699
Assortativity	−0.1367	−0.1296	−0.1284

show that in 2005, there were 12,043 links in the labor flow network, increasing to 15,763 links in 2015. A comparison between Figure 2 and Figure 3 reveals that from 2005 to 2015, the connections between regions became denser, as evidenced by the increasing number of links between nodes; moreover, regions with larger labor flows also exhibited more connections, depicted by the increase in thick links. The density of the labor flow network increased from 0.1498 in 2005 to 0.1961 in 2015, indicating significantly increased connections between network nodes, reflecting the expansion of labor flow and enhanced economic interactions between cities.

The diameter of the labor flow network ranges from 3 to 5, with an average path distance between 1.8205 and 1.9883, implying that on average, a city can be reached from another city in about 2.5 steps, and the longest path distance does not exceed 6, conforming to the “small-world” phenomenon. The average shortest path decreased from 1.9883 to 1.8205 during the sample period, indicating enhanced efficiency in the labor flow network, suggesting that labor flows between regions became more rapid and unimpeded. This may be attributed to advances in transportation, information technology, or optimization of labor market policies.

In the labor flow network, reciprocity indicates that the flow of personnel between two cities is mutual, with labor flowing bidirectionally between the two cities. During the sample period, the reciprocity index increased steadily from 0.2729 in 2005 to 0.4254 in 2015, indicating an upward trend in reciprocity in China’s labor flow network, suggesting that during this period, close interactions between cities promoted the circulation of the labor force. The clustering coefficient ranges from 0.4232 to 0.4699, indicating a certain degree of clustering in the labor flow network. Negative assortativity indicates that nodes with high degrees tend to be connected to nodes with low degrees, suggesting that the network is disassortative. The increase in the maximum value of the degree centrality index during the sample period indicates that a few central cities in the network continue to occupy a relatively core position, with power and influence firmly held by these central cities.

3.2.2. Regional Degree Distribution Characteristics

The free movement of labor is an important channel for optimizing the spatial allocation of labor and is one of the important research areas in development economics. More than half of the world’s production activities are concentrated in major cities within each country, and the world’s economy and population are increasingly concentrated in a few large cities or metropolitan areas. The phenomenon of economic concentration in developed countries is very evident. So, does China’s floating population also exhibit the same network characteristics of concentration?

This paper uses the 1% sample survey data from 2005 and 2015 for comparative analysis to obtain a longer time dimension for comparison. Figure 4 shows the regional distribution characteristics of the in-degree and out-degree of the labor flow network in 2005 and 2015. The eastern region has the highest average in-degree, while the central region has the highest average out-degree. It can be seen that the out-degree centrality of the labor flow network is much lower than the in-degree centrality, indicating a pattern of “concentration of inflow, dispersion of outflow”. This means that certain cities have become centers for talent aggregation, while the sources of talent outflow are more diverse and dispersed. From a longitudinal time perspective, the difference between the average in-degree and out-degree in the eastern region has increased during the sample period, while the difference in the central region has gradually decreased. The difference between the average outflow and inflow in the western and northeast regions has significantly widened. By comparing the geographical distribution of the floating population in 2005 and 2015, it is evident that the eastern region has maintained its attractiveness to labor, while the attractiveness of the western and northeast regions has declined significantly. The trend of labor flow towards regions with faster economic development in China has become more pronounced, and overall population migration shows a pattern of higher levels in the east and lower levels in the west.

3.2.3. Node-Level Characteristics

To observe the node-level characteristics of the labor flow network, we analyze the in-degree and out-degree of the 284 nodes in the labor flow network constructed above and compare the top 20 prefecture-level cities in 2005 and 2015. The results are shown in

Table 2. Top 20 cities from 2005 to 2015 in China’s labor mobility network and their centrality.

	2005		2015		2005		2015
Rank	City	Indegree	City	Indegree	City	Outdegree	City	Outdegree
1	Beijing	0.975	Shanghai	0.958	Wenzhou	0.410	Beijing	0.512
2	Shenzhen	0.965	Beijing	0.919	Chongqing	0.389	Shenzhen	0.509
3	Shanghai	0.961	Shenzhen	0.894	Zhoukou	0.368	shanghai	0.470
4	Tianjin	0.901	Tianjin	0.869	Chengdu	0.353	Guangzhou	0.459
5	Guangzhou	0.855	Guangzhou	0.809	Zhumadian	0.346	Chongqing	0.456
6	Dongguan	0.707	Suzhou	0.753	Zhengzhou	0.318	Wenzhou	0.435
7	Zhuhai	0.657	Dongguan	0.703	Anqing	0.315	Zhoukou	0.406
8	Foshan	0.647	Hangzhou	0.650	Nanyang	0.315	Nanyang	0.396
9	Huizhou	0.611	Wuhan	0.636	Nanchong	0.307	Chengdu	0.392
10	Suzhou	0.601	Nanjing	0.622	Harbin	0.307	Wuhan	0.385
11	Zhongshan	0.562	Xi’an	0.618	Dazhou	0.304	Hangzhou	0.382
12	Hangzhou	0.509	Xiamen	0.594	Mianyang	0.300	Fuyang	0.375
13	Ningbo	0.509	Wuxi	0.583	Wuhan	0.293	Hefei	0.375
14	Xi’an	0.491	Foshan	0.572	Shaoyang	0.290	Nanchong	0.368
15	Wenzhou	0.452	Jinhua	0.569	Fuyang	0.286	Nanchang	0.360
16	Jiangmen	0.449	Jiaxing	0.562	Guiyang	0.276	Tianjin	0.360
17	Quanzhou	0.445	Zhuhai	0.558	Xuzhou	0.269	Zhumadian	0.357
18	Kunming	0.445	Wenzhou	0.548	Guang’an	0.269	Heze	0.353
19	Haikou	0.435	Huizhou	0.537	Xinyang	0.269	Harbin	0.346
20	Fuzhou	0.431	Ningbo	0.534	Yibin	0.265	Xinyang	0.339

. The in-degree centrality results indicate that in 2005, Beijing had the highest in-degree, followed by Shenzhen, Shanghai, Tianjin, and Guangzhou. In 2015, Shanghai had the highest in-degree, followed by Beijing, Shenzhen, Tianjin, and Guangzhou, indicating the presence of some “super cities” in China that attract labor. In addition, the top 20 cities are mainly from the Beijing–Tianjin–Hebei metropolitan area, the Yangtze River Delta metropolitan area, and the Guangdong–Hong Kong–Macao Greater Bay Area. The population continues to flow to first-tier and second-tier cities and regional center cities, showing a trend of urbanization and metropolitanization. The centrality of the top cities in terms of in-degree in 2015 has decreased compared to 2005, but other cities in the top 20 have seen an increase in in-degree centrality, indicating a more balanced distribution within core cities.

From the out-degree centrality results, it can be observed that in 2005, labor from cities with lower living conditions and lower levels of economic development tended to flow out. However, in 2015, the outflow of residents from first-tier cities became more pronounced. This may be due to the continuously rising cost of living, such as housing prices, in first-tier cities, leading to an increase in the out-degree centrality indicator for these cities. Labor from cities with lower levels of economic development tends to flow to regions with greater differences. However, labor does not only flow between cities with high differences. In cities with higher resource levels, the trend of strong collaboration becomes more evident.

4. Research Design

4.1. Econometric Model Specification

In classic literature assuming the relationship between economic activities and the environment, sustainability and green development are often regarded as functions of scale, technology, and structure [25,26]. Drawing from previous research [27], this paper extends the theoretical framework influencing GTFP by incorporating additional significant factors such as labor mobility network characteristics. The basic function is as follows:

$$GTFP=F(Scale,Technology,Structure,otherinfluceningfactors)$$

(1)

where $Sacle$ represents scale effects, reflecting the impact of economic activity scale on green productivity. This paper employs per capita GDP (PGDP) to characterize scale effects, a common practice in many studies. $Technology$ represents technological effects, reflecting the influence of technological progress on green productivity. Technological innovation and technology penetration are characterized using two aspects: the quantity of patent technology (PQ) and the number of internet users (TEL). $Structure$ represents structural effects, reflecting changes in economic structure. Energy consumption structure (ES) and industrial structure (IS) are used to measure structural effects. Among other influencing factors, network centrality is considered a key variable in this study. It is measured in two ways: out-degree centrality and in-degree centrality to distinguish different flow directions. Based on previous research, we also include levels of human capital (EDU), infrastructure (INF), and degree of openness (OP) as additional control variables. Based on the above analysis, the specific model can be described as:

$$\begin{gathered} {GTFP}_{i,t}={\alpha }_0+{\alpha }_1{Centrality}_{i,t-1}+{\alpha }_2{PGDP}_{i,t-1}+{\alpha }_3{FS}_{i,t-1}+{\alpha }_4{PQ}_{i,t-1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\alpha }_5{TEL}_{i,t-1}+{\alpha }_6{ES}_{i,t-1}+{\alpha }_7{IS}_{i,t-1}+{\alpha }_8{X}_{i,t-1}+{\epsilon }_{i,t-1} \end{gathered}$$

(2)

where $i$ represents the cross-sectional units involving 284 cities in China, $t$ represents the year, and $\epsilon$ is the random disturbance term. It is worth noting that, in order to address the issue of reverse causality and make the conclusions more robust, we regress both the core explanatory variables and control variables with a one-period lag, as the promotion of labor mobility network status in a given year may take some time to manifest its impact on GTFP. However, future GTFP cannot influence the current labor mobility network status in advance. The coefficient measures the impact of network centrality on GTFP and is the core parameter of interest in this study. If it remains significantly positive after controlling for a series of city-specific variables, it indicates that the improvement in labor mobility network status contributes to the increase in GTFP. Otherwise, the relationship is reversed. represents other factors that may affect the dependent variable and includes control variables consistent with the current study. To control for potential heteroscedasticity and serial correlation issues, this study adjusts the standard errors of all regression coefficients using heteroscedasticity adjustment and applies “clustering” at the firm level. Additionally, to control for the effects of macroeconomic changes over time and differences between regions, this study includes year and regional fixed effects in the regression model [28].

4.2. Measurement of Main Variables

4.2.1. Choice of Dependent Variable

Different from the traditional measurement of total factor productivity, GTFP takes into account the constraints of energy and environmental factors on economic development, in addition to minimizing inputs of labor, capital, and other production factors and maximizing economic output. This means that in addition to the traditional calculation of total factor productivity, we should incorporate non-desirable indicators such as energy consumption and environmental pollution [29]. Building upon existing research [30], we use the directional distance function of non-desirable outputs and the Green Malmquist–Luenberger index to measure GTFP. The indicators used to measure GTFP are as follows: we use the directional distance function of non-desirable outputs and the Globe-Malmquist–Luenberger (GML) index to measure green total factor productivity. Within a non-parametric framework, this paper constructs a non-angular, non-radial Malmquist Productivity Index (MPI) based on the foundation of an undesired output super-efficiency SBM (Slack-Based Measure) efficiency measurement model. The indicators used to measure green total factor productivity are as follows:

$$\begin{gathered} {GML}_0^{t,t+1}=\frac{{\rho }_0^{t+1}(x_0^{t+1},y_0^{g,t+1},y_0^{b,t+1})}{{\rho }_0^t(x_0^t,y_0^{g,t},y_0^{b,t})} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \left[\frac{{\rho }_0^g(x_0^{t+1},y_0^{g,t+1},y_0^{b,t+1})}{{\rho }_0^{t+1}(x_0^{t+1},y_0^{g,t+1},y_0^{b,t})}\times \frac{{\rho }_0^t(x_0^t,y_0^{g,t},y_0^{b,t})}{{\rho }_0^g(x_0^t,y_0^{g,t},y_0^{b,t})}\right] \end{gathered}$$

(3)

• In Equation (3), ${GML}_0^{t,t+1}$ measures the change in the green total factor productivity of cities from period $t$ to $t+1$. ${\rho }_0^t(x_0^t,y_0^{g,t},y_0^{b,t})$ and ${\rho }_0^{t+1}\left(x_0^{t+1},y_0^{g,t+1},y_0^{b,t+1}\right),$ respectively, represent the efficiency values of a city at periods $t$ and $t+1$; ${\rho }_0^g(x_0^{t+1},y_0^{g,t+1},y_0^{b,t+1})$ is the efficiency value based on the global production technology across all periods and the input–output values at time $t+1$; ${\rho }_0^g(x_0^t,y_0^{g,t},y_0^{b,t})$ is the efficiency value based on the global production technology across all periods and the input–output values at time $t$. $\frac{{\rho }_0^g(x_0^{t+1},y_0^{g,t+1},y_0^{b,t+1})}{{\rho }_0^{t+1}(x_0^{t+1},y_0^{g,t+1},y_0^{b,t})}$ reflects the proximity of the frontier at time t+1 to the global frontier, while $\frac{{\rho }_0^t(x_0^t,y_0^{g,t},y_0^{b,t})}{{\rho }_0^g(x_0^t,y_0^{g,t},y_0^{b,t})}$ reflects the proximity of the frontier at time t to the global frontier. If ${GML}_0^{t,t+1}=1$, it indicates that there has been no change in green total factor productivity. If ${GML}_0^{t,t+1}<1$, it signifies a regression in green total factor productivity. If ${GML}_0^{t,t+1}>1$, it indicates an improvement in green total factor productivity.
• Input indicators include labor input, capital input, and energy input. Labor input is measured by the number of employees in the city’s administrative area at the end of each year (in tens of thousands). Capital input is estimated using the perpetual inventory method, $k_{i,t}=k_{i,t-1}\left(1-{\delta }_{i,t}\right)+I_{i,t}$, with $k_{i,t}$ representing the capital stock of the city in year and ${\delta }_{i,t}$ representing the depreciation rate of the city $i$ in year $t$. $I_{i,t}$ represents the total fixed asset investment of the city $i$ in year $t$. All data are adjusted to the base year of 2000. Energy input: Due to the availability of data on energy consumption only for provinces and municipalities directly under the central government, and with only some prefecture-level cities providing energy consumption data, most cities only provide data on energy consumption by industrial enterprises above a certain scale and overall electricity and gas consumption for the city as a whole. To ensure comparability, this study uses the annual electricity consumption in the city’s administrative area (in ten thousand kilowatts) to measure energy input.
• In terms of output indicators, this study considers both the maximization of expected outputs such as economic development and green ecological benefits, as well as the constraints of undesired outputs such as carbon emissions and environmental pollution on economic development. Specifically, the expected output indicators are measured by the actual GDP (in CNY ten thousand) of each prefecture-level city calculated at constant prices in 2000 and the urban green coverage rate (%). The undesired outputs are measured by the industrial wastewater emissions (in ten thousand tons), industrial carbon dioxide emissions (in ten thousand tons), and industrial smoke emissions (in ten thousand tons) of each prefecture-level city. These indicators are then fitted into an environmental pollution composite index using the entropy method.

Based on the selected indicators, this study uses MaxDEA Pro to calculate the GML index for the selected 284 prefecture-level cities. Additionally, following the cumulative thinking, the green total factor productivity index is transformed into a cumulative productivity index based on the year 2000 and logarithmically transformed, which is then used as the dependent variable in the model. We compared the city-level green total factor productivity calculated from our dataset with the study by Zhou et al. [31]. While these numbers do not perfectly match, which is expected due to their different time frequencies and sources, the trends are nearly identical, with a correlation exceeding 85%.

4.2.2. Core Explanatory Variables

In order to comprehensively analyze the labor mobility characteristics in different regions and consider the complex interrelationships between regions, this study uses the in-degree and out-degree centrality indicators in the SNA method to measure the labor mobility network characteristics in each region. As mentioned earlier, a higher value indicates a stronger influence of the region in the global labor mobility network. A high in-degree centrality means that the region is in a central position for population inflow and has labor mobility relationships with more regions, attracting more people to move to the region. Conversely, a high out-degree centrality means that the region is in a central position for population outflow and has labor mobility relationships with more regions, leading to more people moving out of the region.

4.2.3. Control Variables

Labor mobility is usually non-random. This study collects city-level data from various sources to differentiate the impact of population migration on the labor market from concurrent regional factors, in order to avoid spurious correlations between labor inflow and labor market outcomes due to omitted variables [32,33,34]. The regional control variables mainly include the following:

• Per capita GDP (PGDP): PGDP is measured by the ratio of actual GDP to the total population of each prefecture-level city.
• Patent quantity (PQ): The patent data in this study are sourced from the National Intellectual Property Administration, including 5,649,241 domestic patent applications from 1985 to 2017. These data encompass detailed information for each patent, including applicant, location, application date, approval date, and International Patent Classification (IPC) code. The patents are aggregated by patent category (123 categories) and year at the city level, resulting in patent data for 284 prefecture-level cities between 2005 and 2015.
• Internet users (TEL): The improvement of urban technological levels facilitates the cross-regional and long-distance flow of factors such as labor and capital among cities, thereby promoting regional economic development. However, if urban technological advancements focus solely on hardware infrastructure rather than improving the soft environment, the increase in informatization may not necessarily enhance urban productivity. Hence, this study employs the number of internet users to represent technological penetration.
• Industrial structure (IS): The adjustment of urban industrial structure mainly involves the gradual transition from the primary industry to the tertiary industry. The larger the proportion of industries with higher production efficiency in a city, the higher the production efficiency, energy utilization efficiency, and environmental efficiency may be. The industrial structure is represented by the proportion of output value from the secondary industry and the tertiary industry.
• Human capital level (EDU): Considering the differences in human capital under different education levels, this study uses the average years of education per capita (EDU) to estimate the human capital level of cities. Assuming that primary education lasts for 6 years, junior high school education lasts for 9 years, high school education lasts for 12 years, and college education or above lasts for 16 years, the average years of education per capita in a city can be calculated as: Average years of education per capita = 6S1 + 9S2 + 12S3 + 16S4. Here, S1, S2, S3, and S4 represent the proportions of the population at each education level in the total population.
• Infrastructure (INF): The construction of urban infrastructure not only improves the operating environment for the economy and reduces transaction costs for businesses with the external environment but also accelerates the pace of transformation and upgrading of traditional industries, promoting regional economic growth. If the improvement of urban infrastructure only exists at the internal level of the city and cannot form a close network of connections with the external environment, the improvement of urban infrastructure cannot effectively enhance the efficiency level of the city. This study measures urban infrastructure using the per capita area of urban roads.
• Degree of openness (OP): Foreign direct investment not only influences the economic output of cities through industry linkages, technology spillovers, and management experience but also enhances the openness of cities by increasing the capital stock. Therefore, this study uses the proportion of annual actual foreign investment in the city’s GDP (converted based on the average exchange rate of the Chinese yuan over the years) as a control variable OP.

4.3. Data Sources and Descriptive Statistical Analysis

The variables of out-degree centrality, in-degree centrality, and average years of education per city were calculated using the 1% sample survey data from China in 2005, the 2010 China Population Census data, and the 1% sample survey data from China in 2015. In addition, the patent data for each city in this study are sourced from the National Intellectual Property Administration, while the remaining control variables measuring city characteristics are obtained from the “China City Statistical Yearbook” for each respective year. Descriptive statistics of the main variables are shown in

Table 3. Data description and descriptive statistical analysis.

Variable	Description	Mean	Median	Std.
gtfp	Green Total Factor Productivity	0.988	0.991	0.032
indegree	In-Degree Centrality	0.173	0.113	0.169
outdegree	Out-Degree Centrality	0.173	0.159	0.084
pgdp	the Gross Domestic Product divided by the total population of a city	3.074	4.327	1.649
pq	Number of Patent Applications for Inventions in the Entire City (in Ten Thousand)	1.291	0.286	3.764
tel	Number of Internet Users (in ten thousand households)	46.813	21.276	121.090
is	Share of Secondary Industry Output in GDP (%)	39.411	40.106	7.931
edu	Average Years of Education in Cities	9.475	9.398	3.141
inf	Per Capita Road Area in Cities (m2)	10.732	8.643	27.241
op	Actual Foreign Direct Investment as a Percentage of City’s Gross Domestic Product (GDP)	14.876	8.973	16.214

.

5. Empirical Results

5.1. Network Centrality and Green Total Factor Productivity

Table 4. Baseline regression.

	(1)	(2)	(3)	(4)
Indegree	0.046 ***	0.032 **
	(2.62)	(2.21)
Outdegree			0.058 **	0.053 *
			(2.09)	(1.63)
Pgdp		0.664 ***		0.396 ***
		(6.68)		(7.20)
Pq		0.259		0.298
		(0.37)		(0.28)
Tel		1.137 **		0.799 *
		(2.48)		(1.87)
Is		−0.056		−0.251
		(−1.48)		(−1.15)
Edu		0.560 ***		0.098
		(3.85)		(1.05)
Inf		0.111 ***		0.043 **
		(3.01)		(2.02)
Op		0.092		0.235
		(0.76)		(0.65)
Constant	1.077 ***	1.737 ***	2.127 ***	2.135 ***
	(7.83)	(6.02)	(4.05)	(3.11)
City fixed effect	Yes	Yes	Yes	Yes
Year fixed effect	Yes	Yes	Yes	Yes
Observation	852	852	852	852
R2	0.186	0.189	0.106	0.121

T-statistics in parentheses. *** p < 0.01, ** p < 0.05, * p < 0.1.

presents the static analysis of the relationship between network centrality (including in-degree centrality and out-degree centrality) and green total factor productivity. From models (1)–(4), it can be observed that the characteristics of labor flow networks have a significant impact on the green total factor productivity of a prefecture-level city. Being in a more central position in the network has a significant positive effect on the green total factor productivity of the region. The regression coefficient for in-degree is 0.032 and is significant at the 5% level, indicating that, holding other variables constant, a 1-percentage-point increase in the in-degree centrality of a city in China’s labor flow network is associated with a 0.032 increase in its green total factor productivity index. The regression coefficient for out-degree is 0.053 and is significant at the 10% level, indicating that, holding other variables constant, a 1-percentage-point increase in the out-degree centrality of a city in China’s labor flow network is associated with a 0.055 increase in its green total factor productivity index. The estimation results are consistent with expectations because, for a specific region, a higher network centrality implies a greater number of prefecture-level cities directly connected to the region and a higher volume of personnel exchanges among them. This means the region has more channels for technology and information learning. For cities with higher in-degree centrality, the inflow of labor factors drives the aggregation of other production factors to the region, which can not only enhance the overall production efficiency but also improve the overall energy utilization efficiency. In the post-industrialization development stage, the aggregation of labor and the allocation of other factor resources to high-efficiency regions can promote economic growth and improve green total factor productivity through scale effects and re-allocation effects. For cities with higher out-degree centrality, even if there is an outflow of labor, it also means that the region has more frequent capital and information exchanges with other regions, which helps to form a more environmentally friendly and greener development model, ultimately promoting the improvement of the region’s green total factor productivity.

5.2. Robustness Checks

To enhance the robustness of our baseline regression analysis and address potential endogeneity issues, we conducted a series of robustness checks to ensure more accurate conclusions.

Firstly, endogeneity issues. Directly examining the relationship between labor mobility networks among cities and GTFP may face endogeneity challenges. For instance, unobservable city characteristics could influence both the network formation due to labor mobility and GTFP. If other unobserved factors are at play, the direction of bias in OLS estimates becomes uncertain. To ensure robustness, we attempted to find instrumental variables for labor outflow rates and re-estimated the aforementioned econometric model using two-stage least squares (2SLS) estimation. A reasonable instrumental variable should be closely related to labor mobility networks while being uncorrelated with a set of observable variables. In our study, we chose the average centrality of geographically adjacent cities and the distance of each prefecture-level city from the coastline as our instrumental variables and conducted a two-stage least squares regression analysis. We selected geographic information from adjacent areas to construct instrumental variables because labor mobility in a city is influenced by labor flows from neighboring cities, which evidently do not directly affect local GTFP. The method of constructing distances from each area to the nearest coastline was inspired by the study of Nunn and Wantchekon [35], with data sourced from the National Basic Geographic Information Center. In reality, closer distances to the coastline facilitate personnel exchanges, making it easier to become the center of labor mobility networks. The closest distance of each area to the coastline is determined by geographic factors, reflecting the influence of geographical factors on GTFP and meeting the exogeneity condition of instrumental variables.

It is worth noting that, in terms of data features, the distance from the coastline as an inherent natural characteristic of sample cities is city cross-sectional data, while endogenous variables and dependent variables contain panel data with both city and time information. Therefore, following the approach used by Angrist and Krueger [36] in estimating the returns to education in the US labor market, we introduced the original variables and interaction terms between annual dummy variables as instrumental variables into the model. This approach overcomes the data dimension limitations of cross-sectional instrumental variables, with variations existing in both dimensions, while also fully reflecting the impact of different annual instrumental variables on endogenous variables.

Table 5. Robustness checks.

	2SLS				Tobit		Different Sample
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Indegree		0.054 ***			0.030 ***		0.015 ***
		(3.12)			(3.14)		(3.59)
Outdegree				0.067 **		0.028 **		0.019 *
				(2.12)		(2.08)		(1.86)
Iv1	1.326 **		0.474 ***
	(2.42)		(4.01)
Iv2	0.003 ***		0.006 ***
	(15.08)		(5.15)
Kleibergen–Paaprk Lm Statistic	8.626		16.588
Stock-Yogo10% Maximal Iv Size	7.39		8.21
Cragg-Donald Wald F Statistic	1347.340		35.349
Kleibergen–Paaprk Wald F Statistic	109.145		15.319
Constant	0.303 *	0.241	2.131 ***	2.048 ***	0.997 ***	0.984 ***	1.029 ***	1.008 ***
	(1.89)	(1.48)	(7.89)	(8.45)	(0.003)	(0.007)	(0.009)	(0.010)
Control variables	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
City fixed effect	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Year fixed effect	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Observation	852	852	852	852	852	852	852	852
R2	0.254	0.189	0.233	0.121			0.108	0.103

T-statistics in parentheses. *** p < 0.01, ** p < 0.05, * p < 0.1.

’s first four columns present the robustness test results using the instrumental variable approach, with columns (1) and (3) showing the first-stage regression results of two-stage least squares regression and columns (2) and (4) showing the second-stage regression results of two-stage least squares regression. In the first-stage estimation results, the estimated coefficients of the average centrality of geographically adjacent cities and the distance of cities from the coastline are both significantly positive, indicating that higher average centrality of geographically adjacent cities and closer distances from the coastline are associated with higher levels of city centrality. Regarding the effectiveness of instrumental variables, both the Kleibergen–Paaprk Wald F statistic and the Kleibergen–Paaprk LM statistic reject the null hypothesis of weak instrumental variables and inadequate instrumental variable identification. This ensures the validity of the instrumental variables used in our study. Therefore, even considering potential endogeneity issues, our conclusions remain robust.

Secondly, Tobit model estimation results. The dependent variable studied in this paper, GTFP, ranges from 0 to 2, making it a bounded variable. This could introduce bias in traditional mean effects estimation models. Therefore, drawing on the approach of Cassiman and Veugelers [37], this paper opts for re-estimation using the Tobit model. Robustness test results, presented in columns (5)–(6) of Table 5, indicate that the regression coefficients of the core explanatory variables pass the 5% confidence level, with their directions and magnitudes largely consistent with the baseline regression results. This suggests that the baseline regression results in this paper are robust.

Thirdly, we consider a different sample. To test the robustness and mitigate endogeneity concerns, we directly exclude cities with a high proportion of high-paying industries from the sample to examine whether the conclusions obtained in this chapter apply only to these specific cities or have similar effects on all cities [38]. We exclude the first-tier cities, Beijing and Shanghai, from the sample and re-estimate Equation (1). The results in columns (7)–(8) of Table 5 show similar results to those in Table 4, with significant positive regression coefficients, indicating that an increase in the centrality of labor inflows or outflows in a region will enhance its GTFP.

5.3. Mechanism Examination

According to the empirical results in Table 4, the regression coefficient of patent quantity (PQ) on GTFP is positive but not significant. This could be due to the fact that the impact of technological innovation on GTFP requires some time to materialize, and the sample period in this paper only covers the years 2005 to 2015, during which this impact may not have been evident. Additionally, industrial structure (IS) does not exhibit the expected positive effect on GTFP, possibly because of the current stage of China’s economy, which dictates a reliance on the secondary sector for economic growth. Simply relying on changing the industrial structure to enhance green total factor productivity would thus be a slow process. Therefore, this paper only analyzes the pathway of technological diffusion effects.

The results in

Table 6. Mechanism testing of technological diffusion effects.

	(1)	(2)	(3)	(4)
	FE	2SLS	FE	2SLS
Indegree	0.028	0.030
	(0.98)	(0.89)
Tel × Indegree	0.073 *	0.087 **
	(1.90)	(1.99)
Outdegree			0.033	0.033
			(0.17)	(0.17)
Tel × Outdegree			0.076 *	0.251 *
			(1.78)	(1.69)
Tel	0.035	0.036	0.008	0.008
	(0.87)	(0.87)	(0.19)	(0.19)
Constant	1.737 ***	0.241	2.135 ***	2.048 ***
	(6.02)	(1.48)	(3.11)	(8.45)
Control variables	Yes	Yes	Yes	Yes
City fixed effect	Yes	Yes	Yes	Yes
Year fixed effect	Yes	Yes	Yes	Yes
Observation	852	852	852	852
R2	0.190	0.190	0.121	0.121

T-statistics in parentheses. *** p < 0.01, ** p < 0.05, * p < 0.1.

indicate that the interaction terms between in-degree centrality and out-degree centrality with the number of internet users are significant at least at the 10% level. This suggests that cities located in central positions within labor mobility networks facilitate the diffusion of technology, thereby promoting GTFP. Overall, the technological diffusion effect outweighs other pathways, indicating that even if cities in China cannot achieve GTFP enhancement through sustained technological innovation and optimal resource allocation, technological diffusion can still play a crucial role in promoting GTFP.

5.4. Heterogeneity Analysis

First, we examine the differences in the impact of labor mobility on GTFP across different regions in China. We divide China into four regions: east, central, west, and northeast, and estimate the regression equation separately for each region. The results are presented in

Table 7. Heterogeneity analysis.

	Indegree		Outdegree
	Coefficient	Std.	Coefficient	Std.
Part A
Eastern	0.079 ***	(0.023)	0.055 *	(0.030)
Central	0.028	(0.026)	0.041	(0.037)
Western	0.066	(0.150)	0.037	(0.063)
Northeastern	0.019	(0.072)	0.005	(0.029)
Part B
Tightened	0.060 ***	(0.020)	0.041	(0.032)
Lenient	0.063 ***	(0.022)	0.105 ***	(0.028)

*** p < 0.01, * p < 0.1.

. The results indicate that the regression coefficients for the eastern regions are significant and have larger absolute values. This is primarily because the eastern regions inherently have a higher quality of talent, and the inflow and outflow of labor can drive more resources and technological communication and exchange. The synergistic effect of labor factors and other factors enhances the economies of scale, thereby improving the efficiency of resource allocation. Therefore, in the eastern regions, labor mobility plays a more significant role in promoting green total factor productivity.

In line with the latest outline for new urbanization construction in our country, cities with an urban permanent population of less than 3 million have essentially lifted restrictions on household registration. Thus, this paper defines cities with an urban permanent population exceeding 3 million as large cities with relatively difficult household registration, whereas cities with a population below 3 million are considered small cities with relatively easy household registration. Through a sub-sample analysis based on the ease of city registration, the results shown in Table 7 demonstrate that in places with fewer registration restrictions, improvements in the centrality of labor inflow and outflow more noticeably enhance green total factor productivity. The main reason is that in areas with fewer registration restrictions, reduced migration costs facilitate smoother personnel exchanges, driving more convenient exchanges of capital, technology, and other production factors, which is more conducive to the region’s green development.

6. Conclusions

This paper employs social network analysis methods, utilizing data from the 2005 China 1% Population Sample Survey, the 2010 Census data, and bilateral labor flow data between 284 prefecture-level cities in China from the 2015 China 1% Population Sample Survey database to construct the labor flow network of China. It examines the overall layout of China’s labor flow network and the characteristics of each prefecture-level city within the network. The study finds that between 2005 and 2015, the density of China’s labor flow network exhibited an overall increasing trend, with deeper connections between prefecture-level cities. The network displays a clear pattern of “concentrated inflows” and “dispersed outflows”, fostering a network of cities linked by resources and economic power, thus strengthening the pattern of “strong collaboration” in labor mobility. Building upon this analysis, considering the impact of regional labor flow on environmental issues such as carbon emissions for producers and consumers, this paper empirically tests the influence of regional labor flow network characteristics on green total factor productivity (GTFP). For specific regions, the characteristics of the labor flow network have a robust and significant impact on their GTFP. Specifically, an increase in network centrality contributes to enhancing the region’s control over core resources in the labor network, thereby promoting an increase in GTFP. Whether through an increase in out-degree or in-degree centrality, both contribute to maintaining and advancing high-quality green economic development in the region. The paper also examines the technological diffusion effect channel driving the relationship between network centrality and GTFP. The empirical results suggest that cities situated in central positions within the labor flow network are more likely to obtain valuable funds and information from the network, aiding in making more efficient decisions and thus achieving an increase in GTFP.

The research findings of this paper hold both academic and policy significance. The relationship between urban patterns and the environment remains contentious in the literature, and this paper deepens our understanding of this issue. On the policy front, discussing the environmental outcomes of internal urban population migration can help governments and urban planners optimize policies. People migrating to larger cities often aspire to improve their living standards, which typically entail higher energy consumption and increased carbon emissions. However, hindering people’s pursuit of a better life is undesirable. More importantly, the exchange and dissemination of information and technology facilitated by human mobility ultimately led to an increase in green total factor productivity. This is crucial because it allows us to improve energy efficiency by optimizing urban patterns and achieving green development, especially in destination cities for immigrants rather than discouraging those seeking higher income and better living conditions.

This paper could be expanded in several areas. Firstly, focusing on the labor flow network and covering the period from 2005 to 2015, the study may lack a comprehensive understanding of the effects of labor mobility networks in the current flourishing digital economy. Future research could combine the impact of labor flow networks on GTFP in the context of the digital economy to provide a more accurate explanation of the current situation. Additionally, collecting more years of panel data would facilitate a more in-depth analysis of the nonlinear relationship between labor flow network characteristics and GTFP. Secondly, the locations of labor mobility are often the result of individuals’ self-selection, which may lead to omitted variable bias in the conclusions of this paper, posing a significant challenge in addressing endogeneity issues. Future research could collect more micro-level sample data to identify cleaner causal effects by examining the relationship between changes in high-level network structures and GTFP. Alternatively, utilizing China’s household registration system as a quasi-experiment and employing more advanced econometric methods could better address endogeneity issues, further enhancing the significance of this paper’s research.

This paper can be extended into two significant dimensions. Firstly, while focusing on the labor mobility network over the sample period of 2005–2015, the influence of the digital economy on labor mobility is not accounted for, potentially rendering the results less timely. The world is currently in the midst of a digital technology boom [39,40,41], future research could integrate the effects of labor mobility networks under the digital economy on GTFP, offering more accurate insights for the present context. Secondly, the destinations of labor mobility often result from personal choice, leading to potential omitted variable bias that poses a considerable challenge to addressing endogeneity issues [42,43]. Future studies could explore more comprehensive datasets to examine the causal relationship between labor mobility and GTFP through changes in high-level network structures, thereby enhancing the significance of this research.