Data-Driven Algorithms for Two-Location Inventory Systems

Abstract

In this paper, we consider a multiperiod, two-location inventory system with unknown demand distributions and perishable products. Products can be transshipped from the location with excess inventory to the other with excess demand to better fulfill customer demand. The demand distributions are assumed to follow a family of parametric distributions and can only be learned on the fly. To address the challenge, we propose a data-driven inventory management algorithm called DD2LI that achieves a good performance in terms of regret. This algorithm, DD2LI, employs maximum likelihood estimation to approximate the unknown parameter and determines the order quantity based on these estimations. In addition, we emphasize a key assumption that tightens regret bound. Finally, we test the effectiveness of our proposed algorithm by conducting numerical experiments for two scenarios.

1. Introduction

Inventory management research is a significant branch of operations research that addresses the challenges businesses face in meeting customer demand while minimizing costs associated with excess and insufficient inventory. The traditional newsvendor model has long been a cornerstone of inventory management theory, providing a framework for single-location inventory decisions under uncertainty. However, in today’s globalized and interconnected business environment, companies often operate across multiple locations, each with its own unique demand dynamics and inventory [1]. For instance, a clothing store chain may operate multiple outlets in a city [2]. In this way, the store chain can carry out transshipment if one store has excess inventory and another is experiencing a stockout [3]. In such a system, efficient management of inventory across multiple locations is vital to maintaining customer satisfaction and operational efficiency.

The current literature on inventory management and transshipment primarily presupposes a known demand distribution, hence the inventory managers can derive optimal inventory levels and transshipment strategies [3,4]. Yet in practice, the specific form of the demand distribution is generally unknown, and inventory decisions must be made based on limited demand samples. This serves the starting point for research on data-driven inventory management strategies that can adapt to unknown demand patterns. When demand distribution is unknown a priori, inventory managers must learn the demand on the fly and make inventory decisions by past demand data [5,6]. Despite the prevalence of data-driven inventory management studies, current studies mainly focus on single-location inventory decisions.

Given the aforementioned challenges, this paper considers a multiperiod, two-location inventory system with perishable products. The firm can incur a cost to transship excess inventory in one location to the other experiencing stockout. The model with full demand information has been explored in [3,4]. Our work differs from previous research by assuming the demand distributions are unknown and by proposing data-drive algorithms tailored for the two-location inventory system. In this paper, the demand distributions in the two locations are assumed to follow a parametric family of distributions and are unknown a priori. Inventory decisions can only be made by past demand data. The objective of our paper is to design an adaptive algorithm for two-location inventory systems and to establish the theoretical performance of the algorithm.

Next, we summarize the main results of our work. First, we propose a parametric data-driven algorithm called DD2LI, specifically designed for the two-location inventory system with transshipment. This algorithm utilizes past demand data, employs maximum likelihood estimation to approximate the unknown demand parameters, and determines the order quantity based on the estimations. Second, we characterize the regret bound of our proposed algorithm based on asymptotics of the maximum likelihood estimator. The regret bound of our algorithm is $O\left(\sqrt{T}\right)$ and can be strengthened to $O(logT)$ with an additional assumption that the optimal order quantity is Lipschitz continuous with respect to parameters. Finally, the proved regret bound is validated through numerical experiments.

There are two main contributions in this paper. First, we design adaptive inventory control algorithms for two-location inventory systems with unknown demand distributions. This algorithm holds significant practical value, given the common scenario of unknown demand in real-world applications. We also hope that our study will offer valuable insights to store managers tasked with inventory management across multiple locations. Second, our paper is among the first to explore data-driven inventory management strategies for problems with more than one location. The novelty of our work lies in the performance analysis of DD2LI, where we bound the difference between expected cost functions using demand parameters. We provide proof that our proposed algorithm achieves an optimal convergence rate.

The remainder of this paper is organized as follows. The literature is reviewed in Section 2. In Section 3, we outline the classic standard newsvendor model and the two-location inventory system with transshipment. In Section 4, we present the formulation of a multiperiod, two-location inventory system. In Section 5, we propose a data-driven algorithm called DD2LI, and we present its performance analysis in the section Performance Analysis. In Section 6, we present results of numerical experiments under two scenarios. We conclude our paper in Section 7.

2. Literature Review

We review the relevant literature from two aspects: two-location inventory systems with transshipment and data-driven inventory management.

2.1. Two-Location Inventory Systems with Transshipment

First, our paper relates to the literature on two-location inventory systems with transshipment. Ref. [7] first introduced the concept of inventory sharing across multiple locations. It is demonstrated that, when the demand at each location follows an independent normal distribution, inventory sharing can reduce the system’s total cost to $O\left(1/\sqrt{n}\right)$, where n is the number of locations, without considering transportation costs. Ref. [7] serves as a foundation for expanding the standard newsvendor model to incorporate multilocation extensions. An important research stream is the study of inventory transshipment. For a comprehensive review, please refer to [8]. When multiple locations can adjust inventory through transshipment, Ref. [9] studied a centralized transshipment network of n newsvendors, establishing the optimality of a base-stock policy. Refs. [10,11,12,13] conducted research on optimal strategies for two-location production and sales systems, considering various settings and using different demand and supply models. Ref. [14] examined single-warehouse multilocation inventory systems and proved that there are five possible optimal strategies. Ref. [4] considered the impact of the manufacturer’s pricing on multi-retailer systems, finding that the manufacturer’s profit is significantly influenced by whether the manufacturer is the price setter or price taker in the presence of retailer inventory sharing. Recent literature has examined general multilocation systems. Ref. [15] investigated multi-warehouse, multi-store systems with no external replenishment, designing asymptotically optimal policy via Lagrangian relaxation. Ref. [16] applied distributionally robust optimization to analyze a multilocation newsvendor network with demand ambiguity. The authors applied a moment-based uncertainty set and derived inventory levels that minimize the worst-case expected cost. Ref. [17] studied a multilocation inventory system with an additive or multiplicative random yield. They found the comparison between centralization and decentralization hinges significantly on demand uncertainty.

Another important stream explores the strategic behavior of decentralized newsvendors. Ref. [3] investigated the behavior of two newsvendors maximizing profits through mutual transshipment, deriving equilibrium order quantities and transshipment prices. Ref. [18] explored the impact of demand information asymmetry and designed an optimal information coordination mechanism. Ref. [19] developed a two-stage game model to examine the inventory and end-of-season transshipment decisions between competing retailers. Ref. [20] examined the impact of inventory transshipment network structures on transshipment equilibria. Additionally, from a behavioral perspective, Ref. [21] studied the transshipment equilibrium between bounded rational newsvendors. Ref. [22] found that overconfidence could undermine the benefits brought by transshipment. Ref. [23] discovered from the practices of procurement managers that they tend to order less when inventory sharing is involved. Based on this observation, the authors in [23] constructed a behavioral model to explain this phenomenon.

The existing literature on inventory transshipment primarily assumes that the underlying demand distribution is known. We complement this line of research by developing data-driven inventory control strategies for a two-location inventory system with transshipment when the demand distribution is unknown a priori.

2.2. Data-Driven Inventory Management

Our work is also related to data-driven inventory management, particularly focusing on the parametric stream. The data-driven research on inventory management can primarily be categorized into two parts: one assumes that the demand distribution falls within a specific parametric family, while the other approach does not make such an assumption. Our work belongs to the former category. Early studies in this category are mainly based on Bayesian dynamic programming. Ref. [24] assumed that the demand distribution was generated from a certain parametric family with unknown parameters, but the posterior distribution of the parameters could be obtained from demand samples, thereby modeling inventory decisions as a Bayesian Markov decision process. Refs. [25,26] examined cases where the demand distribution follows a specific parametric family. Ref. [26] provides explicit solutions for inventory control strategies when the demand distribution follows the Weibull distribution. Ref. [27] studied nonstationary demand process. Nevertheless, methods based on Bayesian Markov decision processes only guarantee the convergence of the algorithm, providing no performance analysis compared to full information benchmarks. The methods’ performances are solely described through limited numerical experiments, offering only a partial understanding of their effectiveness.

Recent research on parametric methods utilizes maximum likelihood estimation (MLE) and concentration inequalities to obtain the regret bound. Ref. [5] studied a joint pricing and inventory management problem for perishable products with changing demand distributions. The authors in [5] considered that the random error in the demand distribution follows an exponential family distribution and then used the maximum likelihood estimation to estimate the parameters of the exponential family distribution. Refs. [28,29] investigated joint pricing and inventory management with limited price adjustments and parametric demand. Ref. [29] provided the concentration properties of the maximum likelihood estimator for censored demand. In addition, there are other research studies that employ different underlying methods. Ref. [30] studied the network revenue management problem, assuming a parameterized prior distribution for the demand. They designed an algorithm based on Thompson sampling by calculating the Bayesian posterior distribution from demand samples. Ref. [31] introduced operational statistics, which integrate demand estimation and inventory optimization.

Contrary to existing studies that mainly investigate single-location inventory problems, our work contributes to the literature by proposing a parametric learning algorithm tailored for two-location inventory systems. Moreover, we have successfully established the performance of our algorithm and validated its effectiveness through numerical experiments.

3. Preliminaries

3.1. The Standard Newsvendor Model

This section provides a review of the setup and solution to the standard newsvendor model. For a more comprehensive review of the newsvendor model, readers may refer to [32,33].

The newsvendor model assumes that the demand distribution for a product is stochastic, represented by the random variable D. At the beginning of the period, the risk-neutral newsvendor must decide on the order quantity y. The product has a fixed unit retail price of p, a unit purchase cost of $c(\mathrm{with}p>c)$, and, for simplicity, the salvage cost is normalized to zero.

For a real number x, let $x^{+}$ represent $max\{x,0\}$. The expected profit of the newsvendor, denoted as $\Pi \left(y\right)$, is a function of the order quantity y. It is defined as follows:

$$\Pi \left(y\right)=p\mathbb{E}min\{y,D\}-cy.$$

When D is a continuous random variable, $\Pi$ is differentiable. Setting the derivative of $\Pi$ to zero, it can be found that the optimal order quantity $y^{*}$ satisfies the equation

$$F\left(y^{*}\right)=\frac{p-c}{p},$$

which shows that the optimal order quantity is the $(p-c)/p$ quantile of the demand distribution.

3.2. Two-Location Inventory System with Transshipment

To fulfill demand efficiently and maximize profits, a firm operating two outlets can carry out transshipments whenever a stockout occurs in one location, while excess stock is available at the other location.

We follow the framework established by [4]. Consider two retailers designated as i and j (where $j=3-i$). The two retailers are operated by a single firm. In the event of a stockout at one location, excess demand can be met through transshipment if another location has surplus inventory. We represent the random demand in the two locations as $D_1$ and $D_2$. It is assumed that the demands are continuous random variables, each characterized by differentiable cumulative distribution functions $F_1$ and $F_2$, as well as continuous probability density functions $f_1$ and $f_2$.

A central planner decides the order quantity $y_1$ and $y_2$ for the two locations. The product has a unit price p and a unit purchase $c(\mathrm{with}p>c)$, and transshipment can be carried out at a cost of $\tau$.

The transshipment quantity between the two retailers is the minimum of excess demand and demand shortage. It can be expressed as $min\{{(D_1-y_1)}^{+}+{(D_2-y_2)}^{+},{(y_1-D_1)}^{+}+{(y_2-D_2)}^{+}\}$.

The central planner aims to maximize the per-period expected profit:

$$\begin{array}{cc}\hfill Q(y_1,y_2)& =\mathbb{E}\left[p(min\{D_1,y_1\}+min\{D_2,y_2\})\right]-c(y_1+y_2)\hfill \\ \hfill & +\mathbb{E}[(p-\tau )min\{{(D_1-y_1)}^{+}+{(D_2-y_2)}^{+},{(y_1-D_1)}^{+}+{(y_2-D_2)}^{+}\}]\hfill \\ \hfill & =-\mathbb{E}\left\{(p-c-\tau ){(D_1+D_2-y_1-y_2)}^{+}+\tau [{(D_1-y_1)}^{+}+{(D_2-y_2)}^{+}]\right\}\hfill \\ \hfill & +(p-c)\mathbb{E}[D_1+D_2].\hfill \end{array}$$

(1)

The expected profit comprises three components: the expected revenue generated from direct sales at both locations, minus the associated costs, and the additional revenue obtained through transshipment.

The equality (1) follows from the observation that

$$\begin{array}{l}min\{{(D_1-y_1)}^{+}+{(D_2-y_2)}^{+},{(y_1-D_1)}^{+}+{(y_2-D_2)}^{+}\}\hfill \\ =min\{D_1+D_2,y_1+y_2\}-(min\{D_1,y_1\}+min\{D_2,y_2\}),\hfill \end{array}$$

and the fact that $min\{a,b\}=a-{(a-b)}^{+}$ and $a=b-{(b-a)}^{+}+{(a-b)}^{+}$.

Taking partial derivatives of Q with respect to $y_1,y_2$, we obtain

$$\begin{array}{cc}\hfill \frac{\partial Q}{\partial y_1}& =p-c-(p-c-\tau )F_{12}(y_1+y_2)-\tau F_1\left(y_1\right),\hfill \\ \hfill \frac{\partial Q}{\partial y_2}& =p-c-(p-c-\tau )F_{12}(y_1+y_2)-\tau F_2\left(y_2\right)\hfill \end{array}$$

and

$${\nabla }^{2}Q=\left[\begin{array}{cc}-(p-c-\tau )f_{12}(y_1+y_2)-\tau f_1\left(y_1\right)& -(p-c-\tau )f_{12}(y_1+y_2)\\ -(p-c-\tau )f_{12}(y_1+y_2)& -(p-c-\tau )f_{12}(y_1+y_2)-\tau f_2\left(y_2\right)\end{array}\right],$$

where and $F_{12},f_{12}$ represent the distribution function and probability density function of $D_1+D_2$, respectively.

Following the analysis in [4,9], we claim that $Q(y_1,y_2)$ is jointly concave in $(y_1,y_2)$, and the profit-maximizing central planner chooses optimal order quantity $(y_1^{*},y_2^{*})$ satisfying the first order condition if the distributions of $D_1$ and $D_2$ are known:

$$\frac{\partial Q}{\partial y_1}(y_1^{*},y_2^{*})=0,\frac{\partial Q}{\partial y_2}(y_1^{*},y_2^{*})=0.$$

4. Problem Formulation

In this section, we consider a T-period two-location inventory system with parametric demand distributions.

For each period $t=1,2,\cdots ,T$, we denote $D_t^1,D_t^2$ as the demand distributions for the two locations and $d_t^1,d_t^2$ as their realizations. For ease of exposition, we introduce the random vector ${\mathit{D}}_t=(D_t^1,D_t^2)$ and its realization ${\mathit{d}}_t=(d_t^1,d_t^2)$. Specifically, we assume $\mathit{D}$ is parameterized by $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^k$, where $\Theta$ is a compact subset of ${\mathbb{R}}^k$ and represents the domain of $\mathit{\theta }$. We denote this parameterized demand distribution as $\mathit{D}(\mathit{\theta })$ and its corresponding probability density function as $f(\mathit{d};\mathit{\theta })$.

We make the following assumptions about the demand distributions.

Assumption 1.

The random vector ${\mathit{D}}_t$ is independently and identically distributed (i.i.d.) across time period t.

Assumption 2.

The family of distributions $\left\{f\right(\mathit{d};\mathit{\theta }):\mathit{\theta }\in \Theta )\}$ is identifiable: the probability function $f(\mathit{d};{\mathit{\theta }}_1)\ne f(\mathit{d};{\mathit{\theta }}_2)$ for ${\mathit{\theta }}_1\ne {\mathit{\theta }}_2$.

Assumption 3.

The Fisher information matrix $I(\mathit{\theta })$ is bounded and positive definite. $I(\mathit{\theta })$ is defined by

$${\left[I(\mathit{\theta })\right]}_{ij}=\mathbb{E}\left[-\frac{{\partial }^2}{\partial {\mathit{\theta }}_i\partial {\mathit{\theta }}_j}log{\mathcal{L}}^{\mathit{\theta }}\left(\mathit{D}\right)\right],$$

where ${\mathcal{L}}^{\mathit{\theta }}\left(\mathit{D}\right)$ is the likelihood function.

Assumption 1 assumes the demand process is stationary. This assumption is common in inventory literature [6,34,35]. Assumption 2 assumes the family of parametric demand distributions under consideration is identifiable, ensuring that each parameter vector uniquely determines the corresponding probability distribution. Identifiability is an important concept in mathematical statistics, and it has been extensively employed in the literature [36]. Assumption 3 ensures the convergence of the maximum likelihood estimator (MLE). Notably, exponential family distributions inherently satisfy both Assumptions 2 and 3. Consequently, the analysis presented in our paper applies to a wide range of common parametric distribution families.

At the beginning of each period t, the central planner decides the order quantities ${\mathit{y}}_t=(y_t^1,y_t^2)$ for both outlets. The central planner has no knowledge of the true underlying demand distribution a priori but can rely on historical demand data and make adaptive inventory decisions based on the available information.

In this work, we consider only perishable products, implying there are no inventory carryovers across periods. Therefore, in each period t, the central planner collects the profit $(p-c-\tau ){(d_t^1+d_t^2-y_1-y_t^2)}^{+}+\tau [{(d_t^1-y_t^1)}^{+}+{(d_t^2-y_t^2)}^{+}]+(p-c)(d_t^1+d_t^2)$. We define $Q({\mathit{y}}_t,\mathit{\theta })$ as the per-period expected profit function when the order quantity is ${\mathit{y}}_t$ and when the demand parameter is $\mathit{\theta }$:

$$\begin{array}{cc}\hfill Q({\mathit{y}}_t,\mathit{\theta })& =-{\mathbb{E}}_{\mathit{D}\sim \mathit{D}(\mathit{\theta })}\left\{(p-c-\tau ){(D_t^1+D_t^2-y_t^1-y_t^2)}^{+}+\tau [{(D_t^1-y_t^1)}^{+}+{(D_t^2-y_t^2)}^{+}]\right\}\hfill \\ \hfill & +(p-c)\mathbb{E}[D_t^1+D_t^2].\hfill \end{array}$$

(2)

Let $\{{\mathcal{H}}_t:t\ge 0\}$ represent the sequence of filtrations generated by demand data and decisions accumulated up to time t. Precisely, ${\mathcal{H}}_t$ is defined as the sigma algebra $\sigma ({\mathit{y}}_k,{\mathit{d}}_k:k=1,2,\cdots ,t)$ with ${\mathcal{H}}_0=\varnothing$. A feasible policy $\varphi$ is a sequence of functions ${\mathit{y}}_t=\varphi \left({\mathcal{H}}_{t-1}\right)$, which maps the historical information to current inventory decisions.

According to the analysis in Section 3.2, if the underlying demand distribution is known, then there exists an order quantity ${\mathit{y}}^{*}$ that maximizes the per-period profit, i.e., ${\mathit{y}}^{*}=\underset{\mathit{y}}{\arg \max }Q(\mathit{y},\mathit{\theta })$. In the system with perishable products, the optimal policy is a myopic policy ${\varphi }^{*}$ that sets the order quantity as ${\mathit{y}}^{*}=(y_1^{*},y_2^{*})$. We refer to ${\mathit{y}}^{*}$ as the clairvoyant optimal solution and ${\varphi }^{*}$ as the clairvoyant optimal policy.

To measure the performance of data-driven policy $\varphi$, we use regret as the criterion, which is defined as the expected total profit loss incurred by $\varphi$ when compared to the clairvoyant optimal policy ${\varphi }^{*}$:

$$R_T\left(\varphi \right)=Q({\mathit{y}}^{*},\mathit{\theta })-\mathbb{E}\left[\sum _{t=1}^{T}Q({\mathit{y}}_t,\mathit{\theta })\right].$$

(3)

Regret is a widely adopted metric in the literature on data-driven inventory management [6,29,37]. The metric quantifies the reduced profit caused by a lack of demand information. A lower regret value indicates a more effective policy. Thus, the central planner’s goal is to devise an algorithm that minimizes regret.

Finally, we make the following assumptions about the problem.

Assumption 4.

The clairvoyant optimal order quantity ${\mathit{y}}^{*}$ is upper-bounded by $M>0$: $y_1^{*}$, $y_2^{*}\le M$.

Assumption 5.

The profit function $Q(\mathit{y},\mathit{\theta })$ is Lipschitz continuous with respect to θ: there exists a constant $L_1>0$ such that $|Q(\mathit{y},{\mathit{\theta }}_1)-Q(\mathit{y},{\mathit{\theta }}_2)|\le L_1{\parallel {\mathit{\theta }}_1-{\mathit{\theta }}_2\parallel }_2$ for ${\mathit{\theta }}_1,{\mathit{\theta }}_2\in \Theta$.

Assumption 6.

${\mathit{y}}^{*}(\mathit{\theta })$ is Lipschitz continuous with respect to θ: there exists a constant $L_2>0$ such that $\parallel {\mathit{y}}^{*}\left({\mathit{\theta }}_1\right)-{\mathit{y}}^{*}\left({\mathit{\theta }}_2\right){\parallel }_2\le L_2{\parallel {\mathit{\theta }}_1-{\mathit{\theta }}_2\parallel }_2$ for ${\mathit{\theta }}_1,{\mathit{\theta }}_2\in \Theta$, where ${\mathit{y}}^{*}(\mathit{\theta })$ is the optimal order quantity given the demand parameter θ.

Assumption 4 is mild. It claims the clairvoyant optimal order quantity is upper-bounded, which can be met with common demand distributions. This assumption facilitates our theoretical analysis. Assumption 5 assumes that the per-period profit function exhibits Lipschitz continuity with respect to demand parameters. This assumption suggests that an accurate estimation of the unknown demand parameter can lead to a close approximation of the actual per-period profit function. Assumption 6 assumes the optimal order quantity is Lipschitz continuous with respect to demand parameters. This assumption implies that minor changes in the parameter will not result in significant variations in the optimal order quantity. Similar assumptions can be found in [5,29].

While Assumption 6 is not an absolute necessity for our algorithm, it plays a pivotal rule in improving the regret bound. We remark that, although Assumption 6 is generally satisfied in most situations, there exist degenerate cases where it may not hold true by the following example.

Example 1.

Consider a two-location system where one location’s demand is equal to zero and where the demand distribution in the other location is a Bernoulli distribution with a cumulative distribution function (CDF)

$$F\left(0\right)=(p-c)/p+\theta ,F\left(1\right)=1,$$

where θ is the parameter under consideration. For a small enough $ϵ>0$, the slight change in θ from $\theta =-ϵ$ to $\theta =ϵ$ will lead to a shift in its optimal order quantity, from 1 to 0.

5. Data-Driven Inventory Control Algorithms

Without any knowledge of the true underlying distribution of ${\mathit{D}}_t$ a priori, we aim to find a provably good, adaptive, data-driven inventory control policy that makes the total expected system profits close to the optimal strategy. In this section, we introduce the data-driven algorithm DD2LI (Data-Driven Two-Location Inventory Management Algorithm) and prove its theoretical performance.

Detailed steps of DD2LI are presented below.

DD2LI: Data-Driven Two-Location Inventory Management Algorithm

Step 0. 

(Initialization.) In period $t=1$, order an initial quantity ${\mathit{y}}_1=\mathbf{0}$ or select any other permissible value. Collect demand ${\mathit{d}}_1$ and initialize the demand dataset $S=\left\{{\mathit{d}}_1\right\}$ to be the available demand data up to decision time.

For each period $t=2,3,\cdots ,T$, repeat the following steps:

Step 1. 

(Maximum Likelihood Estimation.) Given the past demand dataset S, compute the maximum likelihood estimation of parameter $\mathit{\theta }$:

$${\displaystyle {\widehat{\mathit{\theta }}}_{t-1}=\underset{\mathit{\theta }\in \Theta }{\arg \max }\sum _{i=1}^{t-1}logf({\mathit{d}}_i;\mathit{\theta }).}$$

(4)

Step 2. 

(Order Quantity Optimization.) Using the estimated parameter ${\widehat{\mathit{\theta }}}_{t-1}$ from Step 1, compute ${\mathit{y}}_t=\underset{\mathit{y}}{\arg \max }Q(\mathit{y},{\widehat{\mathit{\theta }}}_{t-1})$, and order ${\mathit{y}}_t$ for the current period t.

Step 3. 

(Demand Data Update.) Observe the realized demand ${\mathit{d}}_t$, and update the demand dataset S by adding the new data point: $S\leftarrow S\cup \left\{{\mathit{d}}_t\right\}$.

Throughout the algorithm, we maintain a set containing past demand data that can be used to make adaptive inventory decisions. In Step 1, given the available demand data, we compute the MLE of the unknown demand parameter constrained on the compact parameter set $\Theta$. In Step 2, we use the MLE estimator to obtain an empirically optimal order quantity and implement it. Lastly, in Step 3, we update the demand dataset.

Performance Analysis

In this subsection, we analyze the performance of our proposed algorithm. To facilitate our analysis, we initially introduce several lemmas that serve as useful tools in our investigation.

Lemma 1 is the direct result of Theorem 36.3 in [36].

Lemma 1.

Defining ${\check{\mathit{\theta }}}_t$ as the unconstrained maximum likelihood estimator given demand data $\{{\mathit{d}}_1,{\mathit{d}}_2,\cdots ,{\mathit{d}}_t\}$:

$${\displaystyle {\check{\mathit{\theta }}}_t=\underset{\mathit{\theta }}{\arg \max }\sum _{i=1}^{t}logf({\mathit{d}}_i;\mathit{\theta }),}$$

then there exists the positive constant $K_1,K_2>0$, such that, for $ϵ>0$,

$$\mathbb{P}(\sqrt{t}\parallel {\check{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2⩾ϵ)\le K_1{e}^{-K_2{ϵ}^2}.$$

(5)

It is well-known in mathematical statistics that maximum likelihood estimators are asymptotically normal under proper conditions. Additionally, Lemma 1 provides a further concentration inequality pertaining to MLE, which plays a vital role in performance analysis.

Corollary 1.

For $ϵ>0$, the projection onto Θ of the maximum likelihood estimator ${\widehat{\mathit{\theta }}}_t$ defined in (4) satisfies

$$\mathbb{P}(\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2\ge ϵ)\le K_1{e}^{-t{K}_2{ϵ}^2}.$$

Proof. 

Note $\parallel {\check{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2\ge \parallel {\widehat{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2\Rightarrow \mathbb{P}(\parallel {\widehat{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2\ge ϵ)\le \mathbb{P}(\parallel {\check{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2\ge ϵ)$. Replacing $ϵ$ with $\sqrt{t}ϵ$ in (5) yields the result. □

Below, we introduce a lemma that is widely used in probability. Lemma 2 states the expectation of X can be obtained by the integral of its survival function.

Lemma 2.

Suppose a continuous random variable $X\sim F(·)$ is nonnegative; if $\mathbb{E}\left[X\right]<\infty$, then

$$\mathbb{E}\left[X\right]={\int }_0^{\infty }[1-F\left(x\right)]\mathrm{d}x.$$

Proof. 

We relegate the detailed proof of Lemma 2 to Appendix A.1. □

Theorem 1 below presents one of the main results in our paper.

Theorem 1.

With Assumption 6, there exists some positive constant $A_1>0$ such that, for $T\ge 1$,

$$R_T=Q({\mathit{y}}^{*},\mathit{\theta })-\mathbb{E}\left[\sum _{t=1}^{T}Q({\mathit{y}}_t,\mathit{\theta })\right]\le A_{1}logT,$$

where ${\mathit{y}}_t$ is the order quantity generated by algorithm DD2LI.

Proof. 

First, we apply Taylor’s expansion to $Q({\mathit{y}}_t,\mathit{\theta })$ at the maximizer $\mathit{y}={\mathit{y}}^{*}$,

$$\begin{array}{cc}\hfill Q({\mathit{y}}_t,\mathit{\theta })& =Q({\mathit{y}}^{*},\mathit{\theta })+⟨{\nabla }_{\mathit{y}}Q({\mathit{y}}^{*},\mathit{\theta }),{\mathit{y}}_t-{\mathit{y}}^{*}⟩\hfill \\ & +⟨{\mathit{y}}_t-{\mathit{y}}^{*},{\nabla }_{\mathit{y}}^{2}Q(\xi {\mathit{y}}_t+(1-\xi ){\mathit{y}}^{*},\mathit{\theta })({\mathit{y}}_t-{\mathit{y}}^{*})⟩,\xi \in [0,1].\hfill \end{array}$$

Since $Q(\mathit{y},\mathit{\theta })$ is maximized at $y={\mathit{y}}^{*}$, we have ${\nabla }_{\mathit{y}}Q({\mathit{y}}^{*},\mathit{\theta })=\mathbf{0}$.

In addition, given Assumption 4, we claim that ${\nabla }^{2}Q$ is continuous and hence upper-bounded in a compact set. Therefore, we get the inequality that there exists a constant $K_3>0$ such that

$$|Q({\mathit{y}}_t,\mathit{\theta })-Q({\mathit{y}}^{*},\mathit{\theta })|\le K_3\parallel {\mathit{y}}_t-{\mathit{y}}^{*}{\parallel }_2^2\le L_2{K}_3{\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }\parallel }_2^2.$$

(6)

The second inequality follows from Assumption 6.

Next, we define an event ${\mathcal{E}}_1$ by

$${\mathcal{E}}_1=\left\{\parallel {\widehat{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2<\sqrt{\frac{logt}{K_{2}t}}\right\}.$$

(7)

According to Corollary 1, we have

$$\mathbb{P}\left({\mathcal{E}}_1\right)>1-\frac{K_1}{t},\mathbb{P}\left({\mathcal{E}}_1^c\right)\le \frac{K_1}{t}.$$

Now, we decompose $\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2^2]$ by event ${\mathcal{E}}_1$:

$$\begin{array}{cc}\hfill \mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2^2]& =\mathbb{P}\left({\mathcal{E}}_1\right)\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2^2\mid {\mathcal{E}}_1]+\mathbb{P}\left({\mathcal{E}}_1^c\right)\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2^2\mid {\mathcal{E}}_1^c]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \le \mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2^2\mid {\mathcal{E}}_1]+\frac{K_1}{t}{(diam\mathbf{\Theta })}^2\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \le {\int }_0^{logt/\left(K_{2}t\right)}{K}_1{e}^{-t{K}_2ϵ}\mathrm{d}ϵ+\frac{K_1}{t}{(diam\mathbf{\Theta })}^2\hfill \end{array}$$

(9)

$$\begin{array}{c}\le \frac{K_4}{t}.\hfill \end{array}$$

(10)

The inequality (8) follows from $\mathbb{P}\left({\mathcal{E}}_1\right)\le 1,\mathbb{P}\left({\mathcal{E}}_1^c\right)\le K_1/t$ and $\parallel {\widehat{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2\le diam\Theta$. Here, ${\displaystyle diam\Theta =\underset{{\mathit{\theta }}_1,{\mathit{\theta }}_2\in \Theta }{max}{\parallel {\mathit{\theta }}_1-{\mathit{\theta }}_2\parallel }_2}$ is the diameter of the set $\Theta$. The inequality (9) is due to Lemma 2 and Corollary 1. By inequality (10), we claim the result is bounded by $O(1/t)$.

Combining (6) and (10) yields

$$\begin{array}{cc}\hfill Q({\mathit{y}}^{*},\mathit{\theta })-\mathbb{E}\left[\sum _{t=1}^{T}Q({\mathit{y}}_t,\mathit{\theta })\right]& \le \sum _{t=1}^T\mathbb{E}\left[\right|Q({\mathit{y}}^{*},\mathit{\theta })-Q({\mathit{y}}_t,\mathit{\theta })\left|\right]\hfill \\ & \le L_2{K}_3\sum _{t=1}^T\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2^2]\hfill \\ & \le L_2{K}_3{K}_4\sum _{t=1}^T\frac{1}{t}.\hfill \end{array}$$

Recall a well-known result in mathematical analysis that the sequence

$$f\left(n\right)=\sum _{k=1}^n\frac{1}{k}-logn$$

converges to Euler’s constant as $n\to \infty$, which indicates ${\displaystyle \sum _{t=1}^T\frac{1}{t}\sim logT}$. Hence, we claim the theorem holds. □

Theorem 1 states the regret bound is $O(logT)$ if Assumption 6 holds. According to [37], it will never be possible to find a policy with a regret smaller than $O(logT)$. Hence, our proposed algorithm can achieve the best possible regret bound.

In contrast, for cases where Assumption 6 does not hold, we have the following theorem:

Theorem 2.

Without Assumption 6, there exists some positive constant $A_2>0$ such that, for $T\ge 1$,

$$R_T=Q({\mathit{y}}^{*},\mathit{\theta })-\mathbb{E}\left[\sum _{t=1}^{T}Q({\mathit{y}}_t,\mathit{\theta })\right]\le A_2\sqrt{T},$$

where ${\mathit{y}}_t$ is the order quantity generated by algorithm DD2LI.

Proof. 

First, we decompose the per-period regret $\mathbb{E}[Q({\mathit{y}}^{*},\mathit{\theta })-Q({\mathit{y}}_t,\mathit{\theta })]$ into three parts:

$$\begin{array}{cc}\hfill \mathbb{E}[Q({\mathit{y}}^{*},\mathit{\theta })-Q({\mathit{y}}_t,\mathit{\theta })]& =\mathbb{E}[Q({\mathit{y}}^{*},\mathit{\theta })-Q({\mathit{y}}^{*},{\widehat{\mathit{\theta }}}_t)]+\mathbb{E}[Q({\mathit{y}}^{*},{\widehat{\mathit{\theta }}}_t)-Q({\mathit{y}}_t,{\widehat{\mathit{\theta }}}_t)]\hfill \\ \hfill & +\mathbb{E}[Q({\mathit{y}}_t,{\widehat{\mathit{\theta }}}_t)-Q({\mathit{y}}_t,\mathit{\theta })].\hfill \end{array}$$

(11)

Since $Q(·,{\widehat{\mathit{y}}}_t)$ is maximized at $\mathit{y}={\mathit{y}}_t$, the second part in (11) is

$$\mathbb{E}[Q({\mathit{y}}^{*},{\widehat{\mathit{\theta }}}_t)-Q({\mathit{y}}_t,{\widehat{\mathit{\theta }}}_t)]\le 0.$$

(12)

For the first and third parts, by Assumption 5 we have

$$\mathbb{E}[Q({\mathit{y}}^{*},\mathit{\theta })-Q({\mathit{y}}^{*},{\widehat{\mathit{\theta }}}_t)]+\mathbb{E}[Q({\mathit{y}}_t,{\widehat{\mathit{\theta }}}_t)-Q({\mathit{y}}_t,\mathit{\theta })]\le 2L_1\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2].$$

(13)

Recall the definition of ${\mathcal{E}}_1$ in (7). Now, we decompose $\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2]$ by event ${\mathcal{E}}_1$:

$$\begin{array}{cc}\hfill \mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2]& =\mathbb{P}\left({\mathcal{E}}_1\right)\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t{-\mathit{\theta }\parallel }_2\mid {\mathcal{E}}_1]+\mathbb{P}\left({\mathcal{E}}_1^c\right)\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2\mid {\mathcal{E}}_1^c]\hfill \\ \hfill & \le \mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2\mid {\mathcal{E}}_1]+\frac{K_1}{t}diam\mathbf{\Theta }\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \le {\int }_0^{\sqrt{logt/\left(K_{2}t\right)}}{K}_1{e}^{-t{K}_2{ϵ}^2}\mathrm{d}ϵ+\frac{K_1}{t}diam\mathbf{\Theta }\hfill \end{array}$$

(14)

$$\begin{array}{c}\le \frac{K_5}{\sqrt{t}}.\hfill \end{array}$$

(15)

Since ${\int }_0^{\infty }{e}^{-t{ϵ}^2}=\frac{\sqrt{\pi }}{2\sqrt{t}}$, the integral in (14) can be bounded by $O(1/\sqrt{t})$. By (15), we claim the result is bounded by $O(1/\sqrt{t})$.

Combining (11), (12), (13), and (15) yields

$$\begin{array}{cc}\hfill Q({\mathit{y}}^{*},\mathit{\theta })-\mathbb{E}\left[\sum _{t=1}^{T}Q({\mathit{y}}_t,\mathit{\theta })\right]& \le 2L_1\sum _{t=1}^T\mathbb{E}[\parallel {\widehat{\mathit{\theta }}}_t-\mathit{\theta }{\parallel }_2]\hfill \\ \hfill & \le 2L_1{K}_5\sum _{t=1}^T\frac{1}{\sqrt{t}}\hfill \\ \hfill & \le 4L_1{k}_5\sqrt{T},\hfill \end{array}$$

where the last inequality follows from the fact ${\displaystyle \sum _{t=1}^T\frac{1}{t}\le 2\sqrt{T}}$. □

By comparing the proofs of Theorems 1 and 2, it is shown that Assumption 6 serves to strengthen the continuity between per-period profit function and the parameter (see the difference between (6) and (13)). Specifically, the inclusion of Assumption 6 allows for a more precise estimation of the per-period profit function compared to scenarios where this assumption is not applicable.

In addition, we remark on the analogy between Assumption 6 in our paper and Assumption (iii) in [37]. As discussed in [38], the absence of a key assumption about the optimal quantity and the parameter will lead the cumulative regret to change from $O(logT)$ to $O\left(\sqrt{T}\right)$.

Overall, in this section, we have proposed the algorithm DD2LI and proved its regret bound. The algorithm’s regret bound is at least $O\left(\sqrt{T}\right)$ under proper conditions. Furthermore, with a stronger assumption about the optimal quantity’s continuity with respect to the parameter, we are able to further enhance the regret bound to $O(logT)$. These regret bounds demonstrate that our algorithm is close to the optimal strategy on average when the time periods are large enough.

6. Numerical Experiments

In this section, we conduct numerical experiments for two scenarios. Following [39], we measure the performance of a learning algorithm by the percentage of relative regret defined as

$$\frac{R_T}{T·Q({\mathit{y}}^{*},\mathit{\theta })}\times 100\%.$$

In both scenarios, we set unit price $p=10$, unit cost $c=3$, and unit transshipment cost $\tau =1$.

In the first scenario, we consider that the demand distributions in the two locations follow exponential distributions $Exp\left({\lambda }_1\right)$ and $Exp\left({\lambda }_2\right)$. Hence, the demand parameter $\mathit{\theta }=({\lambda }_1,{\lambda }_2)$.

Given the demand data up to period t, the parameters ${\lambda }_1,{\lambda }_2$ can be estimated by

$${\widehat{\lambda }}_{1,t}=\frac{t}{{\sum }_{k=1}^t{d}_k^1},{\widehat{\lambda }}_{2,t}=\frac{t}{{\sum }_{k=1}^t{d}_k^2}.$$

For two parameter sets, we conduct $N=100$ runs and compute the average. The results are shown in Figure 1 and Figure 2.

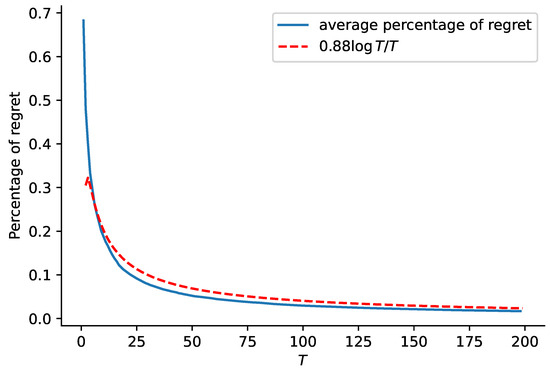
Figure 1. Curve of average percentage of regret in Scenario 1 with ${\lambda }_1=2$ and ${\lambda }_2=3$.

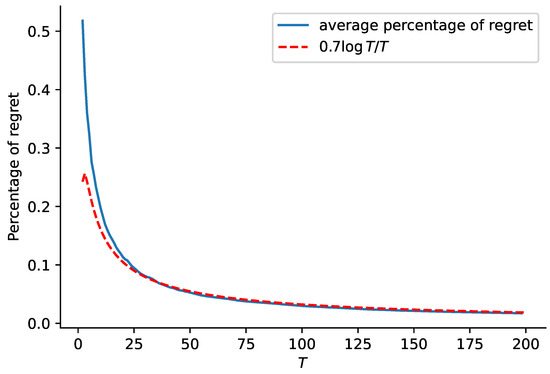
Figure 2. Curve of average percentage of regret in Scenario 1 with ${\lambda }_1=0.5$ and ${\lambda }_2=0.2$.

The blue curves in Figure 1 and Figure 2 show the average percentage of regret for $({\lambda }_1,{\lambda }_2)=(2,3)$ and $({\lambda }_1,{\lambda }_2)=(0.5,0.2)$, respectively, while the red dashed curves in the two figures represent function $\frac{0.88logT}{T}$ and $\frac{0.7logT}{T}$, respectively. This comparison shows that the regret of our proposed algorithm is close to the rate of $O(logT)$.

In the second scenario, we consider that the demand distributions in the two locations follow a multivariate normal distribution with mean vector $({\mu }_1,{\mu }_2)$ and covariance matrix $\left[\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right]$. Hence, the parameter $\mathit{\theta }=\left(({\mu }_1,{\mu }_2),\left[\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right]\right)$. Note that, in this scenario, the demand distributions in the two locations may be correlated.

Given the demand data up to period $t(t\ge 2)$, the parameters can be estimated by

$$\begin{array}{c}{\widehat{\mu }}_{1,t}=\frac{{\sum }_{k=1}^t{d}_k^1}{t},{\widehat{\mu }}_{2,t}=\frac{{\sum }_{k=1}^t{d}_k^2}{t}\\ {\widehat{\sigma }}_{1,t}^2=\frac{{\sum }_{k=1}^t{(d_k^1-{\widehat{\mu }}_{1,t})}^2}{t-1},{\widehat{\sigma }}_{2,t}^2=\frac{{\sum }_{k=1}^t{(d_k^2-{\widehat{\mu }}_{2,t})}^2}{t-1},\rho =\frac{{\sum }_{k=1}^t(d_k^1-{\widehat{\mu }}_{1,t})(d_k^2-{\widehat{\mu }}_{2,t})}{t-1}\end{array}.$$

For two parameter sets, we conduct $N=100$ runs and compute the average. The results are shown in Figure 3 and Figure 4.

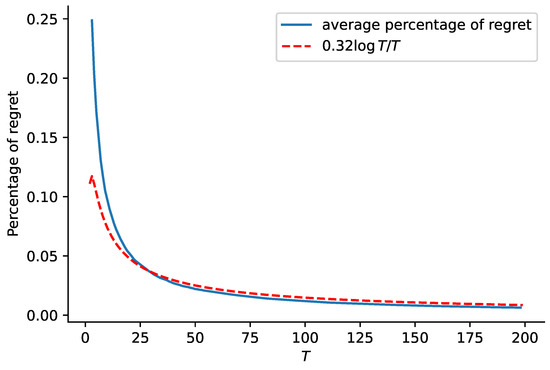
Figure 3. Curve of average percentage of regret in Scenario 2 with ${\mu }_1=8$, ${\mu }_2=12$, ${\sigma }_1^2=4$, ${\sigma }_2^2=9$, and $\rho =0.1$.

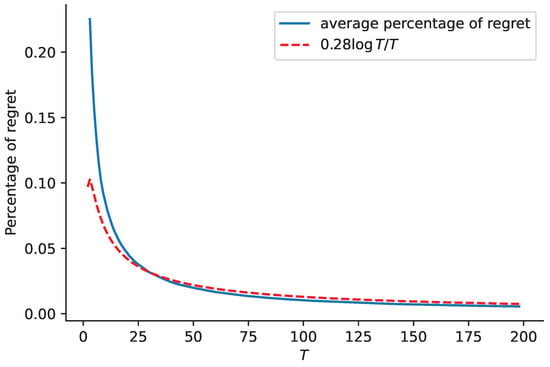
Figure 4. Curve of average percentage of regret in Scenario 2 with ${\mu }_1=5,{\mu }_2=6,{\sigma }_1^2=1,{\sigma }_2^2=4$, and $\rho =-0.5$.

The blue curves in Figure 1 and Figure 2 show average percentage of regret for ${\mu }_1=8,{\mu }_2=12,{\sigma }_1^2=4,{\sigma }_2^2=9,\rho =0.1$ and ${\mu }_1=5,{\mu }_2=6,{\sigma }_1^2=1,{\sigma }_2^2=4,\rho =-0.5$, respectively, while the red dashed curves in the two figures represent functions $\frac{0.32logT}{T}$ and $\frac{0.28logT}{T}$, respectively. This comparison shows that the regret of our proposed algorithm is close to the rate of $O(logT)$, and it is also applicable to correlated demands.

Based on the outcomes of four experiments, we can also conclude that Assumption 6 holds when demand follows exponential distributions or Gaussian distributions.

7. Conclusions

When a firm operates multiple stores, to better fulfill customer demand and make more profit, transshipment can be carried out if one location has excess inventory while another is experiencing a stockout. Despite the extensive research on transshipment between newsvendors, most assume the demand distribution is known a priori.

In this work, we introduce a data-driven inventory management algorithm for a multiperiod, two-location inventory system with perishable products and unknown demand distributions, which are assumed to follow a family of parametric distributions. The proposed algorithm, called DD2LI, uses past demand data to make adaptive inventory decisions. By using maximum likelihood estimation to estimate the unknown parameters, the algorithm determines the order quantity based on these estimations. We successfully derive the regret bound of the proposed algorithm under proper assumptions, which shows the algorithm is close to the optimal strategy on average. Additionally, we emphasize the assumption that the continuity of optimal order quantity with respect to parameters plays a key role in a tighter regret bound. Finally, to validate the effectiveness of our proposed algorithm, we conduct numerical experiments in two distinct scenarios.

There are several future research directions. First, future studies can design algorithms for two-location inventory systems when demand data are censored. Note that the demand censoring may be more intricate in two-location inventory systems with transshipment than in the single-location newsvendor problem. Second, while our work considers the stationary demand process, it is worth exploring algorithms that handle shifting demand. Third, our work only considers two locations, which restrict its use in practice. Future research can try to design algorithms for more complex inventory networks.

Appendix A.1. Proof of Lemma 2

Proof. 

Because the cumulative distribution function gives the probability of a random variable being smaller than a given value, we can obtain $F_X\left(x\right)=\mathrm{Pr}(X\le x)$, and then we have $1-F_X\left(x\right)=\mathrm{Pr}(X>x)$ such that ${\int }_0^{\infty }(1-F_X\left(x\right))\mathrm{d}x={\int }_0^{\infty }\mathrm{Pr}(X>x)$. By the probability density function, it can be written as follows:

$$\begin{array}{cc}\hfill {\int }_0^{\infty }(1-F_X\left(x\right))\mathrm{d}x& ={\int }_0^{\infty }{\int }_x^{\infty }{f}_X\left(z\right)\mathrm{d}z\mathrm{d}x\hfill \\ & ={\int }_0^{\infty }{\int }_0^z{f}_X\left(z\right)\mathrm{d}x\mathrm{d}z\hfill \\ & ={\int }_0^{\infty }{f}_X\left(z\right){\int }_0^z\mathrm{d}x\mathrm{d}z\hfill \\ & ={\int }_0^{\infty }z·f_X\left(z\right)\mathrm{d}z.\hfill \end{array}$$

Then, we apply the definition of the expectation and obtain

$$\begin{array}{cc}\hfill {\int }_0^{\infty }(1-F_X\left(x\right))\mathrm{d}x& ={\int }_0^{\infty }z·f_X\left(z\right)\mathrm{d}z=\mathbb{E}\left[X\right].\hfill \end{array}$$

This completes the proof. □