Unrelated Parallel Machine Scheduling Problem Considering Job Splitting, Inventories, Shortage, and Resource: A Meta-Heuristic Approach
Abstract
1. Introduction
2. Literature Review
- Proposing a new mathematical formulation for the UPMSP with the aim of minimizing the completion time (Makespan) considering job splitting, inventories, and shortages in the production planning horizon, resource constraints, and machine eligibility.
- Developing a heuristic algorithm to produce an initial feasible solution.
- Solving the proposed model using the novel Grey Wolf Optimizer algorithm developed by Mirjalili et al. [1];
- Measuring the performance of the formulation and solution methodology in a real-world production environment, implemented at Bronze Industrial Manufacturing Company (BIMC) in Iran as a decision support system.
3. Mathematical Model
- ✓
- ✓
- The capability of a machine to complete a job is provided [12].
- ✓
- The Kanban planning of each job is presented based on the days of the week. In other words, the required number of products for each job is known during the production planning phase.
- ✓
- The setup time of the machine is with respect to the changes in the machine’s frames. Moreover, the sequence limitations are provided here.
- ✓
- There are two different working hours and shift duration, six days a week or seven days a week. There are three different working hours have been provided by the BIMC [37].
- ✓
- At the beginning of the planning horizon, the production planner needs to know the inventory levels.
4. Solution Methodology
4.1. Solution Representation
4.2. Initial Population Generation
| Algorithm 1: Randomly created feasible solutions. |
| Input Jobs, Economic Production, Machines, Machines Eligibility Based on economic production job, create splits Every split is equal to or greater than economic production. Every split contains the number of products that need to be produced. Assign the previous step to solution coding, 2nd segment “No. of Product per Split”. Create a random permutation of splits. Assign the previous step to solution coding, 1st segment “Permutation”. For each machine, create an empty list of assigned splits. For each split from each job, randomly assign it to a machine. While not an eligible machine is assigned, repeat the previous step. Assign this step to solution coding, 3rd segment “Split of Job Assigned to eligible Machine”. Evaluate the cost of solution coding. Assign this step to solution coding, 4th segment “Cost”. Output Create structured data containing all 4 segments |
4.3. Original Grey Wolf Optimizer
| Algorithm 2: The original GWO algorithm. |
| Input: Set the parameters of the GWO such as for I = 1 to number of search agents do Create a random solution. Calculate the value of the objective function (Minimization or Maximization) end for Set the best solution as Alpha. Set the second-best solution as Beta. Set the third-best solution as Delta. Initialize iteration it = 1 while it < MaxIteration do for it = 1 to number of search agents do Update the position of each grey wolf using Equation (26) end for Decrease the value of Alpha from 2 to 0 using Equation (22) Decrease A and C parameters. Calculate the value of the objective function of each grey wolf. Update , , and it = it + 1 end while Return the best wolf alpha |
4.4. Discrete Grey Wolf Optimizer
| Algorithm 3: The discrete GWO algorithm. |
| Input: Set the parameters of the GWO such as for i = 1 to number of search agents do Create a random solution. Calculate the value of the objective function (Minimization or Maximization) end for Set the best solution as Alpha. Set the second-best solution as Beta. Set the third-best solution as Delta. Initialize iteration it = 1 while it < MaxIteration do for it = 1 to number of search agents do Update the position of each grey wolf using Hamming Distance in Equations (27)–(29) end for Decrease the value of Alpha from 2 to 0 using Equation (22) Decrease A and C parameters. Calculate the value of the objective function of each grey wolf. Update , , and it = it + 1 end while Return the best wolf alpha |
5. Computational Experiments
5.1. Test Problem and Parameter Setting
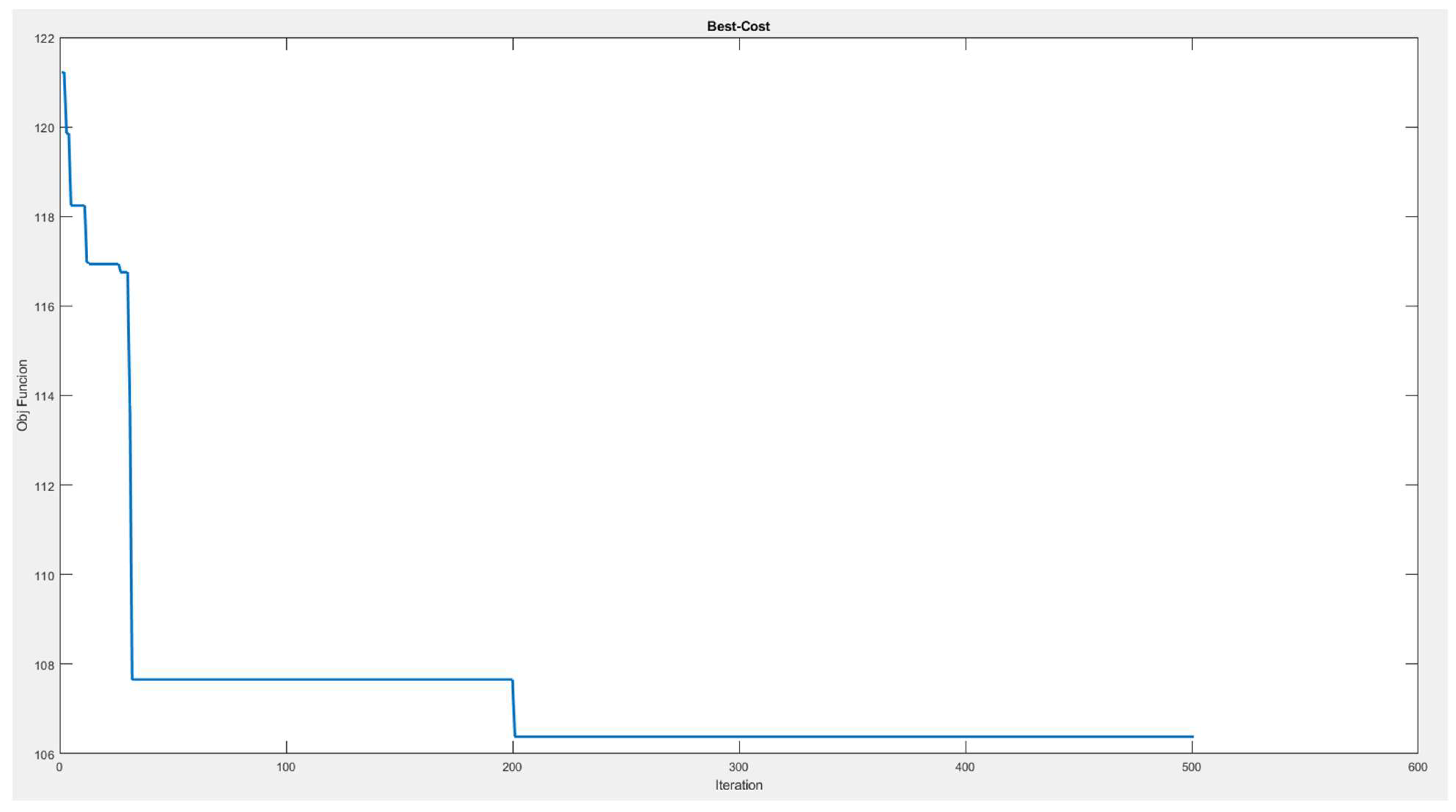
5.2. Computational Results
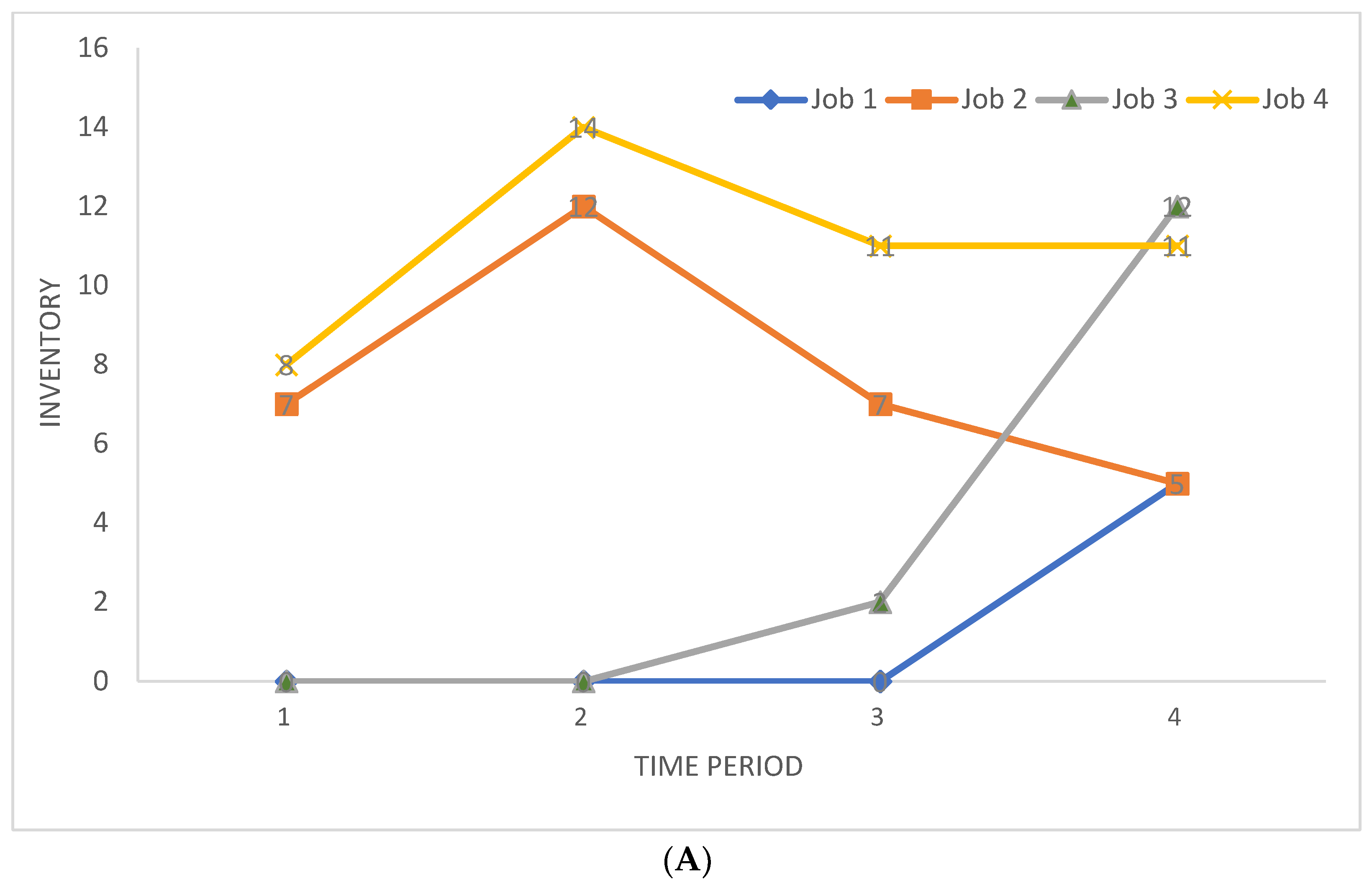
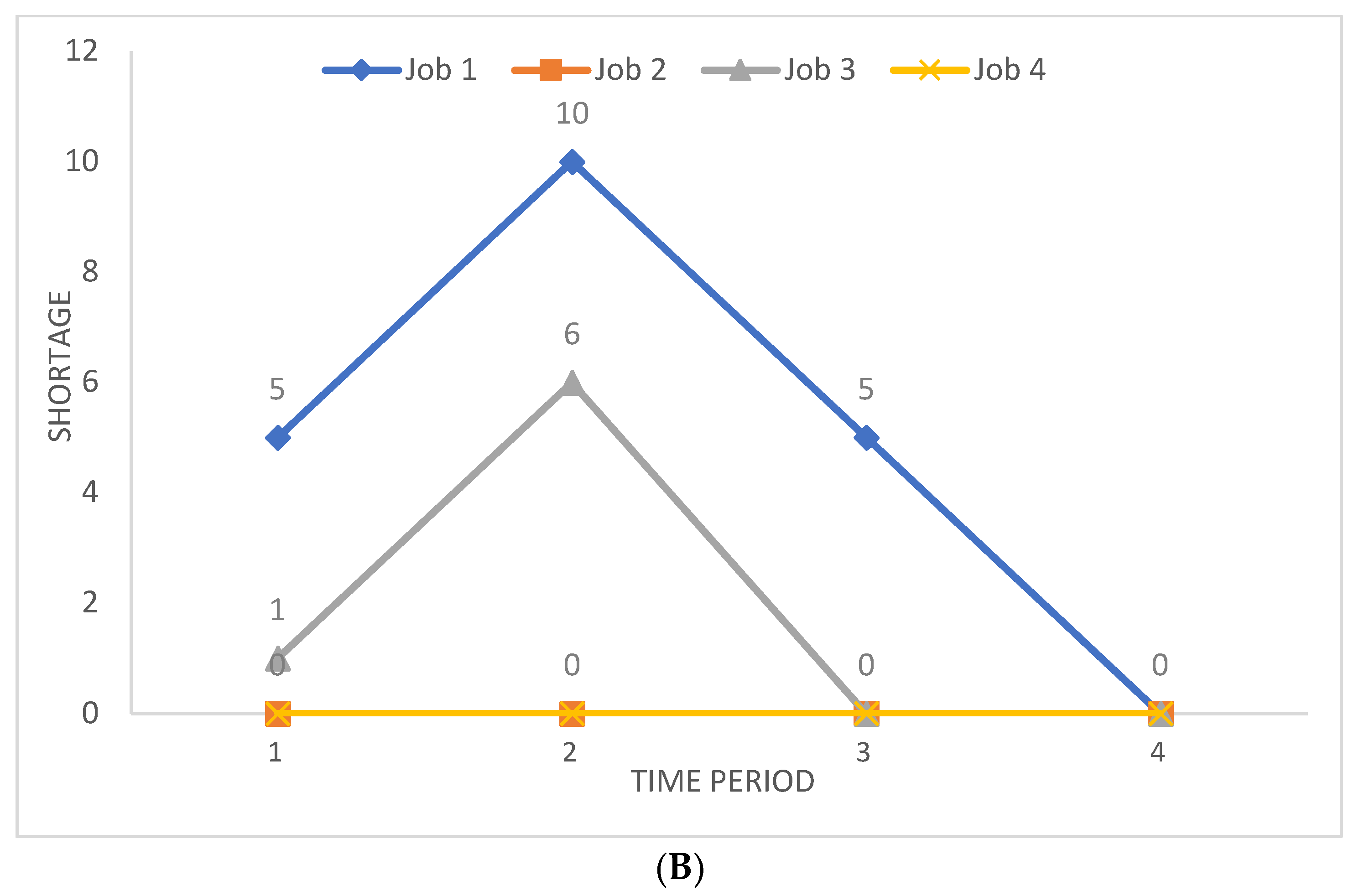
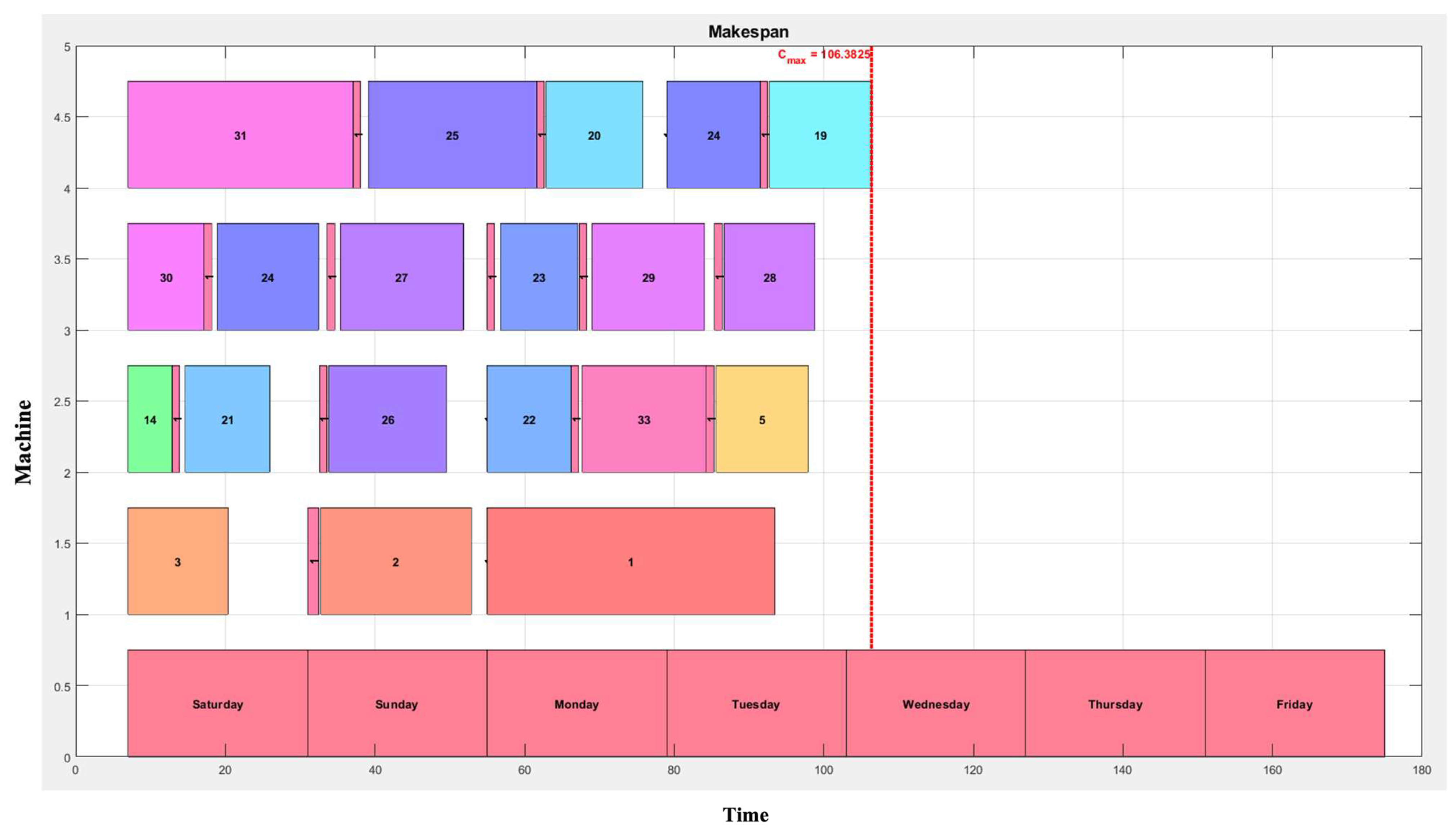
5.3. Results of a Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Afzalirad, M.; Rezaeian, J. Resource-constrained unrelated parallel machine scheduling problem with sequence dependent setup times, precedence constraints and machine eligibility restrictions. Comput. Ind. Eng. 2016, 98, 40–52. [Google Scholar] [CrossRef]
- Alharkan, I.; Saleh, M.; Ghaleb, M.A.; Kaid, H.; Farhan, A.; Almarfadi, A. Tabu search and particle swarm optimization algorithms for two identical parallel machines scheduling problem with a single server. J. King Saud Univ.-Eng. Sci. 2020, 32, 330–338. [Google Scholar] [CrossRef]
- Allahverdi, A. The third comprehensive survey on scheduling problems with setup times/costs. Eur. J. Oper. Res. 2015, 246, 345–378. [Google Scholar] [CrossRef]
- Arani, M.; Dastmard, M.; Momenitabar, M.; Liu, X. Unrelated Parallel Machine Scheduling Problem (UPMSP) Considering Work-in-Process and Finished Goods Inventories Subject to Resource Constraints and Due Dates: A Simulated Annealing. In Logistics and Supply Chain Management; Springer: Berlin/Heidelberg, Germany, 2020; Available online: https://link.springer.com/bookseries/7899 (accessed on 30 October 2021).
- Arık, O.A.; Schutten, M.; Topan, E. Weighted earliness/tardiness parallel machine scheduling problem with a common due date. Expert Syst. Appl. 2022, 187, 115916. [Google Scholar] [CrossRef]
- Asadpour, M.; Hodaei, Z.; Azami, M.; Kehtari, E.; Vesal, N. A green model for identical parallel machines scheduling problem considering tardy jobs and job splitting property. Sustain. Oper. Comput. 2022, 3, 149–155. [Google Scholar] [CrossRef]
- Bilge, Ü.; Kıraç, F.; Kurtulan, M.; Pekgün, P. A tabu search algorithm for parallel machine total tardiness problem. Comput. Oper. Res. 2004, 31, 397–414. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Y.; Tang, Z.; Luo, Q. A hybrid algorithm combining glowworm swarm optimization and complete 2-opt algorithm for spherical travelling salesman problems. Appl. Soft Comput. 2017, 58, 104–114. [Google Scholar] [CrossRef]
- Cheng, B.; Wang, Q.; Yang, S.; Hu, X. An improved ant colony optimization for scheduling identical parallel batching machines with arbitrary job sizes. Appl. Soft Comput. 2013, 13, 765–772. [Google Scholar] [CrossRef]
- Cheng, T.C.E.; Sin, C.C.S. A state-of-the-art review of parallel-machine scheduling research. Eur. J. Oper. Res. 1990, 47, 271–292. [Google Scholar] [CrossRef]
- Croes, G.A. A Method for Solving Traveling-Salesman Problems. Oper. Res. 1958, 6, 791–812. [Google Scholar] [CrossRef]
- de Souza, E.A.G.; Nagano, M.S.; Rolim, G.A. Dynamic Programming algorithms and their applications in machine scheduling: A review. Expert Syst. Appl. 2022, 190, 116180. [Google Scholar] [CrossRef]
- Fanjul-Peyro, L.; Perea, F.; Ruiz, R. Models and matheuristics for the unrelated parallel machine scheduling problem with additional resources. Eur. J. Oper. Res. 2017, 260, 482–493. [Google Scholar] [CrossRef]
- Fowler, J.W.; Mönch, L. A survey of scheduling with parallel batch (p-batch) processing. Eur. J. Oper. Res. 2022, 298, 1–24. [Google Scholar] [CrossRef]
- Gedik, R.; Kalathia, D.; Egilmez, G.; Kirac, E. A constraint programming approach for solving unrelated parallel machine scheduling problem. Comput. Ind. Eng. 2018, 121, 139–149. [Google Scholar] [CrossRef]
- Kaabi, J.; Harrath, Y. Scheduling on uniform parallel machines with periodic unavailability constraints. Int. J. Prod. Res. 2019, 57, 216–227. [Google Scholar] [CrossRef]
- Karagul, K.; Aydemir, E.; Tokat, S. Using 2-Opt based evolution strategy for travelling salesman problem. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2016, 6, 103–113. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility among Combinatorial Problems. In Complexity of Computer Computations; Springer: New York, NY, USA, 1972; pp. 85–103. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Shim, S.-O.; Kim, S.-B.; Choi, Y.-C.; Yoon, H.M. Parallel machine scheduling considering a job-splitting property. Int. J. Prod. Res. 2004, 42, 4531–4546. [Google Scholar] [CrossRef]
- Kim, J.-G.; Song, S.; Jeong, B. Minimising total tardiness for the identical parallel machine scheduling problem with splitting jobs and sequence-dependent setup times. Int. J. Prod. Res. 2020, 58, 1628–1643. [Google Scholar] [CrossRef]
- Koulamas, C.; Kyparisis, G.J. A modified LPT algorithm for the two uniform parallel machine makespan minimization problem. Eur. J. Oper. Res. 2009, 196, 61–68. [Google Scholar] [CrossRef]
- Kress, D.; Meiswinkel, S.; Pesch, E. Mechanism design for machine scheduling problems: Classification and literature overview. OR Spectr. 2018, 40, 583–611. [Google Scholar] [CrossRef]
- Lee, C.-H. A dispatching rule and a random iterated greedy metaheuristic for identical parallel machine scheduling to minimize total tardiness. Int. J. Prod. Res. 2018, 56, 2292–2308. [Google Scholar] [CrossRef]
- Lee, W.-C.; Chuang, M.-C.; Yeh, W.-C. Uniform parallel-machine scheduling to minimize Makespan with position-based learning curves. Comput. Ind. Eng. 2012, 63, 813–818. [Google Scholar] [CrossRef]
- Lee, W.-C.; Wu, C.-C.; Chen, P. A simulated annealing approach to makespan minimization on identical parallel machines. Int. J. Adv. Manuf. Technol. 2006, 31, 328–334. [Google Scholar] [CrossRef]
- Lei, D.; Yuan, Y.; Cai, J. An improved artificial bee colony for multi-objective distributed unrelated parallel machine scheduling. Int. J. Prod. Res. 2021, 59, 5259–5271. [Google Scholar] [CrossRef]
- Lin, Y.K.; Pfund, M.E.; Fowler, J.W. Heuristics for minimizing regular performance measures in unrelated parallel machine scheduling problems. Comput. Oper. Res. 2011, 38, 901–916. [Google Scholar] [CrossRef]
- Logendran, R.; Subur, F. Unrelated parallel machine scheduling with job splitting. IIE Trans. 2004, 36, 359–372. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Nait Tahar, D.; Yalaoui, F.; Chu, C.; Amodeo, L. A linear programming approach for identical parallel machine scheduling with job splitting and sequence-dependent setup times. Int. J. Prod. Econ. 2006, 99, 63–73. [Google Scholar] [CrossRef]
- Park, T.; Lee, T.; Kim, C.O. Due-date scheduling on parallel machines with job splitting and sequence-dependent major/minor setup times. Int. J. Adv. Manuf. Technol. 2012, 59, 325–333. [Google Scholar] [CrossRef]
- Rudek, R. A fast neighborhood search scheme for identical parallel machine scheduling problems under general learning curves. Appl. Soft Comput. 2021, 113, 108023. [Google Scholar] [CrossRef]
- Sarıçiçek, İ.; Çelik, C. Two meta-heuristics for parallel machine scheduling with job splitting to minimize total tardiness. Appl. Math. Model. 2011, 35, 4117–4126. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, T.C.E. A heuristic for scheduling jobs on two identical parallel machines with a machine availability constraint. Int. J. Prod. Econ. 2015, 161, 74–82. [Google Scholar] [CrossRef]
- Yang, D.-L.; Yang, S.-J. Unrelated parallel-machine scheduling problems with multiple rate-modifying activities. Inf. Sci. 2013, 235, 280–286. [Google Scholar] [CrossRef]
- Yeh, W.-C.; Chuang, M.-C.; Lee, W.-C. Uniform parallel machine scheduling with resource consumption constraint. Appl. Math. Model. 2015, 39, 2131–2138. [Google Scholar] [CrossRef]
- Yepes-Borrero, J.C.; Villa, F.; Perea, F.; Caballero-Villalobos, J.P. GRASP algorithm for the unrelated parallel machine scheduling problem with setup times and additional resources. Expert Syst. Appl. 2020, 141, 112959. [Google Scholar] [CrossRef]
- Yunusoglu, P.; Topaloglu Yildiz, S. Constraint programming approach for multi-resource-constrained unrelated parallel machine scheduling problem with sequence-dependent setup times. Int. J. Prod. Res. 2022, 60, 2212–2229. [Google Scholar] [CrossRef]
- Zeng, Y.; Che, A.; Wu, X. Bi-objective scheduling on uniform parallel machines considering electricity cost. Eng. Optim. 2018, 50, 19–36. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, Q.; Gong, G.; Han, W. A new unrelated parallel machine scheduling problem with tool changes to minimise the total energy consumption. Int. J. Prod. Res. 2020, 58, 6826–6845. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, Q.; Lin, R.; Gong, G.; Han, W. A combinatorial evolutionary algorithm for unrelated parallel machine scheduling problem with sequence and machine-dependent setup times, limited worker resources and learning effect. Expert Syst. Appl. 2021, 175, 114843. [Google Scholar] [CrossRef]

| References | Types of PMSP | Objective Function | Splitting Jobs | Inventories | Shortage | Resource Constraints | Machine Eligibility | Sequence-Dependent Setup Times | Solution Methodology |
|---|---|---|---|---|---|---|---|---|---|
| [7] | IPMSP 1 | Minimize tardiness | ✓ | - | - | - | - | - | Heuristic algorithm |
| [8] | IPMSP | Minimize completion time | ✓ | - | - | - | - | ✓ | Heuristic algorithm |
| [9] | IPMSP | Minimize completion time | - | - | - | - | - | - | Simulated Annealing |
| [9] | IPMSP | Minimize tardiness | ✓ | - | - | - | - | - | Tabu search and simulated annealing |
| [10] | IPMSP | Minimize tardiness | ✓ | - | - | - | - | ✓ | Heuristic algorithm |
| [11] | IPMSP | Minimize completion time | ✓ | - | - | - | - | - | Ant colony optimization |
| [12] | IPMSP | Maximize the number of on-time jobs | - | - | - | - | ✓ | - | Heuristic algorithm |
| [13] | IPMSP | Minimize tardiness | - | - | - | - | - | - | Iterated greedy-based metaheuristic |
| [14] | IPMSP | Minimize completion time | - | - | - | - | - | - | Tabu search and particle swarm optimization |
| [15] | IPMSP | Minimize lateness | - | - | - | - | - | - | Fast neighborhood search |
| [16] | IPMSP | Minimize tardiness and energy consumption | - | - | - | - | - | - | Simulated annealing and harmony search |
| [17] | UPMSP 2 | Minimize tardiness | ✓ | - | - | - | - | ✓ | Tabu search |
| [18] | UPMSP | Regular | - | - | - | - | - | - | Heuristic algorithm |
| [19] | UPMSP | Minimize completion time | - | - | - | - | - | - | Heuristic algorithm |
| [20] | UPMSP | Minimize completion time | - | - | - | ✓ | ✓ | ✓ | Genetic algorithm and artificial immune system |
| [21] | UPMSP | Minimize completion time | - | - | - | ✓ | - | - | Greedy-based fixing algorithm |
| [22] | UPMSP | Minimize completion time | - | - | - | ✓ | - | ✓ | Heuristic algorithm |
| [23] | UPMSP | Minimize completion time and total energy consumption | - | - | - | - | - | - | Heuristic algorithm |
| [24] | UPMSP | Minimize completion time | - | - | - | ✓ | - | ✓ | Heuristic and GRASP algorithms |
| [25] | UPMSP | Minimize completion time | - | - | - | ✓ | - | ✓ | Combinatorial evolutionary algorithm |
| [26] | UPMSP | Minimize completion time and tardiness | - | - | - | - | - | - | Heuristic algorithm |
| [27] | UPMSP | Minimize completion time | - | - | - | ✓ | ✓ | ✓ | Heuristic algorithm |
| [28] | UPMSP | Minimize earliness and tardiness | - | - | - | - | - | - | Heuristic algorithm |
| [29] | UnPMSP 3 | Minimize tardiness | - | - | - | - | - | ✓ | Tabu search algorithm |
| [30] | UnPMSP | Minimize completion time | - | - | - | - | - | - | Heuristic algorithm |
| [31] | UnPMSP | Minimize completion time | - | - | - | - | - | - | Heuristic algorithm |
| [32] | UnPMSP | Minimize completion time | - | - | - | ✓ | - | - | Genetic and particle swarm optimization algorithms |
| [33] | UnPMSP | Minimize completion time | - | - | - | - | - | - | Heuristic algorithm |
| [34] | UnPMSP | Minimize total electricity costs and number of machines used for processing | - | - | - | - | - | - | Greedy insertion algorithm |
| This study | UPMSP | Minimize completion time | ✓ | ✓ | ✓ | ✓ | - | ✓ | Grey Wolf Optimizer algorithm |
| Notations | Descriptions |
|---|---|
| Sets: | |
| Set of jobs ( and | |
| Set of machines ( and | |
| Set of renewable resources ( and including cranes, workers, and lift trucks | |
| Set of the time period ( and | |
| Set of part of job i ( and | |
| Parameters: | |
| Number of produced part of job i | |
| The demand for job i in period t | |
| A large number | |
| If machine m is eligible to process job i, 1, otherwise 0 | |
| If job j could be followed by job i and processed on machine m is 1, otherwise 0 | |
| Renewable resource requirement of job i per quantity for resource r in period t | |
| Available renewable resource of type r in period t | |
| Variables: | |
| Completion time of part job i (instead of part, job split) | |
| Maximum completion time of all jobs | |
| If machine m started processing part job i in the beginning of period t 1, otherwise 0 | |
| Processed quantity of job i in period t | |
| Shortage amount of job i in period t | |
| Inventory level of job i at the end of period t |
| Parameters | Value |
|---|---|
| Parameter algorithm | |
| Search agents (wolf population) | 50 |
| Maximum iterations | 500 |
| Parameter model | |
| Number of parts of each job | 2 |
| Demand of job | Uniform (30, 50) |
| Renewable resource of each job for each resource in each period | Uniform (30, 50) |
| Available renewable resources in each period | Uniform (30, 50) |
| Problem | Problem Dimension | Results | Solution Time (Seconds) | ||
|---|---|---|---|---|---|
| CPLEX | GWO | CPLEX | GWO | ||
| 1 | 4*2*2*2*4 | 20.00 | 20.00 | 1.02 | 1.00 |
| 2 | 5*2*2*2*4 | 23.00 | 23.00 | 16.00 | 2.05 |
| 3 | 7*4*2*2*4 | 31.00 | 31.00 | 423.00 | 39.00 |
| 4 | 8*4*2*2*4 | 37.00 | 37.00 | 765.00 | 127.00 |
| 5 | 10*5*2*2*4 | 46.00 | 46.00 | 1359.00 | 234.00 |
| 6 | 12*6*2*2*4 | - | 59.00 | - | 357.00 |
| 7 | 15*8*2*2*4 | - | 71.00 | - | 482.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arani, M.; Momenitabar, M.; Priyanka, T.J. Unrelated Parallel Machine Scheduling Problem Considering Job Splitting, Inventories, Shortage, and Resource: A Meta-Heuristic Approach. Systems 2024, 12, 37. https://doi.org/10.3390/systems12020037
Arani M, Momenitabar M, Priyanka TJ. Unrelated Parallel Machine Scheduling Problem Considering Job Splitting, Inventories, Shortage, and Resource: A Meta-Heuristic Approach. Systems. 2024; 12(2):37. https://doi.org/10.3390/systems12020037
Chicago/Turabian StyleArani, Mohammad, Mohsen Momenitabar, and Tazrin Jahan Priyanka. 2024. "Unrelated Parallel Machine Scheduling Problem Considering Job Splitting, Inventories, Shortage, and Resource: A Meta-Heuristic Approach" Systems 12, no. 2: 37. https://doi.org/10.3390/systems12020037
APA StyleArani, M., Momenitabar, M., & Priyanka, T. J. (2024). Unrelated Parallel Machine Scheduling Problem Considering Job Splitting, Inventories, Shortage, and Resource: A Meta-Heuristic Approach. Systems, 12(2), 37. https://doi.org/10.3390/systems12020037







