An Exploration of Groundwater Resource Ecosystem Service Sustainability: A System Dynamics Case Study in Texas, USA
Abstract
1. Introduction
2. Ecosystem Services of Groundwater Aquifer Systems
2.1. Groundwater and Provisioning Services
2.2. Groundwater and Regulating and Supporting Services
2.3. Groundwater and Cultural Services
3. Systems Thinking Case Study: Groundwater in Texas, USA
3.1. What Has Happened? Event-Level Description
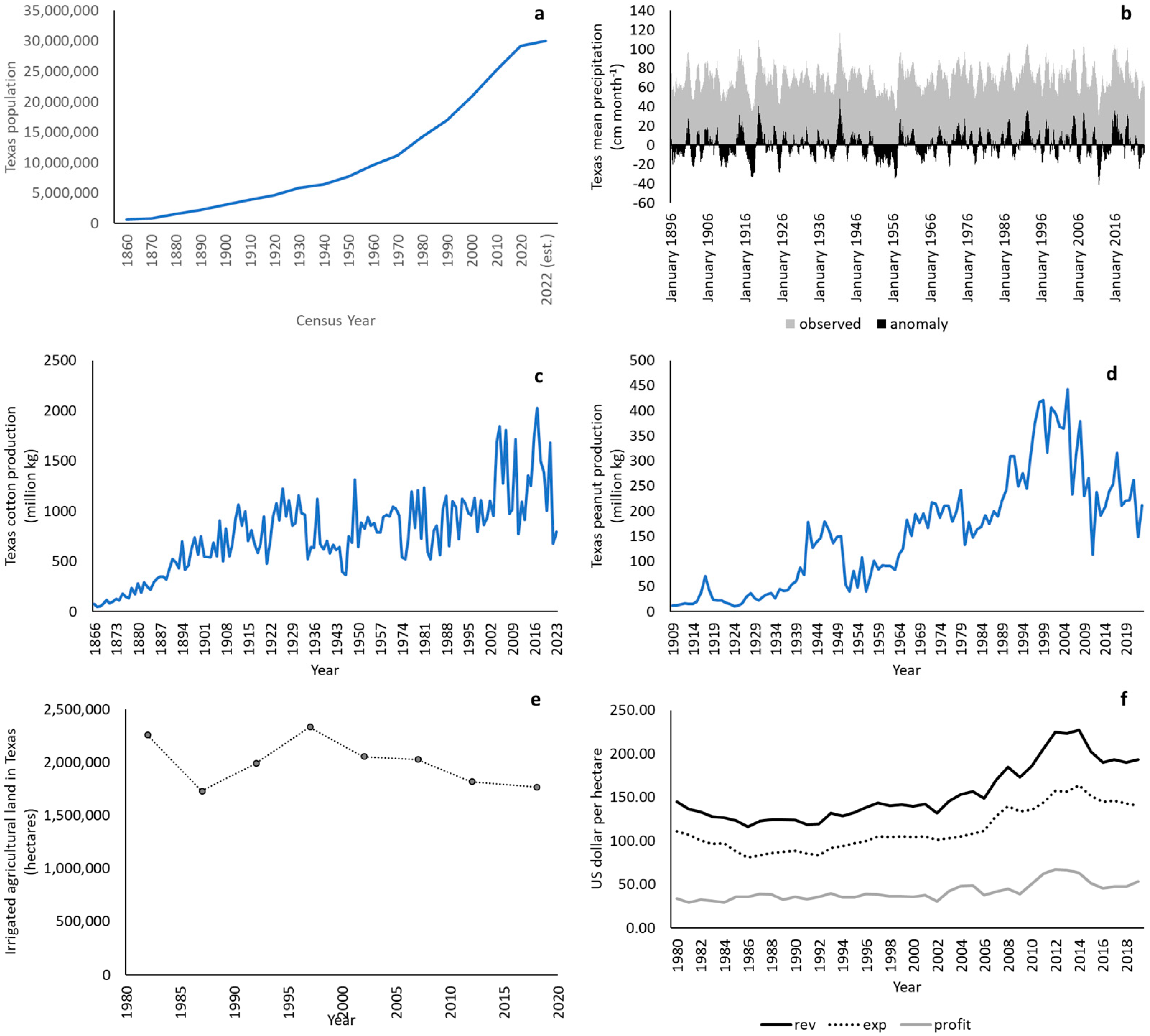
- Urbanization: As communities and population centers grow, the more it becomes appealing for others (both in and out-of-state) to relocate to these areas; as the population within that community grows, so does the need for water supply. With increased urbanization, communities relying on surface water supplies are more susceptible to water quality issues arising from nutrient and runoff pollutants that affect water quality and treatment costs, which in turn incentives cities to acquire groundwater rights to fulfil their water demands. This issue will not be going away as long as the population in Texas continues growing relative to available water supply [41]. In areas with a higher population, greater pumping rates have led to higher costs (due to groundwater level reductions) and the likelihood of externalities such as groundwater contamination or land subsidence is greater [42,43].
- Agriculture: Farmers rely heavily on groundwater for their farms, this allows the farm to generate income, which itself depends on crop yield, that irrigation supports [44]. However, farms experiencing severe stress from either drought (climate variability), productivity (soil degradation), revenue (crop yields and/or quality), or combinations thereof can hit farmers very hard financially, which may incentivize accelerated irrigation pumping as a coping or recovery strategy but lead to increased pumping costs.
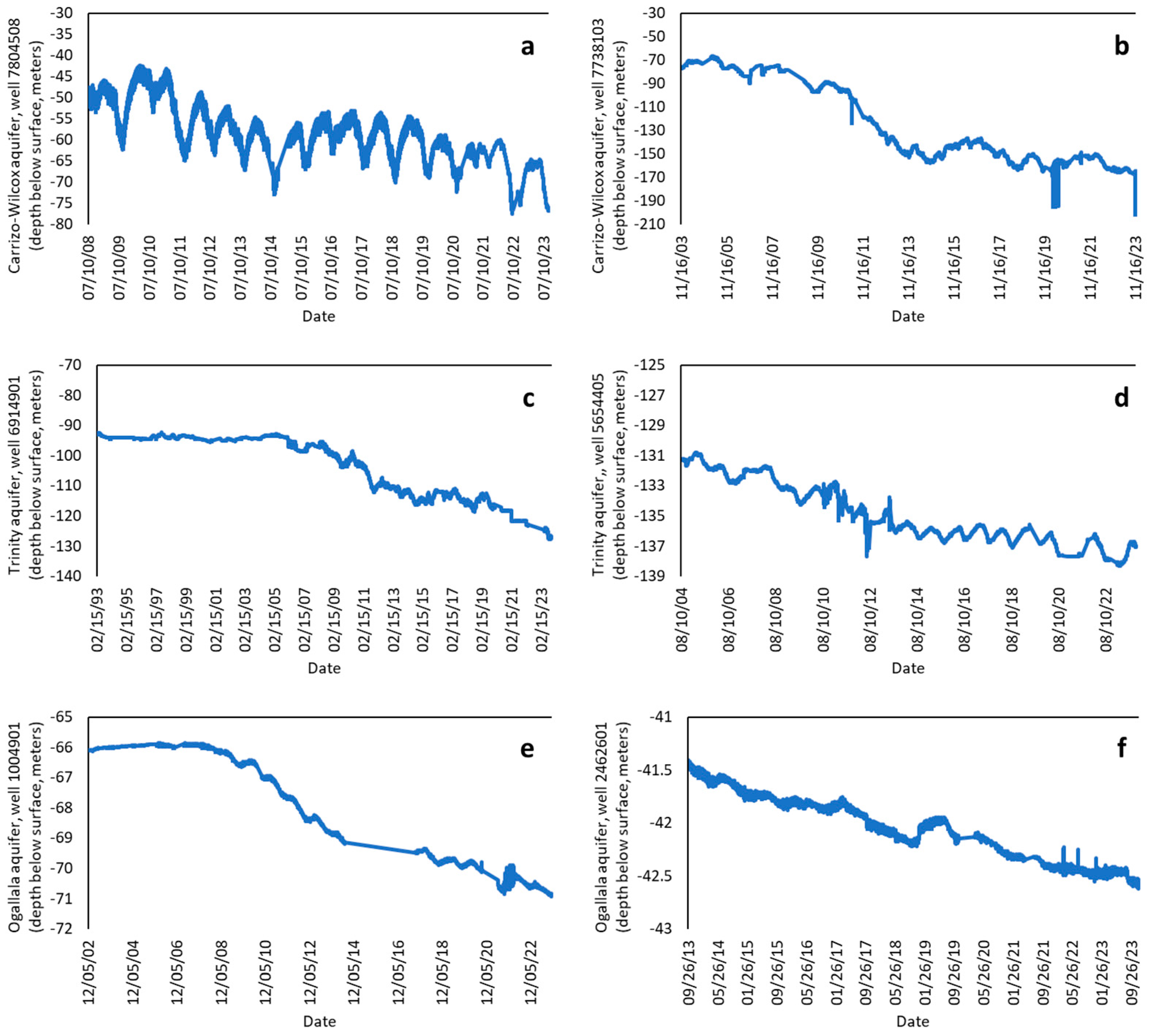
3.2. What Has Been Happening? Trends and Patterns over Time
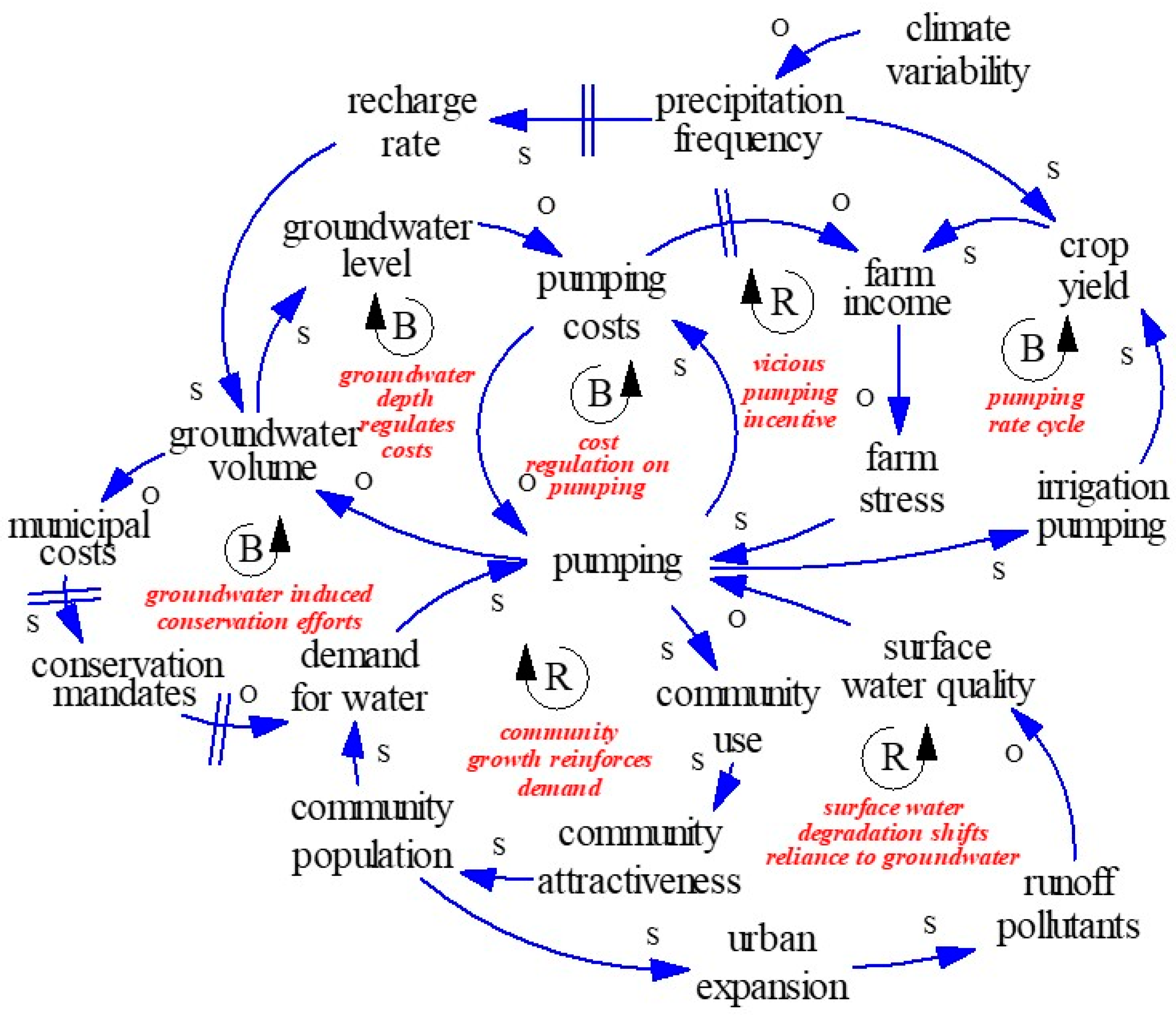
3.3. Why Has It Been Happening? Causal Feedback Structure and Stakeholder Mental Models
- Agriculture: The farmers and ranchers view the situation as they must sustain or improve yield to survive. If they “get more rain, we won’t have to pump more”, but when they are particularly stressed during short-term droughts “I need more water so I pump”. Although they recognized climate variability to be a significant driver (“We need more rain”), it has not been clear if agricultural users recognized how irrigation decisions influence costs as well as yields (“Pumping costs keep rising… we simply need more water”).
- Municipalities (both domestic and industrial users): Likewise, community stakeholders stressed the “need for water to survive and [continue to] grow”. Although groundwater comes at a significant cost, municipal stakeholders recognized another cost factor influencing their water sourcing decisions, namely treatment costs stemming from surface water quality degradation (“We need clean water… becoming more and more important to manage costs of water”).
- Groundwater conservation districts: The GCD managers saw the cycle (or throughput) of water through manmade systems must slow down before groundwater become so scarce it becomes essentially “lost” to productive use, given “accelerated reliance on pumping [by all users] is affecting the amount of water available”. In addition, groundwater quality is growing in concern given “more pollutants in runoff” and “nutrient concentration issues with declining water tables”, especially salts. Lastly GCD managers had a noticeable appreciation for the regulatory mechanisms or constraints on conservation effort implementation, given “not all of the state is in a GCD, some aquifers have multiple GCDs while others have none, and conservation emphasis varies greatly between GCD... in Texas, surface rights holders have a strong legal right to use groundwater [which makes voluntary conservation difficult]”.
4. System Dynamics Model Application
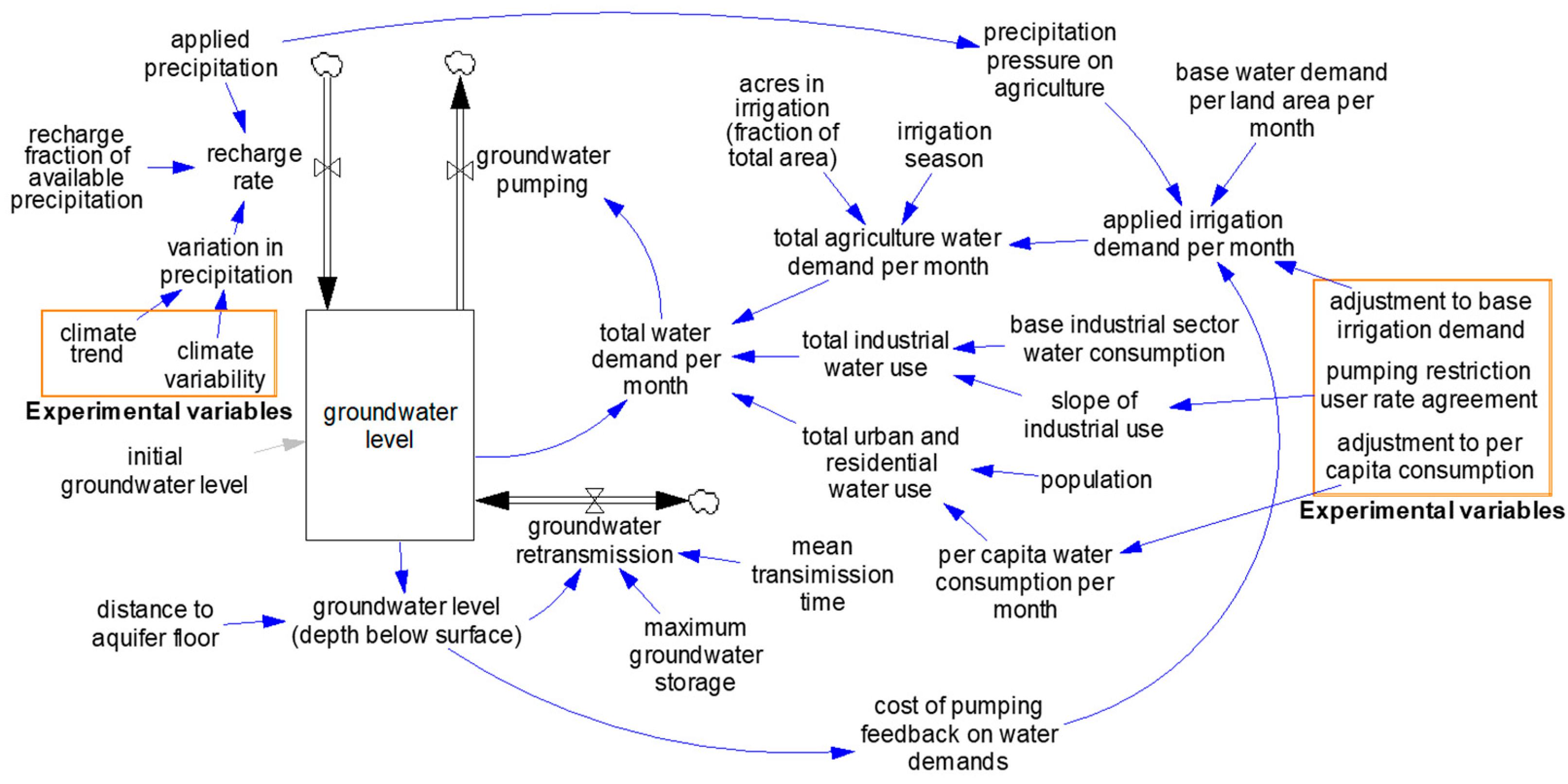
4.1. Model Overview
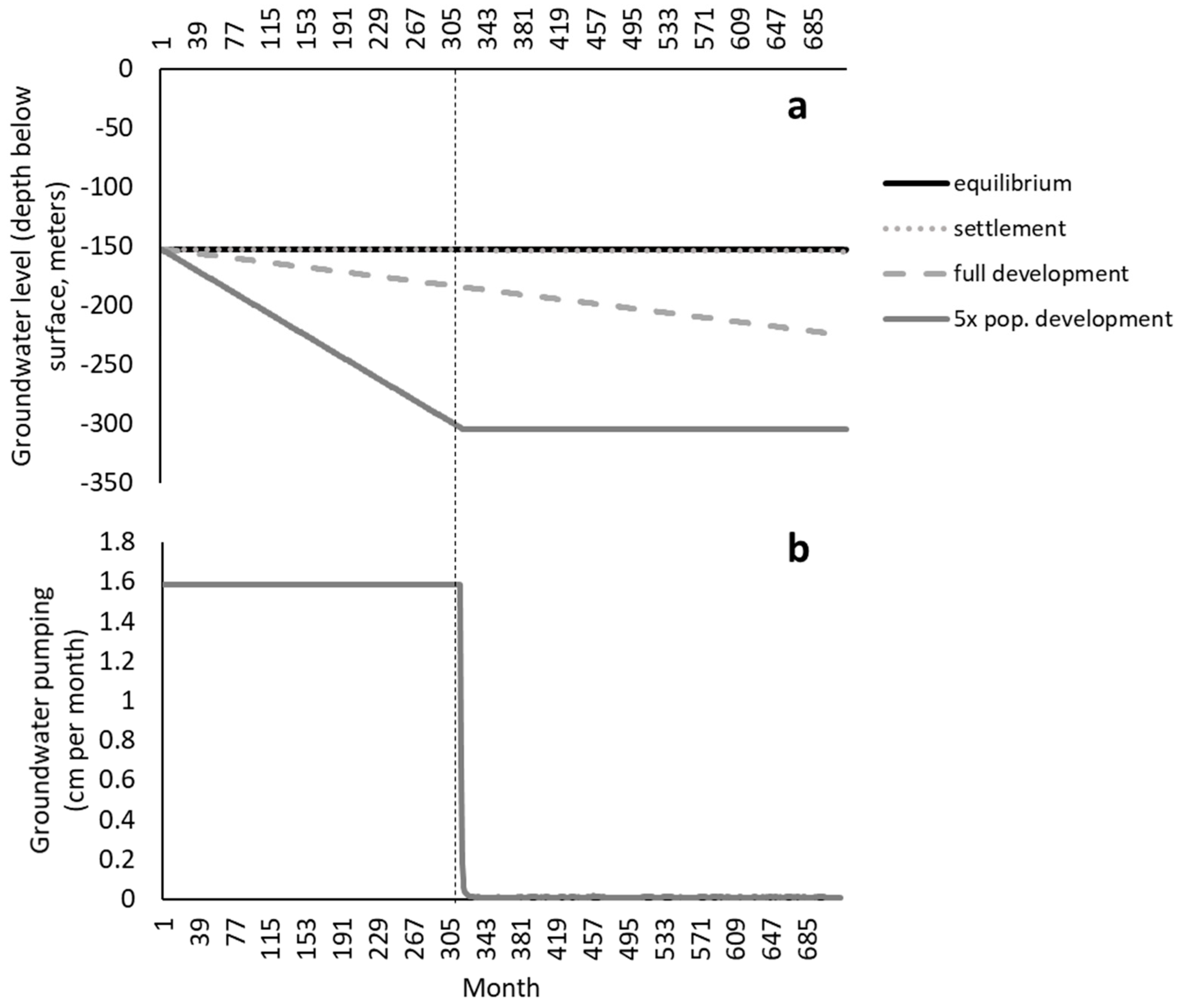
4.2. Model Assessment
- Average recharge (inflow) with no pumping (outflow).
- No recharge (inflow) with pumping (outflow) given surface development in a settlement phase (5% land in agriculture with base demand of 2.4 cm per month, consumptive human use of 1.27 cm per month and industrial use of 2.54 cm per month).
- No recharge (inflow) with pumping (outflow) given the surface completely developed (100% land in agriculture with base demand of 30.48 cm per month, consumptive human use of 6.35 cm per month and industrial use of 12.7 cm per month).
- No recharge (inflow) with pumping (outflow) given the surface fully developed (same parameter values as above) with five times the population demand on consumptive municipal use.
4.3. Experimental Simulation Design
- Improved irrigation efficiency (25%, 50%, 75% reduction in base irrigation demand due to improvements in irrigation efficiency).
- Policies restricting pumping rates in the municipal and industrial sectors (up to 25% reduction in the growth in pumping rates from the base case).
- Cooperative conservation (whereby base agricultural demand in permanently lowered but per capita water consumption is reduced in proportion to agricultural shortfalls during drought to maintain agricultural production). The test represented a feedback loop tradeoff which starts with agriculture base irrigation demand being dropped, but when precipitation declines and stresses agricultural systems, municipal and industrial will proactively conserve.
- A combination treatment which included cooperative conservation, 50% improvement in irrigation efficiency, and 25% pumping rate reduction in municipal and industrial sectors.
5. Results
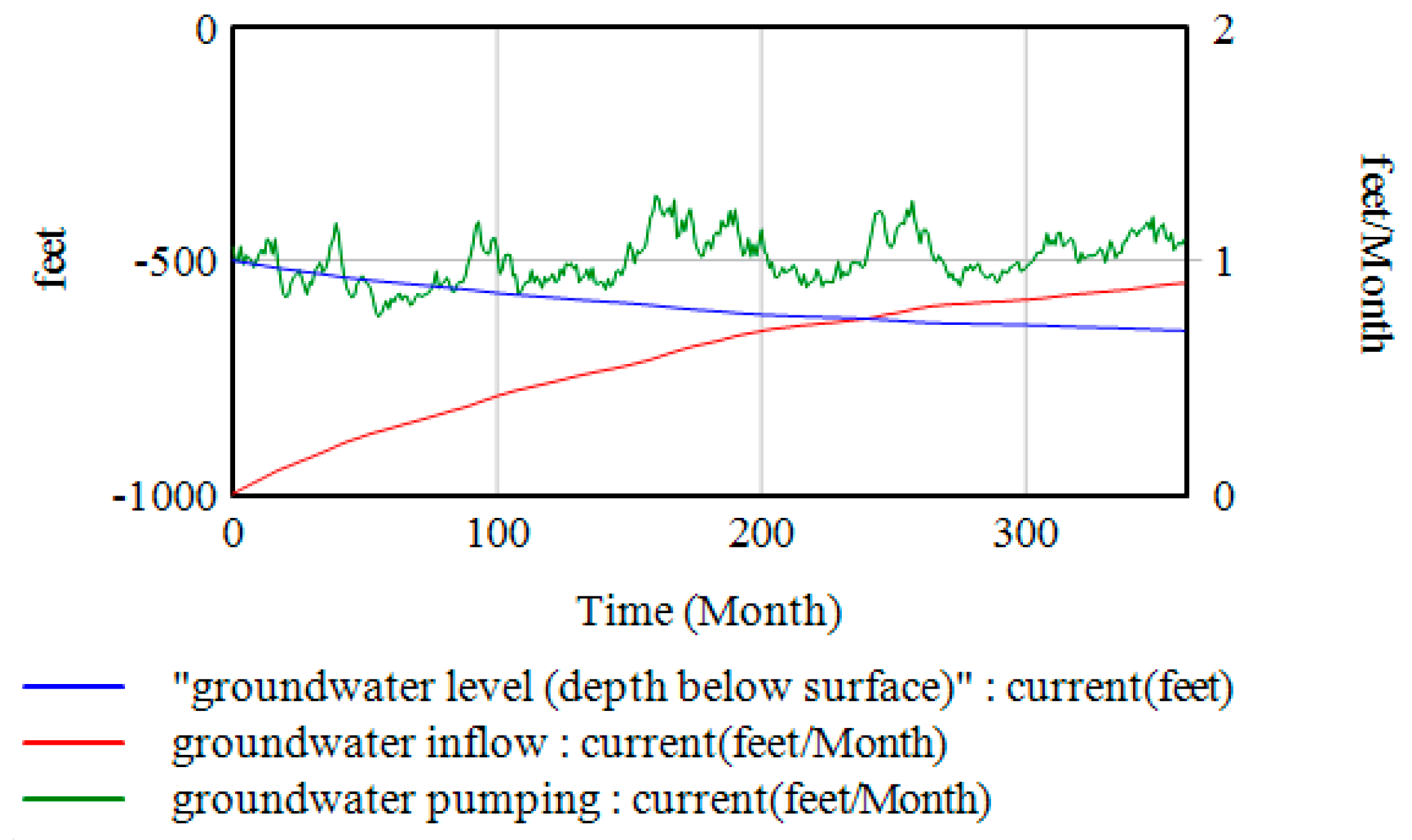
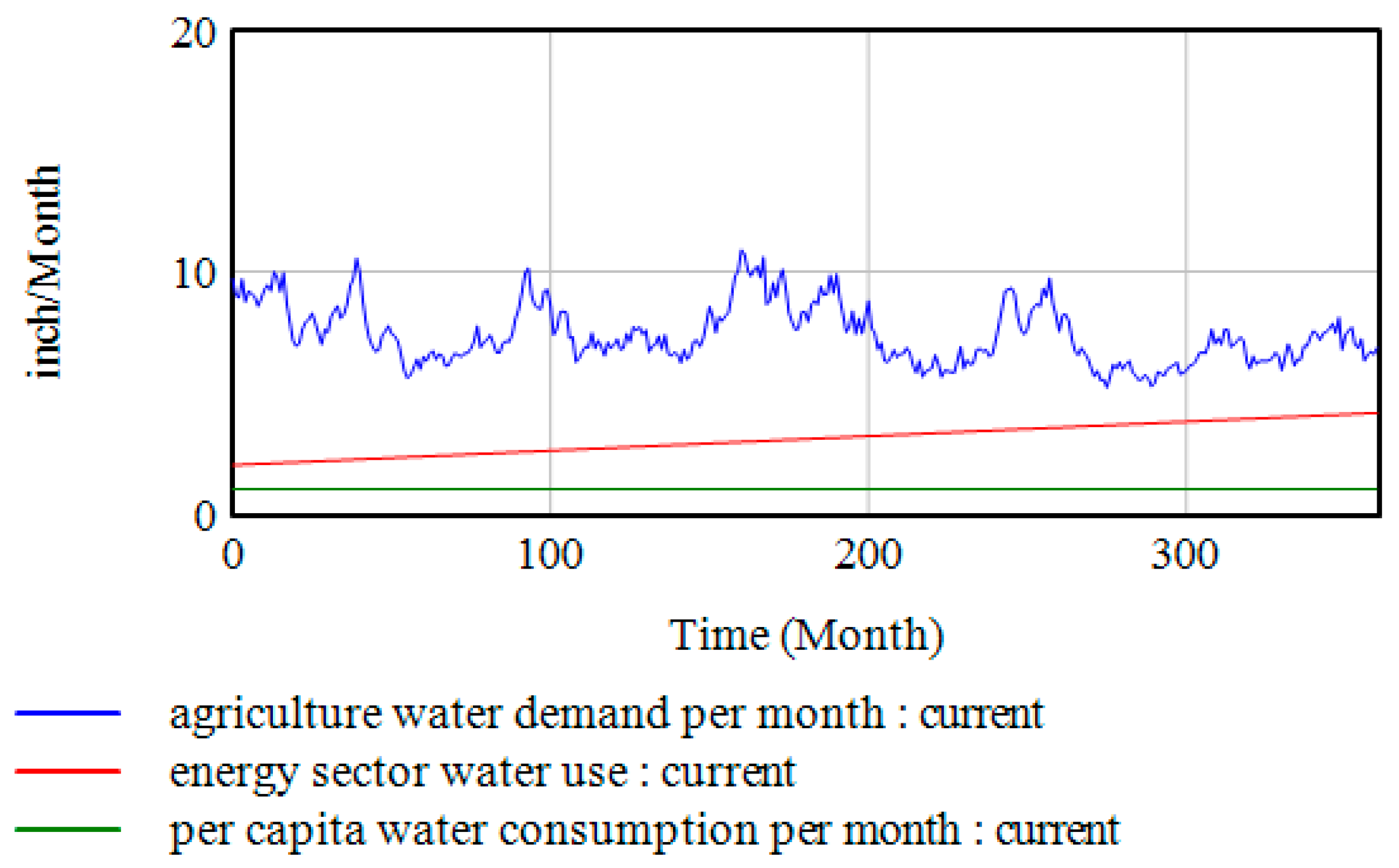
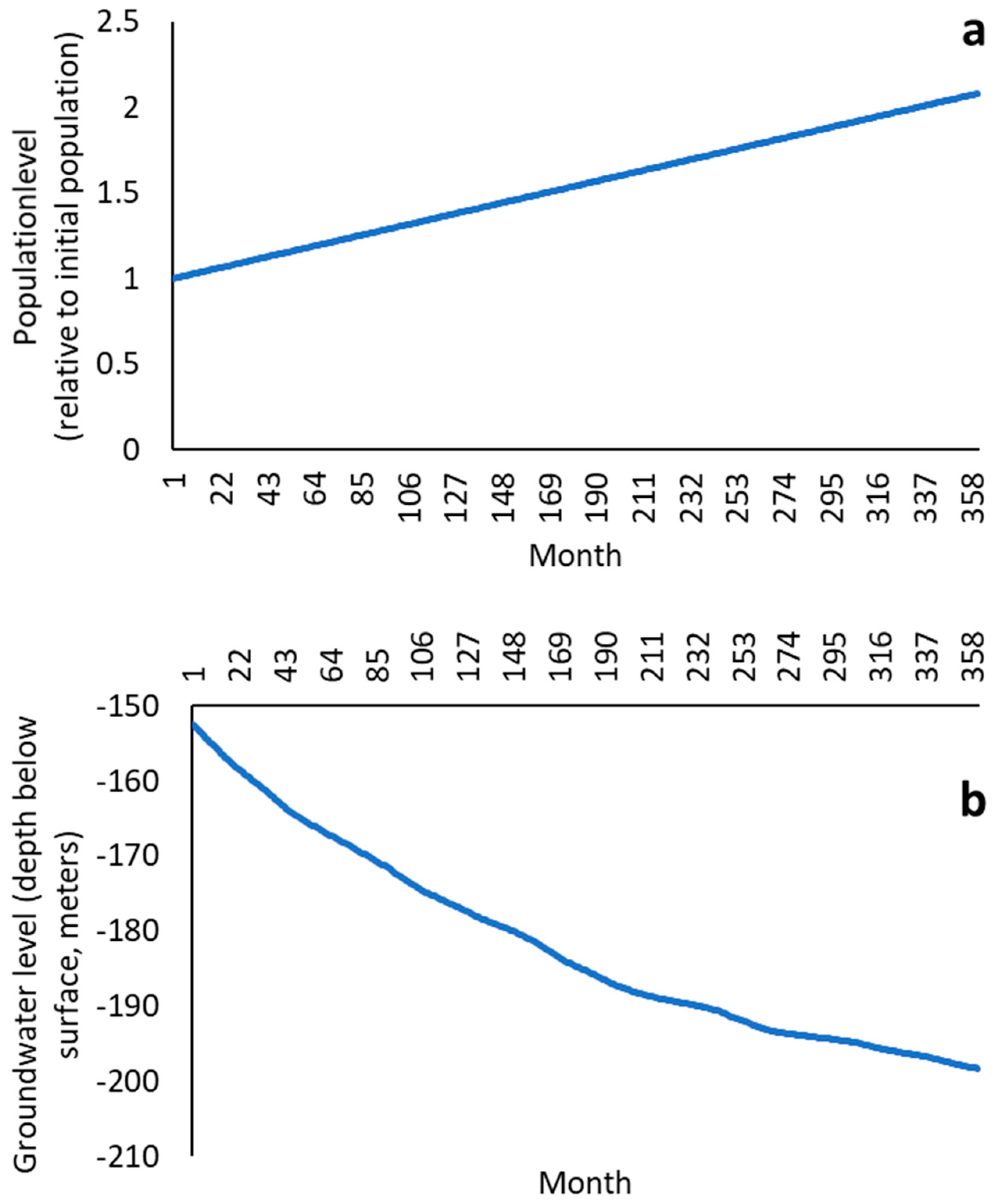
5.1. Model Assessment Results
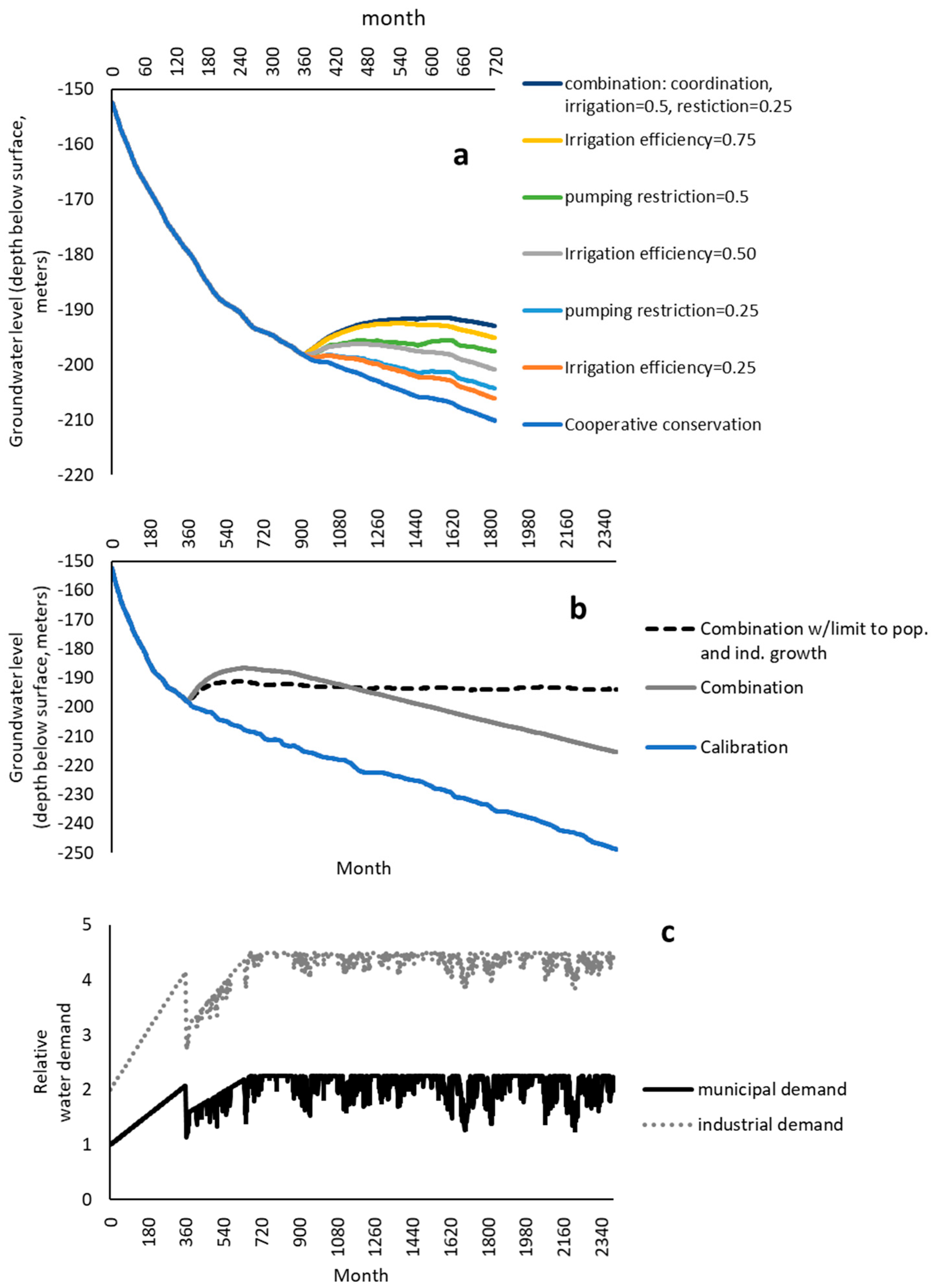
5.2. Experimental Simulation Results
5.3. Systems Thinking as a Methodology to Explore the Groundwater–Ecosystem Service Nexus
5.4. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Serrano, S.E. Hydrology for Engineers, Geologists, and Environmental Professionals; HydroScience: Lexington, KY, USA, 2010. [Google Scholar]
- Griebler, C.; Avramov, M.; Hose, G. Groundwater ecosystems and their services: Current status and potential risks. In Atlas of Ecosystems Services: Drivers, Risks, and Societal Responses; Springer: Berlin/Heidelberg, Germany, 2019; pp. 197–203. [Google Scholar]
- Vollmer, D.; Kremena, B.; Esmail, B.A.; Guerrero, P.; Nagabhatla, N. Incorporating ecosystem services into water resources management—Tools, policies, promising pathways. Environ. Manag. 2022, 69, 627–635. [Google Scholar] [CrossRef] [PubMed]
- Russo, T.A.; Lall, U. Depletion and response of deep groundwater to climate-induced pumping variability. Nat. Geosci. 2017, 10, 105–108. [Google Scholar] [CrossRef]
- Turner, B.L.; Menendez, H.M., III; Gates, R.; Tedeschi, L.O.; Atzori, A.S. System dynamics modeling for agricultural and natural resource management issues: Review of some past cases and forecasting future roles. Resources 2016, 5, 40. [Google Scholar] [CrossRef]
- Ford, A. Modeling the Environment; Island Press: Washington, DC, USA, 2010. [Google Scholar]
- Reid, W.V.; Mooney, H.A.; Cropper, A.; Capistrano, D.; Carpenter, S.R.; Chopra, K.; Dasgupta, P.; Dietz, T.; Duraiappah, A.K.; Hassan, R.; et al. Millennium Ecosystem Assessment. Ecosystems and Human Well-Being: Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Mpanga, I.K.; Idowu, O.J. A decade of irrigation water use trends in Southwestern USA: The role of irrigation technology, best management practices, and outreach education programs. Agric. Water Manag. 2021, 243, 106438. [Google Scholar] [CrossRef]
- Döll, P.; Fiedler, K. Global-scale modeling of groundwater recharge. Hydrol. Earth Syst. Sci. 2008, 12, 863–885. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Williams, J.; Perry, C.J.; Molle, F.; Ringler, C.; Steduto, P.; Udall, B.; Wheeler, S.A.; Wang, Y.; Garrick, D.; et al. The paradox of irrigation efficiency. Science 2018, 361, 748–750. [Google Scholar] [CrossRef]
- Lezzaik, K.; Milewski, A.; Mullen, J. The groundwater risk index: Development and application in the Middle East and North Africa region. Sci. Total Environ. 2018, 628–629, 1149–1164. [Google Scholar] [CrossRef]
- Asadi, A.; Barati, A.A.; Kalantari, K. Analyzing and modeling the impacts of agricultural land conversion in Iraan. Bus. Manag. Rev. 2014, 4, 110–118. [Google Scholar]
- Steward, D.R.; Bruss, P.J.; Yang, X.; Staggenborg, S.A.; Welch, S.M.; Apley, M.D. Tapping Unsustainable Groundwater Stores for Agricultural Production in the High Plains Aquifer of Kansas, projections to 2110. Proc. Natl Acad. Sci. USA 2013, 10, E3477–E3486. [Google Scholar] [CrossRef]
- Partridge, T.; Winter, J.; Kendall, A.; Basso, B.; Pei, L.; Hyndman, D. Irrigation benefits outweigh costs in more US croplands by mid-century. Commun. Earth Environ. 2023, 4, 274. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Gowda, P.H.; Marek, T.H.; Porter, D.O. Irrigation in the Texas High Plains: A brief history and potential reductions in demand. J. Int. Comm. Irrig. Drain. 2009, 58, 257–274. [Google Scholar] [CrossRef]
- Lauer, S.; Sanderson, M.R.; Manning, D.T.; Suter, J.F.; Hrozencik, R.A.; Guerrero, B.; Golden, B. Values and groundwater management in the Ogallala Aquifer region. J. Soil Water Conserv. 2018, 73, 593–600. [Google Scholar] [CrossRef]
- Griebler, C.; Brielmann, H.; Haberer, C.M.; Kaschuba, S.; Kellermann, C.; Stumpp, C.; Hegler, F.; Kuntz, D.; Hertkorn, S.W.; Lueders, T. Potential impacts of geothermal energy use and storage of heat on groundwater quality, biodiversity, and ecosystem processes. Environ. Earth Sci. 2016, 75, 1391. [Google Scholar] [CrossRef]
- Tissen, C.; Benz, S.A.; Menberg, K.; Bayer, P.; Blum, P. Groundwater temperature anomalies in central Europe. Environ. Res. Lett. 2019, 14, 104012. [Google Scholar]
- Gleeson, T.; Wada, Y.; Bierkens, M.F.P.; Van Beek, L.P.H. Water balance of global aquifers revealed by groundwater footprint. Nature 2012, 488, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Gleeson, T.; Befus, K.M.; Jasechko, S.; Luijendijk, E.; Cardenas, M.B. The global volume and distribution of modern groundwater. Nat. Geosci. 2015, 9, 161–167. [Google Scholar]
- Vigerstol, K.L.; Aukema, J.E. A comparison of tools for modeling freshwater ecosystem services. J. Environ. Manag. 2011, 92, 2403–2409. [Google Scholar]
- FAO. Shared Global Vision for Groundwater Governance 2030 and a Call-for-Action; Groundwater Governance: A Global Framework for Action; FAO: Rome, Italy, 2015. [Google Scholar]
- Qiu, J.; Wardropper, C.B.; Rissman, A.R.; Turner, M.G. Spatial fit between water quality policies and hydrologic ecosystem services in an urbanizing agricultural landscape. Landsc. Ecol. 2017, 32, 59–75. [Google Scholar] [CrossRef]
- Larned, S.T. Phreatic groundwater ecosystems: Research frontiers for freshwater ecology. Freshw. Biol. 2012, 57, 885–906. [Google Scholar] [CrossRef]
- Hutchins, B.T. The Conservation Status of Texas groundwater invertebrates. Biodivers. Conserv. 2017, 27, 475–501. [Google Scholar] [CrossRef]
- Cook, B.R.; Spray, C.J. Ecosystem services and integrated water resource management: Different paths to the same end? J. Environ. Manag. 2012, 109, 93–100. [Google Scholar] [CrossRef]
- Herrera-Franco, G.; Montalván-Burbano, N.; Carrion-Mero, P.; Bravo-Montero, L. Worldwide research on socio-hydrology: A bibliometric analysis. Water 2021, 13, 1283. [Google Scholar] [CrossRef]
- Gu, J.; Sun, S.; Wang, Y.; Li, X.; Sun, J.; Qi, X. Sociohydrology: An effective way to reveal the coupled evolution of human and water Systems. Water Resour. Manag. 2021, 35, 4995–5010. [Google Scholar] [CrossRef]
- Breyer, B.; Zipper, S.C.; Qui, J. Sociohydrological impacts of water conservation under anthropogenic drought in Austin, TX (USA). Water Resour. Res. 2018, 54, 3062–3080. [Google Scholar] [CrossRef]
- Gunda, T.; Turner, B.L.; Tidwell, V.C. The influential role of sociocultural feedbacks on community-managed irrigation system behaviors during times of water stress. Water Resour. Res. 2018, 54, 2697–2714. [Google Scholar] [CrossRef]
- Turner, B.L.; Tidwell, V.; Fernald, A.; Rivera, J.A.; Rodriguez, S.; Guldan, S.; Ochoa, C.; Hurd, B.; Boykin, K.; Cibils, A. Modeling acequia irrigation systems using system dynamics: Model development, evaluation, and sensitivity analyses to investigate effects of socio-economic and biophysical feedbacks. Sustainability 2016, 8, 1019. [Google Scholar] [CrossRef]
- Turner, B.L.; Tidwell, V.C.; Fernald, A.; Rivera, J.A.; Rodriguez, S.; Gulden, S.; Ochoa, C.; Hurd, B.; Boykin, K.; Cibils, A. Connection and Integration: A Systems Approach to Exploring Acequia Community Resiliency. In Southwestern United States: Elements of Resilience; New Mexico State University: Las Cruces, NM, USA, 2021; p. 58. [Google Scholar]
- Stroh, D.P. Systems Thinking for Social Change: A Practical Guide to Solving Complex Problems, Avoiding Unintended Consequences, and Achieving Lasting Results; Chelsea Green Publishing: Chelsea, VT, USA, 2015. [Google Scholar]
- Ford, D.N. A system dynamics glossary. Syst. Dyn. Rev. 2019, 35, 369–379. [Google Scholar] [CrossRef]
- Texas Almanac Aquifers of Texas. Available online: https://www.texasalmanac.com/articles/aquifers-of-texas (accessed on 5 December 2022).
- Texas Water Development Board. Aquifers of Texas, Report 380. Available online: https://www.twdb.texas.gov/groundwater/aquifer/index.asp (accessed on 8 December 2024).
- Environment Defense Fund. Available online: https://edf.org/media/texas-groundwater-supplies-are-danger-reports-say (accessed on 5 December 2022).
- Texas Tribune. Available online: https://www.texastribune.org/2013/05/07/texas-groundwater-dropped-sharply-amid-droughtstud/ (accessed on 5 December 2022).
- Holzer, T.L. Preconsolidation stress of aquifer systems in areas of induced land subsidence. Water Resour. Res. 1981, 17, 693–703. [Google Scholar] [CrossRef]
- Baddour, D.; New Study Shows Rate of Groundwater Decline Slowing in Texas. Energy and Environment Reporting for Texas. National Public Radio 2014 (July 17). Available online: https://stateimpact.npr.org/texas/2014/07/17/new-study-shows-rate-of-groundwater-decline-slowing-in-texas/ (accessed on 5 December 2022).
- Federal Reserve Bank of Dallas. Available online: https://dallasfed.org/research/swe/2020/swe20001 (accessed on 5 December 2022).
- Rosepiler, M.J.; Reilinger, R. Land subsidence due to water withdrawal in the vicinity of Pecos, Texas. Eng. Geol. 1977, 11, 295–304. [Google Scholar] [CrossRef]
- Chauduri, S.; Ale, S. Long-term (1930–2010) trends in groundwater levels in Texas: Influences of soils, land cover and water use. Sci. Total Environ. 2014, 490, 379–390. [Google Scholar] [CrossRef] [PubMed]
- Texas Water Development Board. Available online: https://www.waterdatafortexas.org/groundwater (accessed on 8 December 2024).
- NOAA National Centers for Environmental Information. Available online: https://www.ncei.noaa.gov/access/monitoring/climate-at-a-glance/statewide/time-series (accessed on 4 June 2024).
- United States Census Bureau. Available online: https://www.census.gov/data/tables-series/dec/popchange-data-text.html (accessed on 1 May 2021).
- USDA National Agricultural Statistics Service. Available online: https://quickstats.nass.usda.gov/ (accessed on 8 December 2024).
- Flores-Lopez, C.; Turner, B.L.; Hanagriff, R.; Bhandari, A.; Sinha, T. South Texas Water Resource Mental Models: A Systems Thinking, Multi-stakeholder Case Study. J. Contemp. Water Res. Educ. 2022, 176, 15–35. [Google Scholar] [CrossRef]
- De Brito Neto, R.; Santos, C.A.G.; Mulligan, K.; Barbato, L. Spatial and temporal water-level variations in the Texas portion of the Ogallala Aquifer. Nat. Hazards 2016, 80, 351–365. [Google Scholar] [CrossRef]
- Runkle, J.; Kunkel, K.E.; Nielson-Gammon, J.; Frankson, R.; Champion, S.M.; Stewart, B.C.; Romolo, L.; Sweet, W. Texas State Climate Summary; NOAA Technical Report NESDIS 150-TX: Silver Spring, MD, USA, 2022; p. 5. [Google Scholar]
- United States Department of Agriculturee. Available online: https://www.nass.usda.gov/Publications/AgCensus/2012/Online_Resources/Farm_and_Ranch_Irrigation_Survey/ (accessed on 20 October 2019).
- U.S. Department of Agriculture, Economic Research Service. Available online: https://www.ers.usda.gov/topics/farm-economy/farm-sector-income-finances/ (accessed on 7 February 2024).
- Haacker, E.M.K.; Catterman, K.A.; Smidt, S.J.; Kendall, A.D.; Hyndman, D.W. Effects of Management areas, drought, and commodity prices on groundwater decline patterns across the High Plains Aquifer. Agric. Water Manag. 2019, 218, 259–273. [Google Scholar] [CrossRef]
- Watershed Association. Available online: https://wimberlywatershed.org (accessed on 5 December 2022).
- Sustainable Statewide Water Resources Management in Texas. Available online: https://wrap.engr.tamu.edu (accessed on 5 December 2022).
- Forrester, J.W. Principles of Systems; Wright Allen Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Sterman, J. Business Dynamics, Systems Thinking and Modeling for a Complex World; Irwin/McGraw-Hill: Chicago, IL, USA, 2000. [Google Scholar]
- Eberlein, R.L.; Peterson, D.W. Understanding models with Vensim™. Eur. J. Oper. Res. 1992, 59, 216–219. [Google Scholar] [CrossRef]
- Barati, A.A.; Azadi, H.; Scheffran, J. A system dynamics model of smart groundwater governance. Agric. Water Manag. 2019, 20, 502–518. [Google Scholar] [CrossRef]
- Giordano, R.; Brugnach, M.; Vurro, M. System Dynamic Modelling for Conflicts Analysis in Groundwater Management. In Proceedings of the International Congress on Environmental Modelling and Software, Leipzig, Germany, 1 July 2012; p. 105. [Google Scholar]
- Turner, B.L.; Kodali, S. Soil system dynamics for learning about complex, feedback-driven agricultural resource problems: Model development, evaluation, and sensitivity analysis of biophysical feedbacks. Ecol. Model. 2020, 428, 109050. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Laio, F.; Ridolfi, L. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Turner, B.L. Model laboratories: A quick-start quide for design of simulation experiments for dynamic systems models. Ecol. Model. 2020, 434, 109246. [Google Scholar] [CrossRef]
| Dimension | Description |
|---|---|
| Model boundary | Groundwater, its flows, and how groundwater level feeds back to influence future flows (endogenous) Precipitation, population, and irrigation and industrial demand (exogenous) Population and economics and policy feedback processes (excluded) |
| Key variables | Groundwater level, recharge rate, groundwater pumping, cost of pumping feedback on water demands |
| Time parameters | Time unit = 1 month, Time-step = 0.25 months, Time horizon = 360 months |
| Variable or Parameter | Type | Equation or Parameter Value | Equation in Text | Unit |
|---|---|---|---|---|
| Groundwater level | stock | =INTEG (recharge rate-groundwater pumping-groundwater retransmission) | (1) | m |
| Initial groundwater level (depth below surface) | aux | 150 1 | (2) | m |
| Distance to aquifer floor | aux | 300 2 | (3) | m |
| Groundwater retransmission | flow | IF (groundwater level > max groundwater storage), THEN (groundwater level-max groundwater storage)/mean transmission time, ELSE (-groundwater inflow) | (4) | m/month |
| Maximum groundwater flow rate | aux | 0.03 3 | (5) | m/month |
| Mean transmission time | aux | 1/30 3 | (6) | month |
| Recharge rate | flow | rainfall applied * recharge fraction of available precip | (7) | m/month |
| Recharge fraction of available precip | aux | 0.037 4 | (8) | dmnl |
| Groundwater pumping | flow | adjusted water demand per month | (9) | m/month |
| Agriculture demand per month | aux | “acres in irrigation (fraction of total area)” * applied irrigation demand per month*irrigation season | (10) | m/month |
| Acres in irrigation (fraction of total area) | aux | 0.75 5 | (11) | dmnl |
| Applied irrigation demand per month | aux | base water demand per land area per month * cost of pumping feedback on water demands * precipitation pressure on agriculture | (12) | m/ha/month |
| Base water demand per land area per month | aux | 0.3048 5 | (13) | m/ha/month |
| Precipitation pressure on agriculture | aux | mean precipitation/precipitation trend | (14) | dmnl |
| Cost of pumping feedback on water demand | aux | LOOKUP (“groundwater level (depth below surface)”, ([(−750,0)–(0,2)], (−750,0.5), (−500,1), (0,2)) | (15) | dmnl |
| Total industrial use | aux | base industrial sector demand + RAMP(slope of industrial use, INITIAL TIME, FINAL TIME) | (16) | m/month |
| Base industrial sector demand | aux | 0.05 3 | (17) | m/month |
| Slope of industrial use | aux | 0.006 3 | (18) | dmnl/month |
| Total urban and residential water use | aux | Population ratio to initial * per capita water consumption per month | (19) | m/month |
| Population ratio to initial | aux | 1 + RAMP(0.003, INITIAL TIME, FINAL TIME) | (20) | dmnl |
| Per capita water consumption per month | aux | 0.025 6 | (21) | m/month |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leal, J.; Bishop, M.; Reed, C.; Turner, B.L. An Exploration of Groundwater Resource Ecosystem Service Sustainability: A System Dynamics Case Study in Texas, USA. Systems 2024, 12, 583. https://doi.org/10.3390/systems12120583
Leal J, Bishop M, Reed C, Turner BL. An Exploration of Groundwater Resource Ecosystem Service Sustainability: A System Dynamics Case Study in Texas, USA. Systems. 2024; 12(12):583. https://doi.org/10.3390/systems12120583
Chicago/Turabian StyleLeal, Julianna, Morgan Bishop, Caleb Reed, and Benjamin L. Turner. 2024. "An Exploration of Groundwater Resource Ecosystem Service Sustainability: A System Dynamics Case Study in Texas, USA" Systems 12, no. 12: 583. https://doi.org/10.3390/systems12120583
APA StyleLeal, J., Bishop, M., Reed, C., & Turner, B. L. (2024). An Exploration of Groundwater Resource Ecosystem Service Sustainability: A System Dynamics Case Study in Texas, USA. Systems, 12(12), 583. https://doi.org/10.3390/systems12120583








