Abstract
Reducing salt intake is a vital public health measure for combating noncommunicable diseases and mitigating rising social security expenditures in Japan. We developed a system dynamics model to analyze the potential health and cost effects of salt reduction interventions among the Japanese population aged 40 years and above from 2012 to 2040. The simulation findings derived from the model indicate that, in the base run, the disability-adjusted life years (DALYs) for cardiovascular disease (CVD) and chronic kidney disease (CKD) are projected to be approximately 55 and 9.5 per 100,000 people, respectively, contributing approximately 40 trillion yen in social security expenditures by 2040. The model predicts that implementing mandatory reformulation could decrease DALYs for CVD and CKD by 5.7% and 6.2%, respectively, resulting in an approximately 6.7% reduction in social security expenditure. Additionally, voluntary reformulation is estimated to reduce the DALYs for CVD and CKD by 4.7% and 5.2%, leading to a 5.6% decrease in social security expenditure. Finally, accelerating the adoption of a low-salt diet is expected to lower the DALYs for CVD by 2.8% and CKD by 3.2%, thereby reducing social security expenditures by 3.4%. Thus, product reformulation initiatives have a greater impact on health and economic outcomes.
1. Introduction
Excessive salt consumption is a significant dietary risk factor for noncommunicable diseases (NCDs), especially cardiovascular disease (CVD) and chronic kidney disease (CKD) [1], which are the leading causes of death and disability in Japan [2]. In 2021, it was estimated that CVD accounted for around 6 million disability-adjusted life years (DALYs) in Japan, with about 16 million cases of morbidity and 0.37 million deaths. In the same year, CKD resulted in approximately 0.92 million DALYs, with 23 million cases of morbidity and 0.05 million deaths [3]. These NCDs not only affect individual health but also place a significant financial strain on Japan’s healthcare system, comprising more than 30% of the national healthcare costs [4], which is further exacerbated by the country’s rapidly aging population. As of 2021, approximately 29% of Japan’s population was aged 65 years or older [5]. In response to this growing concern, the World Health Organization (WHO) recommends a 30% reduction in average salt intake by 2025 [6], targeting a salt intake of less than 5 g per person per day [7]. In line with global efforts, the Japanese government has prioritized salt reduction in its national health promotion campaigns. The “Health Japan 21 (Second Term),” launched in 2013, aimed to reduce adult salt intake to 8 g per day by 2022 [8]. The subsequent “Health Japan 21 (Third Term)” further lowered this target to 7 g per day by 2032 [9].
Despite global and national initiatives, excessive salt intake has been observed in several countries [10]. In Japan, the problem is particularly pronounced, with the average daily salt intake remaining at approximately 10 g as of 2019 [11], exceeding both the national [8] and global [7] targets. This high salt intake is largely attributable to the traditional Japanese diet, which includes seasonings, such as miso, soy sauce, and salt, contributing to approximately 70 percent of the daily salt intake [12]. Achieving salt reduction targets requires a collaborative approach involving various stakeholders, including the food industry [13]. In Japan, industry-government-academia partnerships are working to increase the availability of healthier food options, particularly reduced-salt products [14,15]. The WHO advocates food product reformulation as a cost-effective strategy for reducing NCDs [16] and has provided global sodium benchmarks to guide national targets and accelerate reformulation efforts [17]. Evidence shows that reducing salt in packaged foods can lead to significant health improvements and economic benefits, including a reduced disease burden and lower healthcare costs [18,19,20,21]. Supporting this, a previous study in Japan emphasized that lowering daily salt intake through reformulation and other interventions can substantially enhance public health outcomes [22].
System dynamics modeling has been extensively applied in previous studies on healthcare [23,24,25] and public health policies [26,27,28,29]. A significant example is the Prevention Impacts Simulation Model (PRISM) [30], a large system dynamics model designed to predict long-term health outcomes and evaluate the cost-effectiveness of population-level interventions in the United States from 1990 to 2040. This model has been adapted in several countries to assess various CVD intervention policies. For instance, system dynamics models applied in public health studies in New Zealand [31] and Singapore [28,32] have utilized PRISM as a guide. A recent study by George et al. [33] employed system dynamics modeling to simulate the effects of thirteen preventive interventions on health status, healthcare utilization, and costs in the population of Kent in southeast England. However, the method has been relatively underutilized in addressing public health issues in Japan, particularly in the prevention of NCDs. In Japan [34], there is only one study that has used an age-specific system dynamics model to examine the long-term impact of reduced salt intake on cardiovascular mortality between 1950 and 2017. Thus, this study aimed to utilize system dynamics modeling to assess the long-term effects of salt reduction interventions on the prevention of CVD and CKD, as well as on mitigating rising social security expenditures at the national level in Japan.
2. Materials and Method
2.1. System Dynamics Simulation Model
We applied a system dynamics simulation model to predict the long-term effects of salt reduction policies on the prevention of CVD and CKD, as well as their impact on social security expenditures by lowering blood pressure. In this study, we developed and validated the simulation model using Vensim DSS 10.2.0 [35].
System dynamics is an approach to analyze the behavior of complex systems over time, revealing how various entities influence each other. It is a particularly effective tool for long-term policy analysis because it considers indirect relationships and feedback loops to reproduce the behavior of complex problems [36]. This method captures both the structure and dynamics of a system, helping researchers and policymakers understand the effects of changes and anticipate the impact of interventions, especially in conditions where pathways to outcomes may be indirect, delayed, or influenced by nonlinear feedback loops [37].
System dynamics modeling typically encompasses both qualitative and quantitative components. The qualitative aspect often involves creating causal loop diagrams (CLDs) to visualize causal interactions within a system [38]. CLDs use causality links and feedback loops to map how different variables influence each other, with arrows indicating causal relationships. Each arrow indicates a causal link between the independent variable at its tail and the dependent variable at its head. There are two types of feedback processes [37]: reinforcing, in which all the arrows are positive or there is an even number of negative arrows, and balancing, in which there is an odd number of negative arrows. Reinforcing feedback processes drive exponential growth or decay in the system, whereas balancing feedback processes counteract these changes until the system reaches equilibrium.
The quantitative aspect involves constructing stock and flow diagrams to encapsulate how the system elements interact and change over time. In these diagrams, the stocks represented by box-shaped icons denote elements that accumulate or are depleted, such as the number of individuals with a disease or the volume of water in a reservoir. The flows depicted by double arrows entering (inflows) and exiting (outflows) the stock represent the movement of entities that cause changes in the stock level. For instance, in an epidemiological study, a stock may represent disease prevalence, with inflows indicating new cases and outflows representing deaths or recoveries.
2.2. Model Conceptualization
We developed a conceptual framework for our system dynamics model to assess the effects of interventions targeting salt intake reduction (Figure 1). The model comprises four components: salt intake reduction interventions, salt intake, noncommunicable diseases, and social security costs. Within the salt intake reduction intervention component, we considered two approaches: (1) promoting the adoption of low-salt diets among the population, and (2) reformulating food products by companies to reduce salt content. The primary outcome of interest for the salt intake component was the average dietary salt intake among adults in Japan, which was influenced by both the adoption of low-salt diets and food reformulation. The noncommunicable disease component examines the incidence and prevalence of hypertension, CVD, and CKD, with CVD and CKD being indirectly affected by salt intake through its impact on elevated blood pressure. The social security cost component includes the medical and long-term care costs covered by the social security system. We expect salt reduction interventions to decrease the disease prevalence and associated costs.
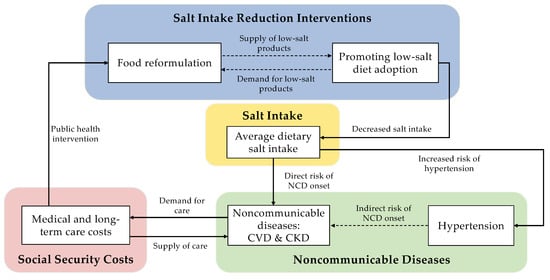
Figure 1.
Conceptual framework of the system dynamics simulation model for evaluating the health and economic effects of salt reduction interventions. Solid arrows indicate causal relations between sectors, and dashed arrows represent causal relations within sectors. CKD, chronic kidney disease; CVD, cardiovascular disease; NCD, noncommunicable disease.
2.3. Dynamic Hypothesis
To formulate the dynamic hypotheses, we constructed a CLD as a qualitative component of our system dynamics model (Figure 2). The CLD includes two reinforcing loops (R1 and R2) and two balancing loops (B1 and B2). In our dynamic hypothesis, we assume that people who are aware of the need to consume less salt in their diet tend to purchase the low-salt products available in the market. This growing demand for these products leads to higher consumption, fostering wider adoption of low-salt diets within the population (R1). As demand for the products continues to increase, the food industry is incentivized to reformulate food products. Subsequently, this expanded supply of low-salt options further boosts overall consumption, as more people are inclined to purchase them (R2), thus reinforcing the cycle.
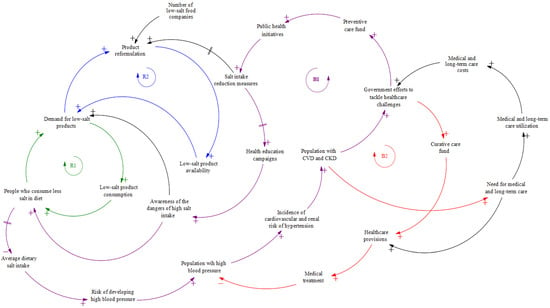
Figure 2.
Causal loop diagram of the system dynamics model for evaluating the health and economic effects of salt reduction policies in Japan. R1, reinforcing loop for low-salt product market growth (green); R2, reinforcing loop for product reformulation (blue); B1, balancing loop for public health awareness (purple); B2, balancing loop for medical treatment (red). The black arrow indicates the connection from the cause to the effect. Plus signs at the arrow-heads indicate that the connected variables change in the same direction, while minus signs indicate that they change in opposite directions. A double line on the arrows indicates a delay in the system. CKD, chronic kidney disease; CVD, cardiovascular disease.
Public health campaigns promoting a low-salt diet raise awareness about the hazards of excessive salt consumption and motivate people to reduce their salt intake. As more individuals recognize the importance of consuming less salt and begin to choose low-salt products, overall dietary salt intake decreases. This reduction lowers the likelihood of hypertension, reduces the incidence of CVD and CKD, and ultimately strengthens public health initiatives, concurrently supported by increased funding for preventive care (B1).
Excessive salt intake, which leads to high blood pressure, increases the incidence of chronic conditions, prompting the government to expand its social security budget for both curative and preventive care. Funding allocated for curative care enables more individuals with early-stage hypertension to receive prompt medical treatment. Early intervention helps prevent the progression of chronic conditions, thereby reducing the risk of developing noncommunicable diseases, such as CVD and CKD (B2).
2.4. Model Formulation
As a quantitative component of the system dynamics modeling, we built stock-flow diagrams based on the relationships outlined in the CLDs. These diagrams integrate five interconnected sectors: general population, dietary salt intake, NCDs, social security expenditures, and salt reduction interventions.
2.4.1. General Population Model
We constructed an aging-chain cohort population model based on age distribution, stratified by sex and 10-year age groups (40–49, 50–59, 60–69, 70–79, 80–89, and ≥90 years). In the model, these age groups are treated as sequentially related stock variables (Figure S1). To improve the model calibration, we included a stock variable representing individuals under the age of 40 in the demographic sector. The general population model incorporated birth, death, and net migration. The population size of each age cohort and sex [5] was calculated using the following equations (Table S1):
where denotes the population by age cohort, , and sex; represents male and female; index i = 0 refers to the cohort under age 40, while i > 0 refers to cohorts aged 40 and above; stands for the current year; represents the number of annual births; and represent net migration and deaths, respectively; denotes the outflow from the previous cohort to the next; and denotes the inflow rate into the next age cohort.
Births enter the model and are initially placed in the stock variable for individuals under 40 years of age, determined as follows:
where brj indicates the birth rate by sex (Table S3) [39]. FW represents the number of women aged 15–49 years and is calculated as follows:
where refers to the total number of women from the under-40 age group () to the 40s age group (). is the proportion of women of reproductive age.
Survivors in each cohort transition to the subsequent cohort, except for the final cohort of individuals aged 90 years and older, at a rate defined by the transition from the last year of the current cohort to the first year of the next (; e.g., age 49 to 50) as follows:
where represents the number of individuals by sex and age, indicates the average duration in each cohort (40 years for individuals under 40 years and 10 years for each 10-year age cohort), and denotes the fraction of the population of each age group. Non-survivors were removed from the model as outflows reflecting deaths based on age-specific mortality rates [40], which were assumed to be constant over time (Table S2). Net migration, the difference between immigration and emigration, was also factored into each cohort population. The net migration rates, which were constant and negative for emigration, were determined by age group (Table S2) [41].
2.4.2. Dietary Salt Intake Model
The dietary salt intake model illustrates the dynamics of salt consumption based on the current mean dietary salt intake [11] and the target for salt reduction (Figure 3) [8].
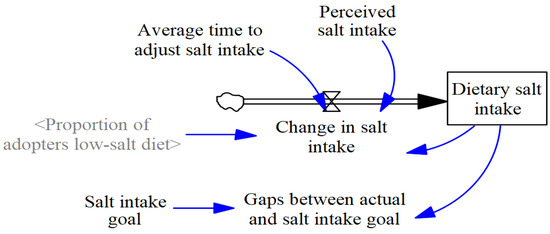
Figure 3.
Stock and flow diagram for the dietary salt intake model. Shadow variable, shown in gray font, represents original variable that appears elsewhere in the model. The cloud-like icon shows the sources of the flow outside the model. The pipe (double arrow) indicates flow that changes the value of stock (rectangle). The valve in the middle of the pipe controls flow. The blue arrow indicates the link between elements in the system.
Mathematically, the current mean salt intake is calculated as follows:
where indicates the mean salt intake at the beginning of the study period.
The rate of change in salt intake, denoted as , is calculated as follows:
where represents the ratio of perceived and actual mean salt intake, indicates the proportion of individuals adopting a low-salt diet, and represents the average adjustment time needed for the population to reduce salt consumption [42]. The model includes to assess the effect of adopting a low-salt diet on average dietary salt intake.
The difference between the salt intake target ( and the current mean salt intake level (), denoted as , was calculated as follows:
2.4.3. NCD Model
We developed an NCD model to demonstrate how dietary salt intake affects the prevalence of CVD and CKD by increasing blood pressure. The NCD model comprised three sub-models of hypertension, CVD, and CKD to project disease events and disabilities (Figures S2–S4). Similar to the general population model, the disease model was constructed as an aging chain process that varies by sex. The sub-models do not include recovery from diseases, considering that once individuals develop hypertension, CVD, or CKD, they will remain in that diseased state until death and will not revert to a susceptible state [43].
Hypertension Sub-Model
The hypertension sub-model (Figure S2) shows the transition of individuals from normal blood pressure to hypertension, describing how those initially classified as normotensive eventually become part of the hypertensive population. Aging is divided into two health states: normotensive (NHTN) and hypertensive (HTN). Individuals are considered to be NHTN if they have a systolic blood pressure < 140 mmHg and a diastolic blood pressure < 90 mmHg, or HTN if they have a systolic blood pressure ≥ 140 mmHg or a diastolic blood pressure ≥ 90 mmHg, or use antihypertensive medication [11].
Equation (9) expresses that the current state of the NHTN population, denoted as , increases with the proportion of NHTN individuals transitioning from the previous cohort (), while it decreases due to the onset of incident HTN cases (), deaths from non-hypertension events (), and the transition of the NHTN population to the next age cohort ().
Equation (10) indicates that the HTN population for each cohort (Table S4) [44] grows owing to HTN patients entering from the previous cohort () and incident cases of HTN (). It declines through death () and the transition of the HTN population to the next age cohort ().
Specifically, the incidence rate of HTN is the product of the normotensive population (, the risk of developing hypertension (, and the fraction of the new HTN population ( as follows:
Finally, the death rates are the product of the HTN population and the fractional mortality rates among HTN individuals, as indicated in Equation (12).
CVD Sub-Model
The CVD sub-model was based on the positive association between blood pressure and CVD risk (Figure S3). The current CVD population in each cohort (Table S4) [3] was calculated as follows:
where the prevalence increases with the proportion of patients with CVD entering from the previous cohort (), and the incidence of CVD associated with HTN and other risk factors (). The CVD population decreases due to death (Table S5) [3] and the proportion of the CVD population turning to the subsequent cohort (. The CVD incidence rate attributed to HTN was calculated as follows:
where indicates the fraction of the first incidence of CVD, and represents the proportion of the CVD population.
CKD Sub-Model
The estimated glomerular filtration rate (eGFR) has been used to define CKD and calculate the different stages of CKD in previous studies that applied system dynamics models [28,45]. Owing to the lack of data on eGFR, our study used the total CKD prevalence in Japan [3]. In general, the CKD sub-model was similar to the CVD sub-model (Figure S4), and the CKD population in each cohort (Table S4) [3] was calculated as follows:
where is the incidence of CKD associated with HTN, and is the incidence of CKD associated with CVD.
Disability-Adjusted Life Years
Our study incorporated disability-adjusted life years (DALYs) as health outcomes. We computed DALYs for each disease as the sum of years of life lost (YLLs) and years lived with a disability (YLDs) [2]. YLLs are defined as the number of years lost owing to premature death compared to the expected average lifespan. The YLLs for CVD and CKD () were calculated as follows:
where and indicate the average years of life lost due to CVD and CKD, respectively. The average years of life lost were calculated by dividing the years of life lost by the number of deaths (Tables S5–S8) [2], using both sets of data sourced from the Global Burden of Disease Study 2019 [3].
The YLDs are defined as the product of the prevalence of the disease and the weight of its disability. The YLDs for CVD () and CKD () were calculated as follows:
where and stand for disability weights for CVD and CKD, respectively. Disability weights reflect the severity of the condition and range from 0 (no loss or burden) to 1 (death) [46]. Disability weights were calculated by dividing the years lived with disability by disease prevalence (Tables S4–S8) [2].
2.4.4. Social Security Expenditure Model
Complications arising from CVD and CKD significantly impact expenditures from both the health sector and individual perspectives. Individual patients may incur high out-of-pocket costs for medications, frequent doctor visits, and potential loss of income due to illness, leading to economic hardship that affects their quality of life and access to necessary care. However, our simulation model did not account for costs borne by individuals. The social security expenditure model in Figure 4 outlines the structure of medical and long-term care (LTC) costs associated with diseases linked to excessive salt intake. It specifically illustrates how the growing population with noncommunicable diseases in Japan impacts annual spending on both the medical and long-term care sectors, represented as stock variables.
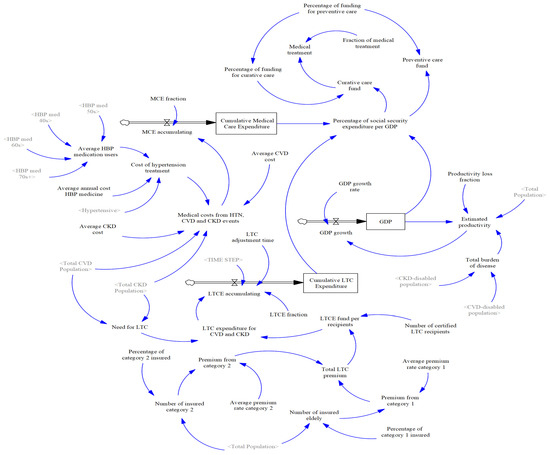
Figure 4.
Stock and flow diagram for the social security expenditures model. The shadow variable, shown in gray font, represents the original variable that appears elsewhere in the model. The cloud-like icon shows sources of the flow outside the model. The pipe (double arrow) indicates flow that changes the value of stock (rectangle). The valve in the middle of the pipe controls the flow. The blue arrow indicates the link between elements in the system. CKD, chronic kidney disease; CVD, cardiovascular disease; GDP, gross domestic product; HBP, high blood pressure; HTN, hypertension; LTC, long-term care; LTCE, long-term care expenditure; MCE, medical care expenditure.
Japan’s national medical care expenditure has grown steadily over the years, reaching 7.93% of its gross domestic product in 2019 [4]. In this study, we assumed that the stock variable for medical care expenditure (Table S9) [4] increases because of the treatment costs associated with individuals with hypertension, CVD, and CKD within the medical sector. Therefore, the annual accumulation rate of these costs () is calculated as follows:
where denotes the total medical treatment costs for hypertension, CVD, and CKD, and indicates the fraction of change in overall medical care spending.
The medical treatment costs were calculated as follows:
where ACCVD and ACCKD denote the average costs per patient for CVD and CKD [47], respectively, indicates the total costs for treating hypertension, denotes the average cost of antihypertensive medications [48], and represents the average number of hypertensive patients on medication [11].
Under the LTC insurance (LTCI) system, the primary source of funding for LTC comes from the premiums paid by insured individuals [49,50]. LTCI is divided into the first category of individuals aged 65 and older, and the second category of individuals aged 40–64 years, and each category has a different premium rate based on LTCI regulations [51]. Other sources for funding LTC, such as grants and investments, are excluded from the analysis as they fall outside the scope of this study. The following formula determines the growth in annual LTC expenditure (:
where represents the total long-term care costs for individuals with CVD and CKD. This includes expenses incurred by older people who require LTC. The percentage changes in LTC expenses and adjustment time are denoted as and , respectively. In addition, the social security expenditure model illustrates how social security costs can be divided into preventive and curative care costs. We assume that social security costs are allocated to preventive care to support public health initiatives, such as media campaigns for salt reduction, while they are allocated to curative care to cover medical treatments, helping increase the percentage of patients recovering from their conditions.
2.4.5. Salt Reduction Intervention Model
The salt reduction intervention model (Figure 5) builds on previous research in Japan [52] and generic innovation diffusion models showing that adopting an innovation ‘infects’ others who have not yet adopted it [37], a process known as social contagion or word of mouth. The model consists of two intervention sub-models. The upper part of Figure 5 illustrates the sub-model of health promotion campaigns to encourage the population to adopt low-salt food products and diets, while the lower part depicts the sub-model of product reformulation.
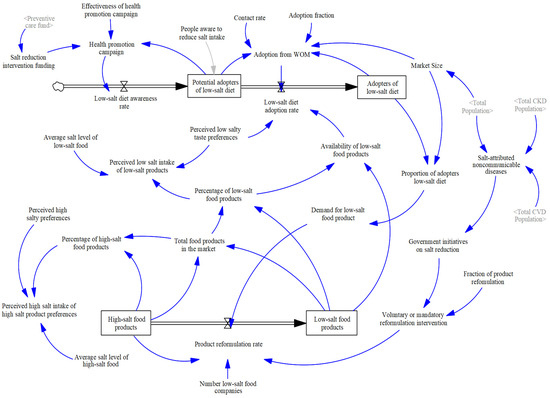
Figure 5.
Stock and flow diagram for the salt reduction intervention sector. CKD, chronic kidney disease; CVD, cardiovascular disease; WOM, word of mouth. The shadow variable, shown in gray font, represents the original variable that appears elsewhere in the model. The cloud-like icon shows sources of the flow outside the model. The pipe (double arrow) indicates flow that changes the value of stock (rectangle). The valve in the middle of the pipe controls flow. The blue arrow indicates the link between elements in the system.
Health Promotion Campaign Sub-Model
In the health promotion campaign sub-model, potential adopters of low-salt diets are defined as individuals who are aware of the need for a low-salt diet but have not yet made a change [53]. Consumers are more likely to buy salt-reduced products if they are more informed, motivated, and have a better understanding of salt-related labels [54]. This stock variable is influenced by the awareness rate of health promotion campaigns [55] and the proportion of social security spending allocated to these interventions [56].
Adopters are individuals who have already adopted a low-salt diet, consume less salt than average, or favor a low-salt diet. Potential adopters adopt a low-salt diet when they encounter individuals who have already adopted this behavior, reflecting the impact of communication within the population, as denoted by “adoption from word of mouth” in the model. This sub-model can be mathematically expressed as
where represents the adoption of low-salt diets among potential adopters, , affected by interactions with adopters and . represents the market size (total population). Contact rate , measures the number of potential adopters persuaded to adopt a low-salt diet within a specific timeframe. The adoption fraction , represents the probability of adoption when a potential adopter comes into contact with an existing adopter. Based on the calibration, we assume that af is 2%. Thus, this imitation effect influences the adoption rate, which is the inflow rate into the stock of low-salt diet adopters. We calculated the adoption rate of a low-salt diet () as follows:
where denotes the availability of low-salt food products in the market and indicates consumer preferences for the taste of low-salt foods. Taste significantly influences food choices [57]. and were linked from the product reformulation sub-model in the lower part of the salt reduction intervention model. This adoption effect demonstrates two key phenomena: (1) changes in the number of potential adopters affect the adoption rate, thereby influencing the balance of potential adopters, and (2) variations in the adoption rate lead to exponential changes in the number of adopters. The ratio represents the percentage of individuals reducing their salt consumption, assuming that it reflects the demand for low-salt food products in this study.
Product Reformulation Sub-Model
The product reformulation sub-model comprises two stock variables: high- and low-salt food products. The flow rate, labeled as the “product reformulation rate”, is influenced by the demand for low-salt products, the number of businesses offering low-salt product options, and policies related to noncommunicable diseases and food product reformulation, which drive this process. In relation to the previous low-salt diet adoption sub-model (the upper part), an increase in the adoption of low-salt diets is expected to boost the demand for low-salt products, prompting food businesses to reformulate these products. Health considerations and government policies aimed at reducing salt intake also motivate businesses to improve the health and nutritional outcomes of their products [58]. This food reformulation sub-model can be mathematically represented as:
where is low-salt product reformulation, , demand for a low-salt food product, is the number of high-salt food products, is the number of food businesses producing or reformulating low-salt products, and refers to the effectiveness estimate for both voluntary and mandatory reformulation.
2.5. Parameterization and Data Sources
The simulation runs from 2012 to 2040 and focuses on adults aged 40 and older in Japan. We chose 2012 as the starting year for the simulation because data on low-salt food products were first available this year. Table 1 lists the key parameters and initial values used for the base run settings in the model.

Table 1.
List of key parameters and initial conditions for base run settings.
2.6. Scenario Assumptions
This study examines three policy scenarios aimed at reducing salt intake. In the base run, the proportion of the population adopting a low-salt diet and the fraction of product reformulation remained constant at initial values of 2% and 5%, respectively, throughout the simulation. This base run serves as a reference for comparing the three scenarios. Scenario 1 focused on encouraging a low-salt diet to influence consumer behavior. In this scenario, the percentage of individuals adopting a low-salt diet increased from the initial 2% to 12%, drawing on prior research related to the adoption of salt restriction behaviors [63]. Scenario 2 involved voluntary reformulation of food products. Based on previous studies [55,64], the fraction of product reformulation increased from 5% to 15%. Scenario 3 introduced mandatory reformulation. Similar to Scenario 2, the fraction of product reformulation increased from the initial 5% to 20%, following prior research [55,64]. Table 2 shows the changes in policy variables for scenario analysis.

Table 2.
Assumptions for scenario analysis.
2.7. Validation Tests
In System Dynamics, several validation tests are used to build confidence in both the model structure and its simulated behavior. These tests evaluate how well the model replicates real-world behavior and ensure that it accurately represents the underlying system dynamics [37,65]. In this study, we conducted behavioral reproduction tests and statistical measures on medical and long-term care expenditure variables to compare their behaviors against historical data. For the statistical evaluation, we assessed four metrics: coefficient of determination, mean absolute error, root mean squared error, and Theil’s inequality statistics.
3. Results
3.1. Model Validation
The behavioral reproduction test results shown in Figure 6 compare the model’s predictions for medical and long-term care costs with reference data from 2012 to 2019 [4,61]. This comparison confirmed that the model was well calibrated. Table 3 summarizes the statistical error measurements, such as the coefficient of determination, mean absolute error, root mean squared error, and Theil’s inequality statistics for medical care and long-term care expenditure. The coefficient of determination exceeded 95% for both variables. The mean absolute error for both variables was <0.5, suggesting that the model values were close to the actual data. Similarly, the root mean squared error for both variables was ≤0.4, indicating a relatively accurate prediction of the data using the model. The results of Theil’s statistics indicated that most of the errors between the simulated and actual data were small and not due to bias or unequal variance. The bias () and unequal variance () components were close to zero, indicating that the model accurately reflected the actual data without systematic overestimation or underestimation and captured the variability well. The covariance component () was close to one, indicating that the model accurately captured the overall trends and patterns of the actual data. Therefore, it is reasonable to conclude that the model can accurately replicate the behavior of a real system.
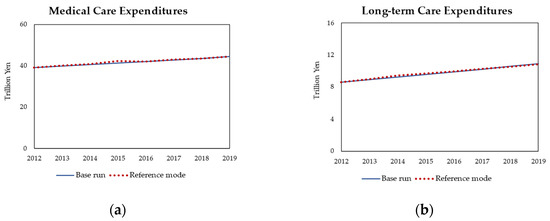
Figure 6.
Comparison of the base run results estimated by the simulation model with actual values on medical care and long-term care expenditures, 2012–2019 [4,61]. (a) Medical care expenditures; (b) Long-term care expenditures.

Table 3.
Results of the statistical validation measures for the model.
3.2. Base Run Analysis
Figure 7 illustrates the projected number of patients with CVD and CKD from 2012 to 2040 without any salt reduction interventions. The prevalence of CVD and CKD gradually increases during this period, with a particularly sharp increase expected among individuals in their 70s and 80s. This upward trend is primarily driven by Japan’s aging population.
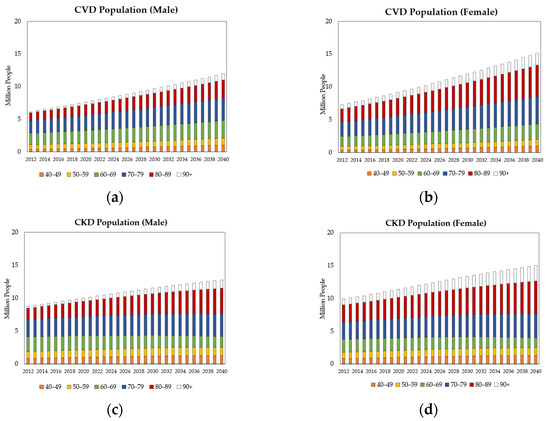
Figure 7.
The number of patients with CVD and CKD without any intervention for salt reduction, projected by the system dynamics simulation model, by 10-year age group and sex, from 2012 to 2040, Japan. (a) CVD population among men; (b) CVD population among women; (c) CKD population among men; (d) CKD population among women. CKD, chronic kidney disease; CVD, cardiovascular disease.
By 2040, the number of CVD patients is projected to be the highest among men in their 70s, reaching approximately 3.4 million. This is followed by those in their 80s and 60s, with approximately 2.8 million and 2.7 million cases, respectively. Among women, those in their 80s are expected to have the highest number of CVD cases, estimated at approximately 4.7 million, followed by women in their 70s, with approximately 4.2 million cases. Overall, CVD prevalence is anticipated to be higher among older women than among older men. Additionally, the prevalence of CKD is forecasted to be highest among individuals in their 80s, with approximately 3.9 million cases for men and 4.9 million for women. Based on these findings, the number of CVD and CKD cases is lower in the 40s and 50s age groups throughout the simulation period.
3.3. Analysis of Scenarios
Table 4 and Figure 8 show the simulation results of the dynamic changes in the key output variables across the salt reduction scenarios over a 29-year period. The mean dietary salt intake gradually decreases toward the target of 8 g per day by 2040 (Figure 8a,b). Figure 8e,f further shows that lower salt intake and improved health outcomes due to food reformulation and increased adoption of low-salt diets would lead to reduced social security expenditures.

Table 4.
Disability-adjusted life years for cardiovascular disease and chronic kidney disease (per 100,000 population) and medical and long-term care expenditures associated with these diseases among individuals aged 40 years and over in Japan in 2040, as projected by the system dynamics simulation model.
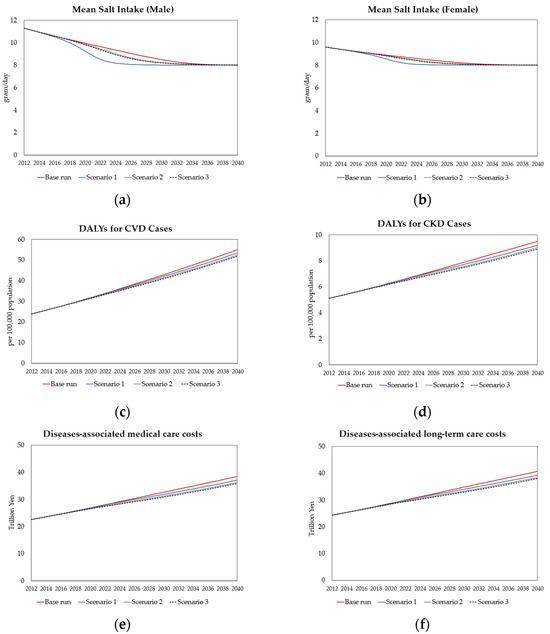
Figure 8.
Simulation outcomes of the proposed intervention scenarios. (a) Mean salt intake among men; (b) Mean salt intake among women; (c) DALYs for CVD cases; (d) DALYs for CKD cases; (e) Disease-associated medical care costs; (f) Diseases-associated long-term care costs. Scenario 1: accelerating adoption of a low-salt diet; Scenario 2: voluntary reformulation; Scenario 3: mandatory reformulation. CKD, chronic kidney disease; CVD, cardiovascular disease; DALYs, disability-adjusted life years.
Compared with the base run, both mandatory and voluntary product reformulation, along with increased adoption of low-salt diets, reduced salt intake, burden of disease rates, and social security expenditures. This is evident in the behavior of these scenarios, indicating lower outcomes compared with the base run behavior represented by the red line. In the base run, by 2040, the cumulative DALYs for CVD and CKD are projected to be approximately 55 and 9.5 per 100,000 people, respectively, contributing approximately 40 trillion yen in social security expenditures (with medical and long-term care costs estimated at approximately 39 trillion yen and 41 trillion yen, respectively).
In Scenario 1, the cumulative DALYs for CVD could be reduced by 2.8%, which is equivalent to 53.5 per 100,000 people. For CKD, the DALYs decreased by 3.2%, which is equivalent to 9.2 per 100,000 people. This scenario could lead to a reduction in social security expenditures of approximately 3.4% (with medical care costs decreasing by 3.5% and long-term care costs decreasing by 3.4%), totaling approximately 37 trillion yen and 39 trillion yen in medical and long-term care costs, respectively. In Scenario 2, the cumulative DALYs for CVD and CKD declined by 4.7% and 5.2%, respectively, resulting in 52.4 per 100,000 for CVD and 9 per 100,000 for CKD. This reduction could lead to a 5.6% decrease in social security expenditures (a 5.6% reduction in medical care costs and a 5.5% reduction in long-term care costs), totaling approximately 36 trillion yen in medical care costs and 39 trillion yen in long-term care costs.
Scenario 3 achieved a 5.7% reduction in DALYs for CVD, bringing the rate to 51.9 per 100,000 population, and a 6.2% reduction in CKD DALYs, resulting in 8.9 per 100,000 population. This scenario could lead to a 6.7% decrease in social security expenditure (with reductions of 6.7% in medical care costs and 6.6% in long-term care costs), with medical care costs totaling approximately 36 trillion yen and long-term care costs amounting to approximately 38 trillion yen. Interestingly, the results also revealed that the disease burden, measured in DALYs, was significantly greater for CVD than for CKD. However, when comparing economic burdens, long-term care expenses slightly exceed expenses associated with the medical care sector.
4. Discussion
The simulation findings from our base run analysis indicated that the prevalence of CVD and CKD in older people were projected to be more than double as the population aged. These findings were consistent with previous studies, which showed that disease prevalence increased with age, making aging one of the most significant risk factors for chronic diseases [66]. Therefore, these projections highlighted the growing challenge of managing noncommunicable diseases in Japan and underscored the need for targeted healthcare strategies and resource planning.
Our study incorporated two key elements of the WHO salt reduction strategy: modifying consumer behavior and reformulating food products [67]. The simulation findings suggested that if all three measures of salt reduction were implemented, dietary salt intake was projected to decrease gradually, approaching the target of 8 g per day set by Japan’s Health Japan 21 dietary goals [8]. However, this still fell short of the WHO Global Action Plan’s 30% sodium reduction target, which required a more comprehensive strategy aligned with the WHO SHAKE Technical Package [68]. These reductions in salt intake were expected to alleviate the disease burden and lower social security costs. This is supported by previous studies in Japan, which suggested that reductions in cardiovascular mortality over time may have been partially attributed to lower salt intake and its blood pressure-lowering effects [69,70]. Similarly, a study by Lackland et al. [71] emphasized that reducing salt intake was crucial for managing blood pressure and preventing chronic diseases, with effective salt reduction policies potentially leading to significant health improvements [72].
In addition, our simulation findings clearly showed that food reformulation by food companies contributed a greater impact on improving health outcomes compared to the strategy of population dietary behavior adoption, with mandatory reformulation policies providing a slight advantage over voluntary reformulation. This advantage was due to mandatory policies ensuring that more companies transitioned from high-salt to low-salt products, increasing the availability of low-salt options and promoting easier adoption of low-salt diets among consumers, even those who were not actively trying to reduce their salt intake [15]. This approach not only accelerated consumer adaptation but also led to improved population health and significant cost savings, reinforcing the evidence that reducing salt intake was both cost-effective and cost-saving [58,73]. Moreover, ongoing product reformulation was essential to ensure that consumers gradually adjusted to the taste of low-salt products over time [74]. Hence, our results suggested that a combined approach was necessary for effective salt reduction: altering eating habits through nutritional education and increasing the availability of reformulated products. While raising consumer awareness was important, achieving global and national salt reduction targets would have been challenging without reformulating food products, because knowledge alone had a limited impact [14].
Despite these insights, our study has several limitations that should be considered in future research, particularly in the context of simulation and modeling studies. First, our model did not differentiate between processed and seasoned low-salt products. Second, our model assumes that changes in salt intake will be sustained from 2012 to 2040, which may not hold if organizations revert to higher-salt products in response to consumer demand. Third, this study focused on two specific types of interventions, overlooking the potential benefits of other interventions, such as food labeling. Fourth, our model did not include delays in the research and development of low-salt products or the need for taste testing. These delays could slow the market introduction of healthier options and impact the overall effectiveness of salt reduction strategies. Future studies should explore ways to expedite research and development for low-salt products and investigate consumer perceptions of taste, which are critical for the successful adoption of low-salt diets. Fifth, we did not estimate the cost-effectiveness of the strategies, such as the cost per unit of improvement in implementation outcomes. Sixth, we did not consider that individuals who chose to reduce their salt intake might have lower consumption levels than those who did not adopt such behaviors. This oversight could affect the accuracy of our findings regarding salt intake and its effects. Seventh, our analysis assumes that consumer acceptance of reformulated products is based on their availability, without data on factors associated with individual perceptions of reformulated products. Eighth, our long-term care sub-model did not differentiate between older people’s demand for various long-term care services, such as home services, nursing homes, and community-based services. The incidence of activities of daily living was also overlooked. This omission may lead to an underestimation of total long-term care expenditure. Future research should address these aspects to provide a more accurate assessment of long-term requirements and costs. Finally, system dynamics is a useful tool for modeling complex real-world systems; however, it depends on certain assumptions when setting up the model. It is also important to note that the results of this study were based on hypothetical experiments using simulation analysis. Further development and analysis are needed to increase confidence in the findings and support policy implementation. As we continue to refine the model, we modify and enhance its formulation and structure, including enhancing the structural equations and accounting for the structural uncertainty.
5. Conclusions
To the best of our knowledge, this study presents the first integrated System Dynamics model in Japan that maps the progression from hypertension to the burden of cardiovascular and chronic kidney diseases while incorporating related social security costs to evaluate the impact of current and future dietary salt policies. The simulation of salt reduction interventions suggests that lowering dietary salt intake could prevent 3–6% of disability-adjusted life years (DALYs) related to CVD and CKD among older people in Japan. This means there would be fewer cases of these diseases, leading to a healthier and more productive population. As salt intake decreases, we can expect a drop in high blood pressure rates, which would significantly reduce the occurrence of heart attacks, strokes, and kidney failure. Consequently, preventing these chronic diseases could result in potential cost savings of about 3–7% in medical and long-term care expenses. This model provides a more detailed analysis and is a valuable educational tool for government stakeholders and the public. The constructed model enhances our understanding of the interconnected elements and the behavioral patterns of key variables. The simulation and experimentation results support the future development of salt reduction hypotheses, provide a testing environment for further research, and offer a pathway for policy development aimed at combating noncommunicable diseases and the costs associated with high salt intake.
Supplementary Materials
The following supporting information can be downloaded from: https://www.mdpi.com/article/10.3390/systems12110478/s1, Supplementary S1: System dynamics model; Supplementary S2: Data used in the national model include Table S1: Population size by age group and sex in 2012, Table S2: Death and migration by age group in 2012, Table S3: Total population, number of births and birth rates for 2012–2019, Table S4: Prevalence of hypertension, cardiovascular disease (CVD), and chronic kidney disease (CKD), in Japan, by age group and sex, in 2012, Table S5: Deaths, years of life lost, and years lived with disability due to cardiovascular disease in Japan, by age group and sex, in 2012, Table S6: Deaths, years of life lost, and years lived with disability due to chronic kidney disease in Japan, by age group and sex, in 2012, Table S7: Estimated average years of life lost and disability weights due to cardiovascular disease in Japan, by age group and sex, in 2012, Table S8: Estimated average years of life lost and disability weights due to chronic kidney disease in Japan, by age group and sex, in 2012 and Table S9: Values used for validation on medical care and long-term care expenditures, 2012–2019; Supplementary S3: Aging chain model include Figure S1: Stock-flow diagram of the population model, Figure S2: Stock-flow diagram of the hypertension sub-model, Figure S3: Stock-flow diagram of the cardiovascular disease sub-model and Figure S4: Stock-flow diagram of the chronic kidney disease sub-model. Reference [75] is cited in the Supplementary Materials.
Author Contributions
Conceptualization, F.A.H., N.N. and N.I.; Methodology, F.A.H., N.N., N.M., T.S. and N.I.; Software, F.A.H. and N.N.; Validation, F.A.H. and N.N.; Formal Analysis, F.A.H. and N.N.; Investigation, F.A.H., N.N. and N.I.; Resources, F.A.H., N.N., N.M., T.S. and N.I.; Data Curation, F.A.H., N.N. and N.I.; Writing—Original Draft Preparation, F.A.H.; Writing—Review and Editing, N.N., N.M., T.S. and N.I.; Visualization, F.A.H., N.N. and N.I.; Supervision, N.N. and N.I.; Project Administration, N.I.; Funding Acquisition, N.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a Health and Labor Sciences Research Grant from the Ministry of Health, Labour, and Welfare of Japan, grant number 23FA1012.
Data Availability Statement
Data presented in this manuscript were extracted from publicly available sources.
Acknowledgments
We thank Yutaka Takahashi (Senshu University, Tokyo, Japan) for his comments on the system dynamics model.
Conflicts of Interest
The authors declare no conflicts of interest. The funder had no role in the design of the study, collection, analyses, or interpretation of data, writing of the manuscript, or the decision to publish the results.
References
- World Health Organization. Noncommunicable Diseases. Available online: https://www.who.int/news-room/fact-sheets/detail/noncommunicable-diseases (accessed on 11 March 2024).
- GBD 2021 Diseases and Injuries Collaborators. Global Incidence, Prevalence, Years Lived with Disability (YLDs), Disability-Adjusted Life-Years (DALYs), and Healthy Life Expectancy (HALE) for 371 Diseases and Injuries in 204 Countries and Territories and 811 Subnational Locations, 1990–2021: A Systematic Analysis for the Global Burden of Disease Study 2021. Lancet 2024, 403, 2133–2161. [Google Scholar] [CrossRef]
- Institute for Health Metrics and Evaluation. Global Burden of Disease 2019. Available online: https://vizhub.healthdata.org/gbd-compare/ (accessed on 30 October 2024).
- Ministry of Health, Labour and Welfare. Overview of National Medical Care Expenditure. Available online: https://www.mhlw.go.jp/toukei/list/37-21.html (accessed on 11 March 2024). (In Japanese)
- Statistics Bureau of Japan, Ministry of Internal Affairs and Communications. Current Population Estimates as of October 1, 2012. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00200524&tstat=000000090001&cycle=7&year=20120&month=0&tclass1=000001011679&result_back=1&tclass2val=0 (accessed on 11 March 2024). (In Japanese).
- World Health Organization. NCD Global Monitoring Framework, Geneva, Switzerland, 2011. Available online: https://www.who.int/publications/i/item/ncd-surveillance-global-monitoring-framework (accessed on 11 March 2024).
- World Health Organization. Guideline. Sodium Intake for Adults and Children, 2012. Available online: https://www.who.int/publications/i/item/9789241504836 (accessed on 11 March 2024).
- Ministry of Health, Labour and Welfare. A Basic Direction for Comprehensive Implementation of National Health Promotion, 2012. Available online: https://www.pbhealth.med.tohoku.ac.jp/japan21/pdf/kenkounippon21_01e.pdf (accessed on 11 March 2024).
- Ministry of Health, Labour and Welfare. Health Japan 21 (Third Term). Available online: https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/kenkou_iryou/kenkou/kenkounippon21_00006.html (accessed on 18 March 2024).
- World Health Organization. Noncommunicable Diseases Data Portal. Available online: https://ncdportal.org/ (accessed on 12 September 2024).
- Ministry of Health, Labour and Welfare. The National Health and Nutrition Survey. Available online: https://www.mhlw.go.jp/bunya/kenkou/kenkou_eiyou_chousa.html (accessed on 11 March 2024).
- Matsumoto, M.; Tajima, R.; Fujiwara, A.; Yuan, X.; Okada, E.; Takimoto, H. Trends in Dietary Salt Sources in Japanese Adults: Data from the 2007–2019 National Health and Nutrition Survey. Br. J. Nutr. 2023, 129, 690–703. [Google Scholar] [CrossRef] [PubMed]
- Vyth, E.L.; Steenhuis, I.H.; Roodenburg, A.J.; Brug, J.; Seidell, J.C. Front-of-Pack Nutrition Label Stimulates Healthier Product Development: A Quantitative Analysis. Int. J. Behav. Nutr. Phys. Act. 2010, 7, 65. [Google Scholar] [CrossRef]
- Takemi, Y. Creating a Healthy Food Environment as a Radical Population Approach and Japanese Initiatives. J. Nutr. Sci. Vitaminol. 2022, 68, S78–S80. [Google Scholar] [CrossRef]
- Tsuchihashi, T. How Much Can Japanese Reduce Dietary Salt Intake? Jpn. Soc. Nutr. Diet. 2020, 78, 49–56. (In Japanese) [Google Scholar] [CrossRef]
- World Health Organization. Tackling NCDs “Best Buys” and Other Recommended Interventions for the Prevention and Control of Noncommunicable Diseases. 2017. Available online: https://www.who.int/publications/i/item/WHO-NMH-NVI-17.9 (accessed on 11 March 2024).
- World Health Organization. WHO Global Sodium Benchmarks for Different Food Categories. 2021. Available online: https://www.who.int/publications/i/item/9789240025097 (accessed on 11 March 2024).
- Cobiac, L.J.; Vos, T.; Veerman, J.L. Cost-Effectiveness of Interventions to Reduce Dietary Salt Intake. Heart 2010, 96, 1920–1925. [Google Scholar] [CrossRef]
- Murray, C.J.; Lauer, J.A.; Hutubessy, R.C.; Niessen, L.; Tomijima, N.; Rodgers, A.; Lawes, C.M.; Evans, D.B. Effectiveness and Costs of Interventions to Lower Systolic Blood Pressure and Cholesterol: A Global and Regional Analysis on Reduction of Cardiovascular-Disease Risk. Lancet 2003, 361, 717–725. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, A.; García Martí, S.; Souto, A.; Ferrante, D.; Augustovski, F. Generalized Cost-Effectiveness Analysis of a Package of Interventions to Reduce Cardiovascular Disease in Buenos Aires, Argentina. Cost Eff. Resour. Alloc. 2009, 7, 10. [Google Scholar] [CrossRef]
- Smith-Spangler, C.M.; Juusola, J.L.; Enns, E.A.; Owens, D.K.; Garber, A.M. Population Strategies to Decrease Sodium Intake and the Burden of Cardiovascular Disease. Ann. Intern. Med. 2010, 152, 481–487. [Google Scholar] [CrossRef]
- Miura, K.; Ando, K.; Tsuchihashi, T.; Yoshita, K.; Watanabe, Y.; Kawarazaki, H.; Matsuura, H.; Kusaka, M.; Kai, H.; Kawamura, M.; et al. [Scientific Statement] Report of the Salt Reduction Committee of the Japanese Society of Hypertension(2) Goal and Strategies of Dietary Salt Reduction in the Management of Hypertension. Hypertens. Res. 2013, 36, 1020–1025. [Google Scholar] [CrossRef]
- Hassan, F.A.; Minato, N. A System Dynamics Analysis of Malaysian Healthcare Resources. Int. J. Jpn. Assoc. Manag. Syst. 2017, 9, 61–69. [Google Scholar] [CrossRef][Green Version]
- Hassan, F.A.; Minato, N. A Systems Thinking Analysis of Healthcare Supply and Demand Management. Int. J. Jpn. Assoc. Manag. Syst. 2019, 11, 103–110. [Google Scholar] [CrossRef]
- Ansah, J.P.; Matchar, D.B.; Love, S.R.; Malhotra, R.; Do, Y.K.; Chan, A.; Eberlein, R. Simulating the Impact of Long-Term Care Policy on Family Eldercare Hours. Health Serv. Res. 2013, 48 Pt 2, 773–791. [Google Scholar] [CrossRef] [PubMed]
- Karanfil, Ö. Dynamics of Medical Screening: A Simulation Model of PSA Screening for Early Detection of Prostate Cancer. Systems 2023, 11, 252. [Google Scholar] [CrossRef]
- Homer, J.; Wile, K.; Yarnoff, B.; Trogdon, J.G.; Hirsch, G.; Cooper, L.; Soler, R.; Orenstein, D. Using Simulation to Compare Established and Emerging Interventions to Reduce Cardiovascular Disease Risk in the United States. Prev. Chronic Dis. 2014, 11, 140130. [Google Scholar] [CrossRef]
- Ansah, J.P.; Wei, S.T.Y.; Min, T.L.S. An Evaluation of the Impact of Aggressive Diabetes and Hypertension Management on Chronic Kidney Diseases at the Population Level: A Simulation Analysis. Syst. Dyn. Rev. 2020, 36, 497–522. [Google Scholar] [CrossRef]
- Ansah, J.P.; Islam, A.M.; Koh, V.; Ly, V.; Kol, H.; Matchar, D.B.; Loun, C.; Loun, M. Systems Modelling as an Approach for Understanding and Building Consensus on Non-Communicable Diseases (NCD) Management in Cambodia. BMC Health Serv. Res. 2019, 19, 2. [Google Scholar] [CrossRef]
- Homer, J. PRISM: The Prevention Impacts Simulation Model. Reference Guide for Model Version 3s, For RTI International and CDC, Voorhees, NJ, May 2015. Available online: https://www.academia.edu/22881706/PRISM_The_Prevention_Impacts_Simulation_Model_Reference_Guide_for_Model_Version_3q (accessed on 12 September 2024).
- Kenealy, T.; Rees, D.; Sheridan, N.; Moffitt, A.; Tibby, S.; Homer, J. A “whole of System” Approach to Compare Options for CVD Interventions in Counties Manukau. Aust. N. Z. J. Public Health 2012, 36, 263–268. [Google Scholar] [CrossRef]
- Ansah, J.P.; Inn, R.L.H.; Ahmad, S. An Evaluation of the Impact of Aggressive Hypertension, Diabetes and Smoking Cessation Management on CVD Outcomes at the Population Level: A Dynamic Simulation Analysis. BMC Public Health 2019, 19, 1105. [Google Scholar] [CrossRef]
- George, A.; Badrinath, P.; Lacey, P.; Harwood, C.; Gray, A.; Turner, P.; Springer, D. Use of System Dynamics Modelling for Evidence-Based Decision Making in Public Health Practice. Systems 2023, 11, 247. [Google Scholar] [CrossRef]
- Sugiyama, T.; Ikeda, N.; Minowa, K.; Nishi, N. Estimation of the Effect of Salt-Intake Reduction on Cardiovascular Mortality Decline between 1950 and 2017 in Japan: A Retrospective Simulation Study. Nutrients 2022, 14, 3747. [Google Scholar] [CrossRef]
- Ventana System Inc. Vensim DSS 10.2.0. Available online: https://vensim.com/software/ (accessed on 10 September 2024).
- Sterman, J.D. Learning in and about Complex Systems. Syst. Dyn. Rev. 1994, 10, 291–330. [Google Scholar] [CrossRef]
- Sterman, J.D. Business Dynamics: System Thinking and Modeling for a Complex World; Irwin McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Hassan, F.A.; Minato, N. Smartphone-Based Healthcare Technology Adoption in Malaysian Public Healthcare Services. Int. J. Jpn. Assoc. Manag. Syst. 2018, 10, 95–104. [Google Scholar] [CrossRef][Green Version]
- National Institute of Population and Social Security Research. Demographic Data Collection 2024. Available online: https://www.ipss.go.jp/syoushika/tohkei/Popular/P_Detail2024.asp?fname=T04-01.htm (accessed on 26 July 2024). (In Japanese).
- Ministry of Health, Labour and Welfare. Vital Statistics of Japan in 2012; Ministry of Health, Labour and Welfare: Tokyo, Japan, 2012. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&toukei=00450011&tstat=000001028897 (accessed on 12 September 2024). (In Japanese)
- Immigration Services Agency. Immigration Control Statistics in 2012; Immigration Services Agency: Tokyo, Japan, 2012. (In Japanese) [Google Scholar]
- Brown, A.D.; Bolton, K.A.; Clarke, B.; Fraser, P.; Lowe, J.; Kays, J.; Hovmand, P.S.; Allender, S. System Dynamics Modelling to Engage Community Stakeholders in Addressing Water and Sugar Sweetened Beverage Consumption. Int. J. Behav. Nutr. Phys. Act. 2022, 19, 118. [Google Scholar] [CrossRef] [PubMed]
- Ito, C.; Kurth, T.; Baune, B.T.; Brinks, R. Illness-Death Model as a Framework for Chronic Disease Burden Projection: Application to Mental Health Epidemiology. Front. Epidemiol. 2022, 2, 903652. [Google Scholar] [CrossRef]
- NCD Risk Factor Collaboration (NCD-RisC). Worldwide trends in hypertension prevalence and progress in treatment and control from 1990 to 2019: A pooled analysis of 1201 population-representative studies with 104 million participants. Lancet 2021, 398, 957–980. Available online: https://www.ncdrisc.org/data-downloads-hypertension.html (accessed on 5 July 2024). [CrossRef]
- Yinusa, A.; Faezipour, M.; Faezipour, M. A Study on CKD Progression and Health Disparities Using System Dynamics Modeling. Healthcare 2022, 10, 1628. [Google Scholar] [CrossRef]
- Struijk, E.A.; May, A.M.; Beulens, J.W.J.; de Wit, G.A.; Boer, J.M.A.; Onland-Moret, N.C.; van der Schouw, Y.T.; Bueno-de-Mesquita, H.B.; Hoekstra, J.; Peeters, P.H.M. Development of Methodology for Disability-Adjusted Life Years (DALYs) Calculation Based on Real-Life Data. PLoS ONE 2013, 8, e74294. [Google Scholar] [CrossRef]
- Ministry of Health, Labour and Welfare. Survey on Medical Benefits. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450389&tstat=000001044924&cycle=0&tclass1=000001044945&tclass2=000001064470&tclass3val=0 (accessed on 24 July 2024). (In Japanese)
- Ministry of Health, Labour and Welfare. Trends in Dispensing Medical Expenses. Available online: https://www.mhlw.go.jp/stf/newpage_06935.html (accessed on 24 July 2024). (In Japanese)
- Ministry of Health, Labour and Welfare. Recent Trends in Long-Term Care. Available online: https://www.mhlw.go.jp/content/12300000/001099975.pdf (accessed on 20 August 2024). (In Japanese)
- Ministry of Health, Labour and Welfare. Long-Term Care Insurance Premiums for Category 2 Insured Persons. Available online: https://www.mhlw.go.jp/topics/kaigo/osirase/jigyo/18/dl/h30_hihokensha.pdf (accessed on 20 August 2024). (In Japanese)
- Ministry of Health, Labour and Welfare. Long-Term Care Insurance System. Available online: https://www.mhlw.go.jp/content/12300000/000614772.pdf (accessed on 24 July 2024).
- Nishi, N. A System Dynamics Model of Salt Reduction at a National Level. In Proceedings of the System Dynamics Society, Cambridge, MA, USA, 21–25 July 2013. [Google Scholar]
- Cabinet Office Food Education Promotion Office. Awareness Survey Report on Dietary Education. Available online: https://www.maff.go.jp/j/syokuiku/ishiki.html (accessed on 18 March 2024). (In Japanese).
- Andrews, J.C.; Netemeyer, R.G.; Burton, S. The Nutrition Elite: Do Only the Highest Levels of Caloric Knowledge, Obesity Knowledge, and Motivation Matter in Processing Nutrition Ad Claims and Disclosures? J. Public Policy Mark. 2009, 28, 41–55. [Google Scholar] [CrossRef]
- Collins, M.; Mason, H.; O’Flaherty, M.; Guzman-Castillo, M.; Critchley, J.; Capewell, S. An Economic Evaluation of Salt Reduction Policies to Reduce Coronary Heart Disease in England: A Policy Modeling Study. Value Health 2014, 17, 517–524. [Google Scholar] [CrossRef]
- The Japan Research Institute. Toward Improving Estimates of Preventive Expenditures in Health Expenditures: Re-Estimation Using “Expenses Required for Social Security Measures”. Available online: https://www.jri.co.jp/MediaLibrary/file/report/jrireview/pdf/13437.pdf (accessed on 24 July 2024). (In Japanese).
- Jessen, N.; Damasceno, A.; Padrão, P.; Lunet, N. Levels of Salt Reduction in Bread, Acceptability and Purchase Intention by Urban Mozambican Consumers. Foods 2022, 11, 454. [Google Scholar] [CrossRef] [PubMed]
- Fanzo, J.; McLaren, R.; Bellows, A.; Carducci, B. Challenges and Opportunities for Increasing the Effectiveness of Food Reformulation and Fortification to Improve Dietary and Nutrition Outcomes. Food Policy 2023, 119, 102515. [Google Scholar] [CrossRef]
- The Japanese Society of Hypertension. Sales Report of Low-Salt Food. 2023. Available online: https://www.jpnsh.jp/data/salt_foodlist_sales.pdf (accessed on 11 March 2024). (In Japanese).
- Statistics Bureau of Japan. National Accounts. Available online: https://www.e-stat.go.jp/en/stat-search?page=1&layout=normal&toukei=00100409&survey=gdp&metadata=1&data=1 (accessed on 18 March 2024).
- National Institute of Population and Social Security Research. The Financial Statistics of Social Security in Japan. Available online: https://www.ipss.go.jp/site-ad/index_english/security-e.html (accessed on 11 March 2024).
- Ministry of Health, Labour and Welfare. Long-Term Care Insurance Business Status Report. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450351&tstat=000001031648&cycle=8&tclass1=000001169206&tclass2val=0 (accessed on 20 August 2024). (In Japanese)
- Du, X.; Fang, L.; Xu, J.; Chen, X.; Bai, Y.; Wu, J.; Wu, L.; Zhong, J. The Association of Knowledge, Attitudes and Behaviors Related to Salt with 24-h Urinary Sodium, Potassium Excretion and Hypertensive Status. Sci. Rep. 2022, 12, 13901. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, N.; Yamashita, H.; Hattori, J.; Kato, H.; Nishi, N. Economic Effects of Dietary Salt Reduction Policies for Cardiovascular Disease Prevention in Japan: A Simulation Study of Hypothetical Scenarios. Front. Nutr. 2023, 10, 1227303. [Google Scholar] [CrossRef]
- Sterman, J.D. Appropriate Summary Statistics for Evaluating the Historical Fit of System Dynamics Models. Dynamica 1984, 10, 51–66. Available online: https://systemdynamics.org/wp-content/uploads/assets/dynamica/volume-10/10-2/4.pdf (accessed on 18 March 2024).
- Atella, V.; Piano Mortari, A.; Kopinska, J.; Belotti, F.; Lapi, F.; Cricelli, C.; Fontana, L. Trends in Age-related Disease Burden and Healthcare Utilization. Aging Cell 2019, 18, e12861. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Reducing Salt Intake in Population. Report of a WHO Forum and Technical Meeting, Paris, France, 5–7 October 2006; Available online: https://iris.who.int/bitstream/handle/10665/43653/9789241595377_eng.pdf?sequence=1&isAllowed=y (accessed on 20 August 2024).
- World Health Organization. The SHAKE Technical Package for Salt Reduction; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Iso, H. A Japanese Health Success Story: Trends in Cardiovascular Diseases, Their Risk Factors, and the Contribution of Public Health and Personalized Approaches. EPMA J. 2011, 2, 49–57. [Google Scholar] [CrossRef]
- Miura, K. Epidemiology and Prevention of Hypertension in Japanese: How Could Japan Get Longevity? EPMA J. 2011, 2, 59–64. [Google Scholar] [CrossRef]
- Lackland, D.T.; Carey, R.M.; Conforto, A.B.; Rosendorff, C.; Whelton, P.K.; Gorelick, P.B. Implications of Recent Clinical Trials and Hypertension Guidelines on Stroke and Future Cerebrovascular Research. Stroke 2018, 49, 772–779. [Google Scholar] [CrossRef]
- Wang, M.; Moran, A.E.; Liu, J.; Coxson, P.G.; Penko, J.; Goldman, L.; Bibbins-Domingo, K.; Zhao, D. Projected Impact of Salt Restriction on Prevention of Cardiovascular Disease in China: A Modeling Study. PLoS ONE 2016, 11, e0146820. [Google Scholar] [CrossRef]
- Bibbins-Domingo, K.; Chertow, G.M.; Coxson, P.G.; Moran, A.; Lightwood, J.M.; Pletcher, M.J.; Goldman, L. Projected Effect of Dietary Salt Reductions on Future Cardiovascular Disease. N. Engl. J. Med. 2010, 362, 590–599. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO Salt Reduction; World Health Organization: Geneva, Switzerland, 2020; Available online: https://www.who.int/news-room/fact-sheets/detail/salt-reduction (accessed on 11 March 2024).
- Homer, J.B.; Hirsch, G.B. System Dynamics Modeling for Public Health: Background and Opportunities. Am. J. Public Health 2006, 96, 452–458. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).