Abstract
Waste management involves the systematic collection, transportation, processing, and treatment of waste materials generated by human activities. It entails a variety of strategies and technologies to diminish environmental impacts, protect public health, and conserve resources. Consequently, providing an effective and comprehensive optimization approach plays a critical role in minimizing waste generation, maximizing recycling and reuse, and safely disposing of waste. This work develops a novel Possibilistic Multi-Objective Mixed-Integer Linear Programming (PMOMILP) model in order to formulate the problem and design a circular–sustainable–reliable waste management network, under uncertainty. The possibility of recycling and recovery are considered across incineration and disposal processes to address the main circular-economy principles. The objectives are to address sustainable development throughout minimizing the total cost, minimizing the environmental impact, and maximizing the reliability of the Waste Management System (WMS). The Lp-metric technique is then implemented into the model to tackle the multi-objectiveness. Several benchmarks are adapted from the literature in order to validate the efficacy of the proposed methodology, and are treated by CPLEX solver/GAMS software in less than 174.70 s, on average. Moreover, a set of sensitivity analyses is performed to appraise different scenarios and explore utilitarian managerial implications and decision aids. It is demonstrated that the configured WMS network is highly sensitive to the specific time period wherein the WMS does not fail.
1. Introduction
Due to the expansion of urban areas and the rising population, the surge in consumption has resulted in a significant rise in waste generation. This excess waste production contributes significantly to pollution in densely populated cities and large metropolitan areas, mainly due to the disorganized utilization of resources [1].
According to the most recent data, it is projected that global waste generation will approach 2.59 billion tons per year by 2030 and 3.4 billion tons per year by 2050 [2]. Typically, between 70 and 80% of organic materials are recyclable; however, only a minimal percentage is actually recycled, particularly in developing nations. Although the swift pace of urbanization and increasing population are the main risks in waste management, there are other challenges that encompass environmental, social, economic, and health concerns. In many countries, particularly developing ones, inadequate infrastructure and lack of public awareness are two main factors making the waste management issue more risky and critical. Implementing effective policies, initiatives, and regulatory measures can be accounted initial solutions in this regard. However, they require product redesign, investing in modern treatment technologies, education, and fostering partnerships between governments, businesses, and communities. Of course, conducting circular-economy approaches, along with Sustainable Development Goals (SDGs), will lead to reducing waste generation, optimizing resource use, and encouraging reuse, recycling and recovery of materials throughout their lifecycle [3,4]. Sustainable development involves using natural resources for human progress in a way that preserves their availability for the future, ensuring that nature can continue to provide these resources over time. On the other hand, the circular economy is a modern approach to production and consumption that promotes long-term sustainable development. By embracing this approach, we can maximize resource efficiency, minimize raw material usage, and recycle waste or repurpose it into new products, giving it a second life.
This research concentrates on the three key terms of “circular economy”, “sustainable development”, and “reliability” in order to establish an efficient optimal Waste Management System (WMS). In this regard, efficient planning and design of waste transfer, treatment, and disposal facilities are crucial constituents of Municipal Solid Waste (MSW) management. The same as with other human-based systems, failures are also indisputable elements of an MSW management system. There are instances where delays, disruptions, or unforeseen alterations in waste center operations can compromise the reliability of processes. These factors often result in a reduction in the average amount of collected waste available for timely processing. The concept of reliability maximization tries to maximize this average amount of collected waste throughout the network. On the other hand, implementing source-separation processes diminishes the separation costs of waste and augments the quality of recycled and recovered materials by minimizing mixed-waste production and facilitating the recycling and recovery process, which also promulgates circular and sustainable practices.
On the other hand, uncertainty remains a significant challenge in waste management, which normally affects the problem due to the above-mentioned failures, unexpected events, and disruptions (e.g., economic recession, pandemics, and wars). The most important parameters susceptible to being influenced in MSW management networks include the rate of waste generation (demand), waste flow rates between facilities, costs, and service quality [5]. Therefore, ensuring the flexibility and adaptability of the MSW system is another crucial aspect that needs attention and preservation, alongside sustainability and circularity principles.
Based on the above-stated requirements, this research attempts to build up a novel Possibilistic Multi-Objective Mixed-Integer Linear Programming (PMOMILP) approach to establish a circular–sustainable–reliable WMS, under uncertainty, where the key contributions are explained below:
- Addressing the principles of the circular economy, sustainable development, and reliability, to configure the waste management network at the same time;
- Employing possibilistic linear programming to treat the uncertainty of demand and flow rates;
- Utilizing the Lp-metric technique to deal with the tri-objectiveness of the model;
- Examining multiple numerical cases (adapted from the literature) to validate the complexity, applicability, and validity of the proposed Decision Support System (DSS).
Eventually, it is shown that managers and policy-makers can leverage this DSS in their decision-making procedures to create a sustainable, circular, and reliable WMS.
2. Background
With respect to the initial research endeavors within the literature, we can refer to those addressing the operational challenges of MSW management. For instance, a periodic Vehicle Routing Problem (VRP) was offered by Shih and Lin [6] to optimally collect and transfer medical waste from hospitals. The other researchers have also applied different versions of VRP to formulate the MSW collection problems, mainly focusing on minimizing total collection/transportation costs [7,8,9]. The main drawback of these studies is their oversight of the importance of strategic and tactical decisions in shaping the overall efficacy of the WMS. Due to this, a major part of the literature is dedicated to the efforts made for designing a thorough WMS, such as MSW network configuration. On the other hand, Multi-Criteria Decision Analysis (MCDA) and multi-objective optimization are known as two main tools to deal with MSW management in the literature. In most MCDA studies, the aim is to rank a list of alternatives subject to a set of criteria as solutions to MSW problems [10,11]. However, the majority of multi-objective optimization studies try to first formulate the MSW problems and provide optimal or near-optimal solutions with detailed information about the network configuration.
In the following, the state-of-the-art multi-objective optimization studies are reviewed. Saeidi-Mobarakeh et al. [12] proposed a bi-level robust optimization method tailored for hazardous WMS design. The goals were to minimize both total cost and total risk, employing Karush–Kuhn–Tucker (KKT) conditions to address the model at both levels. Kargar et al. [13] suggested a linear programming model for optimizing an infectious medical waste Reverse Logistics Network (RLN) during the COVID-19 pandemic. The model minimized costs, transportation risks, and uncollected waste, which was validated through a case study in Iran. Results showed effective balancing of objectives, including installing new treatment centers, with managerial insights provided for health authorities. A multi-objective fuzzy robust optimization model was applied by Mamashli and Javadian [14] for designing a sustainable MSW management network. Their approach aimed to minimize both total cost and environmental effects, while mitigating negative social consequences. They also utilized a risk analysis technique to appraise the social risk value. A real case study was examined using fuzzy Goal Programming (GP) to evaluate the applicability of their model. An MILP model was offered by Ahmed and Zhang [15] to design a multi-phase RLN for managing demolition waste. They explored two cost strategies (with and without facility consideration) to tackle various decisions from both economic and environmental standpoints within a real case-study problem.
A multi-objective optimization model was implemented by Wang et al. [16] for designing reverse logistics networks for MSW. The aim was to optimize collection, transportation, and recycling activities across multiple time periods, accounting for the objectives of minimizing costs, reducing resource use, and diminishing environmental effects, concurrently. Balci et al. [17] developed an RLN tailored for MSW management in Istanbul, Turkey. Their goal was to improve the efficiency of collection, treatment, and transportation operations by incorporating reverse logistics procedures, and recognizing the specific hurdles of waste management. Employing the GP approach, they addressed contradictory objective functions focusing on minimizing total cost, minimizing total carbon cost, and maximizing total profit, respectively. A queuing theory-based MILP model was used by Govindan et al. [18] to establish a sustainable RLN for MSW management. They also implemented a scenario-based approach and augmented ε-constraint technique to tackle uncertainty in waste generation and two objective functions of total cost and population risk minimization, respectively. Joneghani et al. [19] offered a multi-objective MILP model to optimize sustainable medical-waste management, focusing on facility location and waste processing, under uncertainty. The model integrated recycling and waste-to-energy processes, showing potential for cost offsetting, reduced GHG emissions, and positive social impacts, supporting sustainable WMS design in Iran. Nosrati-Abarghooee et al. [20] addressed the configuration of an RLN for MSW management, taking into account epidemic-related disruptions amid uncertainty. Their goal was to optimize the placement of waste collection and treatment centers, to guarantee effective WMS during disruptive events. They utilized the fuzzy GP method to minimize two objectives: total cost and total risk exposure to the population. A multi-objective robust stochastic programming model was offered by Yousefloo et al. [21] to design an MSW recycling network considering operational factors. They applied two quantitative objectives (i.e., total cost and total emission minimization) along with two qualitative objectives (i.e., maximizing the environmental and social outcomes of treatment technologies).
Recently, a parallel heuristic algorithm, along with a two-step MILP model, was offered by Amirteimoori et al. [22] to design a sustainable medical WMS. The model aimed to concurrently minimize population risk, maximize total job opportunity, and minimize total cost. The findings proved the proper efficacy of the algorithm in treating the problem complexity in large-sized problem instances. Tirkolaee et al. [23] developed an integrated approach for establishing a sustainable MSW system coupled with a co-modal transportation network. Employing a robust bi-level DSS, they addressed uncertainties, resilience, and efficiency of waste management operations at the same time. They employed weighted GP to treat the multi-objectiveness of the problem arising from total cost minimization, environmental pollution minimization, and job opportunity maximization, respectively.
As can be found, there is no study in the literature considering the reliability of MSW systems specifically. Moreover, researchers have just focused on sustainable development, and neglected the principles of circular economy while designing a network. In particular, the recycling/recovery facilities, incineration facilities, and secondary markets are established to realize the network circularity in conjunction with SDGs, as much as possible. However, most of the previous research studies ignored one, two, or all of these important facilities. Therefore, a PMOMILP model is developed in this work in order to (i) formulate the proposed MSW network configuration problem, (ii) address sustainable development, circular economy, and reliability principles, and (iii) provide a framework offering valuable insights for decision-makers seeking to develop robust waste-management strategies that can withstand varying conditions and uncertainties. To gain a deeper comprehension of the proposed idea in this work, Figure 1 provides a detailed depiction of the research framework.
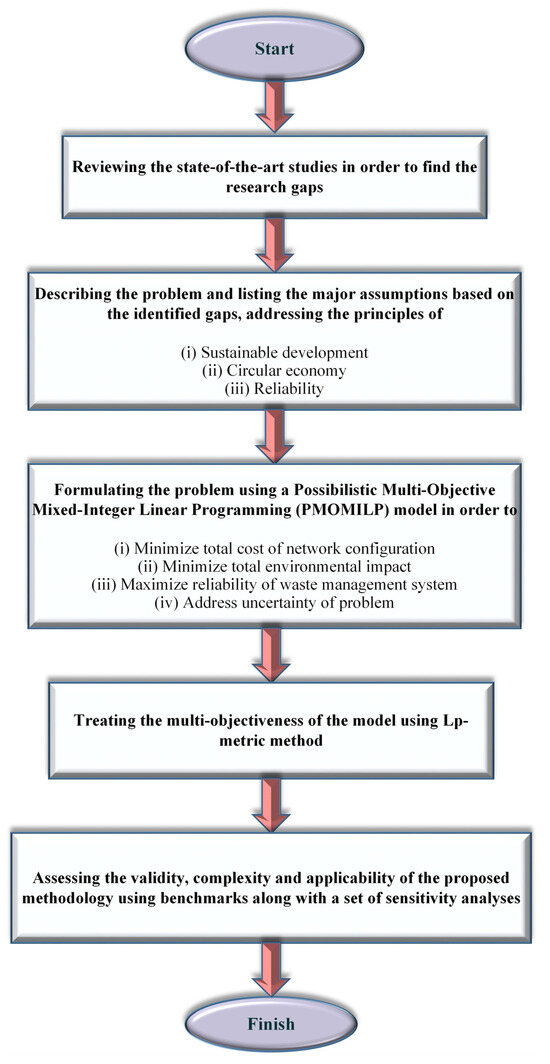
Figure 1.
Proposed research framework.
3. Methodology
This section describes the proposed methodology which is depicted by Figure 2, in four different stages.
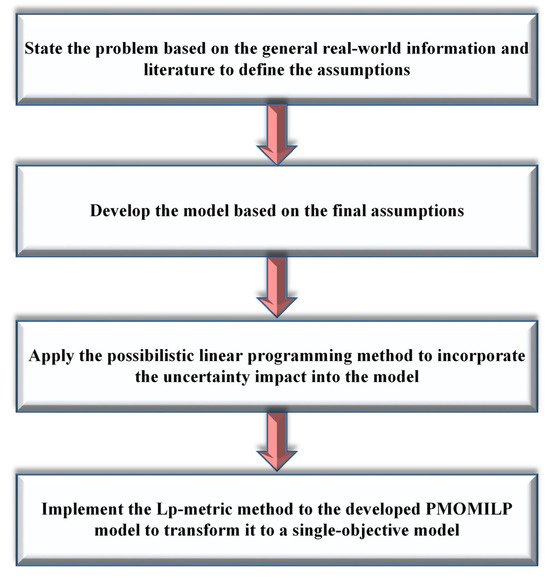
Figure 2.
Proposed methodology.
As the first stage, we need to state the problem, based on the assumptions adopted from the literature and the real world. Assume that the suggested MSW network comprises three echelons, with six different members. In the first echelon, Waste Generation Facilities (WGFs) () and Waste Transfer Facilities (WTFs) () are linked together in order to process and transfer the collected waste. Three pairs of WTFs and Waste Recycling/Recovery Facilities (WRFs) (), WTFs to Waste-to-Energy Incineration Facilities (WEIFs) (), and WTFs to Waste Disposal Facilities (WDFs) () are tied together in the second echelon. Eventually, the third echelon of the network connects three pairs of WRFs to WDFs, WEIFs to WDFs, and WRFs to Secondary Raw Material Markets (SRMMs). The goal is to collect the produced waste at WGFs for different types of waste, throughout a time horizon. Therefore, an MILP model is developed which pursues sustainable development, a circular economy, and reliability requirements addressing the Triple Bottom Line (TBL); i.e., economic, environmental, and social features of the problem. It is noteworthy that the objective functions of the model mainly address these requirements, wherein economic and environmental aspects are tackled with the help of the first and second objective functions, respectively. The third objective function, i.e., reliability maximization, stands for the social aspect in which potential failures of the MSW system negatively affect the timely collection and treatment of waste. The variables used to build up these objective functions are the critical ones handling the levels of sustainability, circularity, reliability of the MSW system. On the other hand, the configuration of the suggested network directly contributes to the system circularity, considering the possibility of recycling/recovery, incineration, and secondary raw materials.
Figure 3 illustrates the network diagram of the problem for clearer comprehension. To assess the feasibility of the proposed DSS, it is important to note that implementing locational decisions typically takes 6 to 18 months. During this time, transportation, loading, and unloading operations occur at various facilities every day. Therefore, locational decisions are generally made at the start of the time horizon.
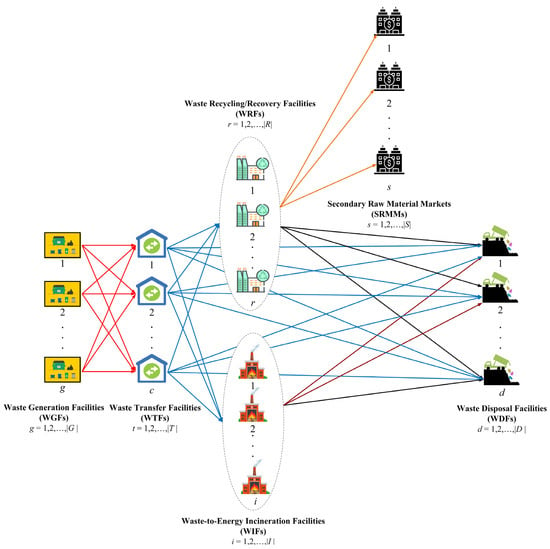
Figure 3.
Representation of the developed WMS network.
On the flip side, there can occasionally be disruptions, delays, or unexpected modifications in the processes to be carried out at different levels, which affect the system reliability negatively. In other words, these factors can lead to a reduction in the average volume of waste that needs to be processed. Hence, the time passed before a failure in processes at time period is assumed to be a variable ( that follows an exponential distribution with parameter . Therefore, , , , and denote the failure rates of cth WTF, rth WRF, ith WEIF, and dth WDF at the tth period. Thus, the reliability of the processes carried out at a facility (RL) is calculated as follows [24,25]:
where stands for the minimum time during which no failure occurs. Accordingly, the RL can be extended and computed for each facility.
Now, the model’s major assumptions are given below:
- Six levels of WGFs, WTFs, WRFs, WEIFs, SRMMs, and WDFs are included in the network;
- WTFs, WRFs, WEIFs, and WDFs are the four levels wherein locational decisions are made at the start of the time horizon. Accordingly, various levels of capacity and fixed establishment costs are defined;
- Multiple types of waste are considered, including wood, metal, plastic, food, and glass;
- The amount of collected waste (demand) and the flow rates are uncertain;
- GHG emissions and environmental pollution result from transportation vehicles and operations at various levels. The GHG emitted from transportation depends on the distance between facilities, transportation mode, and volume of collected waste. On the other hand, the GHG emitted from facilities is contingent on the amount of processed waste;
- The expected amount of collected and processed waste contributes to the reliability function;
- Transportation processes are conducted from WGFs to WTFs, WTFs to WRFs, WTFs to WEIFs, WTFs to WDFs, WRFs to WDFs, WRFs to SRMMs, and WEIFs to WDFs;
- Multimodal transportation is possible, and applicable to various echelons;
- Transportation time is contingent upon both the distance and the mode of transportation;
- Each transportation mode has its own variable and fixed costs, as well as capacity.
3.1. Model Development
Here, the developed model is represented, and the notations used to formulate the problem are delineated in Appendix A.
The model is now built up as follows:
- Objective Functions
Equation (2) shows the 1st objective function of the model, minimizing the total cost. The first five terms represent the operating costs at WTFs, WRFs, WEIFs, SRMMs, and WDFs, while the next four terms display the establishment costs of WTFs, WRFs, WEIFs, and WDFs, respectively. The next seven terms calculate the variable costs of transportation from the WGFs to WTFs, WTFs to WRFs, WTFs to WEIFs, WTFs to WDFs, WRFs to WDFs, WRFs to SRMMs, and WEIFs to WDFs, respectively. Finally, the last three terms represent the fixed costs of using different modes of transportation.
Equation (3) presents the second objective function, minimizing the total environmental pollution resulting from ongoing operations at WTFs, WRFs, WEIFs, SRMMs, and WDFs within the network, respectively. The last seven terms also stand for the amount of GHG emitted from different transportation modes to move waste from WGFs to WTFs, WTFs to WRFs, WTFs to WEIFs, WTFs to WDFs, WRFs to WDFs, WRFs to SRMMs, and WIEFs to WDCs, respectively.
Equation (4) exhibits the third objective function, maximizing the reliability of the designed WMS through increasing the expected amount of processed waste at WTFs, WRFs, WEIFs, and WDFs, respectively.
- Constraints
Constraints (5)–(9) express the capacity limitation of WTFs, WRFs, WEIFs, WDFs, and SRMMs, respectively.
Equation (10) guarantees that all the produced waste must be collected from WGFs. To be more specific, demand should be totally covered in every time period.
Equations (11) and (16) calculate the input flows of different facilities. The flow balances require that the input flows to WTFs must equal their output flows, which could also be achieved by summing Equations (11)–(13). This is also the case for Equations (14) and (16), to create a balance between the input and output flows of WRFs.
Constraints (17)–(23) represent the capacity limitations of various transportation modes. Additionally, these constraints address the requirement to select a transportation mode before allocating it to a flow link. Specifically, Constraint (17) pertains to transportation mode , Constraints (18)–(20) define the capacity limitations for transportation mode , and Constraints (21)–(23) denote the capacity limitations for transportation modes ₁ and ₂.
Constraint (24) exhibits the types of variables.
3.2. Possibilistic Linear Programming
The possibilistic linear programming is implemented into the model in order to tackle the imprecise parameters in the constraints [26]. Otherwise, one cannot guarantee an ideal solution to the problem. To cope with this issue, the weighted-average approach suggested by Lai and Hwang [27] is utilized, which aims to build an equivalent auxiliary crisp model. As can be found from the model presented in the previous section, Equations (10)–(16) cause uncertainty in the model. To be more specific, the imprecise parameters include and which are treated as triangular fuzzy numbers. To do so, we have
The aim is to defuzzify the imprecise parameters and render crisp values. Thus, if the minimum acceptable level of feasibility (or minimum acceptable possibility), Γ, is taken into account, the corresponding crisp constraints can be then given below:
where , ′, and ″ display the weights of the most pessimistic, most possible, and most optimistic values of the fuzzy parameters, respectively. Accordingly, the decision-maker specifies fitting values for these weights and Γ. Here, the weights are set as = ′ = , ″ = and Γ = , in accordance with the theory of most possible values [27].
3.3. Solution Technique: Lp-Metric
The Lp-metric method is used in the proposed DSS model as one of the widely-recognized techniques in the literature [28,29]. The goal is to assess the efficacy of the suggested PMOMILP model through a single objective function. Initially, it is necessary to individually tackle the model with each objective function and attain the ideal values of , , and , which are represented as , , and , respectively. According to the Lp-metric method, three weights of , , and are defined for , , and , respectively. Finally, the single-objective model is built up as follows:
subject to
Constraints (5)–(9), Constraints (17)–(24), and Equations (26)–(32),
- where denotes the final objective function of the model. It is noteworthy that .
4. Results and Discussion
In this section, the offered DSS in this work is evaluated with the help of three numerical cases adapted from Torkayesh et al. [30] and Tirkolaee et al. [23,28] at different scales, which are then slightly modified to comply with the final model. It is worthy of mention that these studies employed the uniform distribution to set most of the parameters. The majority of these parameters are related to the network design addressing locational, tactical and operational decisions, which guarantees a high rate of compliance with our proposed model. Table 1 and Table 2 provide details on the scales and the setting of input parameters for all cases. The weights of the objective functions are then set as (. Our final model is then tackled by means of CPLEX solver/GAMS software.

Table 1.
Scales of the numerical cases.

Table 2.
Parameter setting (U: Uniform).
The final model is now executed on a laptop with a Core™ i7 CPU at 2.60 GHz and 12.00 GB of RAM. Consequently, the ideal (optimal) values of the objective functions are initially attained by optimizing their respective single-objective models (see Table 3). Table 4 presents the final results (i.e., objective functions, CPU times, and absolute gap) obtained from solving all numerical cases. Additionally, Table 5 outlines the strategic decisions to be made.

Table 3.
Ideal (optimal) values of the objective functions.

Table 4.
Final computational results of the numerical cases.

Table 5.
Strategic decisions to establish the required facilities.
Based on Table 4, the proposed DSS can solve the numerical cases in under 468.6 s, finding the optimal values for the objective functions and decision variables. As the problem scale increases, all the objective functions expand, with the most notable increase observed in the second objective function (i.e., ). This issue highlights the significance of the environmental aspect of the problem being accounted for seriously. The objective functions of the Lp-metric method are fewer than 20.5%, which represents the expected deviation values from the optimal values of individual objective functions. As can be seen from Table 5, the number of established facilities in the final case grew significantly, due to the higher number of facilities, waste types, and time periods on which the demand parameters depend.
The last column of Table 4 shows that the solver achieved zero absolute gaps in all cases. Figure 4 represents the upward trend of CPU times for the three numerical cases, with a CPU time of 174.70 s, on average. Here, the blue dashed line stands for the trendline. This figure illustrates an exponential growth in CPU time, indicating the high complexity of the problem. Consequently, for larger scales, the CPU time needed may exceed several hours, highlighting the need for approximate-solution algorithms to manage the complexity.
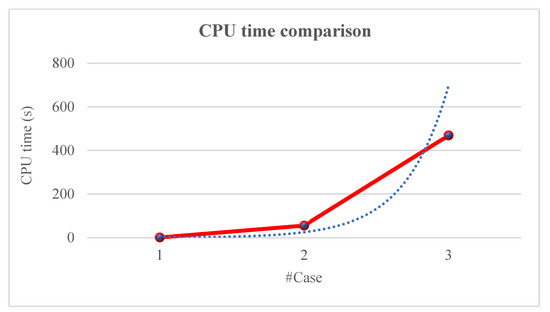
Figure 4.
Comparison of the times.
4.1. Sensitivity Analysis
To further examine the developed DSS, a set of sensitivity analyses is carried out on two main parameters of the model. To do so, multiple combinations of the weights for the objective functions are defined for this purpose (, as well as various change intervals for the specific time period wherein the WMS does not fail (), to evaluate the optimal policies. To proceed with the sensitivity analysis of the weights, we adjust the precedence among the three pillars of sustainability or TBL. Numerical Case 2 is used as a case study for this analysis. The upshots are presented in Table 6 and Table 7. Five different combinations are defined for the weights given to the objective functions in Table 6 and the model is evaluated accordingly. Similarly, five different change intervals are taken into account for the specific time period wherein the WMS does not fail, in Table 7. The change intervals are limited to 20% change in the parameter. Finally, the numerical results of the sensitivity analyses provided by Table 6 and Table 7 are illustrated in Figure 5 and Figure 6, respectively. It is clear that total cost, total pollution, and reliability are highly sensitive to the parameters.

Table 6.
Sensitivity analysis of the weights given to the objective functions.

Table 7.
Sensitivity analysis of the specific time period wherein the WMS does not fail.
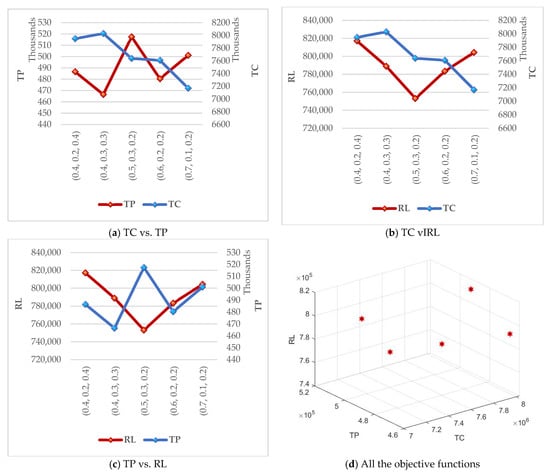
Figure 5.
Sensitivity analysis of (.
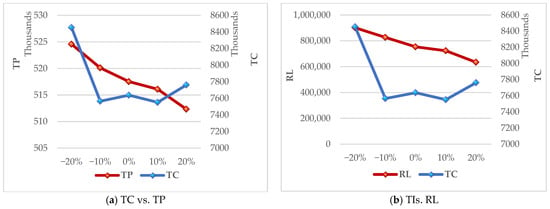
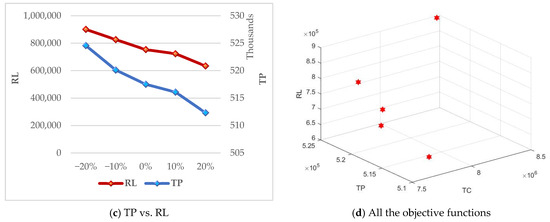
Figure 6.
Sensitivity analysis of .
In accordance with the results attained from the sensitivity analysis, it is observed that various levels of ( and caused diverse fluctuations in the objective functions. It shows that the instability of practical scenarios can directly impact the problem and alter the optimal policy. As expected, assigning higher weights to the objective functions led to better values. As an example, the best value of the total cost is 7,169,560.629, which is provided by (. On the other hand, there is no estimation of the behavior of the objective functions versus the fluctuations of . For example, raising this parameter by 10% led to attaining the best value of the total cost. This is also the case for the other objective functions. As expected, the system reliability has an indirect relation with , wherein diminishing this parameter increased the reliability. Surprisingly, this is the case for the second objective function. As observed, increasing caused a significant reduction in the total amount of environmental pollution, wherein the maximum change occurred at the −20% change interval. Therefore, we can conclude that optimal tuning of for the calculations provides appropriate values for the second and third objective functions; i.e., total environmental and system reliability, respectively. Moreover, an acceptable value can be also achieved for the first objective function, in this regard. For instance, led to an improvement in all objective functions in comparison with . In summary, policy-makers and managers have to evaluate the volume of available resources in the WMS to account for fluctuations that frequently take place in the real world, such as pandemics.
4.2. Discussion: Practical and Theoretical Insights
Despite the previous studies conducted in the literature, our work explicitly introduced the reliability concept and demonstrated its impact on the efficiency of a WMS, which has been ignored so far. The results obtained from the previous research works mostly contributed to the economic and environmental aspects, while it was revealed that social aspect is also significant and depends on the reliability in terms of timely treatment of waste. Furthermore, the circular design of the proposed MSW network led to the fulfillment of SDGs on different levels. In this study, the development and implementation of a PMOMILP model in the design of a circular–sustainable–reliable WMS under uncertainty offered several significant practical implications:
- Enhanced Decision-Making for Waste Management: The model provides an efficient DSS that can aid waste management decisions and policy-makers in settling upon more informed plans. By integrating circular-economy principles, SDGs, and reliability considerations, the DSS guarantees that waste management strategies are both resilient and flexible in the case of fluctuations. This can remarkably enhance the planning and operational efficiency of WMSs, especially in urban areas encountering rapid population growth and increased waste generation.
- Optimization of Resources and Costs: The model’s focus on minimizing total costs while addressing environmental and social impacts allows waste management authorities to optimize resource allocation effectively. By taking into account multiple waste types and utilizing multimodal transportation, the model facilitates sustainable logistics planning, diminishing operational costs and improving the economic viability of waste management practices.
- Enhanced Reliability and Resilience: By defining the possible failures and accounting for uncertainties in waste generation, rates along with waste flow rates, between various facilities, the model augments the reliability and resilience of WMSs. This is crucial in mitigating the risks associated with operational failures, delays, and unforeseen disruptions, such as those caused by pandemics or natural disasters. The model’s ability to adapt to varying situations ensures continuous and efficient waste management operations, even in adverse scenarios.
- Encouragement of Circular-Economy Practices: The integration of circular-economy principles into the model promotes the reuse, recycling, and recovery of materials, thereby diminishing the thorough dependency on landfills and disposal. This not only contributes to environmental sustainability by minimizing waste and resource consumption, but also conforms to global efforts to transition towards more circular and sustainable economic systems.
- Strategic Infrastructure Planning: The model’s application in the configuration of waste management networks, including the selection and establishment of locations for waste transfer, recycling, incineration, and disposal facilities, provides valuable insights for long-term infrastructure planning. Furthermore, the consideration of multiple waste types and the variability of demand guarantees that the designed network is capable of handling diverse waste streams dexterously, leading to more strategic and sustainable infrastructure investments.
On the flip side, the suggested PMOMILP model also contributes to the theoretical advancement of optimization in waste management, as follows:
- Integration of Sustainable Development, Circular Economy, and Reliability in Optimization Models: This work fills a significant gap in the literature by incorporating sustainability and circular-economy principles into reliability considerations in a multi-objective optimization framework. This novel approach offers a deeper insight into how WMSs can be designed to be both sustainable and resilient, contributing to the theoretical development of circular-economy and reliability optimization.
- Application of Possibilistic Programming in Waste Management: The use of possibilistic programming to handle uncertainties in waste management networks is another contribution to the field. Traditional optimization models often rely on probabilistic approaches, which may not adequately capture the vagueness and imprecision inherent in waste management data. The possibilistic approach provides a more flexible and realistic method for modeling uncertainties, taking into account the minimum acceptable degree of feasibility.
- Multi-Objective Optimization with Practical Relevance: The study demonstrates the practical relevance of multi-objective optimization in addressing real-world challenges in waste management. By simultaneously optimizing the sustainability, circularity, and reliability of the system, the model provides a balanced approach to decision-making, which is crucial in treating complex trade-offs. This contributes to the broader literature on multi-objective optimization by showcasing its applicability to pressing global challenges.
- Contribution to SDGs: The research aligns with several United Nations (UN) SDGs, especially those appertaining to responsible consumption and production (SDG 12) and sustainable cities and communities (SDG 11). By providing a framework that supports the achievement of these goals, the proposed DSS contributes to the growing body of literature that seeks to operationalize the SDGs through applicable optimization techniques.
5. Conclusions and Outlook
This research tried to introduce the application of a reliability concept in MSW management, along with the realization of SDGs and circular-economy requirements. To do so, a DSS was offered, based on a PMOMILP model for the configuration of a circular–sustainable–reliable WMS network, under uncertainty. Six levels of WGFs, WTFs, WRFs, WEIFs, SRMMs, and WDFs were taken into account in the network, to guarantee its circular design, to a great extent. Accordingly, a tri-objective model was developed to address the complex challenges encountered by modern WMSs, including the need for sustainability, cost-effectiveness, circularity, reliability, and resilience to uncertainties. Correspondingly, the first, second, and third objective functions were minimizing the total cost, minimizing the environmental impact, and maximizing the reliability of the WMS, respectively. Possibilistic linear programming was then employed to treat the uncertainty of demand and flow rates, with the help of triangular fuzzy numbers. Moreover, the Lp-metric technique was implemented into the model in order to cope with the tri-objectiveness of the model and build up a single objective function to be optimized. To appraise the applicability, complexity, and validity of the proposed model, three numerical cases were created on various scales, on the basis of the benchmarks adapted from the literature. It was revealed that the model is able to treat the cases and find the optimal solutions in a reasonable computational time. Eventually, a set of sensitivity analyses was executed to assess the behavior of the objective functions versus the fluctuations of their corresponding weights and the specific time period wherein the WMS does not fail. The findings demonstrated that the model is notably significant for these parameters where the determination of the final policy to be implemented can directly affect the levels of sustainability, circularity, and reliability of the system.
Along with the limitations of this study, the findings of this research open several avenues for future research. Researchers could focus on implementing other uncertainty-handling techniques such as robust optimization or mixed methods. The obtained results can be then compared and analyzed. Moreover, extending the model to account for dynamic factors, e.g., time-varying waste-generation rates, would provide a more realistic representation of WMSs and enhance the model’s applicability to long-term planning. To treat the computational complexity of the model, future research could explore the development of advanced solution techniques on the basis of heuristic algorithms or parallel computing, in order to enhance its scalability and efficiency. Finally, the principles and methodologies developed in this study could be extended to other sectors that encounter similar challenges, such as water management, energy systems, and supply chain networks. This would extend the research’s influence and aid in advancing more sustainable and resilient infrastructure across various sectors.
All in all, this research provided a valuable contribution to the field of waste management by developing a methodical DSS based on a multi-objective optimization which incorporated sustainability, reliability, and circular-economy principles at various levels of decision-making. While there are limitations to be addressed, the proposed methodology offered a promising framework for making improvements to the design and operation of waste management networks, under uncertainty, with potential applications in a wide range of sectors. For example, the suggested DSS is capable of being generalized to supply-chain-network design, considering manufacturing and distribution activities. To address the main aspects, the total cost of manufacturing and distribution and total environmental pollution must be minimized, along with reliability optimization (i.e., maximizing the expected amount of manufactured and distributed products). Recycling/recovery centers, as well as secondary markets, can be incorporated into the network to address the primary requirements of a circular economy.
Funding
This research received no external funding.
Data Availability Statement
Discussed in Section 4.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Model Notations
| Indices | |
| ) | |
| ) | |
| ) | |
| ) | |
| ) | |
| ) | |
| ) | |
| ) | |
| ) | |
| ) | |
| stands for the index of transportation modes ending at WDFs, while displays the index of transportation modes ending at SRMMs | |
| Parameters | |
| th | |
| th to WRFs | |
| th | |
| th | |
| th | |
| th | |
| th | |
| th-type waste | |
| th-type waste | |
| th-type waste | |
| th-type waste | |
| th-type waste | |
| th | |
| th | |
| th | |
| th | |
| th | |
| th | |
| th | |
| th | |
| th | |
| th | |
| to transfer waste from WTFs to WRFs | |
| to transfer waste from WTFs to WEIFs | |
| to transfer waste from WTFs to WDFs | |
| to transfer waste from WRFs to WDFs | |
| to transfer waste from WRFs to SRMMs | |
| to transfer waste from WEIFs to WDFs | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| Parameter of the exponential distribution expressing the failure rate of cth WTF at tth period | |
| Parameter of the exponential distribution expressing the failure rate of rth WRF at tth period, | |
| Parameter of the exponential distribution expressing the failure rate of ith WEIF at tth period | |
| Parameter of the exponential distribution expressing the failure rate of dth WDF at tth period | |
| A specific time period wherein the WMS does not fail | |
| Variables | |
| th in tth period | |
| th in tth period | |
| th in tth period | |
| th in tth period | |
| th in tth period | |
| th in tth period, | |
| th in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
| in tth period | |
References
- Sharif, N.S.; Pishvaee, M.S.; Aliahmadi, A.; Jabbarzadeh, A. A bi-level programming approach to joint network design and pricing problem in the municipal solid waste management system: A case study. Resour. Conserv. Recycl. 2018, 131, 17–40. [Google Scholar] [CrossRef]
- Eghbali, H.; Arkat, J.; Tavakkoli-Moghaddam, R. Sustainable supply chain network design for municipal solid waste management: A case study. J. Clean. Prod. 2022, 381, 135211. [Google Scholar] [CrossRef]
- Ogunmakinde, O.E.; Egbelakin, T.; Sher, W. Contributions of the circular economy to the UN sustainable development goals through sustainable construction. Resour. Conserv. Recycl. 2022, 178, 106023. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, L.; Zhang, J.; Wang, Z. Using social network analysis to identify the critical factors influencing residents’ green consumption behavior. Systems 2023, 11, 254. [Google Scholar] [CrossRef]
- Cai, Y.; Huang, G.H.; Nie, X.H.; Li, Y.P.; Tan, Q. Municipal solid waste management under uncertainty: A mixed interval parameter fuzzy-stochastic robust programming approach. Environ. Eng. Sci. 2007, 24, 338–352. [Google Scholar] [CrossRef]
- Shih, L.H.; Lin, Y.T. Optimal routing for infectious waste collection. J. Environ. Eng. 1999, 125, 479–484. [Google Scholar] [CrossRef]
- Kim, B.I.; Kim, S.; Sahoo, S. Waste collection vehicle routing problem with time windows. Comput. Oper. Res. 2006, 33, 3624–3642. [Google Scholar] [CrossRef]
- Liang, Y.C.; Minanda, V.; Gunawan, A. Waste collection routing problem: A mini-review of recent heuristic approaches and applications. Waste Manag. Res. 2022, 40, 519–537. [Google Scholar] [CrossRef]
- Singh, D.; Dikshit, A.K.; Kumar, S. Smart technological options in collection and transportation of municipal solid waste in urban areas: A mini review. Waste Manag. Res. 2024, 42, 3–15. [Google Scholar] [CrossRef]
- Achillas, C.; Moussiopoulos, N.; Karagiannidis, A.; Banias, G.; Perkoulidis, G. The use of multi-criteria decision analysis to tackle waste management problems: A literature review. Waste Manag. Res. 2013, 31, 115–129. [Google Scholar] [CrossRef]
- Garcia-Garcia, G. Using Multi-Criteria Decision-Making to optimise solid waste management. Curr. Opin. Green Sustain. Chem. 2022, 37, 100650. [Google Scholar] [CrossRef]
- Saeidi-Mobarakeh, Z.; Tavakkoli-Moghaddam, R.; Navabakhsh, M.; Amoozad-Khalili, H. A bi-level and robust optimization-based framework for a hazardous waste management problem: A real-world application. J. Clean. Prod. 2020, 252, 119830. [Google Scholar] [CrossRef]
- Kargar, S.; Pourmehdi, M.; Paydar, M.M. Reverse logistics network design for medical waste management in the epidemic outbreak of the novel coronavirus (COVID-19). Sci. Total Environ. 2020, 746, 141183. [Google Scholar] [CrossRef] [PubMed]
- Mamashli, Z.; Javadian, N. Sustainable design modifications municipal solid waste management network and better optimization for risk reduction analyses. J. Clean. Prod. 2021, 279, 123824. [Google Scholar] [CrossRef]
- Ahmed, R.R.; Zhang, X. Multi-stage network-based two-type cost minimization for the reverse logistics management of inert construction waste. Waste Manag. 2021, 120, 805–819. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, L.; He, C.X. A multi-objective and multi-period optimization model for urban healthcare waste’s reverse logistics network design. J. Comb. Optim. 2021, 42, 785–812. [Google Scholar] [CrossRef]
- Balci, E.; Balci, S.; Sofuoglu, A. Multi-purpose reverse logistics network design for medical waste management in a megacity: Istanbul, Turkey. Environ. Syst. Decis. 2022, 42, 372–387. [Google Scholar] [CrossRef]
- Govindan, K.; Nosrati-Abarghooee, S.; Nasiri, M.M.; Jolai, F. Green reverse logistics network design for medical waste management: A circular economy transition through case approach. J. Environ. Manag. 2022, 322, 115888. [Google Scholar] [CrossRef]
- Joneghani, N.M.; Zarrinpoor, N.; Eghtesadifard, M. A mathematical model for designing a network of sustainable medical waste management under uncertainty. Comput. Ind. Eng. 2022, 171, 108372. [Google Scholar] [CrossRef]
- Nosrati-Abarghooee, S.; Sheikhalishahi, M.; Nasiri, M.M.; Gholami-Zanjani, S.M. Designing reverse logistics network for healthcare waste management considering epidemic disruptions under uncertainty. Appl. Soft Comput. 2023, 142, 110372. [Google Scholar] [CrossRef]
- Yousefloo, A.; Babazadeh, R.; Mohammadi, M.; Pirayesh, A.; Dolgui, A. Design of a robust waste recycling network integrating social and environmental pillars of sustainability. Comput. Ind. Eng. 2023, 176, 108970. [Google Scholar] [CrossRef]
- Amirteimoori, A.; Tirkolaee, E.B.; Amirteimoori, A.; Khakbaz, A.; Simic, V. A novel parallel heuristic method to design a sustainable medical waste management system. J. Clean. Prod. 2024, 452, 141897. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Simic, V.; Ghobakhloo, M.; Foroughi, B.; Asadi, S.; Iranmanesh, M. Integrated design of a sustainable waste management system with co-modal transportation network: A robust bi-level decision support system. J. Clean. Prod. 2024, 449, 141760. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Faridnia, A.; Soltani, M.; Weber, G.W. Multi-objective optimization for the reliable pollution-routing problem with cross-dock selection using Pareto-based algorithms. J. Clean. Prod. 2020, 276, 122927. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, A.; An, L.; Li, M. Bayesian inference of system reliability for multicomponent stress-strength model under Marshall-Olkin Weibull distribution. Systems 2022, 10, 196. [Google Scholar] [CrossRef]
- Sun, Y. A robust possibilistic programming approach for a road-rail intermodal routing problem with multiple time windows and truck operations optimization under carbon cap-and-trade policy and uncertainty. Systems 2022, 10, 156. [Google Scholar] [CrossRef]
- Lai, Y.J.; Hwang, C.L. A new approach to some possibilistic linear programming problems. Fuzzy Sets Syst. 1992, 49, 121–133. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Aydin, N.S. Integrated design of sustainable supply chain and transportation network using a fuzzy bi-level decision support system for perishable products. Expert Syst. Appl. 2022, 195, 116628. [Google Scholar] [CrossRef]
- Javanmardan, A.; Golpîra, H.; Baradaran, V. A Socio-Economic and Quality-Oriented Optimal Fruit Supply Chain Network Design in a Multi-Market Multi-Product Environment: A Real Case Study. Socio-Econ. Plan. Sci. 2024, 94, 101910. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Vandchali, H.R.; Tirkolaee, E.B. Multi-objective optimization for healthcare waste management network design with sustainability perspective. Sustainability 2021, 13, 8279. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).