Complex Network-Based Resilience Capability Assessment for a Combat System of Systems
Abstract
1. Introduction
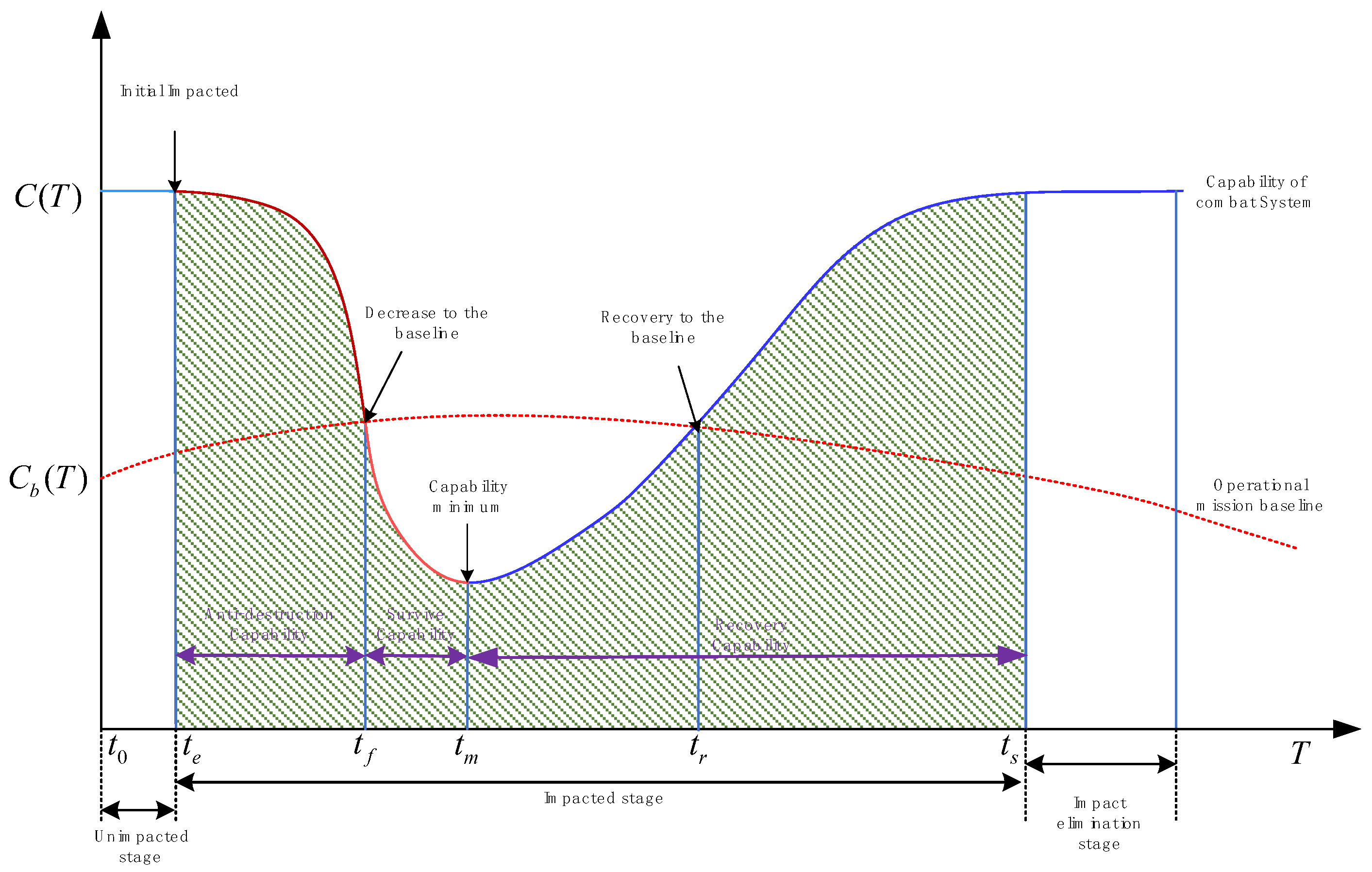
2. Analysis of Elements of Combat SoS Resilience
- (1)
- Despite external strikes or disruptions, the combat SoS retains the ability to fulfill its mission and maintain its fundamental capabilities.
- (2)
- When certain combat elements are damaged or fail, resulting in a reduction in the SoS’s capability, the combat SoS can progressively restore and enhance its overall capability using strategies such as element repair, reconstruction, and dynamic adjustment.
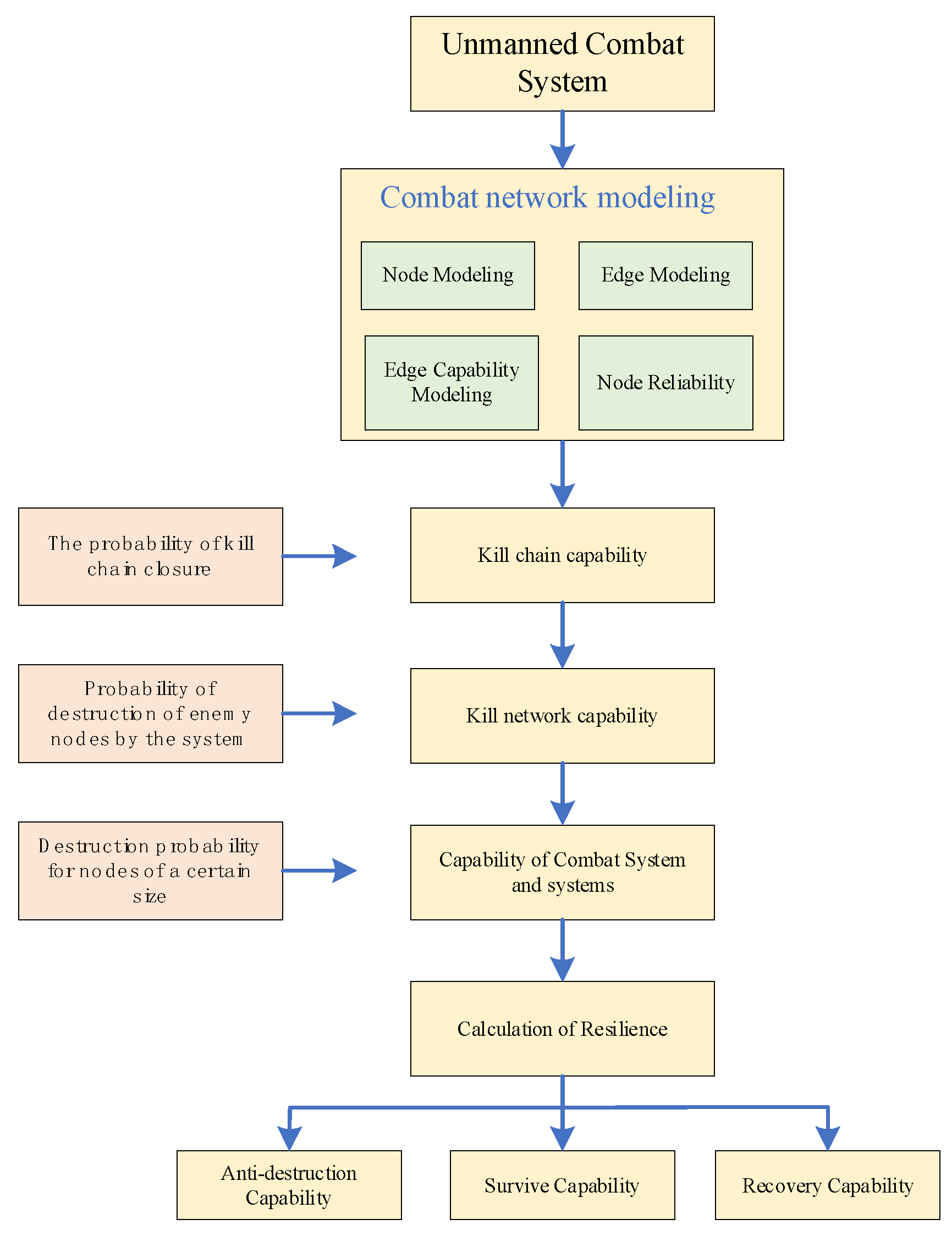
3. Construction of a Networked Model for a Combat SoS
3.1. Combat Network Modeling
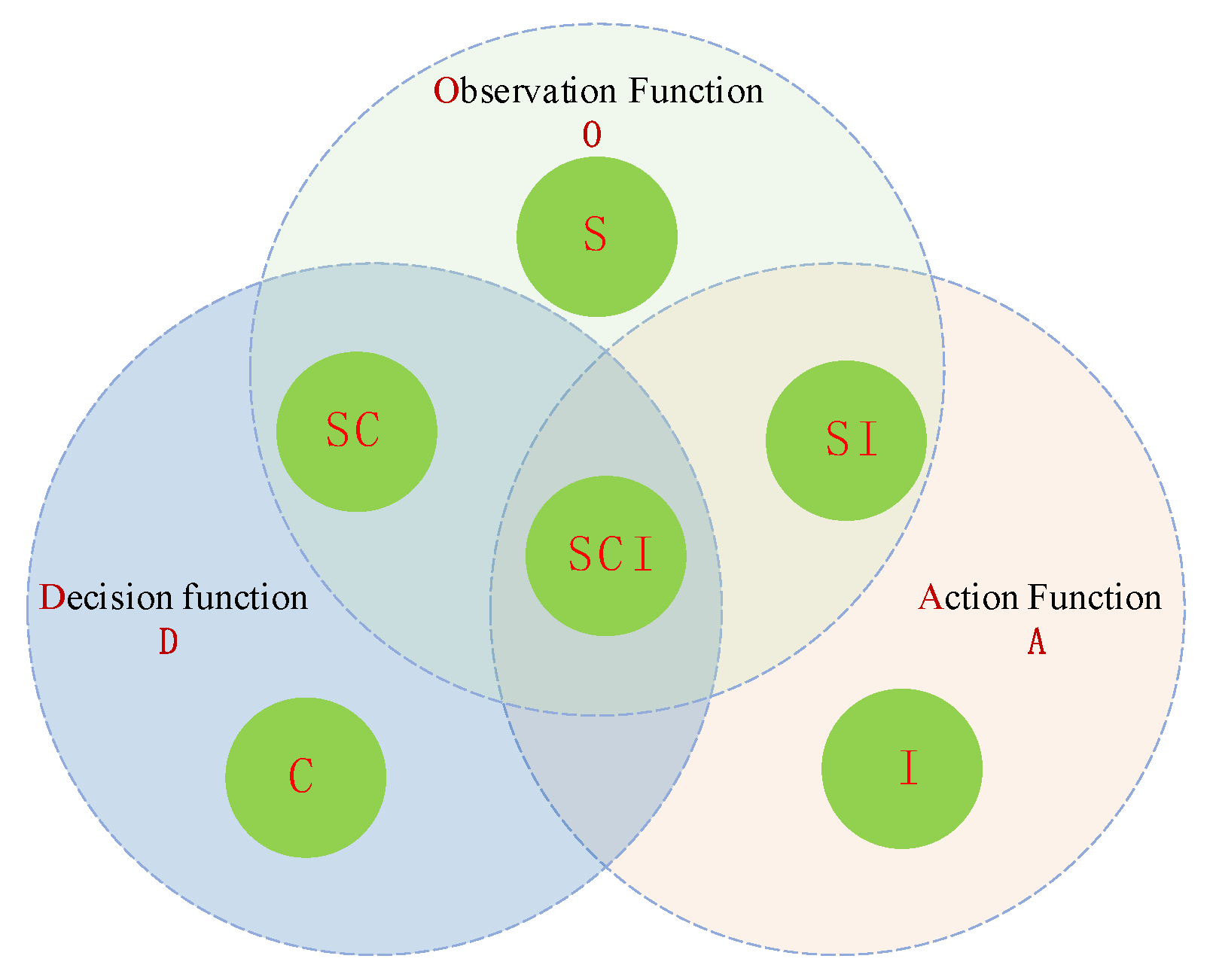
3.1.1. Node Modeling of a Combat Network
3.1.2. Edge Modeling of the Combat Network
3.2. Edge Capability Modeling
4. Combat SoS Capability Model Based on Kill Chain and Kill Network Capability
4.1. Mathematical Model of Kill Chain Capability
4.2. Mathematical Modeling of Kill Network Capability
4.2.1. Description of the Kill Network Capability
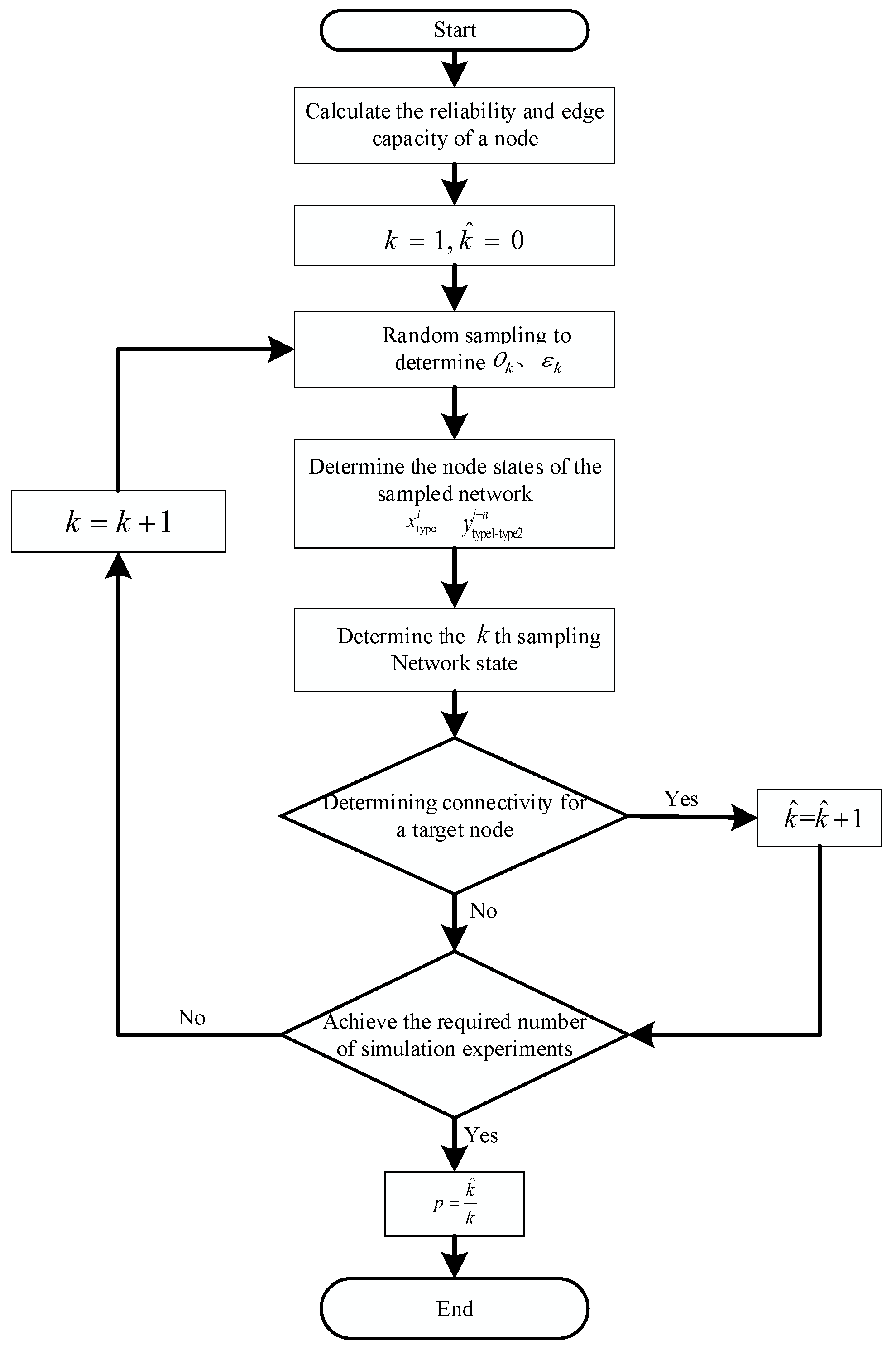
4.2.2. Solving the Kill Network Capability Based on Monte Carlo Simulation
- (1)
- Determine the adjacency matrix
- (2)
- Determining the kill chain on–off situation in the kth sampling
- (3)
- Calculation of the SoS’s capability to attack nodes
4.3. Mathematical Model of Combat SoS’s Capability
5. Analysis and Verification of Indicator Rationality
5.1. Design of Attack and Reconstruction Strategy
5.1.1. Analysis and Design of Attack Strategy
- (1)
- Random attack strategy
- (2)
- Deliberate attack strategy
5.1.2. Reconstruction Strategy
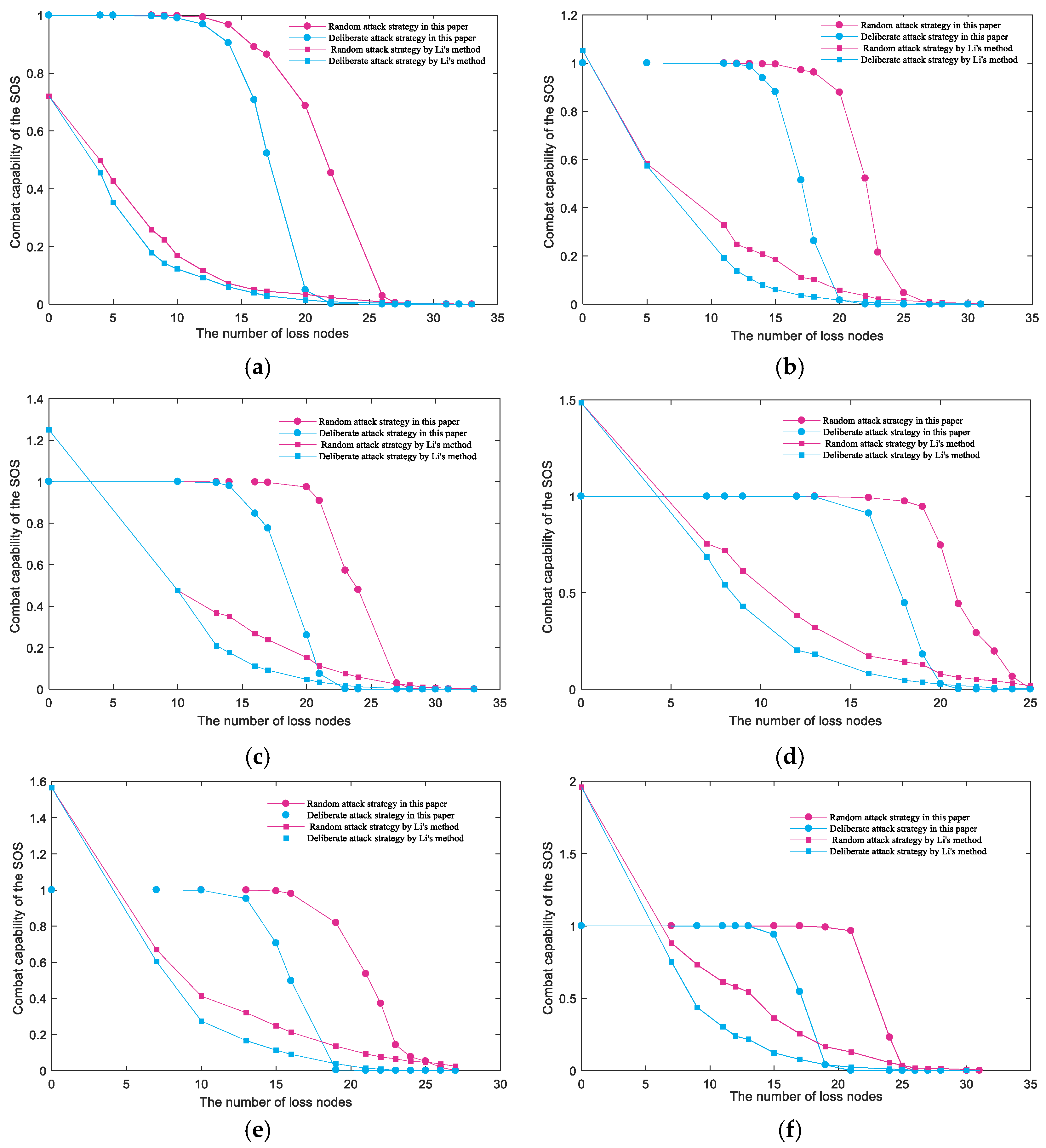
5.2. Rationality Analysis of the SoS Combat Capability Calculation Model
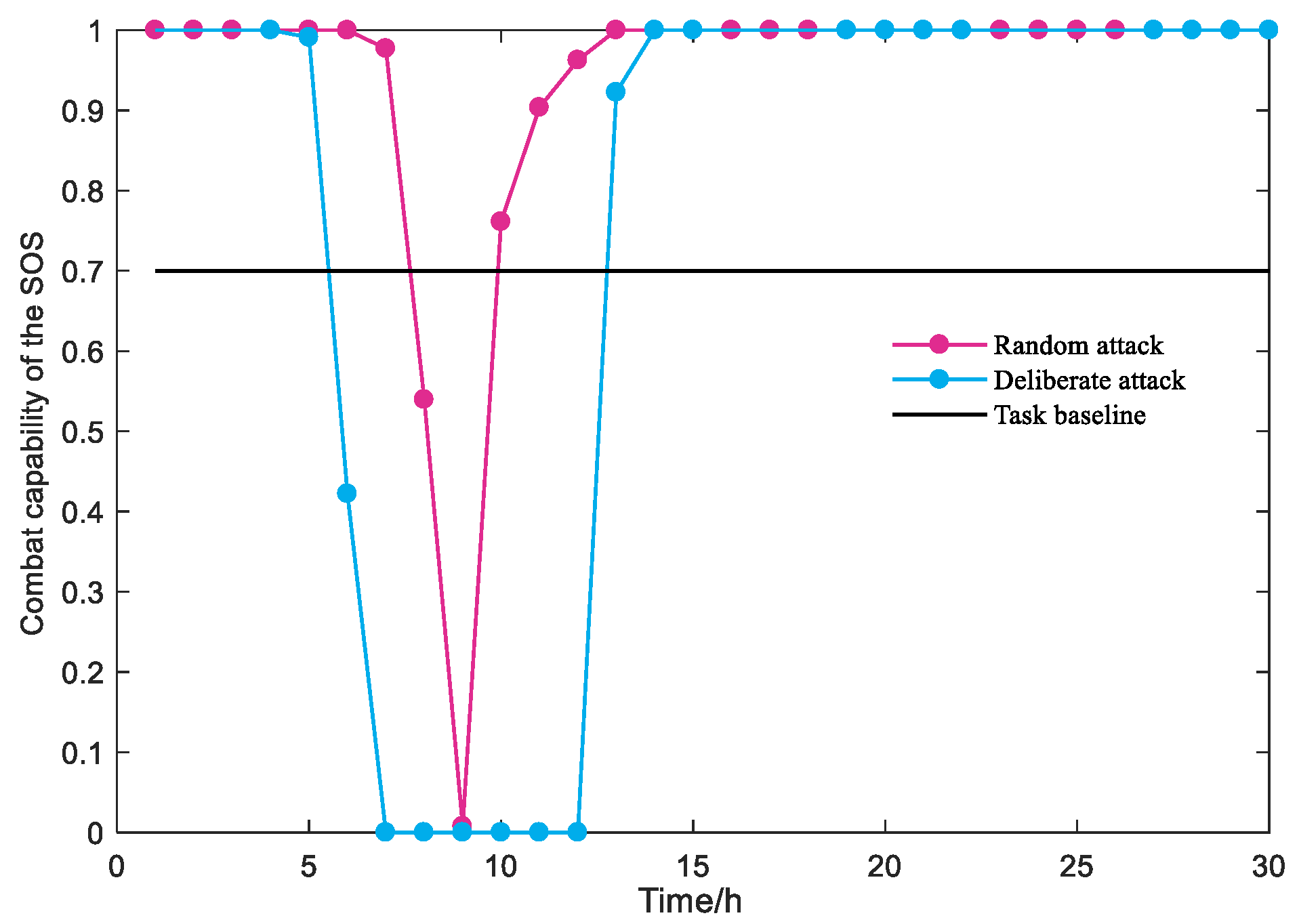
5.3. Resilience Analysis under Different Attack Strategies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, Y.; Dai, G.; Zhou, Y.; Huang, Y.; Zhou, D. Conflicting evidence fusion using a correlation coefficient-based approach in complex network. Chaos Solitons Fractals 2023, 176, 114087. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Pan, C.; Chen, B. Measure of invulnerability for command and control network based on Mission Link. Inf. Sci. 2018, 426, 148–159. [Google Scholar]
- Li, J.; Tan, Y.; Yang, K.; Zhang, X.; Ge, B. Structural robustness of combat networks of weapon system-of-systems based on the Operation Loop. Int. J. Syst. Sci. 2016, 48, 659–674. [Google Scholar] [CrossRef]
- Yang, P.; Hu, S.; Zhou, S.; Zhang, J. A topological sensitive node importance evaluation method in Aerospace Information Networks. Sensors 2022, 23, 266. [Google Scholar] [CrossRef] [PubMed]
- Tian, G.; Yang, X.; Li, Y.; Yang, Z.; Chen, G. Hybrid weighted communication network node importance evaluation method. Front. Phys. 2023, 11, 1133250. [Google Scholar]
- Liu, C.; Wang, J.; Xia, R. Node Importance Evaluation in multi-platform avionics architecture based on Topsis and PageRank. EURASIP J. Adv. Signal Process. 2023, 2023, 27. [Google Scholar] [CrossRef]
- Xu, R.; Liu, X.; Cui, D.; Xie, J.; Gong, L. An evaluation method of contribution rate based on fuzzy Bayesian networks for equipment system-of-systems architecture. J. Syst. Eng. Electron. 2023, 34, 574–587. [Google Scholar] [CrossRef]
- Li, J.; Zhao, D.; Jiang, J.; Yang, K.; Chen, Y. Capability oriented equipment contribution analysis in temporal combat networks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 696–704. [Google Scholar] [CrossRef]
- Nie, J.F.; Chen, X.J.; Shi, H.Q. Dynamic Super-network model of task-oriented naval fleet “Cloud Combat” system. Acta Armamentarii 2021, 42, 2513–2521. (In Chinese) [Google Scholar]
- Koivisto, J.; Ritala, R.; Vilkko, M. Conceptual model for capability planning in a military context—A systems thinking approach. Syst. Eng. 2022, 25, 457–474. [Google Scholar] [CrossRef]
- Anteroinen, J. The Holistic Military Capability Life Cycle Model. In Proceedings of the 2012 7th International Conference on System of Systems Engineering (SoSE), Genova, Italy, 16–19 July 2012. [Google Scholar]
- Kuikka, V. Probabilistic modelling of system capabilities in Operations. Systems 2023, 11, 115. [Google Scholar]
- Han, Q.; Pang, B.; Li, S.; Li, N.; Guo, P.; Fan, C.; Li, W. Evaluation method and optimization strategies of resilience for Air & space defense system of systems based on kill network theory and improved self-information quantity. Def. Technol. 2023, 21, 219–239. [Google Scholar]
- Li, J.; Yang, K.; Fu, C.; Zhang, X.; Chen, Y. An operational efficiency evaluation method for weapon system-of-systems combat networks based on Operation Loop. In Proceedings of the 2014 9th International Conference on System of Systems Engineering (SOSE), Glenelg, Australia, 9–13 June 2014. [Google Scholar]
- Li, J.; Ge, B.; Jiang, J.; Yang, K.; Chen, Y. High-end weapon equipment portfolio selection based on a heterogeneous network model. J. Glob. Optim. 2018, 78, 743–761. [Google Scholar]
- Li, J.; Zhao, D.; Ge, B.; Jiang, J.; Yang, K. Disintegration of operational capability of heterogeneous combat networks under incomplete information. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 5172–5179. [Google Scholar]
- Pan, X.; Wang, H.; Yang, Y.; Zhang, G. Resilience Based Importance Measure Analysis for SoS. J. Syst. Eng. Electron. 2019, 30, 920. Available online: https://apps.dtic.mil/sti/pdfs/AD1032526.pdf (accessed on 20 November 2023).
- Chen, Z.; Zhou, Z.; Zhang, L.; Cui, C.; Zhong, J. Mission Reliability Modeling and evaluation for reconfigurable unmanned weapon system-of-systems based on effective Operation Loop. J. Syst. Eng. Electron. 2023, 34, 588–597. [Google Scholar]
- Chen, Z.; Hong, D.; Cui, W.; Xue, W.; Wang, Y.; Zhong, J. Resilience evaluation and optimal design for weapon system of systems with dynamic reconfiguration. Reliab. Eng. Syst. Saf. 2023, 237, 109409. [Google Scholar]
- Cares, J.R. An Information Age Combat Model; Alidade, Inc.: Newport, PR, USA, 2004; pp. 85–90. [Google Scholar]
- Cares, J.R. Distributed Networked Operations: The Foundations of Network Centric Warfare; iUniverse Inc.: Lincoln, NE, USA, 2005; pp. 63–69. [Google Scholar]
- Yang, S.; Wang, W.; Li, X.; Wang, T.; Li, B.; He, H. A review of the conceptual development and research status of kill chain. In Proceedings of the Third Systems Engineering Conference—Complex Systems and Systems Engineering Management, Zhuhai, China, 28 June–2 July 2021; pp. 67–72. [Google Scholar]
- Wang, Y.; Shang, B.; Song, P.; Ke, E.Q. A method for identifying key nodes of combat system network based on kill chain. Syst. Eng. Electron. 2023, 45, 736–744. Available online: http://kns.cnki.net/kcms/detail/11.2422.TN.20220615.1421.015.html (accessed on 3 November 2022).
- Davila-Frias, A.; Yadav, O.P.; Salem, S.; Jain, R. All-terminal network reliability estimation with Graph Neural Networks. In Proceedings of the 2022 Annual Reliability and Maintainability Symposium (RAMS), Tucson, AZ, USA, 24–27 January 2022. [Google Scholar]
- Brown, J.I.; Colbourn, C.J.; Cox, D.; Graves, C.; Mol, L. Network reliability: Heading out on the highway. Networks 2020, 77, 146–160. [Google Scholar]
- Davila-Frias, A.; Yodo, N.; Le, T.; Yadav, O.P. A deep neural network and Bayesian method based framework for all-terminal network reliability estimation considering degradation. Reliab. Eng. Syst. Saf. 2023, 229, 108881. [Google Scholar]
- Monfared, M.A.S.; Rezazadeh, M.; Alipour, Z. Road networks reliability estimations and optimizations: A bi-directional bottom-up, top-down approach. Reliab. Eng. Syst. Saf. 2022, 222, 108427. [Google Scholar] [CrossRef]
- Brown, J.; DeGagné, C.D. Roots of two-terminal reliability polynomials. Networks 2020, 78, 153–163. [Google Scholar] [CrossRef]
- Dohmen, K. Inclusion-exclusion and network reliability. Electron. J. Comb. 1998, 5, R36. [Google Scholar]
- Ball, M.O. Complexity of network reliability computations. Networks 1980, 10, 153–165. [Google Scholar] [CrossRef]
- Yu, X.; Li, Y.; Zheng, X. Node importance evaluation based on communication network performance grads. J. Tsinghua Univ. (Sci.Technol.) 2008, 48, 542–544. [Google Scholar]
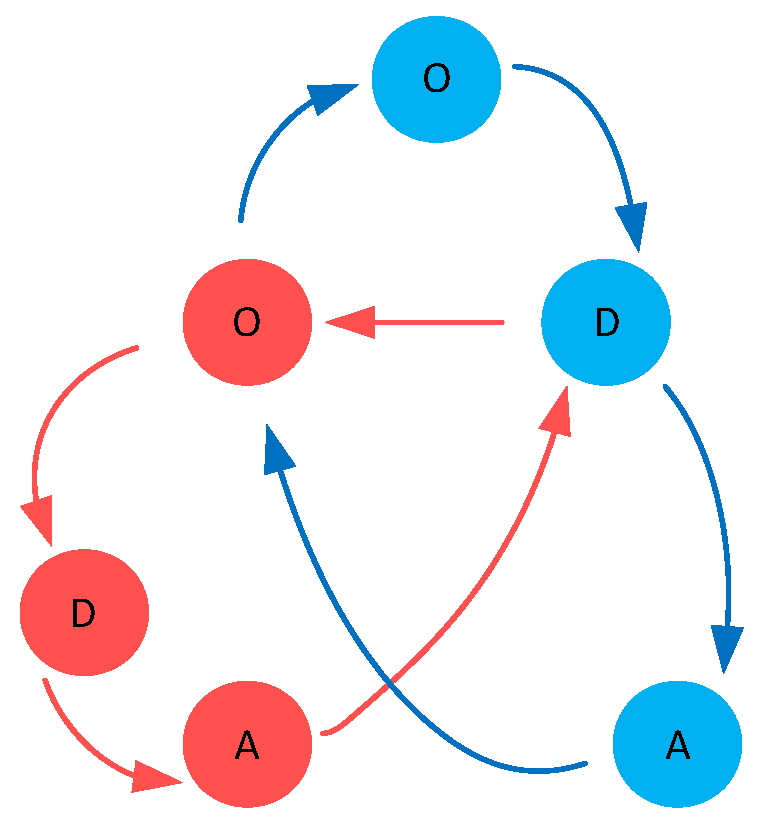


| Number | Edge | Significance |
|---|---|---|
| 1 | Target nodes are detected by observation functional nodes | |
| 2 | Observation functional nodes upload intelligence information to decision functional nodes | |
| 3 | Sharing of reconnaissance intelligence information between observation functional nodes | |
| 4 | Sharing of decision informational between decision function nodes | |
| 5 | Decision functional nodes issue commands to the action functional nodes | |
| 6 | Action functional nodes strike the target enemy nodes |
| Killing Chain | Meaning |
|---|---|
| T-O-D-A-T | Basic kill chain |
| T-O-O-D-A-T | Kill chain including collaborative reconnaissance |
| T-O-D-D-A-T | Kill chain including decision-making synergy |
| T-O-O-D-D-A-T | Kill chain including coordinated reconnaissance and decision-making |
| Node Type | Proportion (%) | Functional Type | Edge Capability Expectation | Edge Capability Variance | Reliability Expectation | Reliability Variance |
|---|---|---|---|---|---|---|
| S | 10 | O | 0.2 | 0.1 | 0.85 | 0.02 |
| C | 20 | D | 0.2 | 0.1 | 0.85 | 0.02 |
| I | 20 | A | 0.2 | 0.1 | 0.85 | 0.02 |
| SC | 20 | O | 0.2 | 0.1 | 0.85 | 0.02 |
| D | 0.2 | 0.1 | ||||
| SI | 20 | O | 0.2 | 0.1 | 0.85 | 0.02 |
| A | 0.2 | 0.1 | ||||
| SCI | 10 | O | 0.2 | 0.1 | 0.85 | 0.02 |
| D | 0.2 | 0.1 | ||||
| A | 0.2 | 0.1 |
| Node Type | S | C | I | SC | SI | SCI |
|---|---|---|---|---|---|---|
| Recovery Duration (h) | 5 | 5 | 5 | 8 | 8 | 10 |
| Node | ||||||||||
| Degree | 21.16 | 21.71 | 22.55 | 21.77 | 16.06 | 16.08 | 15.24 | 15.71 | 17.79 | 17.36 |
| Node | ||||||||||
| Degree | 14.04 | 15.53 | 11.64 | 10.92 | 10.93 | 12.61 | 11.42 | 11.32 | 11.74 | 11.94 |
| Node | ||||||||||
| Degree | 37.45 | 36.93 | 36.67 | 37.11 | 38.09 | 38.45 | 36.24 | 36.12 | 31.94 | 34.64 |
| Node | ||||||||||
| Degree | 34.17 | 31.42 | 35.84 | 35.98 | 31.97 | 34.56 | 47.48 | 48.41 | 49.43 | 49.03 |
| Wave | Random Attack | Deliberate Attack | ||
|---|---|---|---|---|
| The Attacked Nodes | The Number of Attacked Nodes | The Attacked Nodes | The Number of Attacked Nodes | |
| Wave 1 () | ,,,,,,,,,,,, | 13 | ,,,,,,,,,,,, | 13 |
| Wave 2 () | ,, | 3 | ,, | 3 |
| Wave 3 () | ,,, | 4 | ,,, | 4 |
| Wave 4 () | ,,, | 4 | ,,, | 4 |
| Wave 5 () | ,,, | 4 | ,,, | 4 |
| Attack Strategy | Anti-Destruction Capability | Survival Capability | Recovery Capability | Resilience |
|---|---|---|---|---|
| Random attack | 6.6080 | 0.4121 | 20.1311 | 27.1512 |
| Deliberate attack | 4.5165 | 0.3965 | 17.4223 | 22.3353 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Li, W.; Zhang, T. Complex Network-Based Resilience Capability Assessment for a Combat System of Systems. Systems 2024, 12, 31. https://doi.org/10.3390/systems12010031
Chen W, Li W, Zhang T. Complex Network-Based Resilience Capability Assessment for a Combat System of Systems. Systems. 2024; 12(1):31. https://doi.org/10.3390/systems12010031
Chicago/Turabian StyleChen, Wenyu, Weimin Li, and Tao Zhang. 2024. "Complex Network-Based Resilience Capability Assessment for a Combat System of Systems" Systems 12, no. 1: 31. https://doi.org/10.3390/systems12010031
APA StyleChen, W., Li, W., & Zhang, T. (2024). Complex Network-Based Resilience Capability Assessment for a Combat System of Systems. Systems, 12(1), 31. https://doi.org/10.3390/systems12010031





