Simulation and Goal Programming Approach to Improve Public Hospital Emergency Department Resource Allocation

Abstract

Efficient and effective operation of an emergency department is necessary. Since patients can visit the emergency department without making an appointment, the emergency department always treats a lot of critical patients. Moreover, the severity of the ailment determines which patients should be prioritized. Therefore, the patients are greatly impacted as a consequence of longer waiting times caused primarily by incorrect resource allocation. It frequently happens that patients leave the hospital or waiting area without treatment. Certainly, the emergency department’s operation can be made more effective and efficient by examining its work and making modifications to the number of resources and their allocation. This study, therefore, investigates the emergency department of a public hospital to improve its functioning. The goal of this research is to model and simulate an emergency department to minimize patient wait times and also minimize the number of patients leaving the hospital without service. A comprehensive simulation model is developed using the Arena simulation platform and goal programming is undertaken to conduct simulation optimization and resource allocation analysis. Hospital management should realize that all resources must be prioritized rather than just focusing on one or two of them. The case scenario (S3) in this study that implements goal programming with variable weights yields the most favorable results. For example, it is observed in this instance that the number of patients leaving the system without service drops by 61.7%, and there is also a substantial drop in waiting times for various types of patients.

1. Introduction

The healthcare sector has recently undergone substantial transformations. As a result, hospitals as evolving systems must constantly adapt to meet the needs of the modern healthcare system. Hospitals must not only innovate to deliver superior treatment at a cheaper price, but also boost administrative reliability and effectiveness. Healthcare modeling and simulation is one such contemporary technique which can offer a number of benefits, such as lowering expenditures and improving patient satisfaction [1,2,3,4]. In any hospital, an emergency department is a critical section because it cares for patients around the clock. The patients in the emergency department have to undergo various phases [5] such as arrival registration, data retrieving, triage assignment, nurse assignment, doctor evaluation, imaging, and laboratory tests, planning treatment, follow-up for the availability of inpatient beds, and physicians, and finally release or admittance. It is also evident that any emergency department process delays at a specific phase build pressure on the systems and their resources. Thus, simulation along with an optimization tool is an ideal approach that can be adopted by hospital management to enhance the working of the emergency department. Therefore, the goal of this work is to combine simulation with the multi-objective goal programming technique to minimize the waiting times of the patients visiting the emergency department. A simulation model of an emergency department from a public hospital (King Khaled University Hospital, KKUH, Riyadh) in Saudi Arabia is developed and analyzed using the Arena^® Simulation Software, version 16.2 (Rockwell Automation). Subsequently, Arena’s OptQuest tool is deployed to run multiple simulation scenarios created by the goal programming approach. Certainly, when simulation and goal programming are integrated, it is possible to take advantage of the unique benefits of both approaches and exploit their full potential. For example, in this work, the simulation model records and replicates patient movement, while goal programming accomplishes several objectives across a spectrum of opposing requirements. The objective of this research is also to assist hospital administration in better understanding patient movement so that they can make informed and better decisions in an emergency department. The seriousness of the case determines which patients should be prioritized while treating both critical and non-critical patients. A department’s ability to function properly depends on the assigned number of doctors, nurses, beds, etc. The financial burden on a hospital cannot be unfairly increased by increasing the amount of resources, and, on the other hand, patients would suffer if there were to be fewer resources available. It is thus emphasized that there is a necessity of identifying an adequate number of resources and their allocation. Additionally, it has been noted that patients frequently leave hospitals or waiting rooms unsupervised and do not return to the same facility when waiting periods are great. Hence, the appropriate assignment of resources would also minimize the waiting times and thus the number of patients leaving the queue untreated. The details of resources, distinct entities, and their interactions and flow within the model; relevant data collection; model initialization; and goal programming model, the various performance measures and an approach to find an optimal solution that satisfies those targets are presented here, in the following sections and sub-sections.

2. Background

The application of simulation to research various elements of hospital operations has a long history in the scientific community. Indeed, academics and researchers have effectively used simulation and other mathematical-based approaches to address an array of hospital-related issues [6,7,8,9,10,11,12,13]. For instance, Chouba et al. [14] built a simulation model of the emergency department and minimized patient average waiting time. They stated that the quality of treatment could be improved by making optimal use of the resources, which, according to the authors, are a key component. Similarly, Feng et al. [15] observed that due to the hindered access to medical supplies, optimizing resource allocation to reduce patient lengths of stay and unnecessary expenses is imperative. The research findings of Storrow et al. [16] proposed and demonstrated the value of an efficient healthcare simulation model. They suggested reducing the time for implementing emergency services and the response time using the established modeling approaches. Indeed, multiple health and medical domains utilized simulations, and in the past decade, numerous simulation approaches have caught the interest of many healthcare academicians [17]. As reported by Bahari and Asadi [18], the optimal combination of resources must be determined to solve real case studies by applying the simulation and decision-making models with more than one objective. Furthermore, Yeh and Lin [19] used a simulation for minimizing patient queue time in an emergency department as well as provided the use of multi-criteria decision-making for enhancing patient care and staffing in the hospital administration of the Show-Chwan Memorial Hospital in central Taiwan. Subsequently, Oddoye et al. [20] estimated the ideal staffing needs for the medical assessment units and reduced system inefficiencies to optimize the flow of patients.

Recent developments have seen the use of hybrid modeling, operations research, integrated methodologies, and participatory approaches in addition to more conventional techniques. This is due to the fact that using sophisticated modeling techniques or a reliable forecasting system are essential for implementing superior management strategies that maximize resource utilization, cut costs, and boost consumer trust [21]. For example, by taking into account actual emergency department data, Tabar and Zeil [22] created a forecasting model to effectively simulate the consequences of special events on emergency department visits. A simulation approach based on agent-based modeling and exhaustive search was reported by Cabrera et al. [23] to formulate a decision support system for hospital emergency department. They aimed to assist the authorities in establishing guidelines that could enhance emergency department operations. Similarly, as a nurse scheduling strategy, Rerkjirattikal et al. [24] proposed scheduling optimization tools to make an effective nurse shift rotation schedule considering both personal choices for working shifts and day-off assignments and the equitable distribution of the workload. Castanheira-Pinto et al. [25] also emphasized the relevance of simulation and optimization tools for comprehending and efficiently enhancing the operations of any complicated system. They established a simulation methodology to accomplish the desired benchmarks for emergency departments in public hospitals. They devised a number of alternative scenarios using the data collected from the hospital’s database in order to maximize the intricate operations of the emergency department.

Numerous research works also combined optimization models with discrete-event simulation to streamline staffing levels and shorten the average length of stay for patients [26,27,28,29,30]. Hybrid simulation is certainly becoming more popular as healthcare systems have grown more sophisticated and multifaceted [31,32]. Due to complicated systems and large amounts of data, it is difficult for an isolated simulation model to effectively make appropriate decisions. Moreover, studies reveal that the most popular method of developing hybrid simulation models in healthcare is the combination of discrete event simulation with system dynamics [33]. A hybrid modeling approach based on forecasting and real-time simulation introduced by Harper and Mustafee [34] was useful to reduce emergency department overcrowding. The approach used seasonal ARIMA time-series forecasting and could be useful for policymakers, clinicians, and managers at the regional level who are responsible for managing emergency department operational performance. The research study of Tang et al. [35] also described a simulation model to capture a large emergency department’s operation and assess the impact of a COVID-19-like disease on the throughput of an emergency department. In another similar study [36], an optimization model was implemented to identify optimal physician staffing levels for minimizing the combined cost of patient wait times, handoffs, and physician shifts in a hospital emergency department. Likewise, Doudareva and Carter [37] and Mustafee et al. [38] developed discrete event simulation models of emergency departments to diagnose bottlenecks and evaluate performance improvement approaches. A research study by Harper and Mustafee [39] proposed the use of participatory design research methodology for the development of real-time simulation models in healthcare. The methodology emphasized model usefulness and usability using iterative cycles of development and evaluation. Prabhu et al. [40] also explored the impact of delays resulting from the imaging process and bundling the imaging orders on patient flow in the emergency department using discrete event simulation. The results showed that bundling imaging orders can also reduce patient time in the emergency department. Apart from reducing patient waiting time, evaluating staff strength and overcrowding, etc., simulation models have also been utilized by researchers for emergency department evacuation, logistics optimization, layout design, etc. [41,42,43].

It has been repeatedly demonstrated in the literature that simulation modeling is the most effective method for enhancing the performance of any complicated system. Researchers in the healthcare industry have frequently utilized it to increase the effectiveness and efficiency of their particular departments. These improvements have mostly been focused on decreasing patient wait times and raising patient satisfaction by properly scheduling and distributing resources. The need for combining a simulation model with an optimization tool has also been underlined by the researchers as a way to improve the efficacy of the simulations. However, it seems that there are fewer works than anticipated that integrate simulation with optimization. This work is intended to move in that direction by combining goal programming with a simulation model to increase patient satisfaction in an emergency department of a public hospital. Thus, the following sections describe patient flow in the hospital under consideration, its simulation model, and the application goal programming.

3. Simulation Model

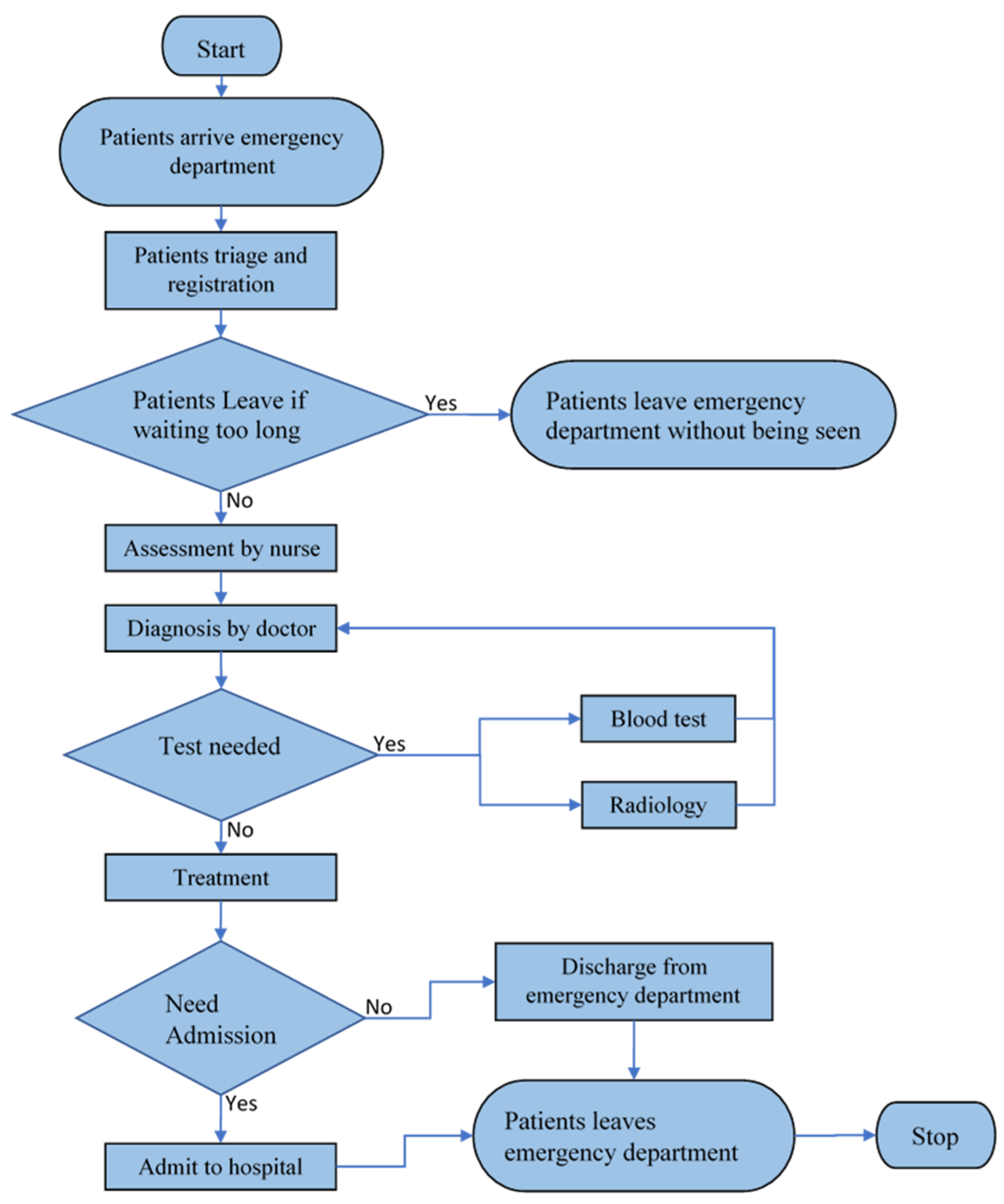
The Arena simulation software is employed to build the desired model. The patient flow in the KKUH’s emergency department as seen in Figure 1 is studied by this simulation model. Furthermore, the input analyzer in Arena is used to create distributions by fitting probability distribution functions to the data. The developed simulation model and the optimization OptQuest model are available at the online repository Zenodo at https://doi.org/10.5281/zenodo.8209820 (accessed on 10 August 2023). The details of resources, process flow, data related to arrival and service rates, model initialization, performance measures adopted are discussed here, below.

3.1. Process Flow

The model operation starts with the arrival of the patient at the triage and registration desk. The triage nurse assesses the severity of the case, assigns the triage level to the patient, and performs registration. The process of sorting patients at a medical facility to receive medical care based on severity of injury or illness after their arrival and assigning priorities is called the triage process. The triage system at KKUH has five levels, as described below.

• Level 1—Resuscitation: life-threatening.
• Level 2—Emergent: could become life-threatening.
• Level 3—Urgent: not life-threatening.
• Level 4—Less urgent: not life-threatening.
• Level 5—Non-urgent: needs treatment when time permits.

The patient has to wait for the availability of bed and nurse. Once they are assigned, each patient is called for a primary checkup. After that, the patient as an entity moves to the doctor for discussion and consultation. Based on the triage level and discussion, the patient is assigned a treatment strategy and laboratory tests if desired. Following the doctor’s diagnosis, the patient has two options: either they undergo the test or receive immediate treatment. If the patient receives the test recommendation, there are, again, two possibilities: either they have a single test or multiple tests. If the patient has to take the tests, the treatment begins only after the results are known. The patient is either admitted to the inpatient department or discharged from the emergency department following their treatment. For further treatment, the patients which need to be admitted are required to wait till the availability of bed in an inpatient department. The bed remains occupied in the emergency department till the patient is moved upwards. The process flow established in the Arena for KKUH’s emergency department is presented in Figure 2.

In Figure 2, patients quit the system after waiting for a certain period of time. With an increase in waiting times, the number of patients leaving the system keeps rising. Therefore, it is crucial to reduce waiting times through efficient scheduling and resource allocation in order to reduce the number of patients leaving the system and serve the greatest possible number of patients.

3.2. Resources

Considering the various phases that the patients have to undergo in the emergency department, doctors and nurses are regarded as resources. The distinct entities are defined for the doctor and nurse to perform interactions within the model. Each entity takes a set of resource states as it flows in the model; these states are waiting, assessment, evaluation, and treatment. After the nurse evaluates the patient, the doctor must be consulted to discuss the treatment strategy. In the developed model, each shift has consulting doctors. The doctor’s job is to either treat patients or issue orders (such as for laboratory or radiology testing). This, in turn, determines the patient’s course of action, including the decision of whether to pursue direct medical treatment, laboratory testing, radiography, or a combination of both tests before treatment. The doctor attends to patients who have the highest triage score on a high-priority basis and vice versa. Similarly, the model has two types of nurses, including triage and bedside nurses. Triage nurses perform initial assessment to determine a patient’s urgency and establish a priority ranking based on that urgency or criticality. On the contrary, prior to the patient being seen by a doctor, bedside nurses perform a secondary evaluation of the patient. Additionally, bedside nurses participate in radiology tests and laboratory blood testing for high-priority patients. Also, they collaborate with doctors to determine the future course of action of a treatment plan. The emergency department is set to operate in three shifts. The following

Table 1. Current resource allocation in emergency departments.

	First Shift	Second Shift	Third Shift	Total
Doctors	1	4	1	6
Triage nurses	1	3	1	5
Bedside nurses	2	8	2	12
Radiologists	1	1	1	3
Beds	16

lists the various resources that are currently allocated during each shift.

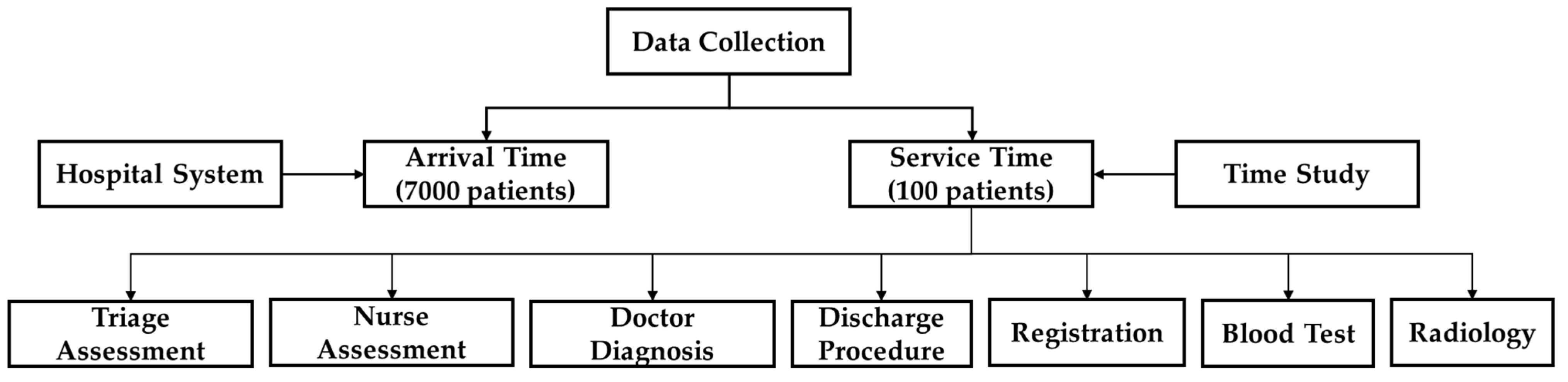
3.3. Data Collection

The first step is the collection of data that is used as input to the model. The data described in Figure 3 are collected from hospital administration as well as through time study. The data are collected between 1 June 2022 to 29 July 2022. The arrival time of about 7000 patients is gathered from hospital administration. Similarly, a member of the research team conducted a time study in the emergency department to determine the service time of about 100 patients. Time spent on triage and nurse assessments, doctor diagnoses, discharge procedures, registration, blood tests, radiology, etc., are all estimated using the time study.

3.4. Arrival Data

The hospital administrative database containing details related to visiting patients is utilized to generate the patients’ arrival times and probabilities employed in the emergency department simulation model. The arrival of patients is based on a schedule, is updated hourly and daily considering peak and off-peak hours. Data are used from approximately 7000 patients, collected over a period of two months. The arrivals are spread out over each hour using a variety of distributions, as illustrated in

Table 2. Hourly distribution of patient arrival.

Period	Distribution	Patient Arrival Expression	Squared Error
00:00–1:00	Exponential	EXPO (0.952)	0.015192
1:00–2:00	Exponential	EXPO (1.05)	0.003993
2:00–3:00	Exponential	EXPO (0.976)	0.001173
3:00–4:00	Exponential	EXPO (0.952)	0.000472
4:00–5:00	Lognormal	LOGN (0.66, 0.313)	0.000874
5:00–6:00	Exponential	EXPO (0.833)	0.009568
6:00–7:00	Lognormal	LOGN (0.742, 0.467)	0.025989
7:00–8:00	Lognormal	LOGN (0.557, 0.167)	0.001615
8:00–9:00	Exponential	EXPO (1.26)	0.006111
9:00–10:00	Normal	NORM (11.3, 5.77)	0.016496
10:00–11:00	Normal	NORM (20.6, 5.81)	0.023891
11:00–12:00	Normal	NORM (21.2, 5.89)	0.014977
12:00–13:00	Normal	NORM (22.6, 7.11)	0.020261
13:00–14:00	Normal	NORM (18.1, 5.74)	0.026783
14:00–15:00	Normal	NORM (14.8, 4.87)	0.008851
15:00–16:00	Normal	NORM (18.8, 5.74)	0.018294
16:00–17:00	Uniform	UNIF (3.5, 26.5)	0.017746
17:00–18:00	Normal	NORM (6.57, 4.8)	0.023369
18:00–19:00	Exponential	EXPO (1.62)	0.003426
19:00–20:00	Exponential	EXPO (1.26)	0.01278
20:00–21:00	Exponential	EXPO (1.02)	0.001825
21:00–22:00	Exponential	EXPO (1.26)	0.013155
22:00–23:00	Exponential	EXPO (1.1)	0.002558
23:00–24:00	Exponential	EXPO (1.33)	0.006698

.

3.5. Triage Level and Percent Distribution

The nurse triages the patients as they enter the model. Patients are assigned a triaged score based on the nurse’s initial evaluation. On a scale from 1 to 5, where 1 denotes the highest priority or most urgency and 5 denotes the lowest priority or least importance, the triaged score is established.

Table 3. Number of patients for each triage level.

Triage Level	Number of Patients (%)	Cumulative (%)
1	1	1
2	15	16
3	56	72
4	25	97
5	3	100

Triage time distribution follows Weibull Expression as 1.5 + WEIB (4, 1.63), where error is 0.0024.

summarizes the percentage of arriving patients in each triage level and the Weibull expression for the triage time. This percentage is calculated using real data from the hospital.

The same nurse performs patient registration once the patients are divided into categories according to their triage level. The triage and registration times are collected from a time and motion study (n = 100) undertaken in the emergency department for 24 h. The triage time and patient registration time, which are calculated for 100 patients, are distributed using the Weibull distribution. The distribution is satisfactory with a fitting error of 0.0024. This distribution os used as input data to the model in order to simulate the operation of the emergency department.

3.6. Probability of Patients Leaving Systems

The patient either waits in the queue or is examined by the nurse depending on the triage level. Patients with less urgent needs enter the queue. However, the number of patients leaving the system rises as waiting times increase.

Table 4. Probability data of patients leaving the system.

Time (h)	Number of Patients Leaving per Hour	Percentage	Cumulative Percentage
0.5	Based on queue length
1	2	2%	2%
2	2	2%	4%
3	4	4%	8%
4	2	3%	11%
5	6	6%	17%
6	9	9%	26%
7	7	7%	33%
8	33% onwards
9
10

summarizes the information about the number of patients leaving the system based on data gathered from the hospital. It is observed that during the first half hour, some patients are seen leaving the system after observing lengthy queues. Moreover, it is noticed that after 7 h, the number of patients leaving the system reaches saturation, with the cumulative percentage remaining at 33% through hours 8, 9, 10, and so on (refer to the following Table 4).

3.7. Probability of Laboratory Test Depend on the Triage Level

Following the doctor’s diagnosis, the patient either undergoes the test or receives immediate treatment. If the patient has to take the test, the treatment begins only after the results are known. It is also observed that the number of patients undergoing tests or direct treatment depends on the triage level (refer to

Table 5. The probabilities of the test and admission.

Triage Level	Probabilities
	Blood Test	Radiology	Admission
1	0.85	0.80	1
2	0.75	0.10	0.54
3	0.50	0.50	0.20
4	0.20	0.30	0.15
5	0.01	0.20	0

). In addition to the doctors, nurses, and test times, the model also incorporates the discharge procedure time as well as the admission time for in-patient treatment (in case the patient is asked to be admitted). The triage level has an impact on admission probability as well. For example, Triage level 1 patient would have an admission probability of 1, while the Triage level 5 would have an admission probability of 0 (refer to Table 5).

3.8. Service Time Data

The patient is either admitted to or discharged from the hospital following their treatment. The patient’s probability of being admitted to the hospital as estimated from administrative data is 0.27. The following

Table 6. Characteristics of Inputs used in the model.

Input (Time in Minutes)		Distribution	Expression	Error
Assessment by the nurse		Triangular	TRIA (7.5, 9.73, 15.5)	0.001621
Diagnosis by the doctor		Normal	NORM (6.28, 0.873)	0.001433
Treatment	Triage levels 1 and 2	Triangular	TRIA (6.5, 8, 11.5)	0.006077
	Triage levels 3, 4, and 5	Normal	NORM (4.18, 1.13)	0.004335
Blood test		Normal	NORM (3.58, 0.681)	0.001122
Radiology		Triangular	TRIA (4.5, 9, 10.5)	0.013475
Discharge procedure		Normal	NORM (9.56, 1.26)	0.007743
Admission time to Inpatient		Exponential	5 + EXPO (102)	0.003841

presents the distributions of various service time data used in the model.

3.9. Performance Measures

The model is established in order to reduce the waiting time, service time, and number of patients leaving the system. It also aims to optimize the number of doctors and nurses in the system with their maximum limit defined. The simulation run is conducted for a week in order to attain the desired results. Moreover, several scenarios are explored using the developed model, for example, a case of resource allocation being raised or optimized.

3.10. Model Initialization

A warm-up period of 24 h is used in the model to eliminate initialization bias. The warm-up period is acquired using Welch’s approach [44] in this research. The number of runs is determined using the statistical method developed by Kelton [45]. After the model is run a predetermined number of times, the output data such as average, half width and standard deviation for all performance measures are collected in this step. Finally, the estimation of the number of simulation runs needed to achieve the 95% confidence level of accuracy is calculated using the statistical t-distribution approach. The estimated number of simulation runs for various performance measures are presented in the following

Table 7. Estimation for the number of runs in the model.

Item	Average	Half Width	STD	Required Half Width (Relative Error = 0.15)	No. of Runs Required
					First Approximation (t)	Second Approximation (z) 95% Confidence Level
Patient triage 1 (wait time, h)	0.23	0.03	0.09	0.03	8.76	28.85
Patient triage 2 (wait time, h)	0.21	0.01	0.03	0.03	1.07	3.52
Patient triage 3 (wait time, h)	0.76	0.04	0.13	0.11	1.52	5.00
Patient triage 4 (wait time, h)	2.83	0.19	0.56	0.42	2.00	6.60
Patient triage 5 (wait time, h)	3.47	0.60	1.76	0.52	13.42	44.18
Patients leave without service	425.89	43.09	126.13	63.88	4.55	14.98

. The results of statistical analysis indicate that a minimum number of 45 simulation runs for this model is required for meaningful results.

3.11. Model Validation and Verification

To validate and verify the number of hospital visits per week produced from the simulation model with those estimated using hospital data, the results were compared to ensure that the simulation model is accurate and validated. The outcome of the simulation model indicated that there are 1001.4 patients on average every week, with a half width of 34.52 and an SD of 114.93. Simulation results showed a 95% confidence interval that covers the calculated database average of 1016.2 patients each week. The overall flow, the analytical characterization of the arrival pattern, and the other processes in the model were all therefore confirmed by this experiment. Due to a lack of information in the hospital database, the simulation model’s results for various performance measures were presented to professionals on the medical staff. Documentation of the model’s structure, assumptions, and limitations were clearly explained to management and staff. The hospital management deemed all of the results to be reliable.

4. Goal Programming (GP) Model

The quality of care provided to patients can be ensured by having enough resources available in the department and ensuring that they are efficiently utilized. Goal programming is a linear programming technique that can be utilized to resolve multiple objectives by treating them as goals with target values and weight. It has, in fact, been widely utilized to simulate and solve scheduling-related issues in the healthcare system. For instance, Mohammadian et al. [46] used goal programming to address the issue of nurse scheduling in a large medical facility in Tehran. Similarly, Anna et al. [47] used the goal programming technique to establish the monthly work shift schedules of nurses, leading to more evenly distributed workloads. Additionally, Jerbi and Kamoun [48] implemented simulation and goal programming to reschedule the shifts of emergency department doctors in a Tunisian hospital. The goal programming model was designed to optimize and choose the most appropriate measures.

In this study, the objectives are to optimize the department resources levels in order to improve the overall efficiency and effectiveness. Therefore, goal programming is used to minimize the number of patients leaving the system without service, patient waiting time, as well as positive deviations from the number of doctors, number of nurses, and number of beds. This, in turn, minimizes the cost of operations in the emergency department of the hospital under consideration. Accordingly, an objective function is set (refer to Equation (1)), and corresponding constraints are defined (refer to Equations (2)–(7)). Weights w₁, w₂, w₃, w₄, w₅, and w₆ are varied to analyze their impact on the objective function. Percentage normalization of the weights is applied to normalize the OptQuest model.

$$\mathrm{Minimize} \mathrm{Z} ={\mathrm{w}}_1\frac{\mathrm{TL}}{\mathrm{TTL}}+{\mathrm{w}}_2\frac{{{\displaystyle \sum }}_{\mathrm{j}=1}^5\frac{{\mathrm{TW}}_{\mathrm{j}}}{{\mathrm{TTW}}_{\mathrm{j}}}}{5}+{ \mathrm{w}}_3\frac{{\mathrm{d}}_3^{+}}{{\mathrm{b}}_3}+{\mathrm{w}}_4\frac{{\mathrm{d}}_4^{+}}{{\mathrm{b}}_4}+{\mathrm{w}}_5\frac{{\mathrm{d}}_5^{+}}{{\mathrm{b}}_5}+{\mathrm{w}}_6\frac{{\mathrm{d}}_6^{+}}{{\mathrm{b}}_6} ,$$

(1)

subject to

$${\displaystyle \sum }_{\mathrm{k}=1}^3{\mathrm{D}}_{\mathrm{k}}-{\mathrm{d}}_3^{+}+{\mathrm{d}}_3^{-}={\mathrm{b}}_3,$$

(2)

$${\displaystyle \sum }_{\mathrm{k}=1}^3{\mathrm{N}}_{\mathrm{k}}-{\mathrm{d}}_4^{+}+{\mathrm{d}}_4^{-}={\mathrm{b}}_4,$$

(3)

$${\displaystyle \sum }_{\mathrm{k}=1}^3{\mathrm{TN}}_{\mathrm{k}}-{\mathrm{d}}_5^{+}+{\mathrm{d}}_5^{-}={\mathrm{b}}_5,$$

(4)

$$\mathrm{B}-{\mathrm{d}}_6^{+}+{\mathrm{d}}_6^{-}={\mathrm{b}}_6,$$

(5)

$${\mathrm{D}}_{\mathrm{k}},{ \mathrm{N}}_{\mathrm{k}},{ \mathrm{TN}}_{\mathrm{k}}, \mathrm{B}\ge 1,$$

(6)

$${\mathrm{d}}_3^{+},{ \mathrm{d}}_3^{-},{ \mathrm{d}}_4^{+},{ \mathrm{d}}_4^{-},{ \mathrm{d}}_5^{+},{ \mathrm{d}}_6^{+},{ \mathrm{d}}_6^{-} \ge 0.$$

(7)

In the above Equations (1)–(7),

• ${\mathrm{w}}_{\mathrm{i}}=\mathrm{weight} \mathrm{or} \mathrm{importance} \mathrm{of} \mathrm{goal} \mathrm{i} \left(\mathrm{i} є 1, 2\dots 6\right);$
• $\mathrm{TL}=\mathrm{total} \mathrm{number} \mathrm{of} \mathrm{patients} \mathrm{that} \mathrm{leave} \mathrm{the} \mathrm{hospital} \mathrm{without} \mathrm{service};$
• $\mathrm{TTL}=\mathrm{target} \mathrm{total} \mathrm{number} \mathrm{of} \mathrm{patients} \mathrm{that} \mathrm{leave} \mathrm{the} \mathrm{hospital} \mathrm{without} \mathrm{service};$
• ${\mathrm{TW}}_{\mathrm{j}}=\mathrm{total} \mathrm{waiting} \mathrm{time} \mathrm{in} \mathrm{queue} \mathrm{for} \mathrm{Triage} \mathrm{level} \mathrm{j} \mathrm{patients} \left(\mathrm{j} є 1, 2\dots 5\right);$
• ${\mathrm{TTW}}_{\mathrm{j}}=\mathrm{target} \mathrm{total} \mathrm{waiting} \mathrm{time} \mathrm{in} \mathrm{queue} \mathrm{for} \mathrm{Triage} \mathrm{level} \mathrm{j} \mathrm{patients} \left(\mathrm{j} є 1, 2\dots 5\right);$
• ${\mathrm{b}}_{\mathrm{i}}=\mathrm{target} \mathrm{values} \mathrm{for} \mathrm{goal} \mathrm{i} \left(\mathrm{i} є 3,4, \dots 6\right);$
• ${\mathrm{d}}_{\mathrm{i}}^{+}=\mathrm{positive} \mathrm{deviation} \mathrm{of} \mathrm{goal} \mathrm{i} \left(\mathrm{i} є 3,4, \dots 6\right);$
• ${\mathrm{d}}_{\mathrm{i}}^{-}=\mathrm{negative} \mathrm{deviation} \mathrm{of} \mathrm{goal} \mathrm{i} \left(\mathrm{i} є 3,4, \dots 6\right);$
• $\mathrm{k}=\mathrm{number} \mathrm{of} \mathrm{shifts} \mathrm{in} \mathrm{the} \mathrm{hospital} \mathrm{emergency} \mathrm{department} \left(\mathrm{k} є 1, 2, 3\right);$
• ${\mathrm{D}}_{\mathrm{k}}=\mathrm{number} \mathrm{of} \mathrm{doctors} \mathrm{assigned} \mathrm{in} \mathrm{shift} \mathrm{k} \left(\mathrm{k} є 1, 2, 3\right);$
• ${\mathrm{N}}_{\mathrm{k}}=\mathrm{number} \mathrm{of} \mathrm{bedside} \mathrm{nurses} \mathrm{assigned} \mathrm{in} \mathrm{shift} \mathrm{k} \left(\mathrm{k} є 1, 2, 3\right);$
• ${\mathrm{TN}}_{\mathrm{k}}=\mathrm{number} \mathrm{of} \mathrm{triage} \mathrm{assesment} \mathrm{nurses} \mathrm{assigned} \mathrm{in} \mathrm{shift} \mathrm{k} \left(\mathrm{k} є 1, 2, 3\right);$
• $\mathrm{B}=\mathrm{number} \mathrm{of} \mathrm{beds} \mathrm{in} \mathrm{hospital} \mathrm{emergency} \mathrm{department}.$

5. Results and Discussion

The simulation runs are performed for seven days and each run is replicated 45 times to eliminate any biases. The existing setting is treated as a base scenario (S0) to depict the current situation in the emergency department of KKUH. Subsequently, the base scenario simulation outcomes are assessed and reported to the hospital’s emergency management. After a discussion with the management, as is customary, the hospital stuff suggested only increasing the amount of human resources, i.e., doctors and nurses to improve the set objectives. This option is treated as Scenario 1 (S1). It is evident that simply increasing the selective resources does not accomplish the set objectives. Thus, the only option ahead is to find the optimum level of all resources. The above-stated goal programming model is developed, and the OptQuest tool is used in combination with the simulation model. In Scenario 2 (S2), experiments utilizing OptQuest are conducted by assigning equal weights to all the set goals. Scenario 2 is implemented to ascertain how well the available resources or workforce level are being utilized. Scenario 2 also explores the trade-offs occurring between available resources, queues, waiting times, and the number of beds based on preferences. The most important management goals in the emergency department are reductions in waiting time and the number of patients leaving service. These goals are not completely met due to an equal weight strategy for all goals. Hence, after analyzing the outcome of Scenario 2 OptQuest simulation results, higher weights are applied to the most important objectives. This option of applying variable weights to a set of goals is treated as Scenario 3 (S3).

The simulation model is utilized to understand both the current scenario (or base scenario) and a number of potential improvements or scenarios. For the current scenario, as shown in Table 1, resources are assigned as follows. One doctor is allocated to the first shift, two doctors are assigned to the second shift, and three doctors are dedicated to the third shift. Similarly, there are two bedside nurses on duty on the first shift, eight on the second shift, and one on the third shift. Additionally, there is one triage nurse on the first shift, three on the second shift, and one on the third shift. The emergency department has a total of 16 beds. For the current scenario, an average performance evaluation of various measures across all replications is presented in the following

Table 8. Performance evaluation of the current situation using the simulation model.

Performance Measure	Average Value	Half Width	Overall SD Across Replications
Patient waiting time to receive a bed	1.28 h	0.06 h	0.20 h
Total time spent in ED (in case patient is admitted)	4.07 h	0.07 h	0.22 h
Total time spent in ED (in case patient is discharged)	2.51 h	0.05 h	0.15 h
Patient waiting in queue: Total waiting time in queue based on triage level
Triage level 1	0.23 h	0.03 h	0.10 h
Triage level 2	0.21 h	0.01 h	0.03 h
Triage level 3	0.75 h	0.04 h	0.12 h
Triage level 4	2.82 h	0.16 h	0.53 h
Triage level 5	3.36 h	0.53 h	1.76 h
Patient leaving queue:
Total time spent in system before leave	2.02 h	0.08 h	0.28 h
Number of patients leaving	423	35	118

.

It is evident that for the base scenario, S0 (refer to Table 7), there is a significant scope for improvement if the resources can be allocated appropriately in different shifts. It can be seen that every performance metric exceeds the targets established in collaboration with hospital management. For example, the target number of patients leaving the system should be 200, but in the current situation, as indicated in the above Table 7, there are currently 423 patients departing the system without treatment. In a similar fashion, the target waiting time for all triage types of patients is set to less than 2 h, but in the current scenario, it is not satisfactory. Thus, improvements are recommended to address the current problem and each improvement is treated as a new scenario one by one. The outcomes of simulated scenarios are presented here, below.

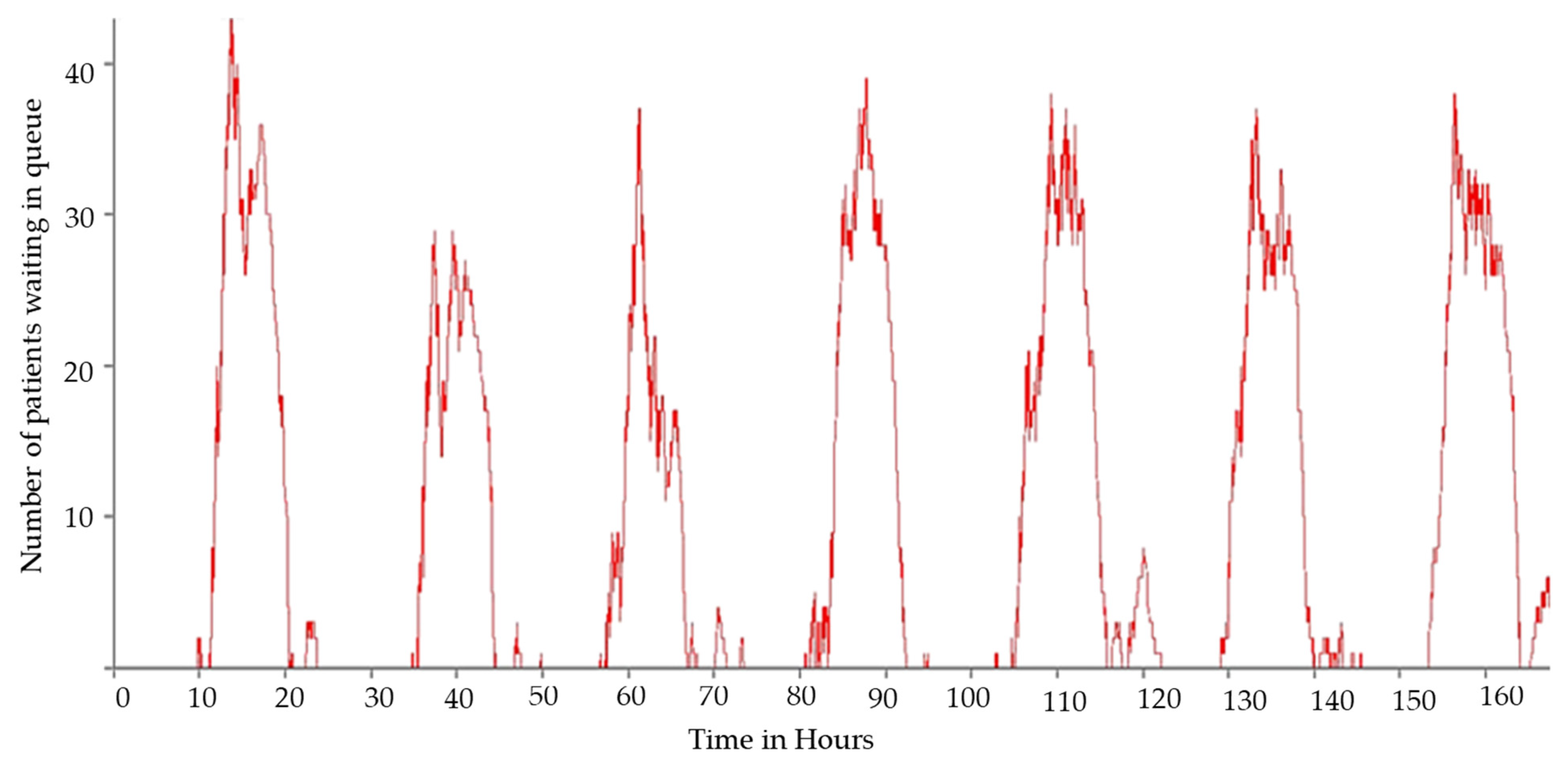
The first improvement, as in Scenario 1, is the employment of additional doctors and nurses to the second shift when a greater number of patients are observed to be waiting in queue. In Figure 4, the number of patients waiting in queue at any given time can be observed. This is the recommendation given by the hospital administration, who believe that resolving the existing situation would require more resources, particularly more doctors and bedside nurses, during the second shift. Hospital management consistently believes that doctors and nurses are the most important people and focuses solely on the increase in the number of doctors and nurses, without considering all options and thoroughly assessing the system, which is never the right approach.

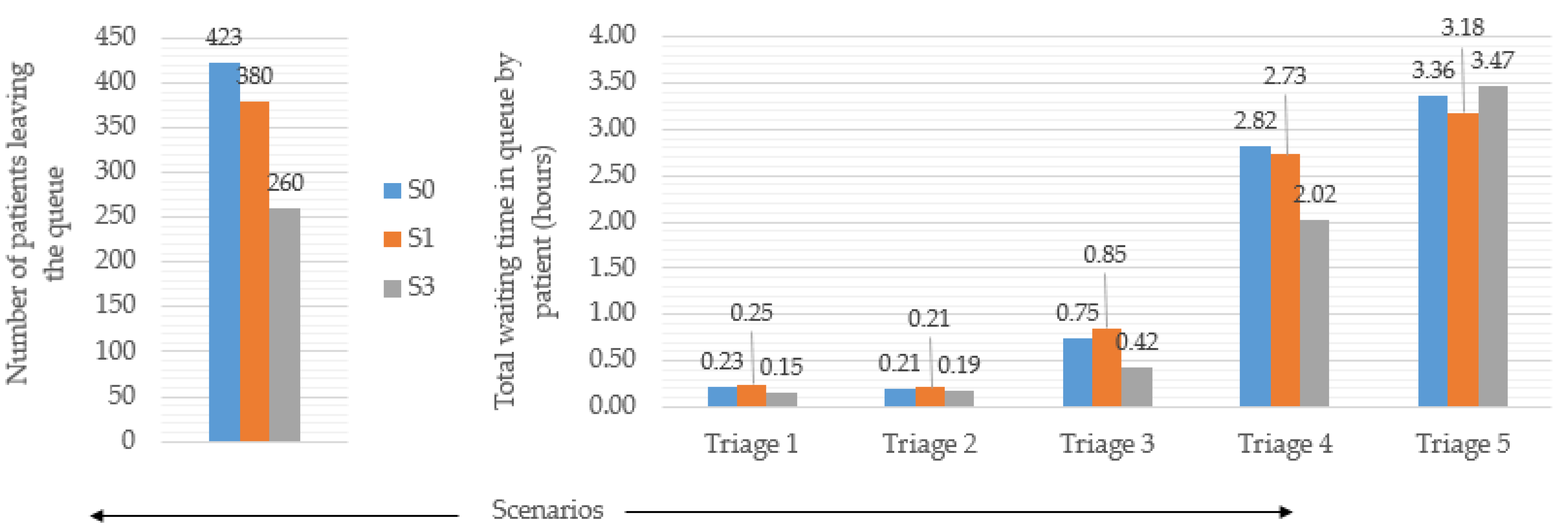
The hospital management recommends increasing the number of doctors and nurses working in the second shift by two and four, respectively. As indicated in the following Figure 5, the results are attained after the simulation model is run using the resource allocation plan suggested by hospital management. Figure 5 compares the base scenario, Scenario 0 and Scenario 1 for the two most important performance measures, i.e., the number of patients leaving the system and the total waiting time of the patients in the triages. Despite the fact that the number of patients leaving the queue drops from 423 to 380, it is still much more than the target value of 200. Similarly, no improvement is observed in patient waiting time in all triages. This shows that the amount of resources is increased, and, as a result, healthcare costs are also increased, yet no improvement is observed. This necessitates the deployment of an appropriate approach that can objectively produce the best results at a minimum cost. Thus, the only option ahead is to find the optimum level of all resources. As in Scenario 2, experiments utilizing OptQuest are conducted by assigning equal weights to all sets of goals.

In Scenario 2, OptQuest finds the best solution after nearly 700 different runs with various combinations of resource assignment, using equal weights for each goal.

Table 9. Number of resources assigned for various scenarios.

Type of Resource	Shift Number	Assigned Number of Resources
		Base Scenario, S0	Scenario 1	Scenario 2	Scenario 3
Doctors	1	1	1	1	1
	2	4	6	3	5
	3	1	1	2	4
Bedside nurses	1	2	2	1	1
	2	8	12	8	9
	3	2	2	5	4
Triage nurses	1	1	1	1	2
	2	3	3	3	3
	3	1	1	2	2
Beds		16	16	16	19

below presents the OptQuest resource assignment for Scenario 2. It is observed that it recommends removing a doctor from the second shift and adding them to the third shift. It also suggests removing a bedside nurse from the first shift while proposing to add three bedside nurses and a triage nurse for total of four nurses to the third shift. It is evident from Figure 4 that a greater number of waiting patients becomes carried over to the third shift from the second shift, even though the arrival rate of patients in the third shift is very low compared to that of the patients in the second shift. Subsequently, comparative assessment of the base scenario and Scenario 2 is performed, and the obtained results are presented in Figure 5.

In Figure 5, it can also be noticed that the emergency department’s performance in Scenario 2 is much better than it is in the base scenario. It is observed that both the number of patients leaving the queue and the average waiting time in triages for the patients are lowered by approximately 38% and 15%, respectively. In spite of this, Figure 5 also shows that the target for the number of patients leaving the system, which is set at 200, is not met. However, the target for waiting times in triages is met successfully in Scenario 2.

As these goals are not completely met due to an equal weight strategy for all goals, Scenario 3 is established in order to further enhance the emergency department’s performance in order to meet the target for the number of patients leaving the queue. In Scenario 3, the total number of patients leaving the queue and the waiting times of the patients are given greater weight than other objectives. Table 9 displays the results and recommendations from Scenario 3. For instance, it is established that the emergency department needs to add three doctors for the third shift and one doctor for the second shift. Similarly, modifications in other resources from Scenario 2 to Scenario 3 can also be observed; refer to Table 9. It must be realized that Scenario 3 changes most of the resources instead of focusing on one or two resources, thereby allowing for effective and efficient resource allocation. The results shown in

Table 10. Scenario 3 simulation outcome with unequal weights.

Performance Measure	Average Value
Patient waiting time to receive a bed	0.48 h
Total time spent in ED (in case patient is admitted)	3.32 h
Total time spent in ED (in case patient is discharged)	1.83 h
Patient waiting in queue: Total waiting time in queue based on triage level:
Triage level 1	0.03 h
Triage level 2	0.11 h
Triage level 3	0.28 h
Triage level 4	1.19 h
Triage level 5	2.12 h
Patient leaving queue
Total time spent in system before leave	0.85 h
Number of patients leaving	162

re related to Scenario 3. It can be recognized that all of the performance indicators reduce noticeably. For instance, in comparison to the base scenario (refer to Table 8), the number of patients leaving the system falls by 61.70%, and the patient waiting time in the case of Triage 1 decreases significantly, by 86.95%. In addition, the desired targets of 200 patients leaving the queue and the patient waiting times in different triages are met. As a result, the need to consider all possible aspects is highlighted rather than presuming that a small number of them are accountable for inefficient operations.

Assessment of All Scenarios Using Process Analyzer

The objective is to perform comparative assessment of all of the four scenarios above. This process is conducted using the Arena process analyzer tool. For this, initially, the created model must be uploaded, inputs and outputs need to be added for examination, and the model needs to be rub in the process analyzer. In parallel, the experiment needs to be configured by defining the input parameter ranges, the number of simulation iterations, and other parameters. Thus, the process analyzer automatically runs numerous distinct scenarios and graphically compares the outcomes of various scenarios. It also helps to perform the assessment of the model modifications and their effects on system goals. The graph displayed in Figure 6 represents the outcome of the process analyzer in the form of box and whisker plots for each scenario, along with the minimum, maximum and median values.

From Figure 6, it is evident that for the performance measure of the ‘number of patients leaving the emergency department without having service’ reaches an average minimum level for Scenario 3 from that of the current scenario (or base scenario, S0). Similarly, the waiting time in hours for patients of all triage levels is gradually minimized from the current or base scenario to Scenario 3. Thus, it is proposed that there is a need to improve the current scenario to Scenario 3.

6. Conclusions

The emergency department in any hospital has a vital role since it interacts with a number of patients every day. It performs numerous interactions between patients, employees, and other resources. Greater patient contentment and favorable hospital credibility depend on the emergency department operating responsibly and efficiently. Furthermore, its operational efficiency and performance depend on the number and allocation of the hospital’s doctors, nurses, beds, and other resources. For example, any change in personnel (e.g., number of nurses or doctors, specific shift assignments) should be carefully considered based on system performance. As a result, it is crucial to provide or assign the proper number of resources to every shift. Prolonged waiting times driven by improper resource allocation have a significant negative impact on patient experience. Therefore, in this study, we explored the emergency department of a hospital in Saudi Arabia and offered recommendations in order to reduce patient wait times and the number of patients that leave the queue untreated. We built a detailed model in Arena and carried out goal programming. For this case, we observed that, if three additional doctors are assigned to the third shift and one to the second shift, the number of patients leaving the system without service decreases from 423 to 162. In a similar manner, for the current scenario, if two additional bedside nurses are added to the third shift and one additional bedside nurse is assigned to the second shift, as well as when an extra triage nurse is added to the first and third shifts each and the number of beds is increased from the 16 beds employed currently to 19 beds, a 61.7% drop in the number of patients leaving without service and a substantial drop in the waiting time for patients with all types of triage are observed. This highlights the fact that hospital management should focus on all available resources instead of emphasizing just one or two of them, because the developed model successfully portrayed the appropriate resource allocation required to improve customer/patient satisfaction levels.

Finally, it can be concluded that simulation and optimization could benefit the hospital by performing reallocation of the existing resources. The proposed model uses the simulation outcome as input to OptQuest and the goal programming model. The few research directions that the researchers can take into consideration for further advancement are as follows: incorporation of resource scheduling using genetic algorithms and/or simulated annealing and development of an artificial intelligence machine learning model to evaluate the performance of emergency departments at different dynamic staffing levels using the multiple simulation output from OptQuest. The authors aim to propose a more generalized model for emergency departments in future publications by incorporating more possibilities and specifics in the current model.