1. Introduction
Energy forecasting is of great significance for understanding and anticipating the future dynamics of the global energy landscape. As a versatile and abundant primary energy, natural gas plays a vital role in meeting the energy demands of various sectors, including power generation, heating, industrial processes, and transportation. Accurate forecasting of natural gas is crucial for policymakers to develop effective energy strategies and make informed decisions about energy infrastructure, environmental regulations, and energy security. However, as countries strive to reduce their reliance on fossil fuels and transition towards cleaner energy alternatives, the demand for natural gas may undergo fluctuations. Additionally, geopolitical factors, such as regional conflicts or trade agreements, can influence natural gas consumption patterns by affecting supply routes and prices. In a word, the time series of natural gas is influenced by multiple factors and exhibits typical complex and irregular characteristics. Traditional forecasting models face challenges in accurately forecasting such patterns. The popular energy forecasting methods include statistical (or empirical) models, machine learning models, and grey system models at present.
The time series models are one of the most used statistical models, which consist of the autoregressive integrated moving average (ARIMA) model, the autoregressive moving average (ARMA) model, and the seasonal autoregressive integrated moving average model [
1]. However, the linear structure of time series models often makes them fail to forecast the nonlinear time series accurately. Machine learning models have unique advantages in handling nonlinear time series. Machine learning models mainly include neural network models [
2,
3,
4], models based on kernel [
5,
6], and ensemble models [
7]. Although machine learning models excel in handling nonlinear system problems, they require a significant amount of training data and impose certain hardware requirements. Furthermore, machine learning models possess intricate nonlinear parameters, which may lead to overfitting. Given the limitations of the aforementioned approaches, grey system models have gained wide applicability due to their ability to model with limited data and accommodate both linear and nonlinear problems.
Since Professor Deng [
8] proposed the grey system theory, many researchers have made contributions to the development of the grey system in different fields. Examples include nuclear energy consumption [
9,
10,
11,
12], wind energy [
13,
14], electricity consumption [
15,
16], and oil production [
17,
18]. Currently, mainstream grey models can be broadly categorized into linear models and nonlinear models. The GM(1,1) model is the most classical linear grey model, while it has inherent issues in modeling mechanisms. Therefore, many scholars have proposed other linear grey models based on the GM(1,1) model. For example, Chen et al. [
19] improved the background value of the grey model using Gaussian–Legendre integration. Xie et al. [
20] first proposed the idea of grey discrete modeling and established the discrete grey model. Xu et al. [
21] firstly demonstrated that grey inputs can vary with time and possess dynamic variability. Then, Cui et al. [
22] employed a linear function of time as the grey input instead of the original constant grey input. However, the forecasting of natural gas is a complex nonlinear problem, and linear grey models have significant limitations when facing such a problem.
Nonlinear grey models can better capture the nonlinear relationships in raw data. In recent years, an increasing number of studies have focused on nonlinear grey system models. For instance, Zhou et al. [
23] proposed a novel discrete grey model considering nonlinearity and fluctuations. Chen et al. [
24] proposed the fractional Hausdorff derivative grey model based on fractional order calculation. Qian et al. [
25] proposed a grey model with time power and demonstrated its feasibility. Zeng et al. [
26] presented a grey model that incorporates lagged dependent variables, linear correction terms, and stochastic disturbance terms. Liu et al. [
27] proposed a grey neural network and input–output combined forecasting model for forecasting the primary energy consumption in Spanish economic sectors. Ma et al. [
28] proposed a novel wavelet kernel-based grey system model by combining the grey system modeling and wavelet kernel-based machine learning and applied it to the urban natural gas consumption forecasting in Kunming, China, which takes advantage of the nonlinearity and periodicity ability of the wavelet kernel. However, existing nonlinear grey system models are often constructed using specific functions, resulting in relatively fixed structures of these models, making them less adaptable to handle more general nonlinear characteristics.
The hyperparameters optimization of nonlinear grey models has also emerged as a popular research topic in recent years. Intelligent optimization algorithms are a class of algorithms based on heuristic search strategies, which are capable of finding solutions that are close to the global optimum within a limited number of iterations. This characteristic makes them particularly effective in handling highly nonlinear, multimodal, and complex optimization problems, leading to their widespread application in recent years. At present, the most popular algorithms are Grey Wolf Optimization (GWO) [
29], Particle Swarm Optimization (PSO) [
30], and the Genetic Algorithm (GA) [
31]. For instance, Cai et al. [
32] introduced GWO for tuning the hyperparameters of long short-term memory networks. Heydari et al. [
33] employed GWO to optimize the Generalized Regression Neural Network. Sebayang et al. [
34] used GWO to tune the hyperparameters of an Artificial Neural Network. Barman et al. [
35] compared the performance of GWO, PSO, and GA, showing that GWO outperformed other algorithms.
In summary, nonlinear grey models can better fit complex data patterns, effectively handle outliers and noisy data, and improve the accuracy of predictions. In previous work, researchers employed specific functions as the grey input to construct nonlinear grey models. In order to address the broader spectrum of nonlinear characteristics, the kernel trick based on the support vector regression with wavelet kernel is employed to build a novel Grey Wavelet Support Vector Regressor. The -insensitive loss function is used to build the optimization problem for training the model, which is transformed to a convex quadratic programming and then solved by the sequential minimal optimization algorithm. The GWO is incorporated to optimize the hyperparameters of the suggested model, thereby finalizing the training and forecasting process of the model.
The subsequent sections of this paper are organized as follows:
Section 2 presents the proposed Grey Wavelet Support Vector Regressor, including all the modeling procedures and algorithms;
Section 3 presents the hyperparameter optimization by the grey wolf optimizer;
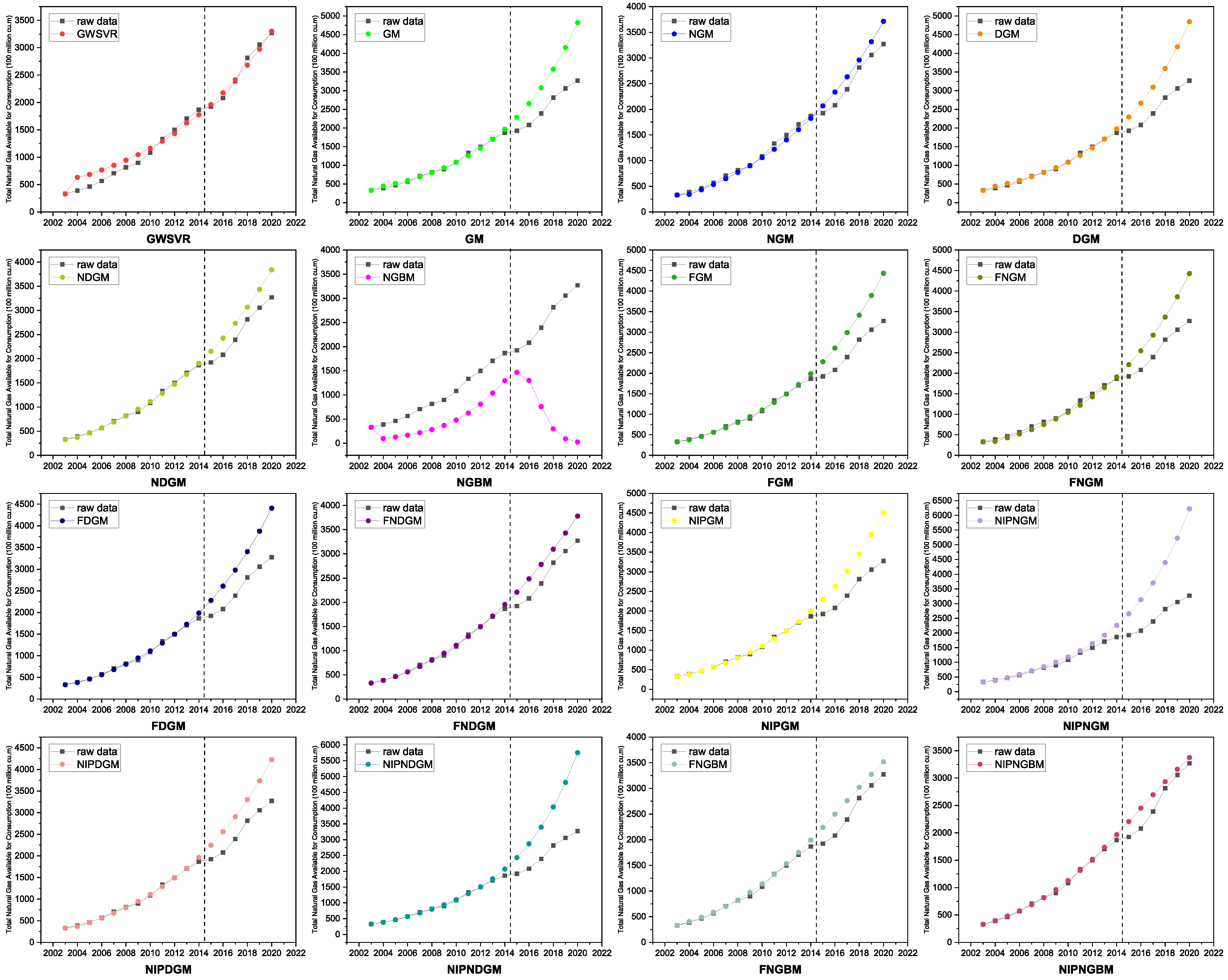
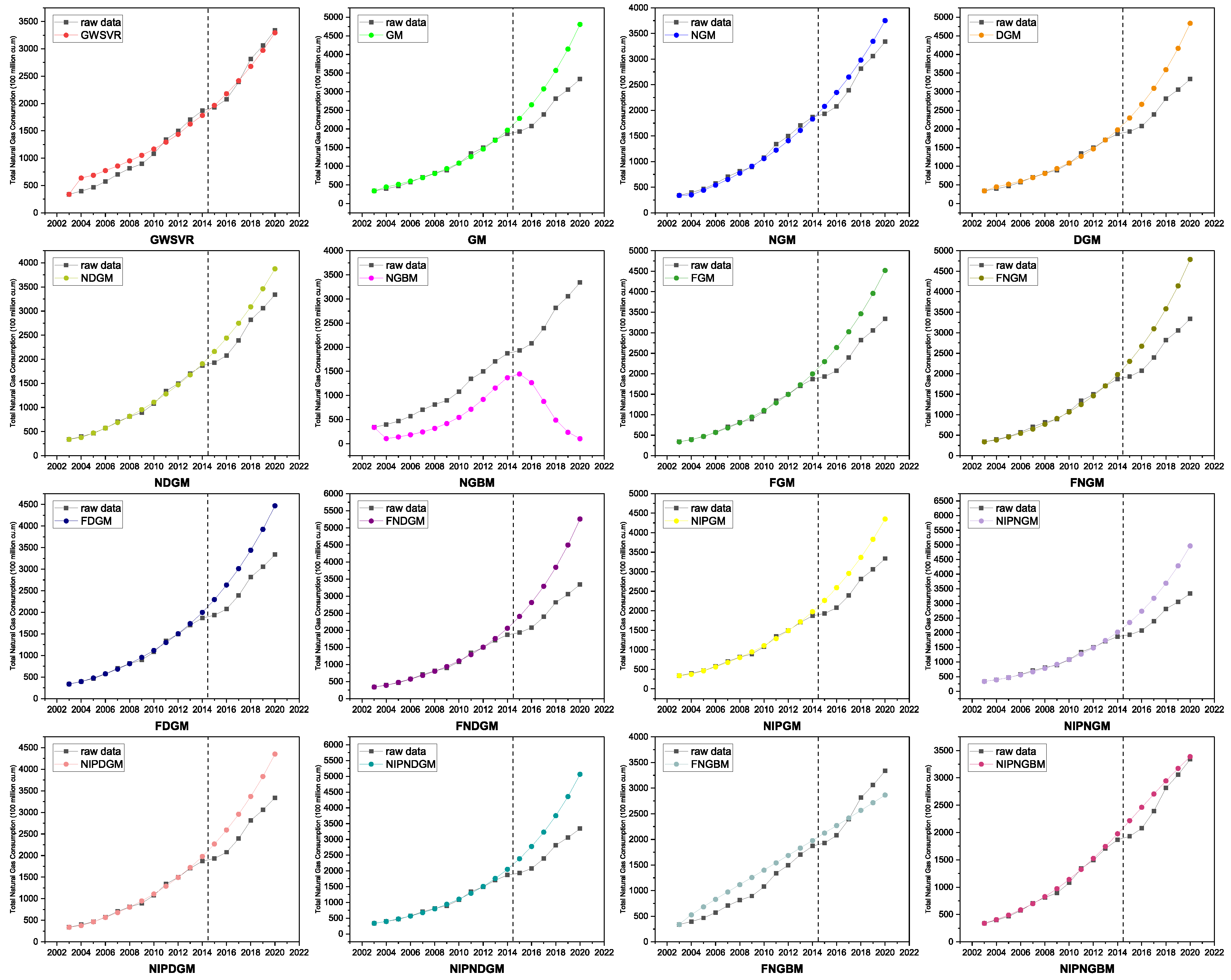
Section 4 demonstrates the case studies conducted to forecast China’s total natural gas supply (available for consumption) and total natural gas consumption using the proposed model. A comparison with other grey system models is provided, and the findings are summarized in
Section 5.
2. The Proposed Grey Wavelet Support Vector Regressor
In this section, the proposed Grey Wavelet Support Vector Regressor (GWSVR) is presented, which uses the main formulation of grey system models and the loss function of the support vector regression.
2.1. Grey System Model with Nonlinear Mapping and Its Solution
A general formulation of the grey system model with nonlinear effect by time can be represented by:
where
is a nonlinear function of time
t, and
is the first order accumulation, which is often abbreviated as 1-AGO. In previous work, researchers used some specific functions such as a linear function and an exponential function to build specific grey system models. In order to deal with more general nonlinear features, a nonlinear mapping is used in this work, which is defined as follows:
where
is the 1-D set of real numbers, and
is the feature space, which is generally high-dimensional linear space. Within this nonlinear mapping, the nonlinear function can be linearly expressed in the feature space as
where the vector
is the weight, and
u is a bias. Then, (
1) of the grey system model can be re-written as
The whitening Equation (
4) is a typical ordinary differential equation, of which the general solution is
2.2. The -Insensitive Loss for the Proposed Model
In order to estimate the parameters and the nonlinear function of the grey system model presented above, we need to first derive its discrete formulation. In previous work, a general way has been to integrate the whitening Equation (
4) in a small interval (e.g.,
). In this work, we make a tiny variation, which averages the time
t of the nonlinear mapping instead of averaging the nonlinear function to make the model simpler without loss of effectiveness. The discrete formulation can be written as
where
are called the background values.
Then, the
-insensitive loss used in this work can be given by
The term C is often called the regularization parameter, which controls the fitting error and scale of the parameters b and . The is a threshold, which limits the fitting errors of the model, and the are the slack variables that make the regularization problem more feasible. This formulation is different to the commonly used least squares method, which not only minimizes the training errors of the model but also reduces the scale of the parameters b and , and this way, the model has higher generality in the real-world cases.
However, the Formulation (
7) is not computable at present, as the nonlinear mapping is still unknown. To make it easier to solve, an extended nonlinear mapping is introduced as
which maps the vector
to
. Let the weighted vector be
, we have
and then we can re-write Equation (
7) as
And now Equation (
10) is essentially equivalent to the primal problem of the support vector regression introduced in [
36]. Within this formulation, the corresponding Lagrangian function can be constructed as
where
are the Lagrangian multipliers, which are nonnegative and satisfy
. By setting the partial derivatives
to be zeros, we can obtain some very important equalities as:
According to Mercer’s condition, a Mercer kernel can be used as the inner product of the feature space, i.e.,
. Within this theorem, we can deduce the following equality
By substituting the equalities in (
12) and (
13) within a Mercer’s kernel, we obtain the dual formulation of the primal (
10) as
It can be seen that the dual formulation is only involved in the computation of the Lagrangian multipliers, and it is now computationally feasible to solve.
2.3. The Kernel Representation and the Wavelet Kernel
Within the above results, the nonlinear function can now be explicitly written as
The wavelet kernel function is used to represent the nonlinear function, which is defined as
where
is the kernel parameter, which governs the degree of nonlinearity and periodicity exhibited by the wavelet kernel. The cosine term of the wavelet kernel function reflects the degree of periodicity of the samples, and the exponential part reflects the nonlinearity of the samples. It is very interesting to see that the exponential part is mathematically equivalent to the Gaussian kernel, which has high performance in dealing with nonlinearities. Considering the structure of the wavelet kernel, it is often more flexible to deal with different spectrums of the datasets, which can be expected to make the forecasting model perform better in nonlinear time series.
2.4. Training Algorithm for the GWSVR
In order to make the model computationally feasible, we should solve the dual problem (
14) to obtain the optimal values of the Lagrangian multipliers
. It can be seen that this formulation is mathematically equivalent to the dual problem of the standard support vector regression model introduced in [
36]; thus, it can also be solved by the sequential minimal optimization (SMO) algorithm, of which the key points are presented in this subsection.
For convenience, the following notation is used
The main idea of the SMO is to minimize the objective function in a “pair-by-pair” way, which minimizes only two variables during each iteration. For the regression problem, two subscripts are selected, and the corresponding variables are optimized at this iteration. Noticing that the multipliers with same subscripts cannot be nonnegative at the same time, only two variables with different subscripts are updated during each iteration.
Let the selected two subscripts be
, and the subproblem of the dual problem (
14) can be written as
where
is the vector of other multipliers, and
is the sum of the rest of the terms, which are independent of the variables
, and it is regarded as constant during each iteration.
Noticing that the multipliers should satisfy the first equation in (
12), the subproblem is essentially a constrained programming. The SMO updates the two variables in the following way
Within this updating rule, the multipliers can always satisfy the constraints during the iterations. By substituting (
19) into the subproblem (
18), the objective function is only with respect to
t, and the subproblem turns to be a univariate optimization problem, which can be solved analytically.
The bias
u can be computed when the optimal multipliers are obtained, which can be approximated by the average value of the partial derivatives of the objective function in (
14) with respect to every multiplier.
By comparing Equations (
13) and (
9), it is easy to obtain the explicit estimation of the parameter
b, which can be written as
Above all, all the parameters can be obtained by using the SMO algorithm and the formulae presented above. The implementation of the SMO is based on the work of Lin et al. [
37], which is one of the most stable versions at present.
2.5. Response Function and the Predicted Values
In order to make predictions, the continuous formulation of the general solution of the whitening Equation (
4) should be discretized. In this work, we average the time point to reach an approximation of the convolutional integral of the solution (
5); then, its discrete formulation can be obtained as
This formulation is different to the previous work but is much easier to implement. Then, the predicted values can be obtained by first order differencing as
and
.
2.6. The Complete Overal Computational Algorithm
For application’s sake, a complete algorithm of the proposed GWSVR (Algorithm 1) is presented in this subsection as a piece of pseudo code.
| Algorithm 1: Overall computation algorithm of GWSVR |
![Systems 11 00428 i001 Systems 11 00428 i001]() |
Within the above computational steps, one can obtain the values predicted by the GWSVR model from the initial point to the point.