Failure Mode and Effect Analysis with a Fuzzy Logic Approach

Abstract

Failure mode and effect analysis (FMEA) is one of the most used techniques in risk management due to its potential to solve multidisciplinary engineering problems. The role of experts is fundamental when developing the FMEA; they identify the failure modes by expressing their opinion based on their experience. A relevant aspect is a way in which the experts evaluate to obtain the indicator of the risk priority number (RPN), which is based on qualitative analysis and a table of criteria where they subjectively and intuitively determine the factor level (severity, occurrence, and detection) for each of the failures. With this, imprecision is present due to the interpretation that each one has regarding the failures. Therefore, this research proposes a fuzzy logic evaluation system with a solid mathematical basis that integrates these conditions of imprecision and uncertainty, thus offering a robust system capable of emulating the evaluation form of experts to support and improve decision making. One of the main contributions of this research is in the defuzzification stage, adjusting the centroid method and treating each set individually. With this, the RPN values approximate to the conventional technique were obtained. Simulations were carried out to test and determine the system’s best structure. The system was validated in a textile company in southern Guanajuato. The results demonstrate that the system reliably represents how experts perform risk assessment.

1. Introduction

Organizations motivated to deliver products and services aligned with customer expectations increasingly use assessment techniques to identify potential risks [1]. Prioritizing failures in a system and planning corrective actions are two essential components of risk management in any organization [2]. The Failure Mode and Effect Analysis (FMEA) is the most widely used structured and qualitative technique to identify failure modes in the system, evaluate their impact, and plan corrective actions. FMEA is the first step in reliability studies [3]. This technique has been applied in manufacturing, food, education, construction, electronics, health, aerospace, and hydrocarbons [4].

Artificial intelligence techniques are increasingly present in solving engineering problems, providing excellent results and greater reliability. A concrete example is the fuzzy logic technique that allows us to develop fuzzy systems that become indispensable tools in risk analysis. 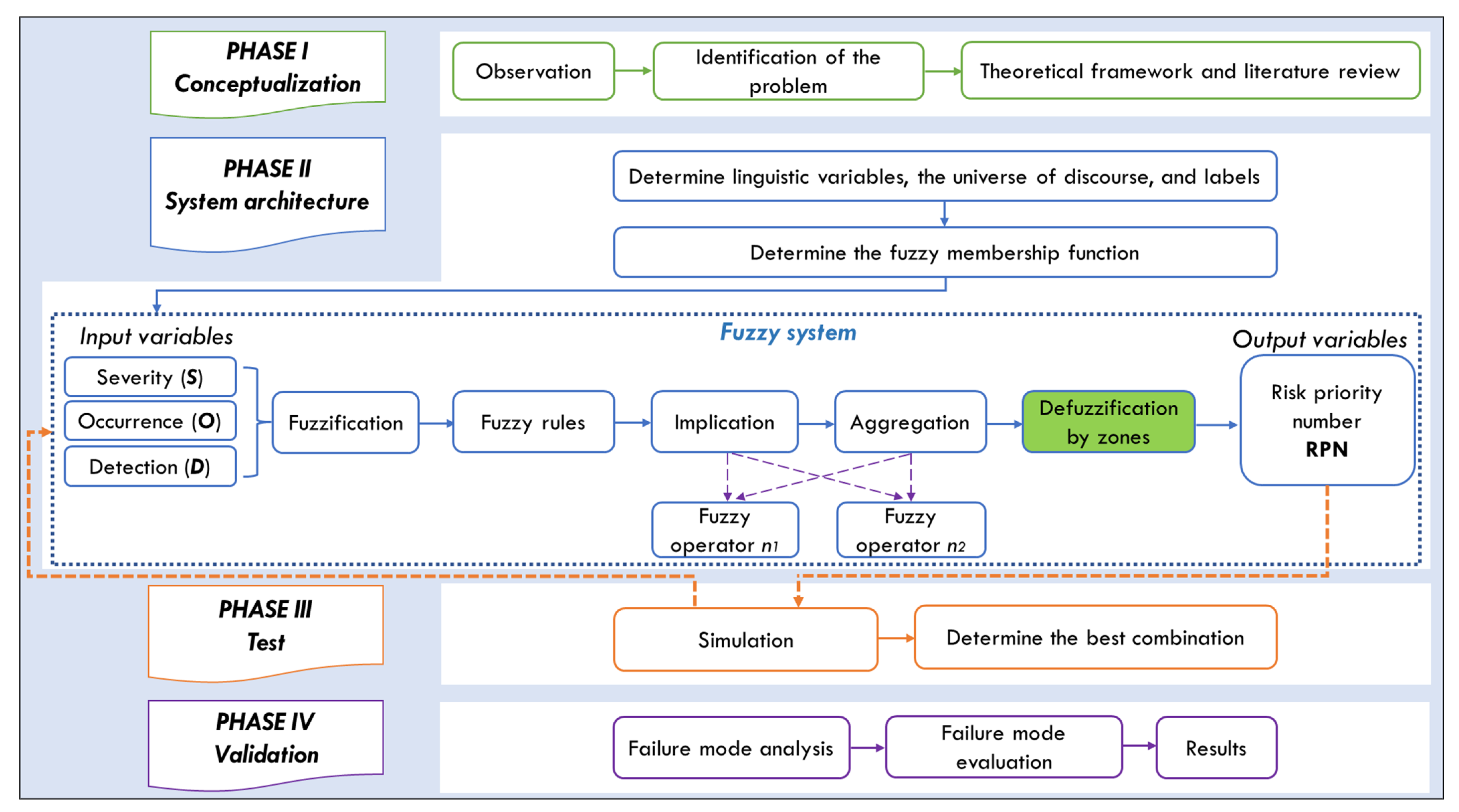A fuzzy-rule-based system is the most common way to represent and systematically model human reasoning, using a rough and linguistic description that reflects our communication language [5]. Considering the aspects of communication and human reasoning, to develop an FMEA, the participation of a multidisciplinary team of experts is necessary to evaluate the different failure modes that can compromise the reliability and correct operation of a system or process. Each team member’s interpretations regarding the failures can generate a degree of imprecision. Therefore, when experts analyze failure modes and consider natural language, they express their point of view based on their knowledge and experience. Likewise, to determine the risk priority number (RPN), the experts develop a qualitative analysis based on a table of specific criteria. Therefore, the evaluation of the severity (S), occurrence (O), and detection (D) factors is highly subjective. Consequently, this research proposes a fuzzy logic evaluation system that mathematically models and emulates experts’ decision making when performing failure mode analysis. In this work, a Mamdani Type-1 fuzzy inference model is proposed. Different scenarios are proposed in the implication and aggregation stages, combining the fuzzy operators. The test of the evaluation system was carried out via simulations to determine the best structure of the system. Therefore, values of the risk priority number (RPN) output variable are obtained with greater reliability.

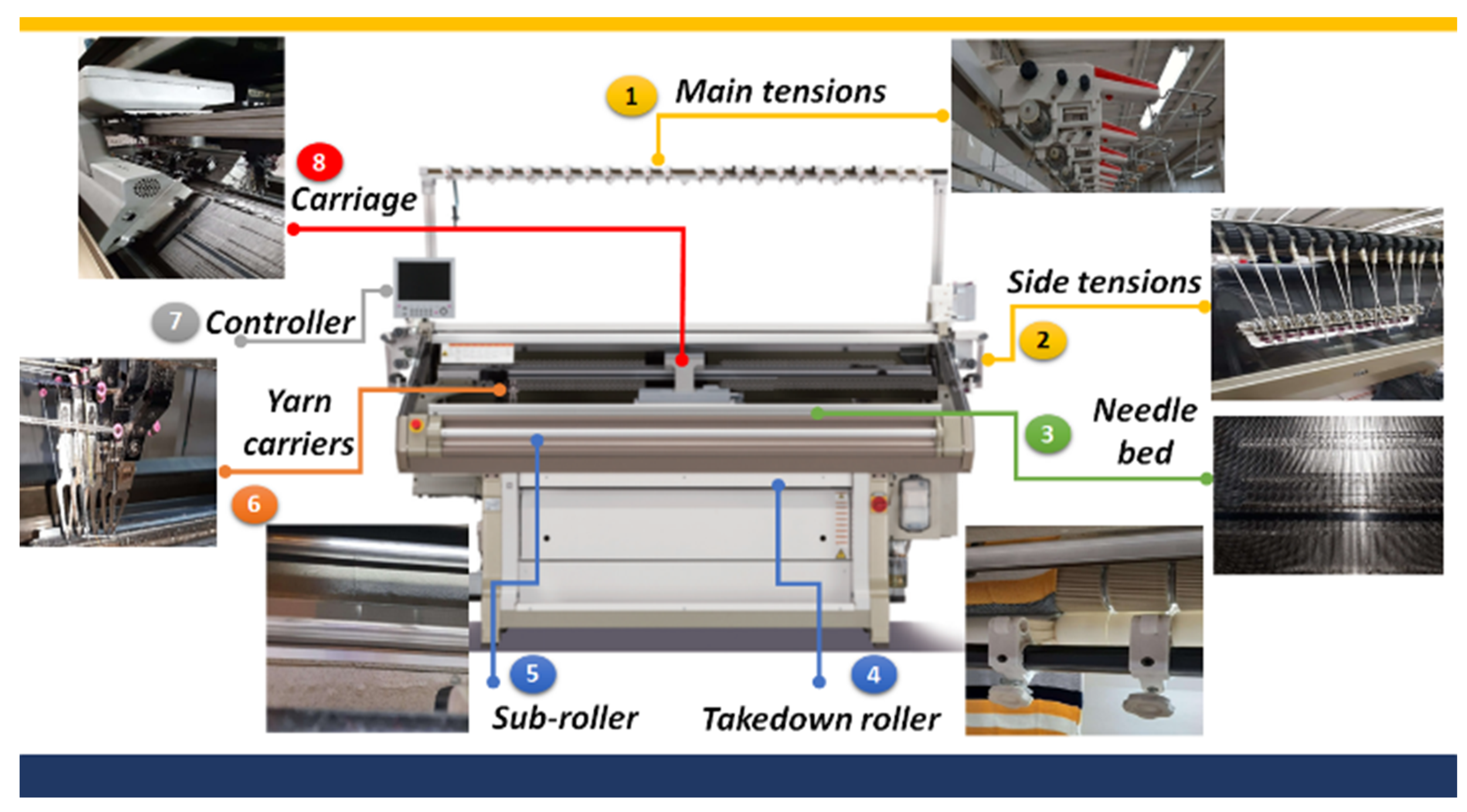
A case study was developed in the knitting department of a company in the textile sector. The evaluation system was validated, and the failure modes of the knitting machinery were prioritized. The main contribution of this research is a modification of the centroid method used in the defuzzification stage. In our proposal, defuzzification is carried out via zones of each fuzzy set to obtain results close to the conventional RPN.

This article is structured as follows. Section 2 presents the literature review, where the authors use fuzzy logic to improve the qualities of FMEA. In Section 3, the proposed methodology and approach are presented. Section 4 presents the development of the fuzzy system with a case study in the textile sector. The discussion is presented in Section 5. Finally, the main findings are concluded in Section 6.

2. Literature Review

The authors of [6] performed a comprehensive risk analysis on public–private partnership (PPP) projects for water treatment. An innovative risk assessment model is proposed based on intuitionistic fuzzy multi-objective optimization and the FMEA tool. Through interviews with experts, the literature, and the statistical frequency method, they identified five primary levels of risk and classified the degree of these risks. It should be noted that they assigned weights to each factor (O, S, and D). The domain of the RPN output variable of the case study is between (0, 1). Moreover, ref. [7] proposed a new method to classify risks in the working environment of an oil refinery. The Mamdani model and the triangular and trapezoidal functions for the linguistic variables were used. Their work is relevant because they develop a further prior evaluation of the input parameters (S, O, and D) by combining fuzzy inference systems into a single evaluation system. Therefore, with the proposed method, they obtain greater precision in risk prioritization.

Furthermore, the work of [8] developed a significant model to analyze the reasons for the failure of the logistics system during the COVID-19 pandemic. The FMEA methodology and the Analytic Hierarchy Process (AHP) method were used to calculate the weights of the factors (O, S, and D). They proposed a new fuzzy risk priority-weighted number (F-RPWN). As a result, it was determined that the most critical types of risk in the logistics system are security, commercial risks, and particular problems. The scale of the output variable in the case study to prioritize risks is less than (0.2). The models proposed by the authors [6,7,8] are novel and relevant to improving the FMEA technique. However, the scales of the RPN output variables differ significantly from the conventional RPN values. Also, ref. [9] proposes a novel methodology that combines the AHP and Partial Risk Map (PRISM) methods to assess risks based on pairwise comparison. They validated the methodology by developing a case study to assess the risks of strategic incidents in the logistic business processes of a nuclear power plant. A relevant aspect was the consistency test of the expert group after the evaluation.

The authors of [10] conducted an FMEA and tested their system in a private hospital, finding nine risk types. They use a Mamdani model with max–min operators. The invaluable implementation of this model in medical sterilization units is highlighted, in which risk analysis has been little explored. They make a comparison between two matrix approaches to classify risks. However, when a matrix approach with five levels is used for the linguistic variables, 125 IF-THEN rules are generated. Expert knowledge is based on relatively few possible combinations between variables. In our research, the knowledge base comprises 27 fuzzy rules, which is computationally practical. However, it also has greater approximation and simplicity when evaluating the RPN factors.

The researchers of [11] analyzed the risks in a hybrid fuel cell and gas turbine system for marine propulsion. With the FMEA, they determine 40 failure modes. A Mamdani-type fuzzy logic model is used for risk assessment. Their study provides an essential framework for developing a new propulsion system with safety in mind. It can be noted that the scale of the RPN output variable was (12.9, 38.0). The model we propose in this work improves the output scale with a closer approximation to the result of the score of the conventional technique. The authors of [12] propose using fuzzy logic and FMEA to analyze risks in student projects. The system integrates the agent-based model to build the membership function and classify the inference rules. They use the Mamdani model, the triangular function, and the max–min operators. The proposal provides a tool to improve the analysis and development of projects in the learning process.

The author’s research [1] focuses on the failure analysis of manufacturing systems proposing an approach based on the fuzzy cognitive map method (FCM), the FMEA for processes, and the delta-rule-learning algorithm considering the opinion of the experts. The results highlight the power of the approach with a food industry case study. The scale of the output variable RPN was (0.65, 0.97). In research [1,12], the most common membership functions are not explicitly related to the meaning of the severity, occurrence, and detection factors. This aspect is relevant and fundamental because the functions represent the degree of membership and the behavior of the system variables.

The work of [13] successfully combines fuzzy logic and product FMEA. The triangular membership function and the Mamdani model with max–min operators were used in the fuzzy system. Sixteen failure modes are analyzed in a family farming equipment cutting module to mechanize artichoke processing. The scale of the RPN output variable for the analyzed failure modes varies between (576.35, 833.47). In a numerical example presented by the authors, the output value is practically twice the value of the conventional RPN. In this present investigation, defuzzification is carried out via zones (sets). With the above, obtaining a value in the output variable close to the conventional RPN is possible.

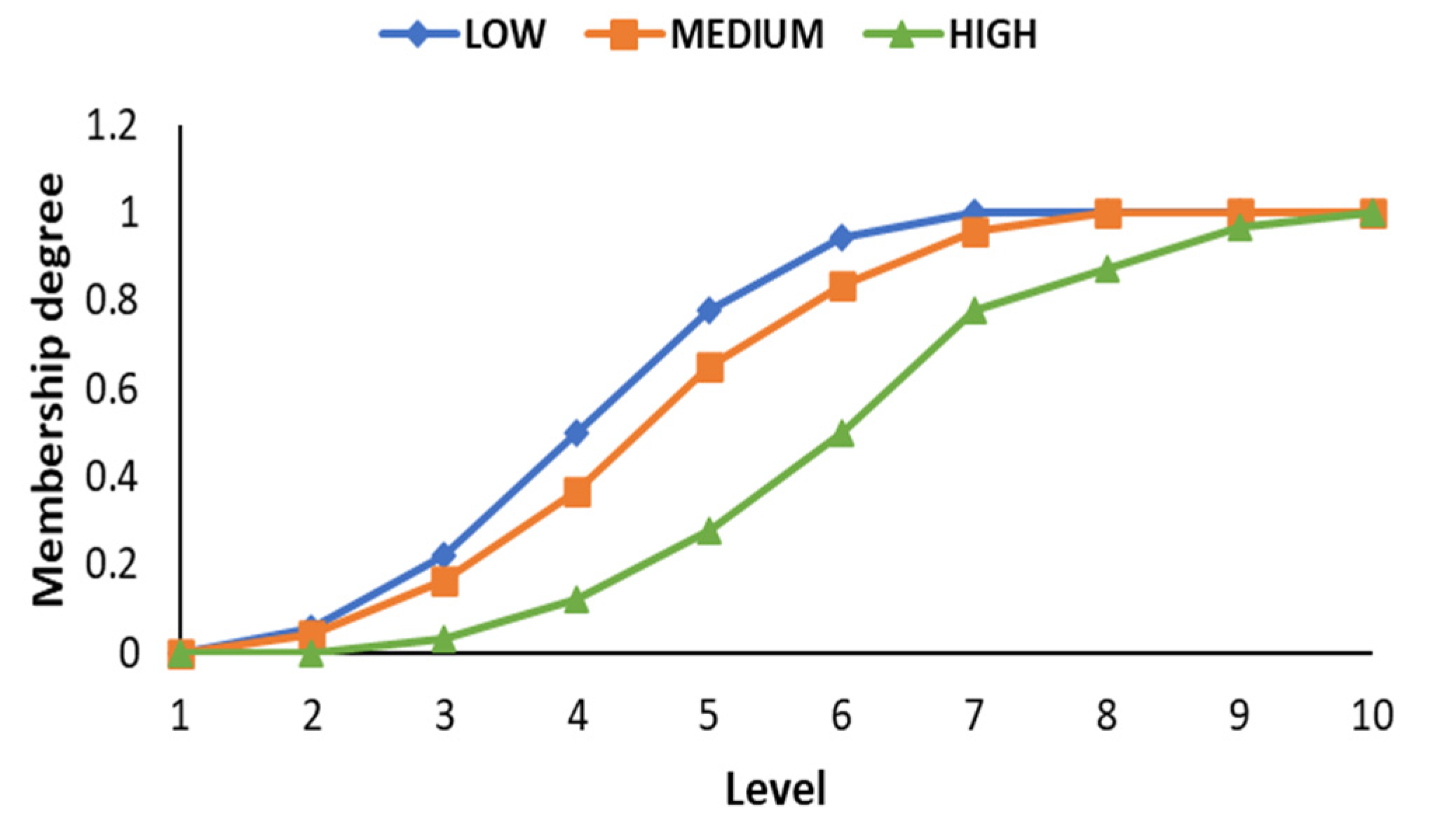
In ref. [14], via an FMEA, the authors evaluated eight risks in Smart Networks. A combination of ICT (Information and Communication Technology) with autonomous energy equipment from the electrical network. The results demonstrate the ability to improve risk perception and classify the impact of failures. The scale of the RPN output variable was (85.2, 116). Their Mamdani-type model incorporated the impact variable as an additional factor. A relevant aspect of this work is the test of the system with two types of membership functions (triangular and Gaussian), and later they perform a comparison of the outputs. However, the functions’ relationship concerning the system variables must be explained. In this present investigation, we explain the relationship of the sigmoidal function concerning the meaning and behavior of the factors (O, S, and D).

The authors of [15] develop an FMEA to study fluid-filling systems in automobile assembly lines, finding 23 failure modes. Aspects such as expert characteristics, scale variation, four membership functions, and four defuzzification algorithms were integrated into the fuzzy model. The scale of the RPN output variable was between (46, 610). Its system improves decision making, maintenance plans, and high levels of availability and security. However, the type of model used is not specified. In this research, a Mamdani model is developed with each stage, and the fuzzy rule base is presented.

In the investigation of [16], an FMEA was carried out with a root cause analysis in mining machinery, finding 16 potential risks via a Mamdani inference model; the Gaussian membership function was used for the input variables, and the triangular function for the output variable, as well as the max–min operators. The electrical subsystem was determined as a priority failure. The scale of the RPN output variable was (32.0, 142.0). The authors of [17] studied the components of a lathe machine via a risk analysis incorporating the fuzzy aspect. The scale of the RPN output variable was (3.50, 7.41). The results show that the fuzzy FMEA approach is superior in criticality analysis.

The researchers in [18] proposed a fuzzy-rule-based model incorporating the Gupta–Ghasemian formula and the Dempster–Shafer theory to quantify uncertainty. Their study analyzed 20 failure modes of an industrial centrifugal pump using an FMEA. Ten experts evaluated the failure modes, and the scale of the RPN output variable was (2.11, 7.49). The studies of [16,17,18] present important models and applications that demonstrate the need to integrate fuzzy logic in the FMEA. However, the result of the output variables is found in ranges with low values. In this present investigation, we propose in the fuzzification stage an adjustment that allows the values of the output variable to be on a scale close to the conventional values of RPN. Moreover, the research of [19] in their study of enterprise architectures carried out an FMEA. The authors analyzed twenty failure modes with a fuzzy model incorporating an eight-step method with multi-criteria optimization. A triangular function and inference rules were used based on expert criteria and weights, best–worst, and min–max operators. The NPR output scale in their case study is (0.63, 9.66). They prioritize and identify significant priorities such as labor practice and infrastructure with their model.

Other studies focused on innovative proposals to build a failure analysis, integrating other techniques to test consistency, pairwise comparison, and ideal solution. For example, the authors of [20] propose a Mamdani-type fuzzy inference system built from the experience of experts. They validate their model in a diesel engine turbocharger system. The analysis of the mechanical system is highlighted by considering its components, subsystems, and the interdependence between failure modes. In addition, they developed a platform as an evaluation interface where experts from different disciplines can share information. In ref. [21], the authors developed a rule-based fuzzy expert system to offer a tool to assess risks associated with marine engineering and offshore transportation issues. They use three membership functions to create fuzzy sets and perform sensitivity analyses for the most critical failure modes. Thus, they demonstrate the effectiveness of their model for risk assessment.

The investigation of [22] proposes a fuzzy inference system implemented in a nuclear reliability engineering problem. They develop an FMEA in a chemical and volume control system. The results demonstrate the potential of the inference system for this class of problems. In addition, it provides the advantage of being used for systems where security data are unavailable or unreliable. The authors of [23] develop an FMEA using the fine-tuned trapezoidal fuzzy-based technique for the order of preference by similarity to the ideal solution. Its objective was to reduce the risks in the preparation or collection of data using hierarchical matrix management. The proposed model considers the interdependencies between failure modes, the relative importance of risk, and the non-subjective nature of conventional RPN functions. In the research by [24], they propose a novel method incorporating the stages of the FMEA technique. The method allows pairwise comparison, calculating the weights of importance and consistency in the evaluation by the groups of experts from the FMEA. With the above, they determine the indices of S, O, and D. By using basic mathematical operations, the method is easily applied. Previous research demonstrates the importance of integrating fuzzy logic and FMEA techniques. The most relevant characteristics of our contribution that motivate the realization of this study are as follows:

• The modification of the centroid method is one of the main contributions of this research since it allows obtaining RPN values close to the conventional technique;
• Likewise, when using the sigmoid function, the relationship with the factors is described, and finally, different scenarios are explored to establish the best combination of fuzzy operators;
• In this study, the proposal of a generalizing system based on a simulation process of multiple runs is made.

3. Methodology

The research methodology is developed in four phases (see Figure 1). The first phase is conceptualization. From the systematic observation, the problem is raised, and the areas of opportunity are identified in the FMEA technique. In addition, the literature review of current research on FMEA and fuzzy logic was carried out. In the second phase, the architecture of the fuzzy evaluation system is carried out. In this phase, we develop the most significant contribution, mainly in the defuzzification stage (highlighted in green). This step will be explained in more detail later.

In the third phase, the fuzzy system is tested with a significant number of simulations to find the combination with the best performance. Finally, in the fourth phase, the validation of the system is developed in a company in the textile sector in the south of Guanajuato.

FMEA

The RPN is the crucial criterion for determining the priorities of the failure modes [25]. The failure mode is how a system or component could fail. The failure effect is a negative consequence. It is essential to determine the RPN accurately. This indicator is the product of three factors: the occurrence estimates the frequency with which possible failures occur. The severity assesses the impact these failures have on the system, and detection is the probability of identifying the failure before it occurs (see Equation (1)).

$$\mathrm{RPN}=\mathrm{Severity}\left(\mathrm{S}\right)\times \mathrm{Occurrence}\left(\mathrm{O}\right)\times \mathrm{Detection}\left(\mathrm{D}\right)$$

(1)

Conducting an FMEA requires a systematic six-step approach as follows:

• Determine the scope of the FMEA and form a multidisciplinary team;
• Analyze potential failure modes;
• Determine the effects, causes, and controls of each failure;
• Find the level of each factor;
• Calculate the RPN of each mode;
• Generate an analysis report and, where appropriate, take the recommended actions to reduce or eliminate risks;

4. Case Study

4.1. Phase I—Conceptualization

Identification of the Problem

Next, the motivation of this work is explained to offer a robust and reliable tool that integrates conditions of linguistic uncertainty to improve decision making during risk analysis. After the first steps, a critical stage is reached when evaluating the factors with which the RPN is determined. The experts perform a qualitative analysis expressing their point of view on each failure mode. Therefore, they are based on commonly used criteria, such as those presented in

Table 1. Evaluation criteria.

	Factors
Rating	Severity	Occurrence	Detection	Evaluation Criteria
1	None	Very remote	Almost certain	No effect for the system.
2	Minimum	Remote	Very high	Minor effects on systems and products.
3	Minor	Very minor	Major	The system operates with few failures.
4	Very low	Minor	Reasonably high	The system operates with some faults.
5	Low	Low	Moderate	Failures with quick repair and minor impacts.
6	Moderate	Moderate	Medium	The system requires changing parts with significant effects.
7	High	Moderate high	Reasonably low	Direct effect on the system, process flow with nonconforming and discarded product.
8	Very high	High	Remote	The system is inoperable due to severe failures.
9	Hazardous	Extreme	Very remote	Failures affect the safety of operators and the system with a warning.
10	Very hazardous	Very high	Absolute uncertainty	The failures affect the safety of operators and the system, causing total stoppage of the process.

.

Each opinion expressed presents a degree of subjectivity and imprecision and is determined by the experience of the expert. For example, the criteria in natural language (labels) for each factor of a failure mode would be as follows: “Failure mode $F_n$ presents Hazardous Severity, has a Very Slight Occurrence, and Detection is Remote”.

In the failure mode analysis, experts determine the criteria based on their reasoning, knowledge, and experience. The interpretation of these criteria varies from one expert to another. For example, three experts (${\mathrm{E}}_1,{\mathrm{E}}_2,{\mathrm{and}\mathrm{E}}_3$) can use the same label (Hazardous). However, there is a difference in the level of meaning because they do not have an established range since it is a qualitative aspect (see Figure 2).

Another area of opportunity is that experts usually analyze many failure modes. By evaluating these failures, multiple possible combinations are formed between the criteria, generating a more complex environment during decision making. Therefore, the need arises to use fuzzy logic to treat subjective and uncertain information, proposing an approach that strengthens decision making and is a robust tool capable of emulating how experts analyze and evaluate the risks that compromise the correct operation.

4.2. Phase II—System Architecture

In this phase, the system architecture was carried out, adopting the approach of a Mamdani model. This approach offers us a tool for logical deductive inference to analyze the results of a model structure in terms of a set of “IF-THEN” rules [26].

4.2.1. Linguistic Variables

The fuzzy set theory is a mathematical tool to translate abstract concepts in natural language into computational language; it offers a way of dealing with imprecise and vague information. Fuzzy logic refers to the concept of partial truth. The ${\mu }_A\left(x\right)=0.0$ and ${\mu }_A\left(x\right)=1.0$ values represent, respectively, a null and complete membership of $x$ in $A$, while all ${\mu }_A\left(x\right)$ values between 0 and 1 indicate a partial membership of $x$ in $A$ [27].

Once the conceptualization phase is complete, the system architecture is developed. The first step is to determine the factors O, S, and D as input variables. The universe of discourse for each factor is in the same range commonly used in the literature (between 1 and 10). Likewise, the RPN was considered an output variable because it is the indicator of interest to prioritize failures. The universe of discourse of the RPN is [1, 1000]. This research proposes to classify the factors into three labels, concentrating on the ten criteria of Table 1 to simplify and make it easy for any decision maker without an expert to evaluate. The linguistic variables or labels were established as low (L), medium (M), and high (H).

4.2.2. Membership Function

The sigmoid membership function is used to fuzzy the input variables. This function is characterized by having an inclusion value other than 0 for a range of values above a certain point $a$, being 0 below $a$ and 1 for values greater than $b$. The inflection point (value 0.5) is $m=\left(a+b\right)/2$. Between points $a$ and $b$, it is quadratic type (smooth) [28].

$$S\left(x;a,m,b\right)=\left\{\begin{array}{c}\begin{array}{c}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x<a\\ 2{\left(\frac{x-a}{b-a}\right)}^2\hspace{0.17em}a \le x \le m\\ 1-2{\left(\frac{x-b}{b-a}\right)}^2\hspace{0.17em}\hspace{0.17em}m \le x \le b\\ 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x>b\end{array}\end{array}\right.$$

(2)

When analyzing the possible functions, it was found that the sigmoid function is the one that reflects a behavior according to the criteria in Table 1. Each factor has a different series of criteria on a qualitative rating scale with gradual growth (from level 1 to 10), where failure modes present a higher risk when the rating increases. In Figure 3, the behavior of this membership function can be observed.

4.2.3. Fuzzy System

Next, the stages that constitute the FMEA fuzzy evaluation system are presented. The fuzzification stage transforms crisp inputs into fuzzy numbers that indicate the degree of membership in the interval [0, 1]; with this, ${\mu }_A\left(x\right)$ indicates that both $x$ belong to the linguistic labels {L, M, H}.

Table 2. Fuzzification parameters.

Linguistic Variables	Labels
	$\mathbf{L}$			$\mathbf{M}$			$\mathbf{H}$
	a	m	b	a	m	b	a	m	b
Occurrence	1	3	7	1	5	8	2	7	10
Severity	1	3	7	1	5	8	2	7	10
Detection	1	3	7	1	5	8	4	7	10
RPN	50	100	150	100	250	400	350	550	700

shows the three input linguistic variables and the output variable. Likewise, the parameters a, m, and b used in the transfer function for each system variable are shown.

Next, the behavior of the membership function of each input variable is described. As shown in the graph of Figure 4, the behavior of the occurrence and severity variables agrees with the evaluation that the experts carry out since by qualifying with a higher criterion, the possibility of failure occur is also greater. Also, the higher the score in the criteria, the higher the severity of the failure.

Likewise, the graph in Figure 5a shows the behavior of the detection variable. The higher the criterion level, the lower the possibility of detecting the failure. Finally, Figure 5b shows the behavior of the output variable. The higher the level in the RPN evaluation, the greater the risk and the higher the failure priority will have to be.

After the fuzzification, the knowledge base of the system was developed. In this stage, the fuzzy rules are established that are the result of different combinations between the number of input variables and linguistic labels. Therefore, 27 rules were defined ($3^3$). The defined rules are of the IF–THEN type, where “IF” is the antecedent and is related to the input variables, and “THEN” is a consequent and is associated with the output variable. Each rule was operated as follows: ${\mathrm{R}}_{\mathrm{i}}:\mathrm{IF}x{\mathrm{is}\mathrm{A}}_{\mathrm{i}}{\mathrm{THEN}\mathrm{N}}_{\mathrm{i}}\mathrm{is}y$.

The rules of the fuzzy system represent in the FMEA the knowledge of the experts when evaluating the factors. In

Table 3. Fuzzy rules.

Rule	Statement	Rule	Statement
R1	IF O is low AND D is low AND S is low THEN RPN is low	R15	IF O is medium AND D is medium AND S is high THEN RPN is medium
R2	IF O is low AND D is low AND S is medium THEN RPN is low	R16	IF O is medium AND D is high AND S is low THEN RPN is medium
R3	IF O is low AND D is low AND S is high THEN RPN is low	R17	IF O is medium AND D is high AND S is medium THEN RPN is medium
R4	IF O is low AND D is medium AND S is low THEN RPN is low	R18	IF O is high AND D is medium AND S is medium THEN RPN is medium
R5	IF O is low AND D is medium AND S is high THEN RPN is low	R19	IF O is low AND D is high AND S is high THEN RPN is high
R6	IF O is low AND D is high AND S is low THEN RPN is low	R20	IF O is medium AND D is high AND S is high THEN RPN is high
R7	IF O is low AND D is high AND S is medium THEN RPN is low	R21	IF O is high AND D is low AND S is medium THEN RPN is high
R8	IF O is medium AND D is high AND S is low THEN RPN is low	R22	IF O is high AND D is low AND S is high THEN RPN is high
R9	IF O is high AND D is low AND S is low THEN RPN is low	R23	IF O is high AND D is medium AND S is low THEN RPN is high
R10	IF O is low AND D is medium AND S is medium THEN RPN is medium	R24	IF O is high AND D is medium AND S is high THEN RPN is high
R11	IF O is medium AND D is low AND S is medium THEN RPN is medium	R25	IF O is high AND D is high AND S is low THEN RPN is high
R12	IF O is medium AND D is low AND S is high THEN RPN is medium	R26	IF O is high AND D is high AND S is medium THEN RPN is high
R13	IF O is medium AND D is medium AND S is low THEN RPN is medium	R27	IF O is high AND D is high AND S is high THEN RPN is high
R14	IF O is medium AND D is medium AND S is medium THEN RPN is medium

, the rules are listed in three groups [low, medium, high]. Thus, the system’s knowledge base is built.

Table 4. Evaluation with the fuzzy system.

Label Group: Low			Label Group: Medium			Label Group: High			Output: RPN
Rule	Implication	Aggregation	Rule	Implication	Aggregation	Rule	Implication	Aggregation	Defuzzification
R1	1.000	1.000	R10	1.000	1.000	R19	0.826	0.875	517.391
R2	1.000		R11	1.000		R20	0.826
R3	0.875		R12	0.875		R21	0.875
R4	1.000		R13	1.000		R22	0.765
R5	0.875		R14	1.000		R23	0.875
R6	0.944		R15	0.875		R24	0.765
R7	0.944		R16	0.944		R25	0.826
R8	1.000		R17	0.944		R26	0.826
R9	0.875		R18	0.875		R27	0.723

shows the rules grouped in the three language labels, the values of implication and aggregation, and finally, the output value in the defuzzification stage. The implication and aggregation constitute the motor of the diffuse system since they allow the interpretation of the rules that form the knowledge base and convert the values of the inputs into outputs, thus achieving a diffuse inference.

In the implication stage, the quantitative analysis is performed individually. Considering the evaluation of Table 4, the fuzzy operator for each rule (implication) was the product. For the aggregation stage, the maximum operator was used, and the quantitative analysis was carried out jointly for each of the three groups of rules; this way, a single fuzzy set is obtained for each label of the output variable. Since there are three factors of interest to obtain the RPN, only three input values are required for the evaluation. For example, an expert may perform the following assessment: $\mathrm{Occurrence}=8$, $\mathrm{Detection}=9$, and $\mathrm{Severity}=8$. The value of the conventional $\mathrm{RPN}=576$. With the diffuse evaluation system, the output value is 517.391. Subsequently, the system was tested and validated with multiple runs of 200 simulations each; this is explained in more detail in Section 4.3. This allows for having a generalizing system in which any expert can reliably evaluate the failure modes.

Once the system’s output is obtained, converting the fuzzy sets into crisp values or natural numbers to facilitate the interpretation of the result and, thus, correctly prioritize the failure modes is necessary to develop the defuzzification stage. Several methods are available for this stage: weighted average, max membership principle, mean-max membership, the center of sums, the first of maxima or last of maxima, and the centroid method. The centroid method is widely used for fuzzy number defuzzification in engineering applications [29].

The centroid method is one of the most used. This method is like the arithmetic mean for frequency distributions of a given variable, with the difference that the weights are the ${\mu }_A\left(x_i\right)$ values, which indicate the degree of compatibility of the $x_i$ value with the concept modeled via the fuzzy set $A$ [30] (see Equation (3)), where $k$ is the number of fuzzy sets, $x_i$ represents the center of the fuzzy set, and ${\mu }_A\left(x_i\right)$ is the output of the aggregation stage of each set:

$$\mathrm{z}=\frac{{{\displaystyle \sum }}_{i=1}^k{\mu }_A\left(x_i\right)x_i}{{{\displaystyle \sum }}_{i=1}^k{\mu }_A\left(x_i\right)}$$

(3)

The aggregation outputs of each set are the values that horizontally segment the membership functions into two areas, the lower area being the one used to calculate the centroid. For example, to obtain the system’s output in the evaluation of Table 4, utilizing the centroid method, the product of the aggregation values (membership degree) is obtained via the inflection points of each membership function (see Equation (4)).

$$\mathrm{Z}=\frac{\left(1\times 100\right)+\left(1\times 250\right)+\left(0.875\times 550\right)}{\left(1\right)+\left(1\right)+\left(0.875\right)}=\frac{100+250+481.25}{2.875}=289.13$$

(4)

The centroid is located at 289.13. Therefore, the value of the output variable is $\mathrm{NPR}=289.13$. The coordinates and position of the centroid are shown in Figure 6.

An essential contribution of this research is in the defuzzification stage. When the centroid method is used to obtain the true value of the output, the areas of each set overlap to form a single area. With this, the point where a vertical line will be located that segments the total area into two areas with equal mass is calculated. Our proposal considers each set individually (see Figure 7). In the same way, each function is cut according to its degree of membership. Initially, it was identified that the maximum values mainly come from the output variable of the fuzzy set high (H). In Equation (3), all the sets have the same importance, but the change is that the high set has higher priority since it is the one that marks the difference between the values.

$$\mathrm{Z}=\left({\mu }_L\left(x\right)\times x_1\right)+\left({\mu }_M\left(x\right)\times x_2\right)+\frac{\left({\mu }_H\left(x\right)\times x_3\right)}{{\mu }_L\left(x\right)+{\mu }_M\left(x\right)+{\mu }_H\left(x\right)}$$

(5)

Unlike Equation (4), now the sum of the output values of the sets is only included in the high label (H). Thus, this set is weighted more (See Equation (5)). For each area, a point is calculated, and the value corresponding to each label is obtained. These values are added to have a broader value on the work scale. With this proposal, a z-value or NPR = 517.391 is obtained.

$$\mathrm{Z}=\left(1\times 100\right)+\left(1\times 250\right)+\frac{\left(0.875\times 550\right)}{\left(1\right)+\left(1\right)+\left(0.875\right)}=100+250+167.391=517.391$$

(6)

Thus, it is possible to contrast the result of Equations (4) and (6) with the conventional $\mathrm{RPN}=576$, achieving for this evaluation a value approaching between the conventional and the diffuse, confirming that with the modification of the original formula, consistent RPN values are obtained.

4.2.4. Combinations

The implication and aggregation stages are crucial. In this research, three scenarios were created using the most common fuzzy operators, as shown in

Table 5. Performance.

Combination	Implication	Aggregation	MSE
1	$\min$	$\min$	6865.06
2	$\min$	$\max$	6132.66
3	$\mathrm{product}$	$\max$	3434.23

.

4.3. Phase III—System Testing

4.3.1. Simulation

In the simulation stage, random numbers are generated for each factor, and the output values of the defuzzification stage are recorded. Therefore, the system was validated via this simulation process generating one hundred runs, and each run consisted of 200 iterations for each combination of operators. Figure 8 presents the results of only one run, where it is possible to compare the behavior of the system outputs with the evaluation of the conventional RPN. In the three scenarios, an approximate behavior is observed. However, It Is essential to evaluate the performance of the system.

4.3.2. Determine the Best Combination

The mean square error (MSE) indicates the best-performing combination. This metric is the most widely used evaluation criterion for model testing purposes. It quantifies the difference between the estimated and real models [31]. The objective is to establish the difference between the values of the real RPN and the values thrown via the fuzzy system. The best configuration of the system will give a lower MSE and, therefore, more closely represent how the expert evaluates. Consequently, this allows having a reliable model that supports decision making by prioritizing failure modes.

Table 5 presents the MSE value for each combination; combination three presents the best performance using the fuzzy operator (product) for implication and the operator (max) for aggregation.

4.4. Phase IV—Validation

To validate the proposed approach, an FMEA was conducted in a clothing factory in the southern region of Guanajuato, Mexico. This factory specializes in making children’s sweaters. The process begins with knitting; the canvases are obtained, which are later basted, ironed, and cut using sewing patterns. Afterward, the garment is sewn and detailed. Finally, the sweater is packed for sale to the customer. The knitting department is the most crucial area because, in this area, knitting machines are used to weave canvases that will be transformed into garments throughout the process. Therefore, the FMEA was developed to prioritize potential risks that affect the operation of the machinery and, consequently, the flow of the manufacturing process.

4.4.1. Failure Mode Analysis

A multidisciplinary team of four experts with knowledge and experience in knitting manufacturing was formed (see

Table 6. Team of experts.

Expert	Area	Experience in the Department
${\mathrm{E}}_1$	Mechanics	40 years
${\mathrm{E}}_2$	Operational	20 years
${\mathrm{E}}_3$	Electronics	26 years
${\mathrm{E}}_4$	Production	10 years

). The team participated in the analysis of potential failures; in addition, they identified the effects, causes, and detection controls. Each expert brought their knowledge to the problem. However, in the evaluation stage, only the specialist of each area participates. In this case, the expert ${\mathrm{E}}_2$ was chosen because they are a specialist in the operational area and have extensive knowledge of knitting machinery.

In Figure 9, the location of the subsystems of the knitting machines are shown and named as follows: (1) main tensions, (2) side tensions, (3) needle bed, (4) takedown roller, (5) sub-roller, (6) yarn carriers, (7) controller, and (8) carriage.

Based on the analysis of the components that generate the highest number of failures during the operation of the machinery, they defined eight subsystems. Derived from the analysis of the subsystems, the experts determined 33 failure modes. In addition, the effect that the failure modes cause in the system was determined, and the components were classified. This information is presented in

Table 7. Failure modes analysis.

Subsystem	ID	Failure Mode	Classification	Effect
1- Main tensions	$F_1$	Large knot	Electronic/Mechanical	-Breakup of the fiber and detachment of the canvas -Deformation of the needle hook
	$F_2$	Small knot	Electronic/Mechanical	-Deformation of the needle hook -Defective knit fabric
	$F_3$	Tensioner out of adjustment	Mechanical	-Modification in fiber tension -Mark and relief on the canvas
	$F_4$	Damaged lamp	Electronic	-Delay in identifying the faulty device
	$F_5$	Up tension wire	Mechanical	-Change in yarn tension
2- Side tensions	$F_6$	Up tension wire	Mechanical	-Change in yarn tension
3- Needle bed	$F_7$	Sinker	Mechanical	-Sinker break
	$F_8$	Jack	Mechanical	-The jack gets stuck
	$F_9$	Needle	Mechanical	-Breaking the needle hook and transfer plate
	$F_{10}$	Needle spacer broken	Mechanical	-The component does not perform its function
	$F_{11}$	Selector inactive	Mechanical	-Rupture
	$F_{12}$	Sele-Jack	Mechanical	-Sele-Jack stuck
4- Takedown roller	$F_{13}$	Rubber	Electronic/Mechanical	-The canvas does not go down correctly
	$F_{14}$	Pressure roller	Mechanical	-In the corresponding section, the canvas is raised
	$F_{15}$	Chain	Electronic/Mechanical	-The Chainmain roller does not accomplish its function
	$F_{16}$	Yarn accumulation	-	-Breakage of the fiber
5- Sub-roller	$F_{17}$	Burr	Electronic/Mechanical	-Breakage of the fiber
	$F_{18}$	Yarn accumulation	Electronic/Mechanical	-Accumulation of fiber in the roller
	$F_{19}$	Roller belt	Electronic/Mechanical	-The roller does not rotate properly
6- Yarn carriers	$F_{20}$	Carrier box	Mechanical	-Yarn carrier inactive, misalignment in the box, retention of the yarn carrier
	$F_{21}$	Yarn feeder	Mechanical	-Loose loops
	$F_{22}$	Porcelain ring	Mechanical	-Breakage of the fiber
7- Controller	$F_{23}$	USB reader	Electronic	-The USB memory is not recognized
	$F_{24}$	Inactive fan	Electronic	-Electronic cards overheating
	$F_{25}$	Screen	Electronic	-Information is not displayed
	$F_{26}$	Card	Electronic	-Information is not processed for the regular operation of the machine
	$F_{27}$	Power supply 30 V	Electronic	-Low voltage
8- Carriage	$F_{28}$	Wear brush	Mechanical	-Does not adjust the tabs of the needles
	$F_{29}$	Stitch Presser	Electronic/Mechanical	-Loops do not go down properly
	$F_{30}$	Actuator set	Electronic	-The loops are not formed according to the programmed instructions
	$F_{31}$	Stitch motor	Electronic	-Knit fabric with loose or tight loops depending on the system
	$F_{32}$	Damaged magnet	Mechanical	-The carriage operates out of time
	$F_{33}$	Damaged solenoid	Electronic	-The yarn carriers do not activate

.

4.4.2. Failure Mode Evaluation

After the development of the system was tested and validated for its operation, the expert ${\mathrm{E}}_2$ evaluated the level of the factors.

Table 8. Expert evaluation.

Subsystem	ID	O	D	S	RPN	F-RPN	Priority
1	$F_1$	5	5	9	225	277.82	2
	$F_2$	10	9	5	450	455.55	1
	$F_3$	3	9	4	108	113.90	3
	$F_4$	4	2	6	48	71.75	4
	$F_5$	3	3	3	27	37.16	5
2	$F_6$	4	2	9	72	77.16	4
3	$F_7$	2	2	2	8	0.04	5
	$F_8$	2	2	3	12	0.16	5
	$F_9$	4	5	6	120	167.01	3
	$F_{10}$	3	3	6	54	50.84	5
	$F_{11}$	3	5	6	90	83.35	4
	$F_{12}$	2	2	4	16	0.36	5
4	$F_{13}$	1	2	3	6	0.00	5
	$F_{14}$	3	5	5	75	72.75	4
	$F_{15}$	3	4	6	72	66.16	4
	$F_{16}$	2	2	4	16	0.36	5
5	$F_{17}$	2	4	3	24	1.45	5
	$F_{18}$	4	2	10	80	77.16	4
	$F_{19}$	2	7	6	84	85.24	4
6	$F_{20}$	3	5	9	135	92.62	4
	$F_{21}$	2	5	8	80	31.46	5
	$F_{22}$	3	4	3	36	40.38	5
7	$F_{23}$	3	2	3	18	35.22	5
	$F_{24}$	9	3	7	189	252.44	2
	$F_{25}$	2	5	3	30	5.83	5
	$F_{26}$	2	4	2	16	0.36	5
	$F_{27}$	2	7	4	56	45.24	5
8	$F_{28}$	10	3	9	270	261.11	2
	$F_{29}$	2	6	5	60	37.25	5
	$F_{30}$	2	7	9	126	127.90	3
	$F_{31}$	3	7	9	189	184.53	3
	$F_{32}$	3	5	6	90	83.35	4
	$F_{33}$	2	7	5	70	63.08	4

presents each of the eight subsystems, their corresponding failure modes, as well as the evaluation with the real data that the expert assigned to the occurrence (O), detection (D), and severity (D).

In the sixth column, the product of the factor values is obtained to obtain the conventional risk priority number (RPN). The seventh column shows the diffuse risk priority number (F-RPN) obtained with the proposed evaluation system for each failure mode. Finally, in the last column, the priority of the failure modes is presented.

As can be seen, the values between the conventional and the diffuse are close. A statistical test is presented below to validate that the means of the conventional and diffuse values are close.

Table 9. Data for comparison of means.

ID	RPN	F-RPN	F-RNP without Change in Centroid
$F_1$	225	277.82	231.14
$F_2$	450	455.55	300.00
$F_3$	108	113.90	209.83
$F_4$	48	71.75	205.38
$F_5$	27	37.16	177.57
$F_6$	72	77.16	212.21
$F_7$	8	0.04	152.58
$F_8$	12	0.16	152.58
$F_9$	120	167.01	207.49
$F_{10}$	54	50.84	186.57
$F_{11}$	90	83.35	189.72
$F_{12}$	16	0.36	152.58
$F_{13}$	6	0.00	0.00
$F_{14}$	75	72.75	187.15
$F_{15}$	72	66.16	186.57
$F_{16}$	16	0.36	152.58
$F_{17}$	24	1.45	152.58
$F_{18}$	80	77.16	212.21
$F_{19}$	84	85.24	216.62
$F_{20}$	135	92.62	195.56
$F_{21}$	80	31.46	181.00
$F_{22}$	36	40.38	177.57
$F_{23}$	18	35.22	177.57
$F_{24}$	189	252.44	294.58
$F_{25}$	30	5.83	159.65
$F_{26}$	16	0.36	152.58
$F_{27}$	56	45.24	188.51
$F_{28}$	270	261.11	300.00
$F_{29}$	60	37.25	181.94
$F_{30}$	126	127.90	248.08
$F_{31}$	189	184.53	248.08
$F_{32}$	90	83.35	189.72
$F_{33}$	70	63.08	201.79
$N=$	33	33	33
$\overline{X}=$	89.5	87.8	193.39
$\sigma =$	91.4	100.8	53.64

presents the data for the conventional RPN and diffuse F-RPN values. In addition, the parameters of each data group are shown.

Using the Minitab software, the analysis of variance was obtained to test the equality of means.

Table 10. ANOVA (F-RNP without centroid adjustment).

ANOVA
Source	df	SS	MS	F-Value	p-Value
Factor	1	178,258	178,258	31.75	0.000
Error	64	359,365	5615
Total	65	537,623

and

Table 11. ANOVA (F-RNP with adjustment to the centroid method).

ANOVA
Source	df	SS	MS	F-Value	p-Value
Factor	1	43	42.58	0.00	0.946
Error	64	592,263	9254.10
Total	65	592,305

present the ANOVA.

A significance level of α = 0.05 is established. Since the p-value = 0.000 is less than the α significance level, there is a significant difference between the means of the RPN and F-RPN risk priority numbers without adjustment to the centroid method (see Table 10).

A significance level of $\alpha =0.05$ is established. Since the p-value = 0.946 is greater than the significance level $\alpha$, no significant difference exists between the means of the RPN and F-RPN risk priority numbers (see Table 11). Therefore, this validates that the proposed approach prioritizes potential failures in most cases as the expert would.

From the results of the F-RPN, the failure modes were prioritized. The prioritization and classification will allow the failure modes to be grouped into five criticality categories (see

Table 12. Criticality classification.

Priority	Range F-RPN
Category 1	[311–500]
Category 2	[201–300]
Category 3	[101–200]
Category 4	[51–100]
Category 5	[0–50]

) to carry out the necessary actions to mitigate and eliminate the potential risks that compromise the operation of the knitting machinery.

The results of Table 8 show that the priority failure modes with the highest risk include the following: $F_2$ (small knot) as Category 1 and $F_1$ (large knot), $F_{24}$ (inactive fan), $F_{28}$ (wear brush) as Category 2. These four failure modes generate machine stoppages, affecting the regular operation of the machinery. Furthermore, these failures affect the quality of the canvases, generating defects in the loops’ formation and the essential structural parameter (stitch graduation). In addition, overheating the electronic card would affect the entire system. Identifying failure modes belonging to the first and second categories allows the team of experts to focus efforts on establishing actions that reduce the probability of occurrence of critical failures to mitigate and eliminate the associated causes.

Figure 10 compares the RPN and the approach proposed in this research (F-RPN). As can be seen, by prioritizing the failure modes, the result of the evaluation with the fuzzy system presents a behavior like that of the conventional technique.

The proposal’s main objective is to have a method that gives us an approximate value to the conventional method based on a robust mathematical model. In graph (b) of Figure 10, the modification of the centroid method is not used as proposed in this study. Therefore, the values of the system are not approximated to the values of the conventional RPN.

5. Discussion

At present, the prioritization and risk analysis with the FMEA technique have become more relevant, and proof of this is the studies that try to overcome the inherent limitations of the method. Risk assessment systems have been proposed in the literature from various approaches. The fuzzy approach is one of the most used, and even integrating it with other techniques forms novel tools. In this research, a fuzzy system was developed to evaluate failure modes to offer a robust tool capable of emulating how an expert in their area of expertise evaluates the risks that limit the operation of a system or process. The evaluation system is based on the Mamdani-type model, where the inference rules allow us to transfer the knowledge of the experts to a mathematical model and strengthen decision making.

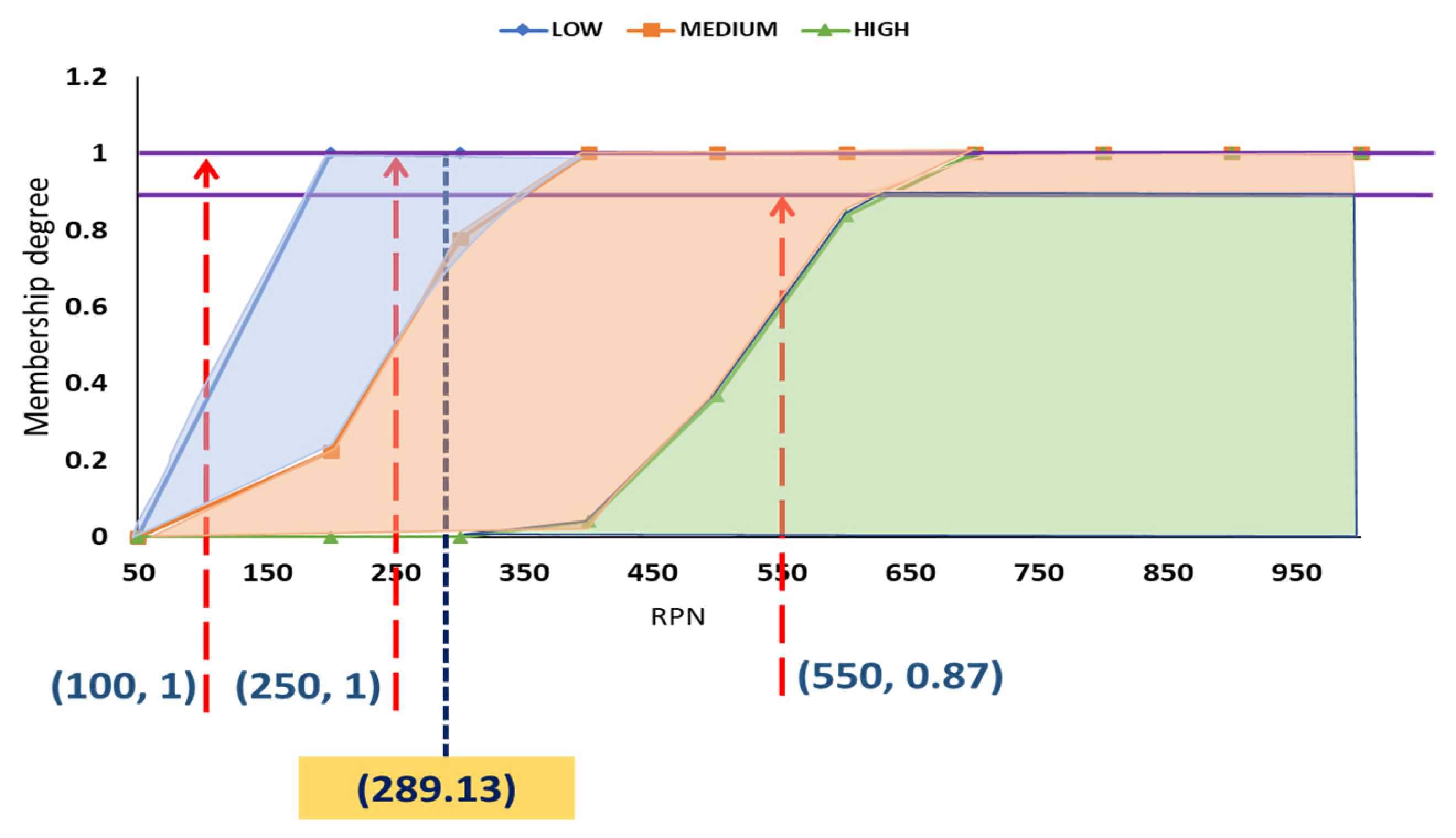
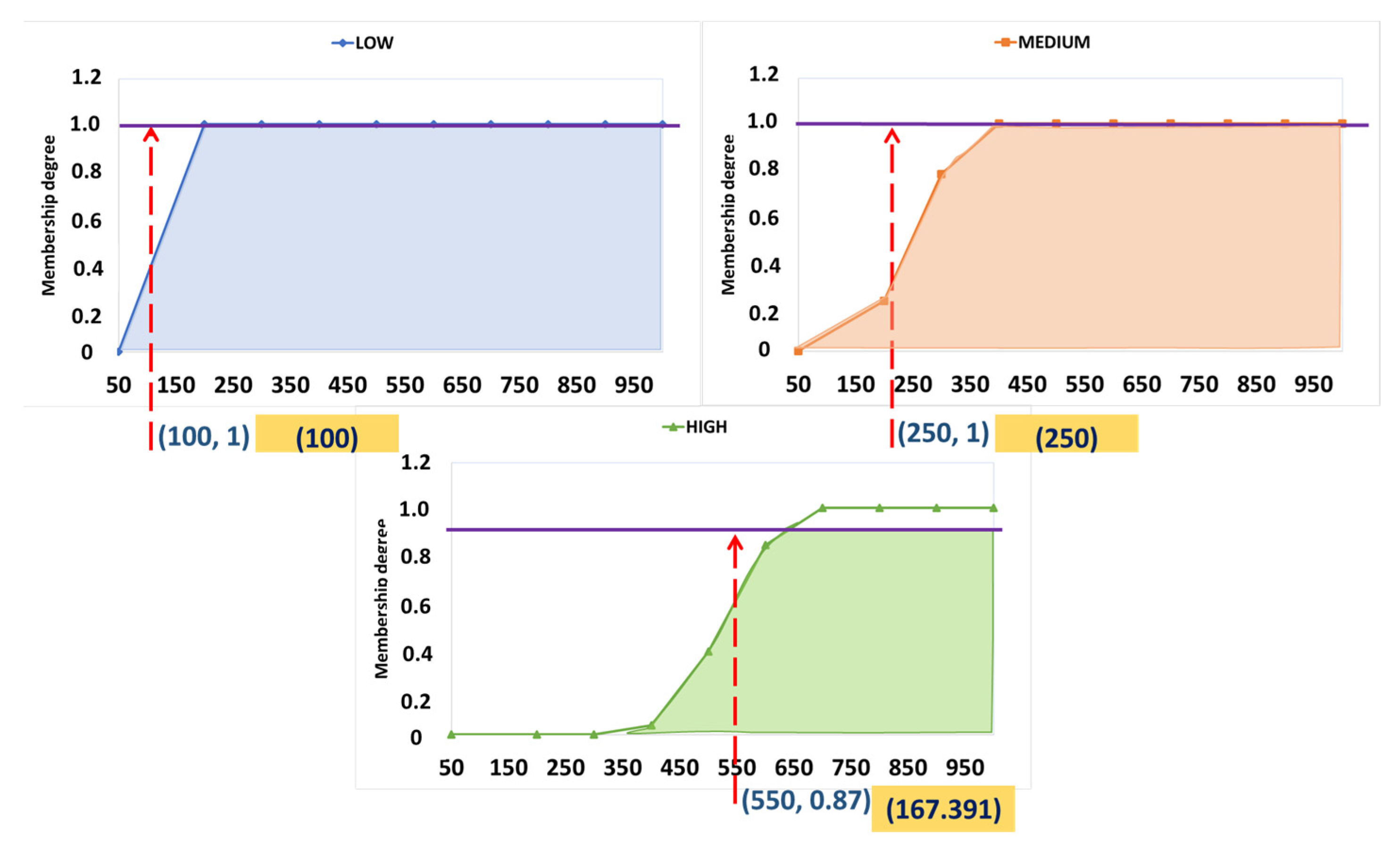
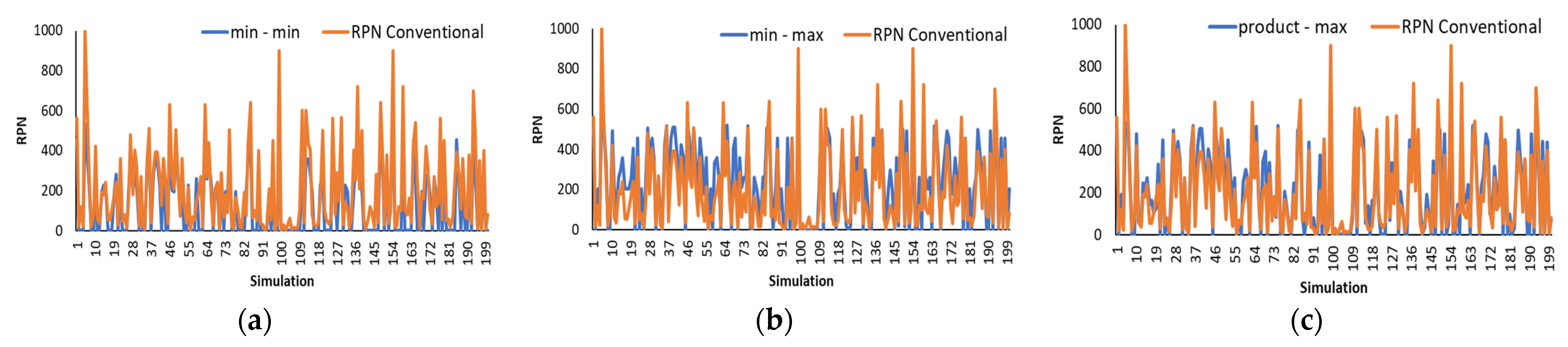
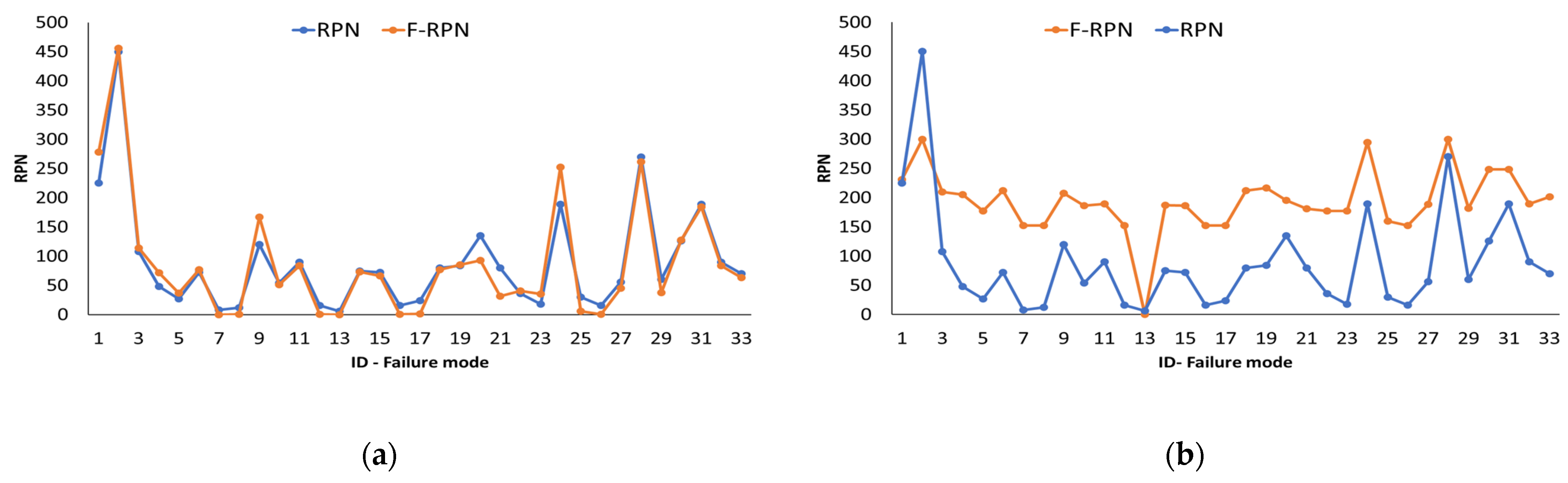
The implications of this present study are in the theoretical and practical aspects. First, a four-phase methodology is offered in the theoretical aspect, in which FMEA steps and the development of a fuzzy system are incorporated. The most relevant contribution of this research that adds value to the literature focuses on the fuzzy system, specifically in the defuzzification stage. One of the most widely used defuzzification methods in fuzzy systems is the centroid method, where the zones of each fuzzy set overlap to form a single zone. Then, the point where a vertical line divides the set into two zones with equal mass is calculated. In this study, a modification of the centroid method is proposed, where the zones that represent the fuzzy sets are treated individually, obtaining a value in each zone; the zone of the highest set is the one of most significant interest because it is the one that marks the difference between the scales of the values and that, when added together, give us the output value. This modification makes it possible to approximate the fuzzy system’s values to the conventional technique’s values. In addition, when statistically validating the results, it is confirmed that the modification allows a good approximation, as shown in the graphs of Figure 10, where it is visualized how the proposed method best approximates the data.

The second relevant aspect is the practical aspect of the proposed approach. Offering a fuzzy evaluation system with an output value that is the F-RPN metric is essential. In a conventional FMEA environment, the RPN metric is obtained directly from the algebraic product of the three factors (O, D, and S). A central feature is the ease of calculation and straightforward interpretation. However, the F-RPN metric is derived from a robust mathematical model that integrates linguistic uncertainty conditions. Trying to approximate the results of the system to the traditional metric allows for preserving a simple interpretation.

Some limitations to consider are the fact that it is necessary to incorporate group decision-making techniques into the proposed system, where a more significant number of specialists in the area participate in evaluating failure modes, incorporate methods of comparison by pairs, consensus, and test the consistency in the opinions of the experts. Future work is contemplated to determine the factors with probability distribution functions to obtain information with a stochastic basis and integrate them into the fuzzy system. In addition, in future work, it is contemplated to develop grouped fuzzy systems and integrate expert consistency tests to reduce subjectivity in evaluating failure modes.

6. Conclusions

FMEA is undoubtedly a simple but helpful technique for people involved in risk analysis. The role of experts was central in this work. The methodology was built to strengthen this technique and offer a tool that emulates how experts evaluate failure modes. In the Type-I fuzzy system, the conditions of imprecision and subjectivity were integrated to give way to a model with a mathematical basis compared to the alternative of solely qualitative analysis.

From the knowledge of the experts, the multidisciplinary team, and how they evaluate the factors, the knowledge base based on 27 fuzzy rules was formed. The sigmoid membership function was used, checking that the relationship and behavior are related to the criteria for each factor. With the defuzzification of each set individually and giving greater importance to the high set, RPN values close to the conventional technique were obtained. This aspect was achieved by modifying the centroid method, the main proposal of this research. Creating scenarios in the implication and aggregation stages and the simulation process made it possible to establish the best structure of the fuzzy system. The validation in a textile sector company allows concluding that the fuzzy evaluation system is consistent and reliable for decision making during the failure mode and effect analysis.

By determining the priorities in the knitting machinery, it is possible to focus material, human, and financial resources on the failures that cause instability in the operations of the knitting area. The most important benefit of the proposed approach is having a system that generalizes adequately, with which any expert can perform the evaluation reliably.