The Distributionally Robust Inventory Strategy of the Overconfident Retailer under Supply Uncertainty

Abstract

To factor in the retailer’s overconfidence when dealing with the inventory problem with supply uncertainty, this paper develops a distributionally robust optimization model by only considering the mean and variance of the yield rate distribution. We first show that overconfidence would prompt the retailer to order more under low-profit conditions, whereas it reduces the order quantity under high-profit conditions. The analysis results imply that the pull-to-center effect still exists when only supply uncertainty applies, and the asymmetry that the deviation is higher under low-profit conditions is proved. The performance of overconfidence is also characterized in the expected profits of both retailer and supplier. Numerical studies show that even though the retailer may suffer losses, the supplier can benefit from the retailer’s overconfidence in the low-profit case, which would positively increase the joint expected profit of the supply chain. Two extensions to the base model are also considered, including the scenario with both demand and supply uncertainties and an overconfident multi-product problem with budget constraints. This research provides tractable results to predict how the decision-maker is biased, and such insights would help the applications of de-biasing techniques in practice.

1. Introduction

Supply uncertainty, also known as yield uncertainty, is common in many industries, such as agriculture [1,2], electronics [3,4], and pharmaceuticals [5,6]. Weather changes, labor shortages, complicated production processes, changes in technology, and so forth may lead to uncertainties in the supply. Reference [2] finds that a major supermarket in China named Century Mart always shows its inefficiency in ensuring a stable supply of agricultural products due to the high uncertain yield. Another example is the Great Global Semiconductor Shortage from 2020 during the COVID-19 outbreaks. Automotive industrial sectors, operating in a just-in-time environment, suffered from the uncertain supply of chips. According to J.P. Morgan Research, global auto production slumped 26% during the first nine months of 2021. Supply uncertainty would affect ordering decisions and supply-chain coordination, which has attracted widespread attention.

Many scholars have carried out relevant research based on a traditional model where the actual supply is proportional to the ordered quantity and the multiplicative factor (i.e., the yield rate) is a random variable. Yano and Lee [7] provide a review and posit this model effectively defines and determines supply uncertainty. There are two underlying assumptions in the traditional uncertain-supply model. One is that the complete information of yield rate distribution is recognized by the decision-maker, and the other is that the decision-maker is unbiased with a precise understanding of the distribution. However, these two assumptions are not practical in real applications for the following reasons.

On the one hand, the decision-maker may face a distribution-free situation, where the accurate probability distribution of the variable is unavailable [8]. It has been well-known that obtaining accurate information on the yield rate distribution can be very challenging, especially for style goods and new products. Even if historical data are collected, it is very difficult to select the most appropriate distribution [9], and reliance on a specific distribution may perform poorly under others. On the contrary, obtaining partial information, such as the mean and variance, is more convenient. Driven by the need for handling decision-making under ambiguity (incomplete distribution information), scholars have developed a distributionally robust optimization (DRO) approach with the max–min rule. The approach derives from [10], where a closed-form solution is proposed by maximizing the expected profit of the worst-case distribution with only the mean and variance known.

On the other hand, numerous real cases and experimental studies have shown that individuals have overconfidence in their beliefs. The overconfident decision-maker tends to underestimate the actual volatility and believes their estimate is more accurate than it actually is. For example, reference [11] introduces the case of a company named Jeppesen Sanderson from America. They show that overconfident managers consistently order too many, which results in USD 800,000 in additional expenses. In the laboratory experiments, overconfidence, identified as underestimating the demand variation, is mainly responsible for driving the pull-to-center (PTC) effect [12]. People show overprecision in forecasts since they pay excessive attention to free and private information [13]. In addition, when the probabilistic information is ambiguous, reference [14] shows that the buyers also exhibit overconfidence, which has been further experimentally supported by [15].

Thus, we consider the overconfidence of retailers under ambiguity in this paper, and a DRO model is proposed to generate the optimal ordering strategy for the scenario. A two-level supply chain is considered that consists of an unreliable manufacturer and an overconfident retailer. The supply uncertainty is modeled as the actual supply being proportional to the ordered quantity, and the overconfidence is introduced as the retailer having a more precise estimate of the outcome, which is modeled by a mean-preserving but variance-reducing transformation. In the base model, we assume the market demand is known and an extension with both demand and supply uncertainties is also considered afterward. With only the mean and variance of the yield rate distribution, a DRO model is developed and the closed-form optimal ordering solution is obtained by maximizing the worst-case expected profit.

To the best of our knowledge, we are the first to study the influence of the retailer’s overconfidence under supply uncertainty when the distribution is incomplete. Our study contributes to the related fields in the following ways.

(1) The retailer’s behavior factor (overconfidence) is incorporated into the traditional inventory problem with supply uncertainty. A DRO model is developed with closed-form solutions for the optimal overconfident ordering quantity with only partial information. The numerical results show that the PTC effect still exists when only supply uncertainty applies, and the asymmetry is proved.

(2) We study the impacts of overconfidence under ambiguity rather than under risk, and we show that the supplier can benefit from the retailer’s overconfidence in the low-profit case, which would positively increase the joint expected profit of the entire supply chain.

(3) Overconfidence is introduced into the constraints of the proposed DRO model, which can make the practical condition softer, and therefore actually beneficial to alleviate the conservatism of this max–min optimization method.

(4) Extensions with both demand and supply uncertainties and an overconfident multi-product problem under supply uncertainty with budget constraints are analyzed. A formula summarizing the results is developed scattered into a framework that can include more factors, such as the correlation between the demand and supply.

The rest of the paper is organized as follows. We present a literature review in Section 2. A theoretical model is formulated that accounts for overconfidence and supply uncertainty in Section 3, and the influences on the ordering strategy and expected profit are studied in Section 4. Extensions are then presented in Section 5. Section 6 concludes the paper. Detailed proofs are provided in Appendix A.

2. Literature Review

Researchers have proposed numerous inventory models and conducted abundant studies on supply-chain management problems. We only review the relevant literature in terms of three aspects, namely, studies on supply uncertainty, inventory problems with overconfidence, and DRO approaches with their applications to inventory problems.

2.1. Supply Uncertainty

Supply uncertainty appears in many industries with many causal factors. For example, reference [1] shows that supply uncertainty arises in agriculture due to the variability of the weather and the amount of nutrients available. In the semiconductor industry, reference [2] introduces the case of Mate 7 of HUAWEI. The output of this innovative product is stochastic since the production process is very complicated with various advanced parts. Reference [16] believes that a high manufacturing lead time, expensive set-up costs, and rapid change of technology contribute to the challenging environment. Reference [17] shows that yield uncertainty led to an influenza vaccine shortage.

Supply uncertainty has received widespread attention recently for its potent effect on ordering decisions and supply-chain coordination. Some researchers develop supply-chain models considering only supply uncertainty. Reference [18] studies an inventory model with an uncertain supply and deterministic demand and obtains the formula for the optimal order policy. When the supply follows a general discrete distribution and the demand is linear with price, reference [19] determines the optimal order quantity under additive and multiplicative pricing policies. Reference [20] studies the newsvendor problem with two types of yield risks (i.e., additive and multiplicative) and shows that supply uncertainty would result in ordering more than needed.

Some other papers study the uncertainties of demand and supply at the same time. Reference [21] examine a supply chain with a manufacturer selling products to a retailer when the supply and demand are both uncertain. They find that both types of uncertainties can benefit the retailer since the manufacturer’s pricing power is weakened. Reference [22] conducts an analysis to compare the impacts of supply uncertainty and demand uncertainty. They show that supply uncertainty is more costly when uncertainty-reduction efforts are absent and the financial consequences of shortages are significant. Reference [23] applies the joint lot-sizing and pricing model to the real agricultural sector where the supply is uncertain and the demand is sensitive to the price. They use data from the California almond industry to show the model’s effectiveness. Dual- or multiple-sourcing problems have been one of the hotspots since supply diversification is beneficial to mitigating the risks caused by supply uncertainty. Reference [24] shows that dual sourcing can reduce the inefficiency caused by a random supply in the presence of end-market competition and thus, bring value to duopolists. Reference [25] finds that dual sourcing is always regarded as a risk-management tool under both demand and supply uncertainties. Reference [26] extends the study to the case where the distributions of demand and supply are both ambiguous. They develop a DRO method to seek the optimal order decisions with only the mean and variance of the distributions.

2.2. Inventory Problems with Overconfidence

Overconfidence is one of the most consistent, powerful, and widespread cognitive biases [27] that has been introduced to operations management recently, just like risk preferences [28] and loss-averse preferences [29]. We refer the readers to [30] for a comprehensive review about overconfidence. They distinguish three types of overconfidence: overestimation, overplacement, and overprecision. Among them, overprecision is the most robust and in this paper, the retailer’s overconfident bias is defined as overprecision, which means the yield rate distribution has a smaller variance than reality.

Overconfidence has been explored widely in fields from psychology to behavioral finance. However, the study of overconfidence in operations and supply-chain management is still at an early stage. To our knowledge, reference [12] is the first to experimentally provide strong evidence that overconfidence is mainly responsible for the PTC effect in the newsvendor problem, which traces back to [31]. They show that the order quantity in the experiments systematically deviates from the optimum. Reference [32] models the overconfident newsvendor problem and finds that the overconfident order quantity is linear with the overconfidence level and the cost of overprecision is convex. Reference [33] extends the study to the competing case and shows that an overconfident newsvendor orders more in a competitive environment than a non-competitive one. More interestingly, competition is beneficial for high-margin products.

The influences of overconfidence on the decision and performance of supply chains have also been studied. Some studies show the negative consequences of overconfidence. Reference [34] investigates a two-echelon supply chain with a supplier and an overconfident manufacturer with an uncertain yield. Overall, they show that overconfidence hurts the performance of both companies. Reference [35] concludes that consumers’ overconfidence negatively influences the product demand and profit in a dual-channel supply chain. Some studies explore the positive side of overconfidence. Reference [36] studies decision-making in a distribution channel. He shows that the profit is decreased when the overconfident supplier and overconfident retailer make a centralized decision, and if they make independent decisions, they can achieve higher profits. In a duopolist supply chain, reference [37] shows that overconfidence does not necessarily damage the supply chain’s performance, no matter whether the rational retailer is aware of the other retailer’s overconfidence. Reference [38] finds that an e-tailer’s overconfidence can promote the financial platform’s profit in a capital-constrained supply chain. Reference [39] studies the allocation problem of inventory responsibilities and shows that each party can benefit from the other’s overconfidence.

Scholars have also studied the combined influence of overconfidence and other behaviors. For example, reference [40] combines overconfidence and optimism into a price-setting newsvendor problem, and they show that the newsvendor’s decision is influenced by overconfidence non-monotonically. Reference [41] studies the inventory problem in a supply chain consisting of a risk-averse supplier and an overconfident manufacturer.

2.3. Distributionally Robust Optimization and Its Application

The distributionally robust inventory problem, also known as the inventory problem under ambiguity, has gained tremendous popularity. The underlying assumption that the supply and demand distributions are known may not hold in practice. Reference [9] points out that selecting the most appropriate distribution is too challenging even with historical data. Moreover, in a fragile market experiencing devastating impacts, it is not easy to predict the future accurately.

To deal with these issues, researchers have developed a DRO method, where the demand-distribution information is not required to be known as in stochastic programming and simultaneously the heavy conservatism of robust optimization is simultaneously avoided [42]. The DRO method dates back to [10], who first build a model to obtain the optimal order quantity for the newsvendor problem under ambiguity. The closed-form solution is obtained by maximizing the worst-case expected profit satisfying the known moment constraints. It was not until after [43] presented a more concise proof that Scarf’s ordering rule was studied and applied more widely.

On the basis of their work, the application of DRO has witnessed explosive growth, including the case where the demand is related to inventory level [44], the constrained-demand case [45], the shortage-penalty case [46], the non-linear inventory cost case [47], the multi-stage case [48], and the multi-product case [26]. Some studies introduce more factors to the DRO of inventory problems. For example, Reference [49] considers the advertising effect, Reference [50] studies the inventory problem under carbon-emission regulations, and Reference [51] investigates the models with dual sourcing.

In [10], the objective is to maximize the expected profit under the worst-case distribution. This criterion is usually referred to as max–min, and the optimal distribution is usually a two-point or three-point distribution. Some argue the conservatism of this rule and introduce other decision criteria [52]. Rreferences [53,54] apply min–max regret, minimizing the maximum regret to control the level of sub-optimality, to the stochastic inventory management. Reference [55] minimizes the worst-case relative regret, the ratio between the objective value based on limited information and the hindsight optimal objective value. Reference [56] introduces the information of semi-variance to capture information on the demand distribution’s asymmetry. In addition, others modify the objective function by introducing risk or loss factors. Reference [57] provides a closed-form solution to the risk-averse and ambiguity-averse newsvendor problem where the profit’s standard deviation measures the risk. Reference [58] maximizes the loss-averse newsvendor’s worst-case expected utility.

2.4. Rationale for Our Model

For each stream of the related research, we contribute to the existing work in the following ways. In the previous studies on supply uncertainty, there are two underlying assumptions: the decision-maker is unbiased and has complete information about yield rate distribution. Nevertheless, they are both compromised in practical applications. We combine overconfidence and ambiguity into the inventory problem with supply uncertainty to obtain the optimal robust ordering strategy with only the mean and variance of the yield distribution. The model is chosen for its tractability, and the results are clear, which helps to obtain managerial insights.

For the second stream of studies on inventory problems with overconfidence, the impacts of overconfidence under ambiguity rather than under risk are studied. We show that overconfidence can positively increase the joint expected profit of the entire supply chain since the supplier can benefit from the retailer’s overconfidence in the low-profit case.

For the third stream of studies on the DRO method, overconfidence is introduced into the constraints of the proposed DRO model, which can make the practical condition softer and thus actually beneficial to alleviate the conservatism of this max–min optimization method.

3. Model Description

In this section, a DRO approach is developed to obtain an optimal ordering strategy for the overconfident retailer. The supply uncertainty is considered in the base model, and, instead of assuming full knowledge of the yield rate distribution, only the first two moments are known.

3.1. The Base Model

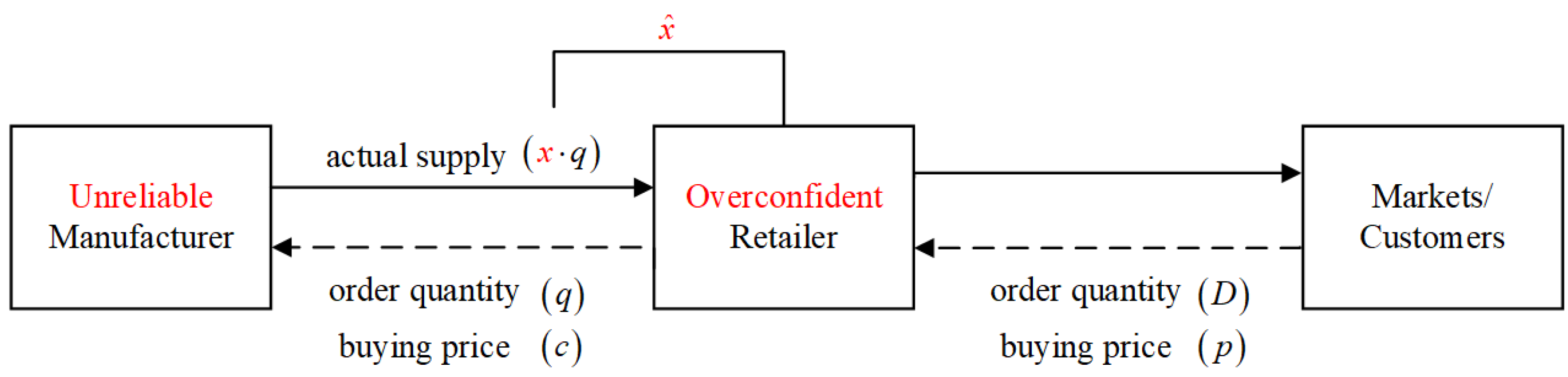
Consider a two-level supply chain that is composed of an unreliable manufacturer and an overconfident retailer (as shown in Figure 1). Before the selling season of a product, the retailer places an order from the manufacturer, and subsequently, the manufacturer starts production. Specifically, the retailer makes an order of q units of the product at a unit cost c and sells to customers at a higher price p ($p>c$). The shortage penalty cost and salvage value are normalized to be zero. Moreover, the market demand is assumed to be known as D by the retailer here, and the stochastic demand case is extended in Section 5.1.

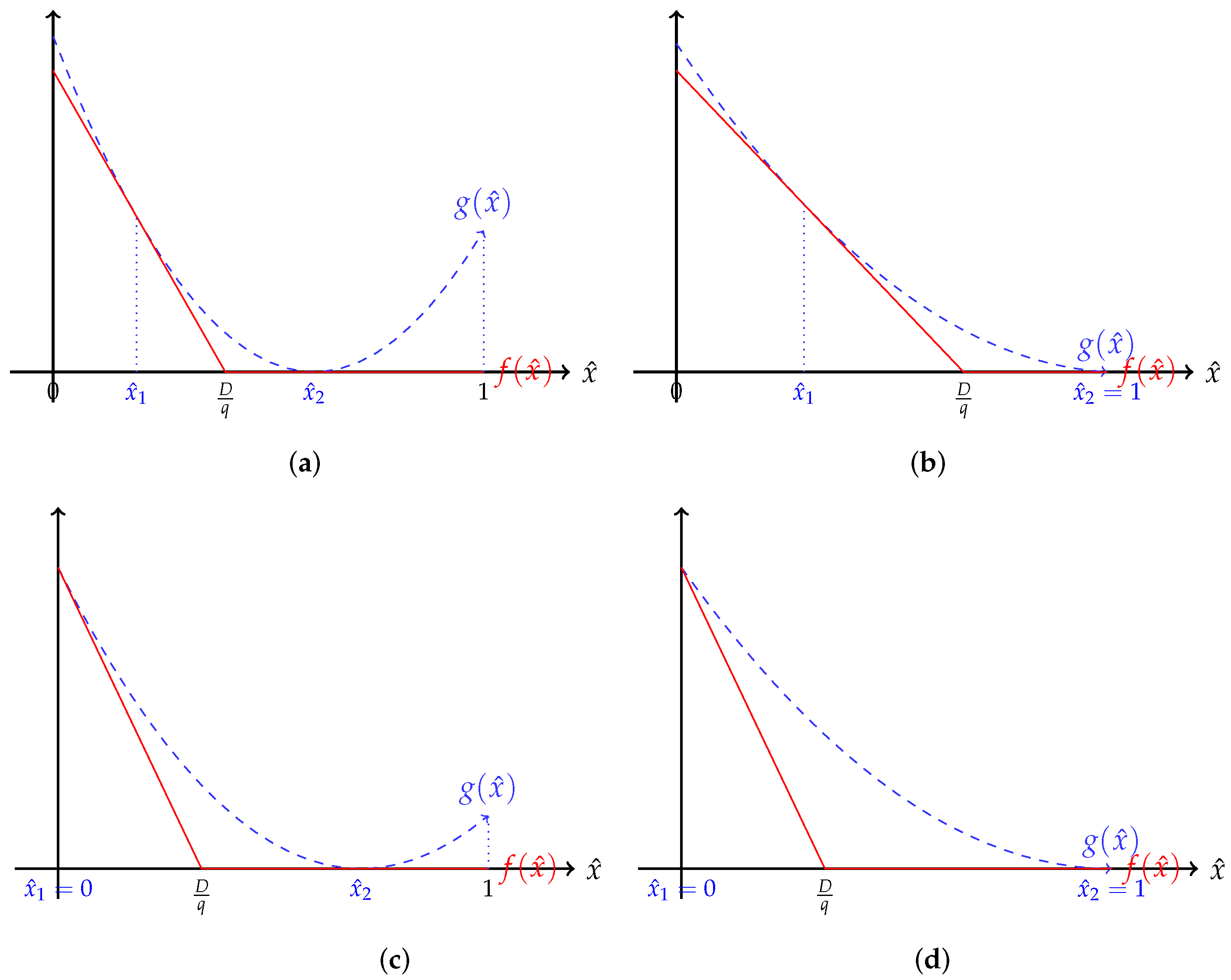
On the supply side, the yield of the manufacturer is assumed to be uncertain due to a long production lead time, complicated production process, or high-quality requirements. The quantity the retailer receives may not necessarily equal the quantity ordered. According to [7], we model the supply uncertainty with a proportional random rule, and the quantity actually received is denoted as $x·q$, where the yield rate x is a random variable following a general cumulative distribution $\pi$ with support [0, 1], mean $\mu$, and variance ${\sigma }^2$ ($0\le \mu \le 1,0\le \sigma \le 1$). The profit for the retailer is thus calculated as $\mathsf{\Pi }(x,q):=p·min\{D,xq\}-c·xq$. Note here that the inequation $q\ge D$ holds, which implies that the retailer should place an order quantity higher than the known market demand to protect against defective items.

Uncertainty encourages overconfidence in the supply chain, as [14,15] point out. The retailer is always overconfident and underestimates the actual extent of the problem, which means the yield rate x is expected to be more precise than it actually is. Based on [12], we model the yield rate considered by the overconfident retailer, $\widehat{x}$, by a mean-preserving but variance-reducing transformation of the true yield rate x, mixing the mean of the distribution $\mu$.

$$\widehat{x}=\alpha x+(1-\alpha )\mu$$

(1)

$\alpha$ ($0\le \alpha \le 1$) is recognized as the overconfidence parameter. From (1), the variance of $\widehat{x}$ is less than or equal to that of x, i.e., $Var\left(\widehat{x}\right)={\alpha }^2{\sigma }^2\le {\sigma }^2$, which means the variability of the yield rate in the belief of the overconfident retailer is lower than the reality. In addition, we show that $0\le \widehat{x}\le 1$, since x and $\mu$ are both on the definite interval [0, 1].

We denote the overconfidence level as $\gamma =1-\alpha$ for convenience. The smaller $\alpha$, the higher the overconfidence level $\gamma$. In particular, $\gamma =0$ ($\alpha =1$) shows the retailer is an unbiased decision-maker, and $\gamma =1$ ($\alpha =0$) represents an infinitely overconfident retailer. Undoubtedly, the overconfidence level $\gamma$ (or overconfidence parameter $\alpha$) is independent of the manufacturer’s random yield rate x.

For a risk-neutral retailer, the objective is to maximize the expected profit, and thus, the overconfident inventory model under supply uncertainty is formulated as follows.

$$\begin{array}{cc}\hfill \underset{q\ge D}{max}& \mathbb{E}\left[\mathsf{\Pi }(\widehat{x},q)\right]\hfill \end{array}$$

(2)

With $min\{D,\widehat{x}q\}=D-{(D-\widehat{x}q)}^{+}$ and ${(·)}^{+}=max\{·,0\}$, problem (2) is equivalent to that stated as (3) in the following

$$\begin{array}{cc}\hfill \underset{q\ge D}{max}& pD-c\mu q-p·\mathbb{E}{(D-\widehat{x}q)}^{+}\hfill \end{array}$$

(3)

Instead of assuming full knowledge of the yield rate distribution, the retailer only acquires the mean and variance, which prompts the use of a DRO method. The DRO method seeks to maximize the expected profit against the worst case over an ambiguity set, which consists of all distributions satisfying the known moment constraints.

Let $\mathsf{\Omega }(\mu ,\sigma )$ denote such an ambiguity set consisting of all distributions with mean $\mu$ and variance ${\sigma }^2$, which is modified as $\mathsf{\Omega }(\mu ,\alpha \sigma )$ in the overconfident case. The robust counterpart of problem (3) can then be formulated as a worst-case expected-profit-maximization model:

$$\begin{array}{ccc}\hfill \underset{q\ge D}{max}& \hfill \underset{\pi \in \mathsf{\Omega }(\mu ,\alpha \sigma )}{min}& pD-c\mu q-p·\mathbb{E}{(D-\widehat{x}q)}^{+}\hfill \end{array}$$

(4)

The max–min model (4) is the main problem where we incorporate the bias of overconfidence into the inventory problem under supply uncertainty in the framework of DRO. We solve this problem in two steps. First, the inner problem (5) is a minimization problem of the decision variable $\pi$, a distribution with incomplete information over the ambiguity set $\mathsf{\Omega }(\mu ,\alpha \sigma )$.

$$\begin{array}{cc}\hfill \underset{\pi \in \mathsf{\Omega }(\mu ,\alpha \sigma )}{min}& pD-c\mu q-p·\mathbb{E}{(D-\widehat{x}q)}^{+}\hfill \end{array}$$

(5)

Second, the outer maximization problem is univariate about q.

3.2. Inner Problem

To obtain the optimal solution to the inner problem (5), the first and most important step is to solve the maximization problem (6). The following Lemma 1 provides detailed insights.

$$\begin{array}{cc}\hfill \underset{\pi \in \mathsf{\Omega }(\mu ,\alpha \sigma )}{max}& \mathbb{E}{(D-\widehat{x}q)}^{+}\hfill \end{array}$$

(6)

Lemma 1. 

Define $H_1=\frac{1}{2}\left[\sqrt{{(D-\mu q)}^2+{\alpha }^2{\sigma }^2{q}^2}+(D-\mu q)\right]$, $H_2=D-\mu q-\frac{(D-q){\alpha }^2{\sigma }^2}{{(1-\mu )}^2+{\alpha }^2{\sigma }^2}$, $H_3=\frac{{\alpha }^2{\sigma }^2}{{\mu }^2+{\alpha }^2{\sigma }^2}D$. For any distribution of π with mean μ and variance ${\alpha }^2{\sigma }^2$(μ, σ, α ∈ [0, 1]), the upper bound for $\mathbb{E}{(D-\widehat{x}q)}^{+}$ is determined as

$$sup\mathbb{E}{(D-\widehat{x}q)}^{+}=H\left(q\right)=\left\{\begin{array}{cc}{H}_2\hfill & D\le q\le \frac{2D(1-\mu )}{1-{\mu }^2-{\alpha }^2{\sigma }^2}\hfill \\ H_1\hfill & \frac{2D(1-\mu )}{1-{\mu }^2-{\alpha }^2{\sigma }^2}<q\le \frac{2D\mu }{{\mu }^2+{\alpha }^2{\sigma }^2}\hfill \\ H_3\hfill & q>\frac{2D\mu }{{\mu }^2+{\alpha }^2{\sigma }^2}\hfill \end{array}\right.$$

(7)

Proof. 

The proof of Lemma 1 is based on duality theory, and we delegate the detailed proof to Appendix A.    □

In light of Lemma 1, the optimal objective value to problem (5), the worst-case expected profit, $\mathsf{\Pi }\left(q\right)$, is described as

$$\mathsf{\Pi }\left(q\right)=pD-c\mu q-p·H\left(q\right)$$

(8)

We further that show $\mathsf{\Pi }\left(q\right)$ is a continuously differentiable concave function in q. The proof can be seen in Appendix A.

3.3. Outer Problem

Since $\mathsf{\Pi }\left(q\right)$ is concave, the first-order condition offers the maximum. Before Theorem 1, which is provided with specific closed-form expressions for the optimal order quantity, we introduce a significant condition in the following.

Assumption 1. 

The profit margin of product a, defined as $\frac{p-c}{p}$, overconfidence parameter α, and yield rate distribution parameters satisfy the following:

$$a\ge \frac{1}{\mu }\frac{{\alpha }^2{\sigma }^2}{{(1-\mu )}^2+{\alpha }^2{\sigma }^2}$$

(9)

Regarding condition (9), which is denoted as the practical condition for convenience, it seems intuitive that the profit margin must be greater than a specific value. More insights are clear in the context of Theorem 1.

Theorem 1. 

For the overconfident inventory problem under supply uncertainty, the robust optimal order quantity, $q^{*}$, is given by

$$q^{*}=\frac{D\mu }{{\mu }^2+{\alpha }^2{\sigma }^2}[1+\frac{(2a-1)\alpha \sigma }{\sqrt{4a(1-a){\mu }^2+{\alpha }^2{\sigma }^2}}]$$

(10)

if and only if the practical condition holds. Otherwise, $q^{*}=D$.

Proof. 

We delegate the detailed proof of Theorem 1 to Appendix A.3.    □

Theorem 1 presents the explicit closed-form results for the overconfident robust optimal ordering strategy under uncertain supply. When the practical condition holds, the optimal order quantity is defined as Equation (10). Otherwise, the retailer only places an order of known demand, D. Some straightforward claims below directly follow the results. Here we mainly discuss the former situation (i.e., the practical condition holds) since it is intuitive for the latter.

(a)

The results in Theorem 1 incorporate the notion of overconfidence into the inventory problem under supply uncertainty with the DRO method. When the retailer is unbiased ($\gamma =0$ or $\alpha =1$), our result is reduced to $\frac{D\mu }{{\mu }^2+{\sigma }^2}\left[1+\frac{(2a-1)\sigma }{\sqrt{4a(1-a){\mu }^2+{\sigma }^2}}\right]$, and when the retailer is infinitely overconfident ($\gamma =1$ or $\alpha =0$), the optimal order quantity is $\frac{D}{\mu }$.

(b)

The relationship between the optimal order quantity and the overconfidence level is complicated. At the intuitive level, it is associated with profit margin $a=\frac{p-c}{p}$, also known as the critical fractile in the classical newsvendor model. We define a product as a high-profit product if $a\ge 0.5$ and as a low-profit one if $a<0.5$. See Section 4.1 for more analysis about the optimal order quantity when the retailer faces different products.

(c)

When the practical condition holds, the overconfident retailer stocks an order quantity higher than D. Compared to the unbiased case where $a\ge \frac{1}{\mu }\frac{{\sigma }^2}{{(1-\mu )}^2+{\sigma }^2}$, the practical condition is softer here. Specifically, our strategy is less conservative, intuitively due to the influence of the additional overconfidence. We will analyze this more in Section 4.3.

The results include overconfidence in the supply-uncertain inventory problem, and this bias arises from different influences. In the following section, we intensively study the managerial insights about how overconfidence and supply uncertainty affect the ordering strategy and expected profit.

4. Managerial Insight

With the exact solutions in Theorem 1, we further explore how overconfidence and supply uncertainty affect the retailer’s decision-making and expected profit in general and the performance of the DRO method. Unless otherwise specified, we focus on the case when the practical condition holds since the managerial interpretation is intuitive if the condition is unsatisfied. Thus, the retailer only places an order of the constant D. For ease of description, we rewrite the condition as shown in (11).

$$\alpha \le {\alpha }_0=\sqrt{\frac{a\mu }{1-a\mu }}\frac{1-\mu }{\sigma }$$

(11)

From (11), along with $\gamma =1-\alpha$, we show that the retailer’s overconfidence level $\gamma$ is preferably bigger than $1-{\alpha }_0$. The critical value ${\alpha }_0$ is only associated with the profit margin a and the yield rate distribution parameters $\mu$ and $\sigma$. Once the values of these parameters are given or calculated using historical data, we can determine whether the condition is true. The scope of the condition’s impact is clear, and then we offer managerial insights.

4.1. Optimal Order Quantity $q^{*}$ and Overconfidence Level $\gamma$

It is worth reiterating that the retailer needs to be more confident, as if the yield rate is more precise than the reality. Underestimating the volatility of the yield rate induces the retailer to make a non-optimal decision systematically. As shown in what follows, we discuss the influence of the retailer’s overconfidence on the optimal order quantity.

4.1.1. Low-Profit Condition

Proposition 1. 

When the product is low-profit, the optimal order quantity $q^{*}$ monotonically increases in the overconfidence level γ.

The detailed proof is omitted here, for it is easy to show that the first-order partial derivative of a function $q^{*}$ in Equation (10) with respect to $\alpha$ is negative. Thus, $q^{*}$ is monotonically increasing in the overconfidence level $\gamma$, since $\gamma =1-\alpha$.

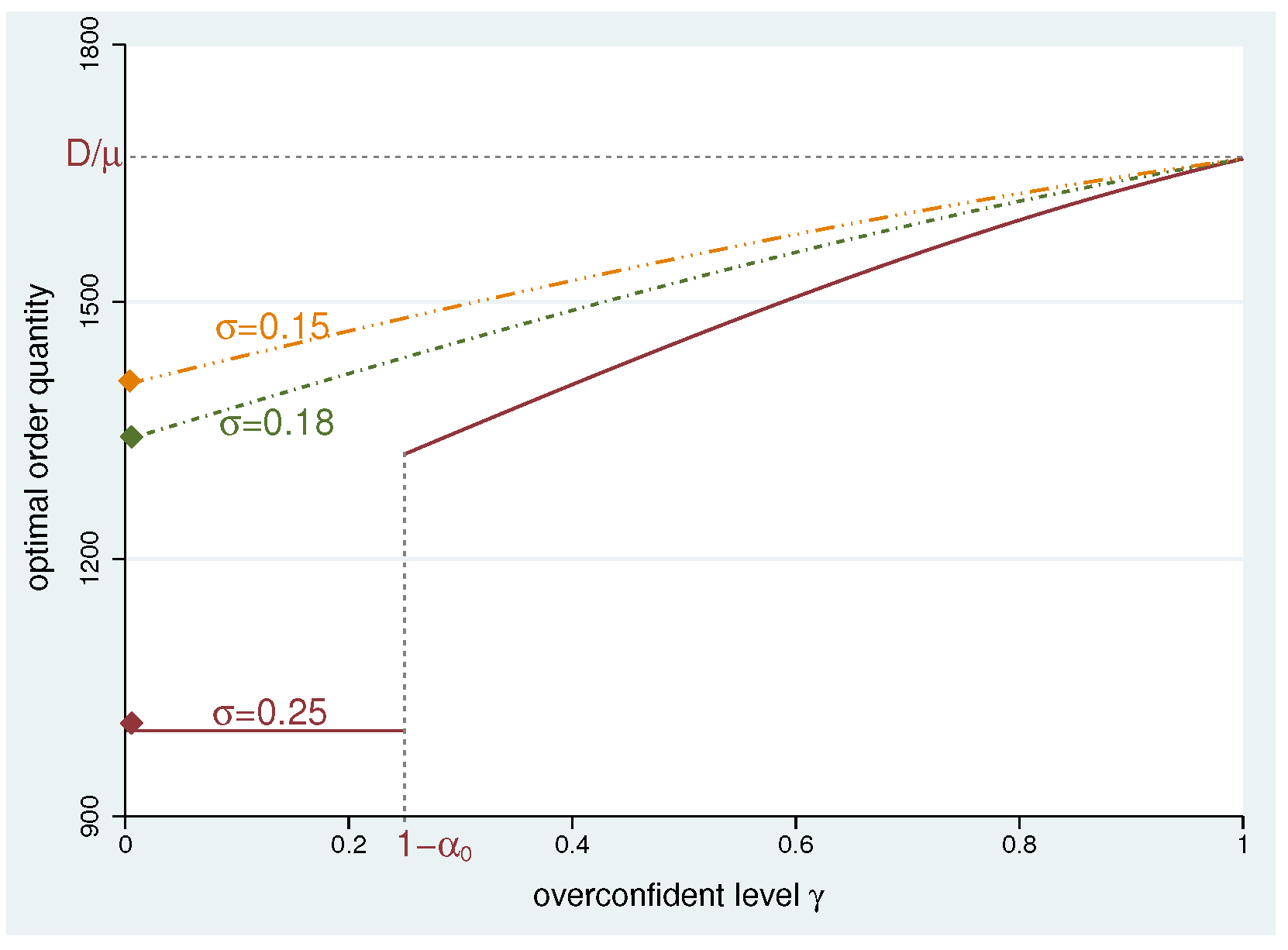
To make Proposition 1 more intuitive, we provide a graphical representation (Figure 2) to show the influence of overconfidence on the optimal order quantity. Figure 2 illustrates the low-profit case, where the profit margin a is 0.3. In the figure, we set the value of $\mu$ to be 0.6, the market demand D to be 1000, and $\sigma$ to be 0.15, 0.18, and 0.25 for three scenarios. Note that we must satisfy the constraint $\mu \ge {\mu }^2+{\sigma }^2$, since $0\le x\le 1$, in the parameter selections.

As shown in Figure 2, the line for $\sigma =0.25$ is piecewise, consisting of two parts. The horizontal line corresponds to the situation when the practical condition (i.e., $\gamma \ge 1-{\alpha }_0$) is unsatisfied and the retailer only orders $D=1000$ units. The other part of the curve with an upward slope represents that the optimal order quantity is positively related to the overconfidence level when the practical condition holds, implying that the retailer’s overconfidence increases the order quantity. The lines for $\sigma =0.18$ and $\sigma =0.15$ are not segmented since the practical condition holds in the whole domain, and the slope is upward, which means the relationship between the optimal order quantity and the overconfidence level is positive.

Note that the point on the vertical axis, identified as the unbiased case ($\gamma =0$), is the optimal order quantity by an unbiased retailer. It is also recognized as the theoretically optimal solution. We show that this optimum is smaller than the result of decisions made by an overconfident retailer under low-profit conditions. Specifically,

$$q^{*}\left(0\right)=\frac{D\mu }{{\mu }^2+{\sigma }^2}\left[1+\frac{2a-1}{\sqrt{1+\frac{4a(1-a){\mu }^2}{{\sigma }^2}}}\right]<q^{*}\left(\gamma \right)$$

(12)

Regarding this result, it implies that overconfidence induces the retailer to order more than the unbiased optimum. Moreover, as the retailer shows a higher overconfidence, the optimality gap is widening.

The other extreme ($\gamma =1$) represents the situation of infinite overconfidence. The retailer is “extremely” confident that the yield rate necessarily equals $\mu$, and therefore “extremely” confidently places an order of $\frac{D}{\mu }$ units. For description convenience, we define $\frac{D}{\mu }$ as the average-supply order quantity (ASOQ). It is apparent that the optimal order quantity under low-profit conditions is smaller than ASOQ, but the deviation becomes smaller as the retailer’s overconfidence level increases.

4.1.2. High-Profit Condition

Proposition 2. 

Under high-profit conditions, $q^{*}$ is affected by the retailer’s overconfidence in the following ways:

(i) 

If ${\alpha }_m<min\{{\alpha }_0,1\}$, $q^{*}$ is concave in γ. More specifically, $q^{*}$ is increasing in the range [$1-{\alpha }_0$, $1-{\alpha }_m$ ] or [$0, 1-{\alpha }_m$] and decreasing in [$1-{\alpha }_m, 1$];

(ii) 

Otherwise, $q^{*}$ is monotonically decreasing in γ.

${\alpha }_m$ is defined as the following Equation (13):

$${\alpha }_m=\frac{\mu }{\sigma }\sqrt{2a(a-1)+\sqrt{a(1-a)}}$$

(13)

Proof. 

Please see the proof in Appendix A.    □

Under high-profit conditions, the insight is complicated, for overconfidence is not monotonically affecting the order quantity. ${\alpha }_m$ in Equation (13) is the extreme point of curve $q^{*}\left(\alpha \right)$. Recall that we defined $\alpha$ on the definite interval [0, 1], and therefore we should decide whether the point ${\alpha }_m$ lies in the interval. If ${\alpha }_m$ lies in the interval, we show that $q^{*}$ is concave in $\alpha$ (or $\gamma$); otherwise, $q^{*}$ is monotonically decreasing in $\gamma$. 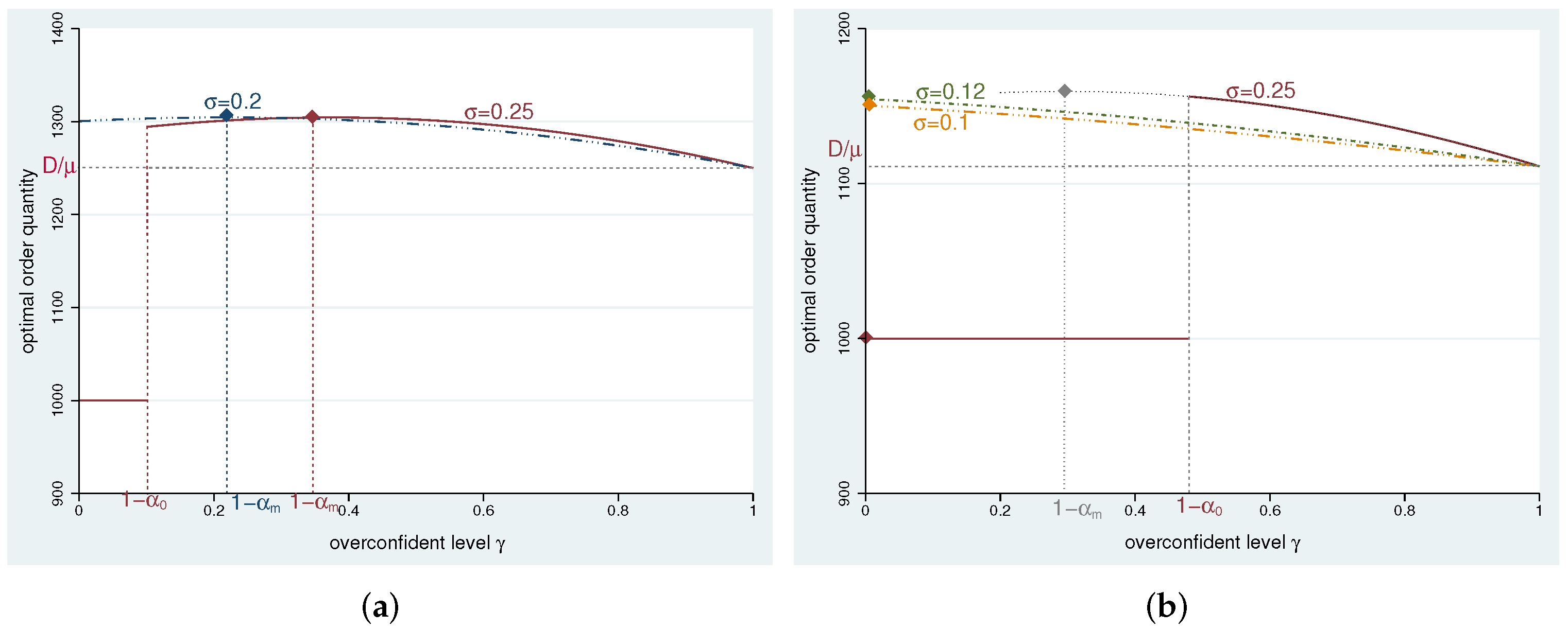We provide Figure 3 to characterize the performance of overconfidence in different scenarios. The profit margin a is set as 0.7 to indicate the product is high-profit here.

In Figure 3a, $\mu =0.8$, $D=1000$. When $\sigma =0.25$, condition ${\alpha }_m<min\{{\alpha }_0,1\}$ is satisfied. As described in Proposition 2, the optimal order quantity is concave in the overconfidence level when the practical condition holds ($\gamma \ge 1-{\alpha }_0$), and the maximizer is achieved at $\gamma =1-{\alpha }_m$. Namely, as the overconfidence level increases, the optimal order quantity by the overconfident retailer increases in the interval [$1-{\alpha }_0$, $1-{\alpha }_m$] and decreases in [$1-{\alpha }_m$, 1]. When $\sigma =0.2$, we show ${\alpha }_0\ge 1$, implying that the practical condition is established in the entire domain, and therefore, the optimal order quantity increases in the interval [0, $1-{\alpha }_m$].

In Figure 3b, the mean of the yield rate distribution $\mu$ is increased to 0.9, and then inequality ${\alpha }_m<min\{{\alpha }_0,1\}$ is invalid. We let $\sigma$ be 0.25, 0.12, and 0.1 for three scenarios. Just as presented in Figure 2, the line for $\sigma =0.25$ consists of two parts: one part is that the practical condition is not satisfied in [0, $1-{\alpha }_0$], and the retailer’s optimal order quantity is equal to the known demand; the other part is that when the practical condition holds, $q^{*}$ is strictly monotonically decreasing in $\gamma$. The curves for $\sigma =0.12$ and $\sigma =0.1$ are continuously downward, which indicates the practical condition is always established, and as the overconfidence level increases, the optimal order quantity monotonically decreases.

We also pay attention to the intersections of the curves and the ordinate axis, representing the unbiased case under high-profit conditions. In Figure 3b, the curves for $\sigma =0.12$ and $\sigma =0.1$ (satisfying $min\{{\alpha }_0,{\alpha }_m\}>1$) are continuous and monotonically decreasing, which means the order quantity by an unbiased retailer is greater than the optimum by an overconfident one, namely, $q^{*}\left(0\right)>q^{*}\left(\gamma \right)$. The overconfident retailer orders fewer items than the unbiased, and the higher the overconfidence level, the greater the deviation. Note the exception that ${\alpha }_0<1$, implying that the practical condition is not satisfied at $\gamma =0$, and the result is conservative, as it equals the demand quantity.

Regarding ASOQ in the high-profit case, we show $q^{*}>\frac{D}{\mu }$ when ${\alpha }_m>{\alpha }_0$ or ${\alpha }_m>1$. This means that the optimal order quantity by the overconfident retailer is greater than the ASOQ, and as the overconfidence level increases, the deviation decreases. When ${\alpha }_m<min\{{\alpha }_0,1\}$, $q^{*}$ is concave in $\gamma$, and we cannot ensure $q^{*}>\frac{D}{\mu }$ in the whole feasible region. However, we are sure that when the overconfidence level is high enough to satisfy $\gamma \ge 1-{\alpha }_m$, the optimal order quantity will move down closer to ASOQ.

4.1.3. Summary on Optimal Ordering Strategy

The relationship between the optimal order quantity and the overconfidence level under different conditions, described in Propositions 1 and 2, can be summarized in

Table 1. The relationship between optimal order quantity and overconfidence level.

Product Attribute	Parameter Range	Relationship
low-profit ($0\le a\le \frac{1}{2}$)	-	monotonically increasing
high-profit ($\frac{1}{2}<a<1$) 1	${\alpha }_m<min\{{\alpha }_0,1\}$	concave function
	otherwise	monotonically decreasing

¹ Note that the practical condition is not satisfied in $\gamma \in [0,1-{\alpha }_0]$ if ${\alpha }_o\le 1$.

. The table shows that a higher overconfidence level prompts the retailer to order more products under low-profit conditions. In contrast, overconfidence is generally inclined to decrease the order quantity under high-profit conditions.

In the discussions above, ${\alpha }_0$ and ${\alpha }_m$, defined as Equations (11) and (13), respectively, are very significant to the analysis. Corollary 1 describes how they relate to the profit margin a and yield rate distribution parameters.

Corollary 1. 

With regard to ${\alpha }_0$ and ${\alpha }_m$, the following holds:

(1) 

${\alpha }_0$ is increasing in a, decreasing in σ, and concave in μ.

(2) 

When $a>0.5$, ${\alpha }_m$ is an increasing function of $\frac{\mu }{\sigma }$ and a concave function of a.

The proof is based on the first-order partial derivative; the details are omitted here. We first show $\frac{\partial {\alpha }_0}{\partial a}>0$, and therefore, it is more likely for the high-profit product than the low-profit product that ${\alpha }_0>1$, which means the practical condition holds in the entire domain. We also show $\frac{\partial {\alpha }_0}{\partial \sigma }<0$ and the first-order condition of ${\alpha }_0$ with respect to $\mu$ offers the maximization point $\mu =\frac{3-\sqrt{9-8a}}{4}$. As a result, if the manufacturer’s supply is relatively stable and the mean yield rate is close to $\frac{3-\sqrt{9-8a}}{4}$, ${\alpha }_0>1$ would be satisfied.

Regarding ${\alpha }_m$, it is increasing in $\frac{\mu }{\sigma }$, and the first-order condition with respect to a offers the maximization point $a=\frac{2+\sqrt{3}}{4}\approx 0.93$. We show that the smaller the coefficient of variation (i.e., the yield rate is high and stable), the closer to 0.93 for the profit margin a, and the higher the potential for ${\alpha }_m>1$. The relationship between the optimal order quantity and the overconfidence level is likely to be monotonically decreasing under high-profit conditions.

4.1.4. Pull-to-Center Effect

In the classic newsvendor problem, reference [59] presents the well-known result, a critical fractile to the stochastic demand distribution. Although this solution has a clear structure and is easy to calculate, experimental studies have shown that decision-makers systematically make non-optimal decisions (e.g., [60,61]). Specifically, subjects place an order between the mean of the demand distribution and the expected profit-maximizing quantity, which means they over-order under low-profit conditions and under-order under high-profit conditions. This behavior is called the PTC effect.

Some explanations for the PTC effect have existed in the literature, such as the anchoring effect [31], psychological costs [62], or impulse balance [63]. References [12,64] show that overconfidence can account for the PTC effect under stochastic demand with known and unknown demand distributions, respectively. In this paper, we seek to explore whether overconfidence accounts for the PTC behavior only under an uncertain supply.

Corollary 2. 

Overconfidence can account for the order bias, the PTC effect, when only supply uncertainty applies.

As the previous lines already suggest, under low-profit conditions, the optimal order quantity by the overconfident retailer is higher than the unbiased one (theoretical optimum) and lower than ASOQ. Under high-profit conditions, the overconfident order quantity is generally lower than the unbiased optimum and higher than ASOQ. The overconfident optimum deviates from the unbiased optimum and moves closer to ASOQ under both conditions as the overconfidence level increases. We, therefore, have every reason to believe that the uncertain supply model with overconfidence shows the existence of the PTC effect when only supply uncertainty applies.

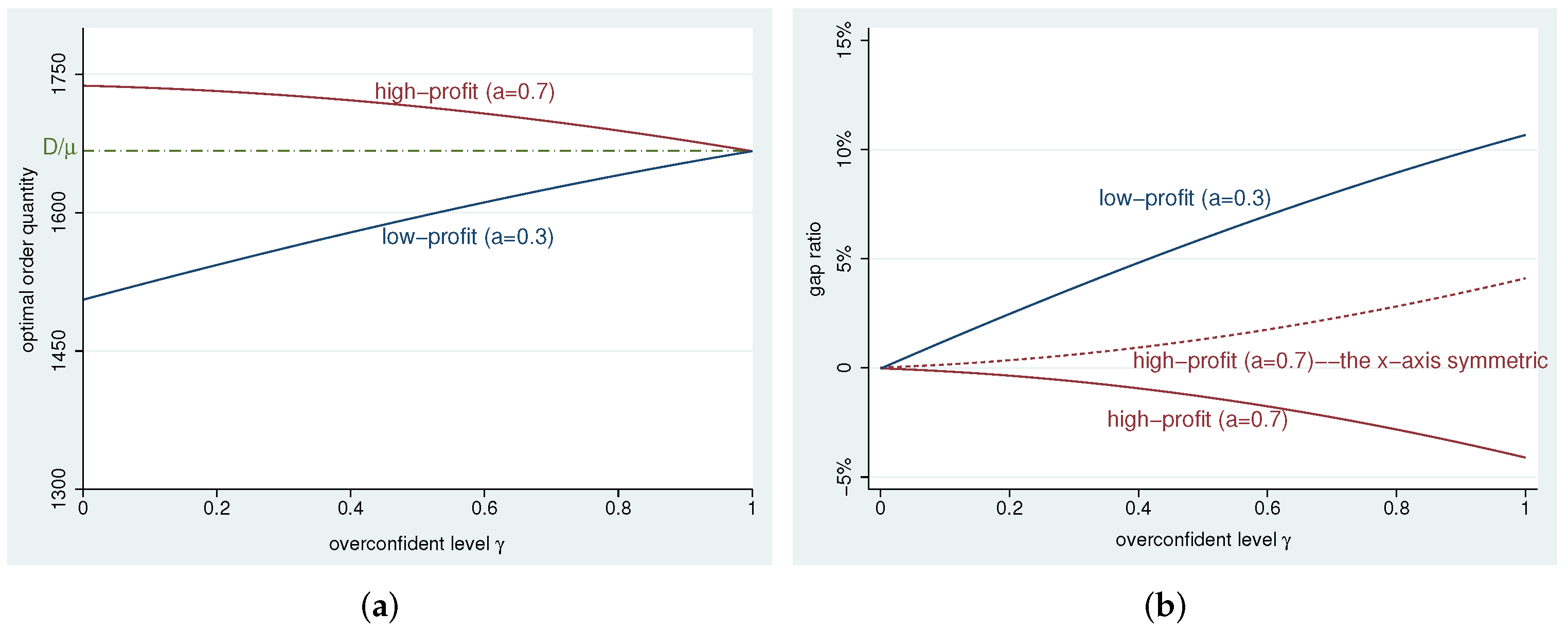
As shown in Figure 4, we set $\mu =0.6$, $\sigma =0.1$, and $D=1000$ and let $a=0.3$ and $a=0.7$ denote low-profit and high-profit conditions, respectively. Figure 4a illustrates that the overconfident optimal order quantity gradually deviates from the expected optimum to ASOQ as the overconfidence level increases. We also find that under different conditions of low and high profit, the deviation of the overconfident optimal order quantity from the unbiased optimum is different. That is, we show asymmetry in the PTC effect. In which condition, high-margin or low-margin, is the overconfident optimum more biased?

To avoid the interference of low bases (the optimal quantity in the low-profit condition is much smaller; a lower deviation from the expected optimum may result in a more significant percentage error than in the high-profit condition), we let g (gap ratio) take the following form to capture the PTC effect asymmetry in the percentage error [65]. A positive value of g indicates higher than the expected optimum, and a higher absolute value indicates a more substantial PTC effect.

$$g=\frac{q^{*}\left(\gamma \right)-q^{*}\left(0\right)}{q^{*}\left(0\right)}\times 100\%$$

(14)

Figure 4b shows the relationship between the gap ratio g and the overconfidence level $\gamma$. First, the positive gap ratio under low-profit conditions shows that the overconfident order quantity has a higher deviation from the expected optimum. In contrast, the negative gap ratio under high-profit conditions shows the overconfident optimum has a lower deviation from the expected result. Second, compared with the high-profit condition, the absolute value of the gap ratio is higher under the low-profit condition, implying that a more substantial PTC effect is shown. As the overconfidence level increases, the deviation percentage error enlarges.

The asymmetry in the PTC effect between the low-profit and high-profit conditions varies significantly from study to study. Reference [31] states that subjects’ order quantities are closer to the optimal order quantity under high-profit conditions than under low-profit conditions. However, reference [62,63] hold the opposite view, that the high-profit condition exhibits a more substantial PTC effect than the corresponding low-profit condition, from the viewpoint of psychological cost, impulse balance, and loss aversion, respectively. Reference [65] concludes that insufficient evidence suggests that the PTC effect is more potent in one margin condition than in the other. This may be related to experimental design factors such as the likelihood of losses, the underage cost, and the existence of a decision-support system.

The previous studies are based on stochastic demand cases rather than supply uncertainty. An experimental result can be referred to in [66]. However, the authors do not distinguish between random demand and random supply. Instead, they conduct experiments in an environment where random demand and supply exist. Thus, in this paper, introducing overconfidence into the inventory problem under only uncertain supply explains the asymmetry of the PTC effect, contributing to the study of PTC’s asymmetry.

4.2. The Influence of Overconfident Decisions on Expected Profits

The overconfident retailer believes he has obtained more accurate information about the yield rate and thus makes a better decision and gains more profits accordingly. In this section, we seek to examine the retailer’s and supplier’s expected profits to decide whether an overconfident retailer makes a better decision.

4.2.1. The Retailer’s Expected Profit

According to Equation (8), the worst-case expected profit considered by the overconfident retailer themself is

$$\mathsf{\Pi }=pD-c\mu q^{*}-\frac{p}{2}\left[\sqrt{{(D-\mu q^{*})}^2+{\alpha }^2{\sigma }^2{\left(q^{*}\right)}^2}+(D-\mu q^{*})\right],$$

(15)

where $q^{*}$ is defined as Equation (10). After substituting into Equation (15), we obtain

$$\mathsf{\Pi }\left(\gamma \right)=(p-c)D-pD(1-\gamma )\sigma \frac{(2a-1)(1-\gamma )\sigma +\sqrt{4a(1-a){\mu }^2+{(1-\gamma )}^2{\sigma }^2}}{2[{\mu }^2+{(1-\gamma )}^2{\sigma }^2]}$$

(16)

$\mathsf{\Delta }\mathsf{\Pi }=\mathsf{\Pi }\left(\gamma \right)-\mathsf{\Pi }\left(0\right)$ denotes the excess profit considered by the retailer. We show $\mathsf{\Delta }\mathsf{\Pi }>0$ and $\mathsf{\Delta }\mathsf{\Pi }$ is increasing in $\gamma$, implying that the higher the overconfidence level, the more profits earned. The overconfident retailer believes that they make a better decision by obtaining more precise information and therefore obtain more excess profits. When they are “extremely” confident ($\gamma =1$), the highest expected profit can be obtained as $(p-c)D$. If that is the case, the retailer satisfies the market demand adequately and appropriately.

However, the real expected profit that can be earned is denoted as

$${\mathsf{\Pi }}^r=pD-c\mu q^{*}-\frac{p}{2}\left[\sqrt{{(D-\mu q^{*})}^2+{\sigma }^2{\left(q^{*}\right)}^2}+(D-\mu q^{*})\right]$$

(17)

After substituting Equation (10) into Equation (17), we show the overconfident retailer actually earns lower expected profits than the unbiased one, i.e., ${\mathsf{\Pi }}^r\left(\gamma \right)<{\mathsf{\Pi }}^r\left(0\right)$. We define $\mathsf{\Delta }{\mathsf{\Pi }}^r={\mathsf{\Pi }}^r\left(0\right)-{\mathsf{\Pi }}^r\left(\gamma \right)$ as the expected loss and show that the higher the overconfidence level, the more losses. That is, overconfidence causes some damage to the retailer by reducing the expected profit under both profit conditions.

4.2.2. The Supply Chain’s Joint Expected Profit

We would examine how overconfidence affects the supply chain’s joint expected profit here. In the first place, we denote the supplier’s expected profit as

$${\mathsf{\Pi }}_s^r=c\mu q-mq=(c\mu -m)q,$$

(18)

where m is the unit production cost. The inequality $m<c\mu$ is satisfied; otherwise, there are no incentives for the supplier to produce.

From Equation (18), we show that the supplier’s expected profit is proportional to the order quantity by the retailer. Therefore, overconfidence has the same impact on the supplier’s expected profit as its impact on the order quantity. That is, the retailer’s overconfidence helps to increase the supplier’s expected profit under low-profit conditions and tends to reduce the profit under high-profit conditions.

The expected joint profit for the supply chain is denoted as

$${\mathsf{\Pi }}_{sc}^r={\mathsf{\Pi }}^r+{\mathsf{\Pi }}_s^r$$

(19)

Recall that overconfidence reduces the retailer’s expected profit under both profit conditions, and we show that the expected joint profit ${\mathsf{\Pi }}_{sc}^r$ is decreasing in the overconfidence level under high-profit conditions. However, under low-profit conditions, overconfidence reduces the retailer’s expected profit but increases the supplier’s. Whether the expected joint profit can be improved depends on the sum of these two changes. If the supplier’s unit profit rate ($c\mu -m$) is high enough, the increase in the supplier’s expected profit would be more significant than the loss in the retailer’s, thus improving the joint revenue; otherwise, overconfidence would reduce the supply chain’s expected joint profit.

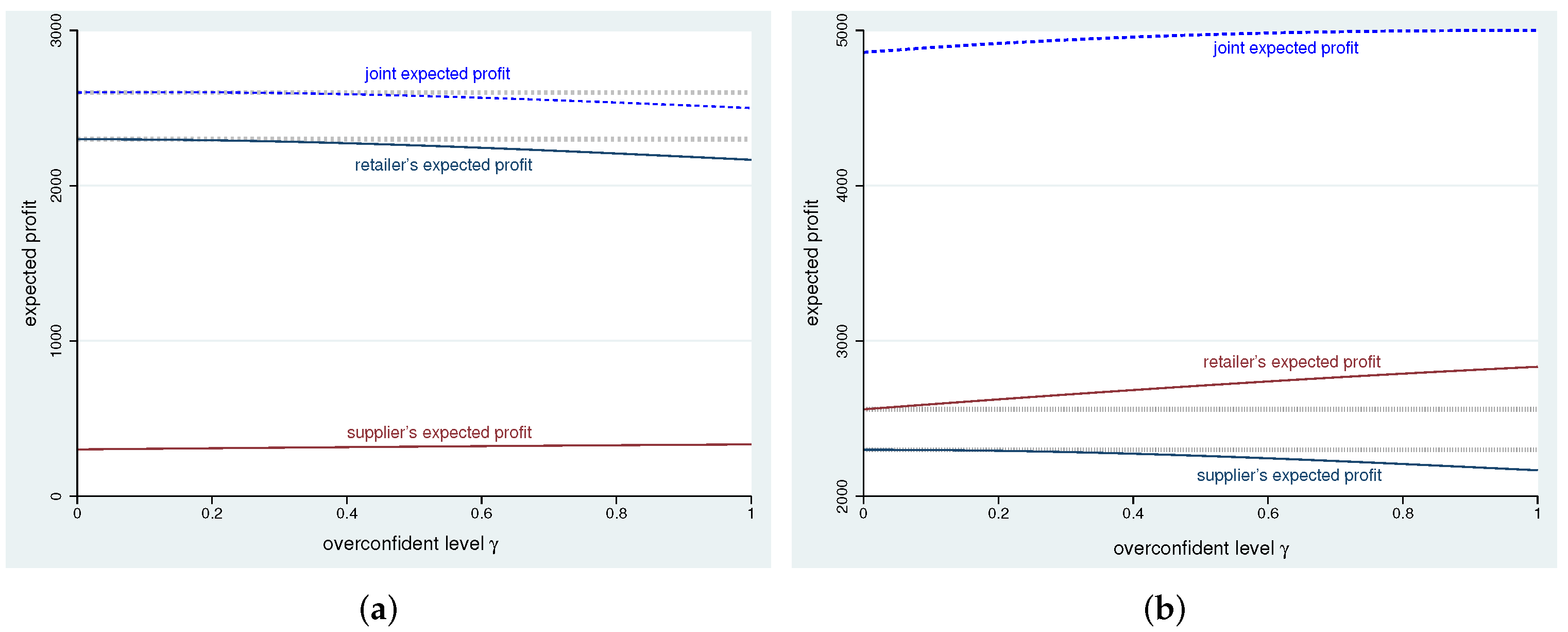
Figure 5 plots the relationship between the supply chain’s expected joint profit and the retailer’s overconfidence level under low-profit conditions, where $p=10$, $c=7$, $D=1000$, $\mu =0.6$, and $\sigma =0.1$. We let $m=4$ and $m=2.5$ denote the supplier’s low unit profit rate and high unit profit rate, respectively. When the unit profit rate for the supplier is low ($m=4$), the increase in the supplier’s expected profit caused by overconfidence cannot make up for the loss in the retailer’s expected profit. Thus, the expected joint profit decreases as the retailer’s overconfidence level increases. When $m=2.5$, the unit profit rate for the supplier is high, and the increase in the supplier’s expected profit is more significant than the loss in the retailer’s expected profit—the expected joint profit increases as the overconfidence level increases. As a result, overconfidence is not always bad for the supply chain, and in some situations, the retailer’s overconfidence increases the expected joint profit by increasing the order quantity.

Related studies mainly focus on the influence of overconfidence on decision-making and performance in a single direction. Some scholars believe overconfidence leads to decision bias and thus damages the expected profits [34,35]. Some other scholars show that overconfidence might increase profits [36]. In this paper, we find that overconfidence has two different sides, and whether overconfidence shows a positive influence depends on the product price and so on.

4.3. Analysis of the DRO Method

4.3.1. The Effectiveness of the DRO Method

The DRO method seeks solutions that perform well independently of the particular distributions. This section sheds more light on the performance of the DRO method in our overconfident inventory model under supply uncertainty. Some numerical experiments are provided to test the robustness of the results, namely, the deviation between the optimal order quantity obtained using the max–min method and the optimum under a particular known distribution, such as a normal distribution or uniform distribution.

In order to evaluate the effectiveness of our method, we introduce an observation indicator called REVAI (relative expected value of additional information), according to [58]. The indicator is calculated as $REVAI=\frac{q^{*}}{q^K}$, where $q^{*}$ denotes the optimal order quantity in Theorem 1 and $q^K$ represents the optimal solution when the yield rate follows a specific known distribution satisfying the given mean and variance constraints.

Recalling that the objective in the model is to maximize the expected profit, we rewrite the objective function as

$$max\mathbb{E}\left[TP\left(q\right)\right]=p·q·{\int }_0^{\frac{D}{q}}xf\left(x\right)dx+p·D·{\int }_{\frac{D}{q}}^{1}f\left(x\right)dx-c\mu q$$

(20)

The derivation of (20) to find the maximum gives (21), the first-order condition for optimality:

$${\int }_0^{\frac{D}{q^K}}xf\left(x\right)dx=(1-a)\mu$$

(21)

According to formula (21), when the probability density function of the yield rate distribution is known, we can calculate the optimal order quantity, $q^K$, with classic stochastic programming. To ensure the uniqueness of the optimum, we assume the cumulative density function is a continuous monotonic increasing function. Most specifically, in the following numerical experiments, we assume the yield rate follows a normal distribution or uniform distribution.

Table 2. The REVAI vs. overconfidence level when demand follows a uniform or normal distribution.

a	$\mathit{\mu }$	$\mathit{\sigma }$	Order Quantity		$\mathit{\gamma }=0$			$\mathit{\gamma }=0.05$
			Normal	Uniform	${\mathit{q}}^{*}$	${\mathit{REVAI}}_{\mathit{n}}$	${\mathit{REVAI}}_{\mathit{u}}$	${\mathit{q}}^{*}$	${\mathit{REVAI}}_{\mathit{n}}$	${\mathit{REVAI}}_{\mathit{u}}$
0.7	0.6	0.18	1778	1803	1719	0.9668	0.9534	1725	0.9702	0.9567
0.7	0.6	0.15	1784	1817	1734	0.9720	0.9543	1736	0.9731	0.9554
0.7	0.6	0.10	1770	1805	1738	0.9819	0.9629	1737	0.9814	0.9623
0.3	0.6	0.18	1345	1283	1339	0.9955	1.0436	1358	1.0097	1.0585
0.3	0.6	0.15	1402	1345	1404	1.0014	1.0439	1419	1.0121	1.0550
0.3	0.6	0.10	1496	1453	1506	1.0067	1.0365	1515	1.0127	1.0427
0.7	0.8	0.15	1332	1359	1304	0.9790	0.9595	1304	0.9790	0.9595
0.7	0.8	0.10	1338	1337	1297	0.9694	0.9701	1296	0.9686	0.9693
0.7	0.8	0.05	1292	1300	1279	0.9899	0.9838	1278	0.9892	0.9831
0.3	0.8	0.10	1173	1132	1164	0.9923	1.0283	1169	0.9966	1.0327
0.3	0.8	0.05	1210	1193	1211	1.0008	1.0151	1213	1.0025	1.0168
MAE (mean absolute error)						0.0147	0.0348		0.0163	0.0381

lists the ratio at different overconfidence levels and yield rate distribution parameters.

In Table 2, we conduct multiple numerical experiments with the parameters randomly selected. The profit margin a is still set as $0.7$ and $0.3$ to represent the high-profit and low-profit conditions, respectively. We let $\mu$ be 0.6 or 0.8 and $\sigma$ be 0.05, 0.10, 0.15, or 0.18. After eliminating some cases where the practical condition could not be met in the whole domain, 11 sets of results are presented in the table. The fourth and fifth columns record the optimum when the yield rate follows a normal and uniform distribution, respectively. The sixth and ninth columns list the optimal solutions for unbiased and overconfident retailers ($\gamma =0.05$), and the corresponding REVAI is calculated as shown in the table, where the subscripts n and u represent a normal distribution and uniform distribution, respectively. In the last line, we calculate each group’s mean absolute error (MAE), namely, the mean absolute error between REVAI and 1.

The table shows that the REVAIs in different situations are all very close to 1, and the MAE is also very small, which shows that the optimal order quantity under the DRO method is quite close to the result of the known normal and uniform distributions. Even if the information about the yield rate distribution is incomplete, the retailer makes a good decision by using the DRO method. For more research on the effectiveness of the DRO method, please refer to [57,64].

The DRO method solves the order-decision problem effectively under ambiguity, which is of great significance in actual scenarios. As we all know, in an uncertain environment, the information about a supplier’s yield rate is too difficult to estimate accurately, even for the supplier themself. In addition, it is costly to dig out all the information. The outstanding performance of the DRO method helps companies save costs by making relatively good decisions with only partial information. Moreover, another advantage is computational simplicity and ease of use. The distribution-free upper bound relies only on the random yield rate’s mean and variance; thus, we can quickly obtain the result through simple algebra. In contrast, exact formulas need to work out a complicated integral problem with a changing upper limit using a computer. The exact result also contains a density function, lacking those structural properties that usually help build intuition.

4.3.2. Overconfidence and the DRO Method

The DRO method performs quite well, but it is undeniable that these results are based on the premise that the practical condition holds.

We take the case shown in Figure 2 as an example. When $a=0.3$, $\mu =0.6$, and $\sigma =0.25$, the point on the vertical axis denotes the unbiased optimum. Since the practical condition is unsatisfactory, the retailer adopting the DRO method only places an order of $D=1000$ units. According to Formula (21), if the yield rate follows a normal or uniform distribution, the optimal order quantity is 1218 or 1151. The optimum in the frame of the DRO method is significantly smaller than the optimum under a known distribution, which shows the conservatism of this method.

When the notion of overconfidence is incorporated into the model, as shown in Theorem 1, the practical condition is softer with the additional overconfidence, and the optimum stays a known demand quantity in a smaller domain. In the example, if the retailer’s overconfidence level is as high as 0.25, the practical condition is satisfied, and the corresponding order quantity increases to 1185, which is very close to the results under the normal and uniform distributions. In other words, if the retailer’s overconfidence level is high enough to make $\gamma \ge 1-{\alpha }_0\ge 0$ hold, the practical condition is not met in the unbiased case, but satisfied in the overconfident case. Accordingly, the overconfident result of the DRO method is more popular than the unbiased situation.

Recall that in Corollary 1, if the profit margin a, the mean yield rate $\mu$ is low, and the volatility of the yield rate is high, the practical condition is not easily satisfied in the DRO method. The conservativeness brought by this max–min criterion has attracted some criticism. Some studies modify the objective function by using risk or loss functions. For example, reference [57] uses the standard deviation of the expected profit to measure the risk and introduces a risk-preference coefficient in the objective function. Reference [58] revises the expected profit to the expected utility function of loss aversion. In this paper, overconfidence is introduced into the constraints and is proved to make the practical condition softer, thereby helping to alleviate the conservatism of worst-case optimization.

5. Some Extensions

In this section, we seek to analyze the impact of overconfidence and ambiguity on order decisions in a broader context and obtain more managerial guidelines for decision-makers.

5.1. The Ordering Strategy under Both Demand and Supply Uncertainties

When making purchasing decisions, not only will we face an uncertain supply, but random changes in the market demand also profoundly impact the result. For example, in the global COVID-19 pandemic, on the one hand, strict prevention measures have resulted in insufficient production and supply shortages; on the other hand, the epidemic has caused significant changes in the market demand for different commodities. Personal protective equipment is urgently needed, whereas industrial raw materials lack demand. Considering the ordering strategy under both demand and supply uncertainties is necessary.

Suppose the market demand D is a random variable in the section and follows the distribution ${\pi }_1$ where only the mean ${\mu }_1$ and variance ${\sigma }_1^2$ are available. The stochastic market demand D is independent of random yield rate x, following the distribution ${\pi }_2$ with mean ${\mu }_2$ and variance ${\sigma }_2^2$. The retailer is assumed to show different overconfidence levels for uncertain demand and supply. ${\alpha }_1$ and ${\alpha }_2$ denote the overconfidence parameter, respectively, and we thus show ${\pi }_1\in {\mathsf{\Omega }}_1({\mu }_1,{\alpha }_1{\sigma }_1)$, ${\pi }_2\in {\mathsf{\Omega }}_2({\mu }_2,{\alpha }_2{\sigma }_2)$. The main problem (4) under only supply uncertainty is changed to a multivariate optimization problem:

$$\begin{array}{ccc}\hfill \underset{q\ge D}{max}& \hfill \underset{{\pi }_1\in {\mathsf{\Omega }}_1,{\pi }_2\in {\mathsf{\Omega }}_2}{min}& p{\mu }_1-c{\mu }_{2}q-p·\mathbb{E}{(D-\widehat{x}q)}^{+}\hfill \end{array}$$

(22)

The key to solving the problem is to calculate the upper bound for $\mathbb{E}{(D-\widehat{x}q)}^{+}$. Recall that random variables D and $\widehat{x}$ are unrelated, and thus, based on Lemma 1, we show the upper bound as

$$\mathbb{E}{(D-\widehat{x}q)}^{+}=\frac{\mathbb{E}|D-\widehat{x}q|+({\mu }_1-{\mu }_{2}q)}{2}\le \frac{1}{2}\left[\sqrt{{({\mu }_1-{\mu }_{2}q)}^2+{\alpha }_1^2{\sigma }_1^2+{\alpha }_2^2{\sigma }_2^2{q}^2}+({\mu }_1-{\mu }_{2}q)\right]$$

With the result, problem (22) is transformed into the following, whose optimal solution is given in Theorem 2.

$$\begin{array}{cc}\hfill \underset{q\ge D}{max}& p{\mu }_1-c{\mu }_{2}q-\frac{p}{2}\left[\sqrt{{({\mu }_1-{\mu }_{2}q)}^2+{\alpha }_1^2{\sigma }_1^2+{\alpha }_2^2{\sigma }_2^2{q}^2}+({\mu }_1-{\mu }_{2}q)\right]\hfill \end{array}$$

(23)

Theorem 2. 

The robust optimal order quantity for the overconfident retailer under both demand and supply uncertainties is derived by

$$q^{*}=\frac{{\mu }_2}{{\mu }_2^2+{\alpha }_2^2{\sigma }_2^2}\left[{\mu }_1+\frac{(2a-1)\sqrt{{\mu }_1^2·{\alpha }_2^2{\sigma }_2^2+{\mu }_2^2·{\alpha }_1^2{\sigma }_1^2+{\alpha }_1^2{\sigma }_1^2·{\alpha }_2^2{\sigma }_2^2}}{\sqrt{4a(1-a){\mu }_2^2+{\alpha }_2^2{\sigma }_2^2}}\right]$$

(24)

Proof. 

We compute the first derivative of (23) with respect to q and set the derivative equal to zero. Solving for q, we obtain Equation (24).    □

Regarding Equation (24), if the demand is known and the supply is stochastic, i.e., ${\mu }_1=D$ and ${\sigma }_1=0$, the result is simplified as

$$q^{*}=\frac{D{\mu }_2}{{\mu }_2^2+{\alpha }_2^2{\sigma }_2^2}\left[1+\frac{(2a-1){\alpha }_2{\sigma }_2}{\sqrt{4a(1-a){\mu }_2^2+{\alpha }_2^2{\sigma }_2^2}}\right],$$

consistent with Theorem 1 in this paper. If the demand is uncertain and the supply is determined (i.e., ${\mu }_2=1$, ${\sigma }_2=0$), then the result is derived to

$$q^{*}={\mu }_1+\frac{(2a-1)}{\sqrt{4a(1-a)}}{\alpha }_1{\sigma }_1,$$

which entirely agrees with the result in [64] that the optimal order quantity decreases in the overconfidence level in the high-profit case and increases in the low-profit case.

Overall, Theorem 2 summarizes the analytical results of Theorem 1 and [64] into a perfect framework and depicts the influence of overconfidence when considering both demand and supply uncertainties. Under low-profit conditions, overconfidence encourages the retailer to order more and, generally, tends to reduce the order quantity under high-profit conditions.

With the formula and given parameter values, we can calculate the expected losses brought by overconfidence under different uncertainties and decide which uncertainty is more costly. For example, we provide an experiment of $p=10$, $c=7$, ${\mu }_1=1000$, ${\sigma }_1=50$, ${\mu }_2=0.6$, and ${\sigma }_2=0.1$. The results show that under only demand uncertainty, the unbiased expected profit is 2771 and the overconfident expected profit is 2758, implying the loss ratio is 0.47%; under only supply uncertainty the loss ratio is 3.98%. As a result, overconfidence under supply uncertainty is more costly, causing more losses.

Moreover, the analysis framework is inclusive and open to including more influencing factors, such as the correlation between demand and supply. In the existing model, we assume the demand and supply are independent, whereas this assumption may not be realistic in practice [66]. For example, a supplier supplies multiple retailers. When the market demand is great and the supplier’s production capacity is relatively insufficient, the supplier chooses to prioritize those intimate retailers. Some other retailers have to face a low supply under high demand, and this is a negative demand–supply dependency. If the supplier opens up a new production line to meet all retailers’ needs, it is a positive demand–supply dependency. We let $\rho$ denote the correlation coefficient between the market demand D and yield rate x and show that

$$\mathbb{E}{(D-\widehat{x}q)}^{+}\le \frac{1}{2}\left[\sqrt{{\mu }_1^2+{\alpha }_1^2{\sigma }_1^2-2({\mu }_1{\mu }_{2}q+\rho {\alpha }_1{\sigma }_1{\alpha }_2{\sigma }_{2}q)+{\mu }_2^2{q}^2+{\alpha }_2^2{\sigma }_2^2{q}^2}+({\mu }_1-{\mu }_{2}q)\right].$$

The optimal order quantity is calculated accordingly.

5.2. An Overconfident Multi-Product Problem under Supply Uncertainty with Budget Constraint

Consider a multi-product inventory problem where a retailer orders N types of products from an unreliable supplier with a budget of B. For each product, the market demand is assumed to be known, while the yield is uncertain, implying the quantity received by the retailer may not necessarily be equal to the quantity ordered. Notations for this case are similar to those used for the single-item case in Section 3.1, and a subscript i is used to indicate product i ($i=1,\cdots ,N$). Note that the retailer shows different overconfidence levels for different types of products; namely, ${\alpha }_i$ are not equal and are independent of each other.

Accurately estimating the yield rate distribution for every product is very difficult using the limited information, which prompts the use of the DRO approach. The robust and overconfident counterpart of the multi-product inventory optimization model with budget constraint is formulated in the following

$$\begin{array}{ccc}\hfill \underset{q_1,q_2,\cdots ,q_N}{max}& \hfill \underset{{\pi }_i\in \mathsf{\Omega }({\mu }_i,{\alpha }_i{\sigma }_i)}{min}& {\displaystyle \sum _{i=1}^N}\left[p_i{D}_i-c_i{\mu }_i{q}_i-p_i·\mathbb{E}{(D_i-\widehat{x_i}{q}_i)}^{+}\right]\hfill \\ \hfill s.t.& \hfill & {\displaystyle \sum _{i=1}^N}{c}_i{q}_i\le B\hfill \end{array}$$

(25)

Based on Lemma 1, and by mathematical deduction, problem (25) is divided into the following:

$$\begin{array}{cc}\hfill \underset{q_1,q_2,\cdots ,q_N}{max}& \hfill \left\{H_j(q_1,q_2,\cdots ,q_N)|{\displaystyle \sum _{i=1}^N}{c}_i{q}_i\le B\right\},\end{array}$$

(26)

where $H_j(q_1,q_2,\cdots ,q_N)={\displaystyle \sum _{i=1}^N}{p}_i{D}_i-c_i{\mu }_i{q}_i-p_i·H_j\left(q_i\right)$, $j=1,2,3$.

The Lagrange multiplier method is one technique that can be applied to solve the constrained optimization model, and we construct the Lagrangian function

$$L(q_1,\dots ,q_N,\lambda )=H(q_1,q_2,\cdots ,q_N)-\lambda \left(\sum _{i=1}^N{c}_i{q}_i-B\right),$$

(27)

where $\lambda \ge 0$ is the Lagrange multiplier associated with the budget constraint. We further show $L(q_1,\dots ,q_N,\lambda )$ is concave in $q_i$, and thus the optimum is achieved by using differentiation. We obtain the results shown in Theorem 3 only when the practical condition holds for each product.

$$1-k_i\ge \frac{1}{{\mu }_i}\frac{{\alpha }_i^2{\sigma }_i^2}{{(1-{\mu }_i)}^2+{\alpha }_i^2{\sigma }_i^2},k_i=(1-a_i)\left(1+\frac{\lambda }{{\mu }_i}\right)$$

(28)

Theorem 3. 

Given an unreliable supplier, the optimal order quantity of the overconfident retailer for product i is given by

$$q_i^{*}=\frac{D_i{\mu }_i}{{{\mu }_i}^2+{{\alpha }_i}^2{{\sigma }_i}^2}\left[1-\frac{(2k_i-1){\alpha }_i{\sigma }_i}{\sqrt{4k_i(1-k_i){{\mu }_i}^2+{{\alpha }_i}^2{{\sigma }_i}^2}}\right]$$

(29)

Proof. 

The proof is omitted here since the optimums for the concave functions can be achieved by using differentiation directly.    □

When $\lambda =0$, implying the budget constraint is insignificant, the result of Theorem 3 is back to Theorem 1, and each product achieves the theoretical optimum.

The problem now is to find the smallest non-negative $\lambda$ such that (28) is satisfied, and we provide a simple search algorithm (Algorithm 1).

Algorithm 1 A simple search algorithm for solving problem (27)

I. Let set $T=\{1,2,\cdots ,N\}$ and we start with $\lambda =0$. If condition (28) for each product is satisfied, $q_i^{*}$ is calculated as (29); otherwise, $q_i^{*}=D_i$. (1) If the budget constraint is also satisfied, stop. The solution is optimum. (2) Otherwise, continue to II. II. Increase $\lambda$ until the first occurrence of either following situation: (1) The budget constraint is satisfied. Stop, and then the solution is optimum. (2) Condition (28) is violated for item $i_0$, $i_0\in T$. Let $q_{i_0}^{*}=D_{i_0}$; remove $i_0$ from set T and go back to I.

Regarding this, we provide a particular case with only two types of products “competing” for a limited budget. We seek to explore the performance of asymmetric overconfidence in competing-inventory problems under supply uncertainty. Assume the retailer shows different overconfidence levels for the two products, without loss of generality, ${\alpha }_1<{\alpha }_2$ (i.e., ${\gamma }_1>{\gamma }_2$), and all other parameters are simplified as equal. When the products are both under-profit, the results show that product 1 with a higher overconfidence level is preferred in the competitive environment for earning more expected profit per unit. Recall that in Section 4.2, we show that overconfidence reduces the expected profit in a non-competitive environment. However, a more unbiased product is preferred in the competitive environment. Therefore, we show that overconfidence can potentially be a positive force under supply uncertainty with only partial information.

6. Conclusions

Inventory problems under uncertain supply have attracted widespread attention and research since emergency situations such as the outbreak of COVID-19 have always impacted the supply chains significantly. This paper enriches the relevant literature by introducing the overconfidence of decision-makers who tend to underestimate the actual volatility, especially in a highly uncertain market, and developing a distributionally robust model with only the mean and variance of the yield rate distribution available. We provide robust expressions for the optimal order quantity by an overconfident retailer under supply uncertainty, which is more realistic for practical application compared to previous studies.

The proposed model has good tractability, and the results are clear to obtain managerial insights. Our analysis results show that overconfidence prompts the retailer to order more under low-profit conditions and order less under high-profit conditions. The ordering strategy is consistent with the PTC effect. We prove the asymmetry in the PTC effect where the deviation is higher in the low-profit case than that in the high-profit case. The performance of overconfidence is characterized in the expected profit, and the results show that even though the retailer suffers losses because of overconfidence, the supplier’s expected profit increases in the low-profit case. The overconfidence may positively increase the expected joint profit of the entire supply chain. The effectiveness of the proposed DRO method is proved in numerical experiments. The results have shown the outstanding performance of our method to be applied in practice, as long as the overconfidence of the retailer would make the practical condition softer, thus helping to alleviate the conservatism of the method. Two extensions to the base model are also considered to analyze the impacts of overconfidence in a broader context. The formula for inventory problems under both demand and supply uncertainties is developed with a solution framework including more factors, such as the correlation between demand and supply. An overconfident multi-product problem with budget constraints is studied, and the analysis results show that the more unbiased product is preferred for earning more expected profit under low-profit conditions. Thus, overconfidence can be a positive force in a competitive environment. The multi-product problem can also be extended to multi-retailer competing problems with symmetrical or asymmetric overconfidence.

Our results predict to what extent the decision-maker is biased and such predictions will help to apply de-biasing techniques, which is of great significance for practical applications. Some problems can be further explored in future studies. For example, one could conduct a small laboratory experiment to check the predictions in our results, or extend the model to multi-stage cases, etc.