Abstract
In the digital economy era, cloud–edge collaboration technology provides the necessary technical support for the digital transformation of enterprises, which can improve the quality of services (QoS), and it attracts extensive attention from scholars and entrepreneurs from all fields. Under the bounded-rationality hypothesis, this paper investigates the service mechanism for the cloud–edge collaboration system considering the quality of experience (QoE) and presents a dynamic evolutionary game model between cloud service providers and edge operators by applying the evolutionary game theory. Then, this paper analyzes the equilibrium and stability conditions for the decision-making of both parties involved to guarantee the QoE reaches the ideal state. In addition, we investigate the factors that influence the stable cooperation between the two evolutionary stable strategies and validate the theoretical analytical results with numerical simulations. The research results show that the final evolution of the cloud–edge collaboration system depends on the benefits and costs of the game matrix between the two parties and the initial state values of the system. Under a specific condition, the cloud–edge collaboration system can eventually be driven to be an ideal state by reducing the collaboration cost and improving the collaboration benefit. The more both parties focus on the QoE, the more conducive it will be for the formation of a cloud–edge collaboration, thus effectively promoting long-term stability and better serving enterprises’ digital transformation.
1. Introduction
The innovation of digital technology has brought tremendous changes in the social and market environments and became disruptive [1]. The digital economy has facilitated a high-quality economic and social development in various countries [2]. The strong resilience demonstrated by Internet-based enterprises based on digital technology has been widely recognized by the international community. The outstanding performance of digital technologies such as big data analytics, cloud computing, and the Internet of things has made all stakeholders more confident that they can achieve the digital transformation of enterprises so as to promote the development of the digital economy. Many countries have paid a lot of attention to the development of digital transformation and proposed a range of strategic decision-making deployments, which have stimulated the demand and endogenous forces for enterprises’ transformation and upgrading. However, the characteristics of traditional enterprises, such as various product types, scattered user data, and different stages of development, affect the overall effect of digital transformation, making it difficult for some enterprises to achieve digital transformation and upgrade in a short period of time.
For businesses, users are the fundamental source of their benefits, and the QoE directly affects their competitiveness in the market, which in turn determines the revenue earned in the face of fierce competition. In previous research and production practices, companies have mainly focused on improving [3], i.e., business sophistication through some measurable hardware and software improvements and guarantees, yet the QoE [4] is the key factor for market success and is not always guaranteed by quantification. The QoE is closely related to the QoS but is not identical to it [5]. The QoE is a user-layer concept and represents both objective and subjective satisfaction of users, while the QoS is a reflection provided by the service provider from the network- and service-layer perspective. For each type of services used by the users, to meet their QoE requirements, the service provider must understand what level of QoS is required, and the network operator needs to consider what QoS mechanism to implement to meet the service provider’s requirements. Thus, how cloud service providers and edge operators focus on the QoE directly affects their benefits and costs and is one of the indispensable factors in studying the behavior of both parties. For both parties, guaranteeing the QoE can improve the level and value of the business, increase user loyalty, and even bring better word-of-mouth communication among users to enhance core competitiveness in a competitive environment.
Since cloud service providers and edge operators have different types of resources and different service storage capabilities, they typically make decisions under diverse conditions. Indeed, based on the premise of bounded rationality, decision-making is an evolutionary game process for cloud service providers and edge operators [6]. In order to improve the QoE and better help various large and small enterprises to achieve digital transformation, we investigate the intrinsic laws of game behavior among digital technology providers based on evolutionary game theory and obtain the following main contributions:
- We establish an evolutionary game model for the collaborative service mechanism of cloud service providers and edge operators and theoretically study the existence conditions and evolution rules of evolutionary stable strategies (ESSs), which contributes to analyzing the behaviors of cloud service providers and edge operators when collaboratively handling user service requests;
- We perform numerical simulations to illustrate the evolution of the cloud–edge collaboration system and show quantitatively the impact of the initial conditions and the variation in decision parameters on the evolutionary results;
- Finally, we propose some specific measures to promote the stability of the cloud–edge collaboration system, based on a theoretical analysis and simulation results.
The rest of the paper is organized as follows: Section 2 introduces the research problem, basic assumptions, and related remarks and constructs an evolutionary game model for the cloud–edge collaboration system. Section 3 theoretically analyzes the evolutionary game in some detailed scenarios and identifies evolutionary stable strategies under different conditions. Section 4 considers the case where there are two evolutionary stable strategies, illustrates the effect of initial values and decision parameters on the evolution process and evolutionary outcomes, discusses evolutionary phenomena, and proposes management measures for the cloud–edge collaboration system. Finally, Section 5 summarizes the conclusions of our work and gives directions for further research.
2. Literature Review
In findings on digital transformation, researchers have always focused on specific aspects such as the influencing factors, processes, and outcomes. For example, Kozanoglu et al. [7] studied the influencing factors of digital transformation in enterprises, including the attitudes of employees. Warner et al. [8] considered the process of digital transformation in enterprises from the perspective of dynamic capability. Bouwman et al. [9] investigated the impact of digital transformation on business models and firm performance. For enterprises, the researchers focused on their digital transformation models, pathways, and the impact of the generalization of digital technologies on business model evolution. Sergei [10] analyzed the variations in nontechnological digital transformation enablers in high-tech and low-tech manufacturing companies. Sjodin et al. [11] studied the digitalization of business models for large manufacturers with an industrial ecosystem coordination framework. Zainal-Abidin [12] explored the antecedents of digital collaboration and developed a framework for microdestination management organizations to enhance effective destination management through digital technologies. Alenezi [13] described some challenges that higher-education institutions encountered, as well as the technological resources and methodologies they used in the current scenario to transform higher-education institutions by embracing digital transformation. It is now agreed that digital technologies are very essential for both large supply-chain enterprises to deeply understand the enterprise value creation brought by digital transformation [14] and small and medium enterprises with numerous resource limitations to realize digital transformation [15,16]. For example, the development of digital finance can promote enterprise innovation, thus facilitating the digital transformation of enterprises [17], which means that digital technologies can better serve digital enterprises to achieve high-quality economic development. Digitization can centralize the scattered data of traditional enterprises and mine the business value of data to promote the organizational transformation of traditional enterprises [18]. A big-data strategy has not only changed the paradigm of economic research [19], but data empowerment is also the key factor to the digital transformation of enterprises. Digital transformation of grassroots governance driven by digital technologies such as the Internet, cloud computing, and big data can achieve a better governance effectiveness. The new infrastructure is guided by the new development concept (innovation, coordination, green, open, sharing), driven by technological change and based on information technology, and faced with the needs of the digital economy era. The infrastructure provides functions such as digital transformation, digital integration, and a digital upgrading of traditional infrastructure. The proposal of a new infrastructure strategy enables enterprises to develop a digital enablement strategy to value innovation. It can be seen that more and more established technologies such as the Internet, cloud computing, and big data strategies provide an optimized development path for solving various problems faced in the digital economy.
Digital technologies include data storage and processing technologies, networking technologies, and computing technologies, such as artificial intelligence, cloud computing, and a wide range of computing algorithms. As cloud infrastructure becomes ubiquitous, the pace of cloud-based intelligence and digitization will continue to accelerate. Microsoft Azure, Amazon AWS, and other public cloud providers offer support for the digital transformation of traditional businesses. However, despite its powerful resource service capabilities, cloud computing suffers from service time delay, energy consumption, and a poor quality of experience due to long-distance transmission between end users and remote cloud centers. Correspondingly, edge computing has the advantage of a low transmission delay and a high service responsiveness due to its deployment at the edge despite certain resource constraints in terms of computation and storage [20]. Thus, cloud–edge collaboration technology can better overcome the shortcomings of both cloud computing and edge computing, and has attracted a lot of research attention from academia and industry in recent years, in areas such as computational offloading [21,22,23], task and resource scheduling [24,25,26], and resource allocation [27,28,29,30], so as to achieve a lower transmission latency and better user experience.
Evolutionary game theory has been widely used in related research on group behavior analysis, providing an effective analytical tool for discussing the strategy selection and evolutionary logic of the players in cloud–edge collaboration systems from a micro perspective, whose core is an “evolutionary stable strategy” and “replication dynamics” [31]. In 1973, Smith and Price proposed the concept of evolutionary stable strategy (ESS) [32], which means that after each player adopts its strategy in the process of an evolutionary game, the population can no longer be affected according to the role of natural selection. In 1978, ecologists Taylor and Jonker proposed the concept of replicator dynamics (RD) [33], which refers to a population simulating the learning and dynamic adjustment process of other populations through “replication dynamics” and then making corresponding optimal decisions through the process of dynamic convergence to an evolutionarily stable strategy. Since some players will not adopt a fully rational equilibrium strategy, they will not find the optimal strategy at the beginning when making decisions. The business processing of the cloud–edge collaboration system is in a dynamic state of continuous development, and the instability of the business makes both parties have a certain degree of distrust; thus, it is difficult for both parties to have complete rationality.
However, it is a critical problem to reasonably describe the collaboration relationship between public cloud service providers offering cloud computing services and edge operators providing edge computing services, who are regarded as bounded rational agents, and also to involve some issues related to their own interests when dealing with user service requests collaboratively. Digital enterprises can gain more benefits in the digital economy market by applying digital technologies, so they can help spur digital technology providers to further provide more technical support for digitalization and high-quality development in a more active and efficient manner.
3. Model Description
The edge cloud relies on the coverage of massive cluster resources to enable end users to access edge computing power with a better experience and lower latency. On the one hand, the flexibility of the user service is enhanced by the upward shift of the terminal computation. On the other hand, the cost and latency are reduced by the downward shift of cloud computing power. Therefore, introducing an edge cloud between the remote cloud center and end users can make the edge service more flexible and achieve quadratic computing with improved territorial performance. We followed the edge cloud architecture [34] and the service-oriented resource allocation cyclic game [35] in edge computing, then simplified the cloud–edge collaboration system into two major decision players, namely, cloud service providers and edge operators, which can operate collaboratively by sharing computing resources and complementing each other to complete the service requests of end users, reduce the cost burden, and share cooperation benefits. Cloud service providers manage service resources via the cloud and deploy them at the edge nodes. They mainly provide the service distribution strategy of SaaS services in the cloud and edge nodes, as well as the SaaS service capability undertaken in the cloud, thus they have the vital resource service and deployment capabilities, but also have the disadvantage of a high latency due to long-distance transmission. The edge operators mainly control the edge node resources because the edge cloud (EC) operators provide small and medium-scale cloud infrastructure on the edge side near the end users and provide edge cloud service capability based on 5G applications, so they can not only realize part of the EC-SaaS services according to the cloud strategy but also realize customer-oriented SaaS through the collaboration of EC-SaaS and cloud SaaS. In addition to the on-demand SaaS services, they also have specific edge service capabilities to meet high-bandwidth, low-latency, and localized-processing business requirements with the advantages of a low transmission latency and the disadvantages of limited resources. Differences between the agents of the cloud–edge collaboration system and the uncertainty of the market competition leave the two parties in an information-asymmetric state. The two types of agents involved in decision-making need to repeatedly try, learn from experience, and adjust their strategies in a game process based on bounded rationality to eventually reach an equilibrium.
3.1. Basic Assumptions and Parameter Descriptions
In this part, we give some basic assumptions and parameter descriptions for the cloud–edge collaboration system. Firstly, we give the following elementary hypothesis by following the generalization of the related literature on evolutionary games, and the parameters are described in Table 1.

Table 1.
Parameter definitions in the model.
Hypothesis 1:
The game process involves cloud service provider
and edge operator , and they are boundedly rational players. The action sets of both and are {solo-processing, coprocessing}. Then, for , the probability of taking the “coprocessing” strategy is , and the probability of choosing the “solo-processing” strategy is ; and for , the probability of choosing the “coprocessing” strategy is , and the probability of choosing the “solo-processing” strategy is .
Hypothesis 2:
Each user sends a service request to the cloud and edge servers. Edge nodes receive the service requests from users earlier than the cloud servers due to their superior low-latency properties. Ifhas deployed the service on the edge node,can choose whether to cooperate or not; ifhas not deployed its service on the edge node,can choose whether to cooperate or not. If bothandchoose “cooperative processing” after receiving the service request, they share the cooperation benefits.
Hypothesis 3:
Here, we do not consider the previous infrastructure investment costs of the cloud–edge collaboration system. Thus, if the two parties choose to collaborate for the end users, they continue to invest in the cost of the collaborative service. We only consider the data transmission cost of andand the service cost of completing the user’s service request and share the service cost during cooperation. Meanwhile, if one party seeks cooperation and the other party refuses, the party who chooses the “coprocessing” strategy has invested costs that cannot be recovered and suffers losses due to a poor service quality delivered to the user, and the other party needs to pay a penalty.
Hypothesis 4:
Now that the Internet is booming, many similar products have emerged with similar or even identical features, making switching behavior very cost-effective for users. QoE directly affects the competitiveness of andin the market, and then affects the revenue gained in the fierce competition. Therefore, it brings more revenue forandwhen they pay much attention to user experience. Moreover, if one party chooses to collaborate while the other chooses not to, then the end users suffer damage since the QoE of each user may not be guaranteed and the benefits of both parties may decrease.
3.2. Construction of Revenue Matrix
According to the above problem description and research hypothesis, we obtained the payoffs of and as shown in Table 2, where and denote the payoff values of and , respectively. Here, can choose the “coprocessing” strategy (i.e., ) or “solo-processing” strategy (i.e., ), and can also choose the “coprocessing” strategy (i.e., ) or “solo-processing” strategy (i.e., ).

Table 2.
Payoff matrix for cloud service providers and edge operators.
Here,
Based on the payoff matrix of the parties in Table 2, we can obtain the replicator dynamic equation for the expected payoff of and the behavioral strategies. Assume that the expected gain of is if it chooses “coprocessing” and if it chooses “solo processing”, and that the average expected gain of is . Then, we have
According to the Malthusian equation, the replicator dynamic equation of can be obtained by combining (1) with Equation (3)
Similarly, we can also obtain the expected gain of and the replicator dynamic equation. Suppose the expected gain of choosing the “coprocessing” strategy is , the expected gain of choosing the “solo-processing” strategy is , and the average expected gain of is . Then, we have
According to the Malthusian equation, the replicator dynamic equation of can be obtained by combining (5) with Equation (7)
Then, the replicator dynamics can be shown as
4. Results
Let , , , and , Then, we rewrite the dynamic equation of as:
and we rewrite the dynamic equation of as:
where
4.1. Stability Analysis of the Evolution of One-Party Strategies
According to the stability theorem for differential equations, the conditions for or to evolve to a stable strategy are and or and .
4.1.1. Evolutionary Stability Analysis of Cloud Service Provider
Let ; there are two definite solutions, i.e., , and , and one possible solution . For the party, we take the derivative of the replicator dynamics system (9) with respect to variable and can obtain .
The solutions satisfying are evolutionary stable strategies (); therefore, we discuss the following cases:
- If , the stable point , and for . When , . Moreover, this type of condition satisfies , i.e., . Thus, in this case, for , its coprocessing gain is larger than the solo-processing gain, i.e., ; hence, chooses the coprocessing strategy no matter how chooses its strategy.
- If , the stable point , and for . When , . Moreover, this type of condition satisfies , i.e., . Thus, in this case, for , its coprocessing gain is smaller than the solo-processing gain, i.e., ; hence, chooses the solo-processing strategy no matter how chooses its strategy.
- If , the stable point , and if . When , . If , , and when , . Moreover, this type of condition satisfies , that is, . Then, in this case, for , its coprocessing gain is less than the solo-processing gain, i.e., ; thus, whether chooses solo-processing or coprocessing is influenced by the strategy choice of .
- From , we know there is no .
4.1.2. Evolutionary Stability Analysis of Edge Operator
Similarly, let ; there are two definite solutions, i.e., , and one possible solution . For the party, we take the derivative of the replicator dynamics system (10) with respect to variable and can obtain .
Only the solution satisfying is the ; thus, we discuss the following cases:
- If , the stable point , and for . When , . This type of condition satisfies , i.e., . Thus, in this case, for , its coprocessing gain is larger than the solo-processing gain, i.e., ; thus, will choose co-processing no matter how chooses its strategy.
- If , the stable points , and for . When , . This type of condition satisfies , i.e., . Then, in this case, the coprocessing gain of is less than its solo-processing gain, i.e., ; thus, chooses solo-processing no matter how chooses its strategy.
- If , the stable point . If , then . When , . If , then . When , . This type of condition satisfies , i.e., , which means that the coprocessing gain of is less than its solo-processing gain, i.e., ; thus, whether chooses solo-processing or coprocessing is indeed influenced by the strategy choice of ;
- From , we know there is no .
4.2. Analysis of the Evolutionary Stability of the Combination Strategies of Both Game Parties in the System
According to the replicator dynamic Equations (4) and (8) and following the single-party strategy evolution analysis in Section 3.1, the local equilibrium point of the system can be obtained as . However, the equilibrium points derived by the replicator dynamic equations are not necessarily the evolutionary stable strategy of the system, so it is necessary to follow the Friedman method [36]. That is, the Jacobi matrix () of the system can be constructed by taking the partial derivatives of Equations (9) and (10) with respect to and , respectively. The local stability of the stationary points can be obtained according to the values of the determinant () and trace () at each stationary point. The Jacobi matrix of the system is given as follows.
Then, the determinant of this matrix is
and the trace of this matrix is
From the evolutionary game theory, it is known that when the Jacobi matrix at the equilibrium point satisfies the condition and , the equilibrium point is . When the Jacobi matrix satisfies the condition and , the equilibrium point is unstable. When the above condition is not satisfied, it is a saddle point. Substituting the five equilibrium points into Equations (11) and (12), we obtain the evolutionary stability points of the system under different conditions, as shown in Table 3.

Table 3.
Evolutionary stable equilibrium points under different conditions.
Following the above study and analysis, we can obtain the following nine scenarios, which are shown in Table 4.

Table 4.
Balanced analysis of cloud–edge collaboration system.
- Mutual influence relationship: From the game process of the and strategy selection, there are three different states:
- The strategy choices of the two parties do not affect each other, as in the case of condition 1;
- One party is affected; for example, is affected by the choice of ’s strategy selection in condition 3;
- The two parties affect each other; for example, and are affected by each other’s strategy choice in condition 9.
We also find that the three states depend on different combinations of conditions, that is, and take different values of costs and benefits during the game evolution, and then the strategy selection process is affected accordingly. As can be seen from conditions 3 and 6, the final evolutionary directions are also different, even with the same strategy influence. Particularly, it can be seen from condition 9 that the final evolutionary outcome of the system may also be related to the initial state of the system. Thus, the final evolutionary direction depends mainly on the factor values of the two-party evolution game matrix and the initial state of the system.
- Evolutionary results: As can be seen from Table 4, there are four evolutionary results, i.e., , and , in the evolutionary game of and . The evolutionary results are in conditions 1, 3, and 7, indicating that in these cases, and choose to collaborate in handling various service requests from users. In other words, regardless of the initial state of the whole system, the two parties eventually reach a stable cloud–edge cooperative relationship after continuously learning and adjusting their strategies, and the common conditions in these three cases are and through a comparative analysis, as shown in Equation (13):that is,
Following the mathematical analysis above, the primary criterion for the constraint loss cost is and . The above essential criterion indicates that if and are to undergo a long-term dynamic evolutionary adjustment to form a cloud–edge collaboration system and eventually achieve joint stability, the constraint loss cost should be at least larger than the difference between the gain when both parties choose to deal with it alone and the gain when they deal with it cooperatively.
- Is the evolutionary stable strategy unique? From condition 9 in Table 4, it can be seen that there are two evolutionary-stable strategies, namely, and , for the cloud–edge collaboration system composed of and , which mainly depend on the values of the cost and benefit in the evolutionary game matrix and the initial state of this system, i.e., the saddle point .
4.3. Factors Affecting Evolutionary Stability and Evolutionary Results
Through the analysis of the evolutionary game system constituted by and under different conditions in Section 3.2, it was found that after a long-term evolutionary game under different conditions, the final evolutionary result of the relationship between and was either cooperation or noncooperation or no equilibrium state. In contrast, there were two evolutionary stable strategies in condition 9, so it is necessary to further explore the variation of each factor of the cloud–edge collaboration system in condition 9 and the influence of the initial state of the system on the final evolutionary result. We derived the following theorem:
Theorem 1.
The probability increases with the increase in , that is, the stronger the willingness of to cooperate, the more inclined is to choose the cooperative processing strategy.
Proof of Theorem 1.
Let ; when , ; then, no matter what value takes, ’s strategy selection is in a stable state. When , two cases are discussed: First, when , is the evolutionarily stable point, that is, when the proportion of ’s cooperative processing is not high, is evolutionarily stable in the “solo-processing” strategy; second, when , is the evolutionarily stable point, that is, when the cooperative proportion of is high, is evolutionarily stable in the “coprocessing” strategy. □
Theorem 2.
The probabilityincreases with the increase in, that is, the stronger the willingness ofto cooperate, the more inclinedis to choose the cooperative processing strategy.
Proof of Theorem 2.
Let ; when , ; then, no matter what value takes, ’s strategy selection is in a stable state. When , two cases are discussed: First, when , is the evolutionarily stable point, that is, when the proportion of ’s cooperative processing is not high, is evolutionarily stable in the “solo-processing” strategy; second, when , is the evolutionarily stable point, that is, when the cooperative proportion of is high, is evolutionarily stable in the “coprocessing” strategy. □
It is known from the assumptions that = in condition 9, and the factors have the values of ; through a mathematical calculation, is satisfied, and the stability analysis can be obtained by judging the signs of the determinant and trace of the Jacobian matrix at each equilibrium point, as shown in Table 5.

Table 5.
Stability analysis of equilibrium points (condition 9).
From Table 5 under condition 9, we can find that among the five possible local equilibria in the system composed of and , and are evolutionary stable strategies, and are unstable points, and is a saddle point. To show the dynamical evolution law between and more graphically, we illustrate the phase diagram of the evolution game between the two parties in Figure 1.
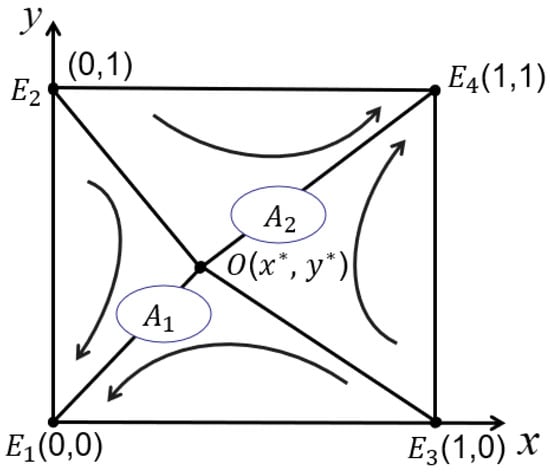
Figure 1.
System phase diagram.
As can be seen from Figure 1, the fold line consisting of the saddle point and the two unstable points constitutes the critical line of the convergence state of the system. If the initial state is in the lower left region of the critical line, denoted as , the final evolution result of the system converges to . If the initial state is in the upper right region of the critical line, denoted as , the final evolution result of the system converges to . The evolution path and final evolution result of the system composed of and are related to the initial state of the system and the payoff matrix, and when the initial state is near the saddle point , a slight variation in the initial state will affect the final evolution result of the game. When , and converge to increase the possibility of cooperative treatment, and the system evolves along toward the equilibrium point . When , and tend to decrease the possibility of coprocessing, and the system evolves along toward the equilibrium point . From Figure 1, the area of is computed as
From Equation (14), it can be found that the factors affecting the area of are the variables , and , which are directly related to , the variables which are directly related to , and the variables , , and , which are related to both parties. The analysis of these parameters leads to the following conclusions:
- With increasing , the possibility of the system evolving to increases;
- With increasing , the possibility of the system evolving to increases;
- For , when , the possibility of the system evolving to increases with an increment in ; when , the possibility of the system evolving to increases with an increment in ;
- For , when , the possibility of the system evolving to increases with an increment in . When , the possibility of the system evolving to increases with an increment in .
5. Numerical Simulation Analysis
5.1. Simulation Analysis
The theoretical derivation of the model does not intuitively reflect how each parameter in the system affects the system’s stability; thus, in this section, we conducted some simulations to further demonstrate the trajectory of each equilibrium point above and the evolution of different initial points of the game to the final equilibrium point. From a practical point of view, the net benefits of both and should be larger than zero, no matter which strategy is chosen. For both and , the aggregated benefit of the cooperative processing strategy should be larger than the aggregated benefit of the individual processing. The cost of service for the coprocessing strategy should be lower than the cost of service for the solo-processing strategy, that is, the total benefit is larger and the cost of service for the two parties to cooperate is less. According to the condition combination, the combination of various cost and benefit values should follow conditions , and . In this paper, we considered the practical scenario of cloud service providers and edge operators and chose the following parameters to discuss the condition combination. The parameters for were , the parameters for were , and the common parameters for both parties were .
- The influence of the initial willingness of both parties on the evolution of the system
Figure 2 depicts the dynamic evolution of the strategy choice of the participating parties over time. The initial values of the game for both parties were taken as . As can be seen from Figure 2, when , the evolutionary stability of the system gradually changes from to with the increase in , verifying that the stronger the willingness of to cooperate is, the more inclined is to evolve to a stable state in co-processing. When , with the increase in , the evolutionary stability of the system gradually changes from to , which verifies that the stronger the cooperative willingness of , the more inclined is to evolve to a stable state in co-processing.
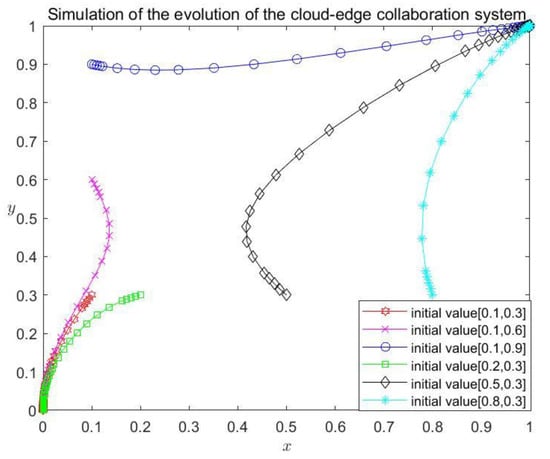
Figure 2.
Simulation of the evolution of the system through initial values.
It can be seen from the figure that when the two parties choose different initial values , the game finally evolve to different results accordingly. In this state, the value of the saddle point can be calculated as . Recall the aforementioned theoretical analysis, it can be seen that when the initial value of falls into region , the initial value finally converges to , and and choose the “solo-processing” game strategy. When the initial value of falls into region , the initial value finally converges to , and and choose the “coprocessing” game strategy. It is obvious that the final evolution of both strategies depends on the initial value of .
- Factors affecting evolutionary stability and evolutionary results
From Equation (14), we know that the parameters in the equation also influence the final evolutionary results of the game. Due to the limited space, we only selected the cooperation benefit , cooperation cost of both parties, data transmission cost of , and complaint loss of as variables and analyzed the influence of the emphasis parameters and on the system evolution results. We set the initial value as to analyze the evolutionary process of the game and verify the theoretical analysis results.
First, we sequentially set the values of to be 40, 41, and 42, to verify the impact of the cooperation gain on the stability of the cloud–edge collaboration service system. As shown in Figure 3, we can find the trend of the evolutionary results of the two parties and with the parameter adjustment of cooperative gain . The result shows that with the increment in , both parties and tend to collaboratively process user service requests faster and faster, which means that increasing the cooperative gain can promote the cloud–edge collaboration system to evolve towards the final evolutionary result {coprocessing, coprocessing}.
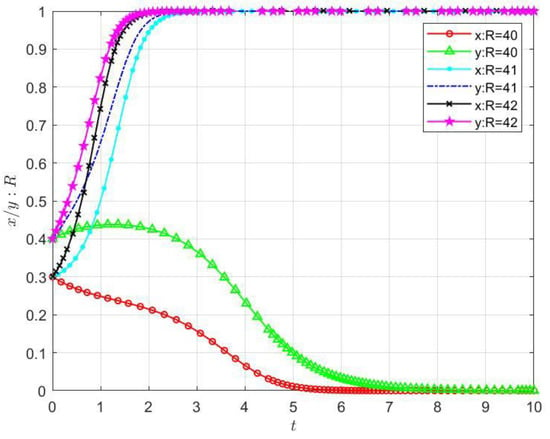
Figure 3.
Impacts of cooperation benefit R on the stability of the cloud–edge collaboration system.
Cost management is an essential part of enterprise management. Thus, we set the values of to be 16, 17, and 18 sequentially to further verify the impact of cooperation cost on the stability of the cloud–edge collaboration service system. As shown in Figure 4, we can derive the trend of the evolutionary results of the two parties and with the parameter adjustment of cooperation cost . The result shows that with the increment in , both parties and tend to process user service requests more and more slowly in collaboration, indicating that increasing the collaboration cost inhibits the cloud–edge collaboration system to evolve towards the evolutionary result {coprocessing, coprocessing}.
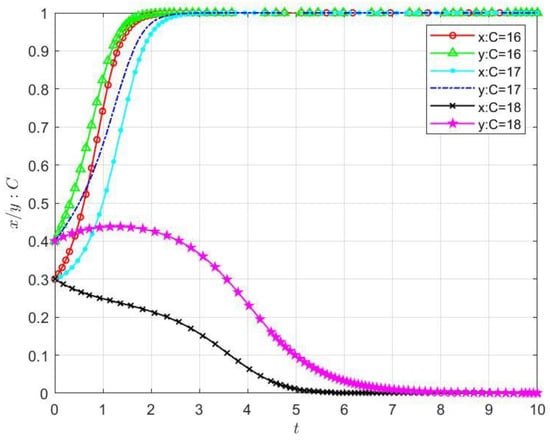
Figure 4.
Impacts of cooperation cost C on the stability of the cloud–edge collaboration system.
The values of were chosen sequentially as to verify the impact of the data transmission cost of on the stability of the cloud–edge collaboration service system with the participation of . As shown in Figure 5, we derived the trend of the evolutionary results of the game party with the parameter adjustment of the data transmission cost . When = 2, the system’s saddle point can be calculated and the initial state falls into the region , indicating that the value of is within the tolerable range. Based on the sensitivity of the evolutionary results to the initial conditions, both parties eventually evolve to . As keeps increasing, the path evolution to slows down, the evolution point of the system gradually evolves from the stable state to the state , and the convergence speed of and choosing their own processing strategies accelerates. The above research result indicates that when gradually increases or even exceeds the budget, rapidly chooses the solo-processing strategy in order to avoid more losses, i.e., the increase in data transmission cost is damaging the stability of the cloud–edge collaboration service system and may even lead to the breakdown of the collaborative processing relationship.
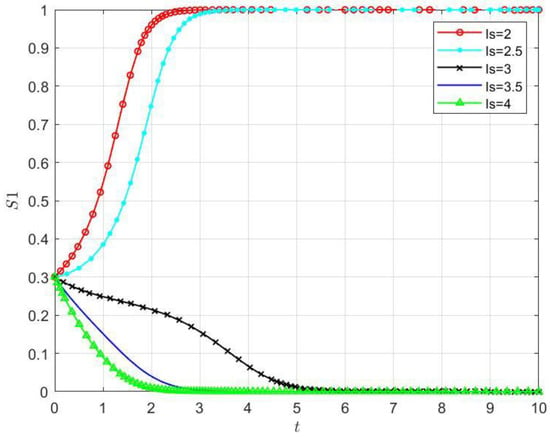
Figure 5.
Impacts of data transmission cost of on the stability of the cloud–edge collaboration system.
Furthermore, the loss cost of was selected sequentially as and to further verify the impact of the loss cost due to user complaints on the stability of the cloud–edge collaboration system with participation. Figure 6 derives the trend of the evolutionary results of the game party with the parameter adjustment of the complaint loss . When = 4, the system’s saddle point is calculated and the initial state falls into the region , indicating that the value of is within the tolerable range. Based on the sensitivity of the evolutionary results of the game system to the initial conditions, both parties eventually evolve to . As increases, the path evolution to slows down, the evolution point of the system gradually evolves from the stable state to the state , and the convergence speed of and choosing to handle the solo-processing strategy accelerates. This indicates that when gradually increases or even exceeds the budget, rapidly chooses the solo-processing strategy in order to avoid more losses, i.e., the benefit loss due to user complaints plays a negative role in the stability of the cloud–edge collaboration system, leading to an increased possibility of relationship breakdown.
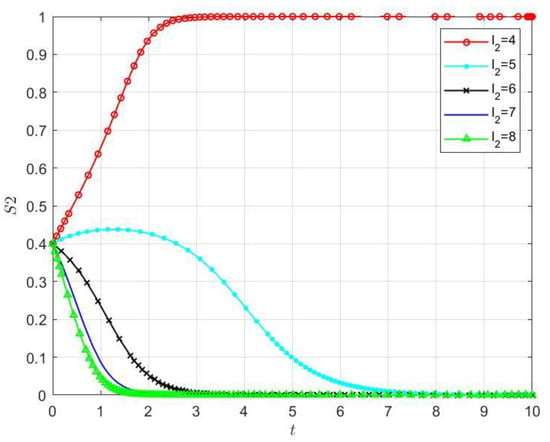
Figure 6.
Impacts of user complaint loss of on the stability of the cloud–edge collaboration system.
Finally, we show the details of the transition from (0, 0) and (1, 1) to the ESS of the cloud–edge collaboration system when increasing the level of emphasis gradually, to verify the influence of the emphasis level on the stability of the cloud–edge collaboration system. We set the values of variables to be , which satisfied . Figure 7, Figure 8 and Figure 9 show the phase diagram of the system when the values of the importance degree α and β were 0, 0.05, and 0.09, respectively, where each different color line describes the evolution path and the final evolution result of the strategies of both parties from a certain initial state of the system, and all lines represent the evolution trend of the system from different initial states. We can find that with the increment in emphasis level parameters and , the combination of variables transitions from satisfying , to satisfying , and finally reaches the state with . The result shows that the cloud–edge collaboration service system evolves from {solo-processing, solo-processing} and {coprocessing, coprocessing} to the evolutionary stable result of {coprocessing, coprocessing}, and gradually eliminates the dependence on the initial value.
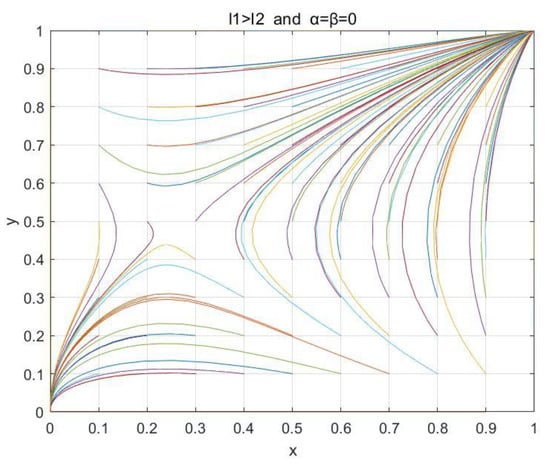
Figure 7.
Impacts of the emphasis level parameters and for the QoE on the stability of the cloud–edge collaboration system when , α = β = 0.
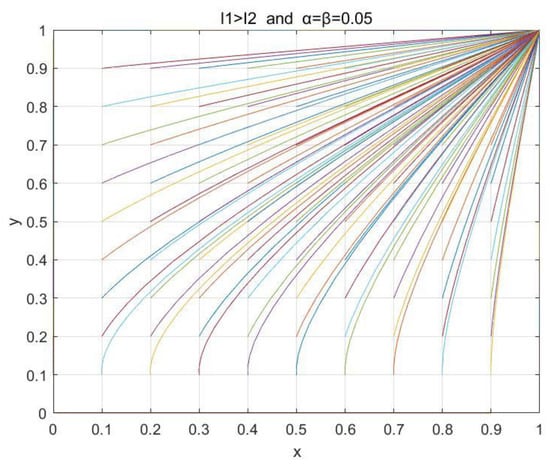
Figure 8.
Impacts of the emphasis level parameters and for the QoE on the stability of the cloud–edge collaboration system when , α = β = 0.05.
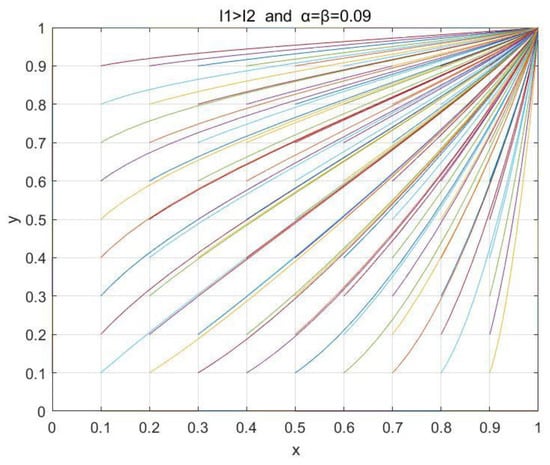
Figure 9.
Impacts of the emphasis level parameters and for the QoE on the stability of the cloud–edge collaboration system when , α = β = 0.09.
Similarly, the variables were assigned the values , which satisfied . Figure 10, Figure 11 and Figure 12 show the phase diagram of the system when the values of the importance degree α and β were 0, 0.05, and 0.09, respectively, where each different color line describes the evolution path and the final evolution result of the strategies of both parties from a certain initial state of the system, and all lines represent the evolution trend of the system from different initial states. We can find that with the increment in emphasis level parameters α and β, the combination of variables transitions from satisfying , to satisfying , and finally reaches the state with . The final evolution results are similar to the former. This fully indicates that the higher the emphasis level of and on the QoE, the more it contributes to the stability of the cloud–edge collaboration system, and when the emphasis level is high enough, the evolutionary result of the system is no longer relying on the initial value.
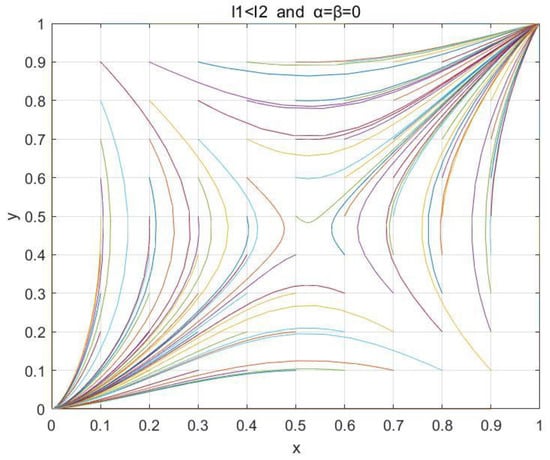
Figure 10.
Impacts of the emphasis level parameters and for the QoE on the stability of the cloud–edge collaboration system when , α = β = 0.
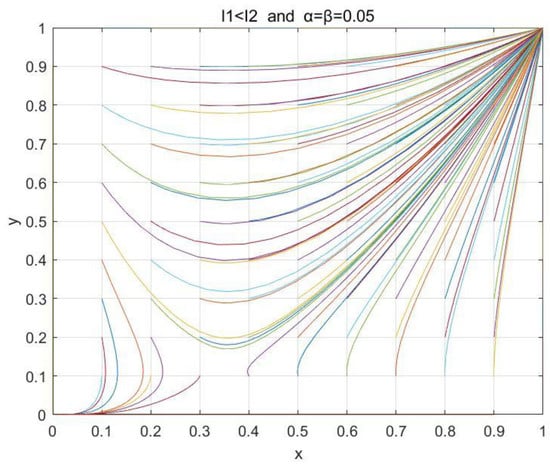
Figure 11.
Impacts of the emphasis level parameters and for the QoE on the stability of the cloud–edge collaboration system when , α = β = 0.05.
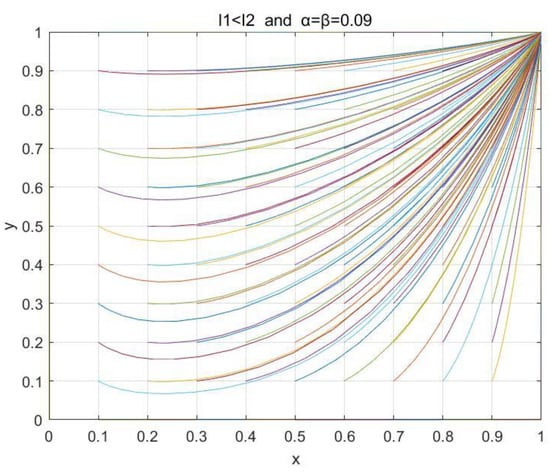
Figure 12.
Impacts of the emphasis level parameters and for the QoE on the stability of the cloud–edge collaboration system when , α = β = 0.09.
Furthermore, this paper also considered the emphasis level parameter of as , when . As shown in Figure 13, with and initial value , the final strategy of is the “solo-processing” one. As increases, evolves towards the “solo-processing” strategy more and more slowly. When reaches a certain value, the final strategy of becomes the “coprocessing” one and evolves faster and faster as increases. As shown in Figure 14, when the value of decreases to a certain value so that , the overall evolutionary trend is consistent with that in Figure 13, but the evolutionary process keeps accelerating. This means that prefers to choose the “co-processing” strategy in that case. This indicates that the higher the emphasis level of , the more favorable it is for the formation and stability of the cloud–edge collaboration system.
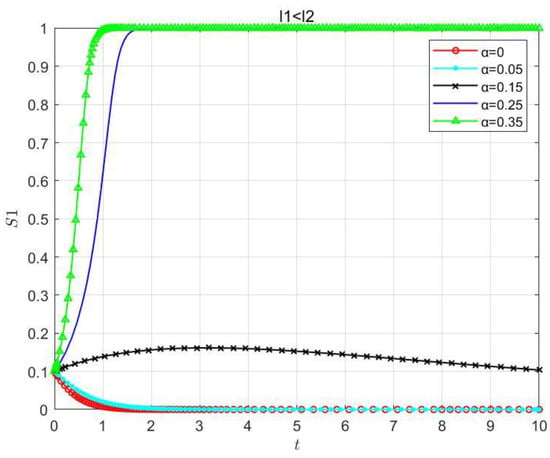
Figure 13.
Impacts of the emphasis level parameter of for the QoE on the stability of the cloud–edge collaboration system when .
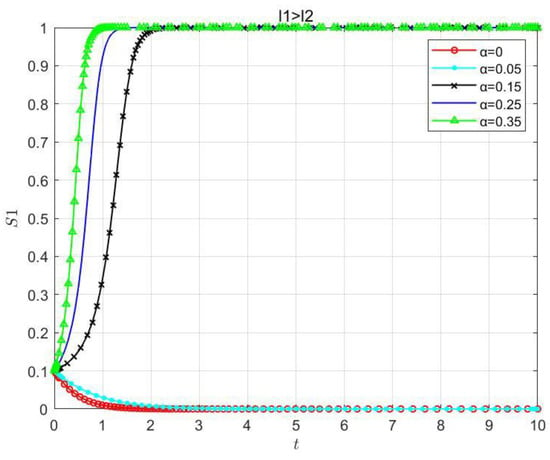
Figure 14.
Impacts of the emphasis level parameter of for the QoE on the stability of the cloud–edge collaboration system when .
Similarly, this paper also considered the emphasis level parameters of as when . As shown in Figure 15, with and initial value , the final strategy of is the “solo-processing” one. As increases, evolves towards the “solo-processing” strategy more and more slowly. When reaches a certain value, the final strategy of becomes the “co-processing” one and evolves faster and faster as increases. As shown in Figure 16, when the value of decreases to a certain value so that , the overall evolutionary trend is consistent with that in Figure 15, but the evolutionary process also keeps accelerating. This means that the acceleration of this evolutionary trend is caused by the decrement in the value of , and is independent of the relationship between the values of and . This indicates that the numerical relationship between and only affects the evolution mechanism of the cloud–edge collaboration system but does not affect the whole evolution process.
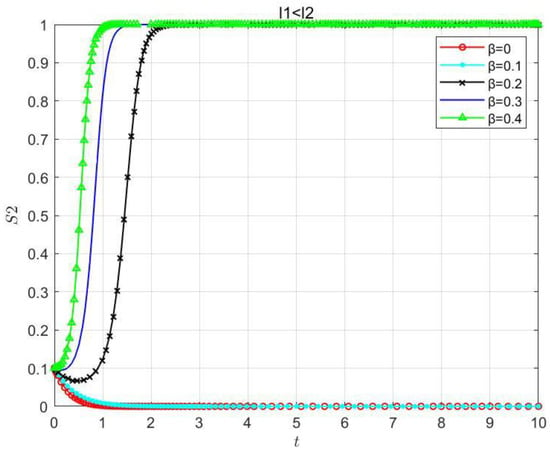
Figure 15.
Impacts of the emphasis level parameter of for the QoE on the stability of the cloud–edge collaboration system when .
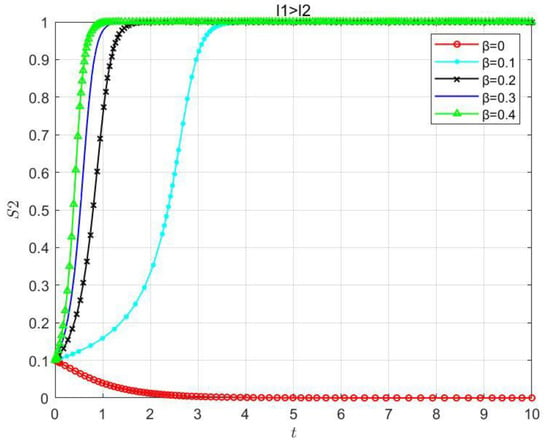
Figure 16.
Impacts of the emphasis level parameter of for the QoE on the stability of the cloud–edge collaboration system when .
5.2. Further Discussion
From the above research analysis, we conclude the following:
- The strategy choices of cloud service providers and edge operators promote each other. The improvement of one party’s willingness to cooperate in processing drives the improvement of the other party’s willingness to cooperate, thus promoting the cooperative stability of the whole cloud–edge system.
- For the cloud service providers and edge operators, the smaller the solo-processing benefit, the larger the solo-processing cost, the less the user loss, the less the cost of data transmission, and the higher the emphasis level on the QoE, thus the more favorable the evolutionary stability of collaborative processing. For the cloud–edge collaboration system, the initial willingness of both parties has a particular influence on the system evolution results. The larger the cooperation benefit, the lower the cooperation cost, and the stronger the stability of the system, the more favorable it is to achieve cooperation.
- The lost fee due to the service constraint agreement breach should be at least larger than the difference between the aggregated benefit when the parties choose to handle processing separately and the benefit when they cooperate to handle processing together, in order to establish a stable cooperative processing relationship between the parties, and to avoid possible speculation by both parties.
- In the cloud–edge collaborative processing, profit-sharing and cost-sharing should be dynamically adjusted in real time with the changes in the market environment, and different shares have different effects on the stability of the cloud–edge collaboration system. This is related to the importance both parties attach to the QoE and the loss of users who quit or complain.
- The higher the emphasis on user experience both parties put, the stronger the cooperation intention is, and this effect is obvious.
To effectively maintain the stability of the cloud–edge collaboration system and promote digital technologies to better serve the digital transformation of enterprises, the following recommendations are proposed in this paper based on the above-mentioned research analysis and results:
- Focusing on improving the cooperation willingness of cloud service providers or edge operators can achieve the effect of improving the cooperation willingness of both parties, so as to promote the harmony and stability of the whole system.
- Cloud service providers and edge operators, as the two major stakeholders of digital services, can reasonably use the policy dividends of the digital economy era and Internet technology to accelerate product development and constantly upgrade and transform to reduce the various costs of user services and improve economic returns, so as to further construct a more stable and mutually reinforcing cooperative relationship between them and jointly promote the high-quality development of the digital economy.
- The governments can supply a sound system to provide a legal basis and guarantee for the cost of service constraint agreement breach, enhance the binding force and enforcement of the agreement, provide credit guarantees for both parties to improve each other’s credit, increase the cooperation stickiness of both parties, integrate all forces together to maintain a stable cloud–edge collaboration system to serve the digital transformation of enterprises, drive the innovation and evolution of business models, and increase the value creation of enterprises.
- The benefit and cost distribution proportion of both parties in the cloud–edge collaboration system should be dynamically adjusted. Cloud service providers and edge operators influence each other in multiple dimensions. Therefore, in the changing market economy environment, both parties should adjust their benefit and cost distribution strategy in real time according to the actual cost and contribution, so that the allocation of benefits and costs can quickly respond to the market and satisfy both parties, thus improving the enthusiasm of cooperation and ensuring the long-term stability of the cloud–edge collaboration system.
- The greater the emphasis on QoE by cloud service providers and edge operators, the more it helps the establishment and stability of the cloud–edge collaboration system. Therefore, we should lower market entry barriers, improve competition in similar services, and create a favorable competitive environment in the future.
6. Conclusions
In this paper, we constructed an evolutionary game model of cloud service providers and edge operators in the cloud–edge collaboration system in the digital economy era and thoroughly analyzed the internal principle of the evolution of the decision-making behavior of both parties and the internal mechanism of collaboratively processing user service requests. We also obtained the equilibrium and stability conditions for the two-party decision to reach the ideal state, performed numerical simulations to verify the two-party evolutionary path, and discussed the parameters that influenced the stability of the cloud–edge collaboration system. We further proposed some specific measures to promote the stability of the cloud–edge collaboration system from the perspective of cloud service providers, edge operators, and external entities, respectively.
A summary of future research directions is given below. First, we will apply other game models to investigate the equilibrium strategies of cloud service providers and edge operators. Second, we will further refine the assumptions to bring the model much closer to the actual scenario. Third, we will further analyze the relevant intrafluid factors, e.g., incentives, penalties, etc. Finally, we will consider the influence of other parties in the system, such as cloud agents and other external entities that may affect the stability of the system.
Author Contributions
Conceptualization, S.L. and W.S.; validation and formal analysis, M.X. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the support from the National Natural Science Foundation of China (no. 71971188), the Humanities and Social Science Fund of Ministry of Education of China (no. 22YJCZH086), the Natural Science Foundation of Hebei Province (nos. G2022203003, G2023203008), the S&T Program of Hebei (no. 22550301D), and the support Funded by Science and Technology Project of Hebei Education Department (no. ZD2022142).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gao, J.-L.; Chen, Y.; Zhang, X.-Q. Digital Technology Driving Exploratory Innovation in the Enterprise: A Mediated Model with Moderation. Systems 2023, 11, 118. [Google Scholar] [CrossRef]
- Huang, J.; Jin, H.; Ding, X.; Zhang, A. A Study on the Spatial Correlation Effects of Digital Economy Development in China from a Non-Linear Perspective. Systems 2023, 11, 63. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. A systematic literature review on QoS-aware service composition and selection in cloud environment. J. Netw. Comput. Appl. 2018, 110, 52–74. [Google Scholar] [CrossRef]
- Sousa, I.; Queluz, M.P.; Rodrigues, A. A survey on QoE-oriented wireless resources scheduling. J. Netw. Comput. Appl. 2020, 158, 102594. [Google Scholar] [CrossRef]
- Díez, I.D.L.T.; Alonso, S.G.; Hamrioui, S.; López-Coronado, M.; Cruz, E.M. Systematic Review about QoS and QoE in Telemedicine and eHealth Services and Applications. J. Med. Syst. 2018, 42, 182. [Google Scholar] [CrossRef]
- Di, X.; Liu, H.X. Boundedly rational route choice behavior: A review of models and methodologies. Transp. Res. Part B Methodol. 2016, 85, 142–179. [Google Scholar] [CrossRef]
- Kozanoglu, D.C.; Abedin, B. Understanding the role of employees in digital transformation: Conceptualization of digital literacy of employees as a multi-dimensional organizational affordance. J. Enterp. Inf. Manag. 2021, 34, 1649–1672. [Google Scholar] [CrossRef]
- Warner, K.; Wäger, M. Building dynamic capabilities for digital transformation: An ongoing process of strategic renewal. Long Range Plan. 2019, 52, 326–349. [Google Scholar] [CrossRef]
- Bouwman, H.; Nikou, S.; de Reuver, M. Digitalization, business models, and SMEs: How do business model innovation practices improve performance of digitalizing SMEs? Telecommun. Policy 2019, 43, 101828. [Google Scholar] [CrossRef]
- Sergei, T.; Arkady, T.; Natalya, L.; Pathak, R.; Samson, D.; Husain, Z.; Sushil, S. Digital transformation enablers in high-tech and low-tech companies: A comparative analysis. Aust. J. Manag. 2023. [Google Scholar] [CrossRef]
- Sjödin, D.; Parida, V.; Visnjic, I. How Can Large Manufacturers Digitalize Their Business Models? A Framework for Orchestrating Industrial Ecosystems. Calif. Manag. Rev. 2021, 64, 49–77. [Google Scholar] [CrossRef]
- Zainal-Abidin, H.; Scarles, C.; Lundberg, C. The antecedents of digital collaboration through an enhanced digital platform for destination management: A micro-DMO perspective. Tour. Manag. 2023, 96, 104691. [Google Scholar] [CrossRef]
- Alenezi, M.; Wardat, S.; Akour, M. The Need of Integrating Digital Education in Higher Education: Challenges and Opportunities. Sustainability 2023, 15, 4782. [Google Scholar] [CrossRef]
- Zioło, M.; Bąk, I.; Spoz, A. Theoretical framework of sustainable value creation by companies. What do we know so far? Corp. Soc. Responsib. Environ. Manag. 2023. [Google Scholar] [CrossRef]
- Kumar, V.; Sindhwani, R.; Behl, A.; Kaur, A.; Pereira, V. Modelling and analysing the enablers of digital resilience for small and medium enterprises. J. Enterp. Inf. Manag. 2023. ahead-of-print. [Google Scholar] [CrossRef]
- Mandviwalla, M.; Flanagan, R. Small business digital transformation in the context of the pandemic. Eur. J. Inf. Syst. 2021, 30, 359–375. [Google Scholar] [CrossRef]
- Luo, S. Digital Finance Development and the Digital Transformation of Enterprises: Based on the Perspective of Financing Constraint and Innovation Drive. J. Math. 2022, 2022, 1607020. [Google Scholar] [CrossRef]
- Dremel, C.; Herterich, M.; Wulf, J.; Waizmann, J.C.; Brenner, W. How AUDI AG Established Big Data Analytics in its Digital Transformation. MIS Q. Exec. 2017, 16, 81–100. [Google Scholar]
- Awan, U.; Shamim, S.; Khan, Z.; Zia, N.U.; Shariq, S.M.; Khan, M.N. Big data analytics capability and decision-making: The role of data-driven insight on circular economy performance. Technol. Forecast. Soc. Chang. 2021, 168, 120766. [Google Scholar] [CrossRef]
- Jiang, C.; Fan, T.; Gao, H.; Shi, W.; Liu, L.; Cérin, C.; Wan, J. Energy aware edge computing: A survey. Comput. Commun. 2020, 151, 556–580. [Google Scholar] [CrossRef]
- Shiraz, M.; Gani, A. A lightweight active service migration framework for computational offloading in mobile cloud computing. J. Supercomput. 2014, 68, 978–995. [Google Scholar] [CrossRef]
- Ali, Z.; Jiao, L.; Baker, T.; Abbas, G.; Abbas, Z.H.; Khaf, S. A Deep Learning Approach for Energy Efficient Computational Offloading in Mobile Edge Computing. IEEE Access 2019, 7, 149623–149633. [Google Scholar] [CrossRef]
- Xu, F.; Xie, Y.; Sun, Y.Y.; Qin, Z.S.; Li, G.J.; Zhang, Z.Y. Two-stage Computing Offloading Algorithm in Cloud-Edge Collabo-rative Scenarios Based on Game Theory. Comput. Electr. Eng. 2022, 97, 107624. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, B.; Lv, Z.; Choo, K.-K.R. A task scheduling algorithm considering game theory designed for energy management in cloud computing. Futur. Gener. Comput. Syst. 2020, 105, 985–992. [Google Scholar] [CrossRef]
- Hamed, A.Y.; Alkinani, M.H. Task Scheduling Optimization in Cloud Computing Based on Genetic Algorithms. Comput. Mater. Contin. 2021, 69, 3289–3301. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, R.; Zhao, X.; Zhu, J.; Xu, J.; Wu, Q. A computational resources scheduling algorithm in edge cloud computing: From the energy efficiency of users’ perspective. J. Supercomput. 2022, 78, 9355–9376. [Google Scholar] [CrossRef]
- Fard, M.V.; Sahafi, A.; Rahmani, A.M.; Mashhadi, P.S. Resource allocation mechanisms in cloud computing: A systematic literature review. IET Softw. 2020, 14, 638–653. [Google Scholar] [CrossRef]
- Karthiban, K.; Raj, J.S. An efficient green computing fair resource allocation in cloud computing using modified deep reinforcement learning algorithm. Soft Comput. 2020, 24, 14933–14942. [Google Scholar] [CrossRef]
- Zhang, J.; Chi, L.; Xie, N.; Yang, X.; Zhang, X.; Li, W. Strategy-proof mechanism for online resource allocation in cloud and edge collaboration. Computing 2021, 104, 383–412. [Google Scholar] [CrossRef]
- Liao, H.; Zhou, Z.; Liu, N.; Zhang, Y.; Xu, G.; Wang, Z.; Mumtaz, S. Cloud-Edge-Device Collaborative Reliable and Communication-Efficient Digital Twin for Low-Carbon Electrical Equipment Management. IEEE Trans. Ind. Inform. 2023, 19, 1715–1724. [Google Scholar] [CrossRef]
- Schmidt, C. Are Evolutionary Games Another Way of Thinking about Game Theory? J. Evol. Econ. 2004, 14, 249–262. [Google Scholar] [CrossRef]
- Smith, J.M.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Liu, H.; Eldarrat, F.; Alqahtani, H.; Reznik, A.; de Foy, X.; Zhang, Y. Mobile Edge Cloud System: Architectures, Challenges, and Approaches. IEEE Syst. J. 2018, 12, 2495–2508. [Google Scholar] [CrossRef]
- Ma, S.; Guo, S.; Wang, K.; Jia, W.; Guo, M. A Cyclic Game for Service-Oriented Resource Allocation in Edge Computing. IEEE Trans. Serv. Comput. 2020, 13, 723–734. [Google Scholar] [CrossRef]
- Friedman, D. Evolutionary Games in Economics. Econometrical 1991, 59, 637–666. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).