Abstract
With the upgrading of people’s consumption patterns, the omni-channel supply chain becomes the mainstream form of e-commerce platform enterprise development. Aiming at two different e-commerce enterprises, we construct an evolutionary game model for enterprises’ “online+offline” omni-channel construction strategy by self-build or cooperating with brick-and-mortar stores. It is based on the Stackelberg and Cournot competition model, combined with the omni-channel pricing strategy, using the theory of perfect rationality and bounded rationality, and combing the non-cooperative game and evolutionary game to realize. Moreover, the evolutionary game process is simulated. Through the dynamic changes of the system, the strategy selection behavior mechanism of the retail channel subjects is deeply analyzed. It is found that enterprises’ strategy choices are influenced by both competitors and profits, and evolutionary stabilization strategies are not unique. In addition, changes in consumer loyalty, physical feelings, and sharing ratio during the evolutionary process will affect the stability rate of enterprises’ behavioral choices.
1. Introduction
With the rapid development of the Internet and mobile communication technology, the e-commerce industry has shown a rapid development trend. According to statistical data, as of December 2022, the number of online shopping users in China exceeded 845 million. At the same time, the explosive growth of e-commerce has brought serious challenges to traditional retailers. Traditional retailers are accelerating the loss of old customers, and people are relying on online product search and price comparison for online and offline integrated shopping [1]. Most consumers will organically combine offline shopping with online shopping in the shopping process, to enjoy the advantages of online convenience and offline self-service as well as in-store experience [2,3,4,5]. For example, the online channel provides consumers with the ability to easily search product assortments, whereas the retail channel allows for direct product interaction and consultation with sales agents [6]. More and more product manufacturers/suppliers are choosing to sell products through e-commerce platforms. For example, in November 2015, Amazon opened a brick-and-mortar bookstore in Seattle, Washington, which is the first brick-and-mortar bookstore established by the company. Warby Parker, a famous online eyewear seller, opened a flagship store in New York in 2013. In addition, Tmall, a famous comprehensive shopping platform, opened its first brick-and-mortar store in Hangzhou in April 2018. Omni-channel retailing is rapidly becoming a predominant norm in the industry [7], with a growing number of purely online e-commerce enterprises actively exploring their offline retail channels. In fact, Apple, Best Buy, and Walmart have started omni-channel programs in the retail market [8].
As a key link in the operation and management of e-commerce, logistics plays an important role in improving business performance and creating differentiated competitive advantages [9,10,11]. The development of electronic technology has forced companies in the distribution supply chain to adapt to consumers’ online and offline purchasing modes. As typical representatives of e-commerce platforms, Amazon and JD have also invested heavily in building their own logistics service systems, aiming to provide high-quality logistics services for platform-owned products and third-party seller products, as e-commerce enterprises would choose different offline retail channel construction methods according to their own development status, financial ability, as well as enterprise strategy.
Modern consumers are becoming sophisticated enough to switch between online and offline channels in the process of purchase decision making [12]. They consider all possible alternatives across all possible channels to optimize their shopping experience [7]. To further model how market characteristics influence e-commerce enterprises’ decisions, in this paper, we investigate how e-commerce enterprises based on the existing online retail channels choose to develop offline retail channel strategies in the process of corporate competition. Based on the bounded rationality assumption and evolutionary game theory, it simulates e-commerce enterprises’ strategic choice of the offline retail channel with cost difference in the evolutionary game process. Additionally, it further analyzes the influence of consumer loyalty, physical feelings, and cost- and revenue-sharing ratio on the evolutionary stability point. We first determine the optimal strategy choice for competitive e-commerce enterprises by establishing a non-cooperative game model under complete rationality. Next, we develop a bounded rational evolutionary game model to analyze the behavioral evolution of competitive enterprises under different revenue conditions.
Motivated by the above-mentioned issues, we pose the following research questions: (1) How do e-commerce enterprises build offline retail channels in the competitive process? (2) How should the evolutionary game among competing e-commerce enterprises be formulated and solved? (3) What are the optimal strategies for e-commerce enterprises in the evolutionary game? (4) What are the effects of enterprises’ cost and profit on enterprises’ decision making?
To answer these questions, we first consider the competitive situation of e-commerce firms in the online retail channel and try to develop the offline retail channel through two strategies (self-built offline retail channels or cooperating with existing brick-and-mortar stores). We calculate the optimal strategy combinations for competing e-commerce enterprises using the non-cooperative game. Based on these results, an evolutionary game method is introduced to explore the long-term evolution process of competing e-commerce enterprises to develop offline retail channels under bounded rationality conditions. In this case, we show that as important members of the e-commerce market, whether enterprises self-build the offline retail channel or cooperate with brick-and-mortar stores depends on the profits and the strategy of competitors. In addition, with the change in enterprises’ profit, competitive enterprises would choose the same offline retail channel strategy, or choose different strategies, respectively, which would both appear in the evolution process. In particular, the evolutionary stabilization strategy is not unique when the enterprises’ profit is within a certain range.
The contributions of this paper include three points. First, from the perspective of e-commerce enterprises’ self-building offline retail channels and cooperation with existing brick-and-mortar stores, it enriches the research of omni-channel retail by considering the evolutionary behavior of enterprise strategy selection under bounded rationality. Second, in the classification strategy of developing offline retail channels, we emphasize consumer channel loyalty and the perceived value of different channels, which provides a new research idea for studying online and offline retail models. Third, we discuss the choice of offline retail channels by e-commerce enterprises in the product competition environment, which helps to further understand the impact of external competitive factors on enterprises’ strategy choices. In addition, we also discuss the implications of our results, while highlighting the management implications of the findings for realistic enterprises behavior strategies.
The rest of this paper is organized as follows: The next section describes and analyzes the existing literature. Section 3 and Section 4 show the problem description, parameters, modeling, and results. Asymptotic stability of the equilibrium points and evolutionary stability strategies are introduced in Section 5. Numerical experiments are executed, and their findings are reported in Section 6. Ultimately, Section 7 summarizes the conclusions and future research opportunities.
2. Literature Review
In recent years, in the context of the technological revolution and the accelerating trend of industrial change, the development of e-commerce enterprises does not rely only on online sales. As a typical representative of new retail, online and offline shopping integration has become one of the key issues in the supply chain link, which is receiving more and more attention.
2.1. Omni-Channel Marketing
In recent years, technological innovation and consumption upgrading have accelerated the rapid development of exploring the “new retail” channel model and reconstructed the traditional retail industry’s value creation mode centered on e-commerce or brick-and-mortar stores, which is fragmented online and offline. [13]. To promote the collaborative development of online and offline in the new retail era, and provide consumers with a high-quality, flexible, and seamless shopping experience, the omni-channel retail supply chain is fully developed [14,15,16].
The maturity of Internet technology and the sophistication of consumer demand have led to continuous changes in retail sales channels, from the initial single-channel retailing to the prosperity of dual [17] and multi-channel [18,19,20]. E-commerce enterprises have also been exploring offline channels, either by building their own offline channels or by expanding their offline channels in cooperation with existing retailers, and omni-channel retailing was first proposed by Rigby in 2011. He argued that as the market changes, digital retailing is rapidly reconfiguring, and retail channels should not be bounded to a single channel, but should develop various channels to satisfy consumers, that is omni-channel retail (OCM) [21]. Showrooms and cyberspaces have become major shopping trends for omni-channel retail shoppers due to technological advances and a surge in purchases from mobile devices. As well as increased engagement with user-generated content on social media platforms [22], it describes the practice of checking out products in a physical store but eventually making an actual purchase online or on a mobile device [23].
How to obtain optimal returns under the omni-channel has been a hot research topic for enterprises and relevant scholars [24,25,26]. Beck and Rygl (2015) argue that the omni-channel, which differs from the dual channel, places more emphasis on the connection between online and offline channels, where consumers can compare between channels to make choices [27]. For example, before purchasing a product, experience the product attributes offline, and then switch to online purchases, and offline pickup. Omni-channel retail integrates the Internet and physical stores, which is a trend of the times. Dzyabura and Jagabathula (2021) studied the problem of display decisions for offline channel products, addressing how firms should choose an optimal offline assortment to maximize the profitability of both channels [28]. To this end, Bell et al. (2014, 2015, 2020) developed numerous models and a comprehensive research practice using a combination of methods, adding an offline showroom channel in addition to considering online and offline channels, and verifying the advantages of showroom services in marketing and operations [13,29,30]. Not coincidentally, Kumar et al. (2012) explored the positive impact of offline showrooms on online channel sales based on retailing issues in the US fashion industry and found that offline physical stores can boost online sales and give a positive complementary effect to online sales [31].
With the development of science and technology, China’s retail industry has made great progress. Supermarket retail has changed from a seller’s market to a buyer’s market, and consumers’ choices are increasing day by day. At the same time, traditional retailers should also scientifically judge the market from many aspects. The aforementioned studies help us to understand the impact of different channel sales models on retailers’ or consumers’ consumption patterns. Controversy between online retailing and offline retailing is also endless. How to strengthen and correctly understand the concept and significance of new retailing, clarify the status and purpose of new retailing, integrate offline and online competition into a new combination and model, discover their respective characteristics and advantages, and gain new retail models and economic growth points has become a new research direction. The above research helps us to understand the influence of different channel sales models on retailers or consumers’ consumption patterns. However, there is little research on e-commerce enterprises choosing the omni-channel marketing model. Therefore, a comprehensive study on the choice of the omni-channel marketing strategy of e-commerce enterprises under the background of online and offline integration will help to expand the scope of existing research. At the same time, in addition to innovating the channel cooperation between enterprises, it is also a problem worthy of attention to carry out new cooperative games between enterprises, so we explore the game between individuals.
2.2. Evolutionary Game
Evolutionary game theory (EGT) integrates the basic ideas of classical game theory and biological evolutionary dynamics to reveal the changing characteristics of animal group behavior, and is a game based on the participants’ “bounded rationality”. The game participants with bounded rationality will not choose the best strategy at the beginning, but through continuous learning, adjustment, and finally reaching a stable state of dynamic evolution [32,33,34]. It is very common to use the classical game model to solve the omni-channel problem in the supply chain. Evolutionary game theory overcomes the defects of traditional game theory, which is widely used in many fields of economic management and other disciplines [35,36].
Numerous scholars have made different attempts in many fields such as population evolution [37], epidemic disease transmission [38], environmental pollution control [39,40,41], and waste product recycling [42,43]. At present, evolutionary game theory has also been applied in a great number of analytical studies related to the field of closed-loop supply chain channel research [44,45]. Among them, Zhu et al. (2007) developed a three-party game model considering government subsidies and penalties to explore the game equilibrium strategy between the government and core firms in green supply chains [46]. To facilitate the effective management of the recycling of e-waste, Liu et al. [47] constructed a tripartite Ito stochastic evolutionary game model to perform analysis of the complex game interaction between national government, local government, and recyclers. Based on omni-channel retailing, considering consumer migration and advertising cost sharing, Chen et al. [48] built a dynamic price and advertising game model of the omni-channel supply chain with BOPS (buy-online-pickup-in store) [48]. Combined with the evolutionary game theory, Hosseini-Motlagh examined the relationship between the evolutionary strategies of SC members towards channel coordination and the profit surplus distribution among them [49]. Soleimani et al. (2022) used evolutionary game theory to explore ordering and pricing policies in a decentralized two-echelon dual-channel supply chain including one manufacturer and one retailer [50]. Ma and Li (2020) develop a dual-channel supply chain model and a dynamic game model based on different display strengths and investigate two online sales models, direct online retailing (the M-R case) and reselling through e-retailers (the e-R case) [45]. The above studies show that evolutionary game theory is used to manage the complex relationships among participants, which has become a common approach to study supply chain problems [51].
To sum up, among the existing studies, more literature discusses the omni-channel model of “online order and physical store pickup”, and only a small amount of literature discusses the role of showrooms from the perspective of empirical evidence or information services. The literature on the impact of omni-channel perspective and enterprises competition on e-commerce retailer’ optimization decisions are rare.
In summary, among the existing studies, more literature explores the omni-channel model of “online ordering and brick-and-mortar stores pickup” from a content perspective, while only a small amount of literature explores the role of exhibition halls from an empirical or information service perspective. At the same time, there is relatively little literature on considering exhibition hall issues from the perspective of online and offline evolutionary games. This article innovatively selects strategies for offline channel construction in different channels from the perspective of integration of online and offline, based on methodology, and explores from the perspective of optimal enterprise benefits to provide optimal decision-making for enterprises.
This paper differs from existing studies in that it considers the situation of self-building or cooperating with existing brick-and-mortar stores to open offline retailing channels in the Internet era. In this situation, we combine the non-cooperative game and the evolutionary game, explore the competing relationship between enterprises’ channel construction strategy choices, and construct an evolutionary game model of self-built and cooperating with existing brick-and-mortar stores channel construction strategies. The evolutionary game process is simulated to analyze the evolutionary stability of the channel construction strategy choices of both sides of the game.
Through the dynamic changes of the system, we deeply analyze the mechanism of strategy selection behavior of retail channel subjects, and we explore the impact of different channel choices on the profit of omni-channel retailers. Moreover, we further analyze the impact of consumer loyalty, physical feelings, and sharing ratio on the evolutionary stability point in order to enrich the relevant theoretical research while providing decision support for enterprises to carry out business innovation model reform.
3. Problem Description
Suppose there are two competing e-commerce companies in the market; , define enterprise 1 and enterprise 2, respectively (Tmall and JD.com). They started with Internet retailing, selling goods on their portal platforms and competing with each other. With the development and expansion of their scale, enterprise 1 and enterprise 2 are no longer satisfied with the commodity profits obtained in the online network market and hope to obtain greater profits in offline market. Enterprise 1 and enterprise 2 can actively explore the offline retail market through two strategies, either by cooperating with existing brick-and-mortar stores (Alibaba Group invested HKD 5.37 billion in Intime Commercial in 2014) or by investing in establishing their own offline sales stores (Alibaba Group opened 1 million Tmall stores in China during 2017), as shown in Figure 1. Among them, the two strategies have different costs for establishing offline channels and different benefits for enterprises. Assume that when the enterprise invests in establishing its own offline sales store, it needs to pay a cost of . When the enterprise cooperates with an existing brick-and-mortar retail store, the cost is ,, and when the enterprise cooperates with the existing brick-and-mortar retail store, the partner will bear part of the cooperation cost and share some of the company’s product sales revenue. Among them, the coefficients of cost and revenue sharing ratio are set as . In the market, enterprise 1 and enterprise 2 sell products through online sales channels at retail prices and , respectively, while in the offline market they sell products at retail prices and .
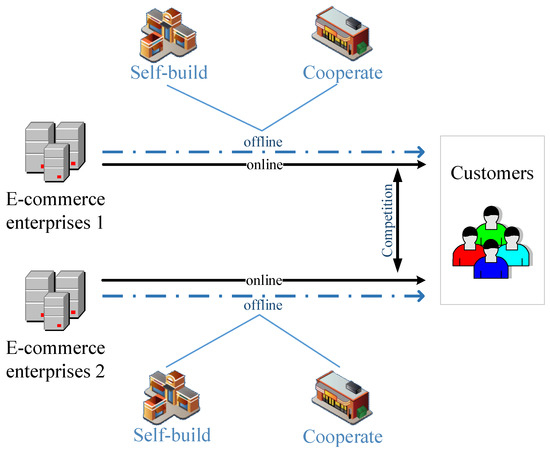
Figure 1.
Online and offline integration omni-channel supply chain.
For the sake of analysis, we use the percentage of consumers who purchase online as a certain indicator in the manuscript to characterize customer loyalty to online retail channels, represented by , where . Accordingly, is the customer loyalty of consumers to offline retail channels. When consumers choose to buy commodities in offline brick-and-mortar stores, they will increase the perceived value of commodities through physical feelings and experiences of commodities, and the degree of increase is set as . Assume that the information of the two enterprises is symmetrical and the operating costs of sales channels are basically the same; in order to simplify the model and better analyze the results, it is normalized to 0.
The demand function in this paper is assumed to be a linear function of price, and the online channel demand of enterprise 1 is ; the online channel demand of enterprise 2 is . The offline channel demand of enterprise 1 is ; the offline channel demand of enterprise 2 is , where represents the product market basis and parameter denotes the sensitivity degree to cross-enterprise; and are the online and offline retail prices of enterprise 1, respectively; and and explain the online and offline retail prices of enterprise 2, respectively.
Based on the above problem descriptions and assumptions, the profit functions of enterprise 1 and enterprise 2 are: when enterprises invest in self-built offline retail channels, the profit of enterprise 1 is , and the profit of enterprise 2 is ; when enterprises establish offline retail channels by cooperating with existing physical stores, the profit of enterprise 1 is , and the profit of enterprise 2 is .
4. Pricing Game Model under Different Offline Channel Establishment Strategies
Science enterprises face two strategic choices to develop offline retail channels; three non-cooperative game scenarios between enterprise 1 and enterprise 2 are considered, namely the Stackelberg game dominated by enterprise 1, and the Stackelberg game and Nash game dominated by both enterprises. Then, the corresponding game models are established, respectively.
4.1. Both Enterprise 1 and Enterprise 2 Choose to Build Their Offline Retail Channels by Themselves
When enterprise 1 and enterprise 2 both choose to build their offline retail channels through investment, enterprise 1 and enterprise 2 play a two-stage Nash game. First, enterprise 1 and enterprise 2 simultaneously decide the retail prices and of commodities in the online retail channel. Then, enterprise 1 and enterprise 2 simultaneously decide the retail prices and of commodities in offline retail channels. The enterprise profit and commodity demand function can be obtained as follows:
By solving the above equation, it can be concluded that when both enterprise 1 and enterprise 2 choose to build their own offline retail channels through investment, the optimal profit is as follows:
4.2. Both Enterprises 1 and Enterprise 2 Choose to Cooperate with Existing Brick-and-Mortar Stores
When both enterprise 1 and enterprise 2 choose to develop offline retail channels by cooperating with offline stores, enterprise 1 and enterprise 2 play a two-stage Nash game. First, enterprise 1 and enterprise 2 simultaneously decide the retail prices and of the online retail channel. Then, enterprise 1 and enterprise 2 simultaneously decide the retail prices and of the offline channel. The enterprise profit and commodity demand function can be obtained as follows:
By solving the above equation, it can be obtained that when both enterprise 1 and enterprise 2 choose to cooperate with existing brick-and-mortar stores, the optimal profit obtained is as follows:
4.3. Enterprise 1 Chooses to Invest in Self-Built Offline Retail Channels, and Enterprise 2 Chooses to Cooperate with Existing Brick-and-Mortar Stores
When enterprise 1 chooses to build its offline retail channel through investment, and enterprise 2 chooses to establish an offline retail channel through a cooperative offline store, enterprise 1 and enterprise 2 play a two-stage Stackelberg game. First, enterprise 1 decides the retail prices and for both online and offline channels at the same time. Then, enterprise 2 decides the retail prices and for both online and offline channels at the same time. The enterprise profit and commodity demand function can be obtained as follows:
By solving the above equation, it can be obtained that when enterprise 1 and enterprise 2 choose different strategies, the optimal profit obtained is as follows:
4.4. Enterprise 1 Chooses to Cooperate with Existing Brick-and-Mortar Stores, and Enterprise 2 Chooses to Invest in Self-Built Offline Retail Channels
When enterprise 1 chooses to establish a retail channel through cooperative offline brick-and-mortar stores, and enterprise 2 chooses to build its own offline retail channel through investment, enterprises 1 and enterprise 2 play a two-stage Stackelberg game. First, enterprise 2 decides the retail prices and for both online and offline channels at the same time. Then, enterprise 1 decides the retail prices and for both online and offline channels at the same time. The enterprise profit and commodity demand function can be obtained as follows:
By solving the above equation, it can be obtained that when both enterprise 1 and enterprise 2 choose different strategies, the optimal profit obtained is as follows:
Assume that the probability that enterprise 1 chooses to build its own offline sales channel through investment is , and the corresponding probability of choosing to cooperate with offline stores to establish an offline sales channel is . The probability that enterprise 2 chooses to build its own offline sales channel through investment is , and the corresponding probability of choosing to establish an offline sales channel in cooperation with an offline store is , where , and are functions of time. The overall profit matrix of enterprise 1 and enterprise 2 can be obtained as shown in Table 1.

Table 1.
Profit matrix.
4.5. Duplicated Dynamic Equation Solving
According to the evolutionary game rule [36], the revenue of enterprise 1 using the self-built strategy is recorded as , the revenue of enterprise 1 using the cooperative strategy is , and the average revenue is .
The revenue of enterprise 2 using the self-built strategy is , the revenue of enterprise 2 adopting the cooperative strategy is , and the average revenue is .
The replicate dynamic equation of the two enterprises is:
Arranging as follows:
According to Friedman’s research [36], when inequality is satisfied, the evolutionary stable point ESS of the system can be obtained.
The joint cubic equation yields 5 equilibrium points , , , , and . Obviously, points , , , and are the equilibrium points of the system. If is also the equilibrium point of the system, they need to be further satisfied , that is .
To further find the stable point of system evolution [52,53,54,55,56], the Jacobian matrix can be constructed:
The Jacobian matrix corresponding to the first equilibrium point :
The eigenvalues,
The determinants and traces at each equilibrium point are shown in Table 2:

Table 2.
Determinant and trace of Jacobian matrix at equilibrium point.
According to the criterion of the Jacobian matrix, this point is an ESS point when the determinant is greater than 0 and the trace is less than 0, i.e., , . According to this criterion, the sign of the determinant and trace can be calculated separately for each equilibrium point under different conditions to determine whether it is a stable point for system evolution.
5. Evolutionary Game Model Analysis
When two enterprises choose different strategic combinations to gain different benefits in developing offline sales markets, the choice of self-build and cooperation strategies will also evolve towards different stable points. The following will further discuss the evolutionary equilibrium results of the two enterprises’ strategy choices in developing offline sales channels under different conditions and analyze the conclusions obtained.
Proposition 1.
When or or , is the equilibrium point of the system.
The results of the Jacobian matrix are shown in Table 3:

Table 3.
Local stability analysis of Case 1.
At this time, is the only ESS point of the system evolution and the evolutionary phase diagram is shown in Figure 2.
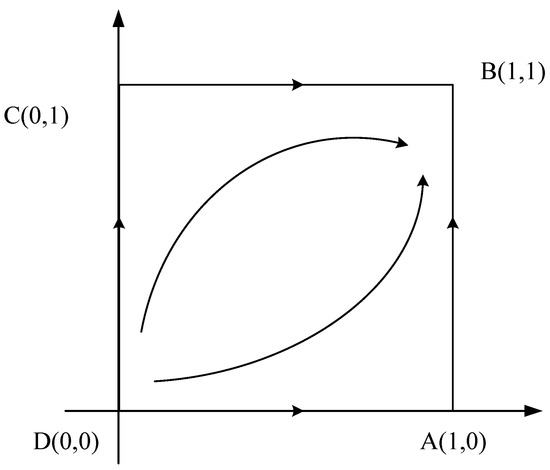
Figure 2.
Case 1 evolutionary game phase diagram.
As can be seen from the figure, no matter what the initial state of the system is, the system will eventually converge to the evolutionary stable strategy , that is, both enterprise 1 and enterprise 2 will choose to build their own offline retail channels through investment. When an enterprise chooses to build its own offline retail channels, the profit obtained by the enterprise is greater than that obtained by the enterprise in cooperation with the existing brick-and-mortar store. Compared to cooperating with existing brick-and-mortar stores, the cost of investment and self-build by enterprises is higher, but they will receive the full retail profits of products without sharing with partners. Driven by the greater economic interest, both enterprises will eventually develop a strategic state in which each chooses to invest in its own offline sales channel.
Proposition 2.
When or or , is the equilibrium point of the system.
The results of the Jacobian matrix are shown in Table 4:

Table 4.
Local stability analysis of Case 2.
At this time, is the only ESS in the system evolution and the evolution phase diagram is shown in Figure 3.
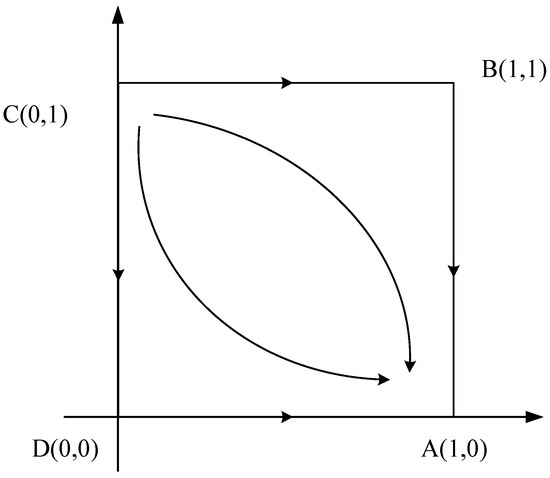
Figure 3.
Case 2 evolutionary game phase diagram.
As can be seen from the figure, no matter what the initial state of the system is, the system will eventually converge to the evolutionarily stable strategy , that is, enterprise 1 chooses to build its own offline sales channels through investment, and enterprise 2 expands its offline sales channels through cooperation. Under this circumstance, compared with the development of offline sales channels through cooperation, the cost of investing in self-built offline sales channels is still higher. Enterprises with competitive advantages can rely on their own advantages to obtain higher sales profits to make up for the cost of investing in the self-built offline retail channel strategy. While due to the lack of strength, competitive inferior enterprises cannot obtain the same high profit as competitive superior enterprises to cover the cost of investing in self-built offline sales channels. Therefore, they choose a lower-cost cooperation strategy to develop offline channels. After the long-term game, enterprises with competitive advantages in the system will choose to invest more in self-built offline sales channels, and enterprises with competitive disadvantages will choose to cooperate more to develop offline channel strategies until they reach the final balance.
Proposition 3.
When or or , is the equilibrium point of the system.
The results of the Jacobian matrix are shown in Table 5:

Table 5.
Local stability analysis of Case 3.
At this time, is the only ESS in the system evolution, and the evolutionary phase diagram is shown in Figure 4.
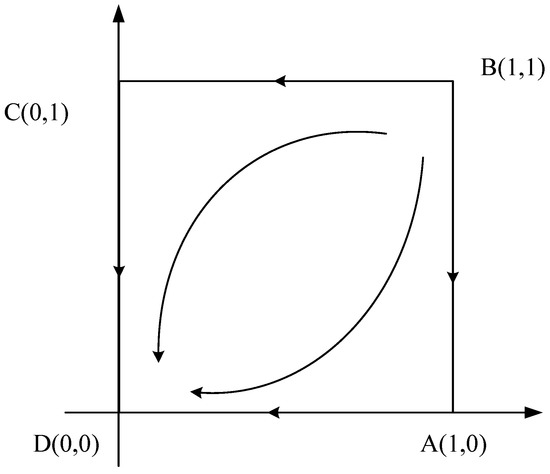
Figure 4.
Case 3 evolutionary game phase diagram.
As can be seen from the figure, no matter what the initial state of the system is, the system will eventually converge to the evolutionarily stable strategy , that is, all enterprises choose to establish offline sales channels by cooperating with existing entities. In this case, the cost of investing in self-built offline channels is significantly higher than the cost of establishing offline channels through cooperation, and the gap between the sales profits obtained by enterprises under the two strategies is relatively small. Even if the sales revenue obtained by the enterprise through cooperation to establish offline channels needs to be shared with its partners, this strategy will not reduce the enterprise’s revenue but will increase the enterprise’s profit. After the long-term game, the proportion of enterprises that choose to invest in self-built offline channels will gradually decrease until all of them choose to establish offline channels through cooperation.
Proposition 4.
When or or , is the equilibrium point of the system.
The results of the Jacobian matrix are shown in Table 6:

Table 6.
Local stability analysis of Case 4.
Conclusion 4: At this time, is the only ESS in the system evolution, and the evolutionary phase diagram is shown in Figure 5.
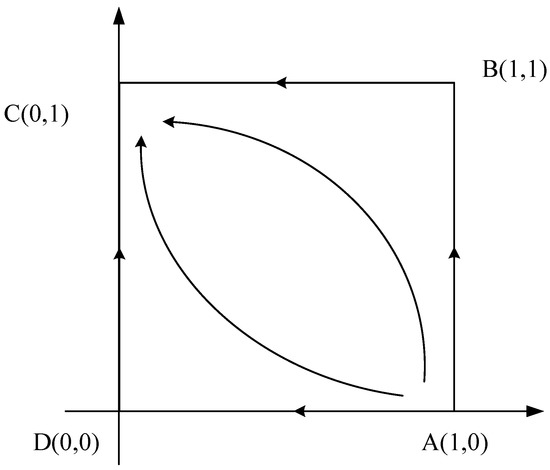
Figure 5.
Case 4 evolutionary game phase diagram.
As can be seen from the figure, no matter what the initial state of the system is, the system will eventually converge to the evolutionarily stable strategy , that is, enterprise 1 chooses to develop offline sales channels through cooperation, and enterprise 2 chooses to build its own offline sales channels through investment. The reason is the same as the management enlightenment and conclusion 2, so it is omitted here.
Proposition 5.
When , and are the equilibrium point of the system.
The results of the Jacobian matrix are shown in Table 7:

Table 7.
Local stability analysis of Case 5.
At this time, and are the ESS of the system evolution and the evolution phase diagram is shown in Figure 6.
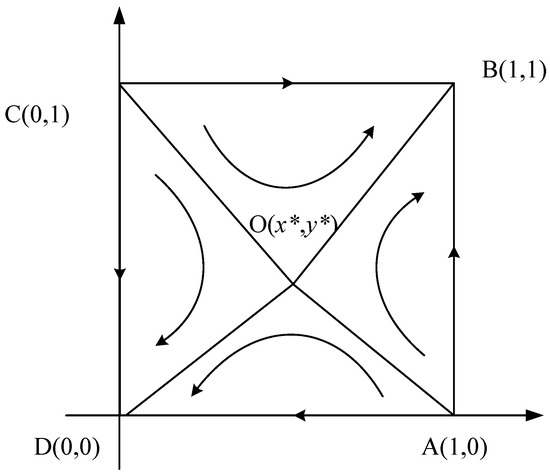
Figure 6.
Case 5 evolutionary game phase diagram.
As can be seen from the figure, the final stable state of the system depends on the initial state and the size of the dividing area formed by the two imbalance points and the saddle point. When the initial state is located in the AOCB area, the system converges to point , and the two enterprises evolve towards investing in self-built offline sales channels; when it is located in the AOCD area, the system converges to point , and the two enterprises evolve towards cooperating with existing brick-and-mortar stores. The probability in which direction the equilibrium result evolves is determined by the size of the quadrilateral AOCB and AOCD. If , the probability of the two enterprises evolving towards investing in self-built offline sales channels is greater than that towards cooperating with existing brick-and-mortar stores; if , the probability of the two enterprises evolving towards cooperating with existing brick-and-mortar stores is greater than the probability of evolving towards investing in self-built offline sales channels; if , the probability of the two enterprises evolving towards investing in self-built offline sales channels is equal to the probability of evolving towards cooperating with existing brick-and-mortar stores.
In this situation, when a competitor chooses to establish offline sales channels through cooperative offline stores, the gap between the two strategies for establishing offline sales channels is relatively small, which is not enough to make up the difference in cost between the two strategies, and enterprises will choose the strategy of cooperating with offline brick-and-mortar stores with lower costs. However, when a competitor chooses to invest in self-built offline sales channels, if the enterprise chooses to cooperate with offline brick-and-mortar stores to develop offline sales channels, the enterprise will lose its competitive advantages in the offline market, and the final revenue will be greatly reduced. Therefore, enterprises will always choose the same strategy as competitors to develop offline sales channels. After the long period of game, the two enterprises finally stabilize their choice of offline channel strategy in {self-build, self-build} and {cooperation, cooperation}.
Proposition 6.
When , and are the equilibrium point of the system.
The results of the Jacobian matrix are shown in Table 8:

Table 8.
Local stability analysis of Case 6.
At this time, and are the ESS of the system evolution, and the evolutionary phase diagram is shown in Figure 7.
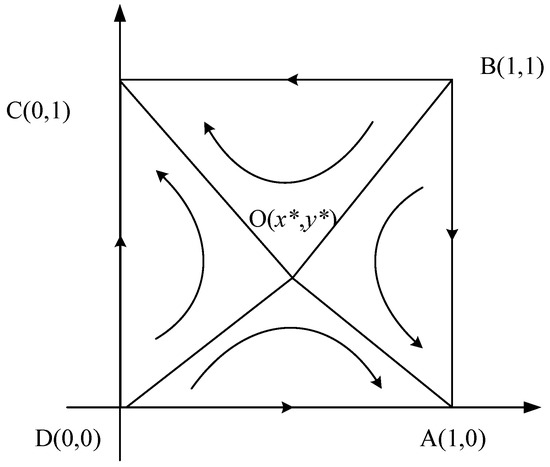
Figure 7.
Case 6 evolutionary game phase diagram.
As can be seen from the figure, the final stable state of the system depends on the initial state and the size of the dividing area formed by the two imbalance points and the saddle point. When the initial state is located in the CDOB area, the system converges to point , the two enterprises strategically choose to cooperate with the existing brick-and-mortar store of the enterprise 1, and the enterprise 2 invests in the self-built offline sales channel and evolves; when located in the ADOB area, the system converges to point , the two enterprises strategically choose to invest in company 1 to build their own offline sales channels, and enterprise 2 cooperates with existing brick-and-mortar stores. The probability of the evolution of the equilibrium result in which direction is determined by the area of the quadrilateral CDOB and ADOB. If , the two enterprises cooperate with company 1 and have brick-and-mortar stores, and the probability of the direction evolution of enterprise 2 to invest in the self-established offline sales channel is greater than the probability of enterprise 1 to invest in the self-established offline sales channel, and the enterprise 2 cooperates with existing brick-and-mortar stores; if , then vice versa; if , the two enterprises cooperate with company 1 and have existing brick-and-mortar stores, and the probability that company 2 invests in self-built offline sales channels is equal to the probability of investing in self-built offline sales channels for company 1, and company 2 cooperates with existing brick-and-mortar stores.
In this case, when a competitor chooses to establish offline sales channels through cooperative offline stores, the gap between the sales profits of the enterprises under the two strategies of developing offline channels is large enough to make up for the cost between the two strategies, while enterprises will choose to pay a higher cost to build their own offline sales channel strategy. When competitors choose to invest in self-built offline sales channels, if the enterprise chooses to invest in self-built offline sales channels to develop offline markets, it will intensify competition between the two enterprises. The increased cost of self-build can be indirectly transferred to consumers through price increasing. Therefore, enterprises will always choose different strategies from their competitors to develop offline sales channels. After a long-term game, the two enterprises finally chose to develop offline channels in two states: {self-built, cooperation} and {cooperation, self-built}.
6. Numerical Simulation
The above analysis relate to strategy selection mechanism of e-commerce enterprises’ sales channels is based on evolutionary game theory. In order to further clarify the operation track and stability of the evolutionary game strategy of e-commerce enterprises’ omni-channel construction from the perspective of online and offline integration, this paper uses MATLAB 2016b to simulate and analyze the above evolutionary game model and draws the corresponding time sequence diagram under the initial probability . Since the actual data set is huge and difficult to obtain and process, the data used in the numerical example are simulated and estimated, as shown in Table 9. To some extent, it does not have practical significance, but it has certain economic significance. Although, these data have been processed before use to strictly comply with certain assumptions of this study. Considering the evolution trend of the system under different conditions, six cases are set up under the condition that the corresponding eigenvalue relationship is satisfied, and simulation verification is carried out. According to the actual situation, the parameters are set as follows:

Table 9.
Parameter value.
We also assume that the initial values of the two enterprises are equal and input the parameters of the six cases into MATLAB, and Figure 8, Figure 9, Figure 10 and Figure 11 simulate the evolution time series plots for different cases and the sensitivity analysis of the parameters , , and to the evolutionary stability of the system.
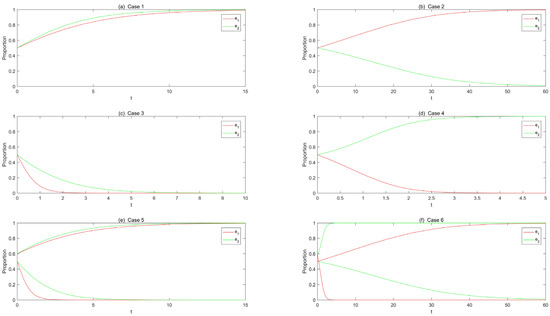
Figure 8.
Evolutionary results under different conditions.
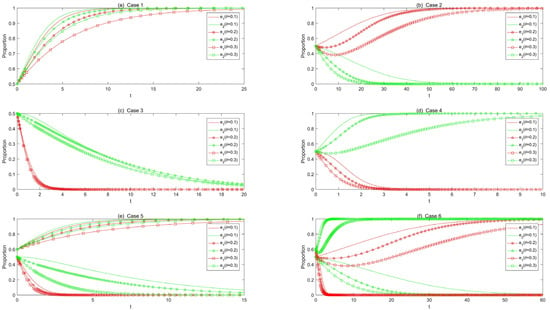
Figure 9.
Effect of customer loyalty for the online retail channel on evolutionary results.
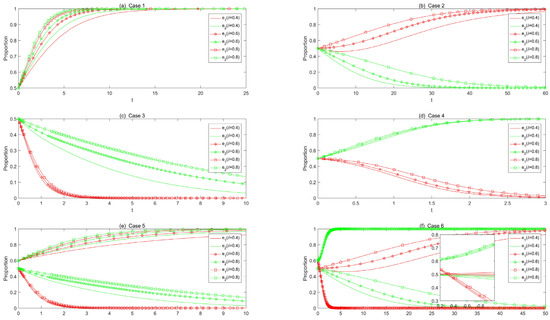
Figure 10.
Effect of customer physical feelings for the online retail channel on evolutionary results.
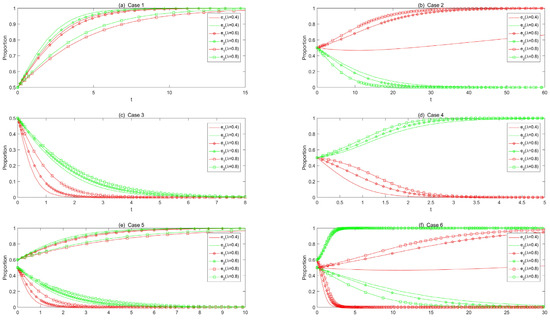
Figure 11.
Effect of coefficients of cost bearing and revenue sharing on evolutionary results.
6.1. The Stability Simulation of Equilibrium Point
With Case 1 to Case 6, we performed the stability simulations of equilibrium points, and the simulation results are shown in Figure 8a–f.
It can be seen from Figure 8 that the final evolution of the system is stable at different points for different conditions. Similarly, as in the results in Section 5, when e-commerce enterprises choose self-built offline retail channels, and the profit under any conditions is greater (or less) than that when enterprises choose to cooperate with existing stores, enterprises’ behavior will tend to choose self-built offline retail channels (or cooperation with existing stores). Namely, the system is stable at (or ) during the evolutionary process. However, if two e-commerce enterprises prioritize profit optimization in choosing different offline retail channel strategies, then they will choose different offline retail channels and not be affected by the competitors’ strategy. At this point, enterprises’ behavior will tend to differ in the evolution process (stable at or ). Expressly, when the profits of two e-commerce enterprises who choose the same establishing offline retail channel strategies is greater than (less than) that of enterprises who choose different strategies, the enterprise behavior will tend to choose the same (different) strategies. Taking Figure 8a,b as examples, when two enterprises choose to build offline channels and the cost difference between establishing their own channels and cooperating with existing brick-and-mortar stores is not significant, an evolutionary stability strategy of {self-built, self-built} will appear, which verifies Proposition 1. On the contrary, when there is a significant difference in required costs, an evolutionary stability strategy of {self-built, cooperation} will appear, which verifies Proposition 2.
In reality, e-commerce enterprises hope to increase their product sales and profit by establishing an omni-channel retail model. When choosing different offline retail channel strategies, enterprises should not only consider the changes in their costs and profits, but also consider the strategic choices of competitive enterprises in the market. This makes it more complex for companies to consider and make strategic choices.
6.2. Impacts of Changes in Customer Loyalty on Evolutionary Paths
With Case 1 to Case 6, we analyzed impacts of changes in customer loyalty for the online retail channel on evolutionary paths, and the simulation results are shown in Figure 9a–f.
In Figure 9a–f, the solid line is used as a benchmark for comparison. When the stable strategy for enterprises is self-built offline retail channels, increasing customer loyalty can enable enterprises to reach a stable equilibrium point later than the initial state. Conversely, when the stable strategy for enterprises is cooperate with existing stores, increasing customer loyalty can enable enterprises to reach a stable equilibrium point earlier than the initial state. As shown in Figure 9a, the red lines represent the strategic evolutions of enterprise 1. As loyalty for the online retail channel () increases from 0.1 to 0.3, the evolution speed of enterprise 1’s choice of self-built offline channels gradually decreases. In other words, as online channel loyalty increases, the willingness of enterprise 1 to choose self-built offline brick-and-mortar stores decreases.
In reality, when consumers are more loyal to online retail channels, they will pay more attention to the convenience of online shopping and ignore the problem of a poor degree of online shopping experience. At this time, e-commerce enterprises are not very motivated to develop offline sales retail channels. In particular, e-commerce enterprises have to pay more costs to establish offline retail channels by themselves than to cooperate with existing brick-and-mortar stores. The higher the loyalty of consumer channels, the harder it is for enterprises to establish their own offline retail channels.
6.3. Impacts of Changes in Customer Physical Feelings on Evolutionary Paths
With Case 1 to Case 6, we analyzed impacts of changes in customer physical feelings for the online retail channel on evolutionary paths, and the simulation results are shown in Figure 10a–f.
In Figure 10a–f, the solid line is used as a benchmark for comparison. When the stable strategy for enterprises is self-built offline retail channels, increasing customer physical feelings can enable enterprises to reach a stable equilibrium point sooner. Conversely, when the stable strategy for enterprises is cooperate with existing stores, increasing customer physical feelings will delay the enterprises from reaching a stable equilibrium point. As shown in Figure 10b, the red lines represent the strategic evolution of enterprise 1, while the green lines represent enterprise 2. By comparing the three red lines, it can be seen that as the customer physical feelings for the online retail channel () increases from 0.4 to 0.8, the evolution speed of enterprise 1’s choice of self-built offline channels gradually increases. In other words, as customer physical feelings for the online retail channel increases, the willingness of enterprises who choose to self-build channels also increases. By comparing the three green lines, it can be seen that as customer physical feelings for the online retail channel increases from 0.4 to 0.8, the evolution speed of enterprise 2’s choice of cooperating with the existing brick-and-mortar store gradually slows down. In other words, as the customer physical feelings for the online retail channel increases, the willingness to choose to cooperate with the existing brick-and-mortar stores decreases.
In practice, when consumers’ physical perception willingness is stronger, they are more inclined to buy goods physically. The reason is that consumers can better understand the attributes and quality of products before buying products. Either self-built offline retail channels or cooperation with existing stores are the ways to develop offline retail channels. Self-built offline retail channels better reflect the importance that enterprises attach to consumers’ perception of entities. Therefore, when e-commerce enterprises find that consumers have a strong physical experience in the process of consumption, they should actively establish their own offline retail physical stores to better reflect the reputation and service of the enterprise.
6.4. Impacts of Changes in Coefficients of Cost Bearing and Revenue Sharing on Evolutionary Paths
With Case 1 to Case 6, we analyzed impacts of changes in coefficients of cost bearing and revenue sharing on evolutionary paths, and the simulation results are shown in Figure 11a–f.
In Figure 11a–f, the solid line is used as a benchmark for comparison. If both enterprises choose the same strategy for offline retail, increasing sharing ratio will slow down the time it takes for the enterprises to reach a stable equilibrium point (shown in Figure 11a,c,e). When both enterprises choose to establish self-built offline retail channels, the increasing sharing ratio makes enterprises observe that they can achieve more profits even when cooperating with offline physical stores. When both enterprises choose to cooperate with offline physical stores, the increasing sharing ratio makes enterprises observe that they would pay the greater cost to cooperate with physical stores. Therefore, when both enterprises choose the same strategy, the increasing share ratio slows their behavioral evolution. However, if both enterprises choose different strategies, the increasing sharing ratio is likely to accelerate the evolution of enterprises choosing to cooperate with offline brick-and-mortar stores (shown in Figure 11b,d,f). As shown in Figure 11d, the red lines represent the strategic evolution of enterprise 1, while the green lines represent enterprise 2. By comparing the three red lines, it can be seen that as the coefficients of cost bearing and revenue sharing () borne by enterprise 1 increases from 0.4 to 0.8, the evolution speed of enterprise 1’s choice to cooperate with existing brick-and-mortar stores gradually slows down. By comparing the three green lines, it can be seen that as the coefficients of cost bearing and revenue sharing () increase, the evolution speed of enterprise 2 choosing to build their own offline channels is gradually accelerating. In other words, as the coefficients of cost bearing and revenue sharing () borne by enterprises increase, they are more inclined to choose to build their own offline channels and give up on cooperating with existing brick-and-mortar stores.
In reality, the cooperation of e-commerce enterprises with offline brick-and-mortar retail stores is a common method of offline channel expansion. E-commerce enterprises can reach cooperation in various ways, such as investment, participation, and acquisition, etc. In the process of cooperation, e-commerce enterprises and offline brick-and-mortar enterprises share profits, while also achieving the sharing of cost and risk.
7. Conclusions
With the upgrading of people’s consumption patterns, today’s society has become a highly online and offline two-dimensional space society, and the consumer market has also become a highly online and offline two-dimensional space market. In order to adapt to the development of the Internet era and overcome the huge impact brought by the single-line and offline sales model, the strategic choice behavior mechanism of retail channel subjects is deeply analyzed. The influence of different channel choices on the profits of omni-channel retailers is also discussed. This study aims at two different e-commerce enterprises and constructs an evolutionary game model of “online+offline” omni-channel construction strategy of enterprises through self-built or cooperation with the existing brick-and-mortar store. It fully considers the influence of consumer loyalty, physical feelings, cost bearing, and revenue-sharing ratio on the evolutionary stability point and discusses the stability of the system and the evolutionary stability strategy of participants by using differential equation theory and MATLAB numerical simulation. While enriching the relevant theoretical research, it provides decision support for enterprises to rebuild their business innovation model.
The findings of this research show the following: (a) as important members of the e-commerce market, whether enterprises self-build the offline retail channel or cooperate with brick-and-mortar stores depends on both the profits and the strategy of competitors. In particular, the evolutionary stabilization strategy is not unique when the enterprises’ profit is within a certain range. (b) With the change in enterprises’ profit, competitive enterprises choose the same developing offline retail channel strategy, or choose different strategies, respectively, which would appear in the evolution process. The reason is that when enterprises choose to self-build the offline retail channel, although they need to pay the cost of building a store, they do not need to share profits with offline retail stores. When a company chooses to cooperate with brick-and-mortar stores, although it only bears a portion of offline retail costs, it also needs to share its retail revenue with offline retail stores. (c) In particular, the evolutionary stabilization strategy is not unique when the enterprises’ profit is within a certain range. (d) Moreover, changes in consumer loyalty, physical feelings, and sharing ratio will affect the steady rate of enterprises’ behavioral choice during the evolution process. Specifically, when the strategies of the two companies are stable in choosing different offline retail channel development strategies, continuously increasing the revenue sharing ratio is likely to accelerate the evolution of the company’s choice to cooperate with brick-and-mortar stores, and at this point, the cooperation costs it pays will also increase.
Through the above analysis, it can be concluded that when enterprises expand their offline retail channels, their strategic decisions are influenced by revenue and competitor strategies, and in the long-term evolution process, they are also influenced by consumer offline experience and channel loyalty. Firstly, when customers have higher loyalty to online shopping channels, enterprises can first cooperate with brick-and-mortar stores to achieve integrated layout of online and offline shopping. This can not only cater to consumers who prefer offline shopping, but also avoid excessive channel construction costs. Secondly, when customers have high requirements for offline experience, enterprises can invest more costs to self-build their own brick-and-mortar stores, which can determine the service level of brick-and-mortar stores themselves and attract more consumers. Whether cooperating with brick-and-mortar stores or self-building their own brick-and-mortar stores, they are commonly used methods for enterprises to expand their offline brick-and-mortar stores in the process of deep integration between online and offline in the retail field.
Although this study proposes a mixed online and offline dual channel model, there are still limitations such as, for the demand function, this research assumes that the demand between two channels of the same enterprise is independent. In practice, online demand is relative to the prices in offline channels, meaning that online demand may be influenced by offline prices. At the same time, the coefficients of cost bearing and revenue sharing are also assumed to be the same in this article, which may actually have some biases. In addition, different development methods of offline channels will lead to different cost structures rather than just different sizes. So, simple cost parameters are not sufficient to describe different cost structures. More complex situations will be presented in future studies. For example, when the enterprise is no longer risk-neutral, how will the different investment costs and risk affect its strategy choice? How can the random characteristics and complex network characteristics of the e-commerce market be integrated into the model, making the model more realistic? These are interesting questions that will be investigated in the future.
Author Contributions
Conceptualization, Y.C. and B.X.; methodology, Y.C.; software, Y.C.; validation, K.A.; formal analysis, B.X.; investigation, B.X.; resources, K.A.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C. and B.X.; supervision, B.X.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation (grant No.: 72031009); the National Social Foundation of China (grant No.: 20BJL135). Key Soft Science Project of Science and Technology Department of Henan Province (grant No.: 222400410021); Philosophy and Social Science Planning Project of Henan Province (grant No.: 2022CZH015); Soft Science Project of Science and Technology Department of Henan Province (grant No.: 232400411173); General research project of Humanities and Social Sciences in Colleges and Universities of Henan Province (2023-ZDJH-053); Henan Province New Liberal Arts Research and Reform Practice Project (Reform and Practice of the Reform and Improvement of Liberal Arts Majors in Local Ordinary Undergraduate Colleges—Taking the National First-Class Undergraduate Majors in E-commerce as an Example).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, C.; Leng, M.; Liu, Z.; Cui, X.; Yu, J. The impact of recommender systems and pricing strategies on brand competition and consumer search. Electron. Commer. Res. Appl. 2022, 53, 101144. [Google Scholar] [CrossRef]
- Chu, J.; Arce-Urriza, M.; Cebollada-Calvo, J.-J.; Chintagunta, P.K. An empirical analysis of shopping behavior across online and offline channels for grocery products, the moderating effects of household and product characteristics. J. Interact. Mark. 2010, 24, 251–268. [Google Scholar] [CrossRef]
- Chu, J.; Chintagunta, P.; Cebollada, J. ResearchNote—A Comparison of Within-Household Price Sensitivity Across Onlineand Offline Channels. Mark. Sci. 2008, 27, 283–299. [Google Scholar] [CrossRef]
- Konuş, U.; Verhoef, P.C.; Neslin, S.A. Multichannel Shop-per Segments and Their Covariates. J. Retail. 2008, 84, 398–413. [Google Scholar] [CrossRef]
- Venkatesan, R.; Kumar, V.; Ravishanker, N. Multi channel Shopping, Causes and Consequences. J. Mark. 2007, 71, 114–132. [Google Scholar] [CrossRef]
- Shriver, S.K.; Bollinger, B. Demand expansion and cannibalization effects from retail store entry: A structural analysis of multichannel demand. Manag. Sci. 2022, 68, 8829–8856. [Google Scholar] [CrossRef]
- Li, G.; Zhang, T.; Tayi, G.K. Inroad into omni-channel retailing, Physical showroom deployment of an online retailer. Eur. J. Oper. Res. 2020, 283, 676–691. [Google Scholar] [CrossRef]
- Gao, F.; Su, X. Omnichannel retail operations with buy-online-and-pick-up-in-store. Manag. Sci. 2016, 63, 2478–2492. [Google Scholar] [CrossRef]
- Ramanathan, R. The moderating roles of risk and efficiency on the relationship between logistics performance and customer loyalty in e-commerce. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 950–962. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Cai, X.; Shan, J. Service channel choice for supply chain: Who is better off by undertaking the service? Prod. Oper. Manag. 2016, 25, 516–534. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Tian, L. The optimal combination between selling mode and logistics service strategy in an e-commerce market. Eur. J. Oper. Res. 2021, 289, 639–651. [Google Scholar] [CrossRef]
- Hybris. U.S. Consumers Want Retailers to Integrate Channels. Technical Report, SAP Hybris. 2012. Available online: http://www.hybris.com/en/news-events/press-releases/120508-multichannel (accessed on 25 October 2022).
- Bell, D.R.; Gallino, S.; Moreno, A. How to win in an omnichannel world. MIT Sloan Manag. Rev. 2014, 56, 45. [Google Scholar]
- Jin, D.; Caliskan-Demirag, O.; Chen, F.; Huang, M. Omnichannel retailers’ return policy strategies in the presence of competition. Int. J. Prod. Econ. 2020, 225, 107595. [Google Scholar] [CrossRef]
- Radhi, M.; Zhang, G. Optimal cross-channel return policy in dual-channel retailing systems. Int. J. Prod. Econ. 2019, 210, 184–198. [Google Scholar] [CrossRef]
- Nageswaran, L.; Cho, S.H.; Scheller-Wolf, A. Consumer return policies in omnichannel operations. Manag. Sci. 2020, 66, 5558–5575. [Google Scholar] [CrossRef]
- Radhi, M.; Zhang, G. Pricing policies for a dual-channel retailer with cross-channel returns. Comput. Ind. Eng. 2018, 119, 63–75. [Google Scholar] [CrossRef]
- Sousa, R.; Voss, C.A. Service quality in multichannel services employing virtual channels. J. Serv. Res. 2006, 8, 356–371. [Google Scholar] [CrossRef]
- Levy, M.; Weitz, B. Retailing Management, 4th ed.; McGraw-Hill/Irwin: Irvine, CA, USA, 2001. [Google Scholar]
- Zhang, J. Crafting integrated multichannel retailing strategies. J. Interact. Mark. 2010, 24, 168–180. [Google Scholar] [CrossRef]
- Rigby, D. The future of shopping. Harv. Bus. Rev. 2011, 89, 65–76. [Google Scholar]
- Kang, J.Y.M. Showrooming, Webrooming, and User-Generated Content Creation, the Moderating Effect of SOLOMO//International Textile and Apparel Association Annual Conference Proceedings; The Iowa State University Digital Press: Ames, IA, USA, 2014; Volume 71. [Google Scholar]
- Richter, F. Showrooming in the Retail Environment. Statista.com. 2013. Available online: http://www.statista.com/topics/871/online-shopping/chart/1024/showrooming-infographic/ (accessed on 27 October 2022).
- Brynjolfsson, E.; Hu, Y.J.; Rahman, M.S. Competing in the age of omni channel retailing. MIT Sloan Manag. Rev. 2013, 54, 23–29. [Google Scholar]
- Frazer, M.; Stiehler, B.E. Omnichannel retailing, The merging of the online and off-line environment. Glob. Conf. Bus. Financ. Proc. Inst. Bus. Financ. Res. 2014, 9, 665. [Google Scholar]
- Oh, L.B.; Teo, H.H.; Sambamurthy, V. The effects of retail channel integration through the use of information technologies on firm performance. J. Oper. Manag. 2012, 30, 368–381. [Google Scholar] [CrossRef]
- Beck, N.; Rygl, D. Categorization of multiple channel retailing in Multi-, Cross-, and Omni-Channel Retailing for retailers and retailing. J. Retail. Consum. Serv. 2015, 27, 170–178. [Google Scholar] [CrossRef]
- Dzyabura, D.; Jagabathula, S.; Muller, E. Accounting for discrepancies between online and offline product evaluations. Oper. Res. Manag. Sci. 2021, 5/6, 61. [Google Scholar] [CrossRef]
- Bell, D.R.; Gallino, S.; Moreno, A. Offline showrooms in omnichannel retail: Demand and operational benefits. Manag. Sci. 2015, 64, 1629–1651. [Google Scholar] [CrossRef]
- Bell, D.R.; Gallino, S.; Moreno, A. Customer supercharging in experience-centric channels. Manag. Sci. 2020, 66, 4096–4107. [Google Scholar] [CrossRef]
- Kumar, S.; Eidem, J.; Noriega Perdomo, D. Clash of the e-commerce titans, A new paradigm for consumer purchase process improvement. Int. J. Product. Perform. Manag. 2012, 61, 805–830. [Google Scholar] [CrossRef]
- Rand, D.G.; Nowak, M.A. Human Cooperation. Trends Cogn. Sci. 2013, 17, 413–425. [Google Scholar] [CrossRef]
- Kalinowski R B W C, O. S B. Models of man, social and rationalby herbert a. simon. Am. Cathol. Sociol. Rev. 1957, 18, 236–237. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary game dynamics. Bull. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
- Friedman, D. Evolutionary games in economics. Econom. J. Econom. Soc. 1991, 59, 637–666. [Google Scholar] [CrossRef]
- Esmaeili, M.; Allameh, G.; Tajvidi, T. Using game theory for analysing pricing models in closed-loop supply chain from short-and long-term perspectives. Int. J. Prod. Res. 2016, 54, 2152–2169. [Google Scholar] [CrossRef]
- Taylor, C.; Fudenberg, D.; Sasaki, A.; Nowak, M.A. Evolutionary game dynamics in finite populations. Bull. Math. Biol. 2004, 66, 1621–1644. [Google Scholar] [CrossRef]
- Amaral, M.A.; de Oliveira, M.M.; Javarone, M.A. An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. Chaos Solitons Fractals 2021, 143, 110616. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Di, Z.; Chen, J. Evolutionary game of inland shipping pollution control under government co-supervision. Mar. Pollut. Bull. 2021, 171, 112730. [Google Scholar] [CrossRef] [PubMed]
- Fan, W.; Wang, S.; Gu, X.; Zhou, Z.; Zhao, Y.; Huo, W. Evolutionary game analysis on industrial pollution control of local government in China. J. Environ. Manag. 2021, 298, 113499. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, Q.; Tang, J. Evolutionary game analysis of environmental pollution control under the government regulation. Sci. Rep. 2022, 12, 474. [Google Scholar] [CrossRef]
- Li, X.; Mu, D.; Du, J. Multi-channel recycling decisions of electric vehicle battery based on SD-dynamic game model. In Proceedings of the 2018 15th International Conference on Service Systems and Service Management (ICSSSM), Hangzhou, China, 21–22 July 2018; pp. 1–6. [Google Scholar]
- Zhang, Y.; Zhang, T. Complex Dynamics of Pricing Game Model in a Dual-Channel Closed-Loop Supply Chain with Delay Decision. Int. J. Bifurc. Chaos 2022, 32, 2250013. [Google Scholar] [CrossRef]
- Yuan, J.; Zhu, J. Stability and Complexity Analysis of Multichannel Supply Chain with Price Competition. Int. J. Bifurc. Chaos 2022, 32, 2250019. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Wang, Z. Analysis of pricing and service effort in dual-channel supply chains with showrooming effect. Int. J. Bifurc. Chaos 2020, 30, 2050241. [Google Scholar] [CrossRef]
- Zhu, Q.H.; Dou, Y.J. Evolutionary game model between governments and core enterprises in greening supply chains. Syst. Eng. -Theory Pract. 2007, 27, 85–89. [Google Scholar] [CrossRef]
- Liu, X.; Lin, K.; Wang, L. Stochastic evolutionary game analysis of e-waste recycling in environmental regulation from the perspective of dual governance system. J. Clean. Prod. 2021, 319, 128685. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, J. The complexity analysis and chaos control in omni-channel supply chain with consumer migration and advertising cost sharing. Chaos Solitons Fractals 2021, 146, 110884. [Google Scholar] [CrossRef]
- Hosseini-Motlagh, S.-M.; Choi, T.-M.; Johari, M.; Nouri-Harzvili, M. A profit surplus distribution mechanism for supply chain coordination: An evolutionary game-theoretic analysis. Eur. J. Oper. Res. 2022, 301, 561–575. [Google Scholar] [CrossRef]
- Soleimani, F.; Pirayesh, M.; Dehghanian, F. A Stackelberg game for ordering and pricing policies in a decentralised dual-channel supply chain. Int. J. Procure. Manag. 2022, 15, 93. [Google Scholar] [CrossRef]
- Kang, K.; Zhao, Y.; Zhang, J.; Qiang, C. Evolutionary game theoretic analysis on low-carbon strategy for supply chain enterprises. J. Clean. Prod. 2019, 230, 981–994. [Google Scholar] [CrossRef]
- Lyapunov, A.M. The general problem of the stability of motion. Int. J. Control 1992, 55, 531–534. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bertram, J.E. Control system analysis and design via the second method of Lyapunov: (I) continuous-time systems (II) discrete time systems. Ire Trans. Autom. Control 1960, 4, 112. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Wake, G.C. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl. Math. Lett. 2002, 15, 955–960. [Google Scholar] [CrossRef]
- Araujo, R.A.; Moreira, H.N. Lyapunov stability in an evolutionary game theory model of the labour market. EconomiA 2014, 15, 41–53. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).