Forecasting per Capita Energy Consumption in China Using a Spatial Discrete Grey Prediction Model
Abstract
1. Introduction
- (1)
- In this paper, spatial characteristics are incorporated into DGM(1,1), which enhances spatial data predictions. SDGM(1,1,m) is proposed and is used to analyze spatial spillover effects in the selected modeling interval, and a grey model is used to process panel data.
- (2)
- SDGM(1,1,m) is compared with DGM(1,n), and the differences between them are analyzed in terms of modeling purposes and requirements.
- (3)
- In this paper, considering the time lag effect that often accompanies spatial interaction processes, L1-SDGM(1,1,m) is proposed, thus providing a conceptual approach for establishing other time-lag-based spatial discrete grey models.
- (4)
- Using the PCEC data from 30 provinces in China, SDGM(1,1,m) and L1-SDGM(1,1,m) are compared with DGM(1,1), DGM(1,n), NDGM(1,1), and BP neural network models to verify the effectiveness and superiority of SDGM(1,1,m) and L1-SDGM(1,1,m) for predicting the PCEC of China.
- (5)
- Based on a metabolic concept, we use SDGM(1,1,m) to predict the PCECs of 30 provinces in China from 2020–2025.
2. Construction of SDGM(1,1,m) and L1-SDGM(1,1,m)
2.1. Introduction of DGM(1,1)
2.2. Definition of SDGM(1,1,m)
2.3. Definition of L1-SDGM(1,1,m)
2.4. Error Evaluation Index
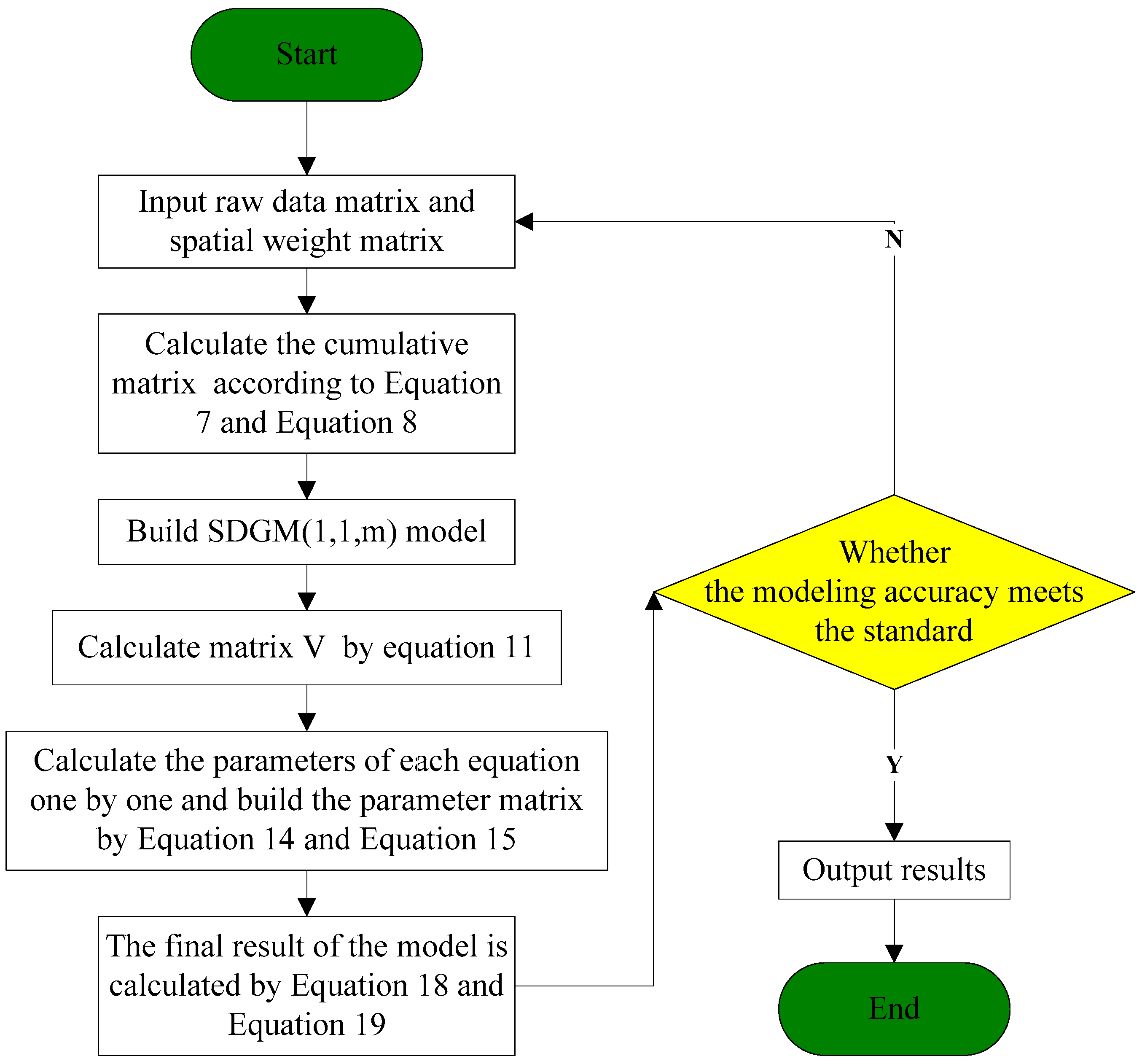
2.5. Flow Chart of SDGM(1,1,m)
3. Applications in Forecasting PCEC in China
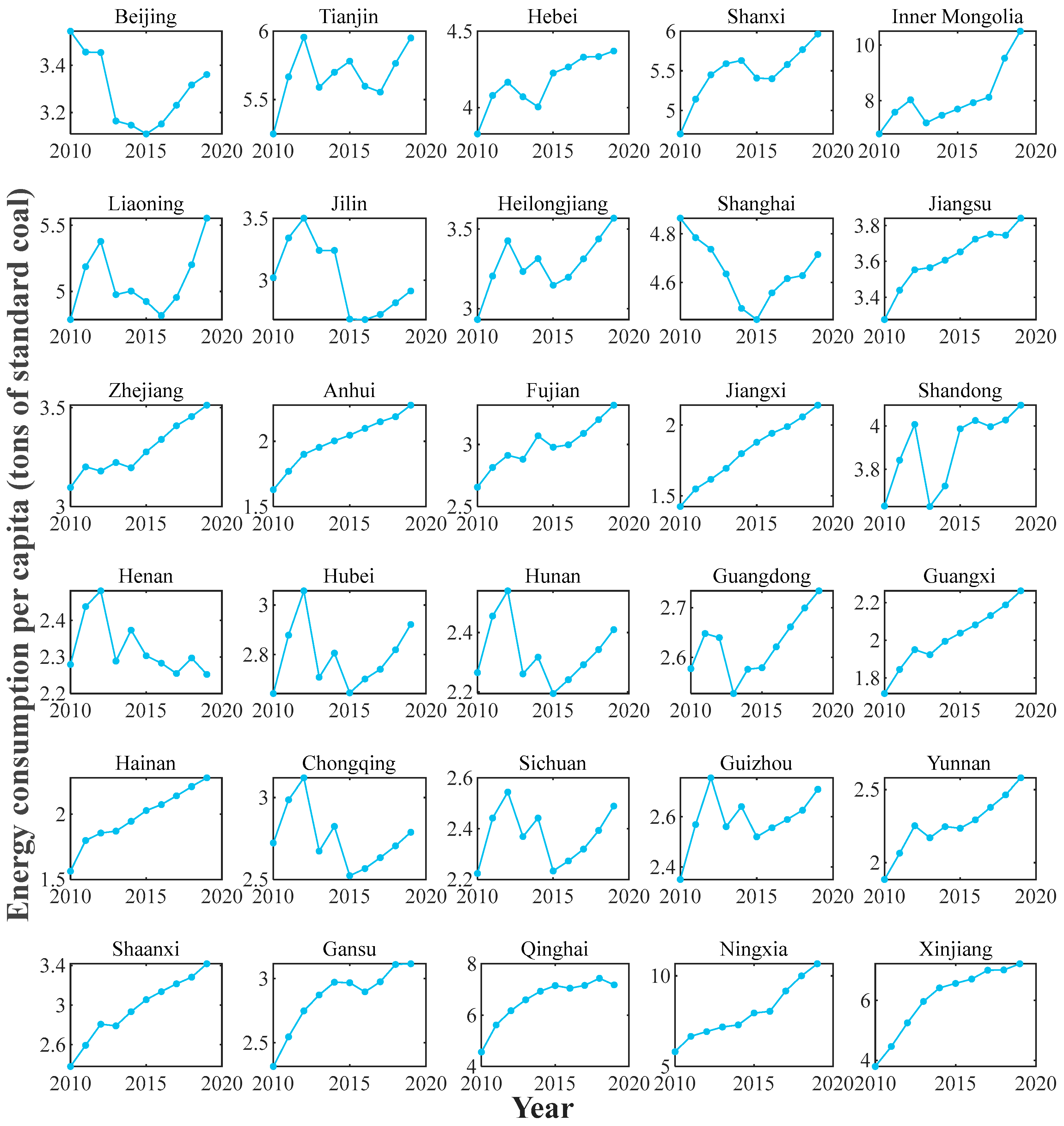
3.1. Data Collection
3.2. Establishment of the Spatial Weight Matrix
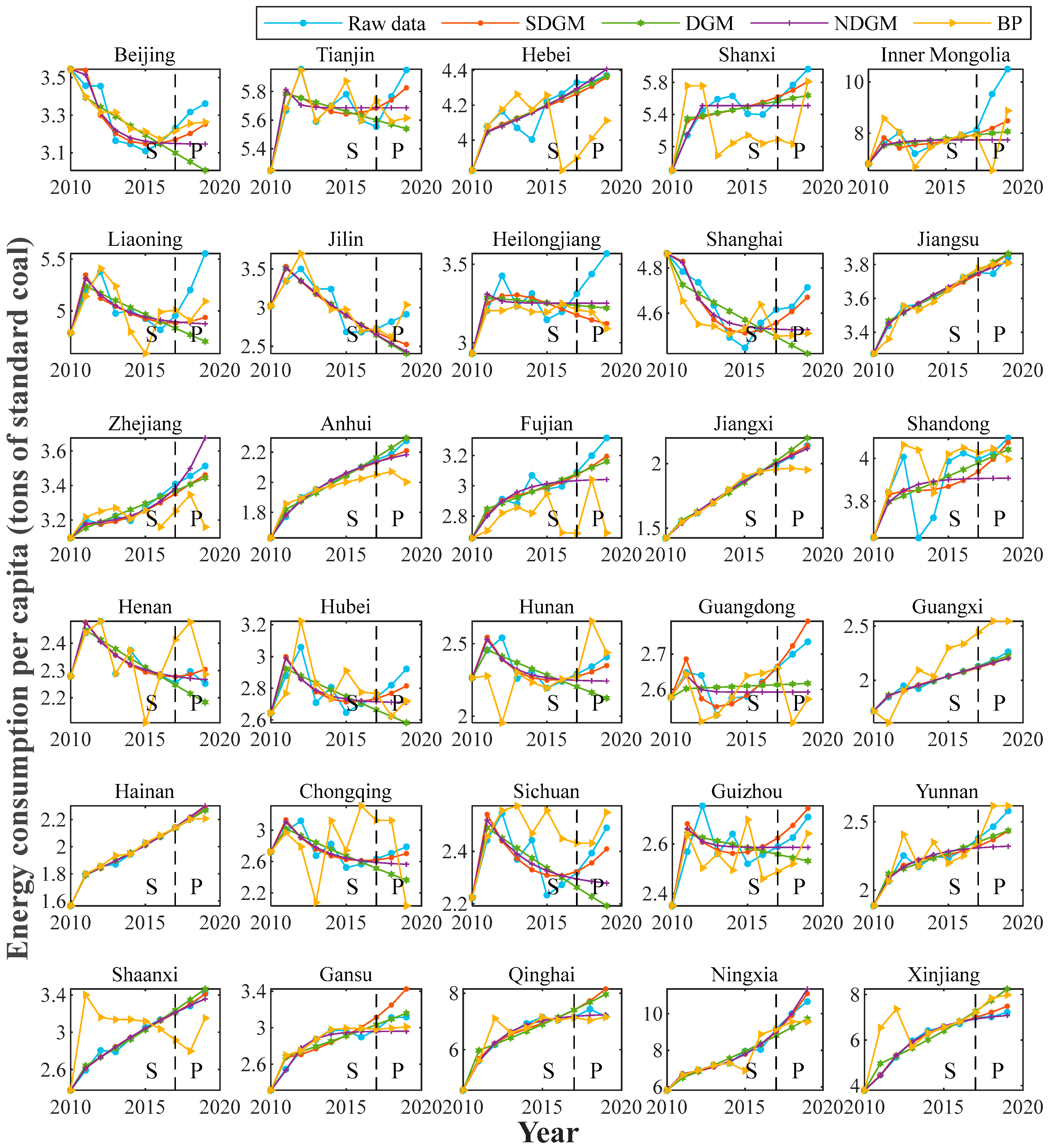
3.3. Model Comparison
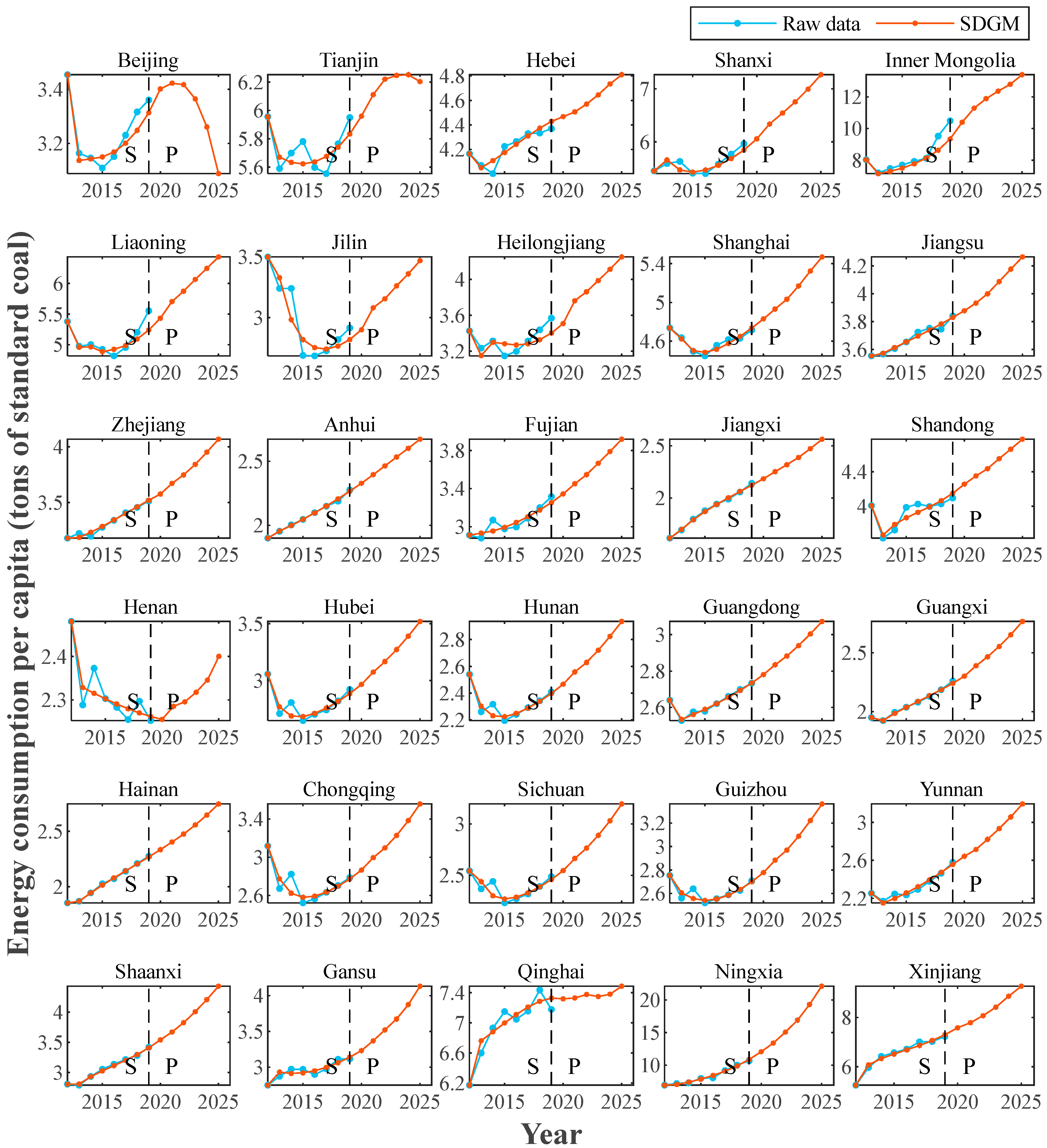
3.4. Projections of PCEC of China
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barak, S.; Sadegh, S.S. Forecasting energy consumption using ensemble ARIMA–ANFIS hybrid algorithm. Int. J. Electr. Power 2016, 82, 92–104. [Google Scholar] [CrossRef]
- Cabral, J.dA.; Legey, L.F.L.; Freitas Cabral, M.V.d. Electricity consumption forecasting in Brazil: A spatial econometrics approach. Energy 2017, 126, 124–131. [Google Scholar] [CrossRef]
- Jamil, R. Hydroelectricity consumption forecast for Pakistan using ARIMA modeling and supply-demand analysis for the year 2030. Renew. Energy 2020, 154, 1–10. [Google Scholar] [CrossRef]
- Shahbaz, M.; Loganathan, N.; Sbia, R.; Afzad, T. The effect of urbanization, affluence and trade openness on energy consumption: A time series analysis in Malaysia. Renew. Sustain. Energy Rev. 2015, 47, 683–693. [Google Scholar] [CrossRef]
- Mirza, F.M.; Kanwal, A. Energy consumption, carbon emissions and economic growth in Pakistan: Dynamic causality analysis. Renew. Sustain. Energy Rev. 2017, 72, 1233–1240. [Google Scholar] [CrossRef]
- Xu, X.; Xiao, B.; Li, C.Z. Analysis of critical factors and their interactions influencing individual’s energy conservation behavior in the workplace: A case study in China. J. Clean. Prod. 2021, 286, 124955. [Google Scholar] [CrossRef]
- Oliveira, E.M.D.; Oliveira, F.L.C. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Tang, L.; Wang, X.F.; Wang, X.L.; Shao, C.C.; Liu, S.Y.; Tian, S.J. Long-term electricity consumption forecasting based on expert prediction and fuzzy Bayesian theory. Energy 2018, 167, 1144–1154. [Google Scholar] [CrossRef]
- Rodger, J.A. A fuzzy nearest neighbor neural network statistical model for predicting demand for natural gas and energy cost savings in public buildings. Expert Syst. Appl. 2014, 41, 1813–1829. [Google Scholar] [CrossRef]
- Ilbeigi, M.; Ghomeishi, M.; Dehghanbanadaki, A. Prediction and optimization of energy consumption in an office building using artificial neural network and a genetic algorithm. Sustain. Cities Soc. 2020, 61, 102325. [Google Scholar] [CrossRef]
- Papadimitriou, T.; Gogas, P.; Stathakis, E. Forecasting energy markets using support vector machines. Energy Econ. 2014, 44, 135–142. [Google Scholar] [CrossRef]
- Tziolis, G.; Spanias, C.; Theodoride, M.; Theocharides, S.; Lopez-Lorente, J.; Livera, A.; Makrides, G.; Georghiou, G.E. Short-term electric net load forecasting for solar-integrated distribution systems based on Bayesian neural networks and statistical post-processing. Energy 2023, 271, 127018. [Google Scholar] [CrossRef]
- Huang, L.Q.; Liao, Q.; Zhang, H.R.; Jiang, M.K.; Yan, J.; Liang, Y.T. Forecasting power consumption with an activation function combined grey model: A case study of China. Int. J. Electr. Power 2021, 130, 106977. [Google Scholar] [CrossRef]
- Xiao, Q.Z.; Shan, M.Y.; Gao, M.Y.; Xiao, X.P.; Goh, M. Parameter optimization for nonlinear grey Bernoulli model on biomass energy consumption prediction. Appl. Soft Comput. 2020, 95, 106538. [Google Scholar] [CrossRef]
- Xie, W.L.; Wu, W.Z.; Liu, C.; Zhao, J.J. Forecasting annual electricity consumption in China by employing a conformable fractional grey model in opposite direction. Energy 2020, 202, 11768. [Google Scholar] [CrossRef]
- Liu, C.; Wu, W.Z.; Xie, W.L.; Zhang, J. Application of a novel fractional grey prediction model with time power term to predict the electricity consumption of India and China. Chaos Solitons Fractals 2020, 141, 110429. [Google Scholar] [CrossRef]
- Şahin, U. Forecasting share of renewables in primary energy consumption and CO2 emissions of China and the United States under Covid-19 pandemic using a novel fractional nonlinear grey model. Expert Syst. Appl. 2022, 209, 118429. [Google Scholar] [CrossRef]
- Saxena, A. Optimized fractional overhead power term polynomial grey model (OFOPGM) for market clearing price prediction. Electr. Power Syst. Res. 2023, 214, 108800. [Google Scholar] [CrossRef]
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 5, 288–294. [Google Scholar]
- Ma, X.; Xie, M.; Wu, W.; Zeng, B.; Wang, Y.; Wu, X.X. The novel fractional discrete multivariate grey system model and its applications. Appl. Math. Model. 2019, 70, 402–424. [Google Scholar] [CrossRef]
- Xu, K.; Pang, X.Y.; Duan, H.M. An optimization grey Bernoulli model and its application in forecasting oil consumption. Math. Probl. Eng. 2021, 2021, 5598709. [Google Scholar] [CrossRef]
- Wu, L.F.; Liu, S.F.; Yao, L.G.; Yan, S.L.; Liu, D.L. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Xie, W.L.; Liu, C.; Wu, W.Z. The fractional non-equidistant grey opposite-direction model with time-varying characteristics. Soft Comput. 2020, 24, 6603–6612. [Google Scholar] [CrossRef]
- Liu, C.; Wu, W.Z.; Xie, W.L.; Zhang, T.; Zhang, J. Forecasting natural gas consumption of China by using a novel fractional grey model with time power term. Energy Rep. 2021, 7, 788–797. [Google Scholar] [CrossRef]
- Wu, L.F.; Liu, S.F.; Yang, Y.J. Using fractional order method to generalize strengthening generating operator buffer operator and weakening buffer operator. IEEE-CAA J. Autom. 2018, 5, 52–56. [Google Scholar]
- Zeng, B.; Duan, H.M.; Bai, Y.; Meng, W. Forecasting the output of shale gas in China using an unbiased grey model and weakening buffer operator. Energy 2018, 151, 238–249. [Google Scholar] [CrossRef]
- Wei, B.L.; Xie, N.M.; Hu, A.Q. Optimal solution for novel grey polynomial prediction model. Appl. Math. Model. 2018, 62, 717–727. [Google Scholar] [CrossRef]
- Ma, X.; Mei, X.; Wu, W.Q.; Wu, X.X.; Zeng, B. A novel fractional time delayed grey model with Grey Wolf Optimizer and its applications in forecasting the natural gas and coal consumption in Chongqing China. Energy 2019, 178, 487–507. [Google Scholar] [CrossRef]
- Şahin, U.; Şahin, T. Forecasting the cumulative number of confirmed cases of COVID-19 in Italy, UK and USA using fractional nonlinear grey Bernoulli model. Chaos Solitons Fractals 2020, 138, 109948. [Google Scholar] [CrossRef]
- Carmona-Benítez, R.B.; Nieto, M.R. SARIMA damp trend grey forecasting model for airline industry. J. Air Transp. Manag. 2020, 82, 101736. [Google Scholar] [CrossRef]
- Kang, Y.X.; Mao, S.H.; Zhang, Y.H. Variable order fractional grey model and its application. Appl. Math. Model. 2021, 97, 619–635. [Google Scholar]
- Xu, N.; Ding, S.; Gong, Y.D.; Bai, J. Forecasting Chinese greenhouse gas emissions from energy consumption using a novel grey rolling model. Energy 2019, 175, 218–227. [Google Scholar] [CrossRef]
- Ceylan, Z. Short-term prediction of COVID-19 spread using grey rolling model optimized by particle swarm optimization. Appl. Soft Comput. 2021, 109, 107592. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.H.; Zeng, B.; Wang, J.Z.; Luo, X.S.; Liu, X.Z. Forecasting Chinese carbon emissions using a novel grey rolling prediction model. Chaos Solitons Fractals 2021, 147, 110968. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Degradation prediction of proton exchange membrane fuel cell based on grey neural network model and particle swarm optimization. Energy Convers. Manag. 2019, 195, 810–818. [Google Scholar] [CrossRef]
- Yang, X.Y.; Fang, Z.G.; Yang, Y.J.; Mba, D.; Li, X.C. A novel multi-information fusion grey model and its application in wear trend prediction of wind turbines. Appl. Math. Model. 2019, 71, 543–557. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Pisarenko, Z. Modeling carbon emission trajectory of China, US, and India. J. Clean. Prod. 2020, 258, 120723. [Google Scholar] [CrossRef]
- Xie, W.L.; Wu, W.Z.; Liu, C.; Zhang, T.; Dong, Z.J. Forecasting fuel combustion-related CO2 emissions by a novel continuous fractional nonlinear grey Bernoulli model with grey wolf optimizer. Environ. Sci. Pollut. Res. 2021, 28, 38128–38144. [Google Scholar] [CrossRef]
- Ye, L.L.; Xie, N.M.; Hu, A.Q. A novel time-delay multivariate grey model for impact analysis of CO2 emissions from China’s transportation sectors. Appl. Math. Model. 2021, 91, 493–507. [Google Scholar] [CrossRef]
- Rajesh, R. Predicting environmental sustainability performances of firms using trigonometric grey prediction model. Environ. Dev. 2023, 45, 100830. [Google Scholar] [CrossRef]
- Sapnken, F.E.; Tamba, J.G. Petroleum products consumption forecasting based on a new structural auto-adaptive intelligent grey prediction model. Expert Syst. Appl. 2022, 203, 117579. [Google Scholar] [CrossRef]
- Comert, G.; Khan, Z.; Rahman, M.; Chowdhury, M. Grey models for short-term queue length predictions for adaptive traffic signal control. Expert Syst. Appl. 2021, 185, 115618. [Google Scholar] [CrossRef]
- Saxena, A. Grey forecasting models based on internal optimization for Novel Coronavirus (COVID-19). Appl. Soft Comput. 2021, 111, 107735. [Google Scholar] [CrossRef] [PubMed]
- Xie, N.M.; Liu, S.F. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2009, 33, 1173–1186. [Google Scholar] [CrossRef]
- Xie, N.M.; Liu, S.F.; Yang, Y.J.; Yuan, C.Q. On novel grey forecasting model based on non-homogeneous index sequence. Appl. Math. Model. 2013, 37, 5059–5068. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Z.B. Research on the novel recursive discrete multivariate grey prediction model and its applications. Appl. Math. Model. 2016, 40, 4876–4890. [Google Scholar] [CrossRef]
- Jiang, S.Q.; Liu, S.F.; Liu, Z.X.; Fang, Z.G. Cubic time-varying parameters discrete grey forecasting model and its properties. Control Decis. 2016, 31, 279–286. [Google Scholar]
- Wei, B.L.; Xie, N.M.; Yang, Y.J. Data-based structure selection for unified discrete grey prediction model. Expert Syst. Appl. 2019, 136, 264–275. [Google Scholar] [CrossRef]
- Ding, S.; Li, R.J.; Tao, Z. A novel adaptive discrete grey model with time-varying parameters for long-term photovoltaic power generation forecasting. Energy Convers. Manag. 2021, 227, 113644. [Google Scholar] [CrossRef]
- Liu, C.; Xie, W.L.; Wu, W.Z.; Zhu, H.G. Predicting Chinese total retail sales of consumer goods by employing an extended discrete grey polynomial model. Eng. Appl. Artif. Intell. 2021, 102, 10426. [Google Scholar] [CrossRef]
- Gou, X.Y.; Zeng, B.; Gong, Y. Application of the novel four-parameter discrete optimized grey model to forecast the wastewater discharged in Chongqing China. Eng. Appl. Artif. Intell. 2022, 107, 104522. [Google Scholar] [CrossRef]
- Ye, L.; Yang, D.L.; Dang, Y.G.; Wang, J.J. An enhanced multivariable dynamic time-delay discrete grey forecasting model for predicting China’s carbon emissions. Energy 2022, 249, 123681. [Google Scholar] [CrossRef]
- Hao, Y.; Peng, H. On the convergence in China’s provincial per capita energy consumption: New evidence from a spatial econometric analysis. Energy Econ. 2017, 68, 31–43. [Google Scholar] [CrossRef]
- Hamilton, J.; Hogan, B.; Lucas, K.; Mayne, R. Conversations about conservation? Using social network analysis to understand energy practices. Energy Res. Soc. Sci. 2019, 49, 180–191. [Google Scholar] [CrossRef]
- Radmehr, R.; Henneberry, S.R.; Shayanmehr, S. Renewable energy consumption, CO2 emissions, and economic growth nexus: A simultaneity spatial modeling analysis of EU countries. Struct. Chang. Econ. Dyn. 2021, 57, 13–27. [Google Scholar] [CrossRef]
- Bu, Y.; Wang, E.; Bai, J.; Shi, Q. Spatial pattern and driving factors for interprovincial natural gas consumption in China: Based on SNA and LMDI. J. Clean. Prod. 2020, 263, 121392. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Wang, H.P.; Zhang, Z. Forecasting Chinese provincial carbon emissions using a novel grey prediction model considering spatial correlation. Expert Syst. Appl. 2022, 209, 118261. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, C.; Pang, H.; Feng, T.; Dong, Z. Forecasting China’s per capita living energy consumption by employing a novel DGM (1, 1, tα) model with fractional order accumulation. Math. Probl. Eng. 2021, 2021, 6635462. [Google Scholar] [CrossRef]


| Name | Formulation |
|---|---|
| The Root Mean Square Percentage Error (RMSPE) | |
| The Root Mean Square Error (RMSE) | |
| The Mean Absolute Error (MAE) | |
| The Index of Agreement (IA) | |
| The Correlation Coefficient (R) |
| Year | Moran’s I | Z-Score | p-Value |
|---|---|---|---|
| 2010 | 0.225 | 2.813 | 0.002 |
| 2011 | 0.197 | 2.517 | 0.006 |
| 2012 | 0.191 | 2.453 | 0.007 |
| 2013 | 0.193 | 2.446 | 0.007 |
| 2014 | 0.181 | 2.328 | 0.010 |
| 2015 | 0.181 | 2.343 | 0.010 |
| 2016 | 0.174 | 2.274 | 0.011 |
| 2017 | 0.170 | 2.251 | 0.012 |
| 2018 | 0.167 | 2.250 | 0.012 |
| 2019 | 0.156 | 2.150 | 0.016 |
| Error Metrics | MDGM | DGM | SDGM | L1-SDGM | NDGM | BP |
|---|---|---|---|---|---|---|
| MRSPE (%) | 1.1887 × 103 | 1.8251 | 1.6163 | 1.6999 | 1.5425 | 3.7021 |
| MRFPE (%) | 1.0076 × 104 | 5.8939 | 3.5159 | 5.2328 | 4.7667 | 7.1758 |
| CMRPE (%) | 2.9661 × 103 | 2.6388 | 1.9962 | 2.4065 | 2.1873 | 4.3968 |
| RMSPE | 6.4272 × 103 | 4.1807 | 3.1759 | 4.7898 | 3.5840 | 7.6856 |
| RMSE | 34,167.3452 | 24.4039 | 18.8417 | 24.2914 | 22.6363 | 35.8206 |
| MAE | 129.7515 | 0.1143 | 0.0847 | 0.1012 | 0.0911 | 0.1711 |
| IA | 0.0049 | 0.8264 | 0.9072 | 0.8807 | 0.8527 | 0.7236 |
| R | 0.0172 | 0.7514 | 0.8644 | 0.8429 | 0.7892 | 0.5647 |
| Province | Spatial Correlation Coefficient-b | Province | Spatial Correlation Coefficient-b | ||
|---|---|---|---|---|---|
| SDGM | L1-SDGM | SDGM | L1-SDGM | ||
| Beijing | 0.3845 | 0.3267 | Henan | 0.1176 | 0.0709 |
| Tianjin | 0.8436 | 0.6084 | Hubei | 0.3368 | 0.2932 |
| Hebei | 0.1196 | −0.1231 | Hunan | 0.3292 | 0.2901 |
| Shanxi | 0.4113 | 0.8088 | Guangdong | 0.6824 | 0.5985 |
| Inner Mongolia | 2.1688 | 1.2967 | Guangxi | 0.1482 | 0.0030 |
| Liaoning | 1.4674 | −0.1139 | Hainan | −0.0448 | −0.0584 |
| Jilin | 0.0669 | 0.0186 | Chongqing | 0.3304 | 0.2542 |
| Heilongjiang | 0.2612 | −0.0964 | Sichuan | 0.2506 | 0.1302 |
| Shanghai | 0.4931 | 0.5391 | Guizhou | 0.6152 | 0.6303 |
| Jiangsu | 0.5556 | 0.1995 | Yunnan | 0.4339 | 0.1157 |
| Zhejiang | −0.7091 | −0.3981 | Shaanxi | 0.1336 | 0.0887 |
| Anhui | 0.1713 | 0.1522 | Gansu | 0.2695 | −0.3935 |
| Fujian | 0.6435 | 0.5127 | Qinghai | 1.1506 | 1.4352 |
| Jiangxi | 0.0582 | 0.0570 | Ningxia | −0.6829 | −0.8404 |
| Shandong | 0.7867 | 0.3192 | Xinjiang | 0.6587 | 0.6787 |
| Province | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 |
|---|---|---|---|---|---|---|
| Beijing | 3.4015 | 3.4225 | 3.4171 | 3.3649 | 3.2611 | 3.0888 |
| Tianjin | 5.9607 | 6.1118 | 6.2208 | 6.2472 | 6.2527 | 6.2041 |
| Hebei | 4.4683 | 4.5062 | 4.5709 | 4.6455 | 4.7347 | 4.8103 |
| Shanxi | 6.0551 | 6.3351 | 6.5418 | 6.7544 | 6.9954 | 7.2678 |
| Inner Mongolia | 10.3993 | 11.2928 | 11.8828 | 12.3648 | 12.7920 | 13.4055 |
| Liaoning | 5.4333 | 5.7046 | 5.8732 | 6.0661 | 6.2458 | 6.4316 |
| Jilin | 2.8981 | 3.0800 | 3.1546 | 3.2611 | 3.3602 | 3.4692 |
| Heilongjiang | 3.5072 | 3.7621 | 3.8624 | 3.9873 | 4.1115 | 4.2505 |
| Shanghai | 4.8301 | 4.9320 | 5.0331 | 5.1702 | 5.3241 | 5.4703 |
| Jiangsu | 3.8777 | 3.9323 | 3.9998 | 4.0874 | 4.1772 | 4.2650 |
| Zhejiang | 3.5749 | 3.6706 | 3.7472 | 3.8415 | 3.9517 | 4.0679 |
| Anhui | 2.3283 | 2.3957 | 2.4640 | 2.5334 | 2.6019 | 2.6726 |
| Fujian | 3.3444 | 3.4510 | 3.5465 | 3.6656 | 3.7879 | 3.9184 |
| Jiangxi | 2.1837 | 2.2514 | 2.3182 | 2.3878 | 2.4714 | 2.5623 |
| Shandong | 4.2566 | 4.3510 | 4.4373 | 4.5540 | 4.6636 | 4.7802 |
| Henan | 2.2553 | 2.2854 | 2.2958 | 2.3177 | 2.3462 | 2.4001 |
| Hubei | 2.9657 | 3.0748 | 3.1673 | 3.2718 | 3.3901 | 3.5205 |
| Hunan | 2.4674 | 2.5592 | 2.6294 | 2.7188 | 2.8234 | 2.9354 |
| Guangdong | 2.7815 | 2.8356 | 2.8822 | 2.9400 | 3.0042 | 3.0731 |
| Guangxi | 2.3030 | 2.3915 | 2.4663 | 2.5548 | 2.6558 | 2.7686 |
| Hainan | 2.3343 | 2.4036 | 2.4748 | 2.5577 | 2.6469 | 2.7466 |
| Chongqing | 2.8665 | 2.9959 | 3.0987 | 3.2294 | 3.3844 | 3.5581 |
| Sichuan | 2.5476 | 2.6653 | 2.7668 | 2.8900 | 3.0316 | 3.1954 |
| Guizhou | 2.7783 | 2.8838 | 2.9696 | 3.0880 | 3.2208 | 3.3631 |
| Yunnan | 2.6431 | 2.7154 | 2.8217 | 2.9346 | 3.0577 | 3.1948 |
| Shaanxi | 3.5389 | 3.6699 | 3.8253 | 4.0066 | 4.2078 | 4.4288 |
| Gansu | 3.2307 | 3.3675 | 3.5202 | 3.6727 | 3.8754 | 4.1317 |
| Qinghai | 7.3175 | 7.3303 | 7.3759 | 7.3487 | 7.3797 | 7.4859 |
| Ningxia | 12.0485 | 13.3855 | 15.0643 | 16.8951 | 19.3048 | 22.1072 |
| Xinjiang | 7.5810 | 7.7859 | 8.0738 | 8.4171 | 8.8585 | 9.2682 |
| Modeling Interval | MRSPE (%) |
|---|---|
| 2012–2019 | 1.1395 |
| 2013–2020 | 0.6917 |
| 2014–2021 | 0.5570 |
| 2015–2022 | 0.4549 |
| 2016–2023 | 0.3510 |
| 2017–2024 | 0.3232 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, Z. Forecasting per Capita Energy Consumption in China Using a Spatial Discrete Grey Prediction Model. Systems 2023, 11, 285. https://doi.org/10.3390/systems11060285
Wang H, Zhang Z. Forecasting per Capita Energy Consumption in China Using a Spatial Discrete Grey Prediction Model. Systems. 2023; 11(6):285. https://doi.org/10.3390/systems11060285
Chicago/Turabian StyleWang, Huiping, and Zhun Zhang. 2023. "Forecasting per Capita Energy Consumption in China Using a Spatial Discrete Grey Prediction Model" Systems 11, no. 6: 285. https://doi.org/10.3390/systems11060285
APA StyleWang, H., & Zhang, Z. (2023). Forecasting per Capita Energy Consumption in China Using a Spatial Discrete Grey Prediction Model. Systems, 11(6), 285. https://doi.org/10.3390/systems11060285







