Cyclical Evolution of Emerging Technology Innovation Network from a Temporal Network Perspective
Abstract
1. Introduction
2. ET-TIN Construction and Measurement
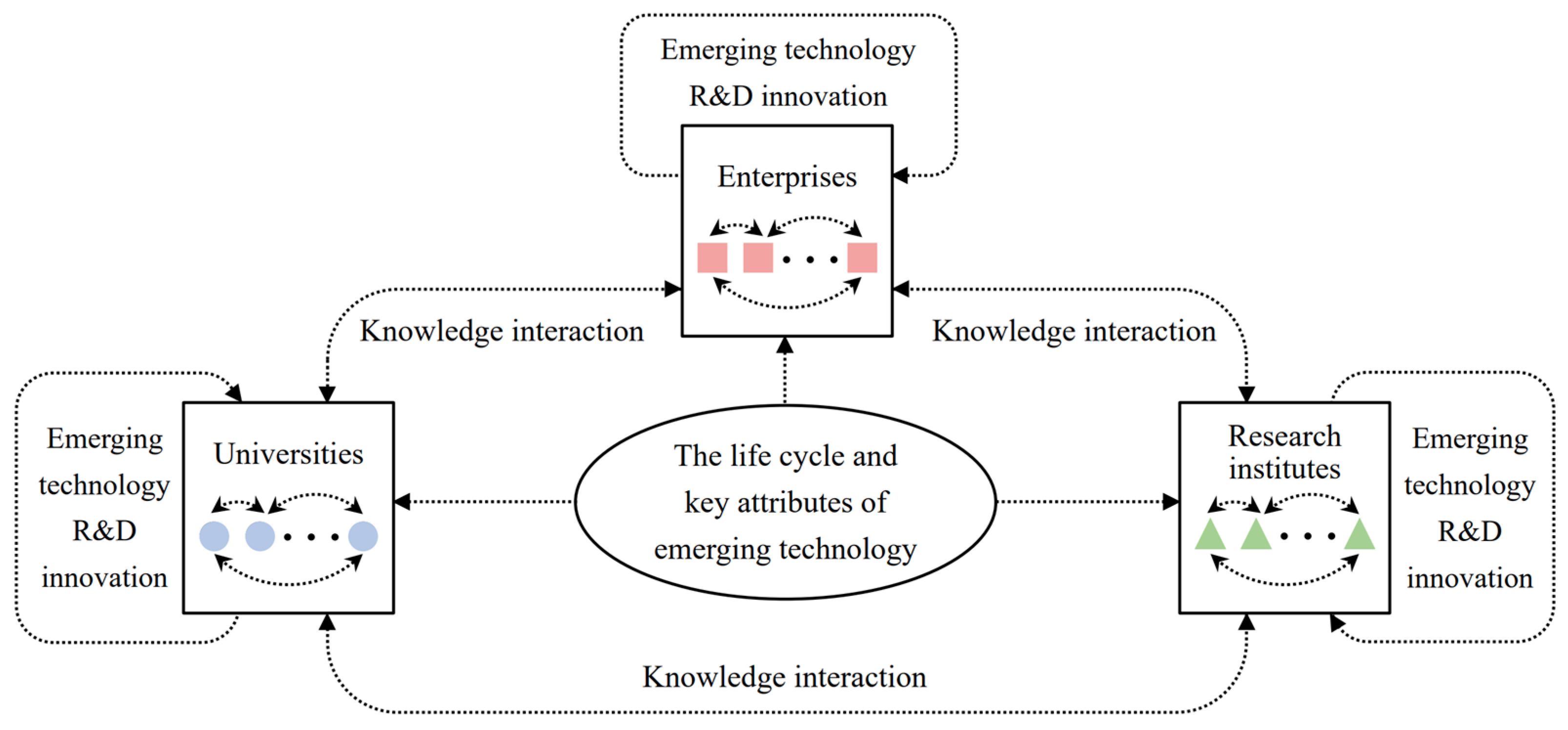
2.1. ET-TIN Construction
2.2. ET-TIN Measurement
2.2.1. Network Scale
2.2.2. Scale-Free Characteristic of Network
2.2.3. Small-World Characteristic of Network
2.2.4. Self-Organizing Characteristic of Network
3. The Modeling of ET-TIN Evolution
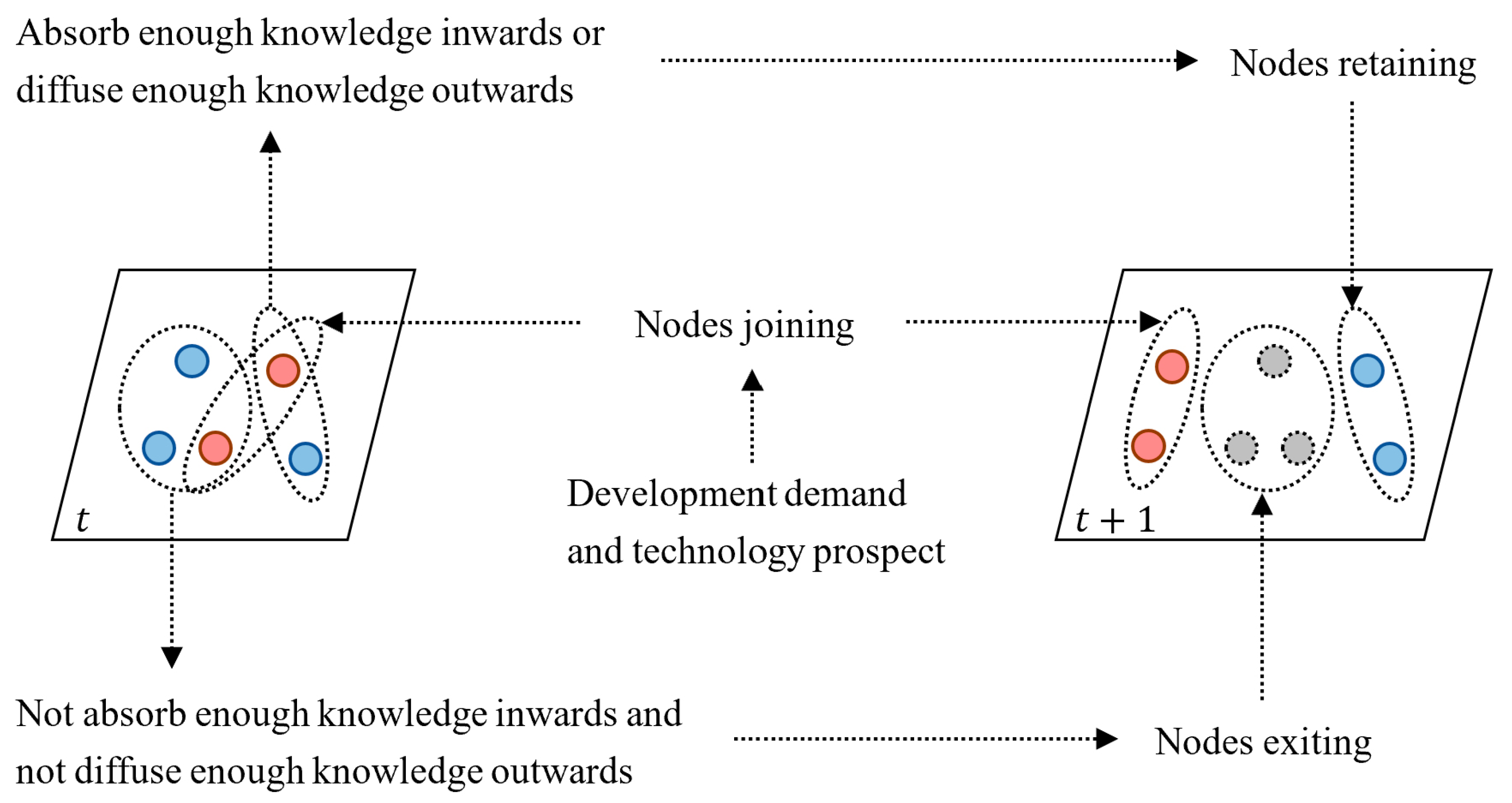
3.1. Network Nodes Evolution Mechanism
3.1.1. Nodes Joining Mechanism
3.1.2. Nodes Retaining and Exiting Mechanism
3.2. Network Edges Evolution Mechanism
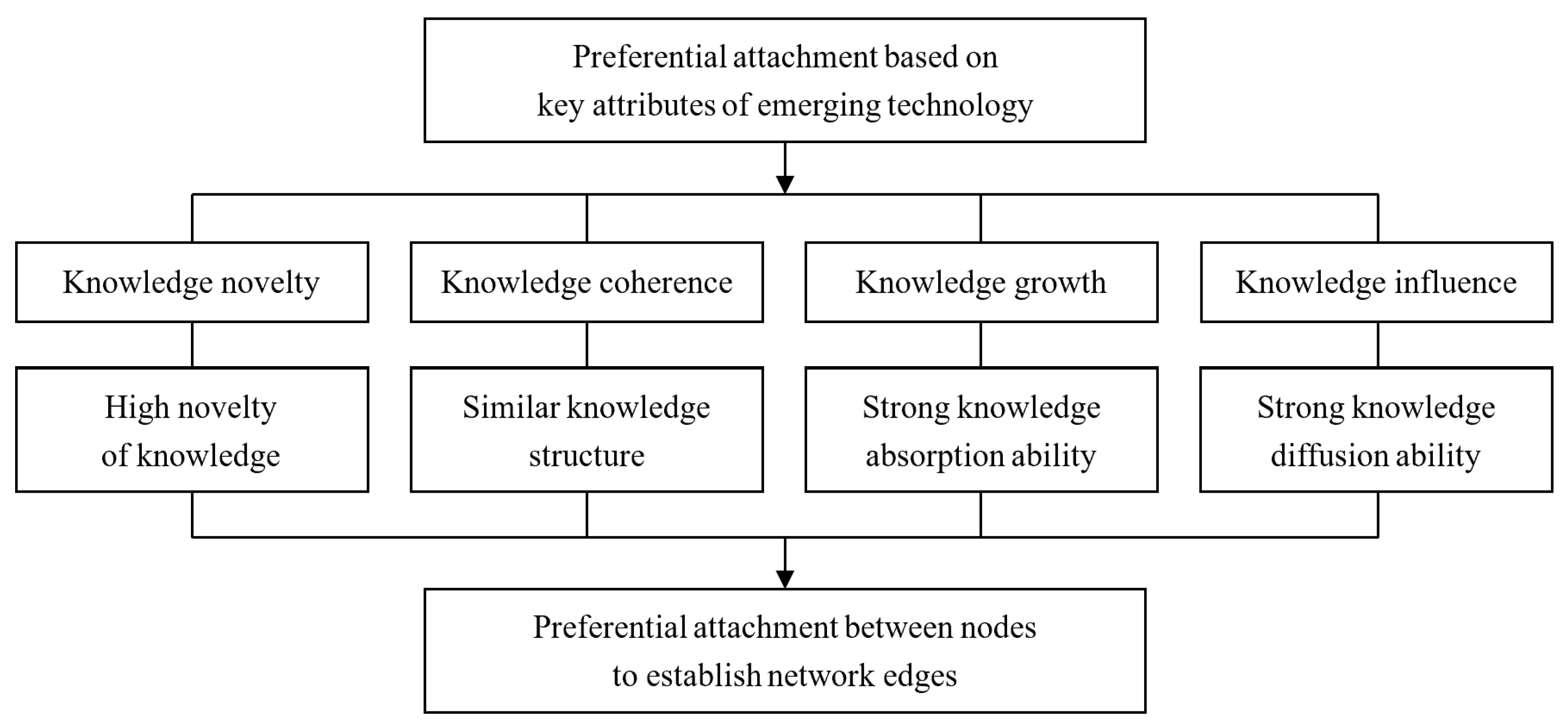
3.2.1. Preferential Attachment Mechanism Based on Knowledge Novelty
3.2.2. Preferential Attachment Mechanism Based on Knowledge Coherence
3.2.3. Preferential Attachment Mechanism Based on Knowledge Growth
3.2.4. Preferential Attachment Mechanism Based on Knowledge Influence
3.2.5. Preferential Attachment Mechanism Based on Multiple Knowledge Attributes
3.3. System Framework of Network Evolution
4. The Simulation Design of ET-TIN Evolution
4.1. Data Sources
4.2. Simulation Steps
5. Results and Discussion
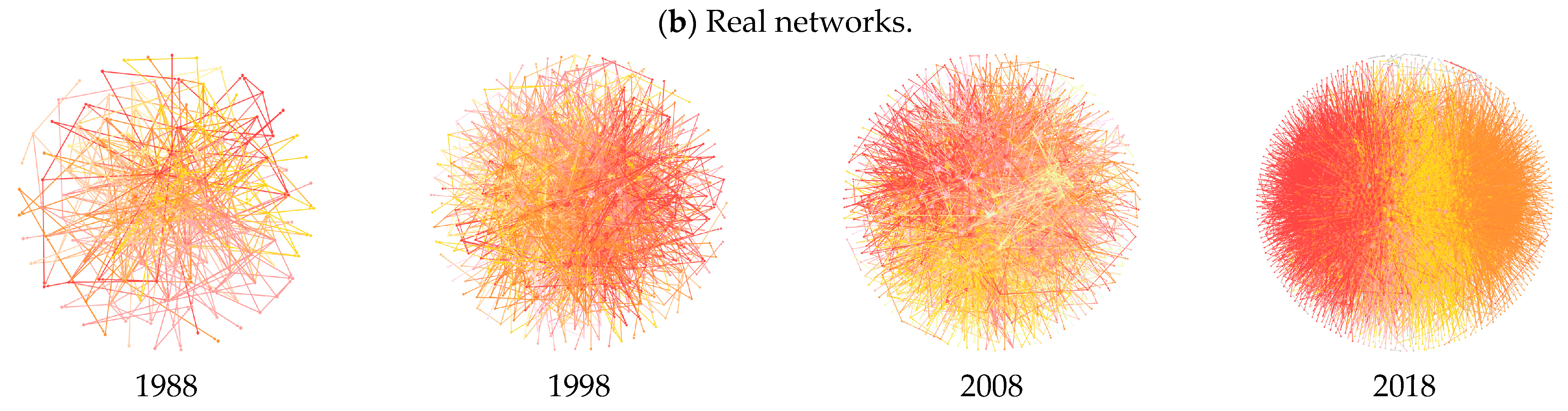
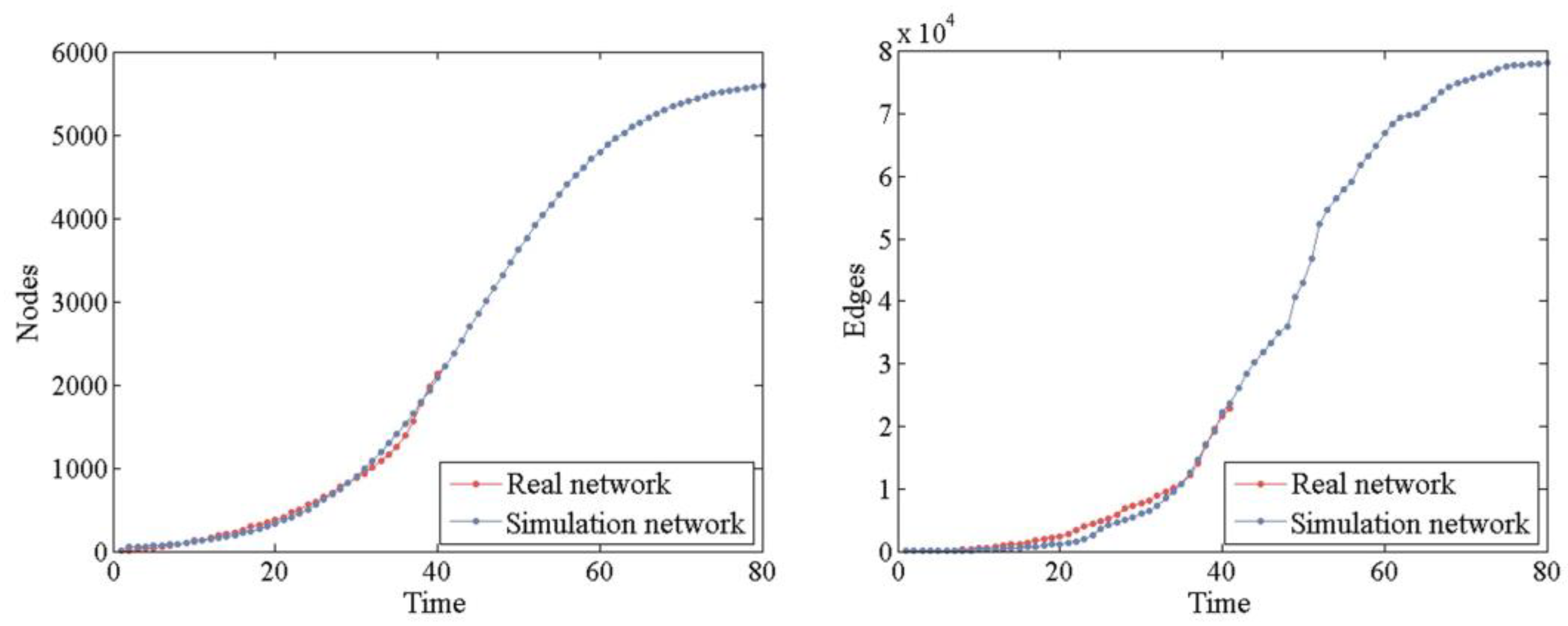
5.1. Analysis of Network Scale
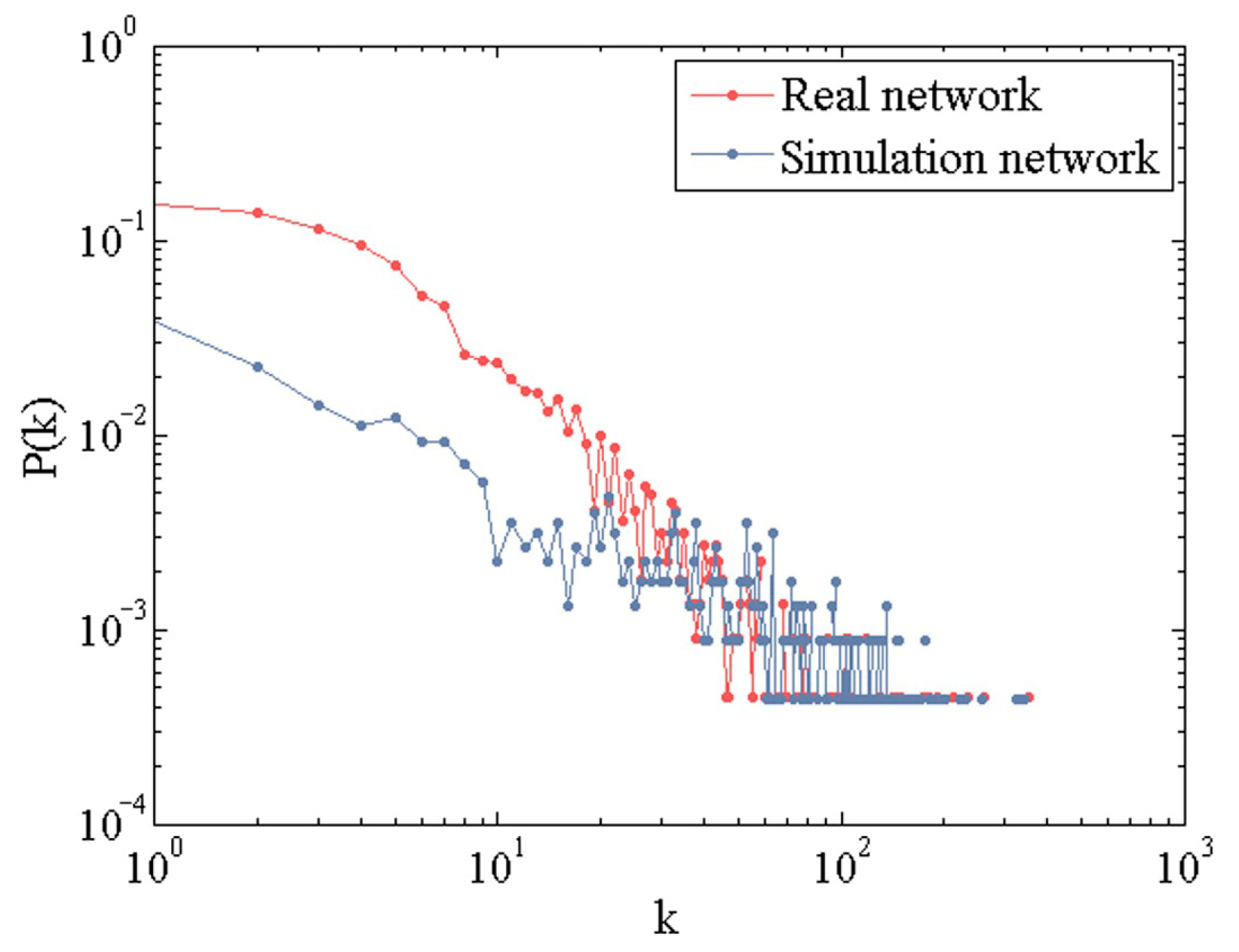
5.2. Analysis of Scale-Free Characteristic of Network
5.3. Analysis of Small-World Characteristic of Network
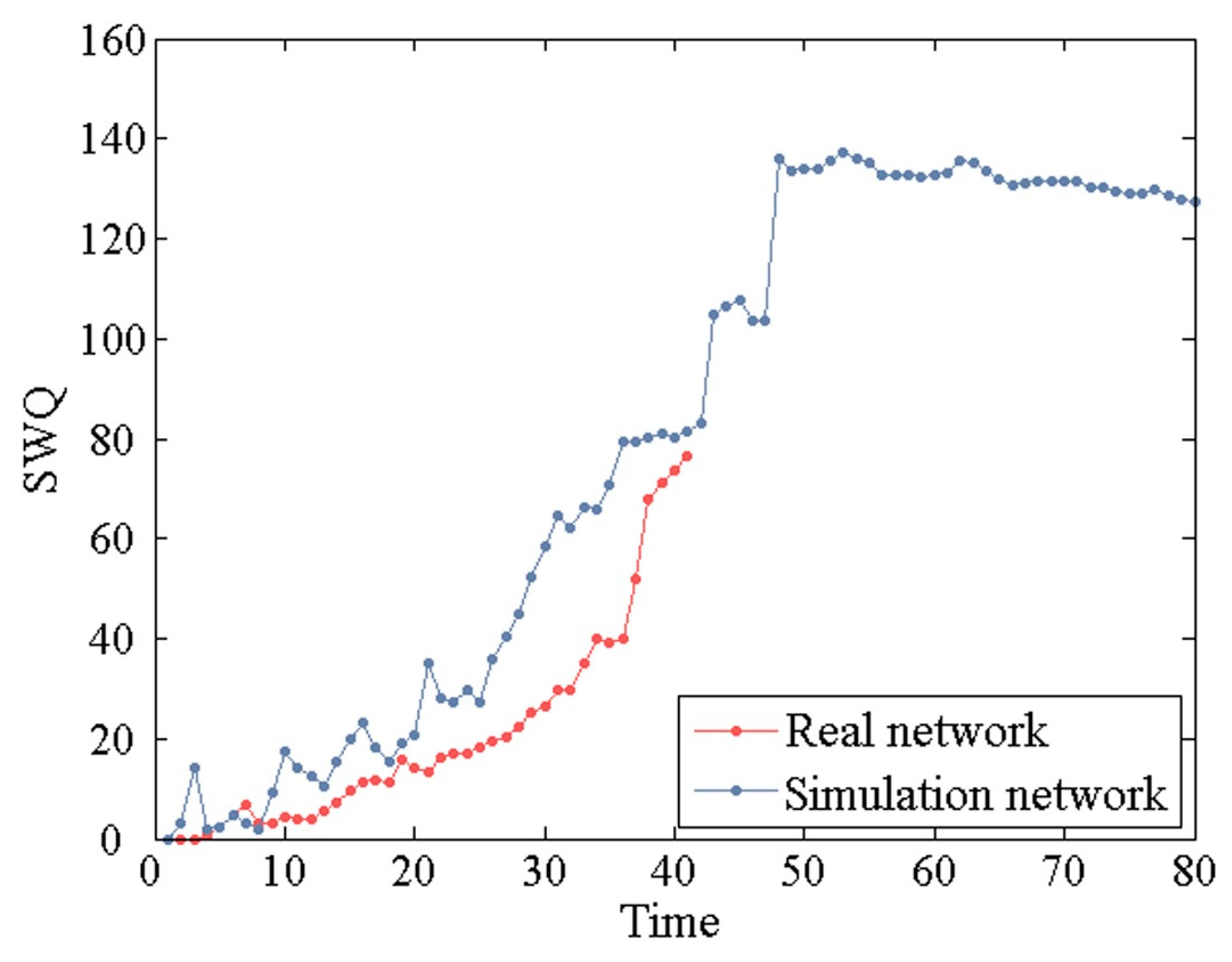
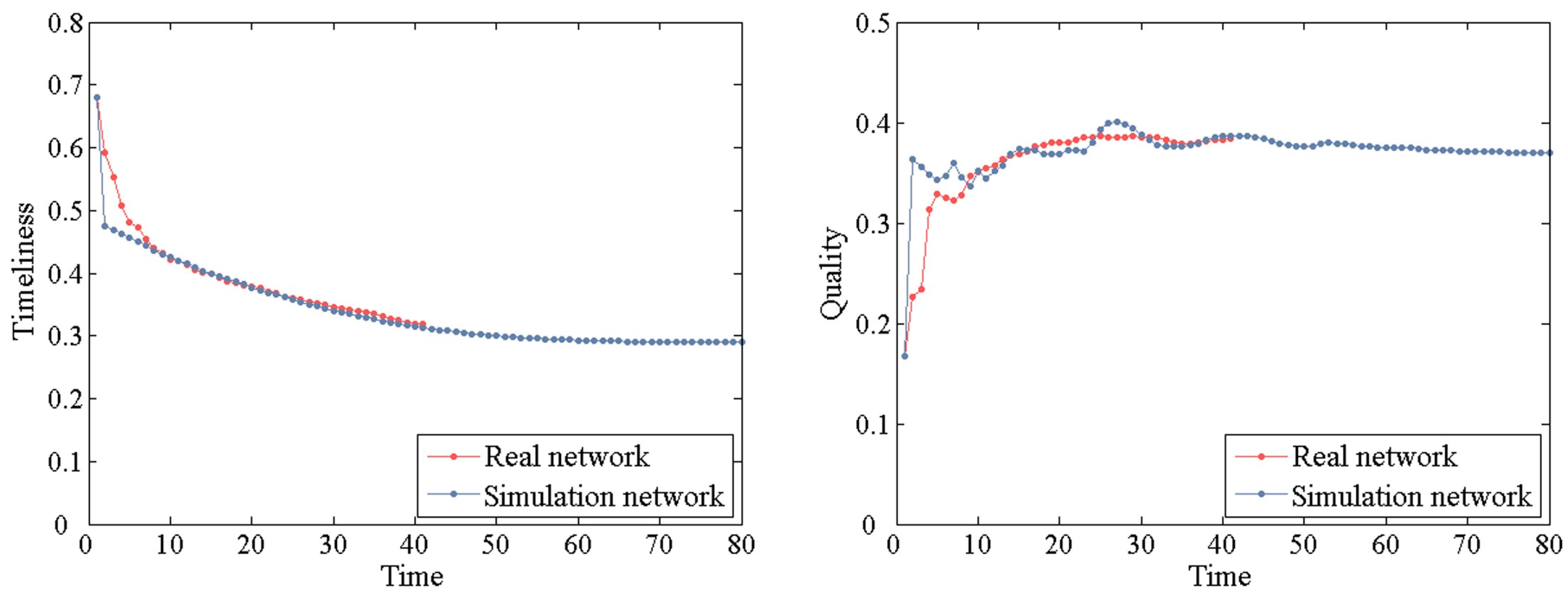
5.4. Analysis of Self-Organizing Characteristic of Network
6. Conclusions
6.1. Summary
6.2. Suggestions
6.3. Limitations and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- van der Pol, J.; Rameshkoumar, J.P. The co-evolution of knowledge and collaboration networks: The role of the technology life-cycle. Scientometrics 2018, 114, 307–323. [Google Scholar] [CrossRef]
- Cabeza-Pulles, D.; Fernandez-Perez, V.; Isabel Roldan-Bravo, M. Internal networking and innovation ambidexterity: The mediating role of knowledge management processes in university research. Eur. Manag. J. 2020, 38, 450–461. [Google Scholar] [CrossRef]
- Benhayoun, L.; Le Dain, M.-A.; Dominguez-Pery, C.; Lyons, A.C. SMEs embedded in collaborative innovation networks: How to measure their absorptive capacity? Technol. Forecast. Soc. Change 2020, 159, 120196. [Google Scholar] [CrossRef]
- Qiao, T.; Shan, W.; Zhang, M.; Liu, C. How to facilitate knowledge diffusion in complex networks: The roles of network structure, knowledge role distribution and selection rule. Int. J. Inf. Manag. 2019, 47, 152–167. [Google Scholar] [CrossRef]
- Meng, X.; Liu, M.; Wang, J. Innovation network economic model of new energy automobile industry based on social network perspective. J. Therm. Anal. Calorim. 2021, 144, 1671–1680. [Google Scholar] [CrossRef]
- Han, J.; Guo, J.-E.; Cai, X.; Lv, C.; Lev, B. An analysis on strategy evolution of research & development in cooperative innovation network of new energy vehicle within policy transition period. Omega-Int. J. Manag. Sci. 2022, 112, 102686. [Google Scholar] [CrossRef]
- Wei, F.; Sheng, D.; Lili, W. Evolutionary Model and Simulation Research of Collaborative Innovation Network: A Case Study of Artificial Intelligence Industry. Discret. Dyn. Nat. Soc. 2018, 2018, 4371528. [Google Scholar] [CrossRef]
- Tu, M.; Dall’erba, S.; Ye, M.Q. Spatial and Temporal Evolution of the Chinese Artificial Intelligence Innovation Network. Sustainability 2022, 14, 5448. [Google Scholar] [CrossRef]
- Lyu, Y.; Zhu, Y.; Han, S.; He, B.; Bao, L. Open innovation and innovation “Radicalness”-the moderating effect of network embeddedness. Technol. Soc. 2020, 62, 101292. [Google Scholar] [CrossRef]
- Rotolo, D.; Hicks, D.; Martin, B.R. What is an emerging technology? Res. Policy 2015, 44, 1827–1843. [Google Scholar] [CrossRef]
- Kwon, S.; Liu, X.Y.; Porter, A.L.; Youtie, J. Research addressing emerging technological ideas has greater scientific impact. Res. Policy 2019, 48, 103834. [Google Scholar] [CrossRef]
- Xu, S.; Hao, L.Y.; Yang, G.C.; Lu, K.; An, X. A topic models based framework for detecting and forecasting emerging technologies. Technol. Forecast. Soc. Change 2021, 162, 120366. [Google Scholar] [CrossRef]
- Borge, L.; Wustmans, M.; Broring, S. Assessing Interdisciplinary Research Within an Emerging Technology Network: A Novel Approach Based on Patents in the Field of Bioplastics. IEEE Trans. Eng. Manag. 2022, 1–18. [Google Scholar] [CrossRef]
- Kim, Y. Exploring Emerging Technologies with Analysis of Bibliographic Data Focused on Plasma Surface Treatment. Coatings 2021, 11, 1291. [Google Scholar] [CrossRef]
- Haessler, P.; Giones, F.; Brem, A. The who and how of commercializing emerging technologies: A technology-focused review. Technovation 2022, 102637. [Google Scholar] [CrossRef]
- Steensma, H.K.; Corley, K.G. On the performance of technology-sourcing partnerships: The interaction between partner interdependence and technology attributes. Acad. Manag. J. 2000, 43, 1045–1067. [Google Scholar] [CrossRef]
- Yoon, J.; Jeong, B.; Lee, W.H.; Kim, J. Tracing the Evolving Trends in Electronic Skin (e-Skin) Technology Using Growth Curve and Technology Position-Based Patent Bibliometrics. IEEE Access 2018, 6, 26530–26542. [Google Scholar] [CrossRef]
- Bergerson, J.; Cucurachi, S.; Seager, T.P. Bringing a life cycle perspective to emerging technology development. J. Ind. Ecol. 2020, 24, 6–10. [Google Scholar] [CrossRef]
- Altuntas, S.; Erdogan, Z.; Dereli, T. A clustering-based approach for the evaluation of candidate emerging technologies. Scientometrics 2020, 124, 1157–1177. [Google Scholar] [CrossRef]
- Cauthen, K.; Rai, P.; Hale, N.; Freeman, L.; Ray, J. Detecting technological maturity from bibliometric patterns. Expert Syst. Appl. 2022, 201, 117177. [Google Scholar] [CrossRef]
- Li, A.; Zhou, L.; Su, Q.; Cornelius, S.P.; Liu, Y.Y.; Wang, L.; Levin, S.A. Evolution of cooperation on temporal networks. Nat. Commun. 2020, 11, y2259. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.S.; Du, W.B.; Shekhtman, L.; Wang, Y.J.; Havlin, S.; Cao, X.B.; Yan, G. Predictability of real temporal networks. Natl. Sci. Rev. 2020, 7, 929–937. [Google Scholar] [CrossRef] [PubMed]
- Li, H.C.; Zhang, X.; Zhao, C.L. Explaining social events through community evolution on temporal networks. Appl. Math. Comput. 2021, 404, 126148. [Google Scholar] [CrossRef]
- Gelardi, V.; Le Bail, D.; Barrat, A.; Claidiere, N. From temporal network data to the dynamics of social relationships. Proc. R. Soc. B Biol. Sci. 2021, 288, 20211164. [Google Scholar] [CrossRef] [PubMed]
- Seabrook, I.E.; Barucca, P.; Caccioli, F. Evaluating structural edge importance in temporal networks. EPJ Data Sci. 2021, 10, 23. [Google Scholar] [CrossRef]
- Perra, N.; Goncalves, B.; Pastor-Satorras, R.; Vespignani, A. Activity driven modeling of time varying networks. Sci. Rep. 2012, 2, 469. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.K.; Liu, Y.H.; Deng, W.W. AST: Activity-Security-Trust driven modeling of time varying networks. Sci. Rep. 2016, 6, 21352. [Google Scholar] [CrossRef]
- Kim, H.; Ha, M.; Jeong, H. Dynamic topologies of activity-driven temporal networks with memory. Phys. Rev. E 2018, 97, 062148. [Google Scholar] [CrossRef]
- Zhu, K.J.; Fletcher, G.; Yakovets, N. Competition-driven modeling of temporal networks. EPJ Data Sci. 2021, 10, 30. [Google Scholar] [CrossRef]
- Qu, C.Q.; Zhan, X.X.; Wang, G.H.; Wu, J.L.; Zhang, Z.K. Temporal information gathering process for node ranking in time-varying networks. Chaos 2019, 29, 033116. [Google Scholar] [CrossRef]
- Yu, E.Y.; Fu, Y.; Chen, X.; Xie, M.; Chen, D.B. Identifying critical nodes in temporal networks by network embedding. Sci. Rep. 2020, 10, 12494. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.L.; Tan, Y.S.; Wu, Q.B.; Chen, B.Z.; Shen, C.X. TM-Miner:TFS-Based Algorithm for Mining Temporal Motifs in Large Temporal Network. IEEE Access 2019, 7, 49778–49789. [Google Scholar] [CrossRef]
- Liu, P.H.; Masuda, N.; Kito, T.; Sariyuce, A.E. Temporal motifs in patent opposition and collaboration networks. Sci. Rep. 2022, 12, 1917. [Google Scholar] [CrossRef]
- Liu, P.; Guarrasi, V.; Sariyuce, A.E. Temporal Network Motifs: Models, Limitations, Evaluation. IEEE Trans. Knowl. Data Eng. 2023, 35, 945–957. [Google Scholar] [CrossRef]
- Qin, H.C.; Li, R.H.; Yuan, Y.; Wang, G.R.; Yang, W.H.; Qin, L. Periodic Communities Mining in Temporal Networks: Concepts and Algorithms. IEEE Trans. Knowl. Data Eng. 2020, 34, 3927–3945. [Google Scholar] [CrossRef]
- Pereira, L.R.; Lopes, R.J.; Louca, J. Community identity in a temporal network: A taxonomy proposal. Ecol. Complex. 2021, 45, 100904. [Google Scholar] [CrossRef]
- Pan, R.K.; Saramaki, J. Path lengths, correlations, and centrality in temporal networks. Phys. Rev. E 2011, 84, 016105. [Google Scholar] [CrossRef]
- Chen, D.B. Empirical study on structural properties in temporal networks under different time scales. Eur. Phys. J. B 2015, 88, 320. [Google Scholar] [CrossRef]
- Batagelj, V.; Praprotnik, S. An algebraic approach to temporal network analysis based on temporal quantities. Soc. Netw. Anal. Min. 2016, 6, 28. [Google Scholar] [CrossRef]
- Wang, D.J.; Yu, W.; Zou, X.F. Tensor-based mathematical framework and new centralities for temporal multilayer networks. Inf. Sci. 2020, 512, 563–580. [Google Scholar] [CrossRef]
- Zhan, X.X.; Hanjalic, A.; Wang, H.J. Information diffusion backbones in temporal networks. Sci. Rep. 2019, 9, 6798. [Google Scholar] [CrossRef]
- Zhong, L.F.; Bai, Y.; Liu, C.J.; Du, J.; Pan, W.J. Information Spreading on Memory Activity-Driven Temporal Networks. Complexity 2021, 2021, 8015191. [Google Scholar] [CrossRef]
- Zhu, H.; Ma, J. Knowledge diffusion in complex networks by considering time-varying information channels. Phys. A 2018, 494, 225–235. [Google Scholar] [CrossRef]
- Sun, Y.; Latora, V. The evolution of knowledge within and across fields in modern physics. Sci. Rep. 2020, 10, 12097. [Google Scholar] [CrossRef]
- Koher, A.; Lentz, H.H.K.; Gleeson, J.P.; Hovel, P. Contact-Based Model for Epidemic Spreading on Temporal Networks. Phys. Rev. X 2019, 9, 031017. [Google Scholar] [CrossRef]
- Masuda, N.; Miller, J.C.; Holme, P. Concurrency measures in the era of temporal network epidemiology: A review. J. R. Soc. Interface 2021, 18, 20210019. [Google Scholar] [CrossRef] [PubMed]
- Guleva, V.Y.; Bochenina, K.O.; Skvorcova, M.V.; Boukhanovsky, A.V. A Simulation Tool for Exploring the Evolution of Temporal Interbank Networks. JASSS J. Artif. Soc. Soc. Simul. 2017, 20, 15. [Google Scholar] [CrossRef]
- Zhao, L.F.; Wang, G.J.; Wang, M.G.; Bao, W.Q.; Li, W.; Stanley, H.E. Stock market as temporal network. Phys. A 2018, 506, 1104–1112. [Google Scholar] [CrossRef]
- Didimo, W.; Grilli, L.; Liotta, G.; Montecchiani, F.; Pagliuca, D. Visual querying and analysis of temporal fiscal networks. Inf. Sci. 2019, 505, 406–421. [Google Scholar] [CrossRef]
- Cai, Q.; Alam, S.; Duong, V.N. A Spatial-Temporal Network Perspective for the Propagation Dynamics of Air Traffic Delays. Engineering 2021, 7, 452–464. [Google Scholar] [CrossRef]
- Urena-Carrion, J.; Saramaki, J.; Kivela, M. Estimating tie strength in social networks using temporal communication data. EPJ Data Sci. 2020, 9, 37. [Google Scholar] [CrossRef]
- Shinkuma, R.; Sugimoto, Y.; Inagaki, Y. Weighted network graph for interpersonal communication with temporal regularity. Soft Comput. 2019, 23, 3037–3051. [Google Scholar] [CrossRef]
- Li, X.G.; Li, X.K. The Impact of Different Internet Application Contexts on Knowledge Transfer between Enterprises. Systems 2021, 9, 87. [Google Scholar] [CrossRef]
- Holme, P.; Saramaki, J. Temporal networks. Phys. Rep. Rev. Sect. Phys. Lett. 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Uzzi, B.; Spiro, J. Collaboration and creativity: The small world problem. Am. J. Sociol. 2005, 111, 447–504. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, J.; Guan, J. Network Embeddedness and Innovation: Evidence from the Alternative Energy Field. IEEE Trans. Eng. Manag. 2020, 67, 769–782. [Google Scholar] [CrossRef]
- Wang, Z.-X.; He, L.-Y.; Li, D.-D. Assessment of the degree of order in the organisational structure of electricity regulatory institution in China based on shannon entropy. Energy Policy 2019, 132, 429–439. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, J.; Li, Y.; David, J. An Appraisal of Manufacturing Structures Using Timeliness-Quality Entropy and Order Index Methods. IEEE Access 2021, 9, 141589–141598. [Google Scholar] [CrossRef]
- Campani, M.; Vaglio, R. A simple interpretation of the growth of scientific/technological research impact leading to hype-type evolution curves. Scientometrics 2015, 103, 75–83. [Google Scholar] [CrossRef]
- Zhuang, E.; Chen, G.; Feng, G. A network model of knowledge accumulation through diffusion and upgrade. Phys. A 2011, 390, 2582–2592. [Google Scholar] [CrossRef]
- Lee, S.; Kim, W.; Lee, H.; Jeon, J. Identifying the structure of knowledge networks in the US mobile ecosystems: Patent citation analysis. Technol. Anal. Strateg. Manag. 2016, 28, 411–434. [Google Scholar] [CrossRef]
- Jaffe, A.B. Technological opportunity and spillovers of R&D: Evidence from firms’ patents, profits and market value. Am. Econ. Rev. 1986, 76, 984–1001. [Google Scholar] [CrossRef]
- Isaksson, O.H.D.; Simeth, M.; Seifert, R.W. Knowledge spillovers in the supply chain: Evidence from the high tech sectors. Res. Policy 2016, 45, 699–706. [Google Scholar] [CrossRef]
- Chen, H.; Xie, F. How technological proximity affect collaborative innovation? An empirical study of China’s Beijing-Tianjin-Hebei region. J. Manag. Anal. 2018, 5, 287–308. [Google Scholar] [CrossRef]
- Arvanitis, S.; Seliger, F.; Woerter, M. Knowledge Spillovers, Competition and Innovation Success. Oxf. Bull. Econ. Stat. 2020, 82, 1017–1041. [Google Scholar] [CrossRef]
- Bianconi, G.; Barabasi, A.L. Competition and multiscaling in evolving networks. Europhys. Lett. 2001, 54, 436–442. [Google Scholar] [CrossRef]
- Tsiotas, D. Detecting differences in the topology of scale-free networks grown under time-dynamic topological fitness. Sci. Rep. 2020, 10, 10630. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Su, J. The spatial-temporal complexity and dynamics of research collaboration: Evidence from 297 cities in China (1985–2016). Technol. Forecast. Soc. Chang. 2021, 162, 120390. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Lee, C.-C.; Li, J. Structural characteristics and determinants of an international green technological collaboration network. J. Clean. Prod. 2021, 324, 129258. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Guan, Y.; Kang, Y. Research on the structural features and influence mechanism of the green ICT transnational cooperation network. Econ. Anal. Policy 2022, 75, 734–749. [Google Scholar] [CrossRef]
- Hu, H.; Wang, X. Evolution of a large online social network. Phys. Lett. A 2009, 373, 1105–1110. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Q.; Liu, W. The structural evolution of an online discussion network. Phys. A 2010, 389, 5871–5877. [Google Scholar] [CrossRef]
- Yu, X.K.; Cui, Y.; Chen, Y.L.; Chang, I.S.; Wu, J. The drivers of collaborative innovation of the comprehensive utilization technologies of coal fly ash in China: A network analysis. Environ. Sci. Pollut. Res. 2022, 29, 56291–56308. [Google Scholar] [CrossRef] [PubMed]
- Dou, Y.D.; Bo, Q.W. Characteristics and Dynamics of BIM Adoption in China: Social Network Analysis. J. Constr. Eng. Manag. 2022, 148, 04022025. [Google Scholar] [CrossRef]
- Zhao, Q.J.; Guan, J.C. International collaboration of three ‘giants’ with the G7 countries in emerging nanobiopharmaceuticals. Scientometrics 2011, 87, 159–170. [Google Scholar] [CrossRef]
- Fang, W.; Xiao, L.M. Simulation of Knowledge Transfer Process Model Between Universities: A Perspective of Cluster Innovation Network. Complexity 2018, 2018, 5983531. [Google Scholar] [CrossRef]
- Yang, H.; Yang, C.; Zhang, X.; Yuan, X. Influences of Different Architectures on the Thermodynamic Performance and Network Structure of Aircraft Environmental Control System. Entropy 2021, 23, 855. [Google Scholar] [CrossRef]
- Zhang, Z.; David, J. Structural order measure of manufacturing systems based on an information-theoretic approach. Expert Syst. Appl. 2020, 158, 113636. [Google Scholar] [CrossRef]
- Dai, Z.X.; Chen, Y.; Li, J.H.; Fam, J.; Bezerianos, A.; Sun, Y. Temporal efficiency evaluation and small-worldness characterization in temporal networks. Sci. Rep. 2016, 6, 34291. [Google Scholar] [CrossRef]
- Waniek, M.; Holme, P.; Rahwan, T. Hiding in Temporal Networks. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1645–1657. [Google Scholar] [CrossRef]

 , ➁ and
, ➁ and  , and ➂ and
, and ➂ and  indicate that nodes join, retain, and exit the network according to Formula (10), Formula (11), and Formula (12), respectively; ➃ indicates that the new nodes added and the old nodes retained are connected preferentially according to Formula (17); ⊕ indicates that the instantaneous networks under each time window are merged to form the integrated networks structures.
indicate that nodes join, retain, and exit the network according to Formula (10), Formula (11), and Formula (12), respectively; ➃ indicates that the new nodes added and the old nodes retained are connected preferentially according to Formula (17); ⊕ indicates that the instantaneous networks under each time window are merged to form the integrated networks structures.
 , ➁ and
, ➁ and  , and ➂ and
, and ➂ and  indicate that nodes join, retain, and exit the network according to Formula (10), Formula (11), and Formula (12), respectively; ➃ indicates that the new nodes added and the old nodes retained are connected preferentially according to Formula (17); ⊕ indicates that the instantaneous networks under each time window are merged to form the integrated networks structures.
indicate that nodes join, retain, and exit the network according to Formula (10), Formula (11), and Formula (12), respectively; ➃ indicates that the new nodes added and the old nodes retained are connected preferentially according to Formula (17); ⊕ indicates that the instantaneous networks under each time window are merged to form the integrated networks structures.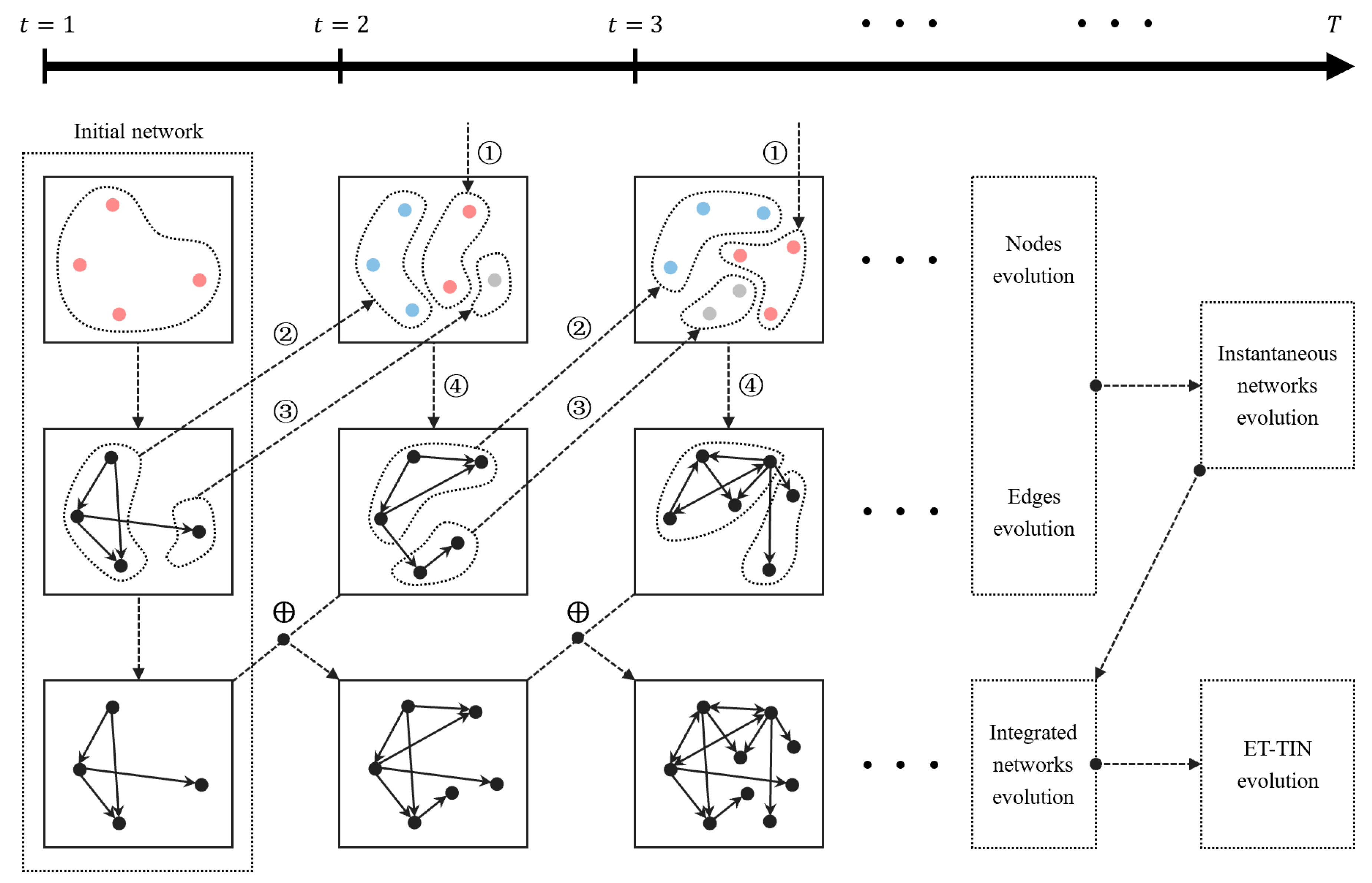


| Notations | Description |
|---|---|
| Level Ⅰ | |
| The probability of node being connected preferentially based on its multiple knowledge attributes. | |
| Level Ⅱ | |
| The probability of node being connected preferentially based on its knowledge novelty. | |
| The probability of node being connected preferentially based on its knowledge coherence. | |
| The probability of node being connected preferentially based on its knowledge growth. | |
| The probability of node being connected preferentially based on its knowledge influence. | |
| The fitness of node , and there is no unified standard for the probability distribution of node fitness, which should be determined according to the real network data. | |
| The upper limit of knowledge absorption of node , which can be set to obey the power law distribution according to the in-degree distribution of nodes in most real networks. | |
| Level Ⅲ | |
| The knowledge novelty of node at time , which is used to calculate . | |
| The knowledge structure vector formed by the innovation outputs of node in different knowledge domains up to time since they joined the network, which is used to calculate . | |
| The in-degree of node at time , which can reflect its knowledge absorption and be used to calculate . | |
| The out-degree of node at time , which can reflect its knowledge diffusion and be used to calculate . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, Y.; He, Q.; Yu, Q. Cyclical Evolution of Emerging Technology Innovation Network from a Temporal Network Perspective. Systems 2023, 11, 82. https://doi.org/10.3390/systems11020082
Liu Y, Chen Y, He Q, Yu Q. Cyclical Evolution of Emerging Technology Innovation Network from a Temporal Network Perspective. Systems. 2023; 11(2):82. https://doi.org/10.3390/systems11020082
Chicago/Turabian StyleLiu, Yaqin, Yunsi Chen, Qing He, and Qian Yu. 2023. "Cyclical Evolution of Emerging Technology Innovation Network from a Temporal Network Perspective" Systems 11, no. 2: 82. https://doi.org/10.3390/systems11020082
APA StyleLiu, Y., Chen, Y., He, Q., & Yu, Q. (2023). Cyclical Evolution of Emerging Technology Innovation Network from a Temporal Network Perspective. Systems, 11(2), 82. https://doi.org/10.3390/systems11020082






