Simplifying the Complexity in the Problem of Choosing the Best Private-Sector Partner

Abstract

Governments frequently partner with the private sector to provide infrastructure and public services. These cooperations, known as public–private partnerships (PPPs), have often failed. Sometimes, due to the problem’s complexity, the public sector cannot choose the right partner for these projects, which is one of the main reasons for failures. Complexity in such problems is associated with a large number of indicators, imprecise judgments of decision-makers or problem owners, and the unpredictability of the environment (under conditions of uncertainty). Therefore, presenting a simplified algorithm for this complicated process is the primary goal of the current research so that it can consider the problem’s various dimensions. While many researchers address the critical risk factors (CRFs) and others focus on key performance indicators (KPIs), this research has considered both CRFs and KPIs to choose the best private-sector partner. In addition, we used single-valued neutrosophic sets (SVNSs) to collect decision-makers’ views, which can handle ambiguous, incomplete, or imprecise information. Next, by defining the ideal alternative and using the similarity measure, we specified the ranks of the alternative. Additionally, to face the uncertain environment, we examined the performance of options in four future scenarios. The steps of the proposed algorithm are explained in the form of a numerical example. The results of this research showed that by employing a simple algorithm, even people who do not have significant operations research knowledge could choose the best option by paying attention to the dimensions of the problem complexity.

1. Introduction

The public–private partnership (PPP) is an alternative procurement method that has gained popularity in many countries over recent decades [1]. Governments have adopted it widely worldwide to provide quality public goods and services [2]. Generally speaking, PPPs are partnerships between the public and private sectors, with varying responsibilities, to deliver public services [3]. The public sector holds expertise in administrative matters and the safety and well-being of its citizens, while the private sector can adapt skills, innovate, assess risks, and use technology. Therefore, public and private expertise must be combined, as neither sector can deliver projects independently without collaborating [4]. Investing in PPPs allows the private sector to increase long-term returns and improve the reputation of companies.

In contrast, the public sector utilizes capital, technologies, and management skills to achieve sustainable development [5]. Notwithstanding, according to the literature, PPP failures have not been rare [6]. Because of the long-term agreement and high levels of uncertainty, various failures are inevitable in PPP projects [7]. In addition, the lack of government capacity and incorrect interference in managing PPP projects may lead to failure [8]. Moreover, selecting partners is often challenging and poses a significant risk of PPP failures [4]. Selection of the optimum private partner with the necessary qualities and capabilities is critical to successful completion. Failure to choose the right partner hinders the execution of the project, resulting in substantial negative economic impacts [9]. The preliminary selection of partners, which often leads to the failure of the concluded agreement and is fraught with loss of state budget funds, is confirmed by much statistical data [10]. Researchers have explored the current state of the research in PPP and identified partner selection as a research gap and future research trends in the PPP literature [11].

In a PPP, the public and private sectors are parties to a long-term contract. Since PPP contracts are long-term, they are susceptible to the environment [12]. One of the ways to deal with environmental uncertainty is to choose a robust partner [13]. While selecting the right private-sector partner is a crucial problem in PPP projects, a few researchers have addressed the decision-making problem [10]. Choosing partners can be challenging, resulting in conflict and failure of PPP relationships [4]. In such projects, the public sectors are essential in determining suitable private sectors [14]. Therefore, it is believed that there needs to be a focus on well-structured and practical decision methods obligatory to improve the performance of PPPs [15]. Decision-making methods can facilitate partner selection decisions partially intuitively [16]. An important question is evaluating conflicting targets and criteria when estimating alternatives [17].

Unlike the supplier selection problems [18], the literature focusing on partner selection in PPP projects is limited [9]. Recently, researchers have proposed a novel integrated private partner selection framework applying the best–worst method (BWM) and the technique of order preference similarity to the ideal solution (TOPSIS). They evaluated partners’ performance considering economic, social, technological, and environmental aspects [11]. Others applied the analytic hierarchy process (AHP) and multi-attribute utility theory (MAUT) to develop an approach for selecting private partners in the housing industry. Their findings categorized criteria into four categories: financial, technical, managerial, and safety/environmental [9]. Grey rational analysis-VIekriterijumsko KOmpromisno Rangiranje (GRA-VIKOR) is proposed in a paper that considers the combined weights of the improved CRITIC-entropy weight method (EWM). In conjunction with the GRA, the VIKOR approach considers the inherent correlation between evaluation indicators, thus improving the validity of selection assessment results [19]. A two-phase framework is used in another paper to select partners. The first phase integrates data envelopment analysis (DEA) and differential evolution (DE) algorithms to compute efficiency scores. In phase two, those efficiency scores are utilized to allocate orders using a multi-objective model [20]. An integrated model was developed using the BWM for evaluating and ranking the selection criteria and the VIKOR for selecting a final partner [21]. Another study uses the AHP and VIKOR to choose the right partner [22].

Some limitations need further improvement when investigating the private-sector partner selection from various perspectives using various multi-criteria decision-making (MCDM) methods. The following two aspects illustrate the need for further improvement: (1) Evaluation of the private sector is usually sophisticated, which can lead to vague and uncertain judgments by decision-makers [23]. (2) Collaborating requires identifying the partner’s characteristics most relevant to problem owners’ needs [24].

For the first limitation, scholars have used fuzzy decision-making methods to deal with the ambiguity of assessment language [25,26,27]. The TOPSIS method using interval-valued intuitionistic fuzzy sets (IVIFSs) was developed to choose a partner for PPP projects [28]. According to researchers, the fuzzy sustainable supplier index is a result of combining the triple bottom-line criteria of sustainable development with performance and using MCDM technology to determine the most sustainable supplier. To control uncertainty, researchers used the trapezoidal fuzzy membership function [29]. Multi-attribute group decision-making (MAGDM) problems were solved using the q-rung orthopair fuzzy entropy-based gained and lost dominance score (GLDS) method as an alternative to the traditional GLDS method. Based on the Hamacher operation laws, the q-rung orthopair fuzzy Hamacher weighting average (q-ROFHWA) and q-rung orthopair fuzzy Hamacher weighting geometric (q-ROFHWG) operators were presented to fuse q-rung orthopair fuzzy information effectively [30].

Moreover, the attribute weights are also determined by q-rung orthopair fuzzy entropy (q-ROFE). A MAGDM model with q-rung orthopair fuzzy information was then constructed based on the q-ROFHWA operator, the q-ROFE, and the traditional GLDS method [30]. A study focused on the Pythagorean fuzzy environment. Partner selection problems with criteria weights are solved using Pythagorean fuzzy sets and TOPSIS methods. A new similarity measure was developed based on the trigonometric function for PFSs to calculate criteria weights [31]. Researchers identified selection criteria for private partners in PPP projects using an extended multi-criteria operation and compromise solution (VIKOR) method. A comprehensive method for selecting an optimal private partner using VIKOR-based tools with an intuitionistic fuzzy set was developed. The factors were divided into five packages: essential ability, management ability, previous performance, credit performance, project performance, and sustainable development [32]. The fuzzy-based approach dealt with vague, uncertain, and qualitative information to present a practical analytical method for selecting a suitable partner. The fuzzy decision-making trial and evaluation laboratory (DEMATEDL) method has been combined with anti-entropy weighting (AEW) and FVIKOR operations to select the most suitable candidate based on the combined weighting technique [33]. An integrated subjective or objective fuzzy group decision-making (FGDM) method and a factor risk scoring system were applied to select private sector partners under the PPP model [34]. Therefore, it can be seen that using neutrosophic sets (NSs) that can express the uncertainty in experts’ judgments more appropriately [35] has not been considered in the literature on private-sector partner selection.

For the second limitation, the development of criteria to select private partners in PPP contracts has been undertaken in multiple prior studies. Still, these studies either pay attention to risk factors or success factors. Some researchers identified five risk groups: financial, political, project-specific, social, and uncontrollable [36]. Scholars have highlighted that the social risks extend to land acquisition, environmental pollution, and demolition [37]. Risk analysis revealed seven critical risk groups. In addition to institutional capacity and the local economy, public sector maturity, project finance, project planning, implementation, and project revenue achieved a high-impact linguistic assessment [38]. Inflation and change in interest rates are some of the financial risks. In contrast, political risks, including unstable policies; economic risks, such as high operating and maintenance costs; technical risks, especially charging technology; and risks posed by the project and the project participant, such as the PPP experience, cannot be ignored [39]. Other researchers have shown that “government intervention” is one of the crucial risk groups, with “government maturity risk” being the second and “economic viability risk” the third [17].

In contrast, other researchers have attempted to recognize CSFs, increasing the possibility of success in PPP projects [40]. It has been shown that the government must implement specific PPP policies, has well-organized and committed public agencies, and provide a stable political and social environment, favorable legal frameworks, and good governance to implement PPP projects effectively. For PPP projects, sector-specific laws, guidelines, standard bidding documents, and contract models should also be used to regulate the PPP procurement process suggested in the PPP proclamation [8]. Researchers surveyed 27 stakeholders to test CSFs identified through a literature review empirically. Results showed that acceptance and support given by the community, project feasibility, the laws, regulations, guidelines, the available financial market, and having a well-organized and committed public agency were the high-priority CSFs [41]. An analysis of 42 CSFs yielded six primary categories: public sector clusters, private sector clusters, procurement process clusters, project information clusters, and external clusters. In implementing PPP infrastructure projects, the private sector, project information, and procurement process clusters had the most significant influence [42]. In developing countries, investigating the case studies indicated that a transparent bidding process, good partnering, and risk allocation are the CSFs in PPP projects [3].

Accordingly, three crucial points have not been considered in previous research, including the use of neutrosophic sets to convert the qualitative judgments of experts into quantitative data, the consideration of CRFs and KPIs in the evaluation of partners simultaneously, and the investigation of the performance of alternatives in case of changes in environmental conditions in the future. Furthermore, there is another criticism about the previous approaches focusing on the problem of selecting a private sector partner: they complicate the process of obtaining the answer (computationally and interpreting it by the decision maker). On the contrary, this research is intended to simplify this process for decision-makers who lack sufficient operations research (OR) expertise. Therefore, the current study aims to provide a practical and straightforward approach that helps decision-makers consider the above characteristics when choosing the best partner. For this purpose, the other sections of the article are organized as follows: in the next section, the proposed methodology is introduced, and in Section 3, by presenting a numerical example, the method of implementing the approach is mentioned. Finally, the last part summarizes the contents and provides suggestions for future research.

2. Methodology

In general, decision-making involves selecting the best option from among a set of other alternatives based on the judgment of a decision-maker or a group of decision-makers [43]. In recent years, decision making has become increasingly complex due to the growing amount of decision information and alternatives, the inherent uncertainty in decision-making, and the fuzzy nature of human reasoning [44]. It is impossible to express the decisions made by people with crisp numerical values [45]. Practical multi-attribute decision-making (MADM) problems are characterized by fast-increasing complex uncertainties requiring effective fuzzy tools to express judgments and preferences [46]. A top feature of fuzziness is its ability to solve engineering and statistical problems efficiently. Several realistic situations can be solved by applying uncertainty theory, including networking problems, decision-making problems, and the impact of uncertainty on social science [47]. With the help of Zadeh’s linguistic variables, Xu’s uncertain linguistic variables proved helpful in dealing with decision-making problems with qualitative attributes [23]. The intuitionistic fuzzy set (IFS) model, with membership μ_A(x_i) ∈ [0, 1] and nonmembership ν_A(x_i) ∈ [0, 1] functions, such that μ_A(x_i) + ν_A(x_i) ≤ 1 for each x ∈ X [48], was introduced to overcome the weakness of fuzzy sets (FS). However, IFSs or FSs cannot manage partial or incomplete information, whereas neutrosophic sets can manage inconsistent and indeterminate information very well [23].

A three-dimensional NS based on three fundamental elements, truth, indeterminacy, and falsity, was developed to handle incomplete information [49]. An intuitionistic fuzzy set theory cannot make a proper decision without the indeterministic part of uncertain data, which appears in NS theory [50]. The most exciting point is that all these three functions are entirely independent, and one function is unaffected by another [50]. NS has the potential to be an investigation tool when dealing with uncertain data sets; Consequently, many different applications have been developed around it [31]. Ratings of alternatives the decision-maker provides can be expressed with NSs in the MADM context. SVNSs were developed to ease the application of neutrosophic sets to real-life scientific and engineering studies [51].

Additionally, as the SVNS model’s membership functions assume values within the standard interval [0, 1], it is compatible with other fuzzy-based models, which can be applied to real-life decision-making problems using actual datasets more efficiently [52]. SVNS has proven helpful in handling various real-life applications due to its flexibility in describing indeterminate and inconsistent information. Several studies have been conducted and applications made in several fields since its appearance [51].

To determine the best alternative in a decision set, we can use the concept of the ideal point. Although the ideal alternative does not exist in the real world, it does provide a sound theoretical construct against which to evaluate options [53]. The similarity measure (SM) measures the similarity between an asset and other entities whose properties are known [54]. Therefore, NS and SVNS theories must include SM, quantifying the similarity between two objects [55]. Researchers and scholars have continually proposed new similarity measures for fuzzy-based models, including the SVNS model, applied to various practical MCDM problems [56]. This section provides the related definitions to compute SVNS in the application.

Definition 2.1.:

Ref. [57] Let $\mathit{X}$ be a universe of discourse. A neutrosophic set$\mathit{N}$ is an object having the farm $\mathit{N}=\left\{\left(\mathit{x}:.{\mathit{T}}_{\mathit{N}\left(\mathit{x}\right)},{\mathit{I}}_{\mathit{N}\left(\mathit{x}\right)},{\mathit{F}}_{\mathit{N}\left(\mathit{x}\right)}\right),\mathit{x}\in \mathit{X}\right\}$ characterized by truth-membership ${\mathit{T}}_{\mathit{N}\left(\mathit{x}\right)},$ indeterminacy-membership ${\mathit{I}}_{\mathit{N}\left(\mathit{x}\right)},$ and falsity-membership functions ${\mathit{F}}_{\mathit{N}\left(\mathit{x}\right)}.$ These functions are real standard or nonstandard subsets of $]0^{-},1^{+}[,$ with the condition $0^{-}\le {\mathit{T}}_{\mathit{N}(\mathit{x})}+{\mathit{I}}_{\mathit{N}(\mathit{x})}+{\mathit{F}}_{\mathit{N}(\mathit{x})}\le 3^{+}.$

Definition 2.2.:

Ref. [58] Let $\mathit{X}$ be a universe of discourse. A single-valued neutrosophic set $\mathit{N}$ is an object having a farm $\mathit{N}=\{(\mathit{x}:{\mathit{T}}_{\mathit{N}(\mathit{x})},{\mathit{I}}_{\mathit{N}(\mathit{x})},{\mathit{F}}_{\mathit{N}(\mathit{x})}),\mathit{x}\in \mathit{X}\},$ where the functions are real standard subsets $[0,1],$ with the condition $0\le {\mathit{T}}_{\mathit{N}(\mathit{x})}+{\mathit{I}}_{\mathit{N}(\mathit{x})}+{\mathit{F}}_{\mathit{N}(\mathit{x})}\le 3$. To make things easier, we apply $\mathit{x}=({\mathit{T}}_{\mathit{N}},{\mathit{I}}_{\mathit{N}},{\mathit{F}}_{\mathit{N}})$ to characterize an element $\mathit{X}$ in SVNS and $\mathit{X}$ is a single-valued neutrosophic number [59].

Definition 2.3.:

Ref. [53] Let $\mathit{N}=\left\{\mathit{x}:〈{\mathit{T}}_{\mathit{N}\left(\mathit{x}\right)},{\mathit{I}}_{\mathit{N}\left(\mathit{x}\right)},{\mathit{F}}_{\mathit{N}\left(\mathit{x}\right)}〉\right\}$ and $\mathit{M}=\left\{\mathit{x}:〈{\mathit{T}}_{\mathit{M}\left(\mathit{x}\right)},{\mathit{I}}_{\mathit{M}\left(\mathit{x}\right)},{\mathit{F}}_{\mathit{M}\left(\mathit{x}\right)}〉\right\}$ be two SVNSs and $\mathit{S}(\mathit{N},\mathit{M})$ be a similarity measure for SVNSs. $\mathit{S}(\mathit{N},\mathit{M})$ satisfies the following properties:

$$\begin{array}{l}1. 0\le \mathit{S}(\mathit{N},\mathit{M})\le 1,\\ 2. \mathit{S}(\mathit{N},\mathit{M})=\mathit{S}(\mathit{M},\mathit{N}),\\ 3. \mathit{S}(\mathit{N},\mathit{M})=1, \mathit{i}\mathit{f} \mathit{N}=\mathit{M},\\ 4. \mathit{S}(\mathit{N},\mathit{M})\le \mathit{S}(\mathit{N},\mathit{K}), \mathit{i}\mathit{f} \mathit{N}\le \mathit{M}\le \mathit{K}.\end{array}$$

Definition 2.4.:

Ref. [56] Let $\mathit{N}=\left\{\mathit{x}:〈{\mathit{T}}_{\mathit{N}\left(\mathit{x}\right)},{\mathit{I}}_{\mathit{N}\left(\mathit{x}\right)},{\mathit{F}}_{\mathit{N}\left(\mathit{x}\right)}〉\right\}$ and $\mathit{M}=\left\{\mathit{x}:〈{\mathit{T}}_{\mathit{M}\left(\mathit{x}\right)},{\mathit{I}}_{\mathit{M}\left(\mathit{x}\right)},{\mathit{F}}_{\mathit{M}\left(\mathit{x}\right)}〉\right\}$ be two SVNSs. We can calculate $\mathit{S}(\mathit{N},\mathit{M})$ applying Equation (1) as follows:

$$\mathit{S}(\mathit{N},\mathit{M})=\frac{{\displaystyle \sum \mathit{x}\in \mathit{X}}({\mathit{T}}_{\mathit{N}}^2(\mathit{x})\cap {\mathit{T}}_{\mathit{M}}^2(\mathit{x}))+(1-{\mathit{I}}_{\mathit{N}}^2(\mathit{x}))\cap (1-{\mathit{I}}_{\mathit{M}}^2(\mathit{x}))+(1-{\mathit{F}}_{\mathit{N}}^2(\mathit{x}))\cap (1-{\mathit{F}}_{\mathit{M}}^2(\mathit{x}))}{{\displaystyle \sum \mathit{x}\in \mathit{X}}({\mathit{T}}_{\mathit{N}}^2(\mathit{x})\cup {\mathit{T}}_{\mathit{M}}^2(\mathit{x}))+(1-{\mathit{I}}_{\mathit{N}}^2(\mathit{x}))\cup (1-{\mathit{I}}_{\mathit{M}}^2(\mathit{x}))+(1-{\mathit{F}}_{\mathit{N}}^2(\mathit{x}))\cup (1-{\mathit{F}}_{\mathit{M}}^2(\mathit{x}))}$$

(1)

Figure 1 shows this practical, straightforward method includes seven steps.

The proposed algorithm begins with listing alternatives (private-sector partners P_i, I = 1, …, n) in the first step. In step 2, after identifying CRFs and KPIs, we should choose some of the most important ones (C_j, j = 1, …, m). Identifying CRFs and KPIs can be accomplished by consulting the literature, as we did in this study. However, it is imperative to remember that these indicators vary for each project. In light of this, it would be better to combine the views of decision-makers (problem owners) with those of the literature. Step 3 defines the ideal Partner (P_I) with the perfect performance in all the criteria. The next step will be to design future scenarios (S_nf, f = 1,…,g). To develop future scenarios, we can apply different approaches to scenario planning, such as three-scenario (optimistic, pessimistic, and probable), four-scenario (taking into account two environmental variables), or robustness analysis (no limit on the number of scenarios). We use the second approach in this research by defining four scenarios according to the considerations that should be considered when using the last one. Suppose that the two indicators, including the interest rate (with two states of stability or decrease) and the floating investment costs (with two states of stability or increase), are the most significant indicators that determine the future. In this case, we will face four scenarios f₁: stability of interest rate and investment floating costs, f₂: decrease in the interest rate and stability of investment floating costs, f₃: stability of the interest rate and increase in investment floating costs, and f₄: decrease in the interest rate and increase in investment floating costs. In step 5, we should construct decision matrices D_f using experts’ viewpoints. Therefore, at this step, a survey of decision-makers (problem owners) should be conducted in as many as the designed scenarios. In step 6, applying Equation (1), we must compute the similarity measure for all partners in all scenarios. Finally, we rank the partners based on their similarity scores.

3. Numerical Example

Here, by a numerical example, we will show how to apply our approach to select the best private-sector partner. In the first step, consider five partners (P₁, P₂, P₃, P₄, P₅); the sixth is the ideal partner (P_I). To choose the criteria (risk and performance factors), we used the factors shown in

Table 1. PPP critical risk and key performance factors.

Factors	Abbreviation
Finance ability [9,36,60]	R1
Performance quality [12,36,61]	R2
Infrastructure equipment [9,21,28]	R3
On-time delivery [12,21,60,62]	R4
Community acceptance [8,40,41,42]	S1
Well-organizing and community [8,11,19]	S2
Resource availability [3,32,34]	S3

.

The decision matrices D_f are available in

Table 2. The decision matrix in Scenario 1 (D₁).

D	R1	R2	R3	R4	S1	S2	S3	S4
P1	(0.7, 0.3, 0.2)	(0.9, 0.1, 0.1)	(0.7, 0.4, 0.1)	(0.7, 0.2, 0.2)	(0.3, 0.4, 0.6)	(0.8, 0.3, 0.1)	(0.3, 0.4, 0.7)	(0.4, 0.5, 0.6)
P2	(0.8, 0.2, 0.2)	(0.8, 0.4, 0.2)	(0.7, 0.3, 0.2)	(0.5, 0.5, 0.5)	(0.4, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.3, 0.4, 0.7)	(0.5, 0.5, 0.5)
P3	(0.6, 0.4, 0.1)	(0.7, 0.3, 0.1)	(0.7, 0.3, 0.2)	(0.8, 0.3, 0.2)	(0.8, 0.1, 0.2)	(0.8, 0.2, 0.2)	(0.7, 0.3, 0.2)	(0.7, 0.4, 0.2)
P4	(0.8, 0.3, 0.1)	(0.6, 0.5, 0.2	(0.8, 0.2, 0.3)	(0.5, 0.5, 0.5)	(0.8, 0.1, 0.2)	(0.7, 0.2, 0.3)	(0.7, 0.3, 0.2)	(0.8, 0.2, 0.1)
P5	(0.7, 0.4, 0.2)	(0.7, 0.2, 0.2)	(0.6, 0.5, 0.3)	(0.7, 0.4, 0.1)	(0.6, 0.3, 0.2)	(0.5, 0.5, 0.5)	(1.0, 0.0, 0.0)	(0.8, 0.1, 0.2)
PI	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)

,

Table 3. The decision matrix in Scenario 2 (D₂).

D	R1	R2	R3	R4	S1	S2	S3	S4
P1	(0.9, 0.1, 0.1)	(0.9, 0.1, 0.1)	(0.8, 0.2, 0.2)	(0.9, 0.1, 0.1)	(0.8, 0.2, 0.2)	(0.8, 0.3, 0.1)	(0.9, 0.1, 0.1)	(0.9, 0.1, 0.1)
P2	(0.8, 0.2, 0.2)	(0.8, 0.4, 0.2)	(0.7, 0.3, 0.2)	(0.8, 0.4, 0.2)	(0.4, 0.5, 0.5)	(0.8, 0.3, 0.2)	(0.9, 0.2, 0.1)	(0.8, 0.2, 0.1)
P3	(0.7, 0.3, 0.2)	(0.7, 0.3, 0.1)	(0.6, 0.3, 0.2)	(0.6, 0.3, 0.2)	(0.8, 0.1, 0.2)	(0.5, 0.5, 0.5)	(0.7, 0.3, 0.2)	(0.8, 0.2, 0.1)
P4	(0.8, 0.3, 0.1)	(0.9, 0.1, 0.1)	(0.6, 0.2, 0.3)	(0.6, 0.3, 0.2)	(0.6, 0.3, 0.2)	(0.5, 0.5, 0.5)	(0.7, 0.3, 0.2)	(0.6, 0.3, 0.2)
P5	(0.5, 0.5, 0.5)	(0.7, 0.2, 0.2)	(0.6, 0.5, 0.3)	(0.5, 0.5, 0.5)	(0.6, 0.3, 0.2)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.6, 0.3, 0.3)
PI	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)

,

Table 4. The decision matrix in Scenario 3 (D₃).

D	R1	R2	R3	R4	S1	S2	S3	S4
P1	(0.7, 0.3, 0.2)	(0.9, 0.1, 0.1)	(0.7, 0.4, 0.1)	(0.7, 0.2, 0.2)	(0.3, 0.4, 0.6)	(0.8, 0.3, 0.1)	(0.3, 0.4, 0.7)	(0.4, 0.5, 0.6)
P2	(0.8, 0.2, 0.2)	(0.8, 0.4, 0.2)	(0.7, 0.3, 0.2)	(0.5, 0.5, 0.5)	(0.4, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.3, 0.4, 0.7)	(0.5, 0.5, 0.5)
P3	(0.9, 0.1, 0.1)	(0.7, 0.3, 0.1)	(0.9, 0.1, 0.1)	(0.8, 0.3, 0.2)	(0.9, 0.1, 0.1)	(0.8, 0.2, 0.2)	(1.0, 0.0, 0.0)	(0.7, 0.4, 0.2)
P4	(0.8, 0.3, 0.1)	(0.9, 0.1, 0.1)	(0.8, 0.2, 0.3)	(0.5, 0.5, 0.5)	(0.8, 0.1, 0.2)	(0.7, 0.2, 0.3)	(0.7, 0.3, 0.2)	(0.8, 0.2, 0.1)
P5	(0.8, 0.2, 0.0)	(0.9, 0.1, 0.1)	(0.6, 0.5, 0.3)	(0.7, 0.4, 0.1)	(0.9, 0.1, 0.1)	(0.8, 0.2, 0.2)	(0.9, 0.1, 0.1)	(0.9, 0.1, 0.1)
PI	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)

and

Table 5. The decision matrix in Scenario 4 (D₄).

D	R1	R2	R3	R4	S1	S2	S3	S4
P1	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.7, 0.4, 0.1)	(0.6, 0.3, 0.3)	(0.3, 0.4, 0.6)	(0.6, 0.4, 0.4)	(0.3, 0.4, 0.7)	(0.4, 0.5, 0.6)
P2	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.8, 0.3, 0.2)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)
P3	(0.6, 0.4, 0.1)	(0.7, 0.3, 0.1)	(0.7, 0.3, 0.2)	(0.8, 0.3, 0.2)	(0.8, 0.1, 0.2)	(0.8, 0.2, 0.2)	(0.7, 0.3, 0.2)	(0.7, 0.4, 0.2)
P4	(0.8, 0.3, 0.1)	(0.6, 0.5, 0.2)	(0.8, 0.2, 0.3)	(0.5, 0.5, 0.5)	(0.8, 0.1, 0.2)	(0.7, 0.2, 0.3)	(0.7, 0.3, 0.2)	(0.8, 0.2, 0.1)
P5	(0.7, 0.4, 0.2)	(0.7, 0.2, 0.2)	(0.6, 0.5, 0.3)	(0.7, 0.4, 0.1)	(0.6, 0.3, 0.2)	(0.5, 0.5, 0.5)	(1.0, 0.0, 0.0)	(0.8, 0.1, 0.2)
PI	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)	(1.0, 0.0, 0.0)

:

Now, applying Equation (1), we can compute the similarity measures as shown in

Table 6. Final scores and ranks.

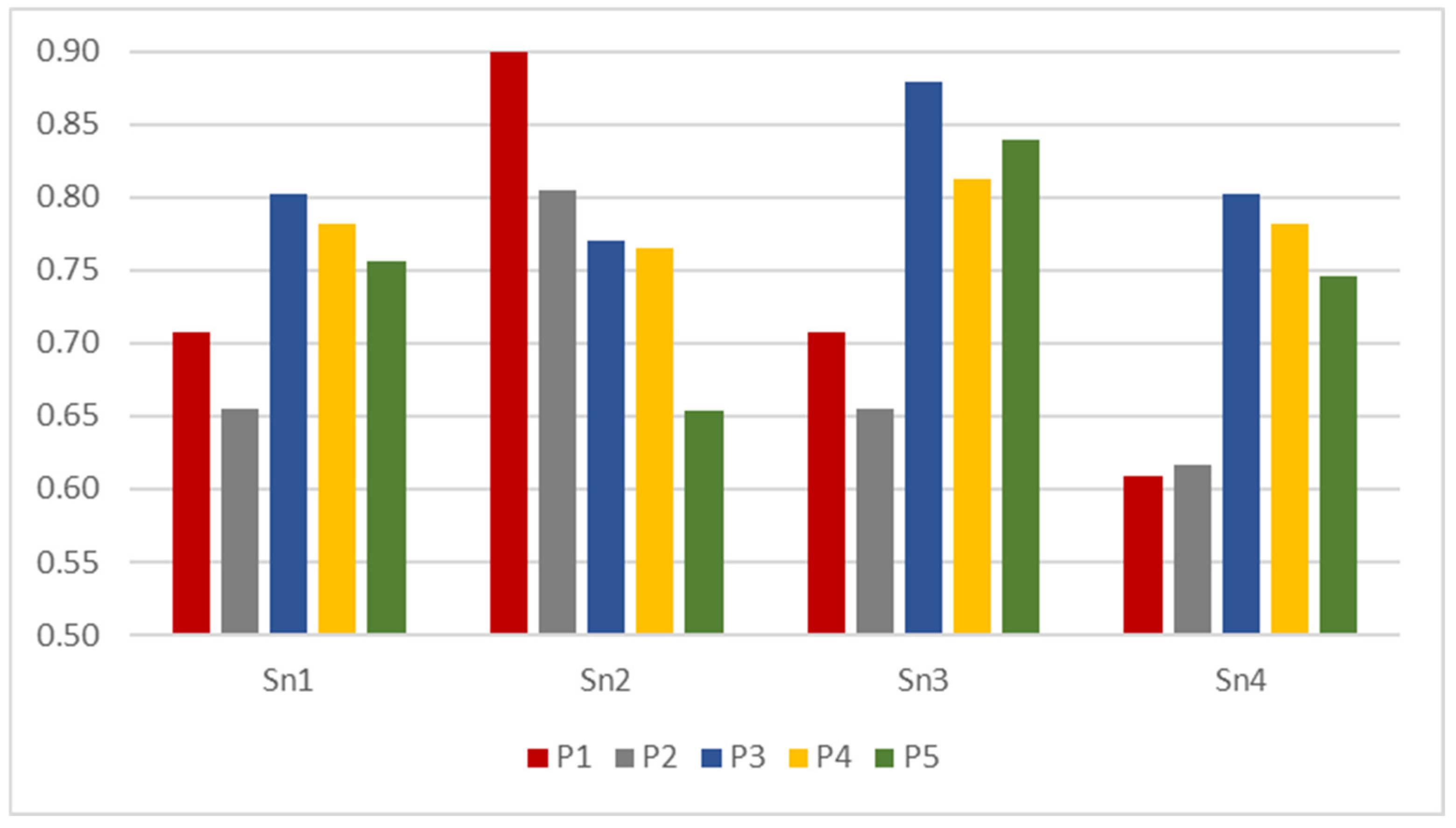
S (Pi, PI)	Scenario 1		Scenario 2		Scenario 3		Scenario 4
	Score	Rank	Score	Rank	Score	Rank	Score	Rank
S (P1, PI)	0.708	4	0.900	1	0.708	4	0.608	5
S (P2, PI)	0.655	5	0.805	2	0.655	5	0.616	4
S (P3, PI)	0.802	1	0.771	3	0.880	1	0.802	1
S (P4, PI)	0.782	2	0.765	4	0.812	3	0.782	2
S (P5, PI)	0.765	3	0.654	5	0.840	2	0.746	3

:

The result depicted in Figure 2 indicates that by considering the most critical risk and key performance factors and using the similarity measure for SVNSs, P₃ is the most similar alternative to the ideal. Furthermore, this partner has the best performance in three future scenarios, while P₁ has the best performance only in Scenario 2.

4. Comparative Study

In this study, it is impossible to compare the results of the proposed approach with other existing ones because what is examined in this study is the ranking of options in the form of future alternative scenarios. As stated earlier, this analysis did not exist in the previous approaches in the field of PPP. Therefore, in this section, we compare the simplicity of implementing the proposed approach with some approaches that have been developed in recent years. A study suggested a hybrid model including the best–worst method to identify the importance weights of the criteria, the weighted influence non-linear gauge system to analyze the intertwined criteria and their causal relations using ideographic causal maps, and TOPSIS to rank and select the private partners [11]. The VIKOR method with the grey relational analysis is combined in a paper. Although this approach makes the results of the selection assessment more reasonable, it is a relatively complicated method for decision-makers to operate [19]. A work proposed a combined model based on BWM for evaluating and ranking the selection criteria and VIKOR for the final selection of partners [21]. Another study applied the analytic hierarchy process and multi-attribute utility theory to construct a framework for selection based on weights and utilities [9]. In addition to being complex, the above approaches do not include uncertainty in their analysis.

The private sector partner selection is carried out in a study based on a factor risk scoring system, simple additive weighted, and the integrated subjective or objective fuzzy group decision-making methods [34]. A paper used an extended VIKOR-based method incorporating an intuitionistic fuzzy set to select an optimal private partner [32]. A paper introduced the Shapley value method to modify the index weights determined by the AHP to overcome differences in expert cognition. Based on interval-valued intuitionistic fuzzy sets, the TOPSIS was constructed to choose sustainable suppliers [63]. Even though they cannot maintain the simplicity of implementation, most of these approaches only pay attention to the judgmental dimension of uncertainty and neglect the environmental dimension (alternative future scenarios).

Two unique characteristics distinguish the proposed approach from other approaches. First (and most notably), it is a straightforward approach that addresses the problem of complexity (the existence of multiple variables) and the dimensions of verbal uncertainty (obtaining the problem owners’ judgments in the form of neutrosophic sets) and environmental uncertainty (alternative future scenarios); Meanwhile, it remains methodologically straightforward and can be readily applied by operators without requiring specialized knowledge in operations research. Another feature is that critical risk factors and key performance indicators are considered simultaneously in the proposed approach, while previous approaches only address one of these criteria categories.

5. Managerial Implication

The PPP projects are long-term in nature and are very costly from a financial point of view. As stated earlier, many such projects have failed, and one of the main reasons is the public sector’s inappropriate choice of private sector partner. The public sector should choose the best options for these projects. Therefore, it faces a decision problem. Considering that various indicators play a role in selecting a suitable private sector partner, the upcoming issue is a multi-criteria decision. These indicators (quantitative and qualitative) are numerous and contradictory and force decision-makers to use MCDM approaches. In the face of qualitative indicators, newer techniques in this field try to introduce ambiguity in the judgments of experts (decision makers or problem owners) into the model by using fuzzy sets and fuzzy set extensions. Using these approaches, we can rely on the resulting answer more confidently.

However, in PPP projects that are long-term in nature and changes in environmental variables can affect the results of their analyzes in the long run, future scenarios are not given proper attention. Decision-makers should be aware that multi-criteria decision-making approaches make the best decision for the future based on current or past information. For making decisions that have long-term consequences, the future environmental conditions may not necessarily be the same as the present. Based on this, our approach, in addition to considering various indicators and solving the ambiguity in the verbal judgments of the problem owners, has also considered alternative future scenarios. Referring to the case example presented in Section 3, if we consider the first scenario, the status quo scenario, the results show that the best alternative is in the same in the other two scenarios. This analysis can give decision-makers some confidence in making a decision. For example, if the current results in Scenarios 3 and 4 were the same as Scenario 2, the decision-makers would conclude that the current decision (related to Scenario 1) is no longer suitable.

It is noteworthy that considering all dimensions of a decision-making problem in one approach leads to its methodological complexity. Since many managers do not have expertise in the field of decision-making knowledge (operations research), this issue in practice leads to their non-use of the introduced approaches. Therefore, the main goal of the present study was to show managers and decision-makers that it is possible to consider different dimensions of the problem using a simple approach with minimal computational complexity and to act more rationally in choosing the best option.

6. Conclusions

The government’s funds alone cannot meet the significant investment needs for many massive projects [37]. PPPs combine outsourcing, privatization, and government partnership to utilize private sector resources [4]. In addition to developing public facilities, PPPs create a system of public service provision [64]. There are considerable challenges associated with PPP projects for both the public and private sectors [65]. Governments have been actively promoting PPP projects, increasing their number. However, many PPP projects are still unsuccessful because of implementation difficulties. A PPP project’s large-scale investment, long concession contract duration, and complex technologies create many potential risk factors during implementation [2]. Furthermore, identifying critical success factors before implementing PPP projects is essential if the project is to run smoothly [66]. Simultaneous consideration of these two categories of factors, risk and success, is one of the points not considered in previous research.

PPP projects’ success depends on selecting the right private partners, but few studies have been conducted on the subject [67]. Information uncertainty is a standard paradigm in modern decision-making because perfect information is seldom available to decision-makers [68]. As shown in the research background, previous approaches either have not addressed uncertainty or only have used fuzzy sets. While neutrosophic sets can more effectively represent the uncertainty in judgments [56], they were not considered. In this study, we introduced an uncomplicated, practical approach to address the problem of selecting the best private-sector partner. This approach considers the most critical risk and key performance factors affecting PPP projects. Our proposed methodology copes with uncertainty by using SVNSs.

The current study has several weaknesses that researchers in future studies can address. In this study, only qualitative factors are considered, while the analysis of quantitative factors also significantly impacts the partner selection process. Another weakness is related to not examining the relationships between factors. Researchers can consider the interdependency criteria by applying the analytic network process (ANP) or DEMATEL-based ANP. Additionally, a fuzzy clustering method can identify the internal relations among the indicators [69]. Not thoroughly studying the uncertainty of the future is another shortcoming of this approach, which we plan to address in our future research. Since it is reductionist to consider only two indicators to define future scenarios, we intend to carry out this development while keeping the approach simple.

Moreover, neutrosophic hesitant fuzzy sets (NHFS) represent a practical and general solution to the problem of hesitancy in decision-making. Researchers can keep this point in mind in future studies. In addition, considering the weights of indicators in a multi-criteria decision-making approach has always been emphasized, but this point is not considered in the proposed approach. Researchers can pay attention to this matter in future studies. Finally, when the number of alternatives is large, judgment becomes complicated for decision-makers. Using the DEA model to eliminate inefficient options can be practical. We suggest the study of this subject to other researchers.