Energy-Saving Scheduling for Flexible Job Shop Problem with AGV Transportation Considering Emergencies
Abstract
:1. Introduction
2. Problem Description
2.1. Introduction of FJSP-AMBRO
- (1)
- Each machine can only process one job at the same time.
- (2)
- Each job can only be processed on one machine at a time.
- (3)
- All AGVs, jobs and machines are ready at time 0.
- (4)
- The AGV can proceed to the next task only after completing the current task.
- (5)
- An AGV can only carry one job at one time.
- (6)
- Ignore the power of AGVs; all AGVs have the same speed.
- (7)
- The collision of AGVs are ignored.
- (8)
- The maintenance time of the broken machine is known.
- (9)
- The arrival time of rush orders, the job number in rush orders are random and the rush orders have processing priority. The machine breakdown and the rush order occur only once, respectively.
- (10)
- AGVs and raw materials are in the warehouse at time 0, and AGVs will drive to the finished product warehouse after completing the transportation tasks.
2.2. Symbol Definitions
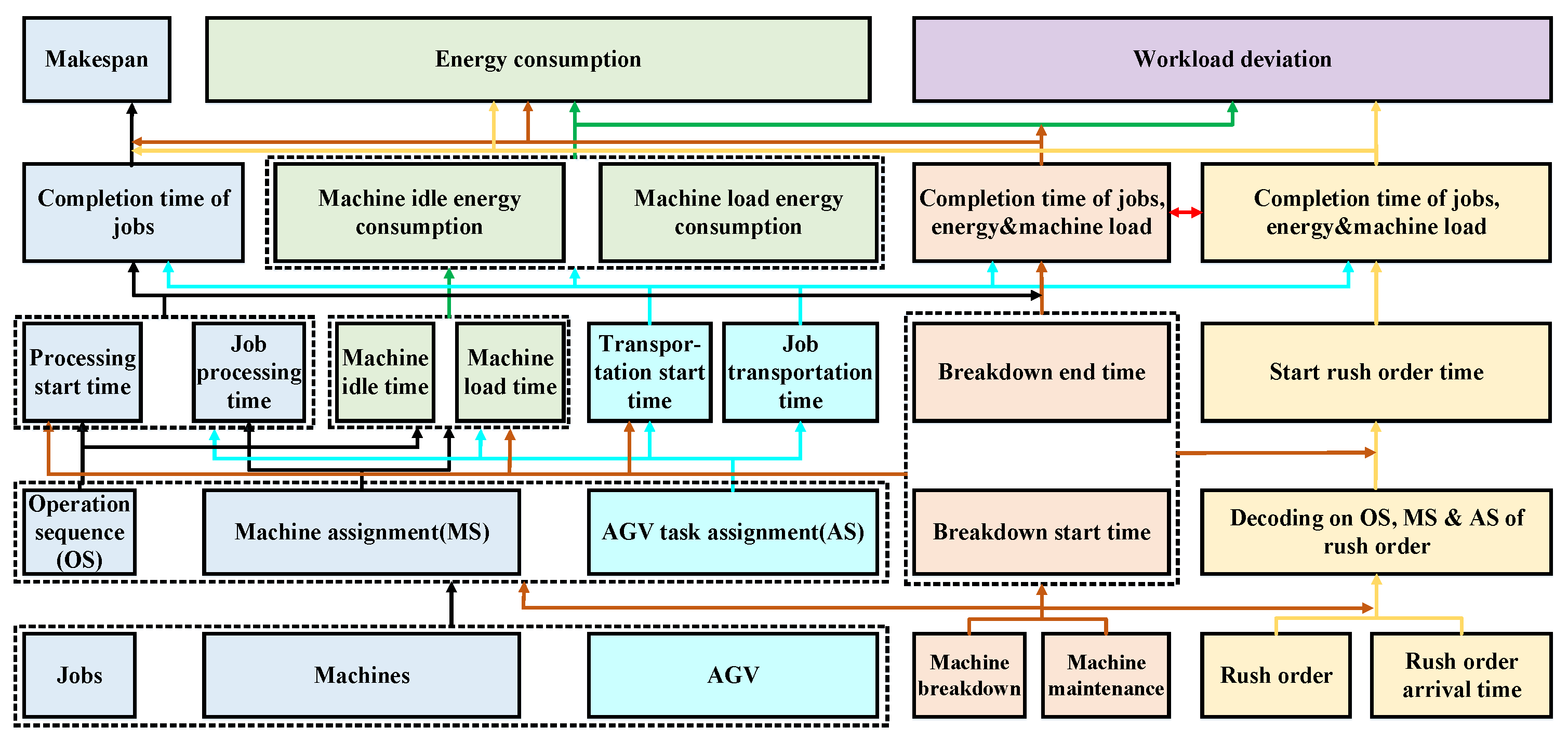
2.3. Mathematical Model
3. Algorithm Design
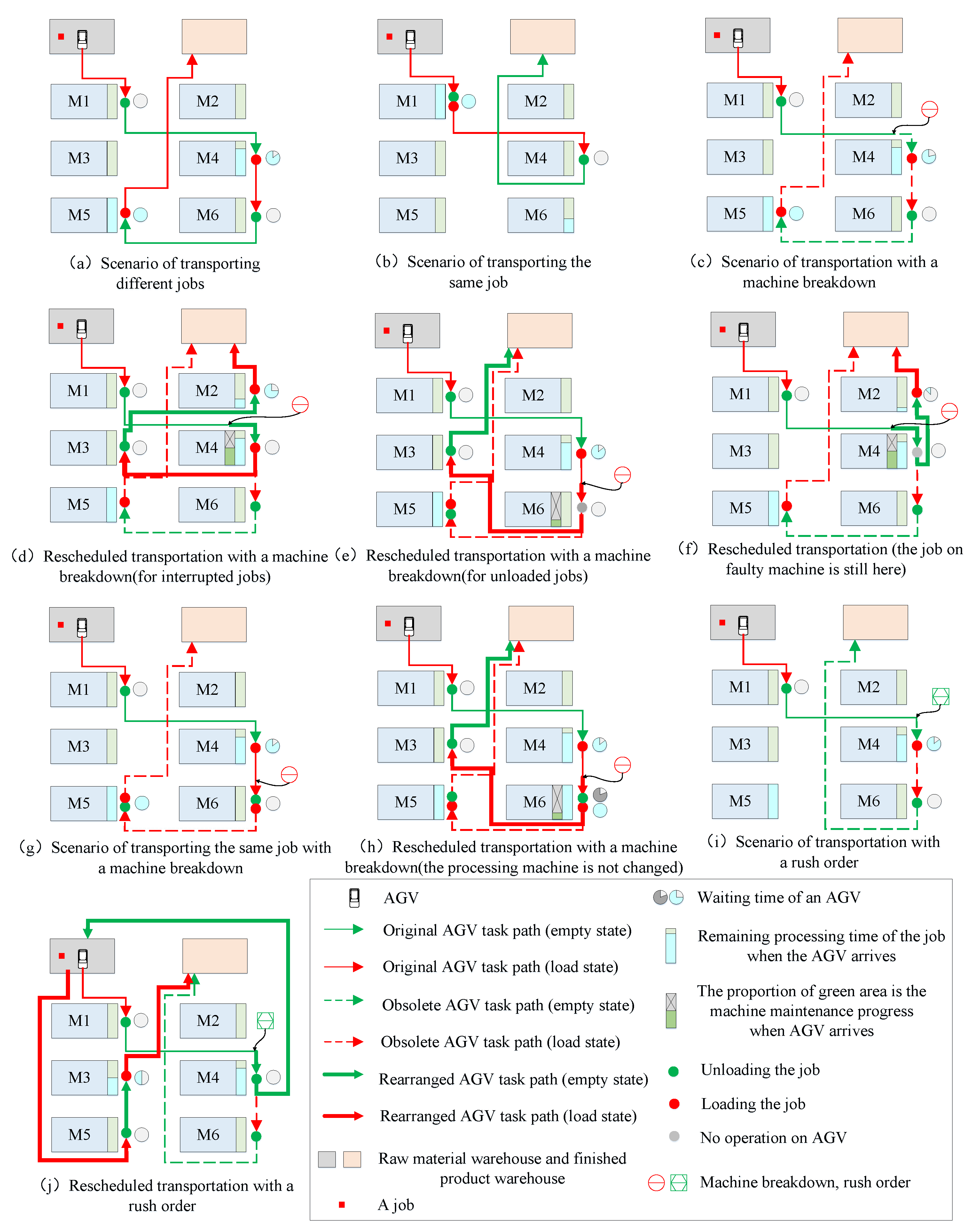
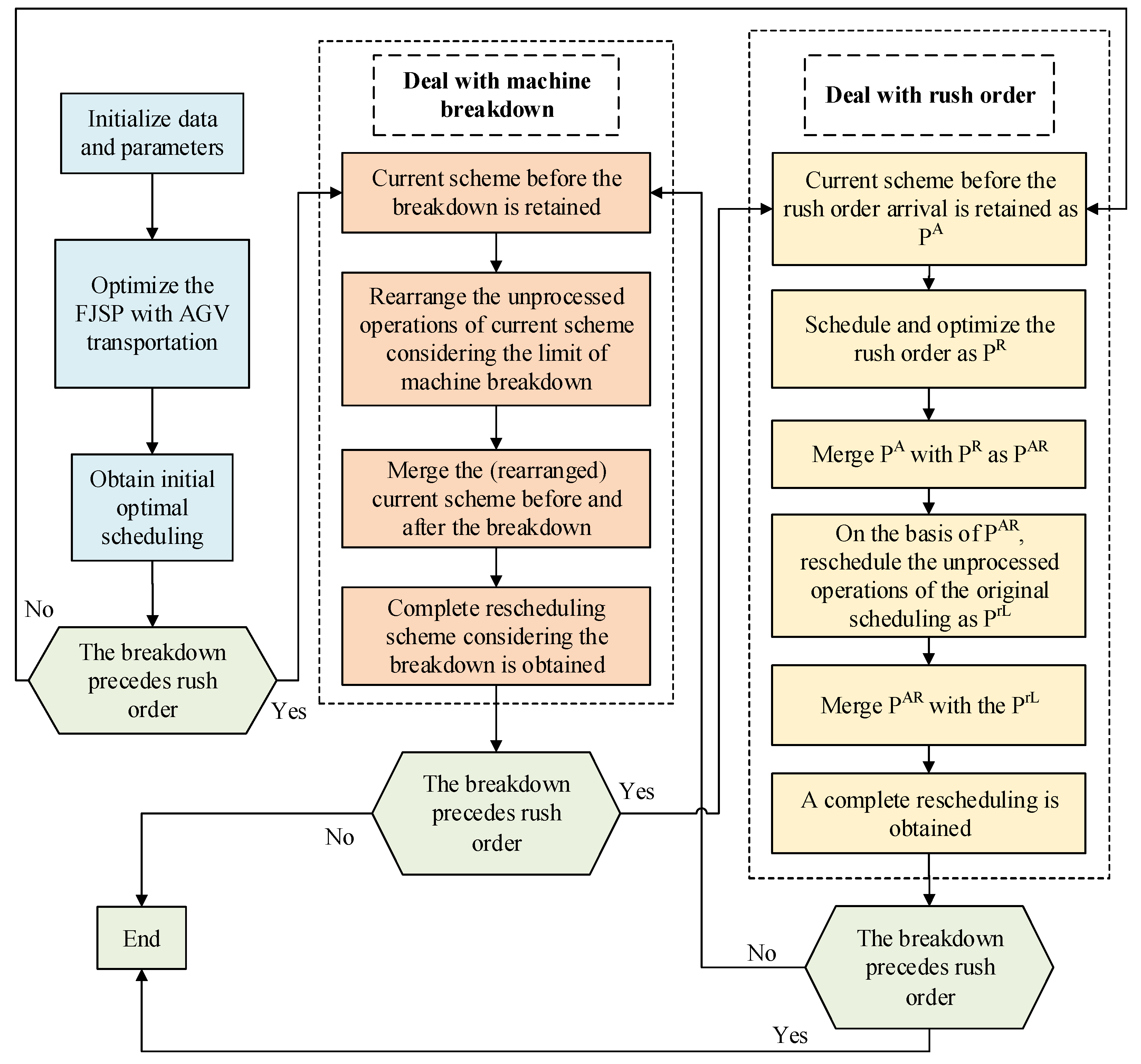
3.1. Emergency Handling Process for FJSP-AMBRO
3.2. Improved NSGA-II
3.2.1. Three-Layer Encoding and Decoding
3.2.2. Selection Operator with Improved Crowding Distance Calculation
3.2.3. POX Crossover Operation
| Algorithm 1: Procedure of POX crossover operation |
| 1: Select two parent individuals. 2: classify the jobs into sets S1 and S2. 3: The genes in set S1 of Parent1 are inherited to the same position of Progeny1. 4: The genes in set S2 of Parent2 are inherited to the same position of Progeny2. 5: The rest positions of genes in progenies are temporarily vacant. 6: The remaining genes in Parent1 are filled into the empty positions of Progeny2 in order. 7: The remaining genes in Parent2 are filled into the empty positions of Progeny1 in order. |
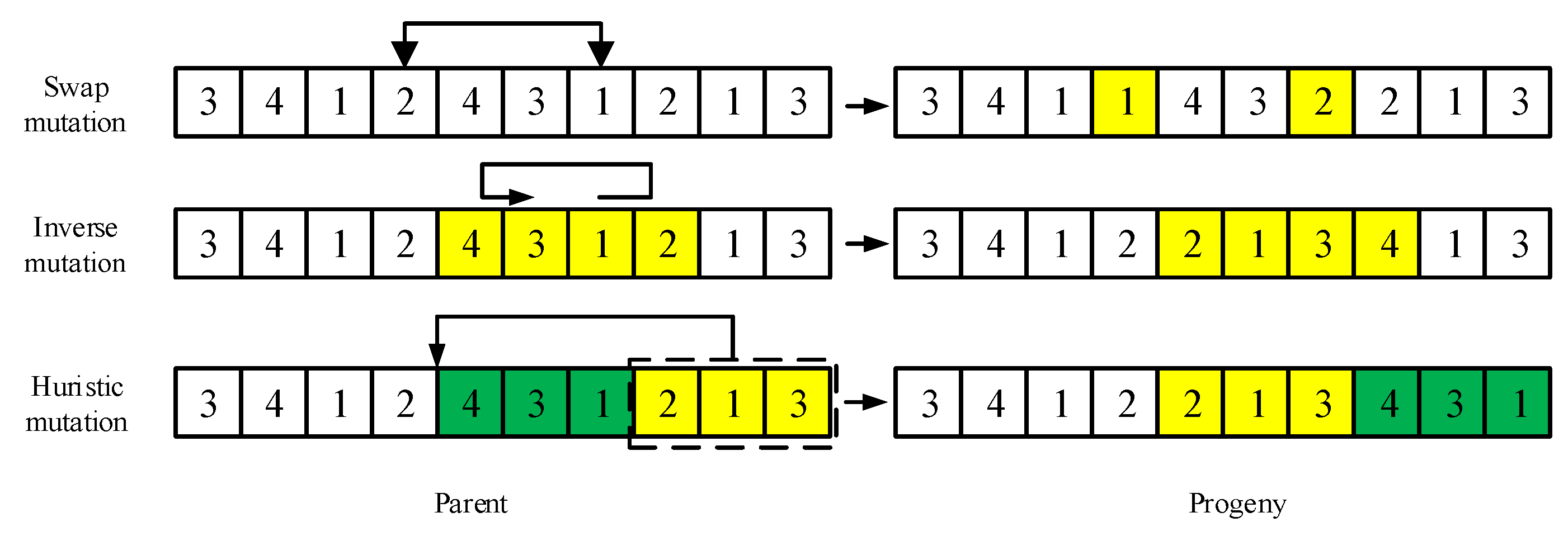
3.2.4. Three-Layer Mutation Operator
| Algorithm 2: Procedure of three layer mutation operator |
| 1: Determine the number of mutation individuals mutate_num. 2: for i in range(mutate_num): 3: Generate a random decimal mutate_num_1 ∈ [0,1]. 4: Randomly select an individual Xi. 5: if rand_num_1 <1/3: 6: (Perform OS mutation.) 7: Generate a random decimal mutate_num_2 ∈ [0,1]. 8: if rand_num_2 <1/3: 9: Perform swap mutation on Xi. 10: elif rand_num_2 <2/3: 11: Perform inverse mutation on Xi. 12: else: 13: Perform heuristic mutation on Xi. 14: Regenerated MS to ensure the feasibility of solutions 15: elif rand_num_1 <2/3: 16: (Perform MS mutation.) 17: Generate a random decimal mutate_num_3 ∈ [0,1]. 18: if rand_num_3 <1/2: 19: (Perform directional mutation on Xi.) 20: Randomly select a position in MS of Xi. 21: Reselect an available machine with the shortest processing time. 22: else: 23: (Perform random mutation on Xi.) 24: Randomly select a position in MS of Xi and randomly reselect an available machine. 25: else: 26: (Perform AS mutation.) 27: Randomly select a different AGV to replace the original one of Xi. |
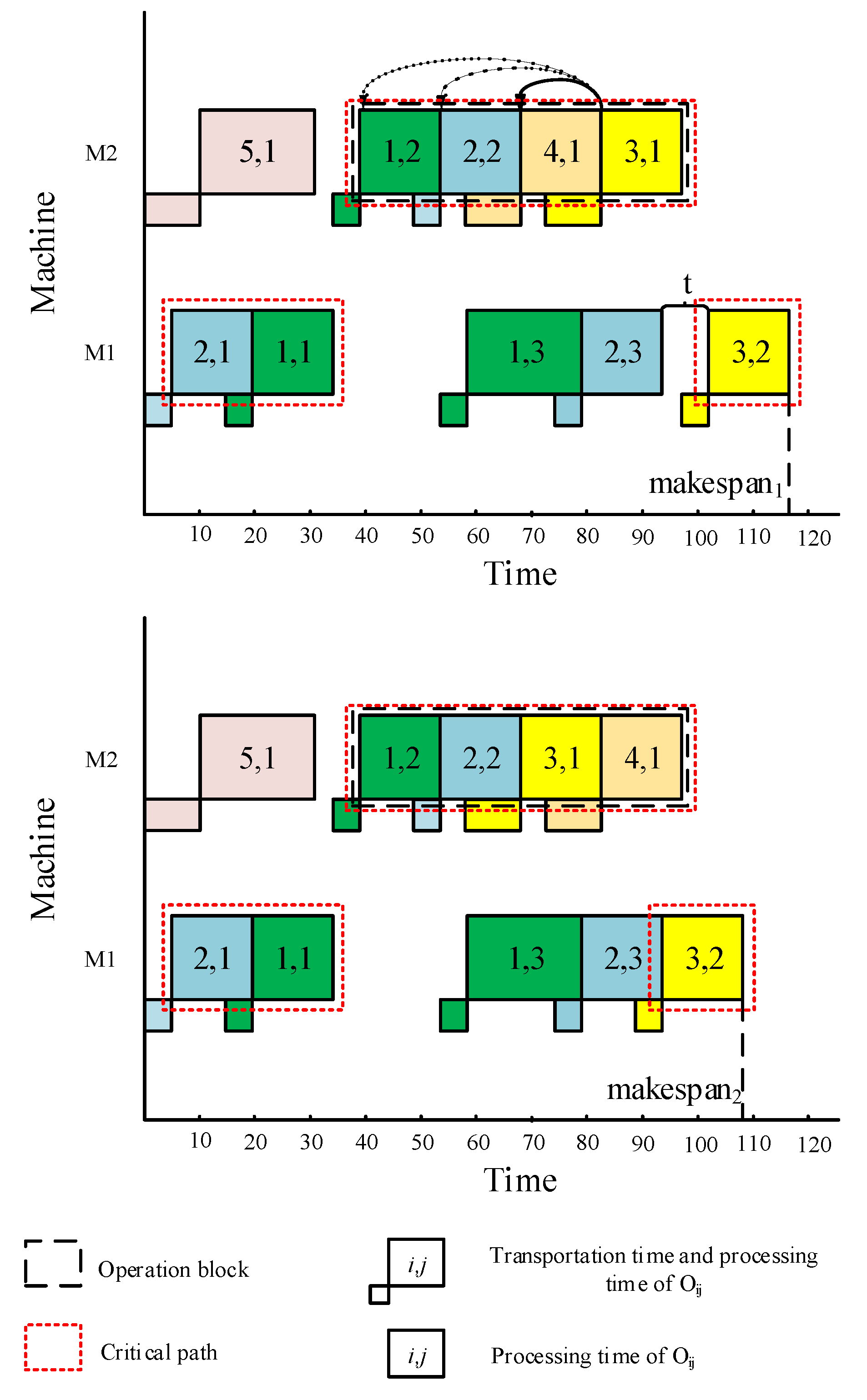
3.2.5. Local Search Based on Critical Path
4. Experimental Analysis
4.1. Example and Performance Metrics
4.2. Parametric Analysis
4.3. Validity Analysis of Improvement Strategies and the Comparison Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; He, Z.; Chan, W.; Chow, C. Deep reinforcement learning with multi-agent graphs for flexible job shop scheduling. Knowl.-Based Syst. 2022, 259, 110083. [Google Scholar] [CrossRef]
- Sun, W.; Pan, Y.; Lu, X.H.; Ma, Q.Y. Research on flexible job-shop scheduling problem based on a modified genetic algorithm. J. Mech. Sci. Technol. 2010, 24, 2119–2125. [Google Scholar] [CrossRef]
- Tang, Q.H.; Chen, S.J.; Zhao, M.; Zhang, L.P. Prediction of optimal rescheduling mode under machine failures within job shops. China Mech. Eng. 2019, 30, 188–195. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, S.N. Research on dynamic flexible job shop scheduling problem based on GABSO algorithm. Syst. Eng. 2021, 40, 143–151. [Google Scholar]
- Mokhtari, H.; Mehrdad, D. Scheduling optimization of a stochastic flexible job-shop system with time-varying machine failure rate. Comput. Oper. Res. 2015, 61, 31–45. [Google Scholar] [CrossRef]
- Ahmadi, E.; Most, Z.; Mojtaba, F.; Seyed, M.E. A multi objective optimization approach for flexible job shop scheduling problem under random machine breakdown by evolutionary algorithms. Comput. Oper. Res. 2016, 73, 56–59. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, M.; Wang, Z.Y.; Zhu, Q.B. Robust scheduling based on extreme learning machine for bi-objective flexible job-shop problems with machine breakdowns. Eepert Syst. Appl. 2020, 158, 113545. [Google Scholar] [CrossRef]
- You, Y.C.; Wang, Y.; Jin, Z.C. Research on flexible job-shop dynamic scheduling based on game theory. J. Syst. Simul. 2021, 33, 2579–2588. [Google Scholar] [CrossRef]
- Zhang, G.H.; Lu, X.X.; Liu, X.; Zhang, L.T.; Wei, S.W.; Zhang, W.Q. An effective two-stage algorithm based on convolutional neural network for the bi-objective flexible job shop scheduling problem with machine breakdown. Expert Syst. Appl. 2022, 203, 117460. [Google Scholar] [CrossRef]
- Jin, P.B.; Tang, Q.H.; Cheng, L.X.; Zhang, L.P. Decision-making model of production rescheduling mode for flexible job shops under machine failures. Comput. Int. Manuf. Syst. 2021, 1–13. Available online: http://kns.cnki.net/kcms/detail/11.5946.tp.20211006.0811.002.html (accessed on 6 February 2023).
- Gao, K.Z.; Ponnuthurai, N.S.; Pan, Q.K.; Mehmet, F.T.; Ali, S. Artificial bee colony algorithm for scheduling and rescheduling fuzzy flexible job shop problem with new job insertion. Knowl.-Based Syst. 2016, 109, 1–16. [Google Scholar] [CrossRef]
- Zhang, C.J.; Zhou, Y.; Peng, K.K.; Li, X.Y.; Lian, K.L.; Zhang, S.Y. Dynamic flexible job shop scheduling method based on improved gene expression programming. Meas. Control 2022, 54, 1136–1146. [Google Scholar] [CrossRef]
- Shen, X.N.; Yao, X. Mathematical modeling and multi-objective evolutionary algorithms applied to dynamic flexible job shop scheduling problems. Inform. Sci. 2015, 298, 198–224. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Y. Optimal scheduling and decision making method for dynamic flexible job shop. J. Syst. Simul. 2020, 32, 2073–2083. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Fatma, S.M.; Alper, H. Greedy randomized adaptive search for dynamic flexible job-shop scheduling. J. Manuf. Syst. 2020, 56, 425–451. [Google Scholar] [CrossRef]
- Zhang, G.H.; Lu, X.X.; Hu, Y.F.; Sun, J.H. Machine breakdown rescheduling of flexible job shop based on improved imperialist competitive algorithm. J. Comput. Appl. 2021, 41, 2242–2248. [Google Scholar] [CrossRef]
- Duan, J.G.; Wang, J.H. Energy-efficient scheduling for a flexible job shop with machine breakdowns considering machine idle time arrangement and machine speed level selection. Comput. Ind. Eng. 2021, 161, 107677. [Google Scholar] [CrossRef]
- Caldeira, R.H.; Gnanavelbabu, A.; Vaidyanathan, T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Comput. Ind. Eng. 2020, 148, 106863. [Google Scholar] [CrossRef]
- Li, C.B.; Kou, Y.; Lei, Y.F.; Xiao, Q.G.; Li, L.L. Flexible job shop rescheduling optimization method for energy-saving based on dynamic events. Comput. Int. Manuf. Syst. 2020, 26, 288–299. [Google Scholar] [CrossRef]
- Duan, J.G.; Wang, J.H. Robust scheduling for flexible machining job shop subject to machine breakdowns and new job arrivals considering system reusability and task recurrence. Expert Syst. Appl. 2022, 203, 117489. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, X.B. Design and optimization of a novel supersonic rocket with small caliber. J. Ind. Manag. Optim. 2022, 19, 3794–3818. [Google Scholar] [CrossRef]
- Li, J.H.; Yan, H.S.; Yang, B.X.; Zhou, Q.H. Improved genetic-harmony search algorithm for solving the workshop scheduling problem of marine equipment. Comput. Int. Manuf. Syst. 2022, 28, 3923. [Google Scholar]
- Li, D.; Xiang, F.H.; Mao, J.L. Many-objective flexible job shop scheduling optimization based on NSGA-II. J. Chongqing Univ. Posts Telecommun. 2022, 34, 341–348. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, G.H.; Hu, Y.F.; Sun, J.H.; Zhang, W.Q. An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints. Swarm Evol. Comput. 2020, 54, 100664. [Google Scholar] [CrossRef]
- Zhang, P.L.; Wang, J.Q.; Tian, Z.W.; Sun, S.Z.; Li, J.T.; Yang, J.N. A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem. Appl. Soft. Comput. 2022, 127, 109339. [Google Scholar] [CrossRef]
- Wang, J.H.; Li, Y.L.; Liu, Z.W.; Liu, J.S. Evolutionary algorithm with precise neighborhood strcture for flexible workshop scheduling. J. Tongji Univ. Nat. Sci. 2021, 49, 440–448. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.Y.; Jin, Y.C. PlatEMO: A matlab platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Gong, G.L.; Deng, Q.W.; Gong, X.R.; Liu, W.; Ren, Q.H. A new double flexible job-shop scheduling problem integrating processing time, green production, and human factor indicators. J. Clean. Prod. 2018, 174, 560–576. [Google Scholar] [CrossRef]




| Symbol | Meaning |
|---|---|
| n | Number of jobs for initial order |
| n* | Number of jobs for initial order and rush orders |
| m | Number of machines |
| g | Number of AGVs |
| i | Job index |
| j | Operation index |
| k | Machine index |
| s | AGV index |
| Operation number of job i | |
| The operation j of job i | |
| The processing time of on machine k | |
| The start time of on machine k | |
| The completion time of on machine k | |
| The earliest transportable time for transportation task from processing machine of to processing machine of by AGV s | |
| The arrival time of the transportation task from the processing machine of to the processing machine of by AGV s | |
| The time for the transportation task from the processing machine of to the processing machine of | |
| The start time of machine breakdown | |
| The available time after machine breakdown | |
| The completion time of job i | |
| Working power of machine k | |
| TE | Total energy consumption of all machines |
| M | A positive number large enough |
| Machine selection decision variable. If is processed on machine k, then ; otherwise | |
| Reschedule machine selection decision variable. If is processed on machine k after rescheduling, then ; otherwise | |
| Machine condition variables. If is the immediately preceding operation of on machine k, then ; otherwis | |
| AGV selection decision variable. If the transportation task from processing machine of to processing machine of is carried out by the AGV s, then ; otherwise | |
| AGV condition variable. If the transportation task of AGV s from processing machine of to processing machine of is earlier than that from to , then ; otherwise | |
| Machine state variable. If there is a breakdown on machine k, = 1; Otherwise, = 0 | |
| Job status variable. If is less than and is more than , =1; Otherwise, = 0 |
| Factor | Levels | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| MaxIt1 | 200 | 300 | 400 | 500 | 600 |
| PC1 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| PM1 | 0.01 | 0.05 | 0.10 | 0.15 | 0.20 |
| MaxIt2 | 200 | 300 | 400 | 500 | 600 |
| PC2 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| PM2 | 0.01 | 0.05 | 0.10 | 0.15 | 0.20 |
| Parameter Combinations | Level | IGD | |||||
|---|---|---|---|---|---|---|---|
| MaxIt1 | PC1 | PM1 | MaxIt2 | PC2 | PM2 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1166.25 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 1211.99 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 1042.18 |
| 4 | 1 | 4 | 4 | 4 | 4 | 4 | 1035.20 |
| 5 | 1 | 5 | 5 | 5 | 5 | 5 | 1019.37 |
| 6 | 2 | 1 | 2 | 3 | 4 | 5 | 1122.31 |
| 7 | 2 | 2 | 3 | 4 | 5 | 1 | 1071.06 |
| 8 | 2 | 3 | 4 | 5 | 1 | 2 | 1108.89 |
| 9 | 2 | 4 | 5 | 1 | 2 | 3 | 1396.53 |
| 10 | 2 | 5 | 1 | 2 | 3 | 4 | 1083.94 |
| 11 | 3 | 1 | 3 | 5 | 2 | 4 | 976.71 |
| 12 | 3 | 2 | 4 | 1 | 3 | 5 | 1150.72 |
| 13 | 3 | 3 | 5 | 2 | 4 | 1 | 1256.44 |
| 14 | 3 | 4 | 1 | 3 | 5 | 2 | 1277.04 |
| 15 | 3 | 5 | 2 | 4 | 1 | 3 | 1141.59 |
| 16 | 4 | 1 | 4 | 2 | 5 | 3 | 1120.62 |
| 17 | 4 | 2 | 5 | 3 | 1 | 4 | 938.70 |
| 18 | 4 | 3 | 1 | 4 | 2 | 5 | 972.39 |
| 19 | 4 | 4 | 2 | 5 | 3 | 1 | 1129.60 |
| 20 | 4 | 5 | 3 | 1 | 4 | 2 | 1404.60 |
| 21 | 5 | 1 | 5 | 4 | 3 | 2 | 1084.39 |
| 22 | 5 | 2 | 1 | 5 | 4 | 3 | 1157.46 |
| 23 | 5 | 3 | 2 | 1 | 5 | 4 | 1372.36 |
| 24 | 5 | 4 | 3 | 2 | 1 | 5 | 1013.42 |
| 25 | 5 | 5 | 4 | 3 | 2 | 1 | 1324.13 |
| Problem | IGD | C | |||||
|---|---|---|---|---|---|---|---|
| NSGA-II | INSGA-II | C(NSGA-II, ) | C(, NSGA-II) | C(INSGA-II, ) | C(, INSGA-II) | ||
| Mk-01 | 10.69 | 10.56 | 10.52↓ | 0.10 | 0.50 | 0.13 | 0.48 |
| Mk-02 | 11.39 | 11.25 | 11.17↓ | 0.03 | 0.63 | 0.22 | 0.23 |
| Mk-03 | 64.75 | 63.37 | 63.10↓ | 0.00 | 0.60 | 0.17 | 0.29 |
| Mk-04 | 14.27 | 14.05 | 13.04↓ | 0.25 | 0.29 | 0.27 | 0.29 |
| Mk-05 | 48.01 | 47.07 | 46.80↓ | 0.20 | 0.33 | 0.25 | 0.28 |
| Mk-06 | 31.09 | 29.74 | 29.09↓ | 0.00 | 0.10 | 0.16 | 0.30 |
| Mk-07 | 26.68 | 26.55 | 26.45↓ | 0.00 | 0.57 | 0.19 | 0.29 |
| Mk-08 | 67.48 | 67.26 | 64.73↓ | 0.27 | 0.31 | 0.03 | 0.43 |
| Mk-09 | 141.63 | 140.25 | 139.42↓ | 0.20 | 0.57 | 0.16 | 0.50 |
| Mk-10 | 164.34 | 161.98 | 161.61↓ | 0.12 | 0.51 | 0.29 | 0.34 |
| Mk-11 | 207.63 | 205.44 | 204.66↓ | 0.15 | 0.29 | 0.26 | 0.36 |
| Mk-12 | 216.12 | 214.10 | 213.51↓ | 0.22 | 0.35 | 0.18 | 0.43 |
| Mk-13 | 226.51 | 221.10 | 219.06↓ | 0.15 | 0.36 | 0.26 | 0.42 |
| Mk-14 | 365.57 | 364.74 | 361.60↓ | 0.21 | 0.45 | 0.27 | 0.32 |
| Mk-15 | 336.60 | 331.41 | 327.76↓ | 0.33 | 0.39 | 0.13 | 0.43 |
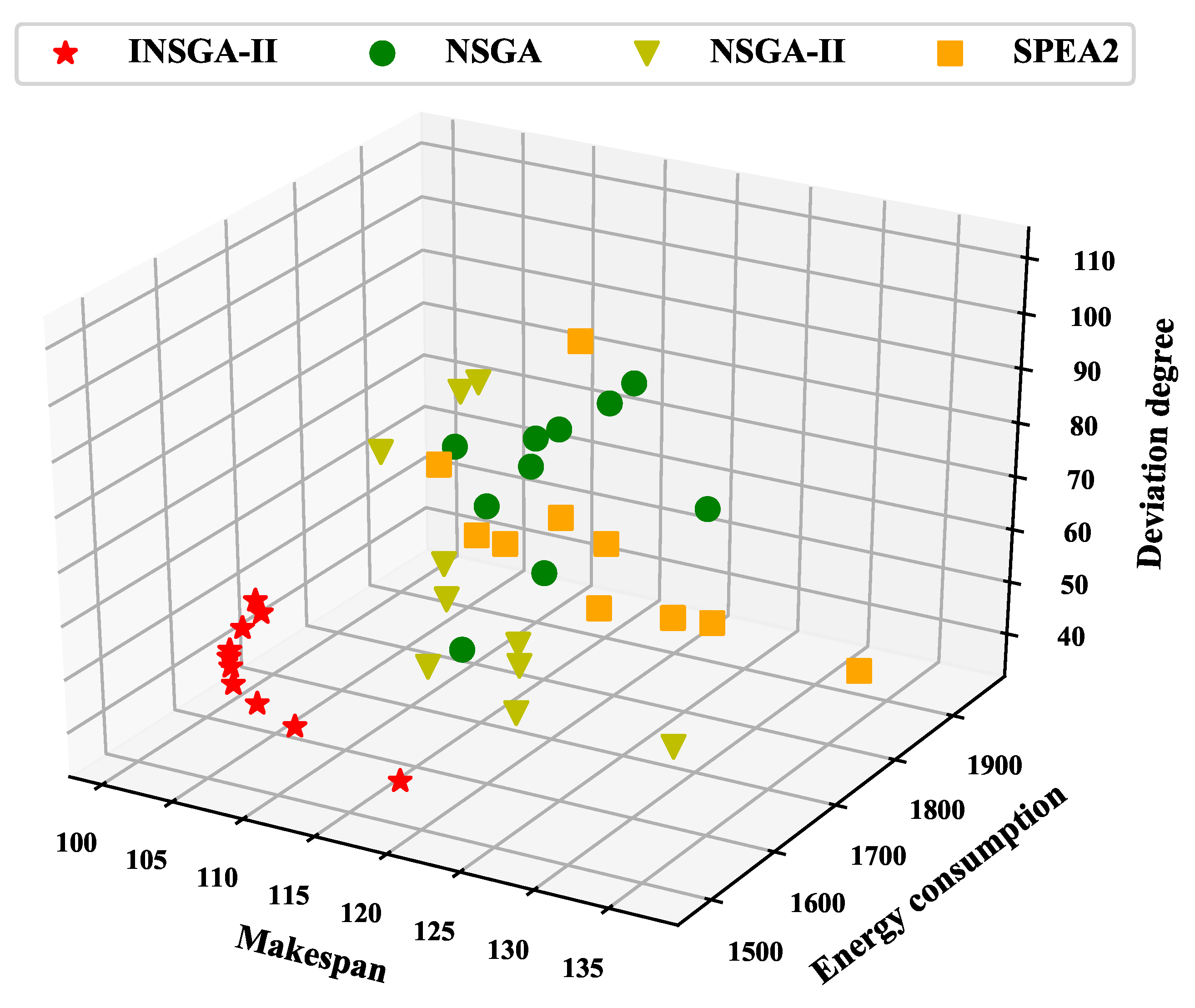
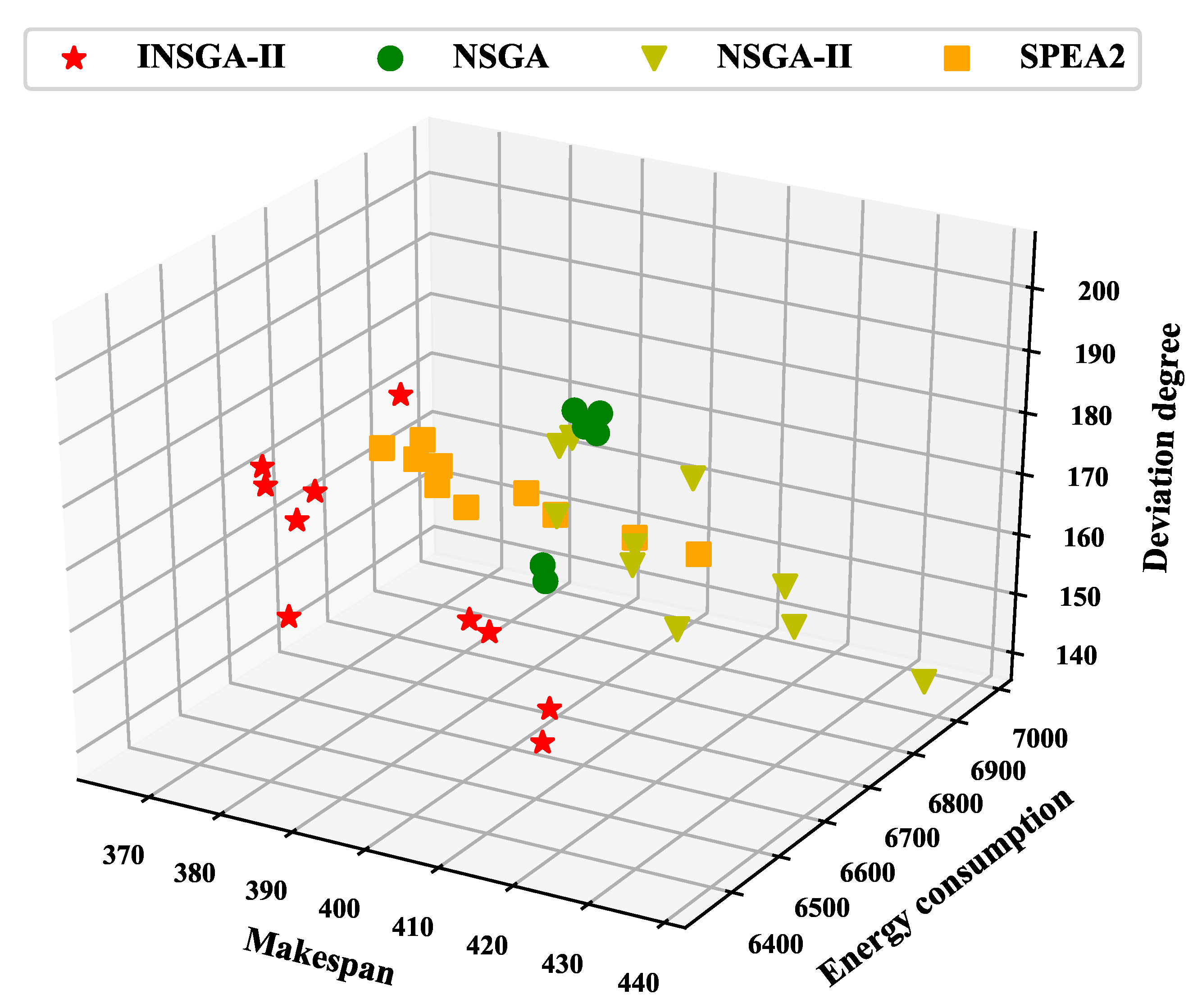
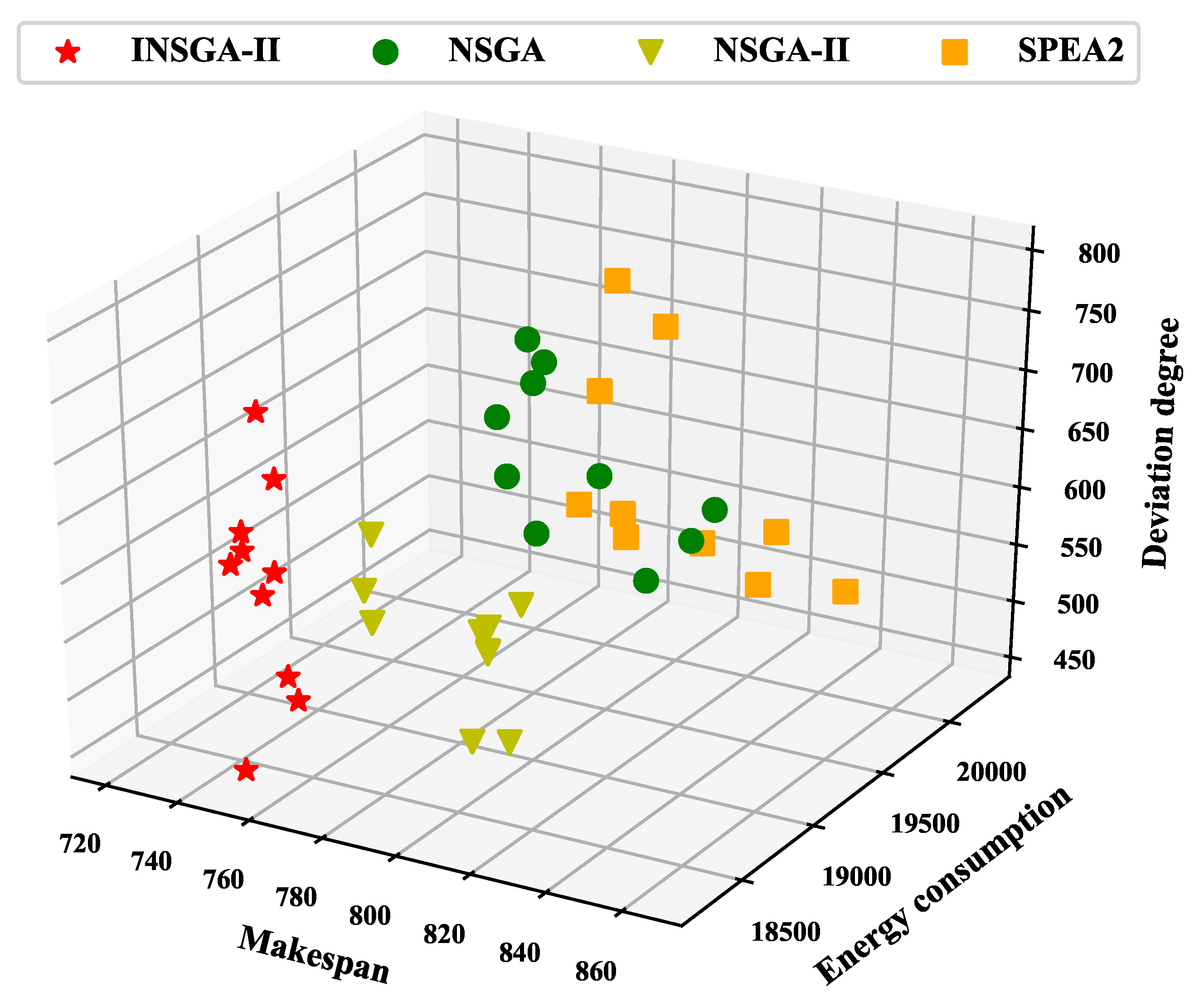
| Problem | n/m | INSGA-II | NSGA | NSGA-II | SPEA2 |
|---|---|---|---|---|---|
| Mk-01 | 10/6 | 10.18 | 10.72 | 11.02 | 11.79 |
| Mk-02 | 10/6 | 12.49 | 12.59 | 13.27 | 11.96 |
| Mk-03 | 15/8 | 63.43 | 66.67 | 63.78 | 67.11 |
| Mk-04 | 15/8 | 11.48 | 13.08 | 12.03 | 12.42 |
| Mk-05 | 15/4 | 44.35 | 45.13 | 44.87 | 45.01 |
| Mk-06 | 10/15 | 28.88 | 30.88 | 29.64 | 33.50 |
| Mk-07 | 20/5 | 27.06 | 30.13 | 27.33 | 33.04 |
| Mk-08 | 20/10 | 64.70 | 65.33 | 64.29 | 64.83 |
| Mk-09 | 20/10 | 141.43 | 145.03 | 142.64 | 146.16 |
| Mk-10 | 20/15 | 162.46 | 167.04 | 163.34 | 165.02 |
| Mk-11 | 30/5 | 202.23 | 206.45 | 206.01 | 203.44 |
| Mk-12 | 30/10 | 209.62 | 217.41 | 215.39 | 211.60 |
| Mk-13 | 30/10 | 221.19 | 227.16 | 223.85 | 231.92 |
| Mk-14 | 30/15 | 363.32 | 368.55 | 365.66 | 368.33 |
| Mk-15 | 30/15 | 337.39 | 346.04 | 341.23 | 344.24 |
| Problem | C(INSGA-II, NSGA) | C(NSGA, INSGA-II) | C(INSGA-II, NSGA-II) | C(NSGA-II, INSGA-II) | C(INSGA-II, SPEA2) | C(SPEA2, INSGA-II) |
|---|---|---|---|---|---|---|
| Mk-01 | 0.48 | 0.11 | 0.30 | 0.21 | 0.34 | 0.20 |
| Mk-02 | 0.51 | 0.14 | 0.34 | 0.20 | 0.92 | 0.00 |
| Mk-03 | 0.42 | 0.12 | 0.35 | 0.17 | 0.58 | 0.04 |
| Mk-04 | 0.48 | 0.08 | 0.29 | 0.18 | 0.72 | 0.08 |
| Mk-05 | 0.30 | 0.08 | 0.31 | 0.18 | 0.44 | 0.03 |
| Mk-06 | 0.34 | 0.10 | 0.14 | 0.12 | 0.99 | 0.00 |
| Mk-07 | 0.54 | 0.07 | 0.35 | 0.26 | 0.84 | 0.00 |
| Mk-08 | 0.55 | 0.10 | 0.28 | 0.19 | 0.57 | 0.00 |
| Mk-09 | 0.65 | 0.05 | 0.25 | 0.19 | 0.83 | 0.01 |
| Mk-10 | 0.59 | 0.03 | 0.38 | 0.09 | 0.77 | 0.01 |
| Mk-11 | 0.41 | 0.18 | 0.17 | 0.17 | 0.32 | 0.02 |
| Mk-12 | 0.50 | 0.06 | 0.32 | 0.17 | 0.40 | 0.02 |
| Mk-13 | 0.70 | 0.05 | 0.25 | 0.16 | 0.89 | 0.00 |
| Mk-14 | 0.63 | 0.06 | 0.37 | 0.17 | 0.44 | 0.05 |
| Mk-15 | 0.63 | 0.09 | 0.30 | 0.07 | 0.80 | 0.00 |
| Algorithm | Mean | Std. Deviation | Std. Error Mean | t | Sig. (2-tailed) |
|---|---|---|---|---|---|
| INSGA-II-NSGA | −3.46733 | 2.64179 | 0.68211 | −5.083 | 0.000 |
| INSGA-II-NSGA-II | −1.61067 | 1.71294 | 0.44228 | −3.642 | 0.003 |
| INSGA-II-SPEA2 | −3.34533 | 3.02869 | 0.78200 | −4.278 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Qin, C.; Zhang, W.; Xu, Z.; Xu, G.; Gao, Z. Energy-Saving Scheduling for Flexible Job Shop Problem with AGV Transportation Considering Emergencies. Systems 2023, 11, 103. https://doi.org/10.3390/systems11020103
Zhang H, Qin C, Zhang W, Xu Z, Xu G, Gao Z. Energy-Saving Scheduling for Flexible Job Shop Problem with AGV Transportation Considering Emergencies. Systems. 2023; 11(2):103. https://doi.org/10.3390/systems11020103
Chicago/Turabian StyleZhang, Hongliang, Chaoqun Qin, Wenhui Zhang, Zhenxing Xu, Gongjie Xu, and Zhenhua Gao. 2023. "Energy-Saving Scheduling for Flexible Job Shop Problem with AGV Transportation Considering Emergencies" Systems 11, no. 2: 103. https://doi.org/10.3390/systems11020103
APA StyleZhang, H., Qin, C., Zhang, W., Xu, Z., Xu, G., & Gao, Z. (2023). Energy-Saving Scheduling for Flexible Job Shop Problem with AGV Transportation Considering Emergencies. Systems, 11(2), 103. https://doi.org/10.3390/systems11020103








