Abstract
This study investigates collaborative route mapping for a collection of connected automated vehicles (CAVs) traversing multi-lane pathways, with a particular emphasis on intersections without traffic signals. A distinctive feature of our research is the prioritization of emergency vehicles, such as ambulances and fire engines, according to their velocity demands. Additionally, a comprehensive analysis of the ethical ramifications of implementing such a prioritised system is engaged, while it is notable that in most of the existing studies, the ethical evaluation of intelligent transportation modalities is neglected. From a technical aspect, trajectories for CAVs in current models tend to be either inflexible or congruent with the collective formation of the fleet. Concurrently, the pre-set velocities for CAVs frequently demonstrate a lack of adaptability, which impedes cohesive operation. Moreover, there exists a pronounced deficiency in catering to the prioritization needs of emergency vehicles within these models. The current research endeavours to address these shortcomings by formulating the intersection management as an optimal control problem (OCP). This formulation enables CAVs to modulate their velocities in response to practical objectives, sidestepping fixed lane regulations at junctions. The control framework also encompasses autonomous vehicles of diverse sizes and velocities. An Adaptive Stepwise Optimization (ASO) methodology is proposed to augment the efficacy of the OCP resolution.
1. Introduction
The challenges posed by traffic bottlenecks and mishaps at crossroads have gained prominence due to the surging number of vehicles and pedestrians on the roads. Several studies, such as those referenced in [1,2,3,4,5], emphasize the growing urgency to address these challenges. In light of this, the development of an advanced transportation framework, as discussed in [6], stands out as a potential remedy. However, with a diverse range of road users, prioritizing one over another can give rise to ethical dilemmas. Hence, any forward-thinking transportation system must not only focus on efficiency and safety but also embed ethical considerations at its core. Incorporating a comprehensive ethical framework ensures that the needs and rights of all users are balanced, fostering trust and acceptance among the community. It’s essential to navigate these intricate moral landscapes to ensure that advancements in transportation truly benefit society.
The realm of smart transportation is seeing a surge in studies centered around connected and automated vehicles (CAVs). The allure of these vehicles lies in their cutting-edge ability to communicate wirelessly, leveraging technologies like DSRC and 5G. The overarching vision is to pave the way for transportation networks that are both dependable and streamlined. One pivotal area of exploration began around 2008, marked by the work of Dresner and Stone. They introduced an approach grounded in a first-come, first-served (FCFS) method for the coordinated navigation of vehicles at intersections [7]. Fast forward to the present, and Xu and colleagues have innovated further, proposing a model wherein vehicles harness geometric topology to dictate the order of passage. This is coupled with an evolved FCFS-inspired method to generate motion paths [8].
Notably, while sequencing remains crucial, an emerging trend in the literature underscores the importance of devising the ideal speed framework for these vehicles. For instance, Mirheli and team framed the conundrum of multi-vehicle speed optimization as a mixed-integer linear programming challenge, turning to the Monte Carlo tree search technique for answers [9]. In a different vein, Malikopoulos and his group broke down the broader speed planning challenge, directing their energies toward deriving analytical resolutions for individual vehicle speed determination [10]. A deep dive into related literature, such as [11,12,13,14], offers a comprehensive overview of the advancements and discussions in this dynamic field.
The cooperative planning techniques mentioned earlier exhibit several shortcomings: firstly, each CAV’s trajectory tends to be static or aligned with the fleet’s structure; secondly, their speeds are typically either set at a constant rate or determined by a rigid pattern; and thirdly, there is a lack of simultaneous planning for the trajectories of the entire CAV ensemble. While some of these design choices aim to enhance the real-time operational performance of the CAVs, they don’t necessarily maximize the team’s cooperative capabilities or the optimal use of time and spatial resources. Moreover, a glaring oversight in previous studies is the absence of priority assignments among vehicles. In real-world scenarios, it’s undeniable that emergency vehicles, like ambulances or fire trucks, should receive precedence in terms of speed over regular vehicles. This critical aspect remains inadequately addressed in existing research.
This paper seeks to bridge these identified gaps. Our primary focus revolves around formulating the intersection management challenge as an optimal control problem (OCP). Within this framework, we emphasize concurrent trajectory planning for all CAVs, ensuring that their speeds can be dynamically adjusted to fit practical objectives. Moreover, this research uniquely incorporates an ethical perspective to validate the logical underpinnings of the proposed design, ensuring that it resonates with real-world values and concerns. This holistic approach guarantees a system that is not only efficient but also considerate of the broader societal implications.
The main contributions of the research are summarized as follows:
- The velocity of each of the CAVs is made manageable by the proposed scheme, with which the velocity priority of emergency cars can be guaranteed; a more realistic OCP model is thus established.
- Without lane discipline at the intersection, the feasible region of each CAV is expanded in a sense that the CAVs can go any directions in the intersection.
- The OCP solution efficiency is improved through the proposed adaptive stepwise optimization (ASO) method.
- The proposed cooperative optimization scheme is ethically verified.
2. Problem Formulation
Within this segment, we articulate an OCP characterized by a multitude of stipulations. The overarching ambition is to augment the collaborative effectiveness of the CAVs. This enhancement is achieved by escalating the collective shift of each CAV’s endpoint in relation to the intersection’s midpoint along its designated coordinate axis, all within a predefined operational timeframe. It’s imperative to highlight that a subset of these CAVs consists of emergency units, inherently demanding precedence in terms of speed. Such prioritization is fundamental in ensuring the rapid response and functionality of these essential vehicles within the network. Note that the intersection is not compartmentalized with delineated lanes in this paper as the assumption is that the intersection is accessible only for CAVs, which are centrally controlled. Collision can effectively be avoided with the trajectory optimization scheme without a lane discipline involved. Under such circumstances, the configuration space of the OCP is expanded compared to that of a strategy with the limitation of a lane discipline [15,16,17,18]. With the current design, each of the CAVs are guided to their corresponding lane by the end of the central control process.
2.1. Kinematic Constraints
Consider an OCP encompassing CAVs, which can be categorized into three distinct dimensions: large, medium, and petite. It’s essential to recognize that a specific subset of these vehicles is designated as emergency units, inherently designed to operate at accelerated speeds. Conversely, the remaining fleet predominantly consists of standard automobiles that traverse at a comparatively subdued pace. To represent the kinematic constraints associated with these vehicles, we resort to the ensuing mathematical formulations. Here, it is pivotal to understand that , , and signify the wheelbase lengths for vehicles of large, medium, and diminutive stature, in that order.
where , . T is the fixed task completion time. The definitions of other variables refer to Figure 1. Some of the above variables need to be within reasonable ranges:
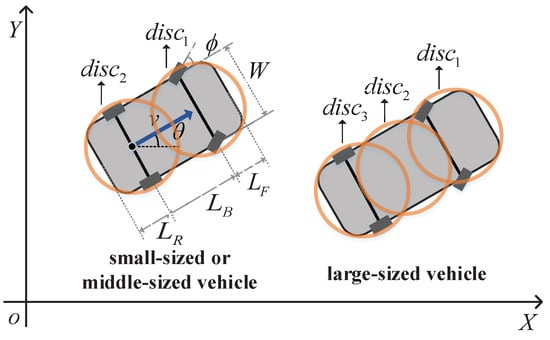
Figure 1.
Kinematic model of CAV. We use different numbers of discs to evenly cover the rectangular body according to the actual size of the vehicle.
In this context, the notation is specifically aligned with emergency vehicles, while pertains to the remaining CAVs. Each vehicle category has been allocated its distinct velocity parameters. Moving forward to Section 4.2, we wll showcase the proficiency of the proposed methodology through a series of simulation-driven evaluations.
2.2. Intersection Scenario Constraints
The setting under examination is an intersection devoid of any signaling system or pre-defined lane structure. In this environment, CAVs possess the flexibility to proceed straight ahead, make a left turn, or steer right, anywhere within the intersection’s confines. These vehicles are delineated with distinctive identifiers ranging from N1 to E3. The combination of alphabets and numerals in these identifiers signifies the direction from which a CAV approaches the intersection and its subsequent exit path, as illustrated in Figure 2. Vehicles grouped under identical identifiers are restricted to specific zones within the intersection, ultimately leading them to their designated target areas.
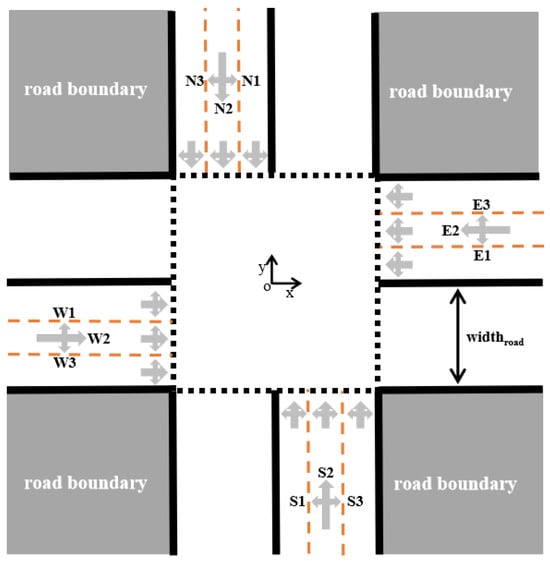
Figure 2.
CAV classification as well as a three-lane intersection where variable turns are allowed at any point within the intersection.
To elucidate the methodology behind crafting feasible region constraints, let’s consider the labels W1–W3 as a guiding example. In this context, W1 symbolizes CAVs approaching from the west and subsequently making a left turn. In contrast, W2 depicts those continuing straight ahead, while W3 signifies vehicles that opt for a rightward turn upon their arrival from the west.
When juxtaposed with conventional intersection management techniques, our method broadens the acceptable zone, as depicted in Figure 3, permitting vehicles to momentarily use the opposing lane. However, for CAVs labeled as W1, maintaining rectangular-shaped vehicles entirely within the L-structured zone presented in Figure 3a becomes a challenge. This results in a constraint that is markedly nonlinear and lacks differentiability. To address this, the quandary is reshaped into a more manageable model by employing circular structures, or discs, to simplify the rectangular vehicle’s shape (as seen in Figure 1) and the perimeter of the road (visible in Figure 4). In the subsequent phase, we moderate the constraint so that the CAV remains inside a rectangular zone, ensuring that vehicle discs steer clear of any overlapping with the environmental discs. It’s worth noting that the discs’ central coordinates and sizes, as represented in Figure 1 and Figure 4, can be ascertained through elementary geometric analysis. Beyond W1, this methodology can seamlessly apply to delineate feasible zones for the remaining 11 CAV categories, substantially diminishing computational intricacies.
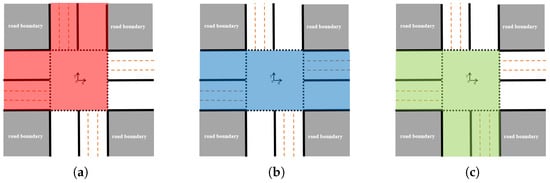
Figure 3.
CAV feasible regions. (a) W1 CAVs, (b) W2 CAVs, (c) W3 CAVs.
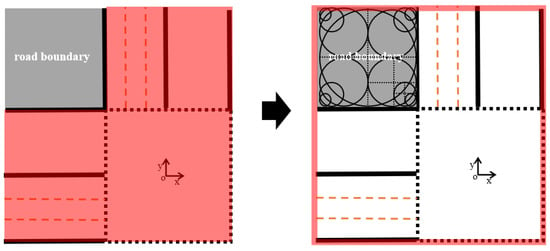
Figure 4.
Schematic diagram of equivalent conversion of W1 CAVs feasible region constraints.
Furthermore, it’s imperative that every CAV navigate towards its designated destination zone, progressing in alignment with the roadway’s orientation as demonstrated in Figure 5. The stipulations for these terminal zones necessitate that each vehicle remains confined within a specific rectangular area upon reaching the conclusion timestamp, denoted as .
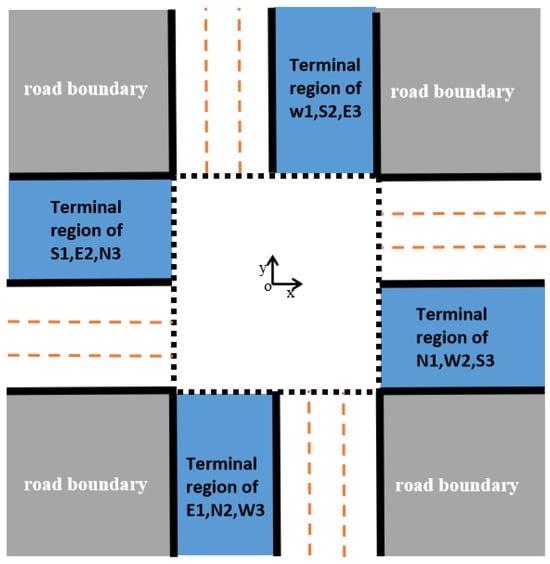
Figure 5.
Terminal region for each category of CAVs.
It’s pivotal to understand that the combination of both feasible zone stipulations and end-zone boundaries together shape the overarching guidelines governing the intersection scenario.
2.3. Cooperative Planning Constraints
The framework for synchronized coordination is comprised of finalization guidelines and mandates for avoiding vehicular clashes. When the timeline begins, represented by , every CAV’s movement status, as it approaches the intersection, is calibrated based on verified data. By the time we reach the endpoint, specifically , to guarantee a seamless and collision-free progression of all CAVs out of the intersection, we establish the ensuing set of closure parameters:
within the designated timeframe, spanning from , it’s imperative that the CAVs avoid any mutual collisions. To ensure such collision-avoidance, the stipulation is set such that the circular boundary of one CAV should never intersect with those of its counterparts. This is implemented by ensuring that the discs representing each vehicle remain distinct and free from overlaps with discs of other vehicles.
2.4. The Optimal Control Problem
In our research, our primary aim with the optimization goal is to promote the greatest possible distance traveled by each CAV in the direction of its final destination.
In summary, the entire task is described as the following OCP:
where are the decision variables of the CAV, the state variables and control variables are defined as and , respectively. Meanwhile, kindly consult Equations (1) and (2) for the determination of the parameters , , , , , and . Furthermore, stands for the feasible region of and is defined as:
in which and are given by kinematic constraints, intersection scenario constraints and cooperative planning constraints, respectively.
3. Methodology
In our quest to unearth the computational solution for Equation (5), we’ve chosen the explicit first-order Runge-Kutta methodology, which reconfigures the Optimal Control Problem (OCP) into a Nonlinear Programming (NLP) challenge. This modified problem is then addressed with the IPOPT NLP resolver, grounded on the foundational principles of the interior-point method [19]. Central to our tactical approach is the generation of an optimum initial conjecture. An adept technique tailored to serve this purpose is elucidated in Section 3.1. Notably, in our foundational strategy, we consciously sideline the inter-vehicle collision-prevention constraints that traditionally exist within cooperative planning. These specific constraints often present substantial complexity when engaged in Equation (5), becoming potential contributors to hefty computational loads. Recognizing this challenge, our strategy, detailed in Section 3.2, advocates for the Adaptive Stepwise Optimization (ASO) methodology. This method contemplates reintroducing these intricate constraints in a phased manner by outlining a sequence of subordinate tasks. By doing so, the overarching computational challenge is parceled out across individual tasks, with each one addressed in a systematic progression. Such a staggered approach lends itself to a marked enhancement in the pace and efficiency of the entire computational process.
3.1. Initial Guess Generation
During the phase of creating the initial estimation, we deliberately set aside the more intricate collision-avoidance constraints, which account for nearly 79% of all constraints in the system. Instead of simultaneously accounting for all CAVs, we meticulously plot the best trajectory for each vehicle sequentially. Since this approach omits considerations of potential vehicular clashes and sidesteps the intricate interdependencies among vehicles, we’re presented with standalone vehicle planning challenges. These isolated planning scenarios offer the advantage of being addressed concurrently. This parallel processing not only speeds up the overall computation (boasting an impressive average resolution time of 0.26 s) but also showcases a scalability that isn’t hindered by the numerical size of the CAV ensemble.
3.2. Adaptively Stepwise Optimization
In discretizing Equation (5) into an NLP problem, each state/control profile is approximated by N equidistance finite element. As many as subproblems are defined, i.e., . Specifically, the does not include any collision-free constraints between CAVs. Compared with , only includes collision-free constraints between CAVs during [0, ]. The whole proposed ASO method process can be summarized as the following pseudo-code (Algorithm 1).
| Algorithm 1: ASO method |
 |
It’s important to highlight a few key aspects of the procedure:
- (1)
- The step size isn’t static but is instead fine-tuned responsively based on the evolving context of the solution.
- (2)
- During the operations in lines 16–18, there’s a verification mechanism in place. This mechanism scrutinizes if the calculated optimal solution aligns with the requisites of the foundational challenge. An intriguing byproduct of this check is that in many scenarios, particularly when confronted with vast constraint cases, it’s not imperative to resolve all the subsidiary issues.
- (3)
- A significant attribute of the ASO method is its consistency. Regardless of the iterative processes it undergoes, the method’s output faithfully mirrors the best possible solution in relation to the parent problem. Subsequently, leveraging the ensuing theorem, the authenticity of the optimum can be corroborated.
Theorem 1.
Suppose there are two NLP problems, and :
In , compared to , we introduce an additional constraint . If the optimal solution of is , and also satisfies the constraint , then is also the optimal solution of .
Proof.
Let us assume that the optimal solutions of is , and . Then the following properties exist:
From Equation (8a,b,e), is a feasible solution of . And is a better solution than for both NLP. Obviously, this goes against the ground truth that is the optimal solution of . Therefore the assumption does not hold. This means that , and is also the optimal solution of . □
4. Simulations
The computational simulations were conducted using the combined environment of Matlab and AMPL. The hardware configuration utilized for these simulations comprised an I5-7300 CPU, operating at a clock speed of 2.50 GHz and bolstered by 8 GB of RAM. In our tests, we iteratively adjusted the parameter through the following values: 4, 8, 12, 16, 20, and 24.
To provide a holistic perspective, for every mentioned value, we generated three distinct scenarios. These unique scenarios were curated at random to ensure variety and a comprehensive examination of potential conditions. All the corresponding parameters and specific configurations are systematically documented in Table 1 for reference.

Table 1.
Parametric settings.
To supplement the written and tabulated data, we’ve curated a comprehensive video presentation. This visual medium encapsulates the intricate nuances and results of the simulations in this section. The objective is to offer viewers a clearer, more intuitive understanding of the findings. The video can be accessed at the following link: https://youtu.be/x8oBZK85r-E (accessed on 3 August 2023).
4.1. On the Efficacy of Optimization Process
The outcomes garnered from applying the ASO method across the test set are meticulously detailed in Table 2. A clear trend emerges from the presented figures: the value of directly correlates with CPU processing time. This correlation is most pronounced when is set at 24, clocking the CPU time at a hefty 7624 s. Such an intensive computational duration can be attributed to the sheer magnitude of the OCP’s scale. With 25,920 variables, 21,288 equality constraints, and 15,424 inequality constraints, the OCP becomes a computational behemoth. The complexity only intensifies due to the factoring in of vehicle dimensions and velocity preferences.

Table 2.
Simulation results with various .
Further deepening our analysis, we introduce the concept of “throughput.” Here, we measure throughput by gauging the time span between the first CAV’s entrance into the intersection and the final CAV’s departure. Predictably, the throughput exhibits a direct relationship with the size of the CAV team. This is because, as escalates, so does the spatial claim on the intersection. This progressive increase in spatial occupancy eventually culminates in noticeable traffic congestion. The manifestations of this congestion, spanning from minor to severe, can be visualized across figures from Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.
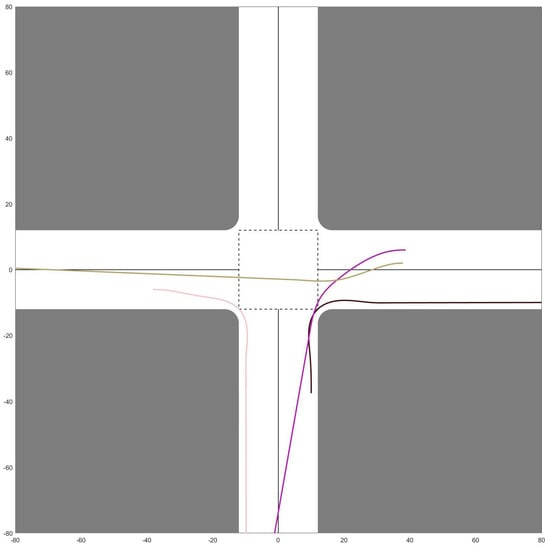
Figure 6.
Optimized CAVs cooperative trajectories. = 4. Note: Different colors represent different CAVs (same below).
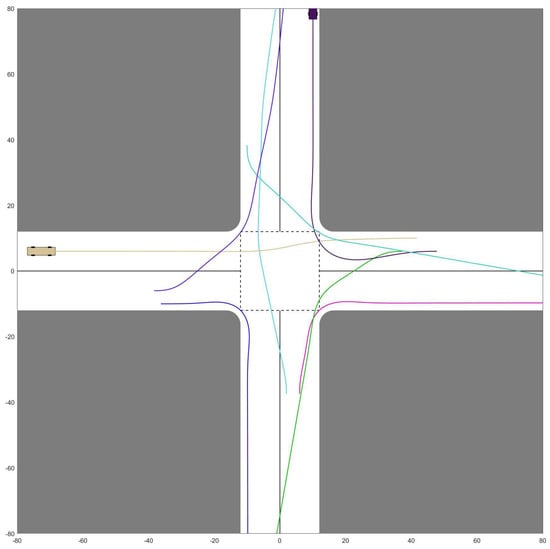
Figure 7.
Optimized CAVs cooperative trajectories. = 8.
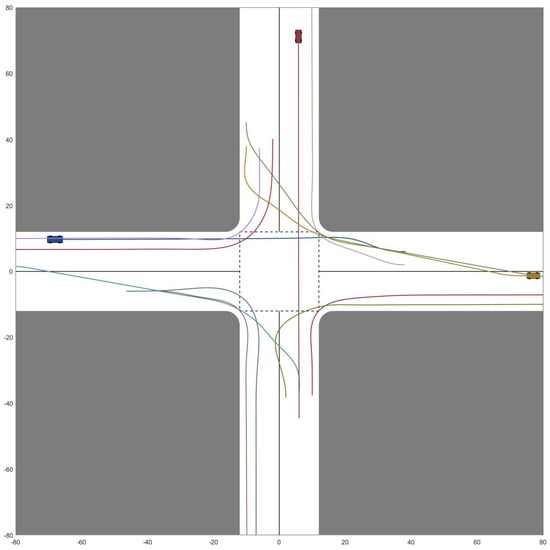
Figure 8.
Optimized CAVs cooperative trajectories. = 12.
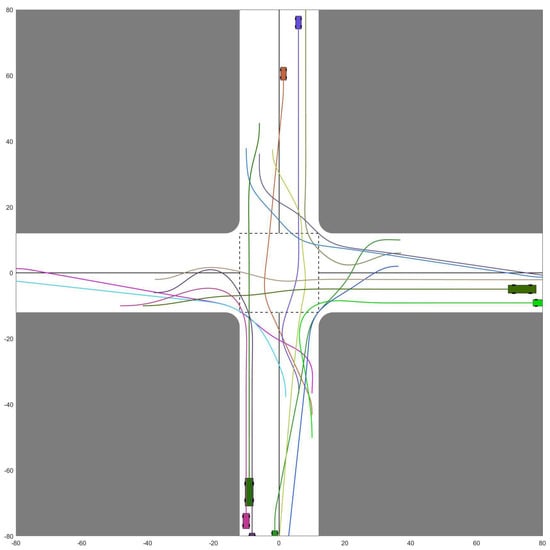
Figure 9.
Optimized CAVs cooperative trajectories. = 16.
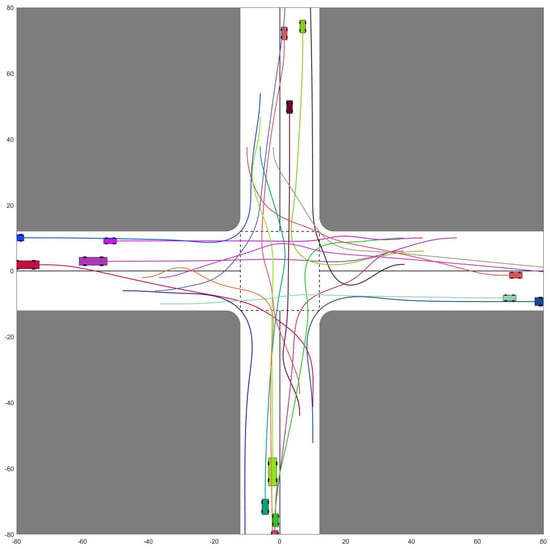
Figure 10.
Optimized CAVs cooperative trajectories. = 20.
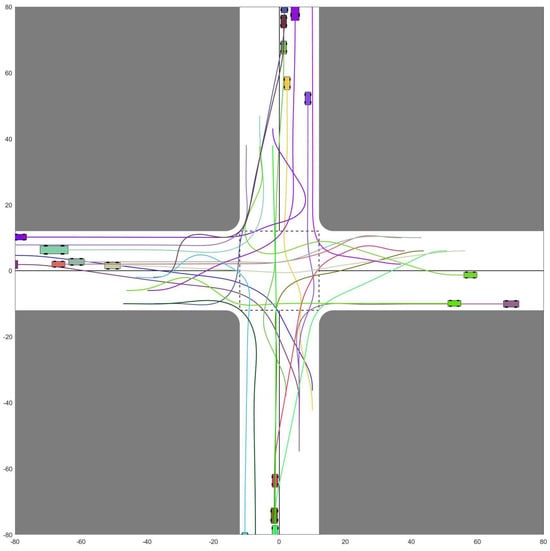
Figure 11.
Optimized CAVs cooperative trajectories. = 24. Note: We added a red pentagram sign on the body of the emergency CAV.
A thorough analysis of Table 2 unveils a significant observation. During each test scenario, we bypass a subset of the collision-free constraints when determining the optimal solution. Given that these collision-free constraints are notably challenging and represent roughly 79% of all constraints, their exclusion is significant. Notably, the total constraint spectrum of OCP broadens as the value of escalates. As a result, even if reaches a sufficiently high value and the percentage of discarded constraints remains small, the absolute number of omitted constraints is still considerable.
For comparative analysis, we introduce an alternative computational approach, referred to as “Algorithm 1*” (shares the same basic structure as that of Algorithm 1). Unlike our ASO method, Algorithm 1* endeavors to directly compute the solution to Equation (5). Strikingly, Algorithm 1* meets its limitations and consistently falls short in all instances where is set at either 20 or 24. The root cause for such a failure can be attributed to a twofold rationale. Firstly, the ASO method’s strategy of reintroducing constraints incrementally circumvents the complexities of addressing them collectively, providing a smoother, more manageable computational pathway. In stark contrast, Algorithm 1*, unwavering in its approach, attempts to process all constraints simultaneously, especially the cumbersome collision-free ones. This uncompromising stance inevitably culminates in an overwhelming computational load, leading to its under-performance in more challenging scenarios.
4.2. On the Efficacy of the Velocity Priority Strategy
To substantiate the efficacy of the configurations delineated in Section 2.1, we formulate an analogous computation method, referred to as “Algorithm 1**” (shares the same basic structure as that of Algorithm 1). The primary distinction between this algorithm and our established methodology is its disregard for the discrepancies in the velocities of the CAVs, as depicted in Equation (2). To conduct a comparative analysis, a specific scenario is concocted wherein both algorithms are subjected to testing, with the resultant outcomes illustrated in Figure 12.
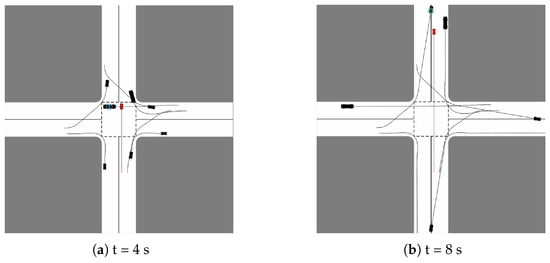
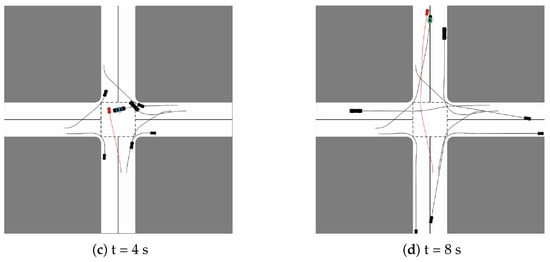
Figure 12.
Comparative simulation results on velocity priority. (a,b) Algorithm 1**; (c,d) This work. Note that we use red and black to denote emergency CAVs and common CAVs, respectively. No. 1 and No. 2 CAVs represent normally moving vehicles that are overtaken by emergency CAVs.
Upon analyzing the yielded results, it is evident that in juxtaposition to Algorithm 1**, our method enables the emergency CAV to surpass No. 1 and No. 2 CAVs at the 4 s and 8 s marks, respectively, securing its precedence in exiting the intersection from the north. This illustrates the nuanced efficiency of our approach, where emergency CAVs, due to their velocity primacy, can navigate swiftly, contributing to the preservation of a harmonious and organized traffic flow. Such structured preferential treatment not only enhances road traffic stability but also prioritizes urgency, reflecting a more intuitive and adaptive response to real-world traffic dynamics. This implementation signifies the integration of optimal functionality with rational responsiveness, aiming to create a harmonious coexistence of varying vehicle types and priorities within the intricate tapestry of urban traffic.
5. Remark on Ethics
The principle underlying the priority accorded to emergency vehicles extends beyond mere convenience or efficiency. In essence, the foundation of such prioritization is rooted in the profound respect and value for human life. The Universal Declaration of Human Rights, for instance, underscores the inherent dignity and inalienable rights of every human being, placing a prime emphasis on the right to life. Consequently, in life-threatening situations, such as medical emergencies or accidents, even a few seconds can drastically alter the outcomes.
Creating intelligent traffic control systems that detect and give way to emergency vehicles is more than a mere integration of technology with infrastructure. It is a reflection of society’s commitment to uphold the sanctity of life. Such systems become emblematic of a society’s collective consciousness, emphasizing the importance it places on safeguarding lives and reducing suffering.
Moreover, the presence of these prioritization mechanisms acts as an omnipresent reminder to citizens about their shared responsibilities. When communal values are constantly reiterated, they are more likely to be internalized by individuals, leading to more responsible and ethical behavior.
Furthermore, as we navigate the age of rapid technological advancements, there’s an amplified call to ensure that our innovations are not just technologically superior but also ethically grounded. Researchers stress the necessity to incorporate ethical considerations at the forefront of technological designs. Hence, in the context of traffic management, while it’s essential to design systems that streamline traffic, it’s equally, if not more, crucial to ensure that these systems are anchored in principles that emphasize the intrinsic value of human life.
6. Conclusions
This research delves into the intricate realm of trajectory design for a myriad of connected and automated vehicles (CAVs) navigating multi-lane roads, converging and diverging at a signal-devoid intersection. A significant emphasis is placed on accommodating emergency vehicles, which are granted precedence in terms of speed. In a bid to enhance the fluidity of traffic flow, the intersection isn’t compartmentalized with delineated lanes but instead perceived as a unified, expansive space.
Diversity in vehicular structure and functionality is acknowledged by factoring in CAVs that vary in dimensions and are assigned hierarchical speed entitlements, ensuring a reflection of real-world traffic intricacies. Augmenting the core structure of this research is the integration of the ASO methodology, meticulously designed to elevate the precision and pace of optimization solutions. Simulation outcomes serve as a testament to the robustness and applicability of the outlined intersection management blueprint. Furthermore, a rigorous ethical analysis is performed to ensure the proposed paradigm adheres to moral standards and prioritizes safety. Looking ahead, there’s an optimistic foresight surrounding this work, hinting at its adaptability to cater to even more multifaceted and dynamic traffic scenarios, thereby potentially revolutionizing intersection management in urban settings.
It is worth our consideration that a more realistic scenario in near future would be intersections with both CAVs and traditional vehicles driven by human, where various other road users, such as pedestrians and bicycles, are also the potential intersection occupiers. An ethical traffic rule and the CAV control strategies adapting to the complicated rule at such an intersection would become rather challenging, which has also boosted the prospects of our future research.
Author Contributions
K.C.: Conceptualization, Data curation, Writing—original draft; B.H.: Methodology, Validation, Writing—review and editing; M.W.: Formal analysis, Investigation, Visualization; H.Z.: Resources, Software, Writing—review and editing; S.C.: Supervision, Project administration; W.L.: Review and editing, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Sanming Project of Medicine in Shenzhen (NO.SZSM202111001).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. There are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, H.; Zhai, G.; Liu, X.; Yang, L.; Liu, Y.; Yuan, Q. Determinants of city-level private car ownership: Effect of vehicle regulation policies and the relative price. Transp. Policy 2022, 115, 40–48. [Google Scholar] [CrossRef]
- Morsali, M.; Frisk, E.; Aslund, J. Spatio-Temporal Planning in Multi-Vehicle Scenarios for Autonomous Vehicle Using Support Vector Machines. IEEE Trans. Intell. Veh. 2021, 6, 611–621. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Z.; Yang, H.; Yang, L. Artificial intelligence applications in the development of autonomous vehicles: A survey. IEEE/CAA J. Autom. Sin. 2020, 7, 315–329. [Google Scholar] [CrossRef]
- Zhang, T.; Song, W.; Fu, M.; Yang, Y.; Wang, M. Vehicle Motion Prediction at Intersections Based on the Turning Intention and Prior Trajectories Model. IEEE/CAA J. Autom. Sin. 2021, 8, 1657–1666. [Google Scholar] [CrossRef]
- Zhou, D.; Ma, Z.; Sun, J. Autonomous Vehicles’ Turning Motion Planning for Conflict Areas at Mixed-Flow Intersections. IEEE Trans. Intell. Veh. 2020, 5, 204–216. [Google Scholar] [CrossRef]
- Guanetti, J.; Kim, Y.; Borrelli, F. Control of connected and automated vehicles: State of the art and future challenges. Annu. Rev. Control 2018, 45, 18–40. [Google Scholar] [CrossRef]
- Dresner, K.; Stone, P. A multiagent approach to autonomous intersection management. J. Artif. Intell. Res. 2008, 31, 591–656. [Google Scholar] [CrossRef]
- Xu, B.; Li, S.E.; Bian, Y.; Li, S.; Ban, X.J.; Wang, J.; Li, K. Distributed conflict-free cooperation for multiple connected vehicles at unsignalized intersections. Transp. Res. Part C Emerg. Technol. 2018, 93, 322–334. [Google Scholar] [CrossRef]
- Mirheli, A.; Hajibabai, L.; Hajbabaie, A. Development of a signal-head-free intersection control logic in a fully connected and autonomous vehicle environment. Transp. Res. Part C Emerg. Technol. 2018, 92, 412–425. [Google Scholar] [CrossRef]
- Malikopoulos, A.A.; Cassandras, C.G.; Zhang, Y.J. A decentralized energy-optimal control framework for connected automated vehicles at signal-free intersections. Automatica 2018, 93, 244–256. [Google Scholar] [CrossRef]
- Mirheli, A.; Tajalli, M.; Hajibabai, L.; Hajbabaie, A. A consensus-based distributed trajectory control in a signal-free intersection. Transp. Res. Part C Emerg. Technol. 2019, 100, 161–176. [Google Scholar] [CrossRef]
- Levin, M.W.; Rey, D. Conflict-point formulation of intersection control for autonomous vehicles. Transp. Res. Part C Emerg. Technol. 2017, 85, 528–547. [Google Scholar] [CrossRef]
- Lin, P.; Liu, J.; Jin, P.J.; Ran, B. Autonomous Vehicle-Intersection Coordination Method in a Connected Vehicle Environment. IEEE Intell. Transp. Syst. Mag. 2017, 9, 37–47. [Google Scholar] [CrossRef]
- Liu, B.; Shi, Q.; Song, Z.; El Kamel, A. Trajectory planning for autonomous intersection management of connected vehicles. Simul. Model. Pract. Theory 2019, 90, 16–30. [Google Scholar] [CrossRef]
- Dixit, A.; Oak, S.; Mantri, S.; Nimkar, A.; Naik, M. Lane Change Prediction based on Trajectory Analysis and Driver Actions Tracking. In Proceedings of the 2021 International Conference on Computing, Computational Modelling and Applications (ICCMA), Brest, France, 13–16 September 2021; pp. 21–26. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.; Rakheja, S. Adaptive Lane Change Trajectory Planning Scheme for Autonomous Vehicles Under Various Road Frictions and Vehicle Speeds. IEEE Trans. Intell. Veh. 2023, 8, 1252–1265. [Google Scholar] [CrossRef]
- Gao, Y.; Gordon, T. Optimal Control of Vehicle Dynamics for the Prevention of Road Departure on Curved Roads. IEEE Trans. Veh. Technol. 2019, 68, 9370–9384. [Google Scholar] [CrossRef]
- Banias, O.; Precup, R.E.; Curiac, D. Multiagent architecture applied in decentralized real-time urban road traffic control. In Proceedings of the 2009 5th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 28–29 May 2009; pp. 271–276. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).