Abstract
With the rise of satellite-as-a-service subscriptions as technology improves, our paper examines how satellite operators (SOs) can choose between traditional channels for selling satellites, satellite-as-a-service (SataaS), and dual-channel strategies. In the space supply chain, commercial satellites display several distinct characteristics that differentiate them from other physical commodities in traditional supply chains, most notably their exposure to significant launch risks. In addition, SataaS suffers from the risk of secure data transmission. However, the emergence of novel technologies such as blockchain technology (BCT) could help to mitigate such risks. Therefore, our study analyzes the optimal strategy among the sell, SataaS, and dual-channel approaches for SOs by considering the above distinctive characteristics in the case without blockchain and the case with blockchain. Our paper reveals the existence of a dual-channel strategy that generates the highest profit for the SO and yields the highest consumer utility when launch success is high and when SataaS fixed costs are low. When the launch success rate is very high, the dual-channel strategy transforms into a pure sell strategy. After the adoption of BCT, when the cost of BCT is low, the SO’s profit is enhanced in all three sales channels compared to the case without blockchain. Notably, in SataaS as well as in the dual-channel approach, the adoption of BCT always improves consumer utility compared to the case without blockchain. However, in the sell channel, the consumer benefits depend on the relatively low cost of blockchain customization.
1. Introduction
1.1. Importance of the Topic
Satellite-as-a-service (SataaS) presents a novel development within the satellite industry, departing from the traditional framework of satellite ownership and operation. This emerging paradigm entails subscribing to satellite services as needed, capitalizing on contemporary satellite technologies like miniaturization, constellation deployments, and cloud-based infrastructure. The mechanism of SataaS is illustrated in Figure 1.
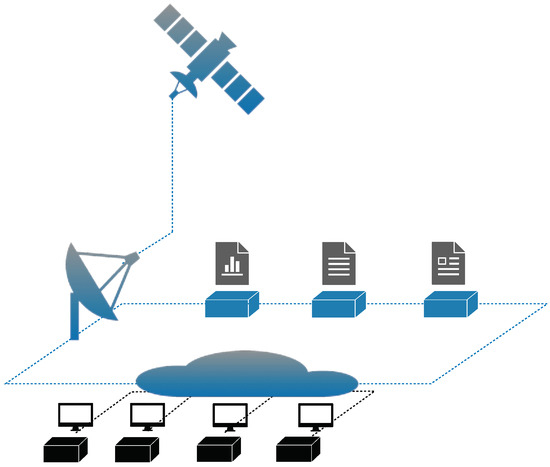
Figure 1.
Diagram of satellite-as-a-service mechanism.
SataaS is distinguished by its potential advantages, including heightened accessibility to satellite data and services, financial efficiency through reduced upfront investments, and adaptability to evolving requirements. Nevertheless, it introduces its own set of challenges, encompassing concerns pertaining to data security and service continuity, specifically in the context of potential satellite system failures or service interruptions. In practice, several SOs have embraced this transformative approach, with notable instances encompassing organizations such as Eutelsat https://www.eutelsat.com/en/blog/satellite-as-a-service-the-future-of-satellite-network-communications.html (accessed on 3 November 2023)), Ellipsis https://ellipsis-drive.com/blog/satellite-as-a-service/ (accessed on 3 November 2023), Xplore https://www.xplore.com/services/satellite-as-a-service.html (accessed on 3 November 2023), and Spacety https://en.spacety.com/index.php/satellite-as-a-service-sataas-2/ (accessed on 3 November 2023).
Traditionally, satellite operations have adhered to the “selling satellites” strategy, characterized by significant upfront costs and attendant risks, wherein customers procure, launch, and maintain their own satellites. In stark contrast, SataaS introduces a subscription-based framework that substantially lowers initial financial thresholds while introducing its own nuances of data transmission risk.
However, the emergence of disruptive technologies, most notably blockchain, has provided ideas for reducing two types of risks. Blockchain technology introduces a layer of security, transparency, and trust that significantly mitigates some of the inherent risks associated with launching and data transmission. Firstly, it plays a crucial role in enhancing the security and integrity of data transmission between satellites and ground stations. The decentralized and tamper-resistant nature of blockchain ensures that data remain unaltered during transmission, reducing the likelihood of data breaches or unauthorized access. Secondly, blockchain technology offers a novel approach to managing launch risks. Through the use of smart contracts, satellite operators can establish contingency plans that trigger automatically in the event of launch failures or other critical incidents. These smart contracts can facilitate swift responses, thereby minimizing disruptions and maintaining service continuity. In the real world, several companies are focusing on integrating blockchain technology with satellite systems, such as SpaceChain https://www.spacechain.com/decentralized-satellite-infrastructure/ (accessed on 3 November 2023) and Spacebit https://spacebit.com/projects (accessed on 3 November 2023).
1.2. Current Gaps
The sell strategy underscores the concept of customer ownership, typically reserved for specialized missions, while SataaS excels in delivering cost efficiency. Based on the characteristics of different strategies in the space supply chain, the satellite data industry is undergoing a transformative shift with the rise of satellite-as-a-service (SataaS), challenging traditional ownership models. Thus, the SO is confronted with a dilemma: how to balance the pros and cons of different distribution channels—selling satellites, SataaS, or a combination of both through dual-channel strategies. This decision is critical for optimizing profitability in an industry marked by launch risks and data transmission challenges.
1.3. Research Goals
This paper aims to provide guidelines for SOs to choose the optimal strategy and demonstrate the proper conditions for adopting BCT. We build three channel models to derive the satellite operator’s strategy by capturing the characteristics of the satellite data business. Our paper delves into the traditional satellite selling channels, SataaS, and the combination of both through dual-channel strategies. Given the distinctive attributes of commercial satellites, including their vulnerability to launch risks and data transmission concerns, our study evaluates optimal strategies in scenarios with and without blockchain technology using game theoretical analysis.
1.4. Study Contributions
Our analysis demonstrates that the dual-channel strategy often emerges as the superior choice, concurrently optimizing profitability and consumer utility, under conditions characterized by high success rates and moderate SataaS fixed costs. Furthermore, blockchain technology always augments consumer utility across SataaS and dual channels. Only when the cost of BCT is low can it improve consumer surplus in the selling channel. Finally, this paper sheds light on the inherent value of BCT for the satellite industry.
The rest of this paper is organized as follows. Section 2 describes the state of the art based on the related literature. In Section 3, we consider the case without BCT and build three models, namely NR, NS, and ND, which correspond to the three channels. In Section 4, BCT is incorporated into the three models. In Section 5, the value of BCT is discussed. Section 6 concludes the paper, presents managerial insights, and suggests future research directions.
2. Literature Review and Marginal Contributions
Our work is related to three streams of research in the literature. After introducing the most similar studies in each stream, we demonstrate the current research gap and compare it with our work to highlight the marginal contributions of this study.
The first stream is the research on satellite services, the second stream focuses on dual channels, and the third stream examines blockchain technology applications in the operations management field.
2.1. Literature Review
2.1.1. Satellite-as-a-Service
As a core component of the Space–Air–Ground Integrated Network (SAGIN), satellite services have drawn attention in the literature. Hein and Rosete [1] clarified the services that satellites may provide from different dimensions. For example, satellites can be used as platforms for running software applications provided by customers, enabling cloud computing [2]. By forming a collaborative computing network in space, invalid data transportation is reduced. In addition, satellite communication has become an important component of the telecommunications industry. Zhang et al. [3] pointed out that typical application areas of satellite communication include video streaming, television relay, and broadband internet, where remote locations are connected to existing high-speed backbone networks through satellites operating in orbit. There are also services that revolve around the full life cycle of a satellite, such as development, launch, and operation [1]. In addition to these, another relevant service is digitization, which allows customers to obtain required data [4]. Spire Global has similar services related to the delivery of Earth observation datasets. There has been extensive research based on the satellite services mentioned above. Shaengchart and Kraiwanit [5] investigated the Starlink satellite project’s impact on internet provider services in emerging economies. Sun et al. [6] found that current satellite–ground IoT task offloading schemes rarely consider service deployment based on network function virtualization (NFV) and proposed a service deployment strategy based on deep reinforcement learning to solve the service deployment problem. Much of the previously discussed research used a technical research methodology. Theoretical research that has examined the impact of satellite services is limited. Here, we consider two types of services provided by satellite operators: selling satellites and SataaS.
2.1.2. Dual-Channel Supply Chain Management
Studies of supply chain management were originally closely related to the research stream of dual-channel supply chain management, including applications of game theory [7,8,9,10,11,12,13,14]. The existing literature in the field of operation management has conducted extensive research on dual-channel supply chains [15,16]. Dan et al. [17] used two-stage optimization techniques and Stackelberg game theory to study the optimal decisions of retail services and prices in centralized and decentralized dual-channel supply chains and evaluated the impact of retail services and consumer loyalty to retail channels on manufacturers and retailers’ pricing behavior, finding that the degree of customer loyalty to the retail channel had a great effect on the retail services and pricing decisions. Li and Mizuno [18] found that the optimal dynamic pricing and inventory policy of a dual-channel supply chain is an inventory-dependent base stock list price policy. Xiao and Shi [19] studied a manufacturer’s product marketing through a dual-channel supply chain, which included online channels and physical retail channels, and found that the main results of pricing and channel priority strategies maintained robustness to the time series of channel priority decisions. Li et al. [20] analyzed the optimal distribution strategy of enterprise software based on the different characteristics of short-term problems (i.e., the software quality was fixed) and long-term problems (i.e., the software quality became a part of strategic decision making) and found that the dual-channel strategy was still viable and brought the highest profits and social welfare to the enterprise even when the cost of adaptation was relatively high compared to the customization cost. Similarly, our paper also considers the optimal channel distribution strategy. Beyond the above research, there is still insufficient research on the dual-channel supply chain for selling satellites and SataaS.
2.1.3. Blockchain Technology
Nakamoto [21] first proposed the concept of Bitcoin, and blockchain technology began to emerge and develop on this basis. With its decentralized structure, distributed nodes, consensus algorithms, smart contracts, and asymmetric encryption, blockchain technology has the potential to enhance network security [22,23,24], transparency [25], and visibility [26]. It has been widely recognized as a technology that has almost unlimited applications in various industries [27]. A large amount of literature has been conducted on the application value of blockchain technology in specific industries [28], especially fields like finance [29,30,31], medicine [32], healthcare [33,34,35], and agriculture [36]. Kim et al. [37] developed a blockchain-enabled supply chain coordination system that facilitated the alignment of diverse decisions made by stakeholders in an off-site construction supply chain. Tan et al. [38] applied a Stackelberg game model to study the feasibility of using blockchain technology in a fresh agricultural product supply chain composed of e-commerce platforms (B2C or O2O) and offline retailers. Jahanbin et al. [39] explored the current status of the agri-food supply chain and how blockchain technology could be useful in addressing existing challenges. Longmei et al. [40] examined the impact of blockchain adoption on online game supply chain pricing and enterprise investment decisions under information asymmetry and found that whether enterprises adopt blockchain technology depends on the comprehensive impact of market demand and input–output on quality. Gupta et al. [41] proposed that blockchain technology is more effective in facilitating the financial resilience of a supply chain under the moderating influence of environmental dynamism compared to artificial intelligence. Similar to the above literature, our paper also captures the characteristics of BCT, such as improving data security. However, most of the operations management literature focuses on the application of BCT in supply chains for areas such as agricultural products, medicine, healthcare, and luxury products, and few studies have focused on the application of BCT in satellite supply chains. This paper fills this gap and explores the value of BCT in satellite business models from an OM perspective. Table 1 shows a comparison between this paper and the relative literature.

Table 1.
Overview of the related literature.
2.2. Marginal Contributions
Our research presents significant contributions in three key areas, strengthening the foundation of knowledge and practice in the evolving satellite industry.
Firstly, a critical gap in Satellite-as-a-Service is filled (SataaS). Our study addresses a noticeable void in the literature concerning SataaS by providing a comprehensive theoretical framework. We offer insights into the impact of selling satellites and SataaS, which, in turn, enriches our understanding of optimal channel distribution strategies within the satellite industry. By doing so, we bridge the knowledge gap that has hindered the industry’s ability to harness the full potential of satellite services.
Secondly, enriching dual-channel supply chain management in satellite data business. Our research goes beyond filling a gap; it enriches the field of dual-channel supply chain management, with a specific focus on the satellite data business. This novel perspective enhances the operations management literature. We delve into the intricacies of dual-channel strategies within the satellite data context, providing actionable insights and theoretical advancements that benefit both researchers and practitioners.
Lastly, pioneering blockchain technology in satellite supply chains. Our study pioneers the application of blockchain technology in satellite supply chains. This innovative approach opens new vistas for enhancing data security, transparency, and efficiency. By exploring and introducing blockchain solutions in the satellite industry, we offer fresh perspectives and practical applications that can revolutionize the management and utilization of satellite data.
In summary, our research not only adds to the body of knowledge but offers valuable insights and practical applications to the satellite industry, cementing our role in shaping its future. These contributions are designed to catalyze innovation, drive operational excellence, and secure the evolving satellite industry’s sustainable growth.
3. Models excluding Blockchain Technology
In this section, we model the optimal strategy for the SO based on business features. The notations and assumptions of the model are described in Table 2 and Table 3. We assume satellite data users are heterogeneous in different channels. We denote customers’ valuation by v, which is uniformly distributed in [0, 1]. If the user chooses to own a satellite to acquire data, they need to pay the SO to purchase the satellite. Plus, they need to take the risk of a failed launch. We assume that the probability of a successful launch is e. Thus, the utility of customers under the sell channel can be measured as

Table 2.
Notations used in this paper.

Table 3.
Summary of assumptions.
If the user chooses the SataaS channel to acquire data, they need to pay as the subscription price to the SO. It is worth noting that users have to face a security risk in acquiring data through the SataaS channel; in order to portray the utility loss of customers, we introduce s. To ensure that the demand is non-negative, we assume that .
We next explore the SO’s payoff, consumer surplus, and social welfare in the NR model, NS model, and ND model when BCT is absent. By analyzing the performance of different channels, we obtain the optimal strategy for the SO.
3.1. NR Model: Sell Channel without Blockchain
By setting Equation (1) to zero, we can derive the marginal customers who are indifferent as to purchasing a satellite and not purchasing a satellite. Since the production cost per satellite unit cannot be neglected, we denote it by . Then, the sell channel demand and the SO’s payoff function can be measured as follows:
After the derivation, we obtain the optimal selling price and profit for the SO in the sell channel, that is, and , respectively.
The closed form of the price and profit indicate that they both increase with the launch success rate and decrease with the per satellite cost, which is intuitive.
3.2. NS Model: SataaS Channel without Blockchain
In this section, we explore the optimal decisions of the SO in the SataaS channel. The market demand derivation for the SataaS channel is similar to that in the sell channel. By taking Equation (2) to be zero, we derive the marginal customers who are indifferent in relation to subscribing to SataaS and not subscribing to SataaS. However, in contrast to the NR model, the marginal cost of SataaS can be ignored. Nevertheless, the upfront investment in the satellite constellation is significant, and we set it as a fixed cost C. Thus, the SataaS channel demand and the SO’s payoff function can be measured as follows:
After solving the equation, the optimal price in the SataaS channel is , and the profit is .
It can be observed that the optimal price is decreasing in s (). The profit of the SO first increases and then decreases as s increases. In other words, the price of SataaS decreases as the degree of loss of consumer utility due to the data risk increases. The variation in profit depends on the trade-off between the price and market demand, which both change with s. This is also intuitive.
3.3. ND Model: Dual Channel without Blockchain
When the SO employs a dual-channel strategy, consumers are free to choose to own satellites or subscribe to SataaS. In this scenario, their consumption decision depends on the comparison of the consumer surplus obtained from purchasing and subscribing: versus . Consumers whose valuation meets will consider purchasing the satellite directly. We denote by the valuation of this type of marginal consumer, i.e., . Consumers whose valuation meets will consider subscribing to SataaS. We denote by the valuation of this type of marginal consumer, i.e., . Eventually, if , marginal consumers with a valuation equal to are indifferent to these two channels. If the valuation is higher than this value, they will tend to subscribe to SataaS.
Thus, there exist two cases, and . In the first case, if , then we can obtain . This means that consumers’ valuations in tend towards purchasing satellites from the sell channel, while consumers in prefer to subscribe to SataaS. Those consumers with a valuation in refuse to spend in either channel. In the second case, no customers prefer to purchase satellites directly. Therefore, consumers whose valuation is in subscribe to satellite data from SataaS channels. Based on the above analysis, we obtain the market segmentation of the dual channels:
Thus, the SO’s payoff function can be written as follows:
By solving the constraint equation, we obtain Lemma 1
Lemma 1.
According to the relationship of e, s, and , there are three strategies for the SO:
- 1.
- When , the dual channel exists, where , , .
- 2.
- When , there is only the SataaS channel, where , .
- 3.
- When , there is only the sell channel, where , .The equilibrium outcomes are summed in Table 4.
 Table 4. Equilibrium outcomes without blockchain technology.
Table 4. Equilibrium outcomes without blockchain technology.
The conditions for dividing the channel in Lemma 1 give us the following insight. Here, e is the probability of satellite launch success, is the cost of manufacturing a satellite, and s represents the utility loss to the user from the data risk of SataaS. Therefore, when the launch success rate is low and the satellite cost is high, no users will choose to purchase the satellite, and the dual channel is reduced to the SataaS strategy; when the utility loss to the user from data security is high, no users will choose SataaS, and the dual channel is reduced to the sell strategy.
Thus, only when the satellite launch success rate remains at can both the SataaS and sell channels exist at the same time. As the launch success rate declines, satellite buyers in the dual channel will no longer choose to own satellites and will shift to the SataaS market. As the launch success rate rises, users will move to the sell market when the utility of launch success outweighs the utility of lost data security.
Furthermore, in order to derive the optimal strategy, this paper compares the profits of the dual-channel strategy with those of the sell and SataaS channels, respectively. From the analysis, we obtain Proposition 1, and the comparison results are summarized in Table 5.

Table 5.
Optimal strategy without blockchain technology.
Proposition 1.
When , the dual channel exists:
(a) , ; (b) if , , .
Proposition 1 sheds light on the conditions for choosing the dual-channel strategy. Proposition 1(a) shows that compared with the pure SataaS strategy, the SO will always obtain a higher profit with the dual-channel strategy. Plus, consumers also benefit more with this strategy. Proposition 1(b) indicates that compared with the pure sell strategy, the important factor for choosing a channel is the fixed cost of SataaS. That is, if C is small, then the dual-channel strategy is better for the SO. Otherwise, the pure sell channel will generate a higher profit. For customers, the consumer surplus of the dual-channel strategy is always higher than that of the pure sell channel. In conclusion, if the dual-channel strategy is possible, it is always the best strategy for consumers. This is because dual channels provide two service options, allowing more consumer needs to be met. For the SO, the condition for the choice of the dual-channel strategy is that C is relatively small.
4. Models including Blockchain Technology
As determined above, while a dual-channel strategy can benefit the SO the most, it is not always possible due to the launch and data transformation risks.
However, with the help of BCT, these risks can be reduced. On the one hand, the choice of a blockchain-embedded launch platform for a satellite launch can reduce the error rate during the launch process to some extent. Through its distributed ledger, it ensures the traceability and immutable recording of critical launch-related information, such as specifications, testing results, and authorizations. This safeguards against unauthorized alterations and enhances data security. By automating and securing various aspects of the launch process, the potential for human error and technical mishaps is considerably diminished, ensuring a smoother and more reliable satellite deployment. For instance, IBM’s transformation of blockchain into satellite launches involves creating a decentralized ledger that records every step of the launch process, from satellite construction to launch vehicle integration and ignition. Each phase of the launch is securely logged and verified, reducing the risk of launch failures and data discrepancies. This blockchain-embedded launch platform, as demonstrated by IBM, provides a high level of transparency and trust among all stakeholders involved. https://www.ibm.com/blog/space-tech-transforming-satellite-launches-with-blockchain/(accessed on 3 November 2023).
On the other hand, the adoption of BCT within the satellite constellation network significantly enhances data security and reduces the risk of unauthorized access or exposure in the satellite network and transmission. Through robust authentication mechanisms, blockchain technology ensures that only authorized users can access and interact with satellite data, minimizing the potential for data breaches and security vulnerabilities. B Sriman and VSS Kandregula [42] mentioned that a satellite can act as a secure node for data transmission. The private key is securely encoded into the satellite software, making it exceptionally resistant to encryption hacking attempts. These insights align with our research, emphasizing the pivotal role of BCT in reducing data risks in SataaS.
Based on real-world observations, we introduce BCT in both the sell and SataaS channels. Through theoretical modeling, we analyze the market segmentation, the profit of the SO for different strategies, and the changes in consumer surplus.
We assume that launching a satellite with the help of BCT can increase the probability of success by a factor denoted as b. Thus, the consumer utility of purchasing satellites through the sell channel changes to
For SataaS, since BCT can reduce the risk of data transmission between satellite networks, we introduce the resilience risk factor () when modeling the utility of this subscriber segment. Thus, the consumer utility of the SataaS channel can be written as follows:
All other settings in the case with BCT remain the same as in Section 3. We next explore the SO’s payoff and the consumer surplus in the BR model, BS model, and BD model when blockchain is adopted.
4.1. BR Model: Sell Channel with Blockchain
By setting Equation (9) equal to zero, we can derive the marginal customers who are indifferent to the choice between the sell channel and SataaS channel. One of the economic aspects that warrants examination is the customization cost associated with integrating blockchain into satellites. This customization cost, denoted as , encompasses the expenses incurred when adapting the satellite infrastructure to accommodate blockchain technology. It includes the development of custom smart contracts for secure data transmission, the integration of cryptographic security measures, and the modification of existing satellite systems to align with the principles of decentralization and data immutability that underpin blockchain [43]. Due to the presence of blockchain-related satellite customization costs and unit satellite costs , to ensure a non-negative demand, we assume that . Since the upper limit of the launch success probability is , to be consistent with reality, we assume that . Then, the sell channel demand and the SO’s payoff function can be measured as follows:
After the derivation, we arrive at the optimal sell price and profit for the SO in the sell channel, that is, and , respectively.
Similar to the NR model, both the price and profit increase with the launch success rate and decrease with the unit satellite cost. The difference is that the price and profit in the BR model also increase with b as well as due to the participation of BCT, and the price in the BR model is higher than that in the NR model because of the added blockchain-related customization costs. The comparison of the returns is not easy to visualize, and we will analyze them in detail in Section 5.
4.2. BS Model: SataaS Channel with Blockchain
The market demand derivation for the SataaS channel is similar to that in the NS model. However, by capturing the features of the BS model, the SO needs to pay an additional blockchain infrastructure cost, assumed to be fixed cost B. This fixed cost mainly includes the costs of satellite operations, blockchain network maintenance, and security measures to ensure continuous service availability [44]. Therefore, we can model the blockchain-embedded SataaS channel market demand and the SO’s profit as follows:
By solving this equation, the optimal price in the SataaS channel is , and the profit is .
Similar to the results for the NS model, both the price and the SO’s profit decrease as the loss of data risk increases. Nevertheless, the difference from the NS model is that the price and profit in the BS model also increase as the coefficient decreases. This is attributed to the adoption of blockchain technology, which reduces the risk of data loss. https://www.codemotion.com/magazine/backend/blockchain/blockchain-data-security/ (accessed on 3 November 2023). In addition, the SO has an additional fixed minus term B which is the cost of employing BCT.
4.3. BD Model: Dual Channel with Blockchain Technology
Analogous to the ND model, when the SO employs a dual-channel strategy, consumers are free to choose to purchase satellites or subscribe to SataaS. In this scenario, the valuation of the marginal consumers who are indifferent to these two channels is equal to . According to the valuation, the market segmentation of the blockchain-embedded dual-channel strategy can be written as follows:
Thus, the SO’s payoff function can be written as follows:
By solving the constraint equation, we obtain Lemma 2. The equilibrium outcomes are summarized in Table 6.

Table 6.
Equilibrium outcomes with blockchain technology.
Lemma 2.
With the adoption of BCT, according to the relationship of e, s, and , there are three strategies for the SO:
- 1.
- When , the dual-channel exists, , , where .
- 2.
- When , there is only the SataaS channel, where , .
- 3.
- When , there is only the sell channel, where , .
Lemma 2 indicates that the conditions for dividing the channel in Lemma 2 are similar to those in Lemma 1, but with slight differences. We will discuss the differences in detailed in Section 5. From the threshold expressions in Lemma 2, we obtain the following insight. Here, is the blockchain-related satellite unit customization cost, b is the coefficient of the launch success rate improved by BCT, and is the coefficient of data security risks reduced by BCT. Therefore, when the launch success rate is low and the satellite cost is high, no users will choose to purchase the satellite, and the dual channel is reduced to the pure SataaS strategy. When the utility loss to the user from data security is high, no users will choose SataaS, and the dual channel is reduced to the pure sell strategy.
Therefore, the SataaS and sell channels can exist simultaneously only if the satellite launch success rate remains at . Similar to the ND model, as the launch success rate declines, satellite buyers in the dual channel will no longer choose to launch satellites and will shift to the SataaS market. As the launch success rate rises, users will move to the sell market when the utility of launch success outweighs the utility of lost data security.
Furthermore, in order to derive the optimal strategy with BCT, we compare the profits of the dual-channel strategy with those of the sell and SataaS channels, respectively. From the analysis, we obtain Proposition 2, and the comparison results are summarized in Table 7.

Table 7.
Optimal strategy with blockchain technology.
Proposition 2.
When , the dual channel exists:
(a) , ; (b) if , , .
Akin to Proposition 1, Proposition 2 provides insight into the conditions for choosing the dual-channel strategy with the adoption of BCT. Proposition 2(a) implies that compared with the pure SataaS strategy, the SO will always obtain a higher profit using the dual-channel strategy. Plus, consumers also benefit more with this strategy. Proposition 1(b) shows that, compared with the pure sell strategy, whether to choose the dual-channel strategy hinges on the sum fixed cost of SataaS and BCT. That is, if is small, then the dual-channel strategy is better for the SO. Otherwise, the pure sell channel will generate a higher profit. For customers, the consumer surplus of the dual-channel strategy is always higher than that of the pure sell channel. In conclusion, Proposition 2 provides a similar suggestion that if the dual-channel exits, it is always the best strategy for consumers. This is because dual channels provide two service options, allowing more consumer needs to be met. For the SO, the condition for the choice of the dual-channel strategy is that is relatively small.
5. Values of Blockchain Technology
After deriving the equilibrium decisions and performance for the sell, SataaS, and dual-channel strategies in the N and B cases, we define the following terms, which represent the value of BCT to the SO, consumers, and social welfare.
The channel can be written as follows:
Proposition 3.
(a) When one chooses the SataaS channel, ⇔ ; . (b) When one chooses the dual channel, ⇔ ; . (c) When one chooses the sell channel, ⇔ and .
Proposition 3 implies the conditions for adopting BCT in different channels and the outcomes are summarized in Table 8. Proposition 3(a) gives the threshold of the BCT cost in the SataaS channel. When , it is better for the SO to adopt BCT. The value of BCT for the SO and customers in Sataas is illustrated in Figure 2. The figure indicates that as the fixed cost of BCT increases, the value of SO’s payoff diminishes, while the value of consumer surplus is always positive. Therefore, as long as the SO adopts the BCT at the proper cost, both they and the consumers gain more from the presence of BCT than the absence of BCT.

Table 8.
The value of BCT.
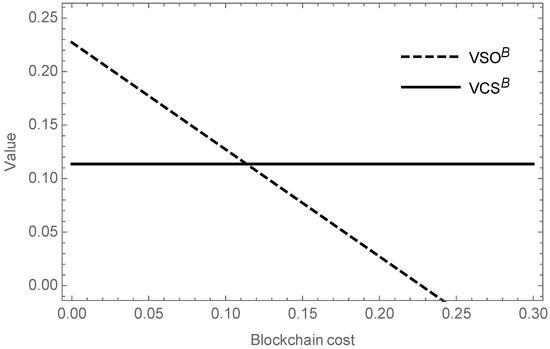
Figure 2.
The value of BCT for the SO and customers in the SataaS channel.
Proposition 3(b) gives the threshold of the BCT cost in the dual channel. When , the SO should adopt BCT. Figure 3 shows the value of BCT in terms of the profit of the SO and the customer surplus. The implication of Figure 3 is similar to that of Figure 2, i.e., both the SO and the consumer can benefit more if they choose to adopt the blockchain at an appropriate BCT cost.
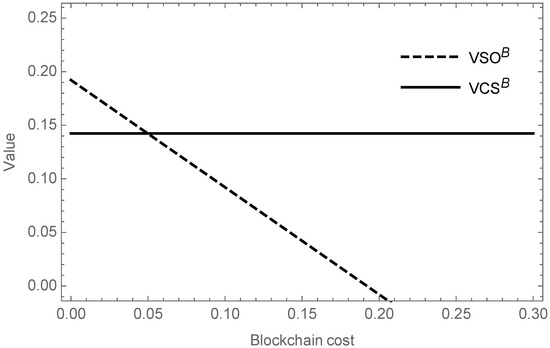
Figure 3.
The value of BCT for the SO and customers in the dual channel.
Proposition 3(c) gives the threshold of the BCT cost in the sell channel. When , it is wise for the SO to adopt BCT. Figure 4 shows the variation in the SO’s profit and consumer surplus with the blockchain-related satellite unit customization cost. The SO’s revenue decreases with an incremental increase in the customization cost. However, the value of consumer surplus is no longer always positive but also decreases with increasing customization costs, which is different from Figure 2 and Figure 3. It shows that consumers in the retail channel do not always benefit more if the SO uses blockchain. Once the cost of customization is high, consumer surplus is instead lower with blockchain than without.
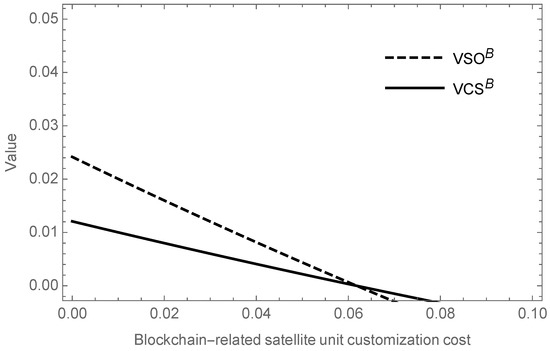
Figure 4.
The value of BCT for the SO and customers in the sell channel.
It is noteworthy that the consumer surplus is always higher when blockchain is adopted in the SataaS and dual channels compared to when it is not adopted. In the sell channel, on the other hand, the consumer surplus is higher with blockchain than without only when the cost is relatively small, which represents the condition for the SO to adopt BCT. As shown in Figure 4, the value of BCT for customers in the sell channel is different to that in the other channels.
6. Managerial Implications and Conclusions
6.1. Managerial Implications
From the analytical results, we arrive at managerial insights for SOs regarding how to choose between the three channels (traditional, SataaS, and dual-channel) and when to use BCT. For the SO, the choice of channel may depend on the expected launch success rate. When th launch success rate is high, traditional sales channels may be more profitable. When it is lower, the SO should consider diversifying into SataaS or a dual-channel approach. As SataaS is an emerging business channel, whether to adopt this new channel depends on the fixed costs related to providing SataaS. If these costs are relatively low, SataaS can be a viable channel. Conversely, if the fixed costs are high, the SO should consider other options.
Furthermore, though blockchain technology provides a method of hedging risks, it cannot be used unconditionally. The SO should adopt BCT for different channels and within the corresponding blockchain cost threshold to achieve benefits. Otherwise, using BCT will lead to a decrease in income.
6.2. Conclusions
As the commercial satellite industry is growing rapidly, there is a limited amount of literature that addresses the business strategies of SOs.
With the rise of SataaS as technology improves, our paper examined how the SO can choose between traditional channels for selling satellites, SataaS, and dual-channel strategies. Commercial satellites display several distinct characteristics that differentiate them from other physical commodities, most notably their exposure to significant launch risks. In addition, SataaS suffer from the risks associated with secure data transmission. However, the emergence of novel technologies such as blockchain could help to mitigate such risks. Therefore, our study analyzed the optimal strategy for the SO by considering the above distinctive characteristics of the sell, SataaS, and dual channels for cases with and without blockchain. Firstly, by deriving and comparing these three channel models in the absence of BCT, we determined the optimal channel under different conditions. Next, akin to the case above, we examined these three channels when embedded with BCT and revealed which channel is optimal with the adoption of BCT. Furthermore, by compare these two cases, this paper shed light on the value of BCT.
Our paper revealed that the dual-channel strategy is possible and generates the highest profit for the SO and the highest consumer utility when the launch success is high and when the SataaS fixed costs are low. The reason for this is that under these two conditions, the dual channel satisfies not only the users who choose to launch their own satellites, but also the needs of users who choose SataaS. Thus, choosing the dual-channel strategy and offering multiple marketing models can reach a larger market of users and increase the overall consumer surplus and the SO’s profitability. When the launch success rate is very high, the dual-channel strategy transforms into a pure sell strategy, because at that point, most users will choose to launch their own satellites. However, when the launch success rate is very low, the dual-channel strategy transforms into pure SataaS, as at this point, satellite users cannot accept the loss of launch failures and most of them choose the subscribe service. After the adoption of BCT, when the cost of BCT is low, the SO’s profit is enhanced in all three sales channels compared to the case without blockchain. Notably, in SataaS as well as in the dual-channel strategy, the adoption of BCT always improves consumer utility compared to the case without blockchain. However, in the sell channel, the consumer benefit depends on the relatively low cost of blockchain customization.
Although this study achieved remarkable results, there are still some limitations to be considered: (1) Our current theoretical model primarily focuses on a single satellite operator, failing to account for the presence of multiple operators in the real-world satellite industry, thereby limiting our exploration of competition between various entities. (2) In the SO’s payoff function, we did not consider the life cycle of satellites. By including the satellite operation cycle in the model, the optimal strategy and conditions may be different. (3) From the perspective of finance, we did not take into account the financial constraints of the SO. Under the fixed-budget constraint, the optimal channel choice and conditions may change. In conclusion, addressing these limitations will facilitate the formulation of more comprehensive and realistic strategies for optimal sales channels in the satellite industry.
Author Contributions
Conceptualization, J.D. and Z.H; methodology, Z.H. and Y.J.; formal analysis, Y.J.; investigation, Y.J.; writing—original draft preparation, Y.J. and C.C.; writing—review and editing, Z.H.; supervision, J.D. and Z.H.; project administration, J.D.; funding acquisition, J.D. and Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 72271227), the Fundamental Research Funds for the Central Universities (grant numbers E1E40810X2 and E2ET0808X2), the Youth Innovation Promotion Association CAS (grant number 110800EAG2), the MOE Social Science Laboratory of Digital Economic Forecasts and Policy Simulation at UCAS, and the Weiqiao Guoke Joint Laboratory at UCAS.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SataaS | Satellite-as-a-service |
| BCT | Blockchain technology |
References
- Hein, A.; Bruce Rosete, C. Space-as-a-Service: A Framework and Taxonomy of-as-a-Service Concepts for Space. In Proceedings of the International Astronautical Congress, Paris, France, 18–22 September 2022. [Google Scholar]
- Orbitals, E. “Satellite-As-A-Service”: A New Approach for Space Industry. 2019. Available online: https://www.exodusorbitals.com/files/whitepaper.pdf (accessed on 3 October 2023).
- Zhang, Z.; Zhang, C.; He, Q.C.; Wang, P. Robust integrated planning for LEO satellite network design and service operations. Oper. Res. Lett. 2023, 51, 575–582. [Google Scholar] [CrossRef]
- Senior, P.; Eckersley, S.; Irwin, V.; Stern, B.; Haslehurst, A.; Cawthorne, A.; da Silva Curiel, A.; Sweeting, M. Can we use low cost small satellites to observe space debris missed by ground systems? In Proceedings of the 8th European Conference on Space Debris, Darmstadt, Germany, 20–23 April 2021; p. 42. [Google Scholar]
- Shaengchart, Y.; Kraiwanit, T. Starlink satellite project impact on the Internet provider service in emerging economies. Res. Glob. 2023, 6, 100132. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Nie, L.; Feng, G.; Zhang, Z.; Liu, J. A joint strategy for service deployment and task offloading in satellite-terrestrial IoT. Comput. Netw. 2023, 225, 109656. [Google Scholar] [CrossRef]
- Bernstein, F.; Song, J.S.; Zheng, X. “Bricks-and-mortar” vs.“clicks-and-mortar”: An equilibrium analysis. Eur. J. Oper. Res. 2008, 187, 671–690. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Sun, Y. Implementing coordination contracts in a manufacturer Stackelberg dual-channel supply chain. Omega 2012, 40, 571–583. [Google Scholar] [CrossRef]
- Deng, Z.; Zheng, B.; Jin, L. Dual-channel supply chain coordination with online reviews. Electron. Commer. Res. Appl. 2023, 60, 101281. [Google Scholar] [CrossRef]
- He, P.; Zhang, G.; Wang, T.Y.; Si, Y. Optimal two-period pricing strategies in a dual-channel supply chain considering market change. Comput. Ind. Eng. 2023, 179, 109193. [Google Scholar] [CrossRef]
- Matsui, K. Should competing suppliers with dual-channel supply chains adopt agency selling in an e-commerce platform? Eur. J. Oper. Res. 2024, 312, 587–604. [Google Scholar] [CrossRef]
- Díaz, Á.; Kaschel, H. Scalable Electronic Health Record Management System Using a Dual-Channel Blockchain Hyperledger Fabric. Systems 2023, 11, 346. [Google Scholar] [CrossRef]
- Zhu, C.; Liang, J.; Liu, Y. Pricing Decision of the Dual-Channel Supply Chain with the Manufacturer’s Extended Warranty. Systems 2023, 11, 313. [Google Scholar] [CrossRef]
- Zhang, R.; Lu, Y.; Liu, B. Pricing Decisions and Game Analysis on Advanced Delivery and Cross-Channel Return in a Dual-Channel Supply Chain System. Systems 2023, 11, 155. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Guo, J.; Zhou, W. Pricing/service strategies for a dual-channel supply chain with free riding and service-cost sharing. Int. J. Prod. Econ. 2018, 196, 198–210. [Google Scholar] [CrossRef]
- Li, G.; Li, L.; Sethi, S.P.; Guan, X. Return strategy and pricing in a dual-channel supply chain. Int. J. Prod. Econ. 2019, 215, 153–164. [Google Scholar] [CrossRef]
- Dan, B.; Xu, G.; Liu, C. Pricing policies in a dual-channel supply chain with retail services. Int. J. Prod. Econ. 2012, 139, 312–320. [Google Scholar] [CrossRef]
- Li, M.; Mizuno, S. Dynamic pricing and inventory management of a dual-channel supply chain under different power structures. Eur. J. Oper. Res. 2022, 303, 273–285. [Google Scholar] [CrossRef]
- Xiao, T.; Shi, J.J. Pricing and supply priority in a dual-channel supply chain. Eur. J. Oper. Res. 2016, 254, 813–823. [Google Scholar] [CrossRef]
- Li, S.; Cheng, H.K.; Jin, Y. Optimal distribution strategy for enterprise software: Retail, saas, or dual channel? Prod. Oper. Manag. 2018, 27, 1928–1939. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. Decentralized Bus. Rev. 2008, 4, 15. [Google Scholar]
- Bocean, C.G.; Vărzaru, A.A. A Two-Stage SEM–Artificial Neural Network Analysis of Integrating Ethical and Quality Requirements in Accounting Digital Technologies. Systems 2022, 10, 121. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhou, X.; Li, D.; Liu, A.; Lev, B. The Impact of R&D Subsidy and IPP on Global Supply Chain Networks System—A Technology Spillover Perspective. Systems 2023, 11, 460. [Google Scholar]
- Xia, J.; Li, H.; He, Z. The Effect of Blockchain Technology on Supply Chain Collaboration: A Case Study of Lenovo. Systems 2023, 11, 299. [Google Scholar] [CrossRef]
- Farooq, M.S.; Riaz, S.; Rehman, I.U.; Khan, M.A.; Hassan, B. A Blockchain-Based Framework to Make the Rice Crop Supply Chain Transparent and Reliable in Agriculture. Systems 2023, 11, 476. [Google Scholar] [CrossRef]
- Dutta, P.; Choi, T.M.; Somani, S.; Butala, R. Blockchain technology in supply chain operations: Applications, challenges and research opportunities. Transp. Res. Part Logist. Transp. Rev. 2020, 142, 102067. [Google Scholar] [CrossRef]
- Choi, T.M. Blockchain-technology-supported platforms for diamond authentication and certification in luxury supply chains. Transp. Res. Part Logist. Transp. Rev. 2019, 128, 17–29. [Google Scholar] [CrossRef]
- Wu, C.; Xu, C.; Zhao, Q.; Zhu, J. Research on financing strategy under the integration of green supply chain and blockchain technology. Comput. Ind. Eng. 2023, 184, 109598. [Google Scholar] [CrossRef]
- Dong, C.; Chen, C.; Shi, X.; Ng, C.T. Operations strategy for supply chain finance with asset-backed securitization: Centralization and blockchain adoption. Int. J. Prod. Econ. 2021, 241, 108261. [Google Scholar] [CrossRef]
- Kowalski, M.; Lee, Z.W.; Chan, T.K. Blockchain technology and trust relationships in trade finance. Technol. Forecast. Soc. Chang. 2021, 166, 120641. [Google Scholar] [CrossRef]
- Su, L.; Cao, Y. Dynamic Evolutionary Game Approach for Blockchain-Driven Incentive and Restraint Mechanism in Supply Chain Financing. Systems 2023, 11, 406. [Google Scholar] [CrossRef]
- Krittanawong, C.; Rogers, A.J.; Aydar, M.; Choi, E.; Johnson, K.W.; Wang, Z.; Narayan, S.M. Integrating blockchain technology with artificial intelligence for cardiovascular medicine. Nat. Rev. Cardiol. 2020, 17, 1–3. [Google Scholar] [CrossRef]
- Haleem, A.; Javaid, M.; Singh, R.P.; Suman, R.; Rab, S. Blockchain technology applications in healthcare: An overview. Int. J. Intell. Netw. 2021, 2, 130–139. [Google Scholar] [CrossRef]
- Hussien, H.M.; Yasin, S.M.; Udzir, N.I.; Ninggal, M.I.H.; Salman, S. Blockchain technology in the healthcare industry: Trends and opportunities. J. Ind. Inf. Integr. 2021, 22, 100217. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Chakraborty, A.; Hasan, M.; Rashid, K.; Siddique, A.H. Blockchain application in healthcare systems: A review. Systems 2023, 11, 38. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, F. Revenue and Risk Sharing Mechanism Design in Agriculture Supply Chains Considering the Participation of Agricultural Cooperatives. Systems 2023, 11, 423. [Google Scholar] [CrossRef]
- Kim, M.; Zhao, X.; Kim, Y.W.; Rhee, B.D. Blockchain-enabled supply chain coordination for off-site construction using Bayesian theory for plan reliability. Autom. Constr. 2023, 155, 105061. [Google Scholar] [CrossRef]
- Tan, C.; Zeng, Y.; Ip, W.; Wu, C. B2C or O2O? The strategic implications for the fresh produce supply chain based on blockchain technology. Comput. Ind. Eng. 2023, 183, 109499. [Google Scholar] [CrossRef]
- Jahanbin, P.; Wingreen, S.C.; Sharma, R.; Ijadi, B.; Reis, M.M. Enabling affordances of blockchain in agri-food supply chains: A value-driver framework using Q-methodology. Int. J. Innov. Stud. 2023, 7, 307–325. [Google Scholar] [CrossRef]
- Longmei, T.; Hu, B. The impacts of blockchain adoption on pricing and efforts decisions in online game supply chains with information asymmetry. Int. J. Prod. Econ. 2023, 266, 109030. [Google Scholar]
- Gupta, S.; Modgil, S.; Choi, T.M.; Kumar, A.; Antony, J. Influences of artificial intelligence and blockchain technology on financial resilience of supply chains. Int. J. Prod. Econ. 2023, 261, 108868. [Google Scholar] [CrossRef]
- Sriman, B.; Kandregula, V.S.S. The Next level of Security Scalable Solution Blockchain (SSSB) in Satellite Communication System. J. Phys. Conf. Ser. 2022, 2335, 012063. [Google Scholar] [CrossRef]
- Li, C.J.; Sun, X.C.; Zhang, Z. Effective methods and performance analysis of a satellite network security mechanism based on blockchain technology. IEEE Access 2021, 9, 113558–113565. [Google Scholar] [CrossRef]
- Choi, T.M.; Ouyang, X. Initial coin offerings for blockchain based product provenance authentication platforms. Int. J. Prod. Econ. 2021, 233, 107995. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).