Abstract
Nowadays, the Internet of Underwater Things (IoUT) provides many marine 5G applications. However, it has some issues with energy efficiency and network lifetime. The network clustering approach is efficient for optimizing energy consumption, especially for underwater acoustic communications. Recently, many algorithms have been developed related to clustering-based underwater communications for energy efficiency. However, these algorithms have drawbacks when considered for heterogeneous IoUT applications. Clustering efficiency in heterogeneous IoUT is influenced by the uniform distribution of cluster heads (CHs). As a result, conventional schemes are inefficient when CHs are arranged in large and dense nodes since they are unable to optimize the right number of CHs. Consequently, the clustering approach cannot improve the IoUT network, and many underwater nodes will rapidly consume their energies and be exhausted because of the large number of clusters. In this paper, we developed an efficient clustering scheme to effectively select the best CHs based on artificial bee colony (ABC) and Q-learning optimization approaches. The proposed scheme enables an effective selection of the CHs based on four factors, the residual energy level, the depth and the distance from the base station, and the signal quality. We first evaluate the most suitable swarm algorithms and their impact on improving the CH selection mechanism. The evaluated algorithms are generic algorithm (GA), particle swarm optimization (PSO), ant colony optimization (ACO), and ABC. Then, the ABC algorithm process is improved by using the Q-learning approach to improve the process of ABC and its fitness function to optimize the CH selection. We observed from the simulation performance result that an improved ABC-QL scheme enables efficient selection of the best CHs to increase the network lifetime and reduce average energy consumption by 40% compared to the conventional ABC.
Keywords:
heterogeneous IoUT; CH selection optimization; ABC; ACO; PSO; GA; reinforcement learning; energy efficiency 1. Introduction
Numerous applications that heavily rely on low-cost, high-performance remote sensing technologies are introduced by the IoUT [1]. By deploying self-organized sensors throughout vast underwater ecosystems, Underwater Wireless Sensor Networks (UWSNs) play a crucial part in data collection [2]. These data are processed and analyzed after they are obtained. The underwater nodes (UNs) are placed in carefully chosen locations, which are frequently characterized by ill-defined topologies. These UNs gather and transmit data about the various undersea areas and are located in a centralized base station (BS). This BS is responsible for sending the collected data directly to end users or via the Internet [3], which was made possible by a cutting-edge UWSN framework built on the idea of the IoUT.
The IoUT needs a pre-defined infrastructure because it is deployed in a distributed and non-deterministic manner. This distribution results in an inherent dynamism in the network topology and organization, which can change over time [4]. Also, the nodes of IoT networks are often heterogeneous, with various configurations for energy sources, storage capacity, and processing energy. As a result, communication lines can be subject to constant change, which may affect communication between nodes or between nodes and base stations [5,6]. Accordingly, UWSNs for constructing the IoUT face various difficulties, including problems with energy stability, communication reliability, and quality of service. To ensure the effectiveness and longevity of IoUT networks, creative solutions are required because underwater settings are dynamic and unpredictable [7].
In the IoUT, when the number of CHs is big and generates a significant number of clusters to communicate with the BS, the energy of these nodes that perform the role of CH will be rapidly depleted [8]. Furthermore, installing a few CHs will result in a small number of clusters with many sensors, as cluster members (CMs) will consume higher energies across long distances to relay data to the CHs. Furthermore, a trade-off between the number of clusters and CHs must be determined to reduce sensor energy consumption while maintaining network lifetime. This means a transmission network topology with a changeable number of CHs based on the distance from the base station is required [9]. Furthermore, when delving into the intricacies of network performance, the heterogeneity of residual node energy, node depth, and the relative distances of the nodes from the base station emerge as important drivers.
Given these concerns, optimizing CH selection requires careful thought. Modifying the CH selection process in response to these complex concerns is critical. A complex CH selection method must be established to reduce the influence of fluctuating residual node energy levels, node depths, and the nodes’ geographical closeness to the base station [10]. Such a technique considers the aspects mentioned above to maintain fair energy consumption among nodes and lengthen the overall endurance of the IoUT system. By fine-tuning the CH selection criteria to account for these complexities, the IoUT may more efficiently negotiate the problems provided by heterogeneous energy distribution and other associated issues, improving the overall efficiency and sustainability of the IoUT network [11].
In the IoUT, CH selection can be improved with the use of swarm intelligence (SI) algorithms, like artificial bee colony (ABC), ant colony optimization (ACO), genetic algorithms (GAs), and particle swarm optimization (PSO). To overcome the complex problems posed by the Internet of Things network dynamics, these algorithms are inspired by the behavior of natural systems. They can help solve some problems related to dynamics according to the state of the network [12]. These algorithms enable to autonomously adjust to the difficulties brought on by uneven energy distribution, variations in node depth, and different distances from the BS. This dynamic and adaptable choice of CH stations optimizes energy utilization. It guarantees the network’s robustness, efficiency, and resilience in the face of the challenging and constantly changing underwater environment [13].
1.1. Study Motivation
Based on what was discussed in the introduction, it becomes apparent that a discernible gap exists related to the lack of capacity to effectively address the demands of efficient energy utilization, reliability, and scalability of the IoUT. This study aims to improve energy efficiency, support network stability, and guarantee reliable communication by considering the specifics of the environments of the IoUT [13]. The improvement will be by taking the revolutionary effects of SI algorithms and Q-learning optimization to maximize the potential of these cutting-edge methods to build dependable, high-performing IoUT networks that can survive the difficulties aquatic ecosystems pose [14]. Following are some of the goals that this study can address:
- ▪
- Identified Energy Issue: This study highlights a clear problem in effectively addressing complex issues related to IoT systems’ reliable and scalable energy usage.
- ▪
- Maximize Energy Efficiency: The main motivation of this study is how to increase the operational lifetime of IoUT networks by improving the CH selection to reduce energy consumption.
- ▪
- Enhancing Network Stability: Study the impact of AI algorithms in reducing the effects of changes in environmental factors of the Internet of Underwater Things (IoUT), changes in node characteristics, and difficulties of underwater ecosystems.
- ▪
- Improve Reliable Communication: Develop an intelligent CH selection process to transmit data efficiently and reduce communication failures using cutting-edge methods, including SI algorithms and Q-learning optimization.
1.2. The Contributions
To overcome the energy consumption challenge in the heterogeneous large-scale IoUT, we proposed an energy-efficient CH selection approach based on the ABC algorithm and learning optimization scenario. The major contributions of this paper are as follows:
- ▪
- Customized for IoUT Challenges: Develop proposed swarm techniques specifically to handle the complexity of IoUT networks, such as variable node depths, varying energy levels, and fluctuating distances from base stations, to provide efficient energy consumption by dynamically adjusting the CH selection.
- ▪
- Advanced CH Election Strategies: Present innovative techniques for CH selection to handle the unique issues provided by the environments of the IoUT by examining the integration of SI algorithms such as ABC, ACO, GA, and PSO with a Q-learning approach.
- ▪
- Improved Energy Efficiency: Establish a more equitable distribution of energy consumption among nodes, hence increasing the network’s operational lifespan, by utilizing the ABC algorithm improved by the Q-learning approach.
- ▪
- Adaptability to Changing Conditions: Provide an intelligent scheme to adjust the CH selection process in response to changes in underwater node attributes by integrating ABC and machine learning approaches.
Accordingly, the aim is to develop an energy-efficient CH selection approach based on the ABC and Q-learning optimization algorithm to reduce the energy consumption for the large-scale IoUT. The rest of this paper is organized as follows: Section 2 reviews the technical background and related works. The heterogeneous IoUT clustering approach model is presented in Section 3. Section 4 discusses different swarm intelligence methods and reviews their impacts on the CH selection process. The proposed study modeling and problem formulation are discussed in Section 5. In Section 6, the methodology and proposed solutions are reviewed. In Section 7, simulation scenarios and parameters are reviewed. Section 8 presents the simulation results and discussion, and, finally, the conclusion is reviewed in Section 9.
2. Background and Related Works
The issue of energy usage is especially important in the context of IoUT large-scale networks. The additional data collecting and packet transmissions inherent in the undersea data exchange operations increase the demands placed on energy resources [15]. As a result, various studies and research projects have gone deep into analyzing tactics to minimize energy use to the greatest extent possible. This approach is consistent with the general goal of maintaining effective and dependable communication in IoUT networks, ensuring the delivery of high-quality services across a wide range of applications.
The IoUT network architecture is precisely developed to handle the obstacles provided by underwater environments. These networks are conscious of their limited communication ranges, severe signal attenuation, and energy constraints [16]. IoUT systems encompass hierarchical clustering, data aggregation and relay schemes, specialized underwater communication protocols, energy-efficient approaches, localization methods, and advanced data processing algorithms to address these issues. These components form a strong foundation for efficient and dependable data transfer, energy conservation, accurate localization, and significant data insights in underwater environments [17].
Numerous approaches and techniques with benefits like accuracy and propagation restriction are used in IoUT applications. Some are also influenced by energy consumption, packet delivery efficiency, and network age [18]. Most recent studies focus mainly on the clustering approach, which is the most suitable technique concerning energy efficiency in IoUT [19]. The clustering concept is an effective strategy for lowering energy usage in large-scale IoUT. Energy resources are conserved through optimizing the transmission process, contributing to the network’s energy efficiency. However, it is worth noting that particular CHs may face problems with early energy depletion, which is impacted by their specific distribution and proximity or distance from the BS [20,21]. These variances underscore the need for enhanced CH selection procedures to enable equal energy resource allocation and to extend the lifetime of CHs.
According to the clustering approach, in the IoUT applications, several UNs can be deployed in clusters. Many UNs exist within each cluster and have a CH and act as underwater cluster members (UCMs) [22]. The UCMs transmit their data in low energy to the CH. Then, the CH collects the data and sends it to the BS using high-energy communication. This method will reduce energy consumption; however, some CHs can lose their energy early depending on their distribution and presence near or far from the BS [23]. Many studies have been conducted to investigate the integration of clustering methodologies in the context of IoUT networks to improve efficiency and expedite CH selection processes.
In [24], the authors provided an efficient game-theoretic clustering approach for a non-cooperative strategy to choose the best relay nodes. To improve CH management in the IoUT, the suggested technique is based on energy heterogeneity and a punishment mechanism. The non-cooperative evolutionary game method selects the best relay as the strategy approaches Nash equilibrium. The examination of the adopted approach reveals that it reduces energy consumption while improving the data delivery ratio.
In [25], the authors present a swarm optimization-based PSO approach. The suggested approach enables the dynamic update of the cluster size depending on the CH load, the CH remaining energy, the distance from the sink node, and the number of times the CHs pass data between clusters. The analyses’ findings indicate that, when compared to other algorithms, the proposed methods can reduce energy use.
The authors in [26] developed an energy-efficient and balanced data-gathering routing protocol based on Q-learning to overcome the problem of high node mobility and void holes. The presented mechanism chose the forwarder nodes based on their residual energy. The authors rely on energy as the primary selection parameter to ensure efficient energy use in the network. The proposed techniques extend the lifetime of underwater sensor networks.
In [27], an energy-aware clustering protocol based on the K-means algorithm was proposed. When using the K-means approach to choose candidate CHs, the procedure is dependent on the node’s location and remaining energy. The authors in [28] introduced a novel optimized CH selection technique based on the tunicate swarm algorithm in their study. Compared to the moth flame optimization routing protocol, the evaluation of the proposed scheme reveals that it improves network stability while also increasing network lifetime by 17%.
In [29], the authors provide a metaheuristics-based architecture of aggregation with the MCR-UWSN routing protocol. The MCR-UWSN technique aims to choose the most effective CHs and travel the path to the target. Experimental findings demonstrate the enhanced performance of cutting-edge MCR-UWSN technology.
The authors in [30] propose using the enhanced remora optimization algorithm (ECERO) in UWSN to select an energy-optimized CH. The scheme enables choosing the CH based on EROA while taking the energy, Euclidean distance from the sink, node density, network’s average energy, and acoustic path loss into account. The suggested method significantly improves the performance of the newly proposed EOCSR algorithm, which promises to alleviate the hot-spot problem but still experiences it because it relays such a big amount of data.
In [31], the authors provide a way to increase the underwater sensor network lifetime while balancing energy consumption, and transmission distance reduction is one of the key problems. The proposed method uses a fitness function that is constructed using several sources of information, including total and residual energy, via the suggested glowworm swarm optimization approach. The comparison’s findings demonstrated that, when comparing alternative methods, the proposed strategy executes the case of total energy usage more efficiently.
A study in [32] proposes two protocols, cooperative delay-reliability and delay-reliability-aware protocols, for UWSNs to avoid the issue of increasing the network’s nodes, which raises the network’s energy consumption. The network is split into two areas in the suggested strategy, with two sink nodes (SNs) in the network’s upper section and two others in its middle region. The protocol chooses the relay node based on residual energy, distance, and bit error rate. The analysis revealed that the proposed method outperforms the depth base routing (DBR) protocol in terms of performance.
The related studies summarized in Table 1 provide different energy consumption solutions. However, they have substantial gaps since they frequently fail to account for the complications caused by diverse energy levels, variable depths, and distances from the surface base station (SBS). These characteristics significantly impact the performance and lifetime of IoUT networks, necessitating a more thorough approach to CH selection [33]. One of the most prominent issues is the availability of UNs with varying energy reserves. Heterogeneous energy levels and other underwater impacts can cause an uneven distribution of energy use across the network, potentially leading to node energy depletion. Variations in the UNs’ depths and distances from the SBS also produce dynamics that must be carefully considered during CH selection.

Table 1.
Summaries of the related works’ shortcomings criteria.
An innovative and robust strategy entails incorporating reinforcement learning (RL) techniques to address these issues. Unlike previous studies, which have concentrated only on static CH selection methods, our methodology employs RL to optimize CH selection dynamically [34]. The network may change CH assignments in real-time based on changing the energy, depth, and closeness to the SBS by applying a Q-learning algorithm with the ABC approach. This adaptability allows the network to deploy resources more efficiently, reducing energy imbalances and improving overall performance.
3. Heterogeneous IoUT Clustering Approach Model
The CHs establish a network on the seabed plane in the heterogeneous IoUT model by being scatted across the ocean floor. These CHs are essential for collecting huge amounts of data from the undersea environment, including multimedia data like films and photos. They are equipped with transmitters to transfer data to and from the surface sea station. CH nodes act as intermediaries, collecting data via multi-hop paths from sensor nodes within their clusters. CHs can store data, messages, and commands via their large storage unit [35]. Acoustic communication sends the gathered data to the mobile sink as it approaches and interacts with a CH. This happens whenever the mobile washbasin approaches the CH closely while moving or visiting. If a CH node stops working, the mobile sink must replace it with a functioning CH node, maintaining the network’s dependability and functionality.
The clustering framework enables the implementation of the large-scale IoUT-based IoT for environmental applications such as monitoring. In addition, it provides a scalable and expandable IoUT with easy energy management. Within the clusters, UCMs send their data directly to the CHs. Some CHs communicate directly to the BS; if the CHs are closed, then the far CHs communicate through the other CHs near the BS by multi-hop mode. Due to this approach, the general energy consumption computation is based on the data packet transmitted and the communication distance [36]. The energy consumption of each underwater node can be calculated as follows:
where and represent the electronic circuit and amplify the transmitted signal energies, respectively, k is data packets in bits, and the term is the acoustic signal attenuation due to absorption and scattering over distance d in the underwater environment. The power factor 2 is denoted for the spherical propagation model in the deep water scenario [37].
The calculation of UCM energy consumption depends on the initial energy of the underwater sensor node, which is given by Equation (2), and the energy consumed by the CH is given by Equation (3).
where represent the underwater node’s initial energy and the node’s standard energy consumption in the CH selection phase, respectively. The depends on the transmitted energy and the node’s energy consumption for the data aggregation process [37].
Since the IoUT is effectively used in acoustic communication, a common acoustic modem used for packet transmission in underwater communications is based on the SNR in dB associated with an acoustic wave at a receiver [37]. The following equation can give the SNR.
where represents the transmitted acoustic wave source level, is the transmission loss, denotes the noise level, and is the directivity index. The following equation can calculate the transmission loss over a distance d for a frequency f signal.
where α (f) is the absorption coefficient in dB/km. For deep water, α (f) can be calculated by the following equation:
For the IoUT, the communication range can be determined using the underwater communication model based on the acoustic SNR, underwater temperature, communication bandwidth, and packet size as shown below.
where Cr represents the communication range of UNs, B is the bandwidth of the communication channel, K is the Boltzmann constant, T is the underwater temperature, and k is the packet size. The Cr indicates whether communication is possible, which indicates the communication range between the UNs.
4. Energy Efficiency Based on SI Methods
The scattered distribution of underwater nodes throughout the underwater area causes energy consumption difficulties in heterogeneous IoUT networks due to varied distances between nodes and their proximity to the BS. Efficient energy management becomes critical to ensuring node energy level equilibrium [38]. While energy-efficient-based clustering approaches have been presented, their appropriateness for large-scale IoUT networks remains insufficient when relied upon. However, swarm algorithms may provide solutions for resolving energy consumption concerns within these expanding networks. The integration of swarm intelligence (SI) algorithms such as GA, ACO, ABC, and PSO is a promising answer to these difficulties. These algorithms provide adaptive decision-making processes, dynamically optimizing methane selection and adapting to changes in energy availability in real-time.
4.1. Generic Algorithm (GA)
GA enables the selection of CHs by representing the CH solutions as chromosomes and evaluating their fitness based on variables like energy consumption and distance. It begins with an initial population of chromosomes and uses the Euclidean formula to determine node distances. Each chromosome serves as a potential CH selection solution, with genes serving as CH node indices. For the IoUT, CH solutions that are chromosomes are viewed as probabilistic groupings that change as a result of the fitness function, mutation, and crossover operations. The best cluster is chosen based on the chromosome with the highest fitness, which takes into account elements like balancing a cluster head’s residual energy, the mean intra-cluster distance, and the distance of the CHs from the SBS [39,40]. As a result, the crossover probability, or crossover, is a crucial element in the crossover operator and is defined as such for random crossover by the following equation:
where k is rand between (0, 1), is the maximum number of genes, and is the minimum number of genes in the chromosome.
To limit the energy consumption in the IoUT, the selection operator, which comes after the crossover and mutation operators, chooses the chromosomes with the highest fitness or the nearly optimal solution among the new population and the chromosomes that are formed as the next generation for the clustering problem [41]. To balance the energy consumption of each cluster in this situation, the CHs are assigned to each cluster with the highest residual energy, the shortest mean intra-cluster distance, and the closest distance to the SBS. GA, however, may run into issues with convergence, parameter tweaking, communication model accuracy, boundary handling, scalability, and real-world validation. To implement successful CH selection in real-world IoUT deployments, several issues must be resolved [42].
4.2. Particle Swarm Optimization (PSO)
PSO optimizes CH selection by leveraging collective intelligence, similar to bird flocking behavior. In PSO, each particle’s location indicates a potential CH structure. The possible CHs are encoded by the position of each particle [43]. The evaluation is based on the objective function-based calculation of each particle’s fitness. Each particle maintains a record of its fitness score and best position configuration. The particle with the best personal best is regarded as the global best among the entire swarm. This is the optimal CH arrangement that the swarm could find. Each particle’s velocity and position are updated based on its present velocity, personal best, and world best [44]. Inertia, cognitive (personal best), and social (global best) variables are all included in the update equations. The velocity update equation for the particle k’s dimension i can be written as follows:
where is the updated velocity of particle k in dimension i at time t + 1, Ω is the inertia weight, and are cognitive and social learning factors, respectively, and are random values between 0 and 1, is the personal best position of particle k in dimension i at time t, is the global best position of particle k at time t, and is the current position of particle k in dimension i at time t.
Using the PSO algorithm enables the identification of an ideal or nearly ideal configuration of CHs in an UWSN while considering variables like energy efficiency, communication range, and other pertinent requirements [45]. However, it faces challenges related to convergence, parameter tuning, accurate modeling of communication conditions, and handling boundary conditions. Addressing these shortcomings is crucial to ensure an effective CH selection in IoUT networks.
4.3. Ant Colony Optimization (ACO)
ACO optimizes CH selection by replicating pheromone trails, taking influence from ant foraging behavior. In the ACO model, CH candidates who travel shorter distances and use less energy leave stronger pheromone trails are selected as a solution candidate. CHs are chosen based on the pheromone value assigned to each UN [46]. The CH is chosen from the UNs by using a probability threshold. Based on the ant’s weight and position, a probability threshold is generated for each node to be chosen as the cluster head. The following equation can be used to determine the probability:
where represents the weight associated with each node (N), is the pheromone concentration associated with each node for an iteration, controls the importance of the pheromone information in the decision-making process, and controls the importance of heuristic information (problem-specific knowledge) in the decision-making process [47].
The usage of the ACO algorithm by the IoUT for CH selection shows many encouraging results and performance factors. Notably, the algorithm prioritizes energy efficiency optimization and enables the balancing of energy efficiency and network coverage [48]. However, when the networks of the IoUT get increasingly sophisticated, the ACO starts to run into scaling problems. The selection of a CH is made more difficult by the requirement for precise modeling of underwater communication conditions [49].
4.4. Artificial Bee Colony (ABC)
ABC mimics bee foraging behavior to optimize CH selection. In ABC, the CH selection process uses the fitness evaluation to evaluate how well a specific CH configuration performs concerning predetermined criteria [50]. Depending on the particular aims and purposes of the IoUT network, the fitness function’s precise parameters may change [51]. For instance, a fitness function might be established to balance these parameters while minimizing energy use and maximizing network coverage. The fitness function of ABC can be represented as f(i) and is specified as follows:
where k is the scaling factor, Re(i) is the residual energies of nodes, is the node degree, which represents the number of connecting nodes to a particular node within its transmission range, and Eu is the Euclidian distance from node i to the sea surface station. The Re(i) is based on the underwater conditions’ impact on energy consumption [52].
In the IoUT networks, the ABC algorithm will provide a thorough method for CH selection. It considers various aspects to analyze and optimize CH setups, such as energy efficiency and underwater consequences [53]. ABC is suitable for tackling the issues of CH selection in IoUT applications because of its flexibility to adapt to the underwater environment and the possibilities for modification [54]. However, the effectiveness of the selected fitness function and the success of parameter adjustment for a given network requirement ultimately determine its performance.
4.5. Exploration and Exploitation Balancing in SI Methods
For optimization algorithms to effectively search the best solution related to the CH selection process, it is crucial to find a balance between exploration and exploitation. When examining the discussed methods, it is shown that GA uses fitness-based selection and genetic diversity. In PSO, particle movement and world-best placements are used. While the ACO relies on ant investigation and pheromone trail updates. The ABC used an employee and onlooker bees for evaluation and exploitation [55]. For CH selection optimization, the exact balance between exploration and exploitation may vary depending on the algorithm’s parameters. However, each algorithm seeks to achieve a balance to identify optimal or nearly optimal CH configurations.
5. Modelling and Problem Formulation
In our proposed method for the IoUT network, we focused a lot on selecting the most efficient CH to reduce energy usage and improve data transmission efficiency. After CH selection, nodes close to CH are arranged within each corresponding CH to form clusters. The potential CH is responsible for supervising the data transfer within their designated clusters. This aggregation provides efficient local data management. The sink nodes are strategically located on the ocean floor and work closely with the underwater data center. Data collection and processing of sensed data are made possible through this integration. After processing, the data are sent to ground stations for further evaluation and action.
The clustering-based IoUT system model is shown in Figure 1. The IoUT underwater nodes are positioned in the 2-dimensional underwater environment. The CH selection process is based on different factors: the residual node energies, the underwater impacts, the node positions, and depth. The coordinate system (x, y) serves as the definition of the 2D underwater environment space. Within this given area, underwater nodes are distributed randomly. The IoUT network clustering approach must efficiently select the optimum number of CHs to reduce energy consumption and increase the network lifetime.
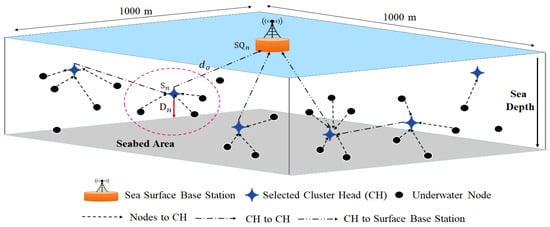
Figure 1.
IoUT CH selection process model.
Several assumptions are made to streamline the modeling and analysis:
- ▪
- The precise position data of surface sea stations and underwater nodes are accessible.
- ▪
- The initial energy levels of UNs are heterogeneous and constant, but there are no energy restrictions on sink nodes. Each node can store locally updated records of recent communications.
- ▪
- Underwater nodes within the cluster only send data to their corresponding CH, passing the packets to the surface sea station.
By applying the SI process such as the ABC algorithm for CH selection within this IoUT network architecture, the proposed approach aims to reduce energy consumption and enhance data transmission efficiency in the context of the IoUT within challenging underwater environments.
5.1. Energy Efficient Heterogeneous CH Selection Process
After defining each of the IoUT, swarm intelligence algorithms, and underwater environment parameters, the selection of CHs is based on the connectivity to the surface water station and fitness function in our suggested clustering approach [55]. To ensure efficient communication and data transfer, the fitness function depends on the quality or fitness of a solution in the context of the optimization issue, energy consumption, and residual energy values of the IoUT. The following equation serves as a representation of the fitness functions [30].
where , , and are the individual fitness criteria for the fitness values of the solution (CH configuration). Each of the functions measures a different aspect of the solution’s quality. , , are weight coefficients or scaling factors that can be introduced for each fitness criterion to adjust their relative importance in the overall fitness evaluation [30,55]. First, the process calculates the residual energy Re(i) of every node in the IoUT network using the following equation.
where = Ie(i) represents the starting energy of the ith IoUT and Ce(i) is the current energy level.
Re(i) = Ie(i) − Ce(i)
The average residual energy of all nodes is calculated after each node’s residual energy calculation, and the average energy of all nodes is then compared to each node’s residual energy. A node will be skipped for the current round to select a CH as the first investigation if its current energy is lower than the average energy [30,56]. The formula for calculating a node’s overall transmit and receive energies is as follows:
where represents the number of transmitted bits by node, is the received bits, and and are the transmission energy and reception, respectively.
By letting Xij represent the position (solution) of the ith food source in the jth dimension of the search space, the ABC function can produce an initial population of food sources (solutions) at random inside the search space [56]. The aim function is to determine each food source’s fitness value depending on the solution to the optimization problem. By allowing f (Xi) to stand in for the suitability (quality) of the ith food source, this function assesses how successfully the solution Xi resolves the issue.
ABC is a three-phase approach that employs bees to investigate and enhance solutions by selecting a food source to be improved. The following can be used to generate new candidate solutions by perturbing the selected solution [53,57].
where j is randomly chosen and ϕ is a random number in the range [−1, 1].
Vi = Xi + ϕ × (Xi − Xj)
The second phase is onlooker bees, which select food sources probabilistically based on fitness. The probability of selecting a food source i proportional to its fitness can be given by the following [53,57]:
where N is the population size. Finally, the third phase is scout bees, who identify abandoned food sources (solutions). Scout bees are responsible for locating sources of unsuitable CHs and replacing them with new CHs as a candidate solution. This determines the fitness value of each potential solution related to selected UNs as candidates as a CH using the objective function f(xi). If a potential solution is abandoned, if it has not been improved after a predetermined number of rounds, or if it has a low fitness value, a scout bee is used to develop a new candidate solution.
To find an optimal or nearly optimal solution to an optimization problem, bees investigate and refine potential solutions using the ABC algorithm, which is captured by these equations and phases [57]. Different fitness functions and issue formulations will be used depending on how the algorithm is used. The fitness of a solution, a set of chosen CHs for the network nodes, serves as the foundation for the optimization technique. Several criteria are used in the provided approach to evaluate fitness. These criteria are as follows:
- ▪
- Residual Energy: This element promotes CH choice for nodes with more residual energy. The payout increases with a node’s leftover energy level. A function is used to calculate it.
- ▪
- Signal Quality: This characteristic promotes CH selection of better signal-quality nodes. The reward increases with a node’s signal quality.
- ▪
- Motion: CH selection for nodes with minimal motion is encouraged by this factor. The payout increases when a node’s speed decreases (signifying less motion).
- ▪
- Depth: This element promotes the use of CHs for nodes located at shallower depths. The payout increases as a node’s depth decreases.
Both cluster heads and non-cluster heads are taken into account when calculating the total IoUT energy consumption depending on the chosen CHs [30,58]. The following is the precise formula for this calculation:
where is the number of cluster heads, is the energy consumption for a cluster head, is the number of non-cluster heads, and is the energy consumption for a non-cluster head. By altering solutions as sets of CHs, following the fitness values, the ABC algorithm iteratively optimizes the selection of cluster heads [58]. Better-fitting solutions are more likely to be chosen or changed.
Overall, while considering variables including residual energy, signal quality, node motion, and depth, the optimization procedure seeks to identify a collection of cluster heads that minimizes energy usage. The needs of challenges and features of the underwater sensor network would need to be taken into consideration when defining the specific formulas for merging these parameters into fitness ratings and for calculating underwater impacts. Remembering that these methods are used to choose the CHs at the start of the selection process, the CHs are evaluated only based on the amount of energy left over without further consideration of their dynamic efficiency.
5.2. Q-Learning for CH Selection Optimization
Our problem definition aims to reduce the overall IoUT network energy consumption. The goal is to determine an optimum number of selected CHs to efficiently hand the data exchanges to the surface sea station while continuously checking the status of selected CH to decide the case of leak energies, depending on the conditions of CH residual energies, depths, and signal quality [59]. The process of CH selection without considering the mentioned conditions could lead to the deterioration of the CH selection process due to the changing conditions of the underwater environment. Therefore, it is important to take the mentioned considerations into account during the selection process [60].
The Q-learning method as shown in Figure 2 can improve the CH selection process for ABC optimization by dynamically building incentive functions. With the help of Q-learning, it is possible to repeatedly gain information from the environmental input until the best course of action is identified. In this instance, it is suitable for the shifting underwater environment [60]. We characterized the nodes as (s, a, r), which represent the direct reward, the node action, and the sensor node status, respectively.
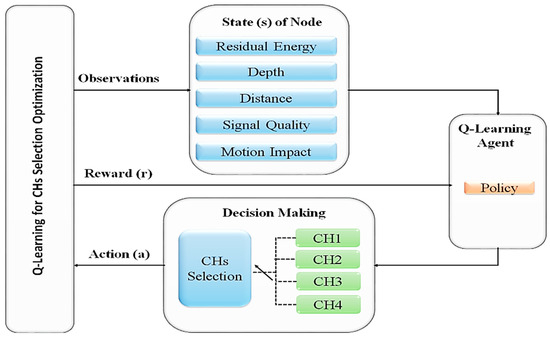
Figure 2.
Dynamic CH selection based on the Q-learning approach.
Depending on the decisions taken, the best CH can be chosen. The agent moves from state si to state sj by performing action ai from strategy. The assessment of an agent’s behavior is called reward. The reward is known as the ( is the sum of the direct reward plus discounted future rewards, as stated below [61].
where denotes the current reward. The future reward’s discount factor is ∈ (0, 1). is the likelihood of an agent in state si leaving state sj. After implementing an optimal policy, the ideal value for a state can be determined. Additionally, it is possible to identify at least one optimal method using the Bellman equation [61]. The policy’s definition of the ideal value is as follows:
The predicted reward earned by carrying out action aj following the best course of action at state si is Q* (si, ai). As a result, the ideal course of action is as follows:
where represents the calculations of the Q-value for each potential action in the current state, enabling the selection of an action with the highest Q-value. The state of random action is chosen when it is less than the exploration rate, and it is always selected between 0 and 1. The agent decides to explore by performing a random action if this random integer is lower than the range within [0, ϵ]. Otherwise, if the outcome is greater than or equal to it, the agent takes advantage of its present knowledge by picking the course of action with the highest Q-value [62].
Our suggested solution uses Q-learning to optimize the ABC process while considering and dynamically checking the CH conditions. To capture the states of nodes and actions of choosing CHs, the Q-table stores the Q-values for state-action pairings. The following equations update the Q-learning during each iteration in both the employed and onlooker bee phases [63].
The current Q-value for the chosen state-action pair is represented by (next state (j)). The (next state (j)) can be described by the Q (current node, neighbor node, next state (current node)). The learning rate regulates how much the new information affects the Q-value. The discount factor weighs potential rewards in priority [63]. The immediate benefit from the chosen action is the reward. is the highest Q-value among potential responses in the upcoming state. Then, the maximum amount of the current Q can provide the best-chosen action.
By iteratively updating the Q-values based on observed rewards and making decisions to maximize expected rewards, Equations (21) and (23) identify an optimal strategy for selecting the best CHs. The following are the fitness rewards that were utilized to optimize CH selection,
where is a residual energy reward, is depth reward, is motion reward, and is a signal quality reward.
Using the aforementioned equations, this improved ABC by Q-learning function assesses the fitness of a CH selection configuration based on several parameters in computing the fitness for each potentially selected node and combining them to create an overall fitness score. The following variables are taken into account: residual energy (, signal quality (, motion (, and depth (. The sum of these rewards determines the fitness of each node, and the sum of the fitness values for all nodes determines the overall fitness of the CH selection configuration [64]. In addition to providing details on the chosen CHs, energy usage, and underwater effects, this tool evaluates the effectiveness of a CH selection strategy.
6. The Methodology and Proposed Solution
To develop solutions for an optimum CH selection mechanism to ensure energy efficiency in IoUT, an energy-efficient CH selection scheme is provided by improving the process of the ABC algorithm by Q-learning, which allows for an effective selection of the best number of CHs for IoUT to ensure stable and reliable IoUT communications. We set an IoUT network in 2D. The prophase scheme allows us to find the best CHs to be served in the network for the nodes based on optimizing the process of an ABC fitness function by Q-learning to learn and update the best solution results during CH selection. Figure 3 describes the proposed energy-efficient CH selection approach.
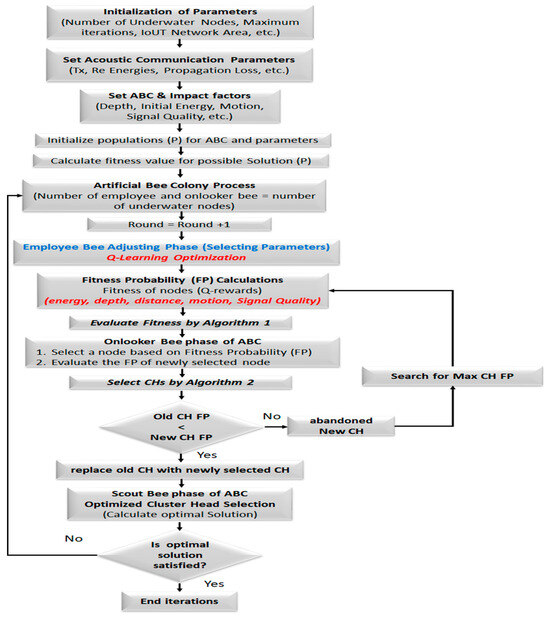
Figure 3.
Improved ABC-based QL optimized CH selection process.
The food source position represents the possible solutions to the optimized problem in the ABC algorithm. In contrast, the amount of food source nectar represents the fitness related to the solution. The improved ABC by Q-learning hybrid is based on how to find the best solutions according to the fitness function evaluation [64]. Algorithm 1 provides and process of the fitness of the best ABC states. The ABC evolves the calculations of its phases by performing a selection in the employee bee and onlooker phases. The Q-table is then initialized with the best state of employee and onlooker bees to the maximum Q-value for the current node that is likely to be selected as a CH.
| Algorithm 1 Evaluated Fitness Function |
|
The Q-learning method selects the best node action for each state. The Q-value is updated using the Q-learning Equations (21) and (23), considering the reward and the maximum Q-value for the following state. The next status of the underwater node will indicate if it will be selected as a CH based on the action selected, and the process is repeated until convergence or the maximum number of iterations is reached. Throughout the process, the proposed technique will update the CHs according to the next best state related to the CH action.
To optimize CH selection in IoUT, the improved ABC based on the Q-learning technique is described in the suggested algorithm. It demonstrates how the ABC and Q-learning components work together to improve the CH selection solution iteratively until an ideal configuration is reached [65]. Additionally, the dynamic CH selection procedure improves the flexibility of adjusting the relative relevance or weightage provided to various fitness components, such as residual energy, signal quality, motion, and depth, when evaluating the fitness of nodes for CH selection. The Q-learning optimization-based dynamic CH selection is shown in Algorithm 2.
| Algorithm 2 Q-learning Optimization based Dynamic CH Selection |
|
Based on learned Q-values, the hybrid ABC-Q-learning optimization enables dynamic modifications of the relative weighting of fitness components such as residual energy, signal quality, motion, and depth. Applying a dynamic CH selection based on these fitness components allows for this adaptability. As the Q-value rises, the dynamic CH modifications will be made, emphasizing the importance of the relevant fitness component in the total fitness assessment [65].
7. Simulation Scenario and Parameters
Given an underwater environment for the IoUT network CH selection optimization problem, the scenario where multiple underwater nodes need to efficiently choose CHs while optimizing various constraints is based on the simulation model in Figure 3. This optimization challenge aims to ensure effective data transmission and network management within the underwater environment, considering underwater communication’s specific characteristics and limitations.
We consider the IoUT network area in a 2D space in a square region (X × Y), where the IoUT nodes are deployed. These nodes need to select CHs strategically to ensure efficient data transfer. For CH selection optimization, the selection process should consider factors such as proximity to other nodes, energy efficiency possible IoUT underwater constraints related to the maximum communication range, energy limitations, and possibly other environmental constraints unique to underwater communication. We assume that the IoUT consists of one surface base station at the center of the (X × Y) region, which can be communicated with different numbers of underwater nodes with different residual energies and depths. By optimizing the CH dynamic selection based on impact factors such as residual energy , depth , motion (), and signal quality () in addition to the distance between the candidate CH and the surface base station (, energy consumption while ensuring the successful operation of the IoUT network can be minimized.
In the given scenario, the nodes are underwater at varying depths and are exposed to currents and potential obstacles. The selection process for the cluster head takes into account the previously mentioned factors, including distance from other underwater nodes and energy efficiency. The ABC algorithm is used and enhanced by incorporating Q-learning, an RL technique, to guide the CH selection process. Q-learning helps to model and adapt to the dynamic underwater environment. The algorithm uses a Q-table to learn and update the quality of CH candidates based on their ability to efficiently manage data transfer, minimize energy consumption, and navigate through underwater challenges.
Since the environment of the IoUT presents unique limitations and challenges, such as limited communication range, power limitations due to battery capacity, and potential interference from underwater obstacles and environmental conditions, Q-learning helps the algorithm to adapt to these constraints and optimize the CH selection accordingly, which achieves the overall goal of this scenario of minimizing the energy consumption of the underwater network while ensuring mission success.
During the process of CH selection, the algorithm, guided by Q-learning, iteratively optimizes the selection of CHs. The algorithm learns and adapts through multiple iterations, eventually converging toward an optimized set of CHs that increases network efficiency and minimizes energy expenditure. In this scenario, the synergy between the ABC algorithm and Q-learning enables the IoUT network to select CHs efficiently, making it a formidable tool for underwater data collection and communications. The simulation results presented in this study for evaluating the effectiveness of the proposed strategy are based on simulation scenario settings according to the criteria specified in Table 2.

Table 2.
Simulation parameters.
The following assumptions underlie the energy IoUT network model: First, the sensor nodes are dispersed randomly over the sea floor in the shape of a two-dimensional plane, with no regard for a specific distribution structure. Second, following deployment, the UNs are stationary, assuming that there is relative movement due to the dynamics of the undersea environment’s velocity. Third, the UNs can only communicate data to the node heads and not directly to the SBS.
8. Evaluation Results and Discussion
The simulations make a comparison for the following evaluations.
- ▪
- Evaluation of the experiment of GA, ABC, PSO, and ACO swarm intelligence methods on the CH selection process.
- ▪
- Evaluation of the performance of improved ABC by Q-learning for CH selection optimization.
- ▪
- Analysis of the proposed algorithm performance in case of increasing the number of underwater nodes.
The testing and evaluation experiments were performed to assess the validity and effectiveness of the proposed methods by using MATLAB 2020 as follows.
8.1. Performance of Swarm Algorithms
The results of swarm intelligence algorithms for CH selection in the IoUT network with 50 underwater nodes and several simulated iterations of 200, 400, 600, 800, and 1000 and the data shown in Table 3 provide a comparison of how each optimization approach performs regarding CH selection.

Table 3.
Numerical performance comparison between GA, ACO, PSO, and ABC algorithms.
In the case of 200 iterations, the performance reveals that the PSO algorithm exhibits the highest mean performance and stability, making it a good contender for CH selection in IoUT networks. While choosing a sizable number of CHs, the ACO algorithm performs with a lower mean and higher variability. With reasonable CH selection ratios, the ABC and GA algorithms provide a balanced performance. The PSO method is notable for its average performance. In contrast, the ABC algorithm provides stability and a fair CH selection ratio. While PSO performs well, ABC also does well. However, PSO’s greater mean performance and lower standard deviation imply that it is more appropriate for the specified CH selection optimization job in the context of IoUT networks with 50 nodes and 200 iterations.
In the case of 400 iterations, the ABC algorithm maintains its excellent mean performance and stability during iteration increase. It keeps up its good work and chooses a respectable number of CHs. ACO algorithm, which has a high CH selection ratio, continues to be reliable. Out of all the algorithms, it chooses the most CHs. With the highest mean performance and smallest standard deviation, the PSO algorithm continues to be effective in CH selection. It selects a large number of CHs. The average mean performance of the GA method is maintained, although it displays more variability. Additionally, it chooses a sizable number of CHs. PSO is still a great candidate if energy stability and efficiency are important factors.
ACO is appropriate if increasing CHs is crucial. While GA may be utilized in situations when a greater number of CHs are needed, ABC offers a balanced approach. On the other hand, the ABC keeps its mean performance high and its standard deviation low, demonstrating both stability and effectiveness in CH selection. With a CH selection ratio of 23%, it chooses a manageable number of CHs that can aid in striking a balance between network coverage and energy efficiency. Through multiple iterations, ABC continuously outperforms, showing its dependability in CH selection. ABC can be a good option since it can provide stability and consistent performance while regulating cluster sizes, allowing for a compromise between CH selection efficiency, stability, and a moderate number of CHs.
In the case of 600 iterations, the PSO algorithm shows good performance having the highest mean performance and steady behavior. Additionally, it keeps a moderate CH selection ratio, which is compatible with controlled cluster sizes and energy efficiency. With a moderate mean performance, ABC exhibits consistent performance. To maximize energy efficiency and manage cluster sizes, it chooses a small number of CHs. Continued use of ACO and GA algorithms that choose many CHs may lead to smaller clusters but more intra-cluster communication. ABC consistently picks just about 18% of CHs. This has the advantage of lowering the danger of cluster congestion by avoiding extensive intra-cluster communication and limiting cluster sizes. Despite its cautious CH choice, ABC retains a good mean performance equal to 0.81. It successfully chooses CHs while striking a decent compromise between network performance and cluster size control, as seen by this. ABC stands out for its cautious CH selection, balanced performance, stability, and dependability in the specific context of the network requirement to regulate cluster sizes and avoid communication difficulties. It is ideal for situations where managing cluster sizes is a crucial factor.
In the case of 800 iterations, ABC retains a high mean performance, demonstrating persistent effectiveness. The average performance of ACO is still very stable. However, it is less than that of other algorithms. Among the algorithms, PSO maintains the greatest mean performance. GA continues to perform at a moderate mean level. The PSO algorithm emerges as the top performer with the highest mean performance and the steadiest behavior. Additionally, it keeps a cautious CH selection with a 15.98% ratio, which aligns with energy efficiency and limited cluster sizes. With an average mean performance, ABC exhibits consistent performance. And because of the controlled cluster sizes and the average amount of CHs chosen with a 22% CH selection ratio, it is good for energy efficiency. Although there is a possibility of smaller clusters and more intra-cluster communication, ACO and GA algorithms continue to choose many CHs. It is possible that this conflicts with the directive to prevent intense intra-cluster communication. According to the most recent data, PSO and ABC are still excellent choices for CH selection optimization. The mean performance is where PSO thrives, whereas ABC strikes a balance between performance and prudent CH selection.
In the case of 1000 iterations, PSO performs better by constantly choosing a small number of CHs with a 15.98% selection ratio, which is in line with energy efficiency and managed cluster sizes. However, ABC has a consistent performance with a reasonable mean performance. Concerning energy efficiency and managed cluster sizes, it chooses many CHs with a 20% selection ratio. It can balance network performance, cluster size control, and reliability. ACO continues to select a reasonable number of CHs and perform at a lower mean performance level. However, it is more variable than PSO and ABC. GA chooses a lot of CHs with a 44% selection ratio, which can result in smaller clusters and more communication within them.
Overall, PSO and ABC are both still excellent choices for CH selection. While ABC balances performance and efficient CH selection, PSO performs better with low iterations. Although PSO gives better average performance and conservative CH selection in mean iterations, the ABC approach is more moderate. It performs better, especially at increasing iterations in scenarios where the trade-off between performance and control of group size is important.
Figure 4 shows the performance of swarm intelligence algorithms regarding the number of CH selections in case the number of underwater nodes increases from 50 to 250. It shows that when managing cluster sizes, ABC frequently beats other methods. Compared to PSO, ABC tends to choose fewer CHs. This cautious method of choosing a CH fits well with the desire to prevent intense intra-cluster communication. The possibility of congestion within clusters can be decreased with smaller clusters, making ABC a preferable option for this particular requirement. PSO may outperform ABC in terms of mean performance. However, ABC consistently achieves a modest mean performance that is frequently adequate for real-world network operations. ABC focuses on striking a balance between controlled cluster sizes and network performance. It aims to provide a stable and reliable network, and this balance can be more aligned with the requirements compared to PSO’s potentially higher but less controlled performance.
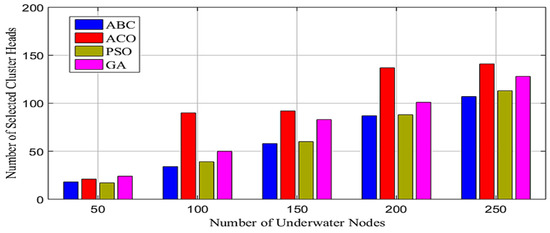
Figure 4.
Performance of swarm algorithms in selecting CHs.
Additionally, ABC is known for being reliable and performing well across iterations. Network stability is essential for reliable communication to continue in unexpected underwater environments. The network’s stability in performance is a result of ABC. The network is kept operational even in the worst-case scenarios thanks to ABC’s reasonable minimum performance level maintenance. This dependability is crucial for mission-critical applications since network outages or performance deterioration might have negative effects.
8.2. Performance of Improved ABC-QL Algorithm
This section discusses the performance evaluation results of the improved ABC algorithm by improving Q-learning compared to the classical ABC algorithm. Through the analysis, the numerical performance of the proposed algorithm was extracted in addition to other metrics, such as the number of live and dead nodes, the number of best CH selections, and the total energy consumption. They consider that all underwater nodes are stationary or in a state of precise movement depending on the vagaries of the underwater environment. The results were drawn in two scenarios: the first is a general evaluation of the proposed algorithm, and the second scenario is an evaluation based on the density of underwater nodes and their impact on the performance of the proposed algorithm.
8.2.1. Numerical and General Case Evaluation
We evaluate the proposed algorithm with 80 underwater nodes in different iterations from 200 to 1000. The underwater nodes are randomly distributed in an underwater environment with a max depth of 50 m. The packet size is 1024 bits. Distances between modes are 50 m. The fractions of residual energy levels are given between 0.7, 0.9, 0.5, and 0.8, with 0.5 for the lowest and 0.9 for the highest level. According to the given simulation settings, the results are obtained in Table 4, and Figure 5, Figure 6 and Figure 7 show the evaluated improved ABC algorithm by Q-learning optimization compared to conventional ABC as follows.

Table 4.
Numerical results for improved ABC-QL and conventional ABC algorithms.
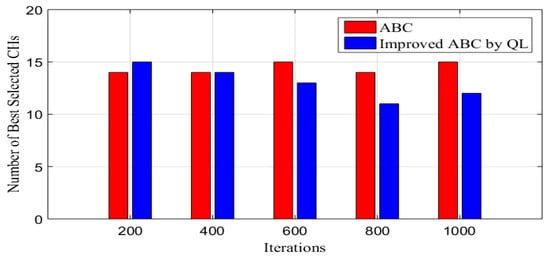
Figure 5.
Performance of improved ABC-QL vs. conventional ABC on the CH selection process.
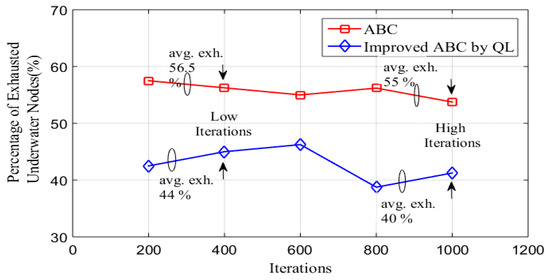
Figure 6.
Number of dead nodes for improved ABC-QL vs. conventional ABC.
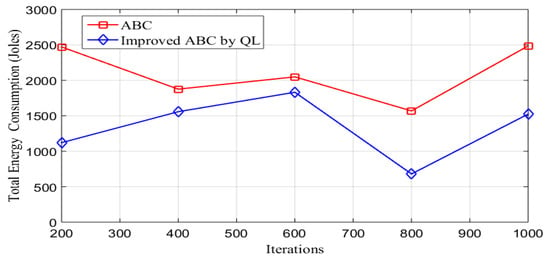
Figure 7.
The energy efficiency performance of improved ABC-QL vs. conventional ABC.
As shown in Table 4. In terms of standard deviation, min and mean fitness values, results show that both classical ABC and improved ABC-QL achieved close min fitness values around 0.03 to 0.05. However, the improved ABC-QL is slightly higher compared to conventional ABC in low iterations, 200, and high iterations, 1000. This means that improved ABC-QL can find solutions with better fitness, indicating a potential advantage in selecting CHs that improve network performance. The mean fitness values for conventional ABC and improved ABC-QL are quite close. This indicates that, on average, both algorithms perform similarly in selecting CHs with reasonable fitness values. However, in the higher iterations 600, 800, and 1000, improved ABC-QL has a slightly higher mean fitness value between 53, 55, and 49 compared to conventional ABC with values of 50, 53, and 48, respectively. This indicates that, on average, improved ABC-QL tends to select CHs with slightly better fitness values, potentially improving network performance. For standard deviation, improved ABC-QL exhibits slightly lower values compared to conventional ABC, which means that it has more consistent performance in the quality of selected CHs.
By considering the CH selection ratios in Table 4 and observing the performance in terms of the number of the best selected CHs in Figure 5, the results show that the improved ABC-QL selects a higher number of best CHs compared to conventional ABC with low iterations. The ABC-QL selects 18% of the total number of underwater nodes to serve as CHs according to adjusted selection parameters. However, it remains low in higher iterations according to optimization in selecting the CH with a stable clustering size. It gives the best CH selection ratio decreased to 13.5% in a high iteration based on the optimization achieved, which means it has been fine-tuned to select the best balance between exploration and exploitation.
The Q-learning enables adjusting the exploration and exploitation parameters based on the underwater nodes’ state. It also helps to explore a broader solution space early in the process to identify potential CHs while exploiting promising solutions and convergence quickly. This implies that improved ABC-QL may offer better coverage or more efficient CH selection, potentially improving network performance. According to these metrics, improved ABC-QL enables the maintenance of a better average best selection cost lower than conventional ABC, which can benefit energy-efficient CH selection.
Figure 6 displays the efficiency of the improved ABC-QL algorithm in terms of the exhausted (dead) underwater nodes. The results show that the improved ABC-QL outperforms the conventional ABC by having significantly fewer average exhausted (avg. exh.) nodes than exhausted nodes by conventional ABC in the initial 200 and 400 iterations, namely 18.5%. This demonstrates that a more stable network setup was initially attained via an enhanced ABC-QL. While the upgraded ABC-QL continues to improve slightly, the conventional ABC performed marginally better with fewer dead nodes through iterations up to 600. However, despite the low number of dead nodes, there was still a big disparity in how well the two methods performed. Improved ABC-QL reduced the number of exhausted nodes in iterations 800 and 1000 by 27.3%, respectively.
These results show that modified ABC-QL performed better regarding the number of exhausted nodes in the initial iterations, demonstrating its capacity to construct a more stable network configuration. Additionally, it offers superior network stability and resource utilization for CH selection optimization in IoUT applications, especially in the early and later iterations. According to the results, improved ABC-QL gives more advantages in configuring a stable IoUT network. It focused on early iterations while adjusting algorithm parameters by incorporating heuristics and prioritizing stability in the initial stages. It can also adapt over time by dynamically re-adjusting parameters to ensure its advantages are maintained and built upon as the optimization process progresses.
The performance of the proposed algorithm’s energy consumption is reviewed in Figure 7. The results demonstrate that the enhanced ABC-QL uses substantially less energy between 1121 and 1524 Joules than the conventional ABC, which uses 2471 to 2485 Joules between 200 and 1000 iterations. As a crucial characteristic for any network, this marked drop in energy consumption shows that improved ABC-QL has a clear energy efficiency advantage, increasing the network lifetime and reducing energy costs. The traditional ABC algorithm shows relatively stable energy consumption levels, which indicates that the algorithm has reached a certain level of convergence in terms of energy consumption; it gives a −0.56% convergence percentage in all iterations. However, ABC-QL showed a significant reduction in energy consumption, giving −36.01% convergence, indicating that it continues converging more energy-efficient solutions with iterations.
When comparing results from all iterations, modified ABC-QL consistently achieved considerably lower energy usage than conventional ABC, indicating a clear benefit in terms of energy efficiency. This is a crucial consideration in IoUT applications where energy supplies are scarce. As demonstrated in Table 4, the enhanced ABC-QL also tended to select CHs with marginally higher mean fitness values. Occasionally, conventional ABC chose more of the best CHs, indicating better coverage or more effective CH selection in some iterations. This benefit, however, was not present in all iterations. A lower CH selection ratio regularly displayed by the enhanced ABC-QL suggests that it was more discriminating when selecting CHs, which can help with energy conservation and network optimization by lowering the number of dead nodes. The improved ABC-QL is also preferred for CH selection in IoUT applications due to its obvious benefit in energy efficiency, which is essential for prolonging network lifetime, keeping individual nodes active for a long time, and lowering operational expenses.
The modified ABC-QL algorithm outperforms standard ABC in terms of energy efficiency in underwater conditions. The incorporation of the Q-learning technique is crucial to its success. Q-learning enables ABC-QL to establish the best balance between exploration and exploitation, guaranteeing that it rapidly converges on energy-efficient solutions. This dynamic adaptation and iterative learning process improves its energy-saving capacities greatly. Another notable feature is ABC-QL’s ability to pick energy-efficient CHs, which reduces energy usage during the selection process. Notably, this improved energy efficiency is not a one-time event; ABC-QL continues to learn and adapt, guaranteeing that its higher performance endures in the face of changing environmental conditions. As a result, ABC-QL increases network lifetime, reduces operational expenses, and shows great promise for sustaining IoT networks in resource-limited underwater environments.
Overall, the improved ABC-QL surpasses the conventional ABC in several important domains, including selection cost, fitness values, standard deviation, the number of best-selected CHs, and energy consumption. These results show that increased ABC-QL enhances CH selection effectiveness, especially when network longevity and energy efficiency are priorities.
8.2.2. Evaluation Based on Underwater Node Density
The performance of the enhanced ABC-QL method is assessed in this section based on the density of the underwater nodes. The results show how more underwater nodes affect the performance of both the enhanced ABC-QL and traditional ABC algorithms. The simulated IoUT network scenarios vary between 50 and 250 nodes, which evaluates the impact of various network sizes on the proposed algorithm.
Figure 8 shows the percentage of exhausted underwater nodes, which indicates the number of dead nodes concerning network size for both improved ABC-QL and conventional ABC. Both algorithms see an increase in dead nodes as the network size grows. However, improved ABC-QL consistently shows fewer exhausted nodes over various network sizes than conventional ABC. This indicates that compared to conventional ABC, improved ABC-QL tends to deliver a more optimized CH selection, resulting in a more stable network with fewer dead nodes. With 50 nodes in a small IoUT network, both algorithms have a close number of exhausted nodes. However, as the network size grows, the modified ABC-QL continues to perform better than conventional ABC, with a 33% reduction in dead nodes.
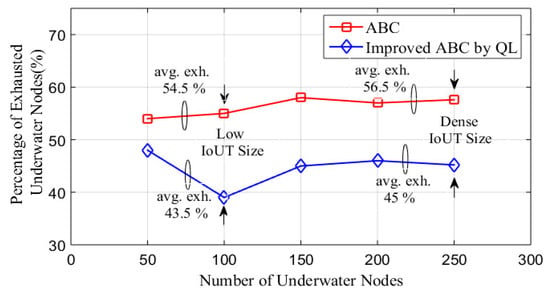
Figure 8.
Performance underwater nodes’ lifetime based on network size variation.
In the proposed algorithm, the use of Q-learning enables a more efficient exploration of different CH selection options. It can focus on actions that have yielded better results regarding fewer exhausted nodes and avoid actions that led to higher dead node counts. The proposed algorithm can adapt and learn from past iterations, improving network stability. The algorithm becomes more adept at choosing CHs that maintain network connectivity and minimize node failures.
The proposed method to improve ABC makes better use of Q-learning to examine different CH selection alternatives. They can focus on measures that produce better results regarding fewer exhausted nodes and avoid those with more exhaustion. This indicates that the ability of the proposed method to adapt and learn from previous iterations helps to improve network stability. The improved ABC algorithm is better at selecting CHs that maintain network connectivity and reduce node failure.
According to Figure 9, the number of top CH selections concerning network size is identical for both improved ABC-QL and conventional ABC. The number of best CH selections increases for both algorithms as the network size grows. Comparing improved ABC-QL with conventional ABC, the number of best CH selections is typically significantly lower. This suggests that the improved ABC-QL may be more sensitive when selecting CHs, concentrating on the most stable nodes to be the best CHs. The improvement in ABC-QL’s selectivity is probably due to the inclusion of Q-learning. The algorithm can learn and modify its CH selection method using Q-learning, emphasizing choosing nodes with the greatest potential to improve network performance.
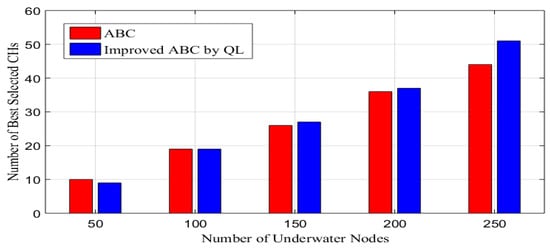
Figure 9.
Performance of the CH selection process based on network size variation.
The more effective and selective CH selection procedure of improved ABC-QL is a good indicator of the improvement by Q-learning. By taking into account previous nodes’ experiences and the state of the network, the proposed algorithm can better choose which nodes to choose as CHs. As a result of this selection, CHs are distributed more optimally, potentially enhancing network efficiency and stability while reducing the unwanted increase in the number of selected CHs. The integration of Q-learning explains the ability of improved ABC-QL to be more selective when selecting CHs compared with conventional ABC.
Using the Q-learning approach allows us to learn from previous iterations and make more informed CH selection decisions. It focuses on nodes that contribute the most to network performance and gives the proposed algorithm the capacity to change its CH selection method depending on historical data and network conditions, resulting in a more optimal CH distribution. This selective strategy may result in improved network stability and efficiency because it reduces the number of selected CHs while maintaining a strong network.
Figure 10 illustrates the energy consumption results, which reveal some interesting behaviors between improved ABC-QL and conventional ABC across various network sizes. Improved ABC-QL consistently shows decreased energy consumption in cases with smaller network sizes of 50 and 100 nodes. This indicates that improved ABC-QL has greater energy efficiency in these smaller-scale scenarios. As the network grows to 150 nodes, the improved ABC-QL retains an energy-efficient profile, consuming 3500 Joules versus 4000 Joules for conventional ABC. Incorporating Q-learning in improved ABC-QL most certainly adds to this efficiency by selecting CHs with the lowest energy consumption.
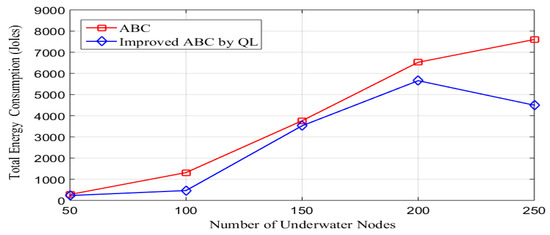
Figure 10.
Energy efficiency performance based on network size variation.
In the case of 200 nodes, improved ABC-QL consumes 5800 Joules, which is somewhat less than the conventional ABC consumption of 6500 Joules. Remarkably, with 250 nodes, the improved ABC-QL regains its energy efficiency advantage, consuming 4500 Joules compared to 7900 Joules for conventional ABC. These results indicate that the improved ABC-QL can adapt to greater network sizes in this scenario. The introduction of Q-learning into improved ABC-QL is most likely responsible for its improved energy efficiency in smaller network sizes.
Q-learning enables the ABC algorithm to learn and change its CH selection method, emphasizing the selection of energy-efficient nodes as CHs. With the aid of Q-learning, the ABC algorithm can adapt to changes in network conditions. It can modify its CH selection approach to maintain performance in response to network size or topology changes. A more effective CH selection process is achieved by integrating Q-learning into the ABC algorithm, which adds adaptive learning and optimization capabilities. The major advancement resides in the algorithm’s capacity to keep as many active nodes as feasible for a long time, contributing to network stability and energy efficiency.
Compared to the conventional ABC algorithm, the improved ABC with Q-learning consistently outperforms it regarding CH selection, network lifetime, and total network energy consumption. This makes it especially valuable in dynamic and evolving network environments. Overall, integrating Q-learning with the ABC algorithm for CH selection optimization in IoUT shows promise in improving energy efficiency, network stability, and adaptability. This approach can be a valuable tool for optimizing underwater communication networks, especially in scenarios with limited energy resources and dynamic conditions.
9. Conclusions
This study proposes an enhanced ABC algorithm for CH selection for IoUT using Q-learning optimization. This study’s inquiry into the ABC algorithm’s Q-learning integration for CH selection optimization in the IoUT has produced insightful information and noteworthy results. The benefits and factors to be considered with this technique are thoroughly understood thanks to the performance evaluation across various network sizes and circumstances. The simulations conducted for this study demonstrate that ABC can perform better than other well-known SI algorithms for CH selection for IoUT. We contribute to using a Q-learning strategy to improve energy efficiency by optimizing the ABC in the CH selection process. This study improved the process of the ABC algorithm by using Q-learning, which shows that it can dramatically increase energy efficiency, particularly in smaller network sizes. The evaluation results demonstrate the outstanding performance of the modified ABC algorithm through the Q-learning approach in CH selection by 10% at a low network size and 5.5% at a higher network size in addition to giving an improvement in energy efficiency by 56.39% at a low network size and 23.53% at a higher network size when compared to the conventional ABC algorithm.
The modified ABC algorithm reduces energy usage and optimizes the CH selection to demonstrate a better level of selectivity, emphasizing nodes that best improve network performance. This selectivity is ascribed to the Q-learning algorithm’s adaptive learning capacity, enabling the algorithm to select CHs with knowledge. The proposed ABC-QL CH selection approach increases network stability and energy efficiency. It helps maintain improved network connectivity and dependability by reducing the number of dead nodes. While improved ABC-QL performs well in smaller network sizes, performance trends in larger networks are more complex. However, adjusting more ABC-QL parameters might prove advantageous in particular circumstances, showing the significance of considering the network size when choosing the optimization strategy. Our next research effort will concentrate on improving intra-cluster communications following CH selection with an enhanced stable selection protocol for clustered heteronomous IoUT networks.
According to this study, future research should look into ways to make improved ABC-QL more adaptable to larger network sizes while preserving its advantages in terms of energy efficiency. We advise developing and researching methods to improve the scalability of the ABC-QL algorithm for additional future research. Large network sizes provide particular difficulties, and the algorithm should successfully increase complexity without lowering performance. Additionally, dynamic parameter tuning techniques let the algorithm dynamically change its parameters in response to network size changes and other factors. This may involve population numbers, mutation probability, or adaptive exploration rates by investigating more sophisticated reinforcement learning methods to increase the adaptability of ABC-QL. Advanced RL techniques like deep reinforcement learning (DRL) and others can help decision-making become more complex.
Author Contributions
Conceptualization, R.A.S., E.S.A., R.A., M.A., R.A.M. and I.K.E.; methodology, R.A.S., E.S.A. and M.A.; software, R.A.M.; validation, I.K.E., R.A., M.A. and E.S.A.; formal analysis, R.A.; investigation, E.S.A. and R.A.; resources, M.A.; data curation, R.A.S., M.A. and R.A.; writing—original draft preparation, R.A.M. and I.K.E.; writing—review and editing, R.A. and M.A. visualization, R.A.S. and E.S.A., supervision, R.A.S., R.A. and M.A.; project administration, R.A., funding acquisition, M.A. and R.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2023R97), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, the authors would like to acknowledge the Deanship of Scientific Research, Taif University for funding this work.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2023R97), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kamalika, B.; Debashis, D. IoUT: Modelling and simulation of Edge-Drone-based Software-Defined smart Internet of Underwater Things. Simul. Model. Pract. Theory 2021, 109, 102304. [Google Scholar]
- Nayyar, A.; Ba, C.H.; Cong Duc, N.P.; Binh, H.D. Smart-IoUT 1.0: A Smart Aquatic Monitoring Network Based on Internet of Underwater Things (IoUT). In Proceedings of the International Conference on Industrial Networks and Intelligent Systems, Ho Chi Minh, Vietnam, 19 August 2019; Volume 257, pp. 1–16. [Google Scholar]
- Kim, H.; Cho, H.-S. SOUNET: Self-Organized Underwater Wireless Sensor Network. Sensors 2017, 17, 283. [Google Scholar] [CrossRef] [PubMed]
- Felemban, E.; Shaikh, F.K.; Qureshi, U.M.; Sheikh, A.A.; Qaisar, S.B. Underwater Sensor Network Applications: A Comprehensive Survey. Int. J. Distrib. Sens. Netw. 2015, 2015, 1–14. [Google Scholar]
- Khan, M.F.; Bibi, M.; Aadil, F.; Lee, J.W. Adaptive Node Clustering for Underwater Sensor Networks. Sensors 2021, 21, 4514. [Google Scholar]
- Gola, K.K.; Arya, S. Underwater acoustic sensor networks: Taxonomy on applications, architectures, localization methods, deployment techniques, routing techniques, and threats: A systematic review. Concurr. Comput. Pract. Exper. 2023, 35, e7815. [Google Scholar]
- Khalifa, O.O.; Roubleh, A.; Esgiar, A.; Abdelhaq, M.; Alsaqour, R.; Abdalla, A.; Ali, E.S.; Saeed, R. An IoT-Platform-Based Deep Learning System for Human Behavior Recognition in Smart City Monitoring Using the Berkeley MHAD Datasets. Systems 2022, 10, 177. [Google Scholar] [CrossRef]
- Shah, S.; Zhaoyun, S.; Khalid, Z.; Altaf, H.; Inam, U.; Yazeed, Y.G.; Muhammad, A.K.; Rashid, N. Advancements in Neighboring-Based Energy-Efficient Routing Protocol (NBEER) for Underwater Wireless Sensor Networks. Sensors 2023, 23, 6025. [Google Scholar]
- Xing, G.; Chen, Y.; Hou, R.; Dong, M.; Zeng, D.; Luo, J.; Ma, M. Game-Theory-Based Clustering Scheme for Energy Balancing in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2021, 8, 9005–9013. [Google Scholar] [CrossRef]
- Sandeep, D.N.; Kumar, V. Review on Clustering, Coverage and Connectivity in Underwater Wireless Sensor Networks: A Communication Techniques Perspective. IEEE Access 2017, 5, 11176–11199. [Google Scholar]
- Ghoreyshi, S.M.; Shahrabi, A.; Boutaleb, T.; Khalily, M. Mobile Data Gathering with Hop-Constrained Clustering in Underwater Sensor Networks. IEEE Access 2019, 7, 21118–21132. [Google Scholar] [CrossRef]
- Jahanbakht, M.; Xiang, W.; Hanzo, L.; Azghadi, M.R. Internet of Underwater Things and Big Marine Data Analytics—A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 904–956. [Google Scholar]
- Figueiredo, E.; Macedo, M.; Siqueira, H.V.; Santana, C.J.; Gokhale, A.; Bastos-Filho, C.J.A. Swarm intelligence for clustering—A systematic review with new perspectives on data mining. Eng. Appl. Artif. Intell. 2019, 82, 313–329. [Google Scholar]
- Elmustafa, S.A.; Rashid, A.S.; Ibrahim, K.E.; Othman, O.K. A systematic review on energy efficiency in the internet of underwater things (IoUT): Recent approaches and research gaps. J. Netw. Comput. Appl. 2023, 213, 103594. [Google Scholar]
- Islam, K.Y.; Ahmad, I.; Habibi, D.; Waqar, A. A survey on energy efficiency in underwater wireless communications. J. Netw. Comput. Appl. 2022, 198, 103295. [Google Scholar]
- Awan, K.M.; Shah, P.A.; Iqbal, K.; Gillani, S.; Ahmad, W.; Nam, Y. Underwater Wireless Sensor Networks: A Review of Recent Issues and Challenges. Wirel. Commun. Mob. Comput. 2019, 2019, 6470359. [Google Scholar] [CrossRef]
- Wei, X.; Guo, H.; Wang, X.; Wang, X.; Qiu, M. Reliable Data Collection Techniques in Underwater Wireless Sensor Networks: A Survey. IEEE Commun. Surv. Tutor. 2022, 24, 404–431. [Google Scholar]
- Kamal, K.G.; Manish, D.; Bhumika, G.; Rahul, R. An empirical study on underwater acoustic sensor networks based on localization and routing approaches. Adv. Eng. Softw. 2023, 175, 103319. [Google Scholar]
- Feng, P.; Qin, D.; Ji, P.; Zhao, M.; Guo, R.; Berhane, T.M. Improved energy-balanced algorithm for underwater wireless sensor network based on depth threshold and energy level partition. J. Wirel. Commun. Netw. 2019, 2019, 228. [Google Scholar]
- Mohan, P.; Subramani, N.; Alotaibi, Y.; Alghamdi, S.; Khalaf, O.I.; Ulaganathan, S. Improved Metaheuristics-Based Clustering with Multihop Routing Protocol for Underwater Wireless Sensor Networks. Sensors 2022, 22, 1618. [Google Scholar]
- Fattah, S.; Gani, A.; Ahmedy, I.; Idris, M.Y.I.; Hashem, I.A.T. A Survey on Underwater Wireless Sensor Networks: Requirements, Taxonomy, Recent Advances, and Open Research Challenges. Sensors 2020, 20, 5393. [Google Scholar] [CrossRef]
- Elmustafa, S.; Rashid, A. Chapter 6: Intelligent Underwater Wireless Communications. In Intelligent Wireless Communications; IET: London, UK, 2021; pp. 271–305. [Google Scholar]
- Sathish, K.; Cv, R.; Ab Wahab, M.N.; Anbazhagan, R.; Pau, G.; Akbar, M.F. Underwater Wireless Sensor Networks Performance Comparison Utilizing Telnet and Superframe. Sensors 2023, 23, 4844. [Google Scholar] [CrossRef]
- Ahmed, G.; Zhao, X.; Fareed, M.M.S. A Hybrid Energy Equating Game for Energy Management in the Internet of Underwater Things. Sensors 2019, 19, 2351. [Google Scholar] [CrossRef]
- Hou, R.; Fu, J.; Dong, M.; Ota, K.; Zeng, D. An Unequal Clustering Method Based on Particle Swarm Optimization in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2022, 9, 25027–25036. [Google Scholar] [CrossRef]
- Khan, Z.A.; Karim, O.A.; Abbas, S.; Javaid, N.; Zikria, Y.B.; Tariq, U. Q-learning based energy-efficient and void avoidance routing protocol for underwater acoustic sensor networks. Comput. Netw. 2021, 197, 108309. [Google Scholar] [CrossRef]
- Li, L.; Qiu, Y.; Xu, J. A K-Means Clustered Routing Algorithm with Location and Energy Awareness for Underwater Wireless Sensor Networks. Photonics 2022, 9, 282. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, N.P. Energy hole mitigation through optimized cluster head selection and strategic routing in Internet of Underwater Things. Int. J. Commun. Syst. 2022, 35, e5283. [Google Scholar] [CrossRef]
- Subramani, N.; Prakash, M.; Youseef, A.; Saleh, A.; Osamah, I.K. An Efficient Metaheuristic-Based Clustering with Routing Protocol for Underwater Wireless Sensor Networks. Sensors 2022, 22, 415. [Google Scholar] [CrossRef]
- Keshav Kumar Tiwari, K.; Singh, S. Energy-optimized cluster head selection based on enhanced remora optimization algorithm in underwater wireless sensor network. Int. J. Commun. Syst. 2023, 36, e5560. [Google Scholar] [CrossRef]
- Salil, B.; Sharma, S.; Alsharabi, N.; Eldin, E.T.; Ghamry, N.A. Energy-efficient clustering protocol for underwater wireless sensor networks using optimized glowworm swarm optimization. Front. Mar. Sci. 2023, 10, 1117787. [Google Scholar]
- Ullah, S.; Saleem, A.; Hassan, N.; Muhammad, G.; Shin, J.; Minhas, Q.-A.; Khan, M.K. Reliable and Delay Aware Routing Protocol for Underwater Wireless Sensor Networks. IEEE Access 2023, 11, 116932–116943. [Google Scholar] [CrossRef]
- Khan, Z.U.; Gang, Q.; Muhammad, A.; Muzzammil, M.; Khan, S.U.; El Affendi, M.; Ali, G.; Ullah, I.; Khan, J. A Comprehensive Survey of Energy-Efficient MAC and Routing Protocols for Underwater Wireless Sensor Networks. Electronics 2022, 11, 3015. [Google Scholar] [CrossRef]
- Almazrouei, K.; Kamel, I.; Rabie, T. Dynamic Obstacle Avoidance and Path Planning through Reinforcement Learning. Appl. Sci. 2023, 13, 8174. [Google Scholar] [CrossRef]
- Natesan, S.; Krishnan, R. FLCEER: Fuzzy Logic Cluster-Based Energy Efficient Routing Protocol for Underwater Acoustic Sensor Network. Int. J. Inf. Technol. Web Eng. IJITWE 2020, 15, 76–101. [Google Scholar] [CrossRef]
- Alsaqour, R.; Ali, E.S.; Mokhtar, R.A.; Saeed, R.A.; Alhumyani, H.; Abdelhaq, M. Efficient Energy Mechanism in Heterogeneous WSNs for Underground Mining Monitoring Applications. IEEE Access 2022, 10, 72907–72924. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Wang, B.; Sun, W.; Du, H.; Zhao, Y. Energy-Efficient Data Transmission for Underwater Wireless Sensor Networks: A Novel Hierarchical Underwater Wireless Sensor Transmission Framework. Sensors 2023, 23, 5759. [Google Scholar] [CrossRef]
- Ahmad, I.; Rahman, T.; Zeb, A.; Khan, I.; Othman, M.T.B.; Hamam, H. Cooperative Energy-Efficient Routing Protocol for Underwater Wireless Sensor Networks. Sensors 2022, 22, 6945. [Google Scholar] [CrossRef]
- Qawqzeh, Y.; Alharbi, M.T.; Jaradat, A.; Abdul Sattar, K.N. A review of swarm intelligence algorithms deployment for scheduling and optimization in cloud computing environments. PeerJ Comput. Sci. 2021, 7, e696. [Google Scholar] [CrossRef]
- Xiao, X.; Huang, H.; Wang, W. Underwater Wireless Sensor Networks: An Energy-Efficient Clustering Routing Protocol Based on Data Fusion and Genetic Algorithms. Appl. Sci. 2021, 11, 312. [Google Scholar] [CrossRef]
- Sajwan, M.; Bhatt, S.; Arora, K.; Singh, S. GAER-UWSN: Genetic Algorithm-Based Energy-Efficient Routing Protocols in Underwater Wireless Sensor Networks. In Data Analytics and Management; Lecture Notes in Networks and Systems; Khanna, A., Polkowski, Z., Castillo, O., Eds.; Springer: Singapore, 2023; Volume 572. [Google Scholar]
- Lilhore, U.K.; Khalaf, O.I.; Simaiya, S.; Romero, C.A.T.; Abdulsahib, G.M.; M, P.; Kumar, D. A depth-controlled and energy-efficient routing protocol for underwater wireless sensor networks. Int. J. Distrib. Sens. Netw. 2022, 18, 1–16. [Google Scholar] [CrossRef]
- Chinnasamy, S.; Naveen, J.; Alphonse, P.J.A.; Dhasarathan, C.; Sambasivam, G. Energy-Aware Multilevel Clustering Scheme for Underwater Wireless Sensor Networks. IEEE Access 2022, 10, 55868–55875. [Google Scholar] [CrossRef]
- Jalal, R.D.; Aliesawi, S.A. Enhancing TEEN Protocol using the Particle Swarm Optimization and BAT Algorithms in Underwater Wireless Sensor Network. In Proceedings of the 15th International Conference on Developments in eSystems Engineering (DeSE), Baghdad, Iraq, 9–12 January 2023; pp. 504–510. [Google Scholar]
- Gadal, S.; Mokhtar, R.; Abdelhaq, M.; Alsaqour, R.; Ali, E.S.; Saeed, R. Machine Learning-Based Anomaly Detection Using K-mean Array and Sequential Minimal Optimization. Electronics 2022, 11, 2158. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, J.; Jiang, S.; Chen, W. A Localization Method for Underwater Wireless Sensor Networks Based on Mobility Prediction and Particle Swarm Optimization Algorithms. Sensors 2016, 16, 212. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Huang, H. A Clustering Routing Algorithm Based on Improved Ant Colony Optimization Algorithms for Underwater Wireless Sensor Networks. Algorithms 2020, 13, 250. [Google Scholar] [CrossRef]
- Maheshwari, P.; Sharma, A.K.; Verma, K. Energy efficient cluster based routing protocol for WSN using butterfly optimization algorithm and ant colony optimization. Ad Hoc Netw. 2021, 110, 102317. [Google Scholar] [CrossRef]
- Aadil, F.; Bajwa, K.B.; Khan, S.; Chaudary, N.M.; Akram, A. CACONET: Ant Colony Optimization (ACO) Based Clustering Algorithm for VANET. PLoS ONE 2016, 11, e0154080. [Google Scholar] [CrossRef] [PubMed]
- Zehra, S.S.; Qureshi, R.; Dev, K.; Shahid, S.; Bhatti, N.A. Comparative Analysis of Bio-Inspired Algorithms for Underwater Wireless Sensor Networks. Wirel. Pers. Commun. 2021, 116, 1311–1323. [Google Scholar] [CrossRef]
- Kim, D.; Wang, W.; Ding, L.; Lim, J.; Oh, H.; Wu, W. Minimum average routing path clustering problem in multi-hop 2-D underwater sensor networks. Optim. Lett. 2020, 4, 383–392. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, P.; Lei, G.; Chen, P.; Yang, G. Energy-Efficient Multiple Autonomous Underwater Vehicle Path Planning Scheme in Underwater Sensor Networks. Electronics 2023, 12, 3321. [Google Scholar] [CrossRef]
- Ghorpade, S.N.; Zennaro, M.; Chaudhari, B.S.; Saeed, R.A.; Alhumyani, H.; Abdel-Khalek, S. Enhanced Differential Crossover and Quantum Particle Swarm Optimization for IoT Applications. IEEE Access 2021, 9, 93831–93846. [Google Scholar] [CrossRef]
- Sun, W.; Tang, M.; Zhang, L.; Huo, Z.; Shu, L. A Survey of Using Swarm Intelligence Algorithms in IoT. Sensors 2020, 20, 1420. [Google Scholar] [CrossRef]
- Nain, M.; Goyal, N.; Awasthi, L.K.; Malik, A. A range based node localization scheme with hybrid optimization for underwater wireless sensor network. Int. J. Commun. Syst. 2022, 35, e5147. [Google Scholar] [CrossRef]
- Sivakumar, V.; Kanagachidambaresan, G.R.; Dhilip kumar, V.; Arif, M.; Jackson, C.; Arulkumaran, G. Energy-Efficient Markov-Based Lifetime Enhancement Approach for Underwater Acoustic Sensor Network. J. Sens. 2022, 2022, 3578002. [Google Scholar] [CrossRef]
- Faheem, M.; Ngadi, M.A.; Gungor, V.C. Energy efficient multi-objective evolutionary routing scheme for reliable data gathering in Internet of underwater acoustic sensor networks. Ad Hoc Netw. 2019, 93, 101912. [Google Scholar] [CrossRef]
- Mukhtar, A.M.; Saeed, R.A.; Mokhtar, R.A.; Ali, E.S.; Alhumyani, H. Performance Evaluation of Downlink Coordinated Multipoint Joint Transmission under Heavy IoT Traffic Load. Wirel. Commun. Mob. Comput. 2022, 2022, 6837780. [Google Scholar] [CrossRef]
- Saeed, M.M.; Saeed, R.A.; Abdelhaq, M.; Alsaqour, R.; Hasan, M.K.; Mokhtar, R.A. Anomaly Detection in 6G Networks Using Machine Learning Methods. Electronics 2023, 12, 3300. [Google Scholar] [CrossRef]
- Touafek, N.; Tayeb, F.B.-S.; Ladj, A. A Reinforcing-Learning-Driven Artificial Bee Colony Algorithm for Scheduling Jobs and Flexible Maintenance under Learning and Deteriorating Effects. Algorithms 2023, 16, 397. [Google Scholar] [CrossRef]
- Fairee, S.; Prom-On, S.; Sirinaovakul, B. Reinforcement learning for solution updating in Artificial Bee Colony. PLoS ONE 2018, 13, e0200738. [Google Scholar] [CrossRef]
- Lu, Y.; He, R.; Chen, X.; Lin, B.; Yu, C. Energy-Efficient Depth-Based Opportunistic Routing with Q-Learning for Underwater Wireless Sensor Networks. Sensors 2020, 20, 1025. [Google Scholar] [CrossRef]
- Chang, H.; Feng, J.; Duan, C. Reinforcement Learning-Based Data Forwarding in Underwater Wireless Sensor Networks with Passive Mobility. Sensors 2019, 19, 256. [Google Scholar] [CrossRef]
- Sun, Y.; Zheng, M.; Han, X.; Li, S.; Yin, J. Adaptive clustering routing protocol for underwater sensor networks. Ad Hoc Netw. 2022, 136, 102953. [Google Scholar] [CrossRef]
- Vijay, M.M.; Sunil, J.; Vincy, V.G.A.G.; IjazKhan, M.; Abdullaev, S.S.; Eldin, S.M.; Govindan, V.; Ahmad, H.; Askar, S. Underwater wireless sensor network-based multihop data transmission using hybrid cat cheetah optimization algorithm. Sci. Rep. 2023, 13, 10810. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).