Assessing the Loss Given Default of Bank Loans Using the Hybrid Algorithms Multi-Stage Model
Abstract
:1. Introduction
2. Literature Review on LGD
2.1. Theoretical Development of LGD
2.2. LGD Modelling
3. Methodology
3.1. Credit Dataset
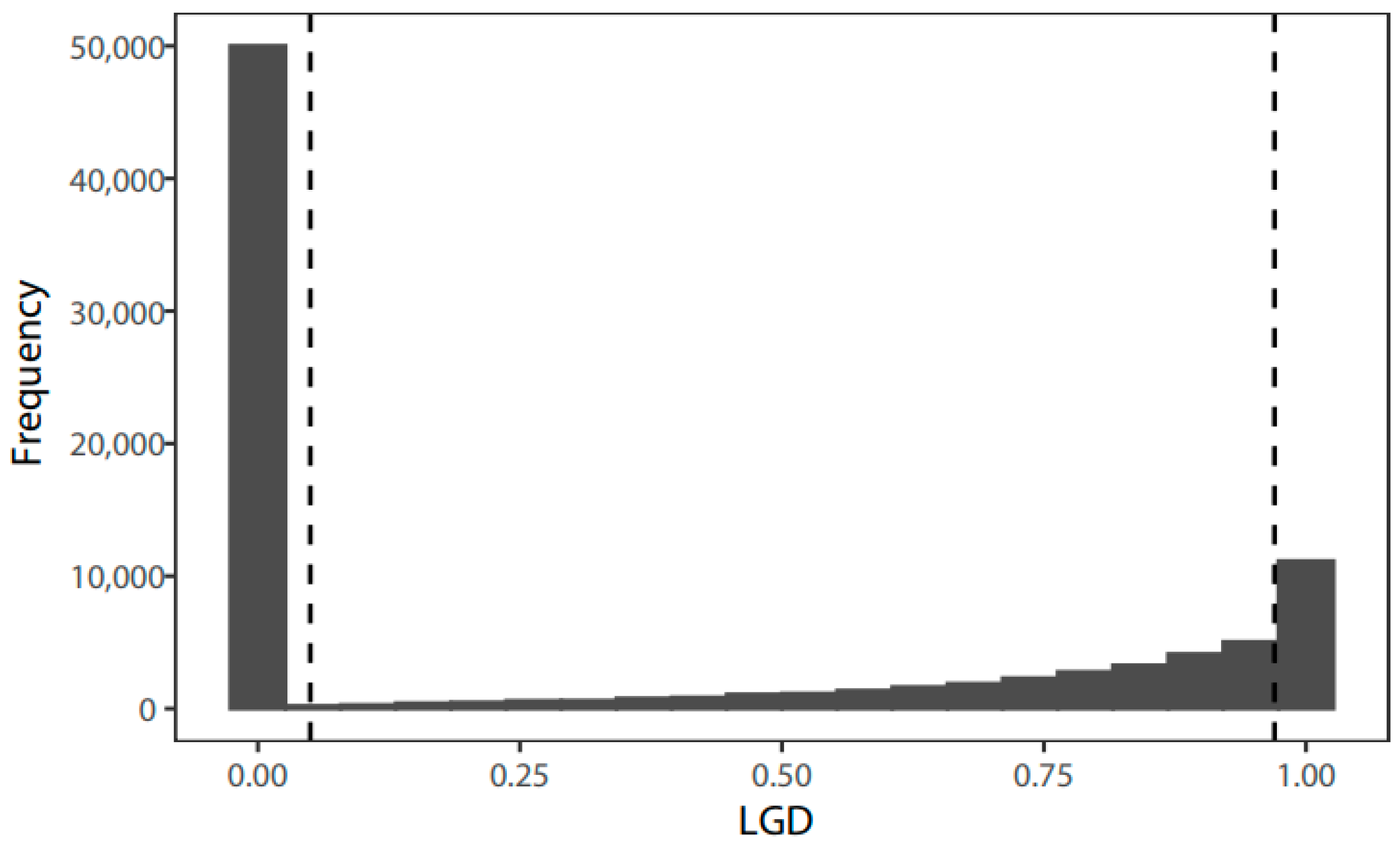
3.2. Data Pre-Processing
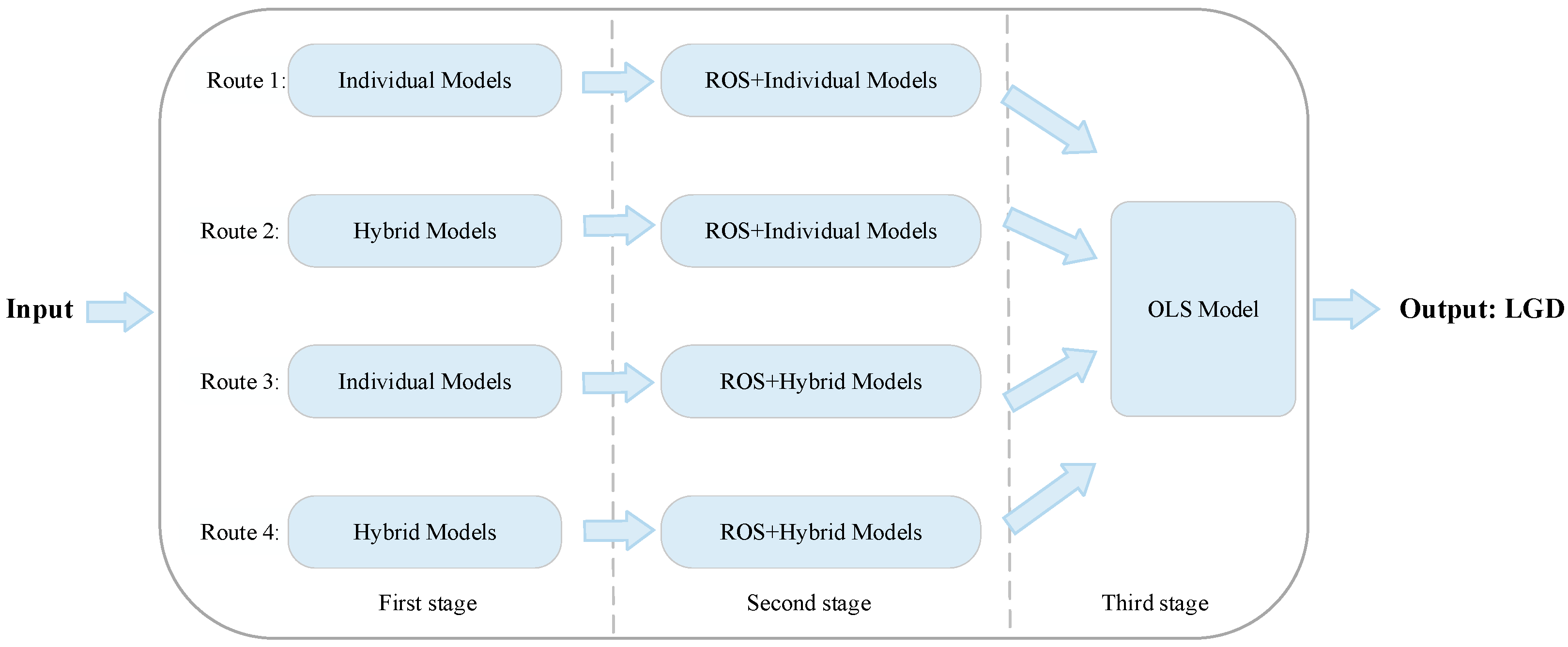
3.3. Model Framework
3.4. Related Algorithms
3.4.1. Unsupervised ML
3.4.2. Supervised ML
3.4.3. Class Imbalance Handling Techniques
3.4.4. Performance Evaluation Metrics
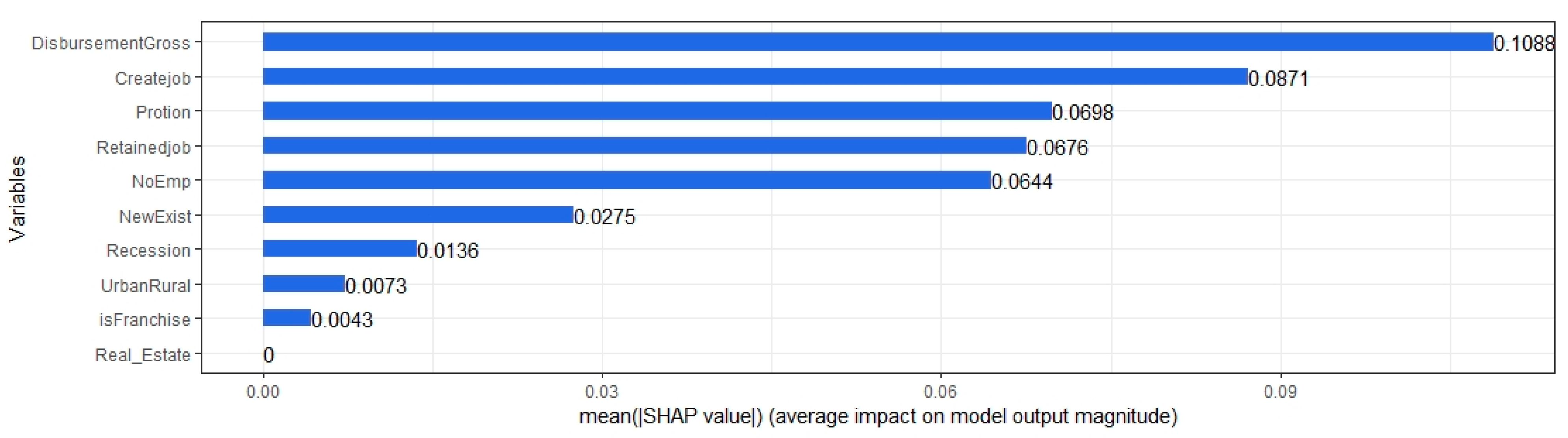
3.4.5. Shapley Additive Explanations (SHAP)
4. Experimental Results and Discussion
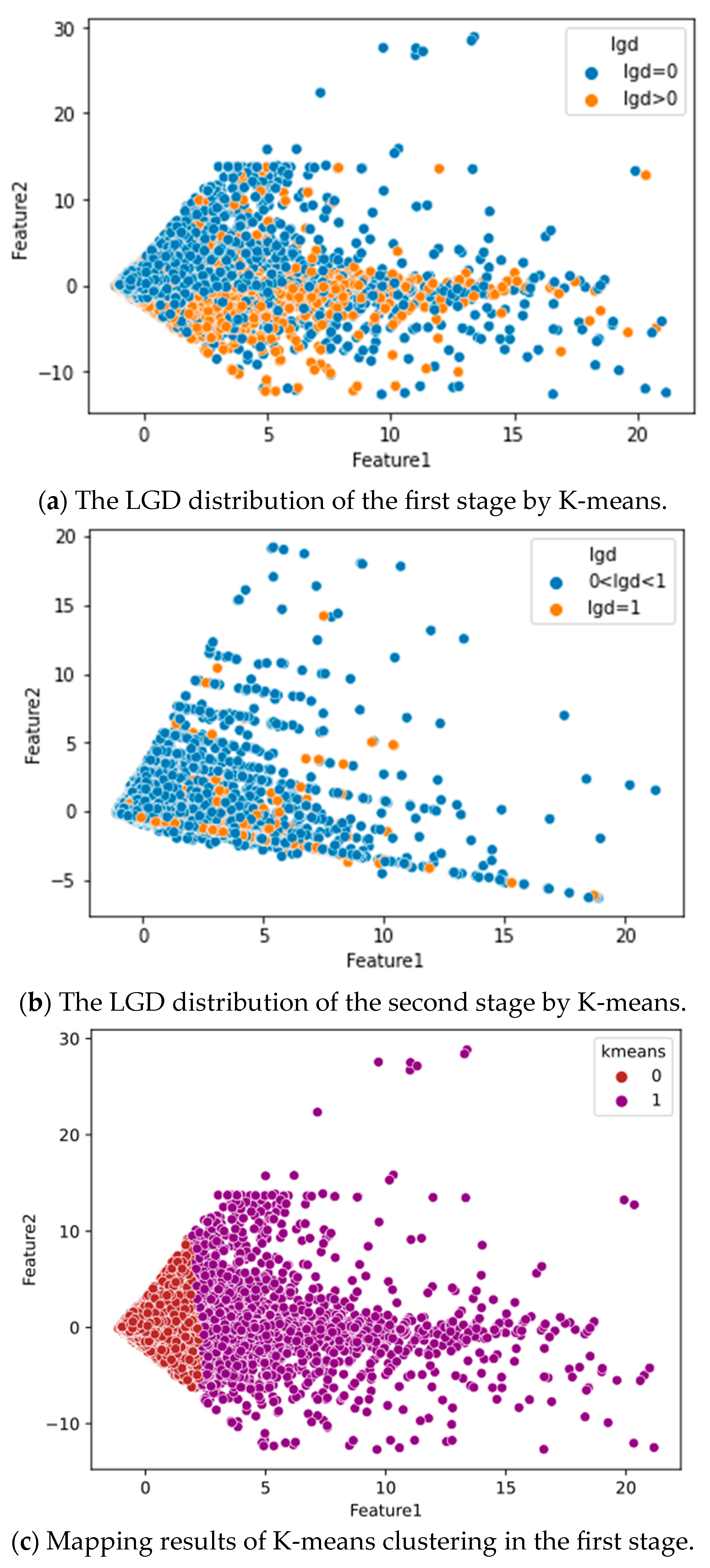
4.1. Dataset Space
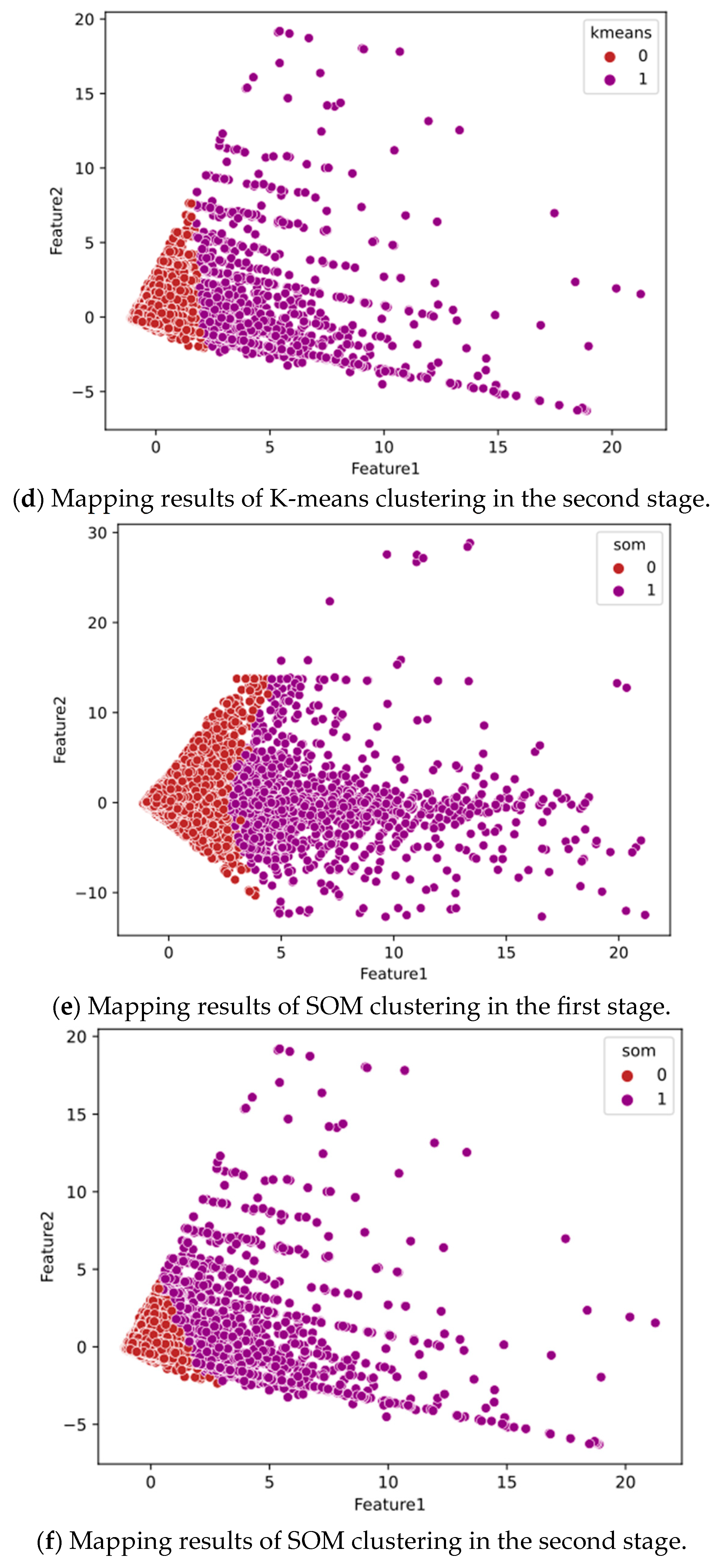
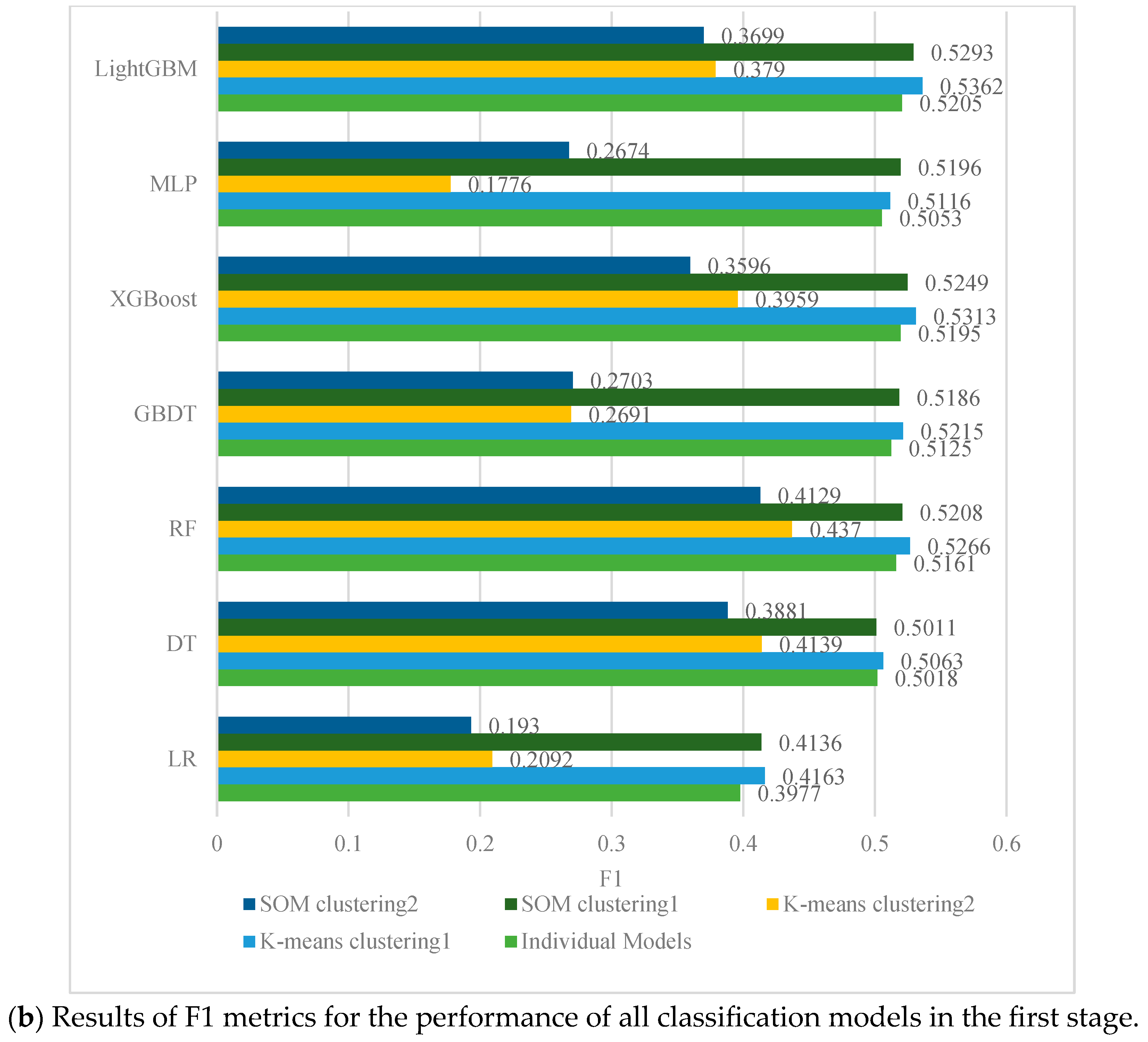
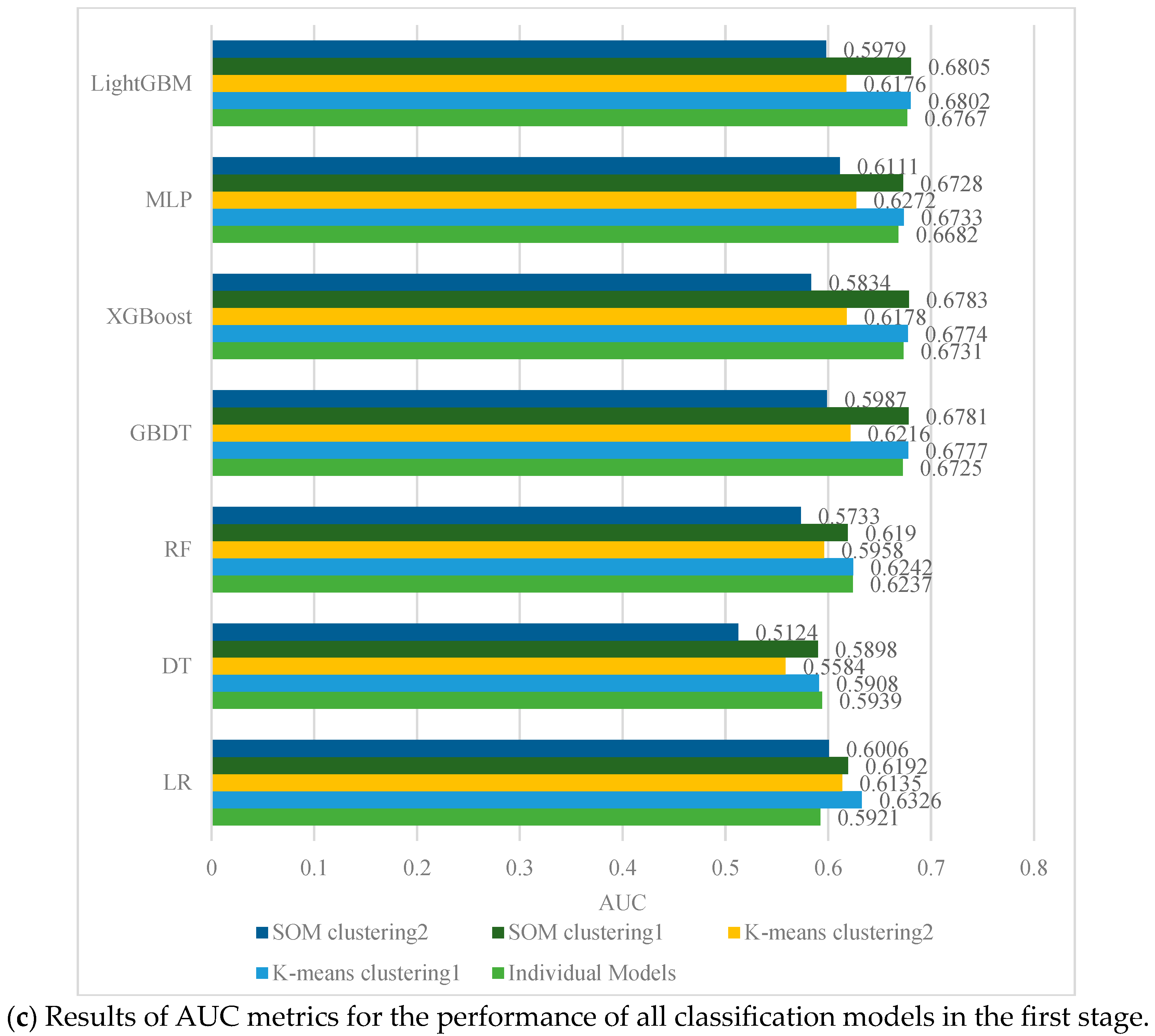
4.2. Performance Evaluation of First-Stage Classification
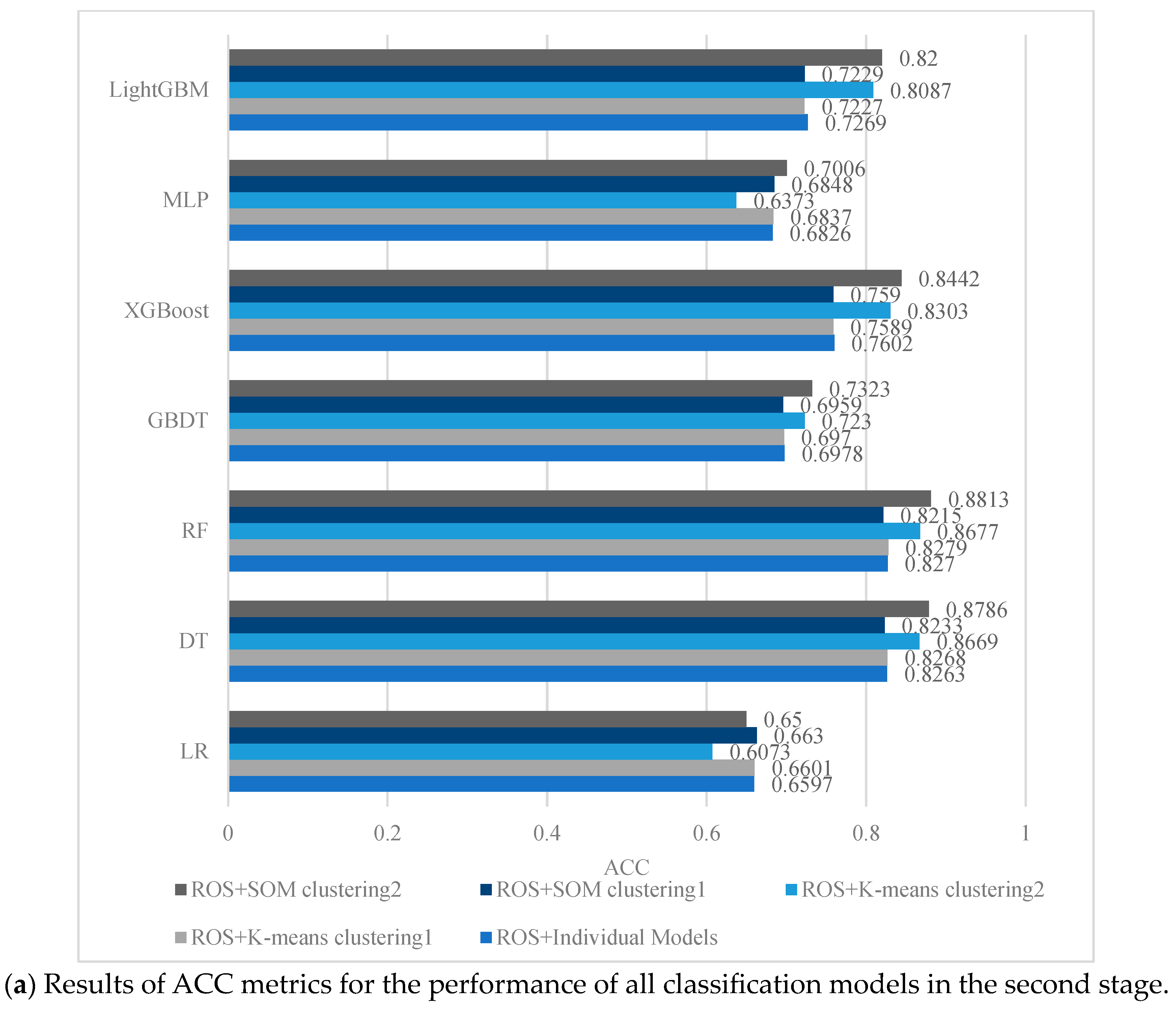
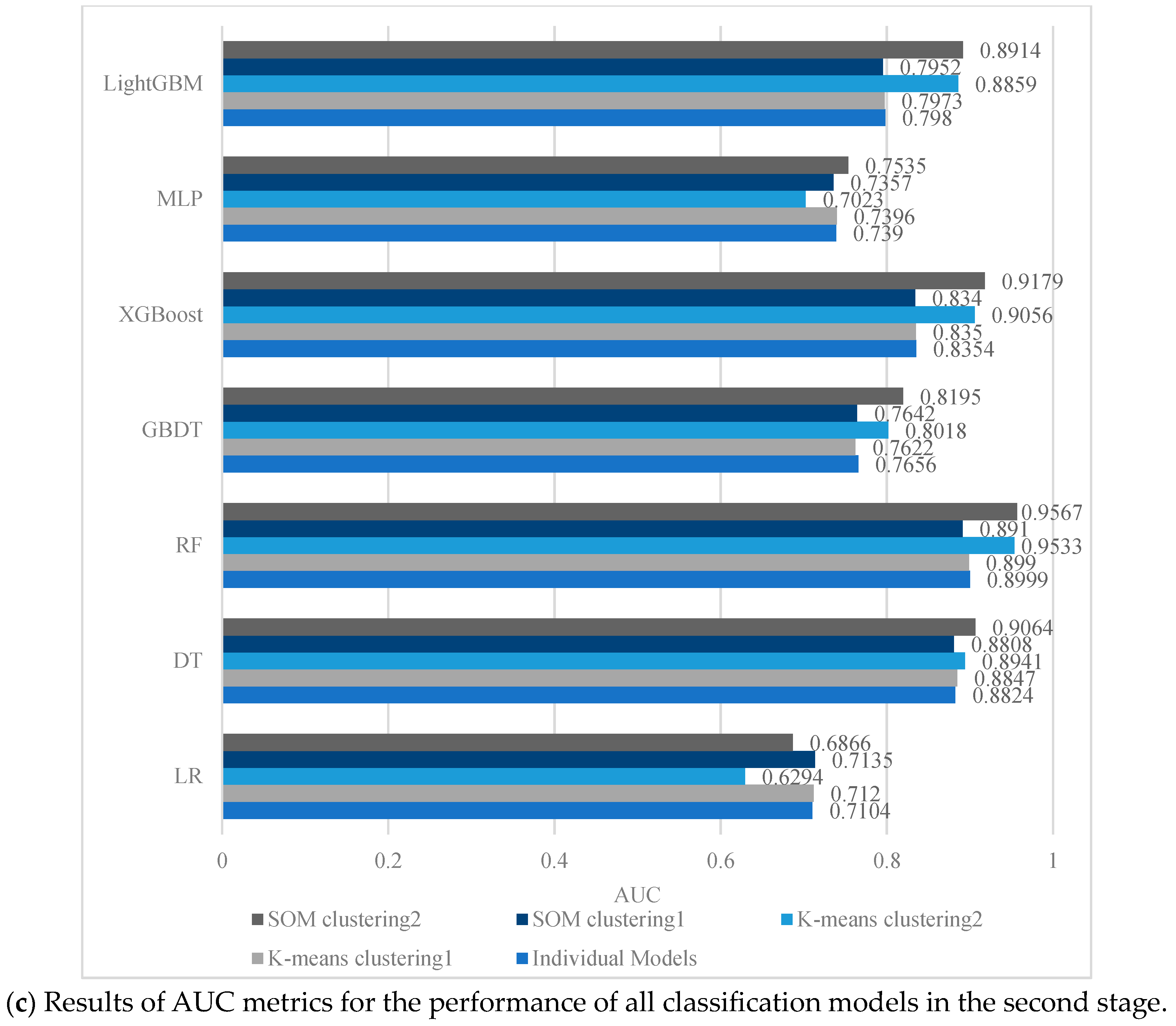
4.3. Performance Evaluation of the Second-Stage Classification
4.4. LGD Prediction Evaluation for the Third Stage
4.5. Robustness Tests
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | For access and download of information on the SBA (Small Business Administration) Credit Dataset, please see the link https://www.kaggle.com/datasets/mirbektoktogaraev/should-this-loan-be-approved-or-denied (accessed on 17 March 2020). The file title of the dataset is “Should This Loan be Approved or Denied?”. |
| 2 | The ROC curve is a visual representation of the classifier performance at different thresholds using the True Positive Rate (TPR), which measures the proportion of positive category samples that are correctly classified as positive, as the vertical coordinate, and the False Positive Rate (FPR), which measures the proportion of negative category samples that are incorrectly classified as positive, as the horizontal coordinate. |
References
- Louzada, F.; Ara, A.; Fernandes, G.B. Classification methods applied to credit scoring: Systematic review and overall comparison. Surv. Oper. Res. Manag. Sci. 2016, 21, 117–134. [Google Scholar] [CrossRef]
- Machado, M.R.; Karray, S. Assessing credit risk of commercial customers using hybrid machine learning algorithms. Expert Syst. Appl. 2022, 200, 116889. [Google Scholar] [CrossRef]
- Twala, B. Combining classifiers for credit risk prediction. J. Syst. Sci. Syst. Eng. 2009, 18, 292–311. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. Overview of The New Basel Capital Accord; Bank for International Settlements: Basel, Switzerland, 2003. [Google Scholar]
- Gürtler, M.; Hibbeln, M. Improvements in loss given default forecasts for bank loans. J. Bank. Financ. 2013, 37, 2354–2366. [Google Scholar] [CrossRef]
- Bellotti, T.; Crook, J. Loss given default models incorporating macroeconomic variables for credit cards. Int. J. Forecast. 2012, 28, 171–182. [Google Scholar] [CrossRef]
- Calabrese, R.; Zanin, L. Modelling spatial dependence for Loss Given Default in peer-to-peer lending. Expert Syst. Appl. 2022, 192, 116295. [Google Scholar] [CrossRef]
- Serrano-Cinca, C.; Gutiérrez-Nieto, B. The use of profit scoring as an alternative to credit scoring systems in peer-to-peer (P2P) lending. Decis. Support Syst. 2016, 89, 113–122. [Google Scholar] [CrossRef]
- Zhang, J.; Thomas, L.C. Comparisons of linear regression and survival analysis using single and mixture distributions approaches in modelling LGD. Int. J. Forecast. 2012, 28, 204–215. [Google Scholar] [CrossRef]
- Kellner, R.; Nagl, M.; Rösch, D. Opening the black box–Quantile neural networks for loss given default prediction. J. Bank. Financ. 2022, 134, 106334. [Google Scholar] [CrossRef]
- Loterman, G.; Brown, I.; Martens, D.; Mues, C.; Baesens, B. Benchmarking regression algorithms for loss given default modeling. Int. J. Forecast. 2012, 28, 161–170. [Google Scholar] [CrossRef]
- Li, K.; Zhou, F.; Li, Z.; Yao, X.; Zhang, Y. Predicting loss given default using post-default information. Knowl.-Based Syst. 2021, 224, 107068. [Google Scholar] [CrossRef]
- Lucas, A. Basel II Problem Solving, QFRMC Workshop and Conference on Basel II & Credit Risk Modelling in Consumer Lending; University of Southampton: Southampton, UK, 2006. [Google Scholar]
- Tanoue, Y.; Kawada, A.; Yamashita, S. Forecasting loss given default of bank loans with multi-stage model. Int. J. Forecast. 2017, 33, 513–522. [Google Scholar] [CrossRef]
- Bao, W.; Lianju, N.; Yue, K. Integration of unsupervised and supervised machine learning algorithms for credit risk assessment. Expert Syst. Appl. 2019, 128, 301–315. [Google Scholar] [CrossRef]
- Li, M.; Mickel, A.; Taylor, S. “Should This Loan be Approved or Denied?”: A Large Dataset with Class Assignment Guidelines. J. Stat. Educ. 2018, 26, 55–66. [Google Scholar] [CrossRef]
- Shi, B.; Chi, G.; Li, W. Exploring the mismatch between credit ratings and loss-given-default: A credit risk approach. Econ. Model. 2020, 85, 420–428. [Google Scholar] [CrossRef]
- Shi, B.; Zhao, X.; Wu, B.; Dong, Y. Credit rating and microfinance lending decisions based on loss given default (LGD). Financ. Res. Lett. 2019, 30, 124–129. [Google Scholar] [CrossRef]
- Xing, H.; Sun, N.; Chen, Y. Credit rating dynamics in the presence of unknown structural breaks. J. Bank. Financ. 2012, 36, 78–89. [Google Scholar] [CrossRef]
- Bijak, K.; Thomas, L.C. Does segmentation always improve model performance in credit scoring? Expert Syst. Appl. 2012, 39, 2433–2442. [Google Scholar] [CrossRef]
- Jankowitsch, R.; Pullirsch, R.; Veža, T. The delivery option in credit default swaps. J. Bank. Financ. 2008, 32, 1269–1285. [Google Scholar] [CrossRef]
- Calabrese, R.; Zenga, M. Bank loan recovery rates: Measuring and nonparametric density estimation. J. Bank. Financ. 2010, 34, 903–911. [Google Scholar] [CrossRef]
- Renault, O.; Scaillet, O. On the way to recovery: A nonparametric bias free estimation of recovery rate densities. J. Bank. Financ. 2004, 28, 2915–2931. [Google Scholar] [CrossRef]
- Acharya, V.V.; Bharath, S.T.; Srinivasan, A. Does industry-wide distress affect defaulted firms? Evidence from creditor recoveries. J. Financ. Econ. 2007, 85, 787–821. [Google Scholar] [CrossRef]
- Altman, E.I.; Brady, B.; Resti, A.; Sironi, A. The link between default and recovery rates: Theory, empirical evidence, and implications. J. Bus. 2005, 78, 2203–2228. [Google Scholar] [CrossRef]
- Bade, B.; Rösch, D.; Scheule, H. Default and recovery risk dependencies in a simple credit risk model. Eur. Financ. Manag. 2011, 17, 120–144. [Google Scholar] [CrossRef]
- Papke, L.E.; Wooldridge, J.M. Econometric methods for fractional response variables with an application to 401 (k) plan participation rates. J. Appl. Econom. 1996, 11, 619–632. [Google Scholar] [CrossRef]
- Barboza, F.; Kimura, H.; Altman, E. Machine learning models and bankruptcy prediction. Expert Syst. Appl. 2017, 83, 405–417. [Google Scholar] [CrossRef]
- Bastos, J.A. Forecasting bank loans loss-given-default. J. Bank. Financ. 2010, 34, 2510–2517. [Google Scholar] [CrossRef]
- Moscatelli, M.; Parlapiano, F.; Narizzano, S.; Viggiano, G. Corporate default forecasting with machine learning. Expert Syst. Appl. 2020, 161, 113567. [Google Scholar] [CrossRef]
- Yao, X.; Crook, J.; Andreeva, G. Support vector regression for loss given default modelling. Eur. J. Oper. Res. 2015, 240, 528–538. [Google Scholar] [CrossRef]
- Bellotti, A.; Brigo, D.; Gambetti, P.; Vrins, F. Forecasting recovery rates on non-performing loans with machine learning. Int. J. Forecast. 2021, 37, 428–444. [Google Scholar] [CrossRef]
- Hurlin, C.; Leymarie, J.; Patin, A. Loss functions for loss given default model comparison. Eur. J. Oper. Res. 2018, 268, 348–360. [Google Scholar] [CrossRef]
- Kaposty, F.; Kriebel, J.; Löderbusch, M. Predicting loss given default in leasing: A closer look at models and variable selection. Int. J. Forecast. 2020, 36, 248–266. [Google Scholar] [CrossRef]
- Miller, P.; Töws, E. Loss given default adjusted workout processes for leases. J. Bank. Financ. 2018, 91, 189–201. [Google Scholar] [CrossRef]
- Gholamian, M.; Jahanpour, S.; Sadatrasoul, S. A new method for clustering in credit scoring problems. J. Math. Comput. Sci. 2013, 6, 97–106. [Google Scholar] [CrossRef]
- Luo, S.-T.; Cheng, B.-W.; Hsieh, C.-H. Prediction model building with clustering-launched classification and support vector machines in credit scoring. Expert Syst. Appl. 2009, 36, 7562–7566. [Google Scholar] [CrossRef]
- Yu, L.; Yue, W.; Wang, S.; Lai, K.K. Support vector machine based multiagent ensemble learning for credit risk evaluation. Expert Syst. Appl. 2010, 37, 1351–1360. [Google Scholar] [CrossRef]
- Zhang, F.; Tadikamalla, P.R.; Shang, J. Corporate credit-risk evaluation system: Integrating explicit and implicit financial performances. Int. J. Prod. Econ. 2016, 177, 77–100. [Google Scholar] [CrossRef]
- AghaeiRad, A.; Chen, N.; Ribeiro, B. Improve credit scoring using transfer of learned knowledge from self-organizing map. Neural Comput. Appl. 2017, 28, 1329–1342. [Google Scholar] [CrossRef]
- Huysmans, J.; Baesens, B.; Vanthienen, J.; Van Gestel, T. Failure prediction with self organizing maps. Expert Syst. Appl. 2006, 30, 479–487. [Google Scholar] [CrossRef]
- Papouskova, M.; Hajek, P. Two-stage consumer credit risk modelling using heterogeneous ensemble learning. Decis. Support Syst. 2019, 118, 33–45. [Google Scholar] [CrossRef]
- Caruso, G.; Gattone, S.; Fortuna, F.; Di Battista, T. Cluster Analysis for mixed data: An application to credit risk evaluation. Socio-Econ. Plan. Sci. 2021, 73, 100850. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Coenen, L.; Verbeke, W.; Guns, T. Machine learning methods for short-term probability of default: A comparison of classification, regression and ranking methods. J. Oper. Res. Soc. 2022, 73, 191–206. [Google Scholar] [CrossRef]
- Qi, M.; Zhao, X. Comparison of modeling methods for loss given default. J. Bank. Financ. 2011, 35, 2842–2855. [Google Scholar] [CrossRef]
- Munkhdalai, L.; Munkhdalai, T.; Namsrai, O.-E.; Lee, J.Y.; Ryu, K.H. An empirical comparison of machine-learning methods on bank client credit assessments. Sustainability 2019, 11, 699. [Google Scholar] [CrossRef]
- Xia, Y.; Zhao, J.; He, L.; Li, Y.; Yang, X. Forecasting loss given default for peer-to-peer loans via heterogeneous stacking ensemble approach. Int. J. Forecast. 2021, 37, 1590–1613. [Google Scholar] [CrossRef]
- Olson, L.M.; Qi, M.; Zhang, X.; Zhao, X. Machine learning loss given default for corporate debt. J. Empir. Financ. 2021, 64, 144–159. [Google Scholar] [CrossRef]
- de Lange, P.E.; Melsom, B.; Vennerød, C.B.; Westgaard, S. Explainable AI for Credit Assessment in Banks. J. Risk Financ. Manag. 2022, 15, 556. [Google Scholar] [CrossRef]
- Moscato, V.; Picariello, A.; Sperlí, G. A benchmark of machine learning approaches for credit score prediction. Expert Syst. Appl. 2021, 165, 113986. [Google Scholar] [CrossRef]
- Brito, L.C.; Susto, G.A.; Brito, J.N.; Duarte, M.A. An explainable artificial intelligence approach for unsupervised fault detection and diagnosis in rotating machinery. Mech. Syst. Signal Process. 2022, 163, 108105. [Google Scholar] [CrossRef]
- Gupton, G.M.; Stein, R.M.; Salaam, A.; Bren, D. LossCalcTM: Model for Predicting Loss Given Default (LGD); Moody’s KMV: New York, NY, USA, 2002. [Google Scholar]






| Dataset | Total | Non-Defaults | Defaults | Defaults Ratio |
|---|---|---|---|---|
| Bank 1 | 51,827 | 31,778 | 20,049 | 38.68% |
| Bank 2 | 20,433 | 11,526 | 8907 | 43.59% |
| Bank 3 | 17,643 | 6656 | 10,987 | 62.27% |
| Bank 1 | Bank 2 | Bank 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | Mean | SD | Min | Max | Mean | SD | Min | Max | Mean | SD | Min | Max |
| NoEmp | 4.948 | 7.044 | 0.000 | 100 | 5.825 | 7.477 | 0.000 | 92 | 3.452 | 5.230 | 0.000 | 100 |
| UrbanRural | 0.925 | 0.263 | 0.000 | 1.000 | 0.860 | 0.347 | 0.000 | 1.000 | 0.932 | 0.252 | 0.000 | 1.000 |
| NewExist | 0.764 | 0.424 | 0.000 | 1.000 | 0.964 | 0.186 | 0.000 | 1.000 | 0.649 | 0.477 | 0.000 | 1.000 |
| Createjob | 0.651 | 2.159 | 0.000 | 50 | 1.041 | 2.288 | 0.000 | 50 | 1.859 | 3.108 | 0.000 | 50 |
| Protion | 0.503 | 0.030 | 0.350 | 0.955 | 0.513 | 0.065 | 0.500 | 0.900 | 0.811 | 0.107 | 0.200 | 1.000 |
| isFranchise | 0.010 | 0.102 | 0.000 | 1.000 | 0.009 | 0.094 | 0.000 | 1.000 | 0.007 | 0.084 | 0.000 | 1.000 |
| Retainedjob | 4.554 | 6.894 | 0.000 | 100 | 4.943 | 7.114 | 0.000 | 90 | 3.362 | 5.190 | 0.000 | 100 |
| DisbursementGross | 52,986 | 73,230 | 4000 | 2,293,500 | 5.825 | 7.477 | 0.000 | 92 | 67,338 | 223,261 | 4729 | 4,200,000 |
| Real_Estate | 0.001 | 0.034 | 0.000 | 1.000 | 0.000 | 0.007 | 0.000 | 1.000 | 0.024 | 0.154 | 0.000 | 1.000 |
| Recession | 0.030 | 0.169 | 0.000 | 1.000 | 0.018 | 0.131 | 0.000 | 1.000 | 0.146 | 0.353 | 0.000 | 1.000 |
| LGD | 0.329 | 0.436 | 0.000 | 1.000 | 0.306 | 0.383 | 0.000 | 1.000 | 0.470 | 0.400 | 0.000 | 1.000 |
| Type | Measure | Description |
|---|---|---|
| Classification | AUC | The area enclosed with the coordinate axis under the Receiver Operating Characteristic (ROC) curve2. |
| Accuracy | The proportion of correctly classified samples. | |
| Precision | The proportion of the truly classified samples to the total number of samples assigned to that class for a class. | |
| Recall | The proportion of true classified samples over the total of samples that belong to that class for a class. | |
| F1-score | This metric combines precision and recall by harmonizing averages and penalizes extreme values. | |
| Regression | MSE | Square of the difference between the true value and predicted value, which is then summed and averaged. |
| RMSE | MSE’s open square root. | |
| EV | The variance score of the explanatory regression model, which takes values in the range [0, 1]. | |
| MAE | Average of the absolute errors. | |
| Coefficient of determination. It is usually between 0 and 1 and reflects how accurately the model fits the data. |
| Clustering | Model | ACC | Precision | Recall | F1 | AUC | |
|---|---|---|---|---|---|---|---|
| Individual Models | no clustering | LR | 0.6025 | 0.6355 | 0.2556 | 0.3645 | 0.5731 |
| DT | 0.5958 | 0.5573 | 0.4570 | 0.5022 | 0.5947 | ||
| RF | 0.5999 | 0.5605 | 0.4775 | 0.5157 | 0.6180 | ||
| GBDT | 0.6295 | 0.6269 | 0.4186 | 0.5020 | 0.6694 | ||
| XGBoost | 0.6274 | 0.6157 | 0.4387 | 0.5123 | 0.6697 | ||
| MLP | 0.6265 | 0.6120 | 0.4449 | 0.5152 | 0.6641 | ||
| LightGBM | 0.6298 | 0.6201 | 0.4389 | 0.5140 | 0.6718 | ||
| K-means | clstering 1 | LR | 0.6052 | 0.6348 | 0.284 | 0.3925 | 0.6077 |
| DT | 0.5968 | 0.5609 | 0.4691 | 0.5110 | 0.5936 | ||
| RF | 0.6003 | 0.5623 | 0.4948 | 0.5264 | 0.6193 | ||
| GBDT | 0.6331 | 0.6316 | 0.4389 | 0.5179 | 0.6743 | ||
| XGBoost | 0.6338 | 0.6275 | 0.4539 | 0.5268 | 0.6744 | ||
| MLP | 0.6304 | 0.6224 | 0.4493 | 0.5219 | 0.6699 | ||
| LightGBM | 0.6341 | 0.6265 | 0.4585 | 0.5295 | 0.6773 | ||
| clustering 2 | LR | 0.6404 | 0.6386 | 0.1045 | 0.1797 | 0.6161 | |
| DT | 0.5788 | 0.4375 | 0.4142 | 0.4255 | 0.5580 | ||
| RF | 0.5958 | 0.4561 | 0.3787 | 0.4138 | 0.5913 | ||
| GBDT | 0.6263 | 0.5137 | 0.1479 | 0.2297 | 0.6157 | ||
| XGBoost | 0.5854 | 0.4358 | 0.3412 | 0.3827 | 0.5902 | ||
| MLP | 0.6397 | 0.641 | 0.0986 | 0.1709 | 0.6199 | ||
| LightGBM | 0.6018 | 0.4589 | 0.3195 | 0.3767 | 0.6055 | ||
| SOM | clustering 1 | LR | 0.6046 | 0.6403 | 0.2711 | 0.381 | 0.5982 |
| DT | 0.5931 | 0.5563 | 0.4605 | 0.5039 | 0.5854 | ||
| RF | 0.5989 | 0.5619 | 0.4816 | 0.5187 | 0.6135 | ||
| GBDT | 0.6296 | 0.6233 | 0.4416 | 0.5169 | 0.6691 | ||
| XGBoost | 0.6274 | 0.6153 | 0.4528 | 0.5217 | 0.6699 | ||
| MLP | 0.6254 | 0.6065 | 0.4701 | 0.5297 | 0.6633 | ||
| LightGBM | 0.6313 | 0.6228 | 0.4522 | 0.524 | 0.6718 | ||
| clustering 2 | LR | 0.6294 | 0.5714 | 0.1265 | 0.2072 | 0.5911 | |
| DT | 0.5866 | 0.4571 | 0.4282 | 0.4422 | 0.5657 | ||
| RF | 0.5866 | 0.4545 | 0.4015 | 0.4264 | 0.5828 | ||
| GBDT | 0.6145 | 0.4886 | 0.1557 | 0.2362 | 0.5967 | ||
| XGBoost | 0.5931 | 0.4558 | 0.326 | 0.3801 | 0.5917 | ||
| MLP | 0.6238 | 0.5321 | 0.1411 | 0.2231 | 0.5895 | ||
| LightGBM | 0.6071 | 0.4804 | 0.3285 | 0.3902 | 0.5998 | ||
| Clustering | Model | ACC | Precision | Recall | F1 | AUC | |
|---|---|---|---|---|---|---|---|
| ROS + Individual Models | no clustering | LR | 0.6597 | 0.6059 | 0.9304 | 0.7339 | 0.7105 |
| DT | 0.8240 | 0.7791 | 0.9085 | 0.8388 | 0.8803 | ||
| RF | 0.8233 | 0.7753 | 0.9147 | 0.8393 | 0.8934 | ||
| GBDT | 0.6998 | 0.6565 | 0.8485 | 0.7403 | 0.7662 | ||
| XGBoost | 0.7568 | 0.7147 | 0.8615 | 0.7813 | 0.8342 | ||
| MLP | 0.6845 | 0.6488 | 0.8159 | 0.7228 | 0.7410 | ||
| LightGBM | 0.7257 | 0.6795 | 0.8631 | 0.7603 | 0.7978 | ||
| ROS + K-means | clustering 1 | LR | 0.6556 | 0.6052 | 0.9033 | 0.7248 | 0.7138 |
| DT | 0.8248 | 0.7761 | 0.9148 | 0.8398 | 0.8807 | ||
| RF | 0.8215 | 0.7704 | 0.918 | 0.8377 | 0.8903 | ||
| GBDT | 0.6999 | 0.6541 | 0.8537 | 0.7407 | 0.7662 | ||
| XGBoost | 0.7582 | 0.7130 | 0.8675 | 0.7827 | 0.8350 | ||
| MLP | 0.6800 | 0.6392 | 0.8319 | 0.7230 | 0.7374 | ||
| LightGBM | 0.7265 | 0.6770 | 0.8704 | 0.7617 | 0.7951 | ||
| clustering 2 | LR | 0.6156 | 0.5908 | 0.8908 | 0.7104 | 0.6414 | |
| DT | 0.8786 | 0.8340 | 0.9620 | 0.8935 | 0.9061 | ||
| RF | 0.8794 | 0.8315 | 0.9684 | 0.8947 | 0.9588 | ||
| GBDT | 0.7429 | 0.7113 | 0.8655 | 0.7809 | 0.8188 | ||
| XGBoost | 0.8333 | 0.7906 | 0.932 | 0.8555 | 0.9172 | ||
| MLP | 0.6993 | 0.6775 | 0.8244 | 0.7438 | 0.7656 | ||
| LightGBM | 0.8057 | 0.7732 | 0.8956 | 0.8299 | 0.8940 | ||
| ROS + SOM | clustering 1 | LR | 0.6521 | 0.602 | 0.9074 | 0.7238 | 0.6875 |
| DT | 0.8773 | 0.8371 | 0.9383 | 0.8848 | 0.9055 | ||
| RF | 0.8847 | 0.8361 | 0.9584 | 0.8931 | 0.9575 | ||
| GBDT | 0.7323 | 0.7033 | 0.8081 | 0.7520 | 0.8165 | ||
| XGBoost | 0.8429 | 0.8168 | 0.8859 | 0.8500 | 0.9228 | ||
| MLP | 0.6871 | 0.6556 | 0.7946 | 0.7184 | 0.7538 | ||
| LightGBM | 0.8139 | 0.7877 | 0.8617 | 0.8231 | 0.8941 | ||
| clustering 2 | LR | 0.6628 | 0.6114 | 0.9001 | 0.7282 | 0.7134 | |
| DT | 0.8190 | 0.7731 | 0.9048 | 0.8338 | 0.8773 | ||
| RF | 0.8160 | 0.7668 | 0.9102 | 0.8324 | 0.8834 | ||
| GBDT | 0.6970 | 0.6522 | 0.8490 | 0.7377 | 0.7638 | ||
| XGBoost | 0.7542 | 0.7100 | 0.8625 | 0.7789 | 0.8311 | ||
| MLP | 0.6808 | 0.6337 | 0.8625 | 0.7306 | 0.7374 | ||
| LightGBM | 0.7244 | 0.6772 | 0.8614 | 0.7583 | 0.7942 | ||
| The Best Classification Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Route | First stage | Second stage | Third stage | MSE | RMSE | MAE | EV | |
| Route 1 | LightGBM | ROS + RF | OLS | 0.0968 | 0.3111 | 0.1838 | 0.4563 | 0.6106 |
| Route 2 | K-means (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS+ RF | 0.0968 | 0.3111 | 0.1837 | 0.4566 | 0.6106 | |
| SOM clustering + LightGBM | ROS+ RF | 0.0978 | 0.3128 | 0.1849 | 0.4508 | 0.6075 | ||
| Route 3 | LightGBM | ROS + K-means clustering + RF | 0.0969 | 0.3112 | 0.1838 | 0.4562 | 0.6104 | |
| LightGBM | ROS + SOM clustering + RF | 0.0967 | 0.3109 | 0.1836 | 0.4573 | 0.6115 | ||
| Route 4 | K-means (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + K-means clustering + RF | 0.0968 | 0.3111 | 0.1837 | 0.4566 | 0.6104 | |
| K-means (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + SOM clustering + RF | 0.0966 | 0.3108 | 0.1835 | 0.4577 | 0.6115 | ||
| SOM clustering + LightGBM | ROS + K-means clustering + RF | 0.0979 | 0.3128 | 0.1849 | 0.4506 | 0.6073 | ||
| SOM clustering + LightGBM | ROS + SOM clustering + RF | 0.0977 | 0.3125 | 0.1847 | 0.4518 | 0.6084 | ||
| The Best Classification Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Route | First stage | Second stage | Third stage | MSE | RMSE | MAE | EV | |
| Route 1 | LightGBM | ROS + RF | OLS | 0.0993 | 0.3151 | 0.1858 | 0.4428 | 0.6015 |
| Route 2 | K-means (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + RF | 0.0983 | 0.3136 | 0.1848 | 0.4479 | 0.6042 | |
| SOM (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + RF | 0.0992 | 0.3150 | 0.1859 | 0.443 | 0.6017 | ||
| Route 3 | Individual Models | ROS + K-means clustering + RF | 0.0995 | 0.3155 | 0.186 | 0.4412 | 0.6006 | |
| Individual Models | ROS + SOM clustering + RF | 0.0992 | 0.315 | 0.1858 | 0.4429 | 0.6018 | ||
| Route 4 | K-means (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + K-means clustering + RF | 0.0986 | 0.314 | 0.1851 | 0.4464 | 0.6032 | |
| K-means (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + SOM clustering + RF | 0.0983 | 0.3136 | 0.1848 | 0.4480 | 0.6045 | ||
| SOM (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + K-means clustering + RF | 0.0995 | 0.3154 | 0.1861 | 0.4414 | 0.6007 | ||
| SOM (clustering 1 + LightGBM) and (clustering 2 + MLP) | ROS + SOM clustering + RF | 0.0992 | 0.315 | 0.1859 | 0.4430 | 0.602 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Wu, T.-H.; Zhao, Q. Assessing the Loss Given Default of Bank Loans Using the Hybrid Algorithms Multi-Stage Model. Systems 2023, 11, 505. https://doi.org/10.3390/systems11100505
Fan M, Wu T-H, Zhao Q. Assessing the Loss Given Default of Bank Loans Using the Hybrid Algorithms Multi-Stage Model. Systems. 2023; 11(10):505. https://doi.org/10.3390/systems11100505
Chicago/Turabian StyleFan, Mengting, Tsung-Hsien Wu, and Qizhi Zhao. 2023. "Assessing the Loss Given Default of Bank Loans Using the Hybrid Algorithms Multi-Stage Model" Systems 11, no. 10: 505. https://doi.org/10.3390/systems11100505
APA StyleFan, M., Wu, T.-H., & Zhao, Q. (2023). Assessing the Loss Given Default of Bank Loans Using the Hybrid Algorithms Multi-Stage Model. Systems, 11(10), 505. https://doi.org/10.3390/systems11100505






