Evaluating Expressway Safety Based on Fuzzy Comprehensive Evaluation with AHP–Entropy Method: A Case Study of Jinliwen Expressway in Zhejiang Province, China

Abstract

To mitigate potential safety hazards during expressway operation, safety evaluation plays a crucial role. This study develops a fuzzy comprehensive evaluation model to assess the safety of expressway operations. First, an expressway operation safety risk assessment index system consisting of four criteria-layer indicators and 10 sub-criteria layer indicators is established. Then, the comprehensive weight of each evaluation index is calculated based on the combined AHP and entropy methods. Finally, the expressway safety level is obtained by converting qualitative indicators into fuzzy sets and defining corresponding membership functions to describe their degree of membership. The evaluation model is applied to the Jinliwen Expressway in a mountainous area in Zhejiang Province, China. The results show that the method could quantitatively and comprehensively evaluate the safety status of expressways and identify the weak links of operational safety management, which can effectively improve the safety level of expressway operations. The research findings will assist decision-makers in gaining a better understanding of the safety issues of expressways and, thus, using corresponding measures to enhance the safety level of the expressway.

1. Introduction

After nearly a century of development, expressways have emerged as crucial components in transportation infrastructure systems. By the end of 2021, China’s expressway network expanded to approximately 170,000 km, accommodating an annual traffic volume of around 5.1-billion passengers and over 3.9-billion tons of freight [1]. However, the rise of expressways has led to increasingly serious traffic safety issues. According to a survey, expressway accidents are expected to become the fifth-leading cause of death worldwide by 2030 [2]. To mitigate potential safety hazards, safety evaluation plays a crucial role in preventing accidents during expressway operations by accurately identifying the main risk factors that affect the safety of expressway operations.

Expressway traffic safety has been extensively studied from various perspectives using different methods. Some scholars evaluate the traffic safety of expressways based on historical traffic accident data, such as accident types, locations, causes, and casualties, to uncover potential safety issues on expressways and provide a basis for improving traffic safety. The current research can be broadly categorized into four types. The first type is accident frequency analysis [3], which primarily involves statistical analysis and identification of high-risk road sections and areas based on the occurrence frequency of traffic accidents, and the implementation of corresponding measures to reduce the probability of accidents. The second type is accident severity analysis [4,5], which focuses on casualties and economic losses in accidents, identifying locations with higher safety risks in order to take measures to reduce the severe consequences of accidents. The third type is accident factor analysis [6,7], which aims to identify the causes and related factors, such as speeding, drunk driving, and road conditions, which increase the probability of accidents. The fourth type is the use of GIS hotspot analysis of traffic accidents for traffic safety assessment [8,9]. Specifically, these studies reveal the geographical distribution patterns and hotspots of road traffic accidents, which aid analysts in achieving a better understanding of the spatial characteristics and influencing factors of accident occurrences. By processing and analyzing traffic accident data, it is possible to accurately identify expressway safety issues and further develop corresponding strategies for safety improvement. However, studies based on accident data also possess certain limitations. First, analyzing historical accident data results in a certain lag for predicting future accidents. Additionally, traffic accident data are limited and could be incomplete, and there may be a lack of analysis of the deeper causes of accidents. Furthermore, evaluating solely from the perspective of traffic accidents may overlook other factors influencing expressway safety.

Due to the complex nature of expressways, researchers have resorted to Multi-Criteria Decision-Making (MCDM) methods to evaluate their safety. The strength of MCDM methods lies in their ability to comprehensively consider multiple indicators and factors, thus providing a comprehensive evaluation result from multiple perspectives and enabling a more accurate assessment system of expressway safety. For expressway safety evaluation, commonly used MCDM methods include the Analytic Hierarchy Process (AHP), Entropy method, Technique for Order Preference by Similarity to Ideal Solution (TOPSIS method, and their modified or combined approaches [10]. AHP evaluates safety by establishing a hierarchical structure, comparing the importance of indicators and calculating weights [11,12]. The Entropy method measures the information and uncertainty of indicators by calculating their information entropy, effectively evaluating differences [13]. The TOPSIS method selects the optimal solution by calculating the degree of proximity between the evaluation schemes and the ideal solution [14]. However, in some complex application scenarios, a single method may not be able to accurately achieve the evaluation objectives. Therefore, researchers often use combined methods or improve individual methods to increase the accuracy and reliability of evaluation results [15,16]. For instance, a combination of the Entropy method and the TOPSIS method has been used. This is known as the Entropy–TOPSIS, where the Entropy method is used to determine the weight of each criterion for each scheme, and then the TOPSIS method is applied to compare the different schemes [17]. Considering the strong subjectivity of the AHP, the Grey Relational Analysis (GRA) technique is employed to analyze indicator data sequences and build grey relational models, providing more accurate and objective weight results. Thus, it improves the credibility of evaluation results [18]. Utilizing game theory to optimize the combination of indicator weights is another approach to overcome the limitations of a single method [19]. This enables a more comprehensive consideration of the relationships between various indicators and generates more scientifically sound weight results. Therefore, the AHP, Entropy method, TOPSIS method, and the combined methods play a crucial role in expressway safety evaluation.

The aforementioned MCDM methods are designed based on precise mathematical theory, employing exact values and accurate computational methods to address expressway safety issues. This is applicable in cases where each influencing factor is precise and a determined quantitative indicator. However, as the complexity of traffic systems increases, expressway safety levels are influenced not only by quantitative indicators, such as vehicle speed and visibility, but also by qualitative indicators. Consequently, precise mathematical methods face challenges when dealing with qualitative indicators since these indicators are often difficult to quantify or lack precise numerical data support. For qualitative indicators, a more suitable approach is to employ fuzzy mathematics [20], which has been validated in various fields such as transportation [21,22], agriculture [23,24], energy [25], environment [26,27], and economics [28]. In comparison to precise mathematical methods, fuzzy mathematics is capable of effectively handling fuzziness and uncertainties in data and indicators. By converting qualitative indicators into fuzzy sets and defining corresponding membership functions to describe their degree of membership, the level of uncertainty can be reflected. For instance, the degree of safety measure assurance can be defined as a fuzzy set of “excellent”, “average”, and “poor”, along with their corresponding membership functions. Subsequently, based on actual circumstances, the specific values of qualitative indicators are mapped to the corresponding membership function values, thereby obtaining a quantitative representation of qualitative indicators. This enables the comprehensive evaluation and decision-making of both qualitative and quantitative indicators simultaneously. In addition, it enables the integration of expert expertise and subjective judgments within the evaluation process, facilitating better utilization of expert knowledge. Therefore, in the safety assessment of expressway, where both quantitative and qualitative indicators are present, a combination of precise mathematical methods and fuzzy mathematics can be employed to consider the influence of various indicators, resulting in more comprehensive and accurate evaluation results. That is, fuzzy mathematics theory has played a significant role in numerous complex and ambiguous problem domains, delivering favorable evaluation outcomes.

This study develops a method for expressway safety evaluation considering both qualitative and quantitative indicators, which essentially falls under the category of complex fuzzy problems. We first analyze and select the main factors affecting the safety of expressway operation and establish an expressway operation safety risk assessment index system. Then, improved AHP and entropy methods are combined to determine the comprehensive weights of each evaluation indicator, mitigating subjective biases of indicator weights [29] while considering the interrelationships among indicators [30]. Finally, the expressway safety level is obtained by converting qualitative indicators into fuzzy sets and defining corresponding membership functions to describe their degree of membership [31]. Compared to the above methods, the fuzzy comprehensive evaluation has the following advantages in evaluating the safety levels of expressways. Firstly, it allows for evaluation from multiple perspectives and levels. Different factors can thus be considered. Secondly, this method transforms qualitative assessment into quantitative assessment using membership degree based on fuzzy mathematics, applying the principle of fuzzy relation synthesis and quantifying some factors with unclear boundaries. Therefore, it has strong practicability for all kinds of non-deterministic problems. Since safety assessments for expressways are a problem with multiple influencing factors, the fuzzy comprehensive evaluation method can thus be well-applied to evaluating the expressway safety level. The proposed evaluation method is illustrated using a case study in a mountainous area of Zhejiang Province in China. Results show that it could identify the safety level by evaluating risk factors during expressway operations. The research findings will assist decision-makers in gaining a better understanding of the safety issues of the Jinliwen Expressway in the Zhejiang Province and using corresponding measures to enhance the safety level of the expressway. It is of both theoretical and practical significance to guide the safety evaluation of expressway operations in China.

The rest of the paper is structured as follows. Section 2 presents the study area and the index system of the expressway safety level. Section 3 presents the evaluation method. Section 4 provides a case study. The last section presents conclusions.

2. Study Area and Establishment of Expressway Safety Evaluation Index System

2.1. Study Area

The Jinliwen Expressway, situated in Zhejiang Province, serves as a vital connection for the Shanghai–Kunming Expressway (National Expressway G60) and the Shenyang–Haikou Expressway (National Expressway G15) in central Zhejiang Province. The location map is shown in Figure 1. Opened on 24 December 2005, this expressway spans a total length of 234 km and includes multiple sections with tunnels, bridges, sharp curves, and downhill segments. Notably, the bridge distance on this expressway exceeds 70 km, while the tunnel distance exceeds 40 km. With a cumulative length of over 110 km, transportation experts often refer to it as the “Bridge and Tunnel Club”. Consequently, certain sections suffer from poor visibility and a limited line of sight. Furthermore, Zhejiang Province experiences a long duration of rainy weather during the plum rain season. Rainfall leads to a decrease in the road surface friction coefficient, resulting in weakened skid resistance. Historical data also indicate that accidents frequently occur on the Jinliwen Expressway. Considering the aforementioned circumstances, there is a need to conduct a study on the safety issues of this expressway. Therefore, this study selects four accident-prone sections (each with a length of 2 km) on this expressway as the research subjects.

2.2. Establishment of Expressway Safety Evaluation Index System

The region traversed by the Jinliwen Expressway encompasses diverse topographies, including mountainous terrain, tunnels, and bridges, resulting in varying meteorological conditions along different sections. Furthermore, there are variations in road design parameters related to the longitudinal, transverse, and vertical aspects, as well as differences in the implementation of traffic safety measures. Moreover, disparities in management and service levels may exist among different segments of the expressway. These factors collectively contribute to significant fluctuations in the safety grading of different sections. Therefore, ensuring an accurate assessment of the safety grading for each segment of the expressway is of utmost importance. The initial step in evaluating the safety grading involves formulating a precise and efficient evaluation framework.

This study constructs an index system to evaluate the expressway safety level following a comprehensive literature review [32,33,34]. Specifically, the evaluation index system includes four criteria-layer indicators, denoted as set $I=\left\{\mathrm{1,2},\cdots ,\left|I\right|\right\}$ and 10 sub-criteria layer indicators, denoted as set $J=\left\{\mathrm{1,2},\cdots ,\left|J\right|\right\}$. The evaluation system is shown in Figure 2.

2.2.1. Road Design

The horizontal curve radius (HCR) represents the arc-shaped curve formed when a road transitions from one straight segment to another. A larger radius results in a more gradual turning process, providing a greater turning radius, thereby facilitating better vehicle control for drivers and reducing the likelihood of emergencies. The size of the radius directly correlates with road safety as a larger radius indicates enhanced safety levels.

Sight distance (SD) refers to the distance at which drivers can consistently observe obstacles within the lane ahead or see the maximum distance of traffic facilities and road markings in front of the roadway from their regular driving position. The distance is measured along the centerline of the lane. A longer sight distance is directly correlated with higher levels of road safety.

The road linear combination (RLC) entails the rational integration of indicators such as curvature radius, straight-line length, and longitudinal slope within road sections. Vehicle speed provides a direct reflection of the linear quality of road segments during travel [35]. Moreover, the “Guidelines for Safety Evaluation of Highway Projects” utilize the ratio of running speed difference between adjacent sections $RV=\left(V_1-V_2\right)/V_2$ as an indication of the rationality of road linear combinations, where $V_1$ represents the current section’s running speed value, and $V_2$ represents the preceding section’s running speed value. A smaller RV value signifies a more appropriate road linear combination and, consequently, a higher level of safety.

2.2.2. Pavement Condition

According to the standard Terminology for Highway Engineering set by the Chinese Ministry of Transport and the national standard Terminology for Road Engineering, pavement roughness (PR) is defined as the vertical deviation between the longitudinal irregularities of the road surface and the ideal plane. This research assesses PR by measuring the vertical cumulative displacement of the suspension system when a vehicle travels a standardized distance at a constant speed of 80 km/h [36]. A smaller cumulative displacement indicates superior pavement roughness. Studies have indicated that as the pavement roughness worsens, the working conditions of the driver become much more complicated. Drivers are constantly forced to monitor the road condition, the presence of potholes, pits, and cracks while slowing down and picking up speed, adjusting to the traffic situation, and often changing the trajectory of movement. Such circumstances lead to the fact that the driver’s attention is concentrated on maneuvers, and not on other important components from the point of view of ensuring traffic safety. Under such conditions, an increase in the accident rate is an inevitable phenomenon [37]. Therefore, deteriorating pavement conditions can add to the traffic safety problem [38,39,40].

The surface skid-resisting capability (SSC) refers to the ability of a road surface to prevent skidding between the tires and the pavement. In this study, texture depth (TD) is used as a measure. According to the Specifications for Design of Highway Asphalt Pavement, the TD value for expressways should be greater than 0.9 mm. A higher TD value indicates stronger surface skid-resisting capability, leading to improved road safety.

2.2.3. Traffic Environment

In this study, maximum travel speed (MTS) refers to the design speed of the target road section. Due to the diverse meanings of travel speed and the difficulty in data acquisition, this study adopts MTS as an indicator reflecting the relationship of road safety. Within a certain range, the higher the MTS, the greater the likelihood and severity of accidents, and the lower the safety.

Road traffic saturation (RTS) refers to a metric used to evaluate the level of traffic load on a road. In this study, the ratio of the maximum traffic volume to the road’s maximum capacity is employed as an indicator of road traffic saturation. When the traffic volume is low, vehicles are in a free-flow state with less interference from other vehicles during normal driving, resulting in relatively low risks of traffic accidents. When the traffic volume is high because of an insufficiently safe distance between vehicles, the frequent overtaking or failure to utilize timely emergency braking actions could occur and, thus, lead to traffic accidents [7]. However, under stable flow conditions, a lower value of RTS indicates a higher level of road safety [41].

2.2.4. Management Measures

In this study, management measures are considered as qualitative indicators, and a four-point rating scale method is used to quantify the following indicators [42,43]. Firstly, the monitoring system and emergency rescue system qualitative indicators are divided into four grades, represented quantitatively using the numbers 1 to 4 (1 = low, 2 = medium, 3 = high, 4 = very high) based on the theory of fuzzy mathematics and the four-point rating scale method, the traffic safety measures [44]. Subsequently, 25 experts (expert details could be found in Section 4.1) evaluated these indicators according to the actual situation. The scores could be averaged, thereby achieving the quantification of qualitative indicators.

Traffic safety measures (TSM) refer to the various actions utilized in the road traffic system with the aim of preventing and reducing traffic accidents and protecting the lives and property of drivers, passengers, and pedestrians.

The monitoring system (MS) refers to the surveillance and management facility deployed on expressways. It employs real-time monitoring and data analysis to provide valuable information and support, ensuring the safety and smooth operation of the expressways. Its primary objective is to safeguard the security and efficiency of the expressway network by continuously monitoring and analyzing data, as well as providing pertinent insights and assistance.

The emergency rescue system (ERS) is a set of equipment and a service system designed to respond quickly to emergency situations. It provides prompt responses and professional assistance, creating a safer environment for road users. This system can reduce the consequences of accidents and enable timely handling of emergencies, thereby enhancing the safety of expressways.

3. Methodology

This study adopts a fuzzy comprehensive evaluation method to determine the safety levels of expressways. Figure 3 depicts the process of evaluating the safety ratings of expressways. Firstly, the improved AHP is used to calculate the subjective weights based on expert evaluations (see Section 3.1). Secondly, the entropy weight method is employed to obtain weights based on objective evaluation factors (see Section 3.2). This process enables a more precise reflection of the relative importance of each indicator in the assessment of safety levels. Subsequently, the Lagrange multiplier method is employed to combine subjective and objective weights, resulting in comprehensive weights (see Section 3.3). Finally, a fuzzy comprehensive evaluation matrix is constructed using membership functions to address the fuzziness and uncertainty between evaluation indicators (see Section 3.4). By employing the weighted average operator, the weights are multiplied by the evaluation matrix to obtain the final assessment of the expressway’s safety level.

3.1. Improved Analytic Hierarchy Process (AHP)

AHP is adopted to calculate the comparative importance of each criterion based on a nine-point scale showing the preference for one criterion against each other. The first step of AHP is to construct a judgment matrix $A$ by employing a pairwise comparison of criteria layer indicators, where each element $a_{i{i}^{\prime }}$ represents the relative importance of indicator $i$ to indicator $i^{\prime }$. In practice, $a_{i{i}^{\prime }}$ can be obtained from experts through a survey. In particular, the value of $a_{i{i}^{\prime }}$ is set based on Satty’s scale weights, including a total of nine degrees with increasing importance. Note that $I$ is in the criteria layer indicator set. The specific explanation is further explained in

Table 1. Importance scale in AHP.

Degree	Descriptions
1	Equally important
3	Moderately important
5	Strongly important
7	Very strongly important
9	Extremely important
2, 4, 6, 8	The intermediate situation between the above two adjacent judgments
Reciprocals	Inverse comparison

.

$$A=\left[\begin{array}{cccc}1& a_{12}& \cdots & a_{1\left|I\right|}\\ a_{21}& 1& \cdots & a_{2\left|I\right|}\\ \cdots & \cdots & 1& \cdots \\ a_{\left|I\right|1}& a_{\left|I\right|2}& \cdots & 1\end{array}\right]$$

(1)

$$A·\gamma ={\lambda }_{max}·\gamma$$

(2)

where ${\lambda }_{max}$ is the maximum eigenvalue of the n-order evaluation matrix $A$; $\left|I\right|$ is the number of indicators in criteria layer; $\gamma$ is the eigenvector corresponding to the maximum eigenvalue ${\lambda }_{max}$.

Inconsistencies may arise due to careless errors or overstated judgments of experts during the process of pairwise comparison. In this study, a consistency test is conducted based on the consistency ratio (CR). CR is computed as the ratio of consistency index (CI) of the judgment matrix and the random index (RI). The value of RI is determined by the order of judgement matrix [45,46], which is shown in

Table 2. RI value.

Order of Judgement Matrix	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

.

$$CR=\frac{CI}{RI}=\frac{{\lambda }_{max}-\left|I\right|}{\left|I\right|-1}·\frac{1}{RI}$$

(3)

If CR is greater than 0.10, the judgments should be revised to detect the source of the inconsistency and resolve it [47]. If the consistency test is satisfied, i.e., less or equal to 0.10, the eigenvector $\gamma$ is normalized to obtain the subjective weight vector ${\zeta }_n$ of the expert group $n$, where $n\in N$ and $N$ is the set of expert groups.

Traditional AHP is influenced by factors such as the research focus and work experience of domain experts, resulting in significant discrepancies in their subjective judgments of the relative importance between indicators. To address this issue, this study applied the improved AHP by introducing correlation coefficients. Firstly, multiple expert groups are utilized to evaluate the criteria layer indicators, resulting in multiple subjective weight vectors. Secondly, the subjective weight vectors from each expert group are arranged in rows to form a weight matrix $C$, as shown in Equation (4). Then, the correlation coefficients are computed using the data from matrix $C$, as shown in Equation (5). Finally, the cumulative similarity between expert group $n$ and other expert groups is computed, as shown in Equation (6).

$$C=\left[\begin{array}{c}{\zeta }_1\\ {\zeta }_2\\ ⋮\\ {\zeta }_{\left|N\right|}\end{array}\right]=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1\left|I\right|}\\ c_{21}& c_{22}& \cdots & c_{2\left|I\right|}\\ \cdots & \cdots & \cdots & \cdots \\ c_{\left|N\right|1}& c_{\left|N\right|1}& \cdots & c_{\left|N\right|\left|I\right|}\end{array}\right]$$

(4)

$$d_{n{n}^{\prime }}=1-\sqrt{\frac{1}{\left|I\right|}{\sum }_{i\in I}{(c_{ni}-c_{n^{\prime }i})}^2},\forall n,n^{\prime }\in N$$

(5)

$$d_n={\sum }_{n^{\prime }\in N}{d}_{{nn}^{\prime }},\forall n\in N$$

(6)

where $d_{{nn}^{\prime }}$ denotes the correlation coefficient between expert $n$ and expert $n^{\prime }$, with $d_{nn}=1$, $d_{{nn}^{\prime }}=d_{n^{\prime }n}$, $d_n$ denote the cumulative similarity between expert group $n$ and other expert groups.

A smaller value of $d_n$ indicates that the weight vector ${\zeta }_n$ corresponding to expert group $n$ exhibits a greater degree of deviation. The significantly deviated subjective weight vectors of expert groups are removed (with an approximate ratio of 20–30%), resulting in a new weight matrix $C^{\prime }$ [48]. Then, the elements in matrix $C^{\prime }$ are averaged column-wise to obtain $\left|I\right|$ criteria layer indicator values, $\Psi =\left({\phi }_1,{\phi }_2,\cdots ,{\phi }_{\left|I\right|}\right)$, where ${\phi }_i$ denote the subjective weight for the indicator $i$ in the criteria layer.

In this study, the method for calculating the subjective weights of sub-criteria indicators is the same as that used for the criteria layer and, therefore, is not reiterated. Let $\Omega =\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_{\left|J\right|}\right)$ denotes the weighting vector, where ${\alpha }_j$ is the subjective weight of indicator $j$ in the sub-criteria layer.

3.2. Entropy Weight Method

In this section, the objective weights of indicators in the sub-criteria layer are calculated based on the idea of information entropy.

Let $M$ denote the set of road sections for evaluation. Let $X$ denote the entropy weight matrix, where $x_{mj}(m\in M,j\in J)$ denotes the value of indicator $j$ for road section $m$. In order to eliminate the influence of different indicator units on the evaluation results, each indicator is standardized. The step transformation method is a standardization method used commonly, as shown in Equations (8) and (9).

$$X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1\left|J\right|}\\ x_{21}& x_{22}& \cdots & x_{2\left|J\right|}\\ ⋮& ⋮& \ddots & ⋮\\ x_{\left|M\right|1}& x_{\left|M\right|2}& \cdots & x_{\left|M\right|\left|J\right|}\end{array}\right]$$

(7)

$$x_{mj}^{\prime }=\left\{\begin{array}{c}\frac{x_{mj}-x_j^{min}}{x_j^{max}-x_j^{min}},x_j^{max}\ne x_j^{min}\\ 1,x_j^{max}=x_j^{min}\end{array}\right.(\mathrm{applicable} \mathrm{benefit} \mathrm{indicators})$$

(8)

$$x_{mj}^{\prime }=\left\{\begin{array}{c}\frac{x_j^{max}-x_{mj}}{x_j^{max}-x_j^{min}},x_j^{max}\ne x_j^{min}\\ 1,x_j^{max}=x_j^{min}\end{array}\right. (\mathrm{applicable} \mathrm{cost} \mathrm{indicators})$$

(9)

where $x_{mj}^{\prime }$ is the normalized value of $x_{mj}$; $x_j^{max}$ and $x_j^{min}$ denote the maximum and minimum values of indicator $j$ in sub-criteria layer, respectively. Then, the objective weight ${\beta }_j$ for indicator $j$ in the sub-criteria is calculated via Equations (10)–(12) [49].

$$p_{mj}=\frac{x_{mj}^{\prime }}{{\sum }_{m\in M}{x}_{mj}^{\prime }},j\in J$$

(10)

$$e_j=-\frac{1}{\mathit{ln}\left|M\right|}{\sum }_{m\in M}{p}_{mj}\mathit{ln}{p}_{mj},j\in J$$

(11)

$${\beta }_j=\frac{1-e_j}{{\sum }_{j\in J}(1-e_j)},j\in J$$

(12)

3.3. Comprehensive Weight Method

In Section 3.1 and Section 3.2, the subjective weights and objective weights of indicators are calculated through improved AHP and Entropy methods, respectively. Due to the different principles of the two methods, there are slight differences in the subjective and objective weights. In this section, comprehensive weights are computed by combinng the two types of weights, which not only reflect the preference of experts but also the influence of objective indicators. According to the minimum relative entropy [50,51], the weights of each indicator obtained from different methods should be close. Therefore, the objective function is shown in Equation (13).

$$minF={\sum }_{j\in J}{\omega }_j\mathit{ln}(\frac{{\omega }_j}{{\alpha }_j})+{\sum }_{j\in J}{\omega }_j\mathit{ln}(\frac{{\omega }_j}{{\beta }_j})$$

(13)

s.t.

$${\sum }_{j\in J}{\omega }_j=1$$

(14)

$${\omega }_j>0,j\in J$$

(15)

where ${\omega }_j$ is the comprehensive weight of indicator $j$ in the sub-criteria layer. The objective function is solved using the Lagrangian function, and the solution is shown in Equation (16).

$${\omega }_j=\frac{\sqrt{{\alpha }_j{\beta }_j}}{{\sum }_{j\in J}\sqrt{{\alpha }_j{\beta }_j}},j\in J$$

(16)

3.4. Fuzzy Comprehensive Evaluation

The fuzzy comprehensive evaluation is based on the theory of maximum membership degree and the principle of fuzzy transformation in fuzzy mathematics [52]. It quantifies indicators that are not clear and comprehensively evaluates the membership degree of the evaluated objects based on multiple indicators [53]. In this study, the multi-level fuzzy comprehensive evaluation method is used to establish the safety evaluation model of the expressway.

Let $L=\left\{\mathrm{1,2},\cdots ,\left|L\right|\right\}$ denote the set of the safety level, where $l$ represents the $l\mathrm{th}$ safety level. Then, the fuzzy evaluation matrix $S$ for the sub-criteria layer indicator is established based on a survey, where participants select the safety level for each indicator based on their circumstances. The relationship between the sub-criteria layer indicators and the evaluation level set $L$ can be demonstrated based on a membership function, which is used to describe the fuzziness of the sub-criteria layer indicators by assigning sub-criteria layer each indicator a level of membership ranging between zero and one. Specifically, the membership degree $s_{jl}$ for indicator $j$ in sub-criteria layer corresponding to the $l\mathrm{th}$ safety level is calculated based on the survey, where $Y_l$ is the number of participants chosen the $l\mathrm{th}$ safety level in the survey.

$$s_{jl}=\frac{Y_l}{{\sum }_{l\in L}{Y}_l},j\in J$$

(17)

$$S=\left[\begin{array}{cccc}{s}_{11}& s_{12}& \cdots & s_{1\left|L\right|}\\ s_{21}& s_{22}& \cdots & s_{2\left|L\right|}\\ ⋮& ⋮& ⋮& ⋮\\ s_{\left|J\right|1}& s_{\left|J\right|2}& \cdots & s_{\left|J\right|\left|L\right|}\end{array}\right]$$

(18)

Then, the fuzzy comprehensive vector $R_i$ for criteria layer is obtained based on the the comprehensive weight vector for indicators in the sub-criteria layer and the fuzzy evaluation matrix, as shown in Equation (19).

$$R_i=W_i·S_i,i\in I$$

(19)

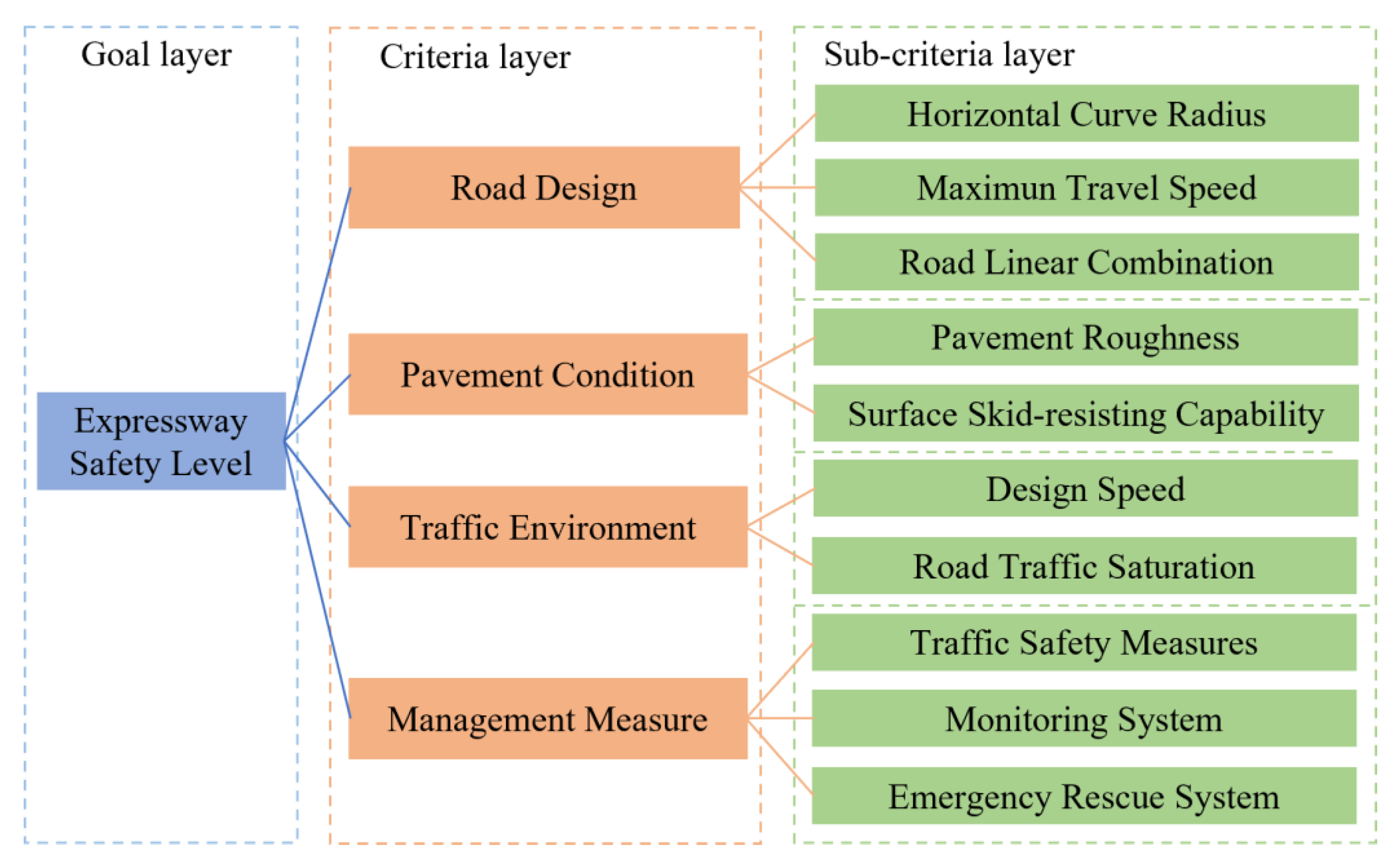
where $W_i={[\omega }_j],j\in H_i$, and where $H_i$ is the set of sub-criteria layer indicators under criteria layer indicator $i$, as illustrated in Figure 1. Similarly, the fuzzy evaluation matrix $S$ is also partitioned into sub-matrices $S_i=\lceil s_{jl}\rceil ,j\in H_i,l\in L$.

Finally, the fuzzy comprehensive vector $B$ of the goal layer indicator is calculated as follows.

$$B=\Psi ·R=(b_1,b_2,\cdots ,b_{\left|L\right|})$$

(20)

where $R=(R_i,i\in I)$ is the fuzzy comprehensive matrix for the criteria layer, composed of four fuzzy comprehensive weight vectors of the criteria layer.

Based on the fuzzy comprehensive evaluation vector B of the goal layer indicators, the safety level of the evaluated road section is determined using the maximum membership principle. That is, $b_l=max\left\{b_1,b_2,\cdots ,b_{\left|L\right|}\right\}$, then the safety level of the evaluated road section is classified as the $l\mathrm{th}$ level.

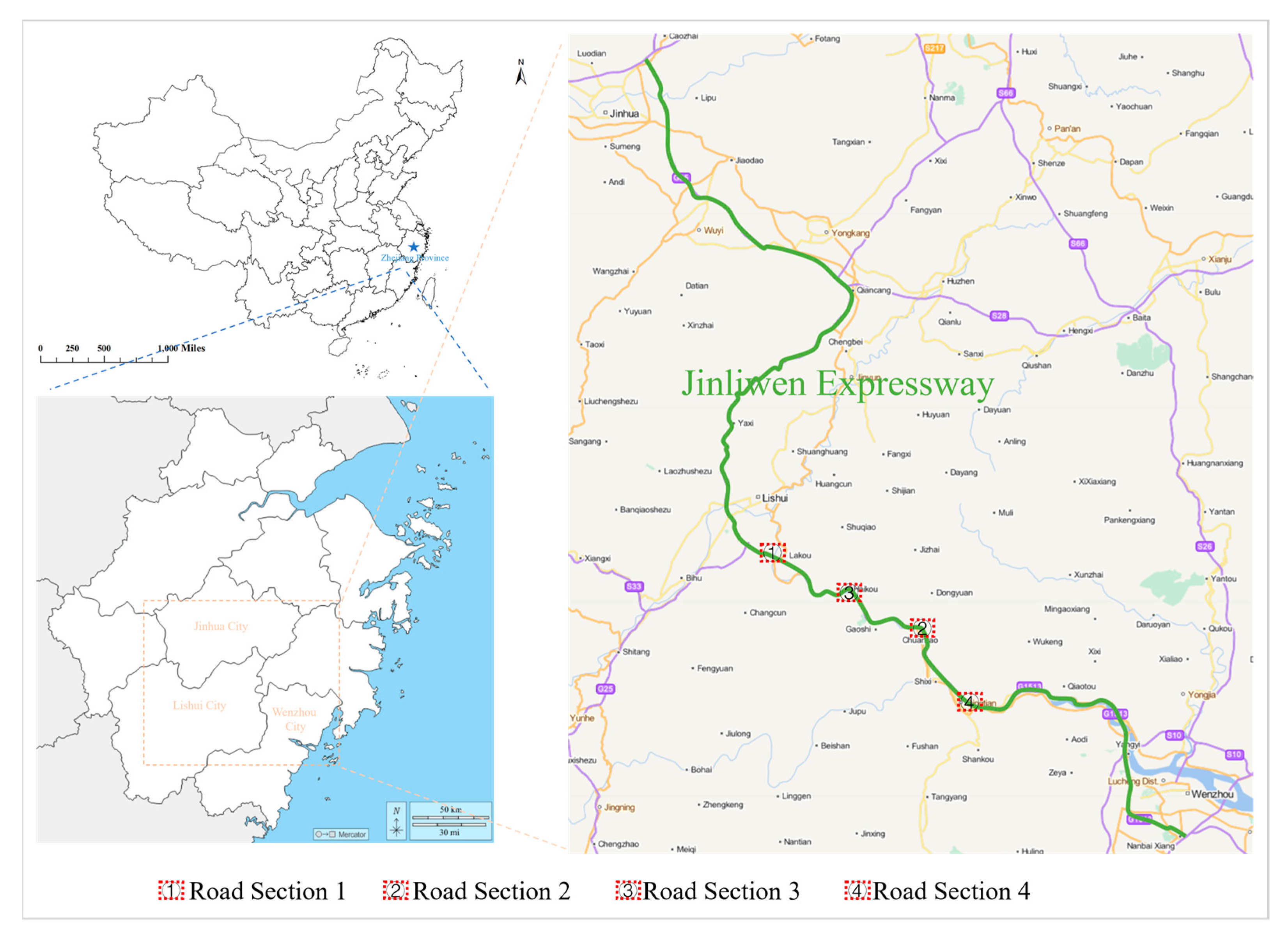
4. Case Study

In this section, the fuzzy comprehensive evaluation method proposed in this study is applied to assess the safety of four road sections on the Jinliwen Expressway in Zhejiang Province.

4.1. Data Sources

In this study, $\left|L\right|=4$, indicating there are four safety levels [54,55], i.e., safe, relatively safe, generally safe, and unsafe.

The relative importance of each indicator for constructing the judgment matrix $A$ in improved AHP is obtained from experts. In order to obtain an accurate judgment matrix, the selection of experts is crucial to the results [26,56]. Experts from different institutions are invited to ensure the credibility of the results. When inviting experts, we first established a database of experts (by selecting appropriate experts from relevant enterprises, universities, and scientific research institutions) and sent invitations to these experts to confirm whether it is convenient to assess the indexes. Finally, 25 experts confirm the invitations. Among them are 10 university professors engaged in traffic safety research, 10 researchers from the Transportation Planning Design and Research Institute (TPD and RI), and five senior expressway traffic maintenance personnel. Details of the experts are shown in

Table 3. Details of the experts.

Institutions	Seniority
	5 Years or Below	5–10 Years	10 Years or Above
University	2	4	4
TPD and RI	3	4	3
Co., LTD	1	2	2

[44]. These experts have the following characteristics: (1) Working and researching expressway safety; (2) Having rich experience or knowledge of safe management and safe assessment. These experts have extensive research or work experience in the field of expressway safety, enabling them to construct accurate judgement matrices.

The objective weights of the indicators in the sub-critera layer are calculated based on the values of indicators $X$, as shown in

Table 4. Sub-criteria layer indicators data for four evaluated road sections of the Jinliwen expressway.

Sub-Criteria Layer Indicators	Unit	Road Section 1	Road Section 2	Road Section 3	Road Section 4
Horizontal curve radius	M	6200	3450	1100	4000
Sight distance	M	210	200	140	190
Road Linear combination	/	0.72	0.79	0.48	0.82
Pavement roughness	mm	2.4	2.8	2.5	3.0
Surface skid-resisting capability	mm	0.94	0.85	0.91	0.85
Maximum Travel Speed	km/h	80	100	80	120
Road traffic saturation	/	0.28	0.33	0.30	0.33
Traffic safety measures	/	3.3	3.2	3.5	3.7
Monitoring system	/	1.8	2.3	2.2	2.8
Emergency rescue system	/	2.3	2.7	2.5	2.6

. The corresponding data are obtained from statistical yearbooks, government portals, traffic white papers, data centers of expressway operation and management departments, expressway performance evaluation reports, and actual measurements.

A survey is conducted to assess the safety level of each indicator in sub-criterion for each road section in order to construct the evaluation matrix $S$. The survey was conducted from 15 May to 20 May 2023, for a duration of 6 consecutive days. Specifically, we distributed questionnaires randomly in the service area and toll stations near the four road sections from 9:00 a.m. to 12:00 p.m. and from 2:00 p.m. to 6:00 p.m. Moreover, each participant is only allowed to participate in the survey once. Therefore, in this paper, we do not compare the impact of participants on the survey results at different times or under different circumstances. Participants include drivers over 18 years old and staff members located at the nearest service areas and toll stations to the road sections, as well as residents living along the road segments. Finally, a total of 600 questionnaires were distributed for the road section 1, and 558 questionnaires were collected. After removing invalid questionnaires such as non-standard filling and unreasonable data, 542 valid questionnaires were obtained. The statistical results of the survey on road section 1 are shown in

Table 5. Statistical description for road section 1 based on the survey.

Sub-Criteria Layer Indicators	Safety Level
	I	II	III	IV
Horizontal curve radius	271	120	109	42
Sight distance	304	163	54	21
Road Linear combination	195	184	98	65
Pavement roughness	249	173	109	11
Surface skid-resisting capability	141	249	130	22
Maximum Travel Speed	314	163	65	0
Road traffic saturation	173	206	141	22
Traffic safety measures	206	195	108	33
Monitoring system	260	163	108	11
Emergency rescue system	217	141	162	22

. For instance, 271 represents there are participants who choose safety level Ⅰ for the Horizontal Curve Radius indicator.

4.2. Results

4.2.1. Weights Calculation

(1) Calculation of the subjective weights. To avoid the potential bias caused by the experience deviation of individual experts in calculating subjective weights and to ensure accurate evaluation results, we have implemented a grouping strategy for the experts. We divided the experts into five distinct groups based on their detailed expertise, including institution and seniority. Each group consists of two university professors engaged in traffic safety research, two researchers from the Transportation Planning Design and Research Institute, and one senior expressway traffic maintenance personnel, and it is ensured that the working years of each group of experts were roughly the same [57]. This approach guarantees that each group consists of experts from different institutions, thereby enhancing both diversity and reliability. Additionally, dividing the 25 experts into five groups facilitates computational efficiency and enables the ease of conducting case studies. The five expert groups mentioned above utilize the AHP to calculate the weights for the criteria level. The calculated weight vectors are as follows: ${\zeta }_1=\left(0.23,0.14,0.55,0.08\right)$, ${\zeta }_2=\left(0.22,0.13,0.52,0.13\right)$, ${\zeta }_3=\left(0.20,0.14,0.53,0.13\right)$, ${\zeta }_4=\left(0.20,0.14,0.51,0.15\right)$, and ${\zeta }_5=\left(0.21,0.13,0.52,0.14\right)$.

The weight vectors of each expert group constitute the weight matrix $C$. According to Equations (5)–(7), the sum of similarities for the five expert groups are $d_1=4.82$, $d_2=4.94$, $d_3=4.94$, $d_4=4.91$, and $d_5=4.94$, respectively. As the value of $d_n$ decreased, the deviation degree of the weight evaluated by an expert n increased. Thus, the cweight vector ${\zeta }_1$ of expert group 1 is eliminated. Next, the four weight vectors ${\zeta }_2$, ${\zeta }_3$, ${\zeta }_4$, and ${\zeta }_5$ are used as row vectors to construct the weight matrix $C^{\prime }$. The improved subjective weight vector $\Psi =(0.21,0.13,0.52,0.14)$ for indicators in the criteria layer is then computed as the column-wise average of matrix $C^{\prime }$.

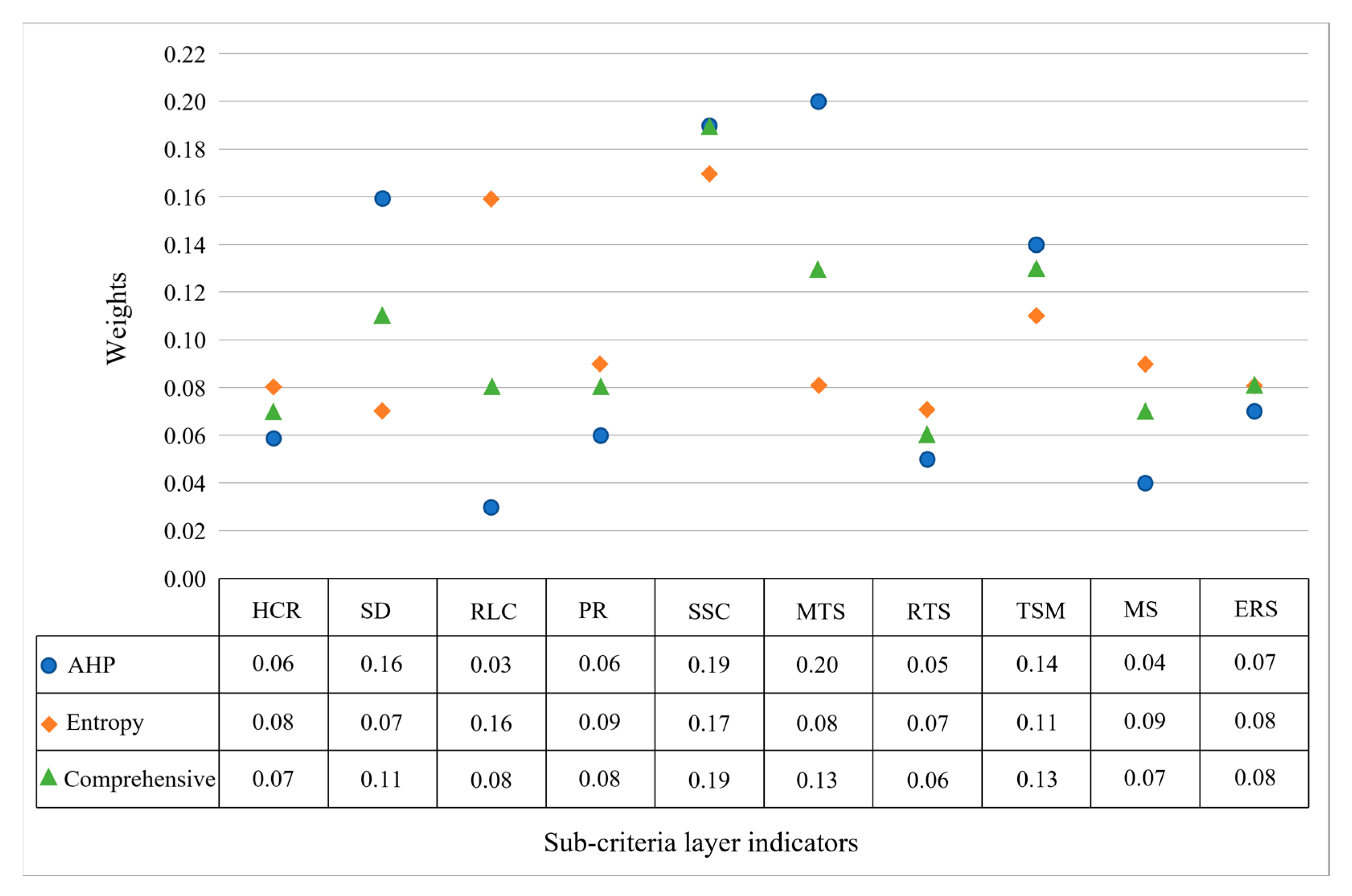
The subjective weights for indicators in the sub-criteria layer are calculated using the same method, and the results are shown in Figure 4.

(2) Calculation of the Objective Weights and the Comprehensive Weights. Through the methods proposed in Section 3.2 and Section 3.3, the objective weights and the comprehensive weights of the sub-criteria layer indicators are solved respectively. The results are shown in Figure 4.

4.2.2. Safety Level Evaluation

We next explore the process of calculating the fuzzy evaluation matrixes. Using road section 1 as an example, the membership degree $s_{jl}$ is computed based on the data provided in Table 5. Then, the fuzzy evaluation matrixes corresponding to the road design, the pavement condition, the traffic environment, and the management measure are obtained.

$$\begin{gathered} S_1=\left[\begin{array}{ccc}0.50& 0.22& \begin{array}{cc}0.20& 0.08\end{array}\\ 0.56& 0.30& \begin{array}{cc}0.10& 0.04\end{array}\\ 0.36& 0.34& \begin{array}{cc}0.18& 0.12\end{array}\end{array}\right],S_2=\left[\begin{array}{ccc}\begin{array}{cc}0.46& 0.32\end{array}& 0.32& 0.02\\ \begin{array}{cc}0.26& 0.46\end{array}& 0.24& 0.04\end{array}\right] \\ {S}_3=\left[\begin{array}{ccc}\begin{array}{cc}0.58& 0.30\end{array}& 0.12& 0.00\\ \begin{array}{cc}0.32& 0.38\end{array}& 0.26& 0.04\end{array}\right],S_4=\left[\begin{array}{ccc}\begin{array}{cc}0.38& 0.36\end{array}& 0.20& 0.06\\ \begin{array}{cc}0.48& 0.30\end{array}& 0.20& 0.02\\ \begin{array}{cc}0.40& 0.26\end{array}& 0.30& 0.04\end{array}\right] \end{gathered}$$

The fuzzy comprehensive vectors of the criteria layer indicators are then calculated by the weighted average method, which are listed as follows.

$$\begin{gathered} R_1=W_1·S_1=(0.13,0.08,0.04,0.02) \\ {R}_2=W_2·S_2=(0.09,0.11,0.07,0.01) \\ {R}_3=W_3·S_3=(0.09,0.06,0.03,0.00) \\ {R}_4=W_4·S_4=(0.12,0.07,0.04,0.01) \end{gathered}$$

The sub-criteria layer evaluation vectors are formed into the fuzzy comprehensive matrix $R={\left[R_1,R_2,R_3,R_4\right]}^T$. Based on weight vector $\Psi =(0.21,0.13,0.52,0.14)$ and the fuzzy comprehensive matrix $R$; the fuzzy comprehensive vector for the goal layer, $B$, is then calculated as follows.

$$B=\Psi ·R=(0.10,0.07,0.04,0.01)$$

Note that $b_{max}=b_1$. According to the principle of maximum membership degree, the safety level of road section 1 is Level Ⅰ, i.e., safe. Similarly, the safety levels of road sections 2–4 are calculated respectively. For the road section 2, $B=(0.08,0.11,0.06,0.01),$ $b_{max}=b_2$. For the road section 3, $B=(0.07,0.12,0.06,0.01)$, $b_{max}=b_2$. For the road section 4, $B=(0.09,0.07,0.10,0.01)$, $b_{max}=b_3$. Thus, the comprehensive evaluation results of road sections 2 and 3 are relatively safe, while the comprehensive evaluation result of road section 4 is generally safe.

4.3. Discussions

The evaluation of the Jinliwen Expressway in Zhejiang sections revealed different safety levels for each road section, providing valuable insights for the optimization work of transportation management departments. According to Figure 4, the comprehensive weights of sight distance, surface skid-resisting capability, maximum travel speed, and traffic safety measures all exceed the average value, that is, greater than 0.1. This result shows that these four factors play an important role in the evaluation of expressway safety. Therefore, a detailed analysis is conducted to assess the impact of the four indicators on the safety of the evaluated road sections.

According to the Highway Alignment Design Specification issued by the Ministry of Transport of China, if the SD indicator value is greater than 160 m, it is considered to meet the safety requirement and will not have a negative impact on the safety level of the road section. Similarly, if the MTS indicator value is less than 120 km/h and the SSC index value is greater than 0.9 mm, they are also considered to meet the safety requirements.

For road section 1, the sight distance, surface skid-resisting capability and traffic safety measures are observed to be of a high level. The values of these three indicators all meet the safety requirements. Additionally, the MTS indicator value is 80 km/h, which is less than the maximum design speed of 120 km/h in the Highway Alignment Design Specification. The speed value also meets the safety requirements. Therefore, road section 1 is considered safe.

For road section 2, with a sight distance of 200 m and a maximum travel speed of 100 km/h, both of these indicators meet the safety requirements in Highway Alignment Design Specification released by the Ministry of Transport of China. However, the SSC index value is less than 0.9 mm, which is not within the safe range. Thus, we focus on the impact of the SSC indicator on the safety level for this road section. Due to the long construction time of section 2, the road surface is severely worn, resulting in a small road surface adhesion coefficient and a long brake distance, especially in rainy and snowy weather. Many rear-end collision accidents occur, which lowers the safety level. According to the road conditions, the road surface should be repaired to improve the surface skid-resisting capability. Additionally, although the sight distance meets the design requirements, the actual surface skid-resisting capability of this section has decreased, resulting in a longer braking distance. Therefore, in order to enable drivers to have earlier awareness of the road conditions ahead and increase their reaction time, it is advisable to consider increasing the sight distance in such situations. This is expected to enhance traffic safety.

For road section 3, the SSC, MTS, and TSM indicators comply with the requirements of the Highway Alignment Design Specification. Therefore, SSC, MTS, and TSM indexes have little influence on the safety level of road section 3. However, the value of the SD indicator is only 140 m, which is less than 160 m. Next, we focus on the influence of SD on the safety level for this road section. Since this section is at a turning point and the terrain consists of a long downhill portion, the sight distance is short, which affects the safety level. According to the road conditions, the line-of-sight guidance facilities should be added at the curved sections to strengthen the warning of drivers.

The safety level of road section 4 of expressway is Level III (general safe), and it is necessary to take targted control measures to reduce risks and imprve the operation. For road section 4, the value of SD indicator is 190 m and the value of TSM indicator is 3.7, which conform to the safety level specified in the Highway Route Design Specification. However, the value of the SSC indicator is 0.85 mm, which is lower than 0.9mm. Additionally, the value of the MTS indicator is 120 km/h, which does not exceed the maximum speed value specified in the specification. However, considering that this segment is located in a mountainous area and is subject to local speed limit policies (where exceeding the speed limit by less than 10% is exempt from punishment), some drivers may travel at higher speeds, undoubtedly increasing the probability of accidents. Thus, the main factors that lead to the safety level of this section only at Level III are the surface skid-resisting capability and speed. This section involves a low surface skid-resisting capability and high-speed regulation, which increases the incidence of traffic accidents and decreases the safety level. According to the road conditions, speed limit signs should be designed in this section, so that drivers reduce driving speed, reducing the incidence of accidents.

5. Conclusions and Recommendations

Expressways are the critical ingredients of the entire transportation infrastructure system, which promotes economic growth and sustainable development. Expressway safety has always been a key research issue in the field of transportation. It is of both theoretical and practical significance to guide the safety evaluation of expressway operation in China. This study presents a fuzzy comprehensive evaluation method, which includes the process of determining evaluation indicators and weights, establishing a fuzzy evaluation matrix, as well as conducting fuzzy operations and de-fuzzification. An index system is constructed to evaluate the expressway safety level following a comprehensive literature review. By establishing a fuzzy evaluation matrix and conducting weighted average fuzzy operations, a fuzzy comprehensive vector of the overall evaluation results is obtained. Finally, de-fuzzification is performed using the maximum membership degree principle to transform the fuzzy comprehensive vector into specific evaluation results. Through the fuzzy comprehensive evaluation method, we can establish and transform the relationship between evaluation indicators and evaluation results, accurately assessing the safety level of expressways. Fuzzy comprehensive evaluation method has the following advantages in evaluating the safety levels of expressways. Firstly, it allows for evaluation from multiple perspectives and levels. Secondly, it transforms qualitative assessment into quantitative assessment using membership degree based on fuzzy mathematics, applying the principle of fuzzy relation synthesis and quantifying some factors with unclear boundaries. Therefore, the proposed evaluation method has more practicability for problems that are fuzzy and difficult to quantify.

The evaluation model is applied to the Jinliwen Expressway in a mountainous area in Zhejiang Province, China. According to the method proposed in this study, the evaluation results of the four road sections are safe, relatively safe, relatively safe, and generally safe, and the main influencing factors are analyzed accordingly. According to Figure 4, the comprehensive weights of sight distance, surface skid-resisting capability, travel speed, and traffic safety measure all exceed the average value, which is greater than 0.1. This result shows that these four factors play an important role in the evaluation of expressway safety. Specifically, the main factors affect the safety level of road section 2, which is the surface skid-resisting capability; the main factors affecting the safety level of the road section 3 is the sight distance; and the main factors affecting the safety level of this section are the surface skid-resisting capability and speed. The results show that the method could quantitatively and comprehensively evaluate the safety status of expressways and identify the weak links of operational safety management, which can effectively improve the safety level of expressway operation. The research findings will assist decision-makers in obtaining a better understanding of the safety issues of Jinliwen Expressway in Zhejiang Province and utilizing corresponding measures to enhance the safety level of the expressway.

In future research, we will collect the actual accident data of the expressway and carry out the fine verification work of the evaluation method. However, future studies should focus on expanding the evaluation system and refining the methodology to ensure its relevance and accuracy in assessing expressway safety in the context of intelligent transportation systems. For instance, with the development of intelligent transportation systems, the evaluation system proposed in this study needs to be modified by incorporating more intelligent transportation indicators. Additionally, further research and refinement could enhance the effectiveness and applicability of the fuzy comprehensive evalution method in assessing expressway safety.