Abstract
The development of a green economy has become a global consensus. More and more manufacturers are greening their production to build green supply chains. At the same time, retailers are employing green marketing efforts for green products. In addition, members who are followers of the green supply chain are prone to fairness-concern behavior. To investigate the impact of fairness concerns on green supply chain decisions, this study develops a two-tier green supply chain in which the manufacturer makes green input and the retailer makes green marketing effort input. The retailer in the follower position of the supply chain has fairness concerns. Stackelberg game models are constructed and compared in three scenarios: one without fairness concerns, one where the manufacturer considers the retailer’s fairness concerns, and one where the manufacturer does not consider the retailer’s fairness concerns. After the manufacturer decides whether to consider the retailer’s fairness concerns, a two-part tariff contract is used to coordinate the green supply chain based on optimal decision-making and profit under a centralized decision-making condition. The study found that: (1) when the manufacturer considers the retailer’s fairness concerns, fairness concerns will negatively impact greenness, green marketing efforts, wholesale price, and retail price. When the manufacturer does not consider the retailer’s fairness concerns, fairness concerns will not impact greenness or wholesale price, but will negatively impact green marketing efforts; (2) the retailer’s fairness concerns have a negative impact on the green supply chain’s profit, and from the supply chain perspective, the retailer should abandon its fairness concerns; (3) it will be more beneficial if the manufacturer can consider the retailer’s fairness concerns; (4) when the manufacturer does not consider the retailer’s fairness concerns, the retailer can make fairness concerns according to the parameter conditions; (5) when a fixed fee meets a certain range, the two-part tariff contract can coordinate the green supply chain when the retailer has fairness concerns. The results will help manufacturers and retailers better understand fairness concerns and provide them with decision-making guidance and coordinated choices.
1. Introduction
1.1. Background and Motivation
Since the 21st century, environmental problems have become increasingly prominent. It has become a global consensus to develop a green economy and promote green production. In this context, the supply chain is facing a great sustainability challenge [1,2]. The development and application of advanced production technologies provide opportunities for sustainable development of the supply chain [3,4]. The green supply chain has been developed extremely rapidly. The construction of the green supply chain can help companies maximize utilization of resources and minimize negative impacts on the environment [5]. More and more, companies are trying to balance economic and environmental benefits by building the green supply chain to achieve ecological improvement and high-quality economic development [6]. For example, the world’s leading smartphone manufacturers, such as Apple and Huawei, are actively building their green supply chains to boost green sustainability. In green supply chains, manufacturers are committed to improving the greenness of their products. For example, in China, Xiaomi invested CNY 9.3 billion in green innovation of electronic products in 2020 [7], and BYD invested CNY 10.627 billion in the research and development of electric vehicles in 2021 [8]. Green products with a high degree of greenness are at the core of competitiveness between manufacturers. In addition, retailers often have a strong interest in employing green marketing efforts for green products [9]. They stimulate consumers to buy green products through advertising [10,11], hiring professional salespeople [12], and other means. For example, Amazon spent USD 11 billion on advertising and promotion in 2019 [13]. Therefore, in the operation of the green supply chain, the way manufacturers and retailers make optimal decisions regarding greenness and green marketing efforts is a problem worthy of attention.
With the development of behavioral economics, irrational fairness concerns have attracted more and more attention from scholars [14,15]. Numerous studies have shown that supply chain members have fairness concerns [16,17]. When a supply chain member has fairness concerns, it believes that its own profits are compared more unfairly with other numbers, which will lead it to make irrational decisions to pursue fairness [17]. For example, the early conflict between Wal-Mart and Procter & Gamble was due to unfair distribution of profits, and the ‘price war’ between GOME and Gree was also due to the unfair distribution of profits [18]. In the green supply chain, although many companies regard sustainable development as their future development strategy, their primary goal is still profit [18]. In particular, members in a follower position in the green supply chain are more likely to have fairness concerns because their profits can be squeezed by members in leadership positions. Therefore, it is worthwhile for scholars to study how the fairness concerns of members in a follower position will affect members’ decisions in the green supply chain. However, the existing literature was conducted with the assumption that the leader will consider the follower’s fairness concerns in supply chain. As a result, this paper discusses the follower’s fairness concerns in two different scenarios. The first scenario is that the leader considers the follower’s fairness concerns. The second scenario is that the leader does not consider the follower’s fairness concerns; that is, this study is more realistic. In addition, whether and how the green supply chain can be coordinated through contracts when members in a follower position have fairness concerns is also an issue that deserves our attention.
1.2. Research Content and Questions
This paper studies a two-tier green supply chain in which a manufacturer makes green input and a retailer makes green marketing effort input. The retailer in a follower position has fairness concerns. Three Stackelberg game models are established: one without fairness concerns, one in which the manufacturer considers the retailer’s fairness concerns, and one in which the manufacturer does not consider the retailer’s fairness concerns. The impact of fairness concerns on the optimal decisions and profits of both parties in the green supply chain is studied. After exploring whether the manufacturer should consider the retailer’s fairness concerns, based on optimal decision-making and profits under centralized decision-making, a contract is introduced to coordinate the green supply chain.
This paper aims to address the following four questions:
(1) What are the optimal decisions for the manufacturer and retailer in the green supply chain when the retailer has fairness concerns?
(2) How do the retailer’s fairness concerns affect green supply chain decisions?
(3) Should the manufacturer consider the retailer’s fairness concerns?
(4) How should the green supply chain be coordinated when the retailer has fairness concerns?
1.3. Contributions and Paper Arrangements
The contributions of this paper are as follows: (1) This paper investigates the problem of optimal decisions for the green supply chain where the manufacturer makes green inputs and the retailer makes green marketing efforts. Related studies such as [19,20] have studied the optimal pricing and sales effort decisions of supply chain members, but not in the context of green supply chains. Therefore, this paper will contribute to green supply chain decisions. (2) This paper investigates the impact of the retailer’s fairness concerns on green supply chain decisions and examines an actual situation in which the manufacturer may or may not consider the retailer’s fairness concerns when the retailer has them. Related studies such as [18,21,22,23] studied the impact of members’ fairness concerns on optimal decisions in the green supply chain but did not study the reality that, when a follower of the supply chain has fairness concerns, the leader may or may not consider its fairness concerns. Therefore, this paper will contribute to the research of fairness concern behavior in supply chains, which is the most important innovation of this paper. (3) This paper coordinates the green supply chain when the retailer has fairness concerns using a two-part tariff contract. Related studies such as [24,25,26] did not use contracts to coordinate green supply chains with fairness concerns, although they studied optimal decisions for green supply chains with fairness concerns. The retailer’s fairness concerns arise because of the unfairness in the distribution of profits. When the manufacturer compensates the retailer for a portion of the profits, it helps to eliminate the retailer’s fairness concerns. Therefore, the use of a two-part tariff contract to eliminate the retailer’s fairness concerns will help enrich the research on green supply chain coordination.
The rest of this paper is organized as follows. Section 2 reviews the existing literature. Section 3 describes and builds the game models. Section 4 solves and analyzes three decision-making models. Section 5 coordinates green supply chains using a contract. Section 6 numerically simulates and discusses the results. Section 7 concludes the paper and presents managerial implications.
2. Literature Review
The literature closely related to this research falls into three categories, namely decisions of the green supply chain, coordination of the green supply chain, and fairness concerns in the supply chain.
2.1. Decisions of the Green Supply Chain
Research on decisions impacting the green supply chain can be divided into two types. The first type includes decisions made under different power structures. Supply chain decision-making models such as a centralized decision-making model, the Stackelberg game decision-making model, and the Nash game decision-making model have been constructed and solved [27,28,29,30]. Scholars obtained the optimal decisions of green supply chain members under different power structures and analyzed the influence of channel structure on optimal decisions. The second type includes decisions that consider influencing factors of the supply chain. With the development of the green supply chain, more and more factors are considered in the field of green supply chain operation decisions [31,32]. External policy factors such as government policies [33], government subsidies [34], and the cap-and-trade mechanism [35] were considered. Internal factors of supply chain members such as risk aversion [36], overconfidence [37], and corporate social responsibility [38] were also considered. Peng et al. [39] and Pal et al. [40] studied optimal green marketing effort decisions in the green supply chain and their impact on pricing decisions. Meng et al. [41] and Ling and Xu [42] studied the impact of consumer behavior on green supply chain decisions from the perspective of consumers. In addition, the symmetry of information also has an impact on green supply chain decisions [43].
Different from these studies, this paper considers the fairness concerns of the retailer in the green supply chain. Price, greenness, and green marketing efforts are used as decision variables, and three Stackelberg game decision-making models are established to study the impact of fairness concerns on the green supply chain.
2.2. Coordination of the Green Supply Chain
Supply chain coordination has been widely considered by scholars in the field of supply chain operations management. For a decentralized supply chain, supply chain coordination can help members improve performance [19,44]. Researchers designed different contracts for different green supply chains to achieve coordination. These contracts include a classic cost-sharing contract [45], a revenue-sharing contract [46], a two-part tariff contract [47,48], and some effective combination contracts. For example, Xu et al. [49] used the combination of the wholesale price contract, cost-sharing contract, and two-part tariff contract to coordinate the green supply chain. Heydaria et al. [50] designed a mixed contract of green cost-sharing and revenue sharing to coordinate the green supply chain. For the coordination of the green supply chain, the applicability of the contract is very important. The result of green supply chain coordination is that the profits of the supply chain members under the contract are higher than for those utilizing decentralized decision-making, and the sum of the profits of the supply chain members under the contract is equal to that under centralized decision-making [20,51,52]. A coordinated green supply chain can obtain more satisfied customers and more profits.
Similar to the green supply chain coordination goals of these studies, this paper aims to achieve the above-mentioned coordination results. However, this paper coordinates the green supply chain where the retailer has fairness concerns. The retailer has fairness concerns because it is dissatisfied with profit distribution, so the retailer prefers for the manufacturer to give itself a certain profit compensation fee. This provides a prerequisite for the application of the two-part tariff contract. Therefore, this paper uses the classic two-part tariff contract for green supply chain coordination.
2.3. Fairness Concerns in the Supply Chain
Many scholars have studied fairness concerns in supply chains. Cui et al. [53] considered fairness concerns for the first time in supply chain management and studied the impact of fairness concerns on supply chain coordination. Ho and Zhang [54] used utility functions to represent fairness concerns. In the green supply chain, the fairness concerns of manufacturers and retailers have attracted much attention [21]. Some scholars have focused on the fairness concerns of manufacturers. For example, Wang et al. [23] studied the green e-commerce supply chain where the green manufacturer has fairness concerns and obtained optimal greenness and service-level decisions. Jian et al. [18] studied the green closed-loop supply chain where the manufacturer has fairness concerns and obtained optimal decisions from the manufacturer and the retailer. Yuan et al. [25] studied the effect of fairness concerns of the green collector on optimal decisions and profits of the green remanufacturer in a reverse green supply chain. Toktas-Palut [55] studied a three-stage green supply chain with fairness concerns and used a two-part tariff contract to coordinate the green supply chain and enable the supply chain members to benefit from the contract in an equitable manner. A few other scholars have studied mainly the fairness concerns of retailers. For example, Zhang et al. [21] studied the impact of the green retailer’s fairness concerns on decisions and profits of the green supply chain and used three contracts to coordinate the green supply chain. Zhang et al. [22] studied a green supply chain in which the retailer has fairness concerns and analyzed the impact of fairness concerns on the environmental quality and pricing of green products. Zhang et al. [24] studied a dual-channel green supply chain with fairness concerns for the retailer and explored green manufacturing strategies for the manufacturer. Mondal and Giri [56] investigated the impact of the retailer’s fairness concerns on supply chain members’ decisions in a closed-loop green supply chain and proposed a restitution-based wholesale price contract to coordinate the supply chain. Zhou et al. [57] studied a green supply chain with retailer fairness concerns in the case of demand information asymmetry, solved the optimal decisions of the supply chain members, and analyzed the impact of fairness concerns on the optimal decisions. Some scholars have also studied the fairness concerns of manufacturers and retailers simultaneously. For example, Adhikari and Bisi [58] studied the fairness concerns of an apparel manufacturer and retailer in a green apparel supply chain and analyzed the impact of fairness concerns on supply chain members under contracts. Yang et al. [26] studied the impact of manufacturers’ and retailers’ fairness concerns on pricing, greenness, and sales effort decisions in a green supply chain under deferred and risk-free interest rates. Some scholars have carried out research from the perspective of horizontal and vertical fairness concerns. For example, Liu et al. [59] studied the horizontal and vertical fairness concerns in the three-stage green supply chain and analyzed the impact of different fairness concerns on the green supply chain. Wang et al. [60] studied a green supply chain with two competing manufacturers and one retailer and analyzed the pricing decisions of the green supply chain when manufacturers have horizontal and vertical fairness concerns. However, all of the above studies assume that when one supply chain member has fairness concerns, the other members will necessarily consider those fairness concerns. They did not explore the fact that when a supply chain member has fairness concerns, its counter-member may or may not consider those concerns. The most relevant studies to this paper are those of Hu et al. [61] and Sun and Zhong [62]. Hu et al. [61] studied the fairness-concern behavior of an agricultural cooperative in the green agricultural product supply chain and examined the situation of the retailer both considering and not considering the fairness concerns of the agricultural cooperative. Compared with Hu et al. [61], this paper considers the fairness concerns of retailers in a supply chain follower position and coordinates the green supply chain. Sun and Zhong [62] studied the fairness-concern behavior of a retailer in the low-carbon supply chain and examined the situation of the manufacturer both considering and not considering the fairness concerns of the retailer. Compared with Sun and Zhong [62], this paper considers retailers’ fairness concerns in the context of green supply chains and coordinates the green supply chain.
2.4. Research Gaps
The literature most relevant to this paper is summarized in Table 1.

Table 1.
Comparison of the related literature.
There has been extensive research on pricing, greenness, and green marketing effort decisions in the green supply chain, but only a few research studies have considered the fairness concerns of supply chain members. In addition, most of research that considers the fairness concerns of members ignores the fact that members’ fairness concerns may or may not be taken into account by other members. The most relevant studies to this paper are those of Hu et al. [61] and Sun and Zhong [62]; but while they studied the fact that fairness concerns may or may not be taken into account, they have not further examined how to coordinate the supply chain in which members have fairness concerns. Therefore, this paper studies the green supply chain where the retailer has fairness concerns. The fact that the manufacturer considers and does not consider its fairness concerns when the retailer has fairness concerns is explored. Whether the manufacturer should consider the retailer’s fairness concerns and when the retailer can have fairness concerns are the focus of this paper. This paper also uses a two-part tariff contract to coordinate the green supply chain.
3. Model Description and Construction
3.1. Model Description
This paper considers a two-tier green supply chain consisting of a manufacturer and a retailer. The manufacturer and retailer follow the Stackelberg game. The manufacturer is the leader, and the retailer is the follower. The decision sequences of the game model are as follows: (1) The manufacturer determines the level of greenness, , and wholesale price, , of the green products and wholesales the products to the retailer. (2) The retailer determines the level of green marketing effort, , and retail price, , according to the decisions of the manufacturer and sells the products to consumers. The green supply chain model diagram is shown in Figure 1.
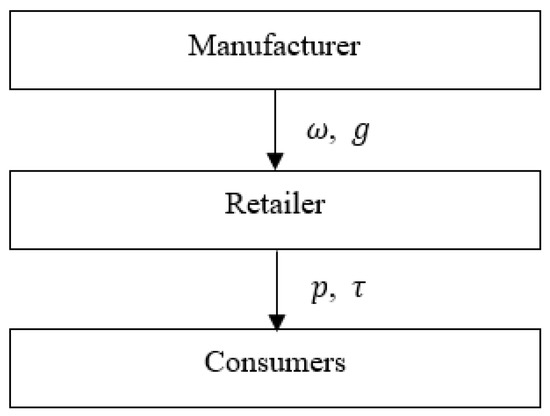
Figure 1.
Green supply chain model diagram.
3.2. Notations
Table 2 presents notations and meanings used in this paper.

Table 2.
Notations and descriptions.
3.3. Assumptions and Model Building
3.3.1. Assumptions
Assumption 1.
The information between the manufacturer and the retailer is completely symmetrical [20,21,22]. The whole process of selling products in the green supply chain does not consider out-of-stock situations [63,64].
Assumption 2.
Basic costs such as product holding costs, product ordering costs, product transport costs, and product inventory costs are not considered, which is consistent with previous studies [20,21,22].
Assumption 3.
To improve the greenness of green products, the manufacturer has to make green investments. The higher the greenness of green products, the higher the green investment [21]. With reference to previous research [63], the green investment of the manufacturer can be expressed as:
Assumption 4.
To increase the sales of green products, the retailer will make green marketing efforts through advertising and other means [48]. With reference to previous research [20,63,64], the green marketing effort cost to the retailer can be expressed as:
Assumption 5.
To attain the demand function, the demand formulations of previous research [20,23,59] are extended. The market demand function is a linear function of the green product retail price, greenness, and level of green marketing effort. The market demand function can be expressed as:
3.3.2. Model Building
According to the above assumptions, the profit functions of the manufacturer, retailer, and entire green supply chain can be expressed as:
According to the profit functions of the manufacturer and retailer, with reference to previous research [17,23,63], the utility function of the retailer with fairness concerns can be expressed as:
4. Decision-Making Model Analysis
4.1. Without Fairness Concerns
When the green supply chain is without fairness concerns, both the manufacturer and retailer make decisions with the goal of maximizing their own profits. The decision objective function of the manufacturer is shown in Equation (4). The decision objective function of the retailer is shown in Equation (5). The Stackelberg game is solved by backward induction. The retailer’s optimal decision is solved first, and then the manufacturer’s optimal decision is analyzed. The superscript is used to denote the optimal situation without fairness concerns.
Theorem 1.
The equilibrium results when the green supply chain is without fairness concerns are:
In the above equations, ,
.
Proof of Theorem 1.
The proof process is shown in Appendix A. □
4.2. With Fairness Concerns of the Retailer
When the retailer has fairness concerns, it pays more attention to the fairness of profit distribution. That is, the retailer will make utility maximization its decision-making goal. For the manufacturer, it has two decision options. The first is that the manufacturer considers the retailer’s fairness concerns when making decisions. The second is that the manufacturer does not consider the retailer’s fairness concerns when making decisions. Accordingly, the manufacturer will make different decisions to optimize its profit.
4.2.1. The Manufacturer Considers the Retailer’s Fairness Concerns
When the retailer has fairness concerns and the manufacturer considers the retailer’s fairness concerns in its decision-making process, the goal of the retailer is to maximize its utility, , and the goal of the manufacturer is to maximize its profit, , while considering the retailer’s utility. The decision objective function of the manufacturer is shown in Equation (4). The decision objective function of the retailer is shown in Equation (7). The Stackelberg game is also solved by backward induction. The superscript is used to denote the optimal situation when the manufacturer considers the retailer’s fairness concerns.
Theorem 2.
The equilibrium results when the manufacturer considers the retailer’s fairness concerns are:
In the above equations, .
Proof of Theorem 2.
The proof process is shown in Appendix A. □
4.2.2. The Manufacturer Does Not Consider the Retailer’s Fairness Concerns
When the retailer has fairness concerns and the manufacturer does not consider the retailer’s fairness concerns in its decision-making process, the goal of the retailer is to maximize its utility, , and the goal of the manufacturer is to maximize its profit, , without the consideration of the retailer’s utility. The decision objective function of the manufacturer is shown in Equation (4). The decision objective function of the retailer is shown in Equation (7). The Stackelberg game is also solved by backward induction. The superscript is used to denote the optimal situation when the manufacturer does not consider the retailer’s fairness concerns.
Theorem 3.
The equilibrium results when the manufacturer does not consider the retailer’s fairness concerns are:
Proof of Theorem 3.
The proof process is shown in Appendix A. □
4.3. Sensitivity Analysis and Model Comparison
Analyzing the equilibrium results of the above three models, the following corollaries can be obtained.
Corollary 1.
(1) . (2) .
Proof of Corollary 1.
The proof process is shown in Appendix A. □
When the manufacturer considers the retailer’s fairness concerns, in order to alleviate the negative effect of the retailer’s fairness concerns on the manufacturer’s profit, the manufacturer will reduce the level of greenness to reduce green investment. When the manufacturer does not consider the retailer’s fairness concerns, the manufacturer will keep the same level of greenness as that without fairness concerns.
Corollary 2.
(1) . (2) .
Proof of Corollary 2.
The proof process is shown in Appendix A. □
When the manufacturer considers the retailer’s fairness concerns, the manufacturer will lower the wholesale price. On the one hand, the manufacturer’s practice can increase the retailer’s purchase volume. On the other hand, it can surrender part of its profit to the retailer to alleviate the retailer’s fairness concerns. When the manufacturer does not consider the retailer’s fairness concerns, the manufacturer will keep the same wholesale price as that without fairness concerns.
Corollary 3.
(1) . (2) . (3) .
Proof of Corollary 3.
The proof process is shown in Appendix A. □
Regardless of whether the manufacturer considers the retailer’s fairness concerns, as fairness concerns increase, the retailer will reduce green marketing effort costs by lowering the level of green marketing efforts to pursue fair profit distribution. When the manufacturer considers the retailer’s fairness concerns, the manufacturer can surrender part of its profit to the retailer. Therefore, the level of green marketing efforts determined by the retailer in this scenario is higher than when the manufacturer does not consider the retailer’s fairness concerns.
Corollary 4.
(1) When , ; when , ; when , . (2) . (3) When , ; when , .
In the above equations, .
Proof of Corollary 4.
The proof process is shown in Appendix A. □
When the manufacturer considers the retailer’s fairness concerns, the manufacturer will lower the wholesale price. Therefore, the retailer has more room to cut the retail price. At this point, the retailer will lower the retail price to increase consumer demand in order to make more profit. When the manufacturer does not consider the retailer’s fairness concerns, the retailer tends to make the following responses. When , the retailer will reduce the retail price to increase consumer demand. When , the retailer will increase the retail price to increase the marginal revenue.
Corollary 5.
(1) . (2) . (3) .
Proof of Corollary 5.
The proof process is shown in Appendix A. □
Regardless of whether the manufacturer considers the retailer’s fairness concerns, as fairness concerns increase, the manufacturer’s profit will go down. The reason is as follows. When the manufacturer considers the retailer’s fairness concerns, the negative impact of decreased greenness and green marketing efforts is higher than the positive impact of the decreased retail price on consumer demand. The manufacturer also reduces the wholesale price. The reduced consumer demand and wholesale price will induce a reduction in the manufacturer’s profit. When the manufacturer does not consider the retailer’s fairness concerns, the lower level of green marketing efforts will lead to lower demand, and the manufacturer’s profit will decrease. However, when the manufacturer considers fairness concerns, the manufacturer will change the wholesale price and greenness level to increase its profit. Therefore, the manufacturer’s profit is higher than when the manufacturer does not consider fairness concerns.
Corollary 6.
(1) When , ; when , ; when , . (2) When , ; when , . (3) .
Proof of Corollary 6.
The proof process is shown in Appendix A. □
When the manufacturer does not consider the retailer’s fairness concerns, the retailer’s profits will go down. The retailer pursues fair distribution of profits on the premise that its own profit is damaged. When the manufacturer considers the retailer’s fairness concerns, the manufacturer will surrender part of its profit to the retailer. When , the retailer’s profit will increase. When , the practices adopted by the retailer in pursuit of a fair distribution of profits are detrimental to itself.
Corollary 7.
(1) When , ; when , . (2) When , ; when , . (3) When , ; when , .
In the above equations, ; .
Proof of Corollary 7.
The proof process is shown in Appendix A. □
Regardless of whether the manufacturer considers the retailer’s fairness concerns, the proportion of the retailer’s profit in the green supply chain’s profit is different under different constraints. Thus, under different constraints, the retailer’s utility may increase or decrease as fairness concerns increase. The greater the retailer’s utility, the stronger the psychological satisfaction that fairness concerns bring to the retailer. But an increase in the retailer’s utility does not necessarily lead to an increase in the retailer’s profit.
Corollary 8.
(1) when , ; when , . (2) . (3) .
In the above equations, .
Proof of Corollary 8.
The proof process is shown in Appendix A. □
When the manufacturer does not consider the retailer’s fairness concerns, both the retailer’s and manufacturer’s profits will decrease. Therefore, the green supply chain’s profit will decrease. When the manufacturer considers the retailer’s fairness concerns, although the retailer’s profit may change, the manufacturer’s profit will decrease. Therefore, the green supply chain’s profit will also decrease.
5. Coordination Model Analysis
From the analysis in Section 4, it can be seen that it is more beneficial for the manufacturer to consider the retailer’s fairness concerns. When the retailer has fairness concerns, the manufacturer should consider the retailer’s fairness concerns and eliminate the negative effects of fairness concerns. However, while it is beneficial for the manufacturer to consider the retailer’s fairness concerns, the retailer’s fairness concerns can hinder cooperation between both parties. Therefore, it is necessary to coordinate the green supply chain through contracting to improve the profits of the two parties. First, the optimal decisions and profit under centralized decision-making are solved. Then, the coordination contract is designed with the goal of optimizing decisions and profit under centralized decision-making to coordinate the green supply chain when the manufacturer considers the retailer’s fairness concerns.
5.1. Centralized Decision-Making
Under a centralized decision-making model, the manufacturer and retailer determine the retail price, greenness level, and green marketing effort level with the goal of maximizing the overall profit of the supply chain. The decision objective function of the manufacturer and retailer is shown in Equation (6). The superscript is used to denote the optimal situation under centralized decision-making.
Theorem 4.
The equilibrium results under centralized decision-making are:
Proof of Theorem 4.
The proof process is shown in Appendix A. □
5.2. Two-Part Tariff Contract
The retailer’s fairness concerns arise from unfair distribution of profits. Therefore, the manufacturer pays the retailer a certain fee, which is a beneficial step toward eliminating the retailer’s fairness concerns. Therefore, the classic two-part tariff contract is introduced to coordinate the green supply chain. Under the two-part tariff contract, the manufacturer sells the green product to the retailer at the wholesale price, . Then the manufacturer pays the retailer a fixed fee, , when the sales process is complete. The superscript is used to denote the optimal situation under the two-part tariff contract.
The profit functions of the manufacturer and retailer can be expressed as:
The utility function of the retailer with fairness concerns can be expressed as:
Theorem 5.
The equilibrium results under the two-part tariff contract are:
Proof of Theorem 5.
The proof process is shown in Appendix A. □
Proposition 1.
When , the two-part tariff contract can coordinate the green supply chain where and .
Proof of Proposition 1.
The proof process is shown in Appendix A. □
6. Numerical Simulations and Discussions
A real case explored by Zhu et al. [65] is used for numerical simulations. The case utilizes a green food supply chain consisting of a well-known Chinese food and beverage producer, A Wu Cate (Retailer AW), and a large ecological breeding base for Yellow River carp in China, Huanghejin (Manufacturer HHJ), located in Zhengzhou City, Henan Province, China, which supplies approximately 300,000 ecological carp to AW each year. Zhu et al. [65] collected data from a representative restaurant (YX Restaurant) of AW, located in Zhengzhou City, Henan Province, China. The specific data collection process is shown in [65]. This paper uses the real data of this case for numerical simulations to verify the reliability of the models. These data are: , /unit, , , . Therefore, the range of the green marketing effort cost coefficient is subject to . Let here.
6.1. Impact of Fairness Concerns
Based on the data from this case, the impact of fairness concerns on the green supply chain is analyzed. It is assumed that the fairness concerns coefficient of the retailer, , varies from 0 to 1. The change of greenness level with is shown in Figure 2.
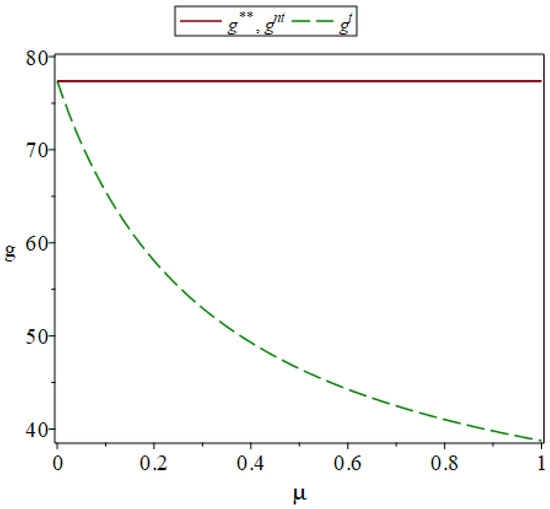
Figure 2.
The change of greenness level with fairness concerns.
It can be seen from Figure 2 that as increases, the greenness level when the manufacturer considers the retailer’s fairness concerns will decrease. This finding is consistent with that of [18,23,24,57]. This is because the manufacturer has to alleviate the negative effect of the retailer’s fairness concerns on its profit by reducing greenness level. Here, , because the manufacturer does not consider the retailer’s fairness concerns and believes that the retailer makes decisions with the goal of maximizing its own profit. The manufacturer will not change the greenness level. The result in Figure 2 is consistent with Corollary 1.
The change in wholesale price with is shown in Figure 3.
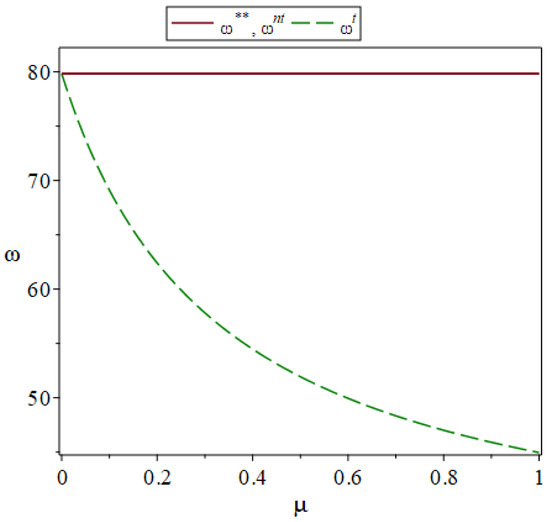
Figure 3.
The change in wholesale price with fairness concerns.
It can be seen from Figure 3 that as increases, the wholesale price when the manufacturer considers the retailer’s fairness concerns will decrease. This finding is consistent with that of [22,26]. This is because the manufacturer wants to increase the retailer’s purchase volume and surrender part of its profit to the retailer. The manufacturer’s practice is beneficial to its own profits and to the elimination of the retailer’s fairness concerns. Here, , which is consistent with the finding of [62]. This is because the manufacturer does not consider the retailer’s fairness concerns and believes that the retailer makes decisions with the goal of maximizing its own profit. The manufacturer will not change the wholesale price. The result in Figure 3 is consistent with Corollary 2.
The change in the green marketing effort level with is shown in Figure 4.
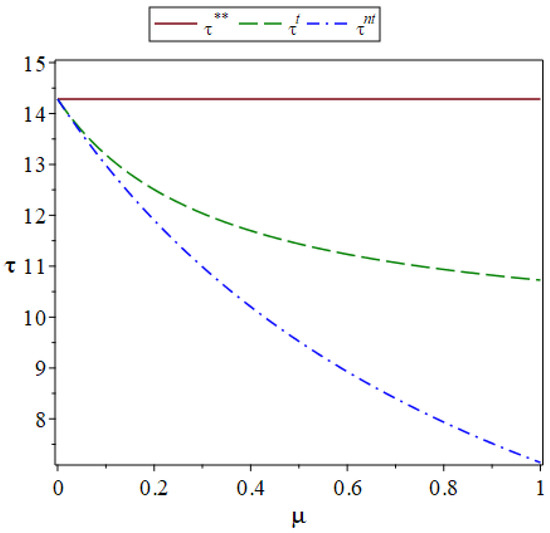
Figure 4.
The change in green marketing effort level with fairness concerns.
It can be seen from Figure 4 that as increases, the green marketing effort level when the retailer has fairness concerns will decrease. This finding is consistent with that of [18], which states that the retailer’s fairness concerns will lead to a decrease in green marketing efforts when the manufacturer considers the retailer’s fairness concerns. This is one of the means by which the retailer to pursue fair profit distribution. No matter whether the manufacturer considers the retailer’s fairness concerns, the retailer will reduce the level of green marketing efforts. Here, , which is consistent with the finding of [62]. This is because when the manufacturer considers the retailer’s fairness concerns, the manufacturer can surrender part of its profit to the retailer. At this point, the retailer only needs to reduce the lower level of green marketing efforts to pursue fair profit distribution. The result in Figure 4 is consistent with Corollary 3.
Then, let vary from CNY 1.77 to CNY 3.77.
The change of retail price with is shown in Figure 5.
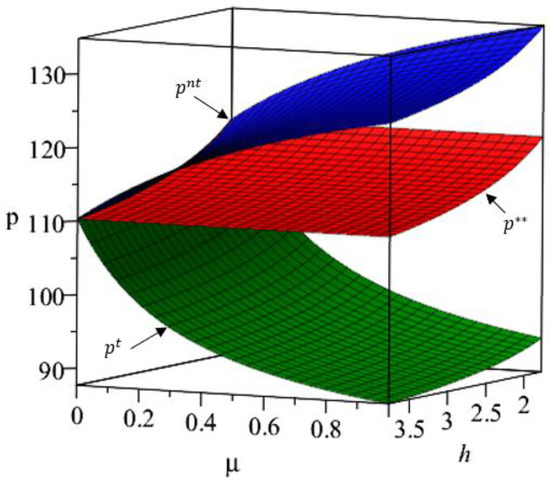
Figure 5.
The change of retail price with fairness concerns.
It can be seen from Figure 5 that as increases, the retail price when the manufacturer considers the retailer’s fairness concerns will decrease. This finding is consistent with that of [22,26]. This is because the retailer has room to lower the retail price and wants to increase consumer demand by lowering the retail price. It can be seen from the numerical simulation data that . Therefore, it can be seen from Figure 5 that when the manufacturer does not consider the retailer’s fairness concerns, as increases, the retail price will increase. It can also be seen from Figure 5 that . These are practices adopted by the retailer to pursue fair profit distribution. The result in Figure 5 is consistent with Corollary 4.
The change of manufacturer’s profit with is shown in Figure 6.
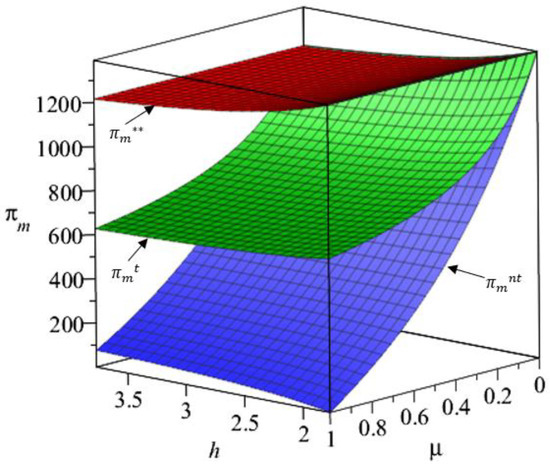
Figure 6.
The change of manufacturer’s profit with fairness concerns.
It can be seen from Figure 6 that regardless of whether the manufacturer considers fairness concerns, as increases, the manufacturer’s profit will decrease, and . This finding is partially supported by [26,56,57,62], which states that the manufacturer’s profit decreases as the retailer’s fairness concerns increase when the manufacturer considers the retailer’s fairness concerns. This shows that it is more beneficial for the manufacturer to consider the retailer’s fairness concerns. This is because when the manufacturer considers the retailer’s fairness concerns, the manufacturer can respond to fairness concerns by adjusting the greenness level and wholesale price, and thus reduce the damage of fairness concerns to itself. If fairness concerns can be eliminated, the manufacturer’s profit will be the greatest. The results in Figure 6 are consistent with Corollary 5.
The change of retailer’s profit with is shown in Figure 7.
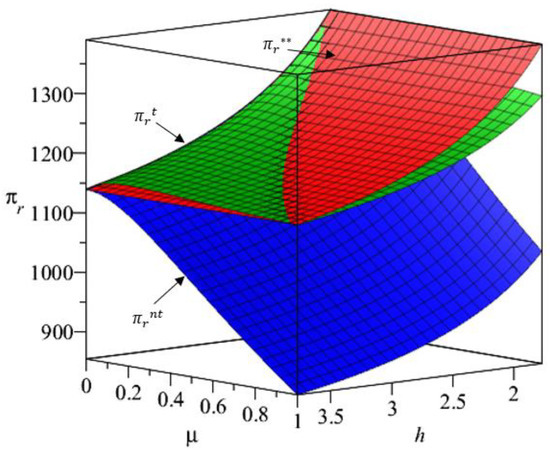
Figure 7.
The change of retailer’s profit with fairness concerns.
It can be seen from Figure 7 that as increases, the retailer’s profit when the manufacturer does not consider the retailer’s fairness concerns will decrease. At this point, the retailer can only pursue fair profit distribution on the basis of its own profits being damaged. From a rational point of view, the retailer should not care about fairness. When the manufacturer considers the retailer’s fairness concerns and , as increases, the retailer’s profit will increase. At this time, the retailer’s fairness concerns have a positive effect on its profit. It can be seen from the numerical simulation data that . Therefore, it can be seen from Figure 7 that when and when . The results in Figure 7 are consistent with Corollary 6.
The change of retailer’s utility with is shown in Figure 8.
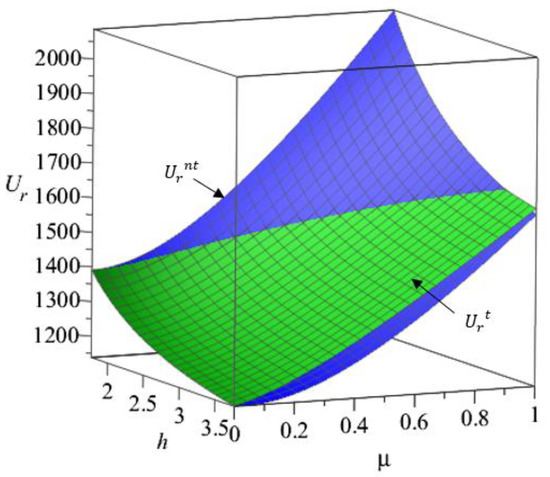
Figure 8.
The change of retailer’s utility with fairness concerns.
It can be seen from Figure 8 that when the manufacturer does not consider the retailer’s fairness concerns and , as increases, the retailer’s utility will increase. It can be seen from the numerical simulation data that . Therefore, it can be seen from Figure 8 that as increases, the retailer’s utility when the manufacturer considers the retailer’s fairness concerns will increase. The retailer’s increased utility will bring psychological satisfaction to itself. It also can be seen from Figure 8 that when and when . The results in Figure 8 are consistent with Corollary 7.
The change of supply chain’s profit with is shown in Figure 9.
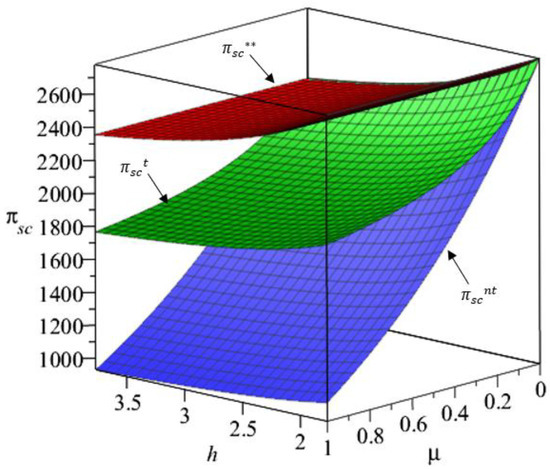
Figure 9.
The change of supply chain’s profit with fairness concerns.
It can be seen from Figure 9 that regardless of whether the manufacturer considers the retailer’s fairness concerns, as increases, the supply chain’s profit will decrease. This finding is partially supported by [21,26,57], which states that the supply chain’s profit decreases as the retailer’s fairness concerns increase when the manufacturer considers the retailer’s fairness concerns. In order to obtain greater profit, the retailer’s fairness concerns should be reduced or even eliminated. It can be seen from the numerical simulation data that . Therefore, it can be seen from Figure 9 that . The results in Figure 9 are consistent with Corollary 8.
6.2. Coordination Contract
The initial data were also used for numerical simulation of the coordination contract, in addition, letting . The value range of can be obtained by calculation. The range of is (−222, 562, 197, −222, 008, 980). Taking random values of , Table 3 can be obtained.

Table 3.
The change of profits with .
It can be seen from Table 3 that when changes in (−222, 562, 197, −222, 008, 980), in the green supply chain coordinated by the two-part tariff contract, both the manufacturer’s profit () and the retailer’s profit () have increased compared with those without coordination ( and ). The supply chain’s profit () after contract coordination is equal to the supply chain’s profit () under centralized decision-making. This is consistent with the case study findings of [65], which found that the coordinated green supply chain could achieve more profits and that the profits of the manufacturer and retailer would increase. It can also be seen from Table 3 that the fixed fee, , paid by the manufacturer to the retailer is negative. This is because under the two-part tariff contract, the manufacturer wholesales green products to the retailer at the cost of production. When the sales process is completed, the profit of the entire supply chain is captured by the retailer. That is, the manufacturer must charge the retailer a fixed fee to realize its own profit. When the fixed fee is valued in the range of (−222, 562, 197, −222, 008, 980), the green supply chain is coordinated under the two-part tariff contract, and the manufacturer and retailer achieve the ‘win–win’ goal. The specific value of is determined by the bargaining power of the manufacturer and retailer.
7. Conclusions, Managerial Implications and Limitations
This paper develops a green supply chain system consisting of a manufacturer making green input and a retailer making green marketing effort input. The retailer in a follower position has fairness concerns. The impact of the retailer’s fairness concerns on the optimal decisions of the green supply chain is analyzed. The results of three Stackelberg game models are compared and analyzed. On the premise of finding that it is more beneficial for the manufacturer to consider the retailer’s fairness concerns, a two-part tariff contract is used to coordinate the green supply chain when the manufacturer considers the retailer’s fairness concerns. The validity of the models is verified by numerical simulations. The results show that: (1) The manufacturer and retailer can quantify the relevant model parameters to obtain optimal decisions. (2) It is beneficial for the manufacturer to consider the retailer’s fairness concerns. This is because the manufacturer’s profit when the manufacturer considers fairness concerns is higher than that when the manufacturer does not consider fairness concerns. The manufacturer’s profit will be highest if the manufacturer can eliminate the retailer’s fairness concerns. In addition, when the parameters meet certain conditions, this will also have a positive impact on the green supply chain’s profits. (3) When the manufacturer does not consider the retailer’s fairness concerns, the retailer can decide whether or not to have fairness concerns based on parametric conditions. When the manufacturer considers the retailer’s fairness concerns, from a rational perspective, the retailer should not have fairness concerns. (4) When the retailer is without fairness concerns, consumers will buy the greenest products, the retailer will make the greatest green marketing efforts, and the green supply chain will be the most profitable. From the supply chain viewpoint, the retailer should not have fairness concerns. (5) The two-part tariff contract can coordinate the green supply chain where the retailer has fairness concerns, which can increase the profits of both the manufacturer and retailer. The fixed fee is determined by the bargaining power of both parties.
According to the above results, the following management implications are provided for members of the green supply chain.
(1) For the manufacturer: when the retailer has fairness concerns, the manufacturer should consider its fairness concerns and not ignore them. The manufacturer could respond to the retailer’s fairness concerns by reducing the wholesale price and greenness. The manufacturer should take positive measures to eliminate the retailer’s fairness-concern behaviour. If the retailer’s fairness concerns are eliminated, the manufacturer’s profit increases significantly. The manufacturer can take the initiative to sign a two-part tariff contract with the retailer to achieve a win–win situation.
(2) For the retailer: when the manufacturer does not consider fairness concerns, from a rational viewpoint, the retailer should not have fairness concerns. When the manufacturer considers fairness concerns, the retailer could make fairness concerns based on parametric conditions and adjust its green marketing effort level and retail price to gain more profit. The retailer can also sign a two-part tariff contract with the manufacturer to further improve its own profit and achieve a win–win situation.
(3) For the entire green supply chain: the retailer should not have fairness concerns. Both parties should coordinate the green supply chain through a two-part tariff contract, provide the market with green products with a high greenness level, improve consumer satisfaction, and earn more profits. This makes the supply chain profit reach the level of centralized decision-making. Even if both parties cannot reach contract cooperation, they should make decisions without fairness concerns.
However, this paper still has some limitations, and these limitations also provide an opportunity for future research. For example, supply chain members are often partially rational in reality [66,67], thus the impact of fairness concerns on the green supply chain can be studied from the perspective that all supply chain members will be partially rational in the future. In addition, the data used in the numerical simulation come from the existing literature. In future research, the real data can be collected for numerical simulation, and the numerical simulation results can be compared with the actual operating conditions of enterprises in order to obtain more realistic guidance for decision-making.
Author Contributions
Conceptualization, H.H. and Y.L. (Yakun Li); methodology, Y.L. (Yakun Li); software, Y.L. (Yakun Li) and M.L.; validation, Y.L. (Yakun Li); investigation, Y.L. (Yakun Li); resources, H.H.; data curation, Y.L. (Yakun Li) and X.Y.; writing—original draft preparation, Y.L. (Yakun Li); writing—review and editing, H.H., Y.L. (Yakun Li), Y.L. (Yingyue Li) and Y.D.; visualization, Y.L. (Yakun Li); supervision, M.L. and X.Y.; project administration, H.H.; funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 71704151; the Soft Science Research Project of Innovation Competence Enhancement Plan of Hebei Province, grant number 21552501D; the Young Top Talent Project of Hebei Higher Education Institutions Humanities and Social Science Research Project, grant number BJ2021079; and the 2021 Hebei Provincial Postgraduate Demonstration Course Construction Project, grant number KCJSX2021021.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the editors and reviewers for their hard work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. The Proof of Theorem 1
According to Equation (5), the Hessian matrix of about and can be obtained by:
It can be seen from this Hessian matrix that . Therefore, when , is a joint concave function of and . Let and , and the optimal retail price and green marketing effort level can be obtained by:
Substituting Equations (A2) and (A3) into Equation (4), it is easy to understand that is the joint concave function of and according to the Hessian matrix of Equation (4) about and . Let and , and can be obtained, as shown in Equations (8) and (9).
Because , can be obtained.
Substituting Equations (8) and (9) into Equations (A2) and (A3), and can be obtained, as shown in Equations (10) and (11).
Substituting Equations (8)–(11) into Equations (4)–(6), , , and can be obtained, as shown in Equations (12)–(14).
Appendix A.2. The Proof of Theorem 2
According to Equation (7), the Hessian matrix of about and can be obtained by:
It can be seen from this Hessian matrix that . Because , can be obtained. Therefore, is a joint concave function of and . Let and , and the optimal retail price and green marketing effort level can be obtained by:
Substituting Equations (A5) and (A6) into Equation (4), it is easy to understand that is the joint concave function of and according to the Hessian matrix of Equation (4) about and . Let and , and can be obtained, as shown in Equations (15) and (16).
Substituting Equations (15) and (16) into Equations (A5) and (A6), and can be obtained, as shown in Equations (17) and (18).
Substituting Equations (15)–(18) into Equations (4)–(6), , , and can be obtained, as shown in Equations (19)–(21).
Substituting Equations (15)–(18) into Equation (7), can be obtained, as shown in Equation (22).
Appendix A.3. The Proof of Theorem 3
The solution process for the manufacturer determines that the optimal wholesale price and greenness level is the same as in Appendix A.1. The optimal wholesale price and greenness level when the manufacturer does not consider the retailer’s fairness concerns can be obtained, as shown in Equations (23) and (24).
After that, the retailer makes decisions based on the manufacturer’s optimal wholesale price and greenness level. Substituting Equations (23) and (24) into Equation (7), the Hessian matrix of about and can be obtained by:
Therefore, is a joint concave function of and . Let and , and can be obtained, as shown in Equations (25) and (26).
Substituting Equations (23)–(26) into Equations (4)–(6), , , and can be obtained, as shown in Equations (27)–(29).
Substituting Equations (23)–(26) into Equation (7), can be obtained, as shown in Equation (30).
Appendix A.4. The Proof of Corollary 1
Because of , it can be calculated that .
Because of , and , it can be calculated that .
Appendix A.5. The Proof of Corollary 2
Because of and , it can be calculated that and .
Because of and , it can be calculated that .
Appendix A.6. The Proof of Corollary 3
Because of , it can be calculated that .
Because of and , it can be calculated that .
Appendix A.7. The Proof of Corollary 4
Because of , it can be calculated that . Because of , it can be calculated that when , ; when , .
Because of , it can be calculated that . Because of , it can be calculated that when , ; when , . Because of , it can be calculated that when , ; when , . Therefore, when , ; when , ; when , .
Appendix A.8. The Proof of Corollary 5
Because of , it can be calculated that . Because of , it can be calculated that .
Because of and , it can be calculated that .
Appendix A.9. The Proof of Corollary 6
Because of , it can be calculated that . Because of , it can be calculated that when , ; when , .
Because of , it can be calculated that when , ; when , . Because of , it can be calculated that . Because of , it can be calculated that when , ; when , . Therefore, when , ; when , ; when , .
Appendix A.10. The Proof of Corollary 7
Because of , it can be calculated that when , ; when , . Because of , it can be calculated that when , ; when , .
Because of , it can be calculated that when , ; when , .
Appendix A.11. The Proof of Corollary 8
Because of , it can be calculated that . Because of , it can be calculated that .
Because of , it can be calculated that . Because of , it can be calculated that . Because of , it can be calculated that when , ; when , . Therefore, when , ; when , .
Appendix A.12. The Proof of Theorem 4
According to Equation (6), the Hessian matrix of about , , and is:
Therefore, is a joint concave function of , , and . Let , and , , , and can be obtained, as shown in Equations (31)–(33).
Substituting Equations (31)–(33) into Equation (6), can be obtained, as shown in Equation (34).
Appendix A.13. The Proof of Theorem 5
According to Equation (37), the optimal retail price and green marketing effort level can be obtained by:
In order to achieve green supply chain coordination, and are set. Therefore, and can be obtained, as shown in Equations (40) and (41).
Substituting Equations (38)–(41) into Equations (35)–(37), , , and can be obtained, as shown in Equations (42)–(44).
Appendix A.14. The Proof of Proposition 1
When the green supply chain is coordinated, and . Therefore:
Therefore, the range of can be expressed as:
To sum up, when , the two-part tariff contract can coordinate the green supply chain.
References
- Gayialis, S.P.; Kechagias, E.P.; Papadopoulos, G.A.; Masouras, D. A review and classification framework of traceability approaches for identifying product supply chain counterfeiting. Sustainability 2022, 14, 6666. [Google Scholar] [CrossRef]
- Dey, B.K.; Yilmaz, I.; Seok, H. A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation. Processes 2022, 10, 1775. [Google Scholar] [CrossRef]
- Kechagias, E.P.; Chatzistelios, G.; Papadopoulos, G.A.; Apostolou, P. Digital transformation of the maritime industry: A cybersecurity systemic approach. Int. J. Crit. Infr. Prot. 2022, 37, 100526. [Google Scholar] [CrossRef]
- Min, H. Blockchain technology for enhancing supply chain resilience. Bus. Horiz. 2019, 62, 35–45. [Google Scholar] [CrossRef]
- Li, G.; Li, L.; Choi, T.M.; Sethi, S.P. Green supply chain management in Chinese firms: Innovative measures and the moderating role of quick response technology. J. Oper. Manag. 2020, 66, 958–988. [Google Scholar] [CrossRef]
- Zhu, Q.; Sarkis, J. Relationships between operational practices and performance among early adopters of green supply chain management practices in Chinese manufacturing enterprises. J. Oper. Manag. 2004, 22, 265–289. [Google Scholar] [CrossRef]
- Xiaomi Group. 2020 Annual Report. 2020. Available online: https://cdn.cnbj1.fds.api.mi-img.com/staticsfile/csr/pdf/3.pdf (accessed on 1 June 2022).
- Wang, M. BYD will Invest 10.627 Billion Yuan in Research and Development in 2021, A Year-on-Year Increase of 24.2%. 2021. Available online: https://baijiahao.baidu.com/s?id=1728641710586085698&wfr=spider&for=pc (accessed on 1 June 2022).
- Roh, T.; Noh, J.; Oh, Y.; Park, K.-S. Structural relationships of a firm’s green strategies for environmental performance: The roles of green supply chain management and green marketing innovation. J. Clean. Prod. 2022, 356, 131877. [Google Scholar] [CrossRef]
- Hu, H.; Li, Y.; Li, M. Decisions and Coordination of Green Supply Chain Considering Big Data Targeted Advertising. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1035–1056. [Google Scholar] [CrossRef]
- Yan, K.; Liu, S.; Zuo, M.; Zheng, J.; Xu, Y. Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value. Systems 2022, 10, 76. [Google Scholar] [CrossRef]
- Gurnani, H.; Erkoc, M.; Luo, Y. Impact of product pricing and timing of investment decisions on supply chain coopetition. Eur. J. Oper. Res. 2007, 180, 228–248. [Google Scholar] [CrossRef]
- Marketing Edge. Amazon Dethrones Procter & Gamble as World’s Largest Advertiser. 2020. Available online: https://marketingedge.com.ng/amazon-dethrones-procter-gamble-as-worlds-largest-advertiser/ (accessed on 1 June 2022).
- Corsten, D.; Kumar, N. Do suppliers benefit from collaborative relationships with large retailers? An empirical investigation of efficient consumer response adoption. J. Mark. 2005, 69, 80–94. [Google Scholar] [CrossRef]
- Loch, C.H.; Wu, Y. Social preferences and supply chain performance: An experimental study. Manag. Sci. 2008, 54, 1835–1849. [Google Scholar] [CrossRef]
- Katok, E.; Olsen, T.; Pavlov, V. Wholesale pricing under mild and privately known concerns for fairness. Prod. Oper. Manag. 2014, 23, 285–302. [Google Scholar] [CrossRef]
- Nie, T.; Du, S. Dual-fairness supply chain with quantity discount contracts. Eur. J. Oper. Res. 2017, 258, 491–500. [Google Scholar] [CrossRef]
- Jian, J.; Li, B.; Zhang, N.; Su, J. Decision-making and coordination of green closed-loop supply chain with fairness concern. J. Clean. Prod. 2021, 298, 126799. [Google Scholar] [CrossRef]
- Tsao, Y.; Sheen, G. Effects of promotion cost sharing policy with the sales learning curve on supply chain coordination. Comput. Oper. Res. 2012, 39, 1872–1878. [Google Scholar] [CrossRef]
- Hu, H.; Wu, Q.; Han, S.; Zhang, Z. Coordination of dual-channel supply chain with perfect product considering sales effort. Adv. Prod. Eng. Manag. 2020, 15, 192–203. [Google Scholar] [CrossRef]
- Zhang, R.; Ma, W.; Si, H.; Liu, J.; Liao, L. Cooperative game analysis of coordination mechanisms under fairness concerns of a green retailer. J. Retail. Consum. Serv. 2021, 59, 102361. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.; Liu, Y.; Lu, R. Optimal environmental quality and price with consumer environmental awareness and retailer’s fairness concerns in supply chain. J. Clean. Prod. 2019, 213, 1063–1079. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, R.; Shen, L.; Jin, M. Decisions and coordination of green e-commerce supply chain considering green manufacturer’s fairness concerns. Int. J. Prod. Res. 2020, 58, 7471–7489. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Pu, X.; Li, Y. Green manufacturing strategy considering retailers’ fairness concerns. Sustainability 2019, 11, 4646. [Google Scholar] [CrossRef]
- Yuan, X.; Tang, F.; Zhang, D.; Zhang, X. Green remanufacturer’s mixed collection channel strategy considering enterprise’s environmental responsibility and the fairness concern in reverse green supply chain. Int. J. Environ. Res. Public Health 2021, 18, 3405. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Shao, E.; Gong, Y.; Guan, X. Decision-making for green supply chain considering fairness concern based on trade credit. IEEE Access 2021, 9, 67684–67695. [Google Scholar] [CrossRef]
- Zhu, W.; He, Y. Green product design in supply chains under competition. Eur. J. Oper. Res. 2017, 258, 165–180. [Google Scholar] [CrossRef]
- Parsaeifar, S.; Bozorgi-Amiri, A.; Naimi-Sadigh, A.; Sangari, M.S. A game theoretical for coordination of pricing, recycling, and green product decisions in the supply chain. J. Clean. Prod. 2019, 226, 37–49. [Google Scholar] [CrossRef]
- Agi, M.; Yan, X. Greening products in a supply chain under market segmentation and different channel power structures. Int. J. Prod. Econ. 2020, 223, 107523. [Google Scholar] [CrossRef]
- Xia, Q.; Zhi, B.; Wang, X. The role of cross-shareholding in the green supply chain: Green contribution, power structure and coordination. Int. J. Prod. Econ. 2021, 234, 108037. [Google Scholar] [CrossRef]
- Agi, M.A.N.; Nishant, R. Understanding influential factors on implementing green supply chain management practices: An interpretive structural modelling analysis. J. Environ. Manag. 2017, 188, 351–363. [Google Scholar] [CrossRef]
- Jamali, M.B.; Rasti-barzoki, M. A game theoretic approach for green and non-green product pricing in chain-to-chain competitive sustainable and regular dual-channel supply chains. J. Clean. Prod. 2018, 170, 1029–1043. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, Z.; Wei, H. Competition and coordination in a dual-channel green supply chain with an eco-label policy. Comput. Ind. Eng. 2021, 153, 107057. [Google Scholar] [CrossRef]
- Khosroshahi, H.; Dimitrov, S.; Hejazi, S.R. Pricing, greening, and transparency decisions considering the impact of government subsidies and CSR behavior in supply chain decisions. J. Retail. Consum. Serv. 2021, 60, 102485. [Google Scholar] [CrossRef]
- Li, Z.; Pan, Y.; Yang, W.; Ma, J.; Zhou, M. Effects of government subsidies on green technology investment and green marketing coordination of supply chain under the cap-and-trade mechanism. Energ. Econ. 2021, 101, 105426. [Google Scholar] [CrossRef]
- Li, B.; Wang, H.; Zheng, W. Who will take on green product development in supply chains? Manufacturer or online retailer. J. Clean. Prod. 2021, 314, 128000. [Google Scholar] [CrossRef]
- Xiang, Z.; Xu, M. Dynamic game strategies of a two-stage remanufacturing closed-loop supply chain considering Big Data marketing, technological innovation and overconfidence. Comput. Ind. Eng. 2020, 145, 106538. [Google Scholar] [CrossRef]
- Tian, G.; Liu, J.; Gong, Y.; Wang, Q.; Sun, H.; Chen, H. Multinational companies’ coordination mechanism for extending corporate social responsibility to Chinese suppliers. J. Clean. Prod. 2020, 267, 121896. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, W.; Li, S.; Veglianti, E. Competition and cooperation in the dual-channel green supply chain with customer satisfaction. Econ. Anal. Policy 2022, 76, 95–113. [Google Scholar] [CrossRef]
- Pal, B.; Sarkar, A.; Sarkar, B. Optimal decisions in a dual-channel competitive green supply chain management under promotional effort. Expert. Syst. Appl. 2023, 211, 118315. [Google Scholar] [CrossRef]
- Meng, Q.; Li, M.; Liu, W.; Li, Z.; Zhang, J. Pricing policies of dual-channel green supply chain: Considering government subsidies and consumers’ dual preferences. Sustain. Prod. Consump. 2021, 26, 1021–1030. [Google Scholar] [CrossRef]
- Ling, Y.; Xu, J. Price and greenness competition between duopoly firms considering consumer premium payments. Environ. Dev. Sustain. 2021, 23, 3853–3880. [Google Scholar] [CrossRef]
- Liu, A.; Luo, S.; Mou, J.; Qiu, H. The antagonism and cohesion of the upstream supply chain under information asymmetry. Ann. Oper. Res. 2021, 1–46. [Google Scholar] [CrossRef]
- Manoj, U.V.; Sriskandarajah, C.; Wagneur, E. Coordination in a two-stage production system: Complexity, conflict and cooperation. Comput. Oper. Res. 2012, 39, 1245–1256. [Google Scholar] [CrossRef]
- Liu, G.; Yang, H.; Dai, R. Which contract is more effective in improving product greenness under different power structures: Revenue sharing or cost sharing? Comput. Ind. Eng. 2022, 148, 106701. [Google Scholar] [CrossRef]
- Shen, Y.; Willems, S.P.; Dai, Y. Channel selection and contracting in the presence of a retail platform. Prod. Oper. Manag. 2019, 28, 1173–1185. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X. Information acquisition and its incentives in an E-Commerce supply chain under the offline showroom model. J. Theor. Appl. Electron. Commer. 2021, 16, 1791–1804. [Google Scholar] [CrossRef]
- Hong, Z.; Guo, X. Green product supply chain contracts considering environmental responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Xu, X.; He, P.; Xu, H.; Zhang, Q. Supply chain coordination with green technology under cap-and-trade regulation. Int. J. Prod. Econ. 2017, 183, 433–442. [Google Scholar] [CrossRef]
- Heydaria, J.; Govindanb, K.; Basiria, Z. Balancing price and green quality in presence of consumer environmental awareness: A green supply chain coordination approach. Int. J. Prod. Res. 2020, 59, 1957–1975. [Google Scholar] [CrossRef]
- Zhang, C.T.; Wang, H.X.; Ren, M.L. Research on pricing and coordination strategy of green supply chain under hybrid production mode. Comput. Ind. Eng. 2014, 72, 24–31. [Google Scholar] [CrossRef]
- Basiri, Z.; Heydari, J. A mathematical model for green supply chain coordination with substitutable products. J. Clean. Prod. 2017, 145, 232–249. [Google Scholar] [CrossRef]
- Cui, T.H.; Raju, J.S.; Zhang, Z.J. Fairness and channel coordination. Manag. Sci. 2007, 53, 1303–1314. [Google Scholar]
- Ho, T.H.; Zhang, J. Designing pricing contracts for boundedly rational customers: Does the framing of the fixed fee matter? Manag. Sci. 2008, 54, 686–700. [Google Scholar] [CrossRef]
- Toktas-Palut, P. An integrated contract for coordinating a three-stage green forward and reverse supply chain under fairness concerns. J. Clean. Prod. 2021, 279, 123735. [Google Scholar] [CrossRef]
- Mondal, C.; Giri, B.C. Investigating a green supply chain with product recycling under retailer’s fairness behavior. J. Ind. Manag. Optim. 2022, 18, 3641–3677. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Q.; Hu, X.; Yang, W.; Chen, W. Optimal contract design problem considering the retailer’s fairness concern with asymmetric demand information. J. Clean. Prod. 2021, 287, 125407. [Google Scholar] [CrossRef]
- Adhikari, A.; Bisi, A. Collaboration, bargaining, and fairness concern for a green apparel supply chain: An emerging economy perspective. Transp. Res. E-Log. 2020, 135, 101863. [Google Scholar] [CrossRef]
- Liu, J.; Wu, X.; Lei, J.L. The combined impacts of consumer green preference and fairness concern on the decision of three-party supply chain. J. Ind. Manag. Optim. 2022, 18, 2749–2782. [Google Scholar] [CrossRef]
- Wang, D.; Ge, G.; Zhou, Y.; Zhu, M. Pricing-decision analysis of green supply chain with two competitive manufacturers considering horizontal and vertical fairness concerns. Environ. Sci. Pollut. R 2022, 29, 66235–66258. [Google Scholar] [CrossRef]
- Hu, H.; Li, Y.; Li, M.; Zhu, W.; Chan, F. Optimal decision-making of green agricultural product supply chain with fairness concerns. J. Ind. Manag. Optim. 2022, 1–23. [Google Scholar] [CrossRef]
- Sun, H.; Zhong, Y. Carbon emission reduction and green marketing decisions in a two-echelon low-carbon supply chain considering fairness concern. J. Bus. Ind. Mark. 2022, 1–25. [Google Scholar] [CrossRef]
- Ma, P.; Li, K.W.; Wang, Z.J. Pricing decisions in closed-loop supply chains with marketing effort and fairness concerns. Int. J. Prod. Res. 2017, 55, 6710–6731. [Google Scholar] [CrossRef]
- Alizadeh-Basban, N.; Taleizadeh, A.A. A hybrid circular economy—Game theoretical approach in a dual-channel green supply chain considering sale’s effort, delivery time, and hybrid remanufacturing. J. Clean. Prod. 2020, 250, 119521. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Zhao, S. Cost-sharing models for green product production and marketing in a food supply chain. Ind. Manag. Data. Syst. 2018, 118, 654–682. [Google Scholar] [CrossRef]
- Hu, H.; Li, Y.; Tian, M.; Cai, X. Evolutionary Game of Small and Medium-Sized Enterprises’ Accounts-Receivable Pledge Financing in the Supply Chain. Systems 2022, 10, 21. [Google Scholar] [CrossRef]
- Xie, B.; An, K.; Cheng, Y. Dynamic Research on Three-Player Evolutionary Game in Waste Product Recycling Supply Chain System. Systems 2022, 10, 185. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).