Encipher GAN: An End-to-End Color Image Encryption System Using a Deep Generative Model
Abstract
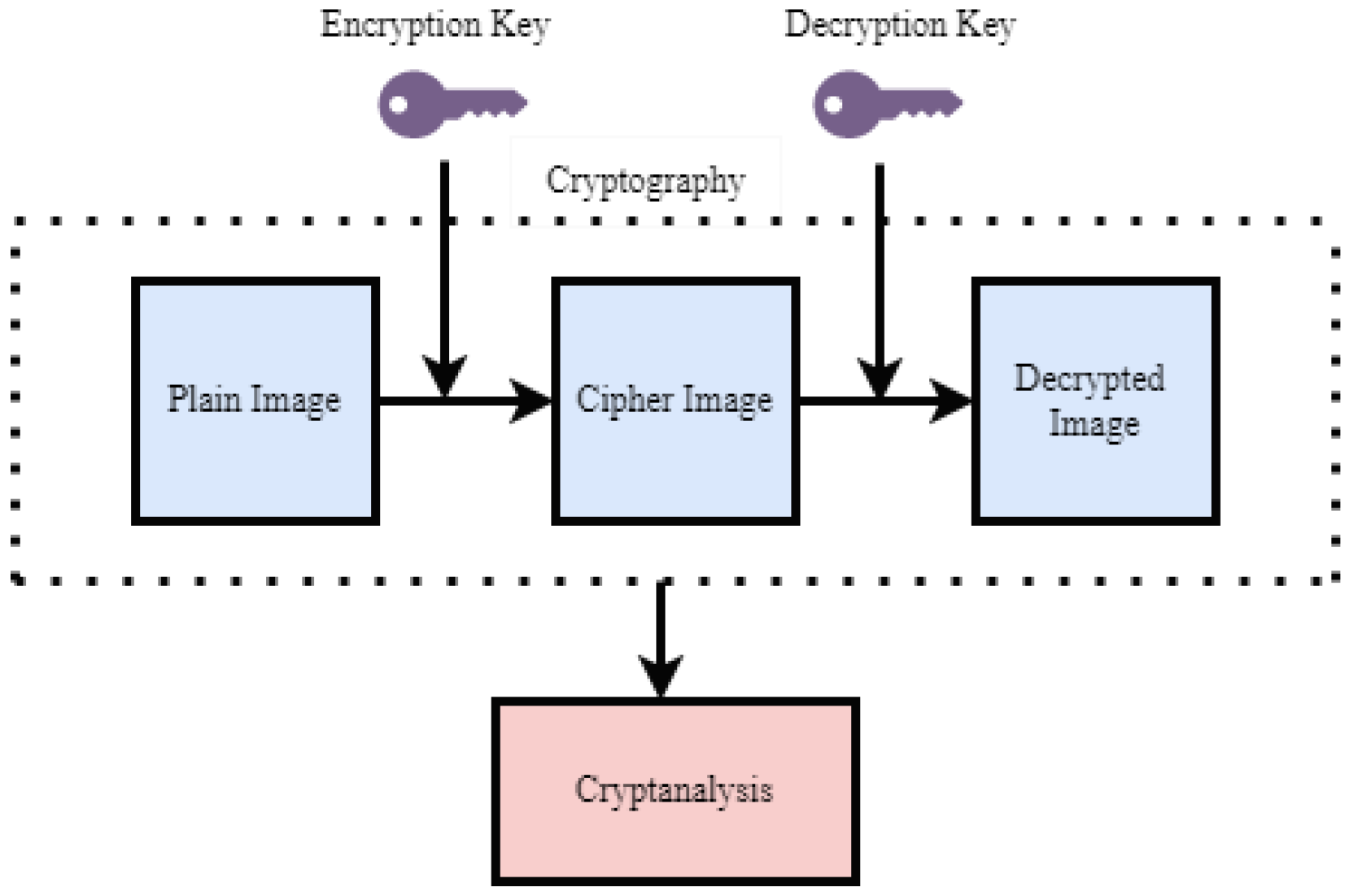
1. Introduction
2. Related Works
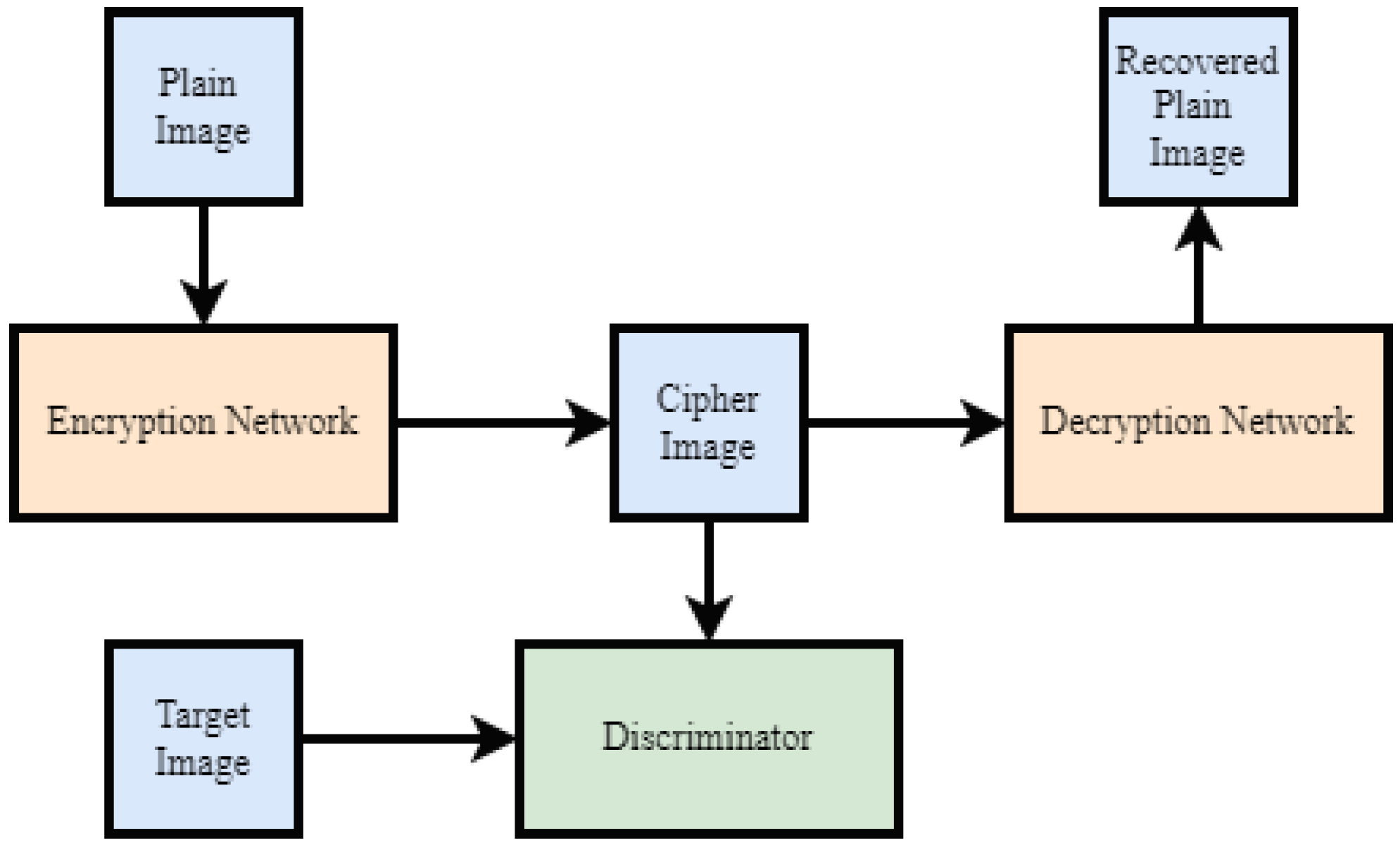
3. Proposed Method
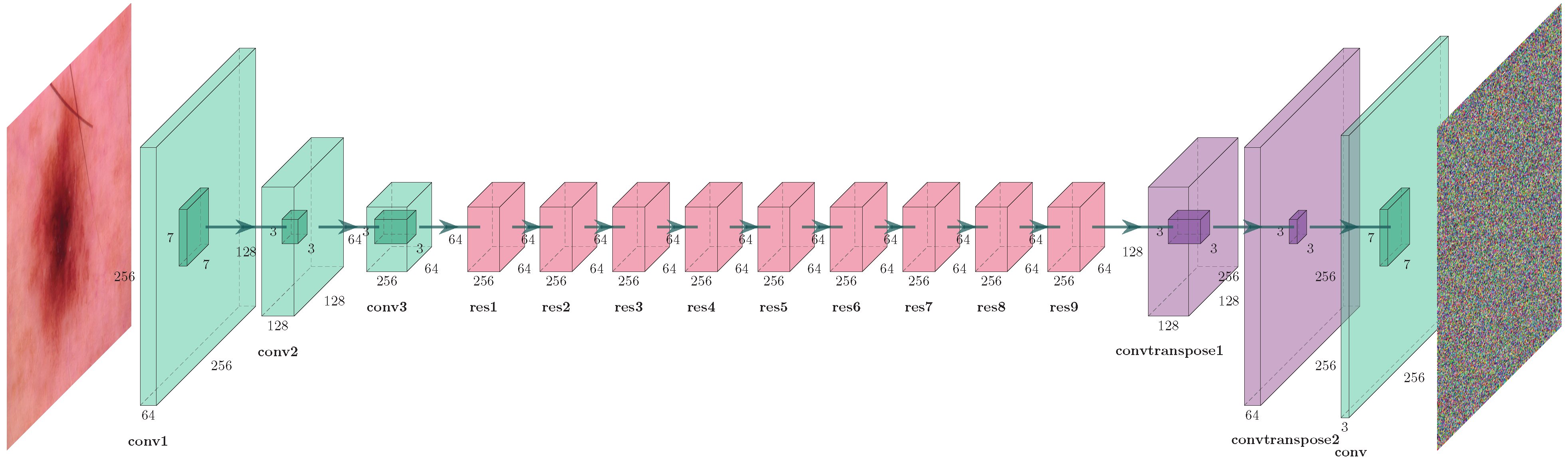
3.1. Encryption Network
- Feature Encoder:The input image is downsampled with three layers of convolution to extract the features of images.The encoder consists of three convolutions, each of which is followed by instance normalization and reLU activation. The first convolution layer has 64 filters of size , followed by convolutions with filters of size . The encoder downsamples the plain image to extract features.
- Transformation Module:In this phase, the features are transformed by residual blocks. The model is optimized using a ResNet based architecture to enhance the stability of the model. These residual blocks consist of convolution–batch normalization–ReLU–convolution–batch normalization–LRelU. The output of each of these blocks are concatenated and then passed to the decoder. The size of input features and output remains the same during transformation.
- Feature Decoder:The decoder upsamples the transformed features using rounds of transpose convolution layers. In the final convolution layer, these features are mapped to output image of size .
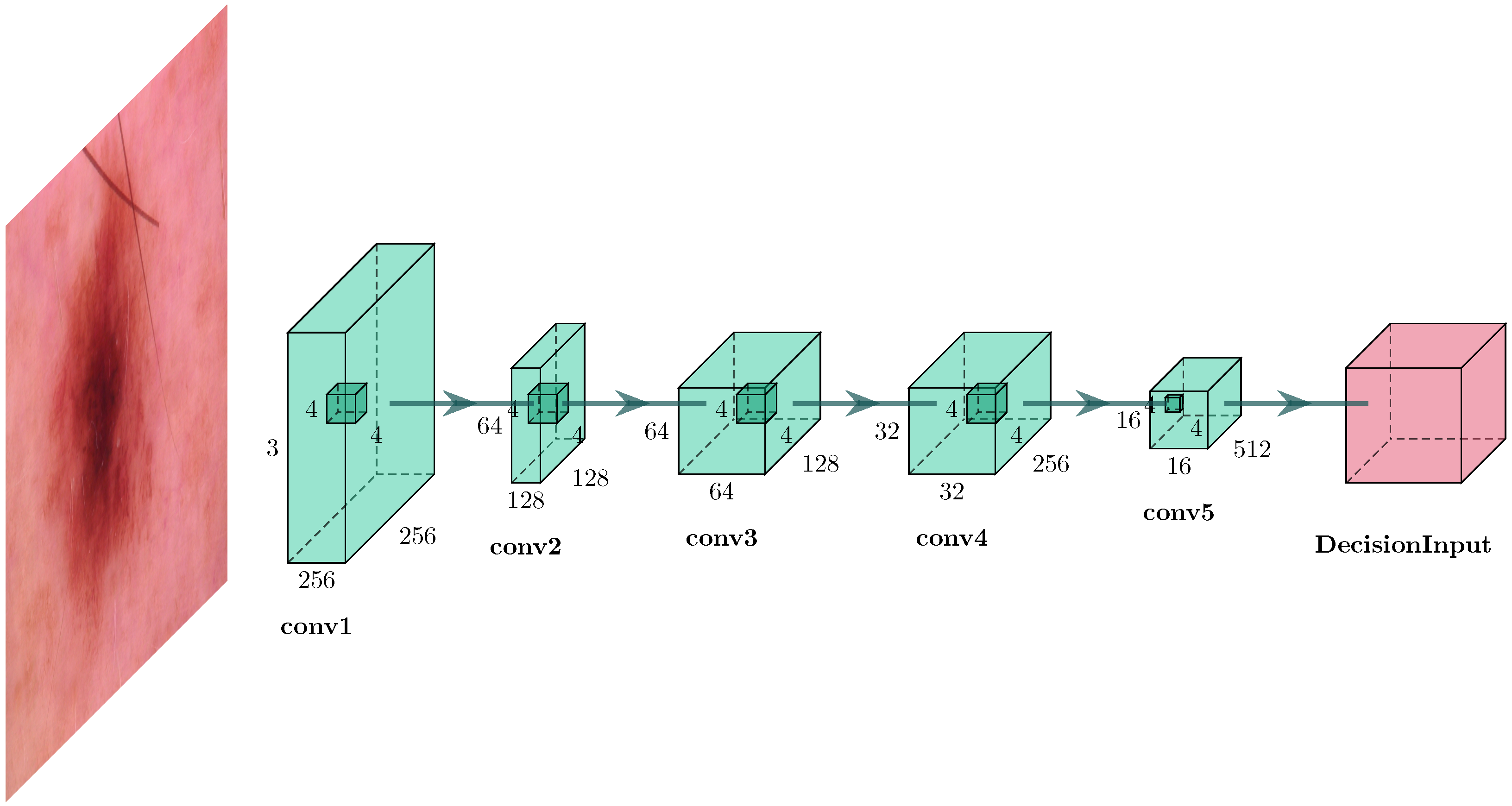
3.2. Discriminator Network
3.3. Decryption Network
3.4. Training
Total Loss of the Network
3.5. Encryption/Decryption Algorithm
| Algorithm 1 Encryption model. |
| Input: Plain Image I of size and Secret Key () Output: Cipher Image, C Initialisation: Assign trained weights to the encryption network using secret key .
|
4. Security Analysis
4.1. Secret Key Space
4.2. Secret Key Sensitivity
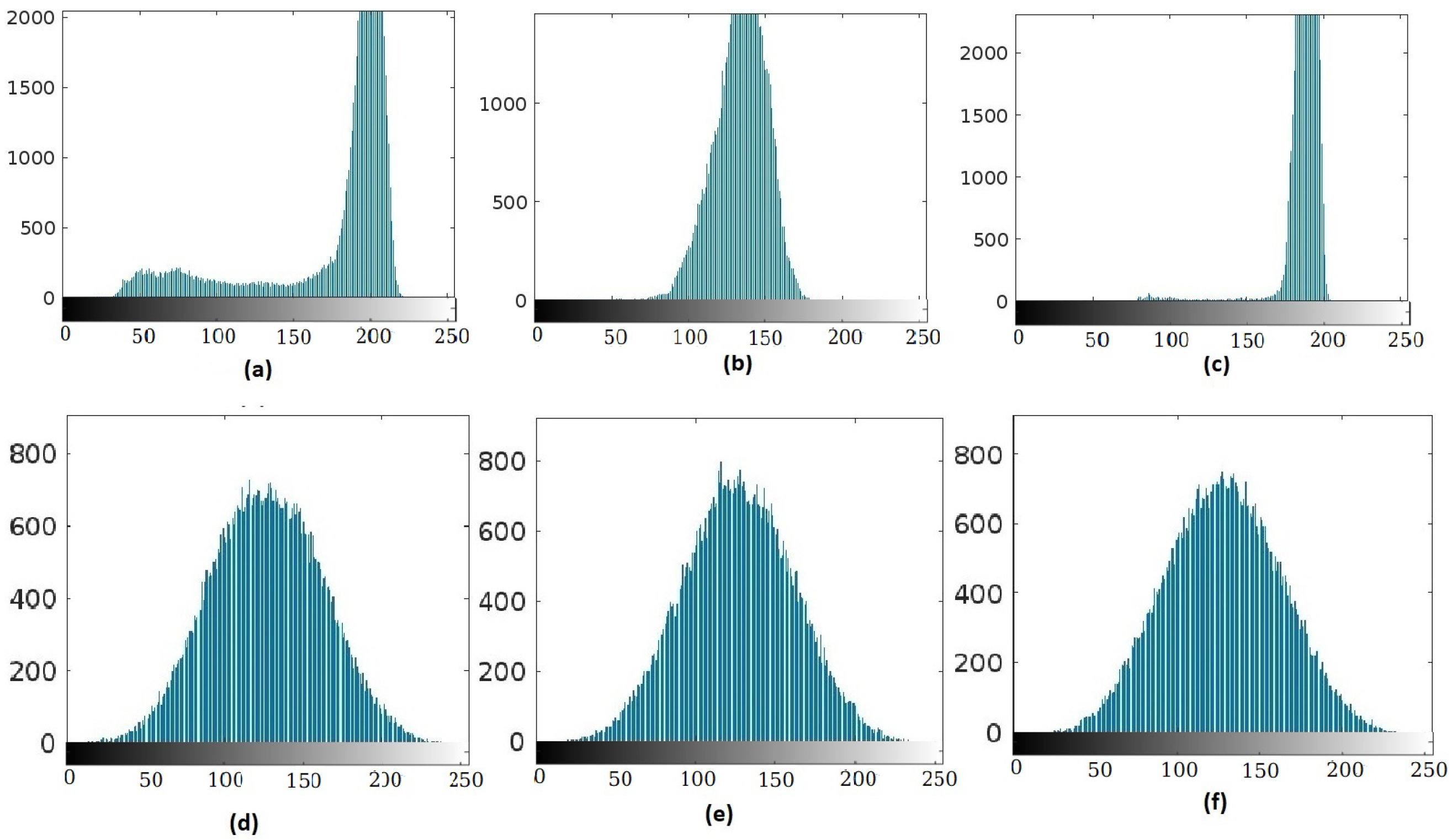
4.3. Analysis of the Histogram of Generated Images
4.4. Image Information Entropy
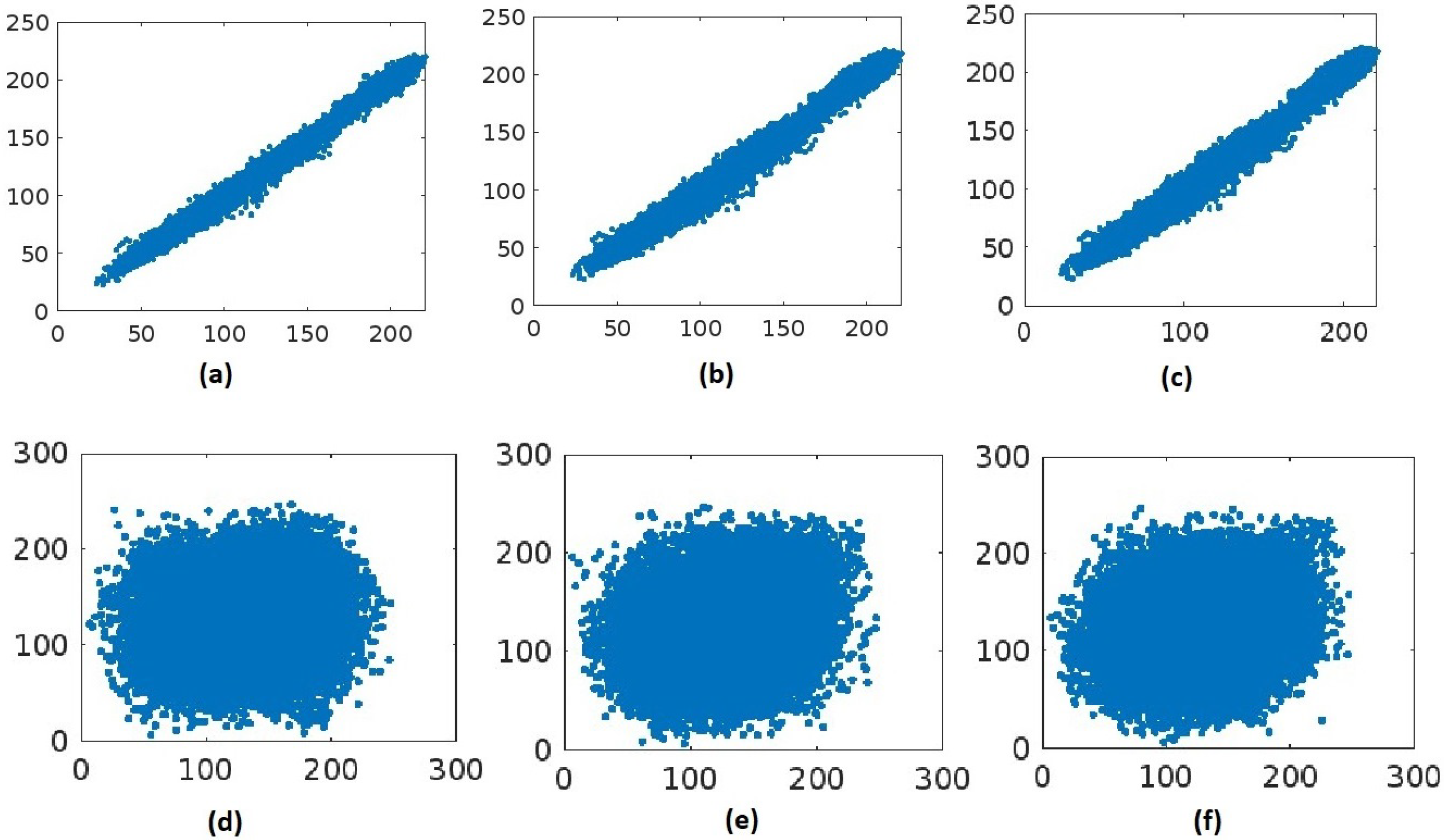
4.5. Correlation Analysis
5. Performance Analysis
5.1. Optimization Process
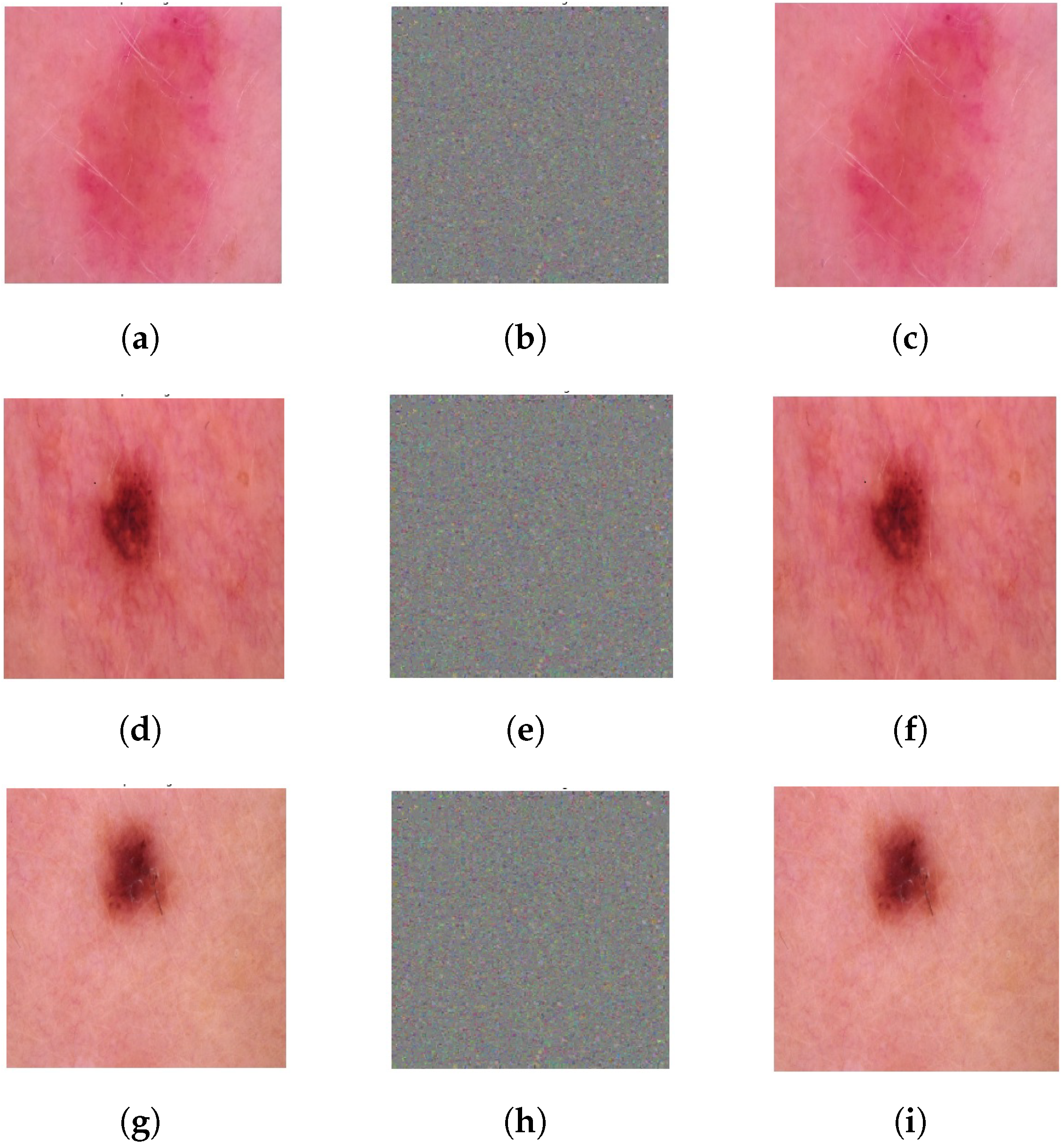
5.2. Quality of Recovered Image
5.3. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DES | Data encryption standard |
| AES | Advanced encryption standard |
| Cycle GAN | Cycle generative adversarial network |
| SSIM | Structural similarity index |
| MSE | Mean-squared error |
| PSNR | peak signal-to-noise ratio |
| CNN | Convolutional neural network |
| DNN | Deep neural network |
| SA | Silica aerogel |
| IE | Image entropy |
| DeepEDN | Deep learning based image encryption and decryption Network |
References
- Zhang, L.Y.; Liu, Y.; Pareschi, F.; Zhang, Y.; Wong, K.W.; Rovatti, R.; Setti, G. On the security of a class of diffusion mechanisms for image encryption. IEEE Trans. Cybern. 2017, 48, 1163–1175. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ding, Y.; Wu, G.; Chen, D.; Zhang, N.; Gong, L.; Cao, M.; Qin, Z. DeepEDN: A deep-learning-based image encryption and decryption network for internet of medical things. IEEE Internet Things J. 2020, 8, 1504–1518. [Google Scholar] [CrossRef]
- Chen, W.H.; Luo, S.; Zheng, W.X. Impulsive synchronization of reaction–diffusion neural networks with mixed delays and its application to image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2696–2710. [Google Scholar] [CrossRef] [PubMed]
- Dridi, M.; Hajjaji, M.A.; Bouallegue, B.; Mtibaa, A. Cryptography of medical images based on a combination between chaotic and neural network. IET Image Process. 2016, 10, 830–839. [Google Scholar] [CrossRef]
- Hu, F.; Wang, J.; Xu, X.; Pu, C.; Peng, T. Batch image encryption using generated deep features based on stacked autoencoder network. Math. Probl. Eng. 2017, 2017, 3675459. [Google Scholar] [CrossRef]
- Hu, D.; Wang, L.; Jiang, W.; Zheng, S.; Li, B. A novel image steganography method via deep convolutional generative adversarial networks. IEEE Access 2018, 6, 38303–38314. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Y.; Chen, M.; Li, F. Research on iris image encryption based on deep learning. EURASIP J. Image Video Process. 2018, 2018, 126. [Google Scholar] [CrossRef]
- Debiasi, L.; Uhl, A. Techniques for a forensic analysis of the casia-iris v4 database. In Proceedings of the 3rd International Workshop on Biometrics and Forensics (IWBF 2015), Gjovik, Norway, 3–4 March 2015; pp. 1–6. [Google Scholar]
- Jaeger, S.; Candemir, S.; Antani, S.; Wáng, Y.X.J.; Lu, P.X.; Thoma, G. Two public chest X-ray datasets for computer-aided screening of pulmonary diseases. Quant. Imaging Med. Surg. 2014, 4, 475. [Google Scholar]
- Jin, J.; Kim, K. 3D CUBE algorithm for the key generation method: Applying deep neural network learning-based. IEEE Access 2020, 8, 33689–33702. [Google Scholar] [CrossRef]
- Maniyath, S.R.; Thanikaiselvan, V. An efficient image encryption using deep neural network and chaotic map. Microprocess. Microsyst. 2020, 77, 103134. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Enginoğlu, S.; Akbacak, E.; Thanh, D.N. An image encryption scheme based on chaotic logarithmic map and key generation using deep CNN. Multimed. Tools Appl. 2022, 81, 7365–7391. [Google Scholar] [CrossRef]
- Fratalocchi, A.; Fleming, A.; Conti, C.; Di Falco, A. NIST-certified secure key generation via deep learning of physical unclonable functions in silica aerogels. Nanophotonics 2021, 10, 457–464. [Google Scholar] [CrossRef]
- Li, J.; Zhou, J.; Di, X. A learning optical image encryption scheme based on CycleGAN. J. Jilin Univ. (Eng. Technol. Ed.) 2021, 51, 1060–1066. [Google Scholar]
- Ding, Y.; Tan, F.; Qin, Z.; Cao, M.; Choo, K.K.R.; Qin, Z. DeepKeyGen: A deep learning-based stream cipher generator for medical image encryption and decryption. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4915–4929. [Google Scholar] [CrossRef] [PubMed]
- Bao, Z.; Xue, R. Research on the avalanche effect of image encryption based on the Cycle-GAN. Appl. Opt. 2021, 60, 5320–5334. [Google Scholar] [CrossRef]
- Bao, Z.; Xue, R.; Jin, Y. Image scrambling adversarial autoencoder based on the asymmetric encryption. Multimed. Tools Appl. 2021, 80, 28265–28301. [Google Scholar] [CrossRef]
- Baluja, S. Hiding images in plain sight: Deep steganography. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2223–2232. [Google Scholar]
- Codella, N.; Rotemberg, V.; Tschandl, P.; Celebi, M.E.; Dusza, S.; Gutman, D.; Helba, B.; Kalloo, A.; Liopyris, K.; Marchetti, M.; et al. Skin lesion analysis toward melanoma detection 2018: A challenge hosted by the international skin imaging collaboration (ISIC). arXiv 2019, arXiv:1902.03368. [Google Scholar]
- Sang, Y.; Sang, J.; Alam, M.S. Image encryption based on logistic chaotic systems and deep autoencoder. Pattern Recognit. Lett. 2022, 153, 59–66. [Google Scholar] [CrossRef]
- Panwar, K.; Purwar, R.K.; Jain, A. Cryptanalysis and improvement of an image encryption scheme using combination of one-dimensional chaotic maps. J. Electron. Imaging 2018, 27, 053037. [Google Scholar]
- Zheng, Z.; Liu, H.; Yu, Z.; Zheng, H.; Wu, Y.; Yang, Y.; Shi, J. Encryptgan: Image steganography with domain transform. arXiv 2019, arXiv:1905.11582. [Google Scholar]
- Chen, J.; Li, X.W.; Wang, Q.H. Deep learning for improving the robustness of image encryption. IEEE Access 2019, 7, 181083–181091. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J. Single Exposure Phase-Only Optical Image Encryption and Hiding Method via Deep Learning. IEEE Photonics J. 2022, 14, 1–8. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lü, J.; Hao, F. Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE Multimed. 2018, 25, 46–56. [Google Scholar] [CrossRef]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. Regul. Pap. 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Lu, X.; Li, C.; Tan, K. Network Analysis of Chebyshev Polynomial in a Fixed-precision Digital Domain. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 8634–8638. [Google Scholar]




| Layer | Size of Kernel | Normalization Technique | Activation Function | Output | Parameters |
|---|---|---|---|---|---|
| Input | |||||
| Convolution | Instance | ReLU | 4704 | ||
| Convolution | Instance | ReLU | 18,432 | ||
| Convolution | Instance | ReLU | 73,728 | ||
| Resnet Blocks (9, each with 2 convolutions) | Batch | ReLU | 2,564,208 | ||
| Transpose Convolution | Instance | ReLU | 73,728 | ||
| Transpose Convolution | Instance | ReLU | 18,432 | ||
| Convolution | Tanh | ReLU | 4704 |
| Layer | Size of Kernel | Normalization Technique | Activation Function | Output | Parameters |
|---|---|---|---|---|---|
| Input (Two Inputs of same size) | |||||
| Convolution | ReLU | 3136 | |||
| Convolution | Instance Normalization | ReLU | 131,456 | ||
| Convolution | Instance Normalization | ReLU | 524,056 | ||
| Convolution | Instance Normalization | ReLU | 2,098,688 | ||
| Convolution | Instance Normalization | 8193 | |||
| linear | Sigmoid | 1 |
| Images | Image 1 | Image 2 | Image 3 |
|---|---|---|---|
| Plain | 7.15 | 6.27 | 6.04 |
| Cipher | 7.40 | 7.36 | 7.38 |
| Images | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| Image 1 | 0.9976 | 0.9986 | 0.9959 |
| Cipher | 0.4812 | 0.4584 | 0.2169 |
| Image 2 | 0.9976 | 0.9984 | 0.9963 |
| Cipher | 0.5090 | 0.4538 | 0.2043 |
| Image 3 | 0.9977 | 0.9986 | 0.9961 |
| Cipher | 0.5203 | 0.4147 | 0.1782 |
| Methods | Average PSNR |
|---|---|
| Proposed Method | 39.9703 |
| DeepEDN [3] | 36.514 |
| EncryptGAN [23] | 17.5992 |
| Image encryption system with CNN denoiser [24] | 24.8975 |
| Optical Image Encryption using Deep Learning [25] | 30.0000 |
| Ref. | Technique | PSNR between Original Image and Recovered Image | SSIM between Original Image and Recovered Image | Correlation Coefficient | Image Entropy of Cipher Image |
|---|---|---|---|---|---|
| Proposed | Deep learning based encryption | 39.9703 | 0.9972 | 0.3855 | 7.36 |
| [12] | Deep learning based secret keys and chaos-based encryption | inf | 1 | 0.0149 | 7.98 |
| [13] | Deep learning based secret keys and chaos-based encryption | inf | 1 | 0.00002 | 7.99 |
| [3] | Deep learning based image encryption scheme | 36.514 | 0.90000 | – | 7.95 |
| [24] | Optical image encryption scheme using deep convolutional neural network | 24.8975 | 0.8885 | – | – |
| [25] | Optical Image encryption and Hiding using deep learning | 30.0000 | 0.9306 | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panwar, K.; Singh, A.; Kukreja, S.; Singh, K.K.; Shakhovska, N.; Boichuk, A. Encipher GAN: An End-to-End Color Image Encryption System Using a Deep Generative Model. Systems 2023, 11, 36. https://doi.org/10.3390/systems11010036
Panwar K, Singh A, Kukreja S, Singh KK, Shakhovska N, Boichuk A. Encipher GAN: An End-to-End Color Image Encryption System Using a Deep Generative Model. Systems. 2023; 11(1):36. https://doi.org/10.3390/systems11010036
Chicago/Turabian StylePanwar, Kirtee, Akansha Singh, Sonal Kukreja, Krishna Kant Singh, Nataliya Shakhovska, and Andrii Boichuk. 2023. "Encipher GAN: An End-to-End Color Image Encryption System Using a Deep Generative Model" Systems 11, no. 1: 36. https://doi.org/10.3390/systems11010036
APA StylePanwar, K., Singh, A., Kukreja, S., Singh, K. K., Shakhovska, N., & Boichuk, A. (2023). Encipher GAN: An End-to-End Color Image Encryption System Using a Deep Generative Model. Systems, 11(1), 36. https://doi.org/10.3390/systems11010036







