The Decision-Making for the Optimization of Finance Lease with Facilities’ Two-Dimensional Deterioration
Abstract
1. Introduction
2. Two-Dimensional Deterioration of Lease Facilities
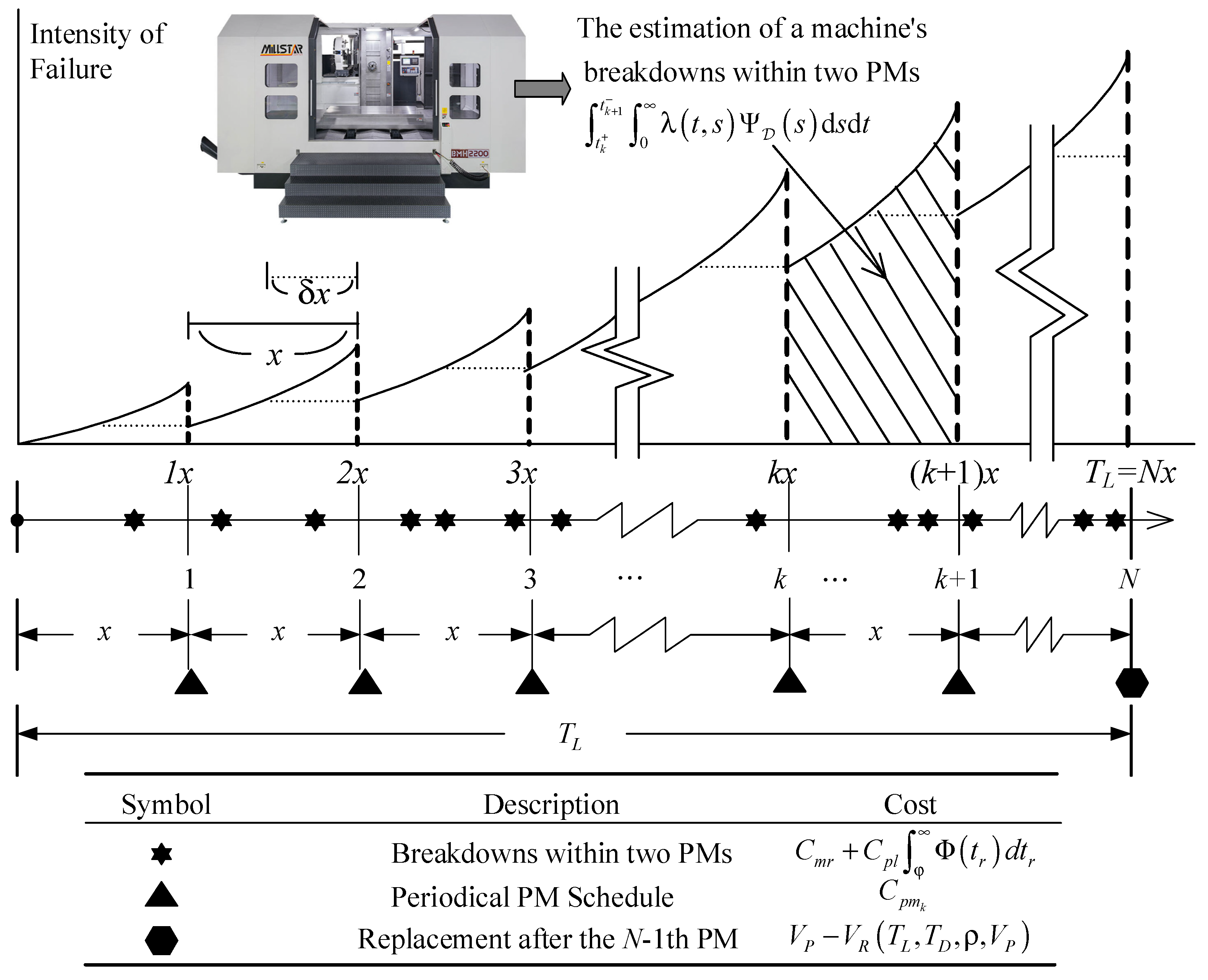
2.1. Two-Dimensional Deterioration Model
- The leased facility deteriorates over time and usage, and an NHPP can describe the failure or breakdown process.
- When a failure or breakdown appears during the leased period, a minimal repair is made. The facility would be immediately returned to its previous state following the repair.
- Because the PM activities are imperfect, the leased facility‘s condition cannot be fully restored after PM.
- The lessor is responsible for covering the costs of repairs and routine PM.
- It is assumed that the usage rate of the leased facilities follows a Gamma, Lognormal or Uniform distribution.
2.2. Estimation of Related Costs under Periodic Preventive Maintenance
3. Optimal PM Decision to Facilities with and without Consideration of Financial Lease Contract Revenue
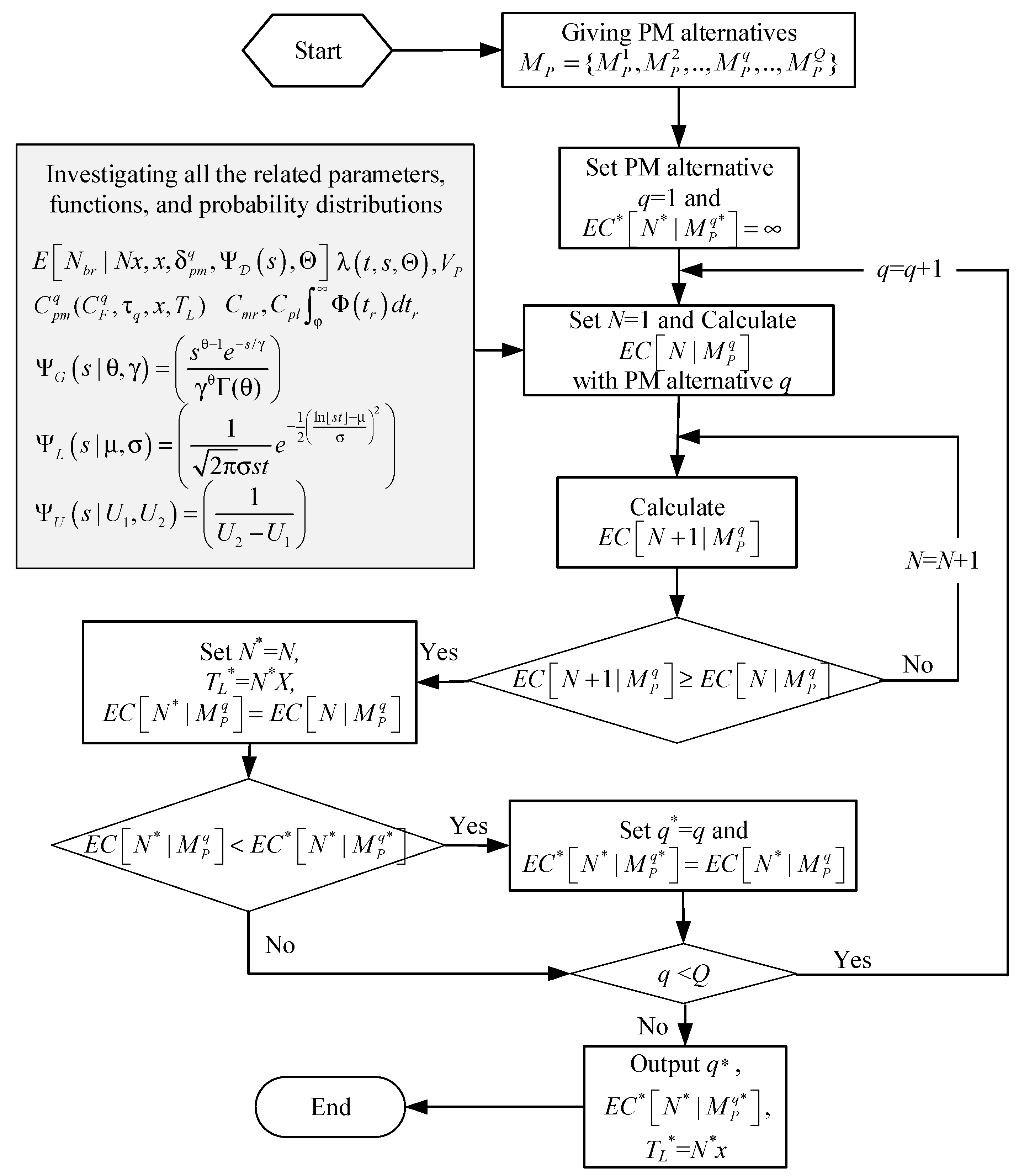
3.1. Optimal PM without Consideration of Financial Lease Contract Revenue
- Step 1: Initially, all the PM alternatives are given as the candidate list .
- Step 2: Start with the first PM alternative (), and the variable of the optimal expected cost is set to infinity.
- Step 3: Set the PM number and calculate the expected cost .
- Step 4: Calculate the expected cost .
- Step 5: Investigating whether the condition is supported or not? If it is supported, go to Step 6. Otherwise, go to Step 4 with .
- Step 6: Set the optimal number as , the optimal lease length as , and the variable of the optimal expected cost as .
- Step 7: Investigating whether the condition is supported or not? If the answer is yes, go to Step 8. Otherwise, go to Step 9.
- Step 8: Set the optimal PM alternative as and the variable of the optimal expected cost as .
- Step 9: Investigating whether the condition has reached? If the answer is yes, go to Step 3 with . Otherwise, go to Step 10.
- Step 10: Output the optimal solution (The best PM alternative , the optimal expected cost , the optimal lease length ) .
3.2. Optimal PM with Consideration of Financial Lease Contract Revenue
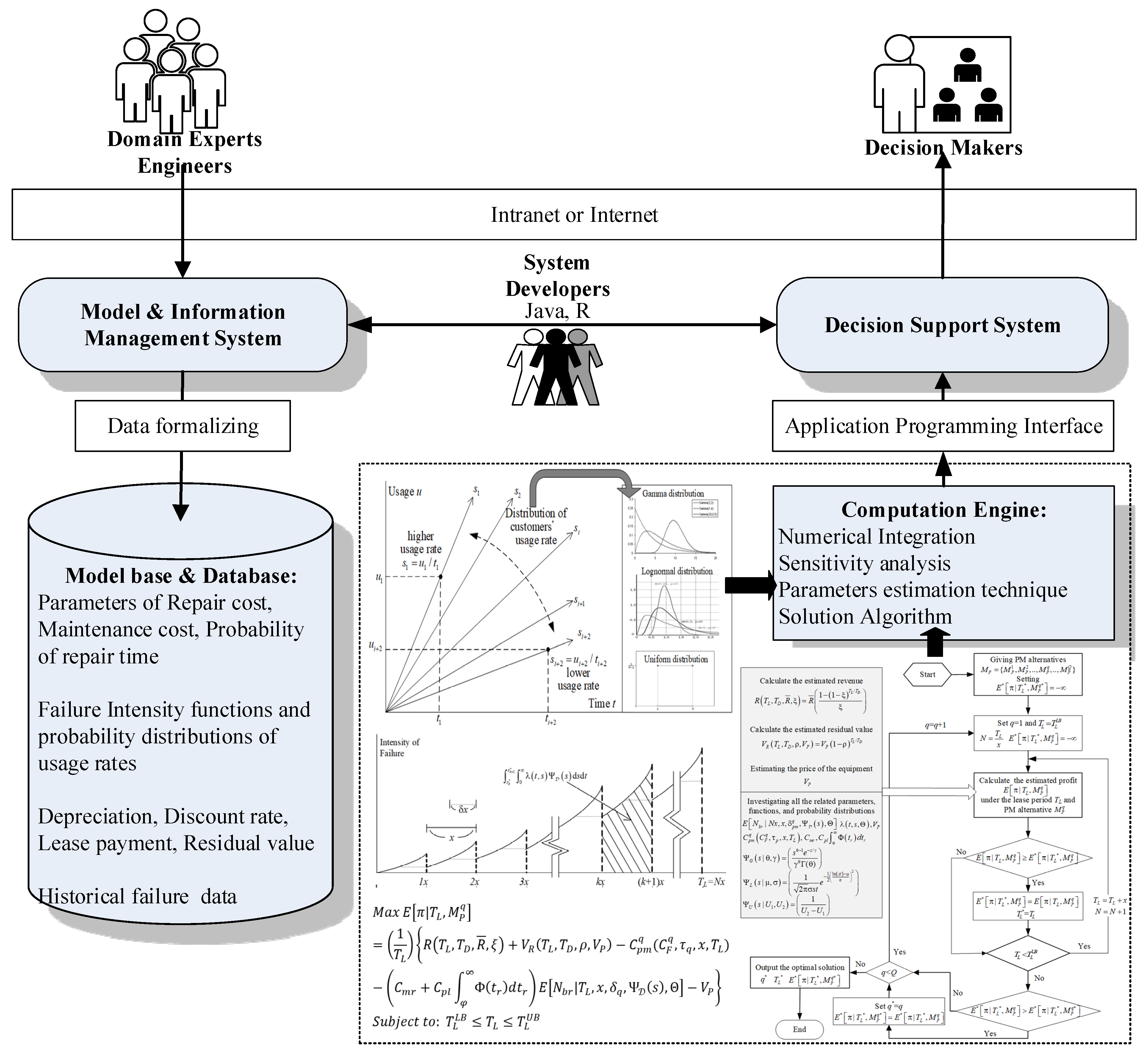
3.3. Computerized Decision Support System Design
4. Application and Sensitivity Analysis
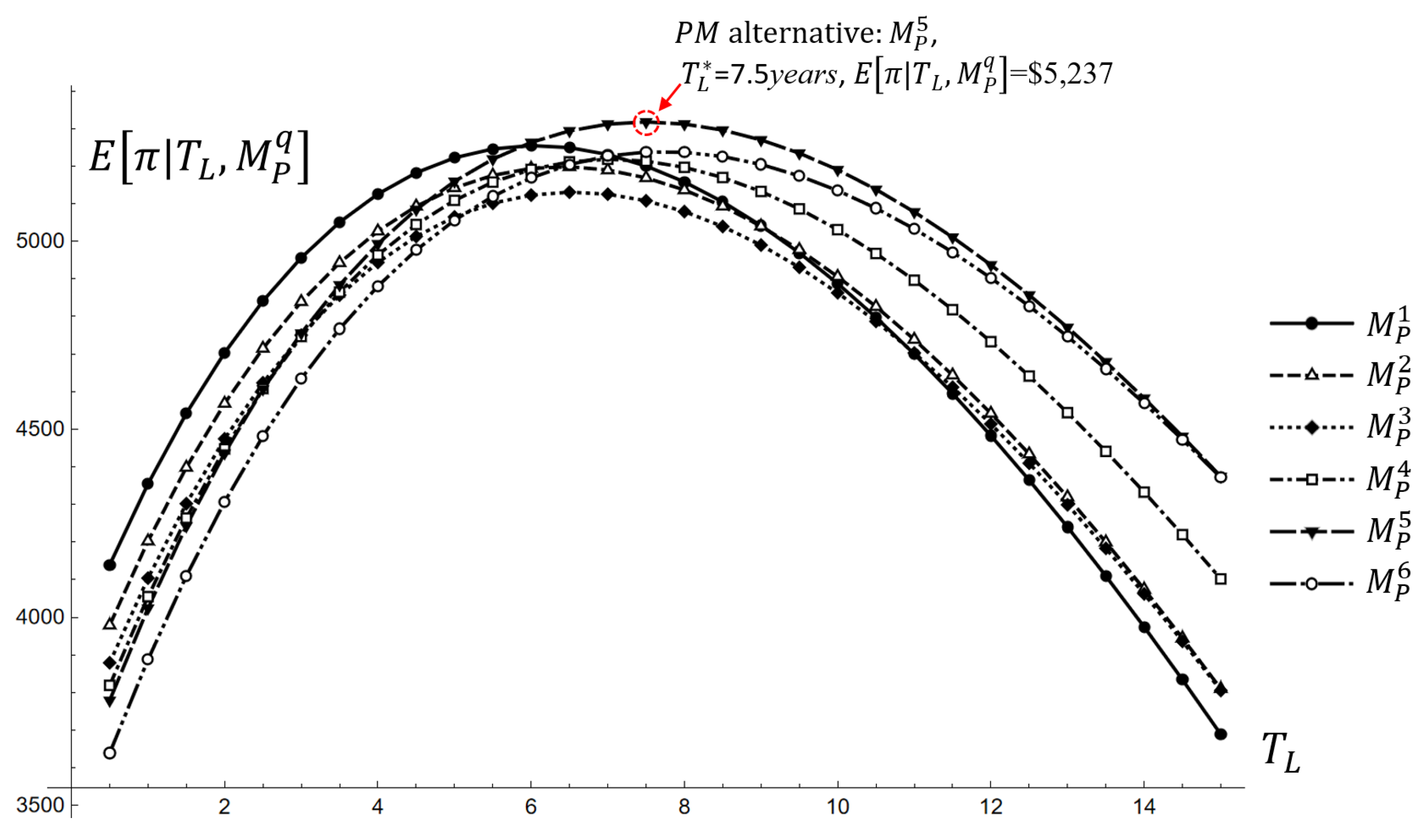
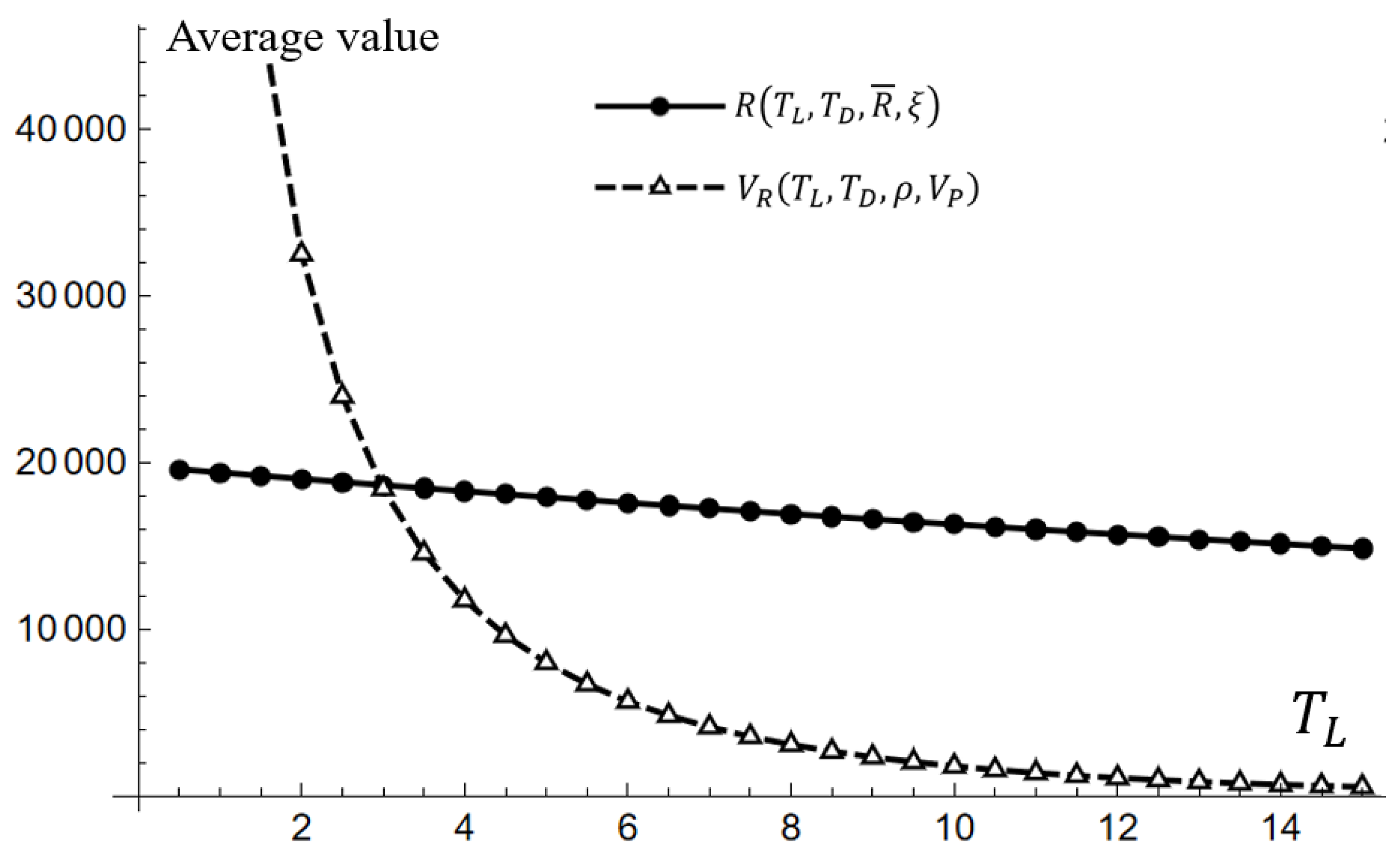
4.1. Application
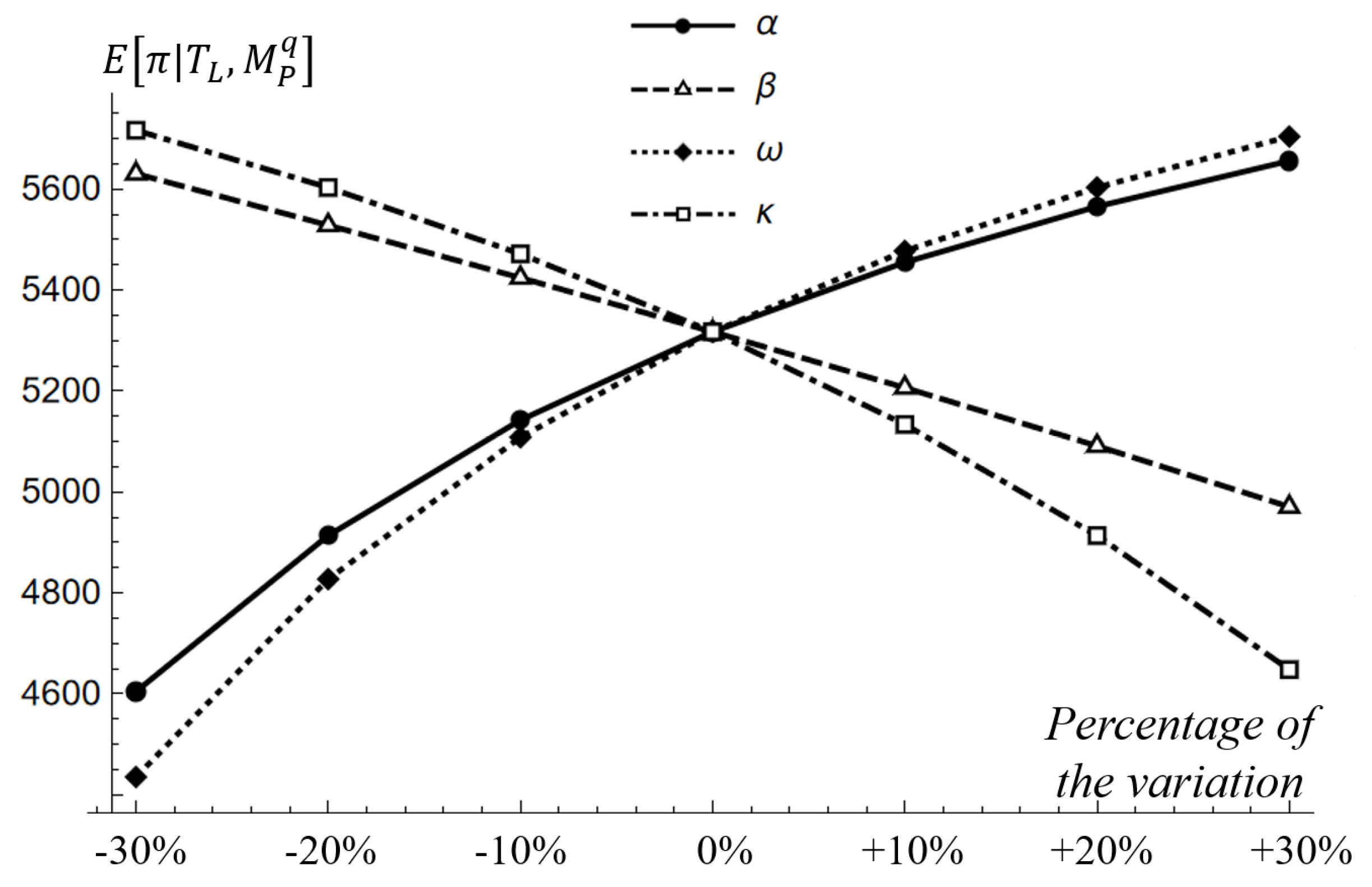
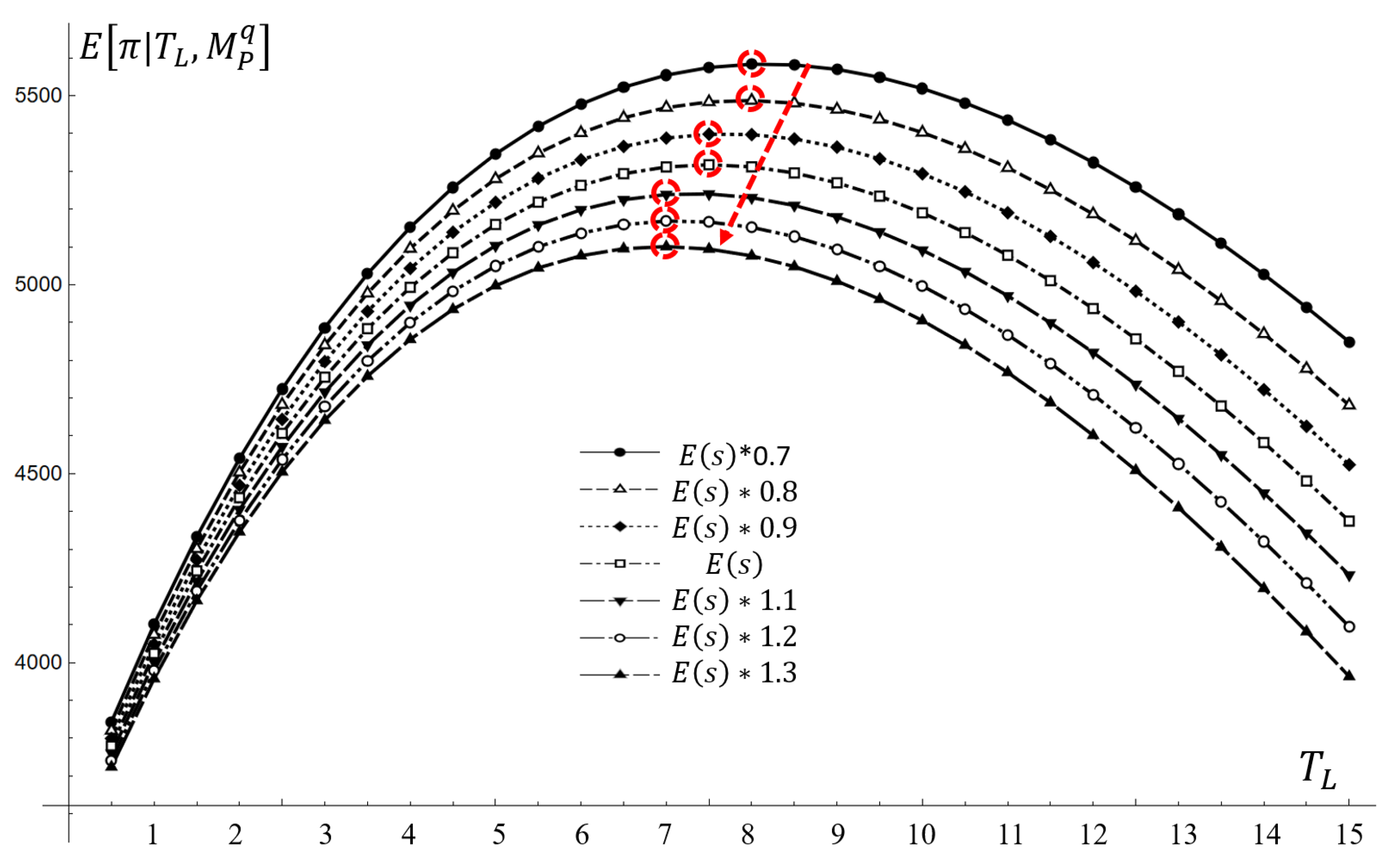
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pongpech, J.; Murthy, D.N.P. Optimal periodic preventive maintenance policy for leased equipment. Reliab. Eng. Syst. Saf. 2006, 91, 772–777. [Google Scholar] [CrossRef]
- Nisbet, A.; Ward, A. Radiotherapy equipment–purchase or lease? Br. J. Radiol. 2001, 74, 735–744. [Google Scholar] [CrossRef] [PubMed]
- Aras, N.; Güllü, R.; Yürülemz, S. Optimal inventory and pricing policies for remanufacturable leased products. Int. J. Prod. Econ. 2011, 133, 262–271. [Google Scholar] [CrossRef]
- Bourjade, S.; Huc, R.; Muller-Vibes, C. Leasing and profitability: Empirical evidence from the airline industry. Transp. Res. Part A 2017, 97, 30–46. [Google Scholar] [CrossRef]
- Yeh, R.H.; Kao, K.C.; Chang, W.L. Preventive-maintenance policy for leased products under various maintenance costs. Expert Syst. Appl. 2011, 38, 3558–3562. [Google Scholar] [CrossRef]
- Schutz, J.; Rezg, N. Maintenance strategy for leased equipment. Comput. Ind. Eng. 2013, 66, 593–600. [Google Scholar] [CrossRef]
- Ben Mabrouk, A.; Chelbi, A.; Radhoui, M. Optimal imperfect maintenance strategy for leased equipment. Int. J. Prod. Econ. 2016, 178, 57–64. [Google Scholar] [CrossRef]
- Iskandar, B.P.; Husniah, H. Optimal preventive maintenance for a two dimensional lease contract. Comput. Ind. Eng. 2017, 113, 693–703. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Zeng, J.; Wang, J.; Xue, S. Lessees’ satisfaction and optimal condition-based maintenance policy for leased system. Reliab. Eng. Syst. Saf. 2019, 191, 106532. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Y.; Yang, H.; Segerstedt, A.; Zhang, L. Maintenance service strategy for leased equipment: Integrating lessor-preventive maintenance and lessee-careful protection efforts. Comput. Ind. Eng. 2021, 156, 107257. [Google Scholar] [CrossRef]
- Park, D.H.; Jung, G.M.; Yum, J.K. Cost minimization for periodic maintenance policy of a system subject to slow degradation. Reliab. Eng. Syst. Saf. 2000, 68, 105–112. [Google Scholar] [CrossRef]
- Yeh, R.H.; Lo, H.C. Optimal preventive-maintenance warranty policy for repairable products. Eur. J. Oper. Res. 2001, 134, 59–69. [Google Scholar] [CrossRef]
- Jung, G.M.; Park, D.H. Optimal maintenance policies during the post-warranty period. Reliab. Eng. Syst. Saf. 2003, 82, 173–185. [Google Scholar] [CrossRef]
- Seo, J.H.; Bai, D.S. An optimal maintenance policy for a system under periodic overhaul. Math. Comput. Model. 2004, 39, 373–380. [Google Scholar] [CrossRef]
- Yeh, R.H.; Chang, W.L. Optimal threshold value of failure-rate for Leased products with preventive maintenance actions. Math. Comput. Model. 2007, 46, 730–737. [Google Scholar] [CrossRef]
- Hu, F.; Zong, Q. Optimal periodic preventive maintenance policy and lease period for leased equipment. J. Tianjin Univ. Sci. Technol. 2008, 41, 248–253. [Google Scholar]
- Das, A.N.; Sarmah, A.N. Preventive replacement models: An overview and their application in process industries. Eur. J. Ind. Eng. 2010, 4, 280–307. [Google Scholar] [CrossRef]
- Chang, W.L.; Lo, H.C. Joint determination of lease period and preventive maintenance policy for leased equipment with residual value. Comput. Ind. Eng. 2011, 61, 489–496. [Google Scholar] [CrossRef]
- Bouguera, S.; Chelbi, A.; Rezg, N. A decision model for adopting an extended warranty under different maintenance policies. Int. J. Prod. Econ. 2012, 135, 840–849. [Google Scholar] [CrossRef]
- Chang, W.L.; Lin, J.H. Optimal maintenance policy and length of extended warranty within the life cycle of products. Comput. Math. Appl. 2012, 63, 144–150. [Google Scholar] [CrossRef]
- Kim, B.S.; Ozturkoglu, Y. Scheduling a single machine with multiple preventive maintenance activities and position-based deteriorations using genetic algorithms. Int. J. Adv. Manuf. Technol. 2013, 67, 1127–1137. [Google Scholar] [CrossRef]
- Shafiee, M.; Finkelstein, M.; Zuo, M. Optimal burn-in and preventive maintenance warranty strategies with time-dependent maintenance costs. IIE Trans. 2013, 45, 1024–1033. [Google Scholar] [CrossRef]
- Khojandi, A.; Maillart, L.M.; Prokopyev, O.A. Optimal planning of life-depleting maintenance activities. IIE Trans. 2014, 46, 636–652. [Google Scholar] [CrossRef]
- Yuan, X.; Lu, Z. Efficient approach for reliability-based optimization based on weighted importance sampling approach. Reliab. Eng. Syst. Saf. 2014, 132, 107–114. [Google Scholar] [CrossRef]
- Lu, B.; Zhou, X.; Li, Y. Joint modeling of preventive maintenance and quality improvement for deteriorating single-machine manufacturing systems. Comput. Ind. Eng. 2016, 91, 188–196. [Google Scholar] [CrossRef]
- Wang, K.; Djurdjanovic, D. Joint Optimization of Preventive Maintenance, Spare Parts Inventory and Transportation Options for Systems of Geographically Distributed Assets. Machines 2018, 6, 55. [Google Scholar] [CrossRef]
- Zhou, Y.; Kou, G.; Xiao, H.; Peng, Y.; Alsaadi, F.E. Sequential imperfect preventive maintenance model with failure intensity reduction with an application to urban buses. Reliab. Eng. Syst. Saf. 2020, 198, 106871. [Google Scholar] [CrossRef]
- García, F.J.Á.; Salgado, D.R. Analysis of the Influence of Component Type and Operating Condition on the Selection of Preventive Maintenance Strategy in Multistage Industrial Machines: A Case Study. Machines 2022, 10, 385. [Google Scholar] [CrossRef]
- Alrifaey, M.; Sai Hong, T.; As’arry, A.; Elianddy Supeni, E.; Ang, C.K. Optimization and Selection of Maintenance Policies in an Electrical Gas Turbine Generator Based on the Hybrid Reliability-Centered Maintenance (RCM) Model. Processes 2020, 8, 670. [Google Scholar] [CrossRef]
- Tsarouhas, P. Reliability, Availability, and Maintainability (RAM) Study of an Ice Cream Industry. Appl. Sci. 2020, 10, 4265. [Google Scholar] [CrossRef]
- Lastra, R.; Pereira, A.; Díaz-Cacho, M.; Acevedo, J.; Collazo, A. Spare Parts Made by Additive Manufacturing to Improve Preventive Maintenance. Appl. Sci. 2022, 12, 10564. [Google Scholar] [CrossRef]
- Diatte, K.; O’Halloran, B.; Van Bossuyt, D.L. The Integration of Reliability, Availability, and Maintainability into Model-Based Systems Engineering. Systems 2022, 10, 101. [Google Scholar] [CrossRef]
- Baik, J.; Murthy, D.N.P.; Jack, N. Two-dimensional failure modeling with minimal repair. Nav. Res. Logist. 2004, 51, 345–362. [Google Scholar] [CrossRef]
- He, Z.; Loh, H.T.; Xie, M. A two-dimensional probability model for evaluating reliability of piezoelectric micro-actuators. Int. J. Fatigue 2007, 29, 245–253. [Google Scholar] [CrossRef]
- Murthy, D.N.P.; Iskandar, B.P.; Wilson, S.P. Two-dimensional failure-free warranty policies: Two-dimensional point process models. Oper. Res. 1995, 43, 356–366. [Google Scholar] [CrossRef]
- Kim, H.G.; Rao, B.M. Expected warranty cost of two-attribute free-replacement warranties based on a bivariate exponential distribution. Comput. Ind. Eng. 2000, 38, 425–434. [Google Scholar] [CrossRef]
- Pal, S.; Murthy, G.S.R. An application of Gumbel’s bivariate exponential distribution in estimation of warranty cost of motor cycles. Int. J. Qual. Reliab. Manag. 2003, 20, 488–502. [Google Scholar] [CrossRef]
- Shahanaghi, K.; Noorossana, R.; Jalali-Naini, S.G.; Heydari, M. Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts. Eng. Fail. Anal. 2013, 28, 90–102. [Google Scholar] [CrossRef]
- Huang, Y.S.; Gau, W.Y.; Ho, J.W. Cost analysis of two-dimensional warranty for products with periodic preventive maintenance. Reliab. Eng. Syst. Saf. 2015, 134, 51–58. [Google Scholar] [CrossRef]
- Huang, Y.S.; Huang, D.D.; Ho, J.W. A customized two-dimensional extended warranty with preventive maintenance. Eur. J. Oper. Res. 2017, 257, 971–978. [Google Scholar] [CrossRef]
- Park, M.; Jung, K.M.; Park, D.H. Optimization of periodic preventive maintenance policy following the expiration of two-dimensional warranty. Reliab. Eng. Syst. Saf. 2018, 170, 1–9. [Google Scholar] [CrossRef]
- Dong, E.; Gao, T.; Cheng, Z.; Wang, R.; Bai, Y. Opportunistic Maintenance Strategy for Complex Equipment with a Genetic Algorithm Considering Failure Dependence: A Two-Dimensional Warranty Perspective. Sensors 2022, 22, 6801. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, L.; Xie, M. An unpunctual preventive maintenance policy under two-dimensional warranty. Eur. J. Oper. Res. 2020, 282, 304–318. [Google Scholar] [CrossRef]
- Dong, E.; Cheng, Z.; Wang, R.; Zhao, J. Optimization of two-dimensional extended warranty scheme for failure dependence of a multi-component system with improved PSO–BAS algorithm. Processes 2022, 10, 1479. [Google Scholar] [CrossRef]
- Lu, J.C.; Bhattacharyya, G.K. Some new construction of bivariate Weibull models. Ann. Inst. Stat. Math. 1990, 42, 543–559. [Google Scholar] [CrossRef]
- Jayabalan, V.; Chaudhuri, D. Cost optimization of maintenance scheduling for a system with assured reliability. IEEE Trans. Reliab. 1992, 41, 21–25. [Google Scholar] [CrossRef]



| : the age of the leased facility. : the effective age of a deteriorating system before the kth preventive maintenance. : the effective age of a deteriorating system after the kth preventive maintenance. : the time required for performing a minimal repair. : the scale parameter of the bivariate Weibull model for the system’s age. : the shape parameter of the bivariate Weibull model for the system’s age. : the scale parameter of the bivariate Weibull model for the system’s usage. : the shape parameter of the bivariate Weibull model for the system’s usage. : the intensity function of age and usage of a deteriorating system. : the intensity function of age and usage rate of a deteriorating system. : the usage of the leased facility. : the usage per unit time, and it varies from lessees’ usual practice. (s = t/u) : the length of a lease contract. : the time segment for time-discounting factor. : the depreciation rate of the leased facility after a time segment. : the purchase price of the leased facility. : the residual value of the leased facility at time . : the payment of the lease facilities. : the expected number of the failures times of the leased facility. The mathematical form is given in Equation (8) , : the time span between two scheduled periodic preventive maintenances. : the expected cost of performing a minimal repair. : the penalty cost when the actual repair time exceeds the time limit . : the pre-specified limit of time for a minimal repair work. : the probability density function of the time for performing minimal repair. : the cost of performing the kth preventive maintenance for alternative . : the base cost for performing a preventive maintenance, and it is influenced by the degree of PM. : the periodically increasing rate of the preventive maintenance cost for alternative . : the age reduction factor in effective age for alternative due to the kth preventive maintenance, where . |
| The estimated values of the parameters of the two-dimensional deterioration | , , , |
| Interval of PM; Time segment | ; |
| The probability distribution of customers’ usage rate | Gamma probability distribution with and |
| Age reduction factors of the alternatives (1..6) | |
| The base cost for a PM action (1..6) | |
| Periodically increasing rates of PM cost (1..6) | |
| Depreciation rate | |
| The lower and upper boundaries of the planned lease terms | ; |
| Rental per half-year | |
| Time discount rate | |
| The purchasing cost of an equipment | |
| Expected cost of performing a minimal repair | = $450 |
| Penalty cost when the repair time exceed the time limit | |
| Expected value and standard deviation of performing a minimal repair | , |
| Tolerable waiting time limit for performing a minimal repair |
| 2 | 32,513 | 1208 | 1388 | 1526 | 1597 | 1652 | 1825 | 621 | 576 | 532 | 488 | 444 | 401 | 4703 | 4568 | 4474 | 4447 | 4436 | 4307 |
| 2.5 | 23,980 | 1231 | 1417 | 1568 | 1643 | 1703 | 1886 | 740 | 680 | 620 | 561 | 503 | 444 | 4841 | 4715 | 4623 | 4608 | 4607 | 4481 |
| 3 | 18,424 | 1254 | 1446 | 1610 | 1688 | 1753 | 1948 | 860 | 784 | 709 | 635 | 561 | 488 | 4956 | 4839 | 4750 | 4746 | 4755 | 4634 |
| 3.5 | 14,559 | 1277 | 1476 | 1652 | 1734 | 1804 | 2009 | 980 | 889 | 799 | 709 | 620 | 532 | 5050 | 4943 | 4856 | 4864 | 4884 | 4767 |
| 4 | 11,745 | 1300 | 1505 | 1694 | 1779 | 1854 | 2071 | 1102 | 995 | 889 | 784 | 679 | 576 | 5125 | 5027 | 4943 | 4963 | 4993 | 4880 |
| 4.5 | 9625 | 1322 | 1534 | 1736 | 1825 | 1905 | 2132 | 1224 | 1101 | 980 | 859 | 739 | 620 | 5182 | 5093 | 5013 | 5044 | 5084 | 4976 |
| 5 | 7987 | 1345 | 1563 | 1778 | 1871 | 1956 | 2194 | 1347 | 1208 | 1071 | 934 | 799 | 664 | 5222 | 5142 | 5065 | 5109 | 5159 | 5056 |
| 5.5 | 6694 | 1368 | 1593 | 1820 | 1916 | 2006 | 2255 | 1470 | 1316 | 1162 | 1010 | 859 | 709 | 5246 | 5175 | 5101 | 5157 | 5218 | 5119 |
| 6 | 5657 | 1391 | 1622 | 1862 | 1962 | 2057 | 2317 | 1594 | 1423 | 1254 | 1086 | 919 | 754 | 5254 | 5194 | 5123 | 5191 | 5263 | 5169 |
| 6.5 | 4815 | 1414 | 1651 | 1904 | 2008 | 2108 | 2378 | 1718 | 1531 | 1346 | 1162 | 979 | 798 | 5249 | 5198 | 5130 | 5211 | 5294 | 5204 |
| 7 | 4122 | 1436 | 1680 | 1946 | 2053 | 2158 | 2440 | 1843 | 1640 | 1438 | 1238 | 1040 | 843 | 5231 | 5190 | 5125 | 5218 | 5312 | 5227 |
| 7.5 | 3547 | 1459 | 1710 | 1988 | 2099 | 2209 | 2501 | 1968 | 1749 | 1531 | 1315 | 1101 | 889 | 5200 | 5169 | 5108 | 5213 | 5317 | 5237 |
| 8 | 3066 | 1482 | 1739 | 2030 | 2144 | 2259 | 2563 | 2093 | 1858 | 1624 | 1392 | 1162 | 934 | 5158 | 5136 | 5079 | 5197 | 5312 | 5237 |
| 8.5 | 2660 | 1505 | 1768 | 2072 | 2190 | 2310 | 2624 | 2219 | 1967 | 1717 | 1469 | 1223 | 979 | 5105 | 5093 | 5039 | 5169 | 5296 | 5225 |
| 9 | 2316 | 1528 | 1797 | 2114 | 2236 | 2361 | 2686 | 2345 | 2077 | 1811 | 1546 | 1284 | 1025 | 5042 | 5040 | 4990 | 5132 | 5270 | 5204 |
| 9.5 | 2023 | 1550 | 1827 | 2156 | 2281 | 2411 | 2747 | 2472 | 2187 | 1904 | 1624 | 1346 | 1070 | 4969 | 4977 | 4931 | 5086 | 5234 | 5174 |
| 10 | 1772 | 1573 | 1856 | 2198 | 2327 | 2462 | 2809 | 2599 | 2298 | 1998 | 1701 | 1407 | 1116 | 4887 | 4906 | 4863 | 5031 | 5190 | 5135 |
| 10.5 | 1556 | 1596 | 1885 | 2240 | 2373 | 2513 | 2870 | 2726 | 2408 | 2093 | 1779 | 1469 | 1162 | 4797 | 4826 | 4787 | 4967 | 5138 | 5088 |
| 11 | 1369 | 1619 | 1914 | 2282 | 2418 | 2563 | 2932 | 2853 | 2519 | 2187 | 1857 | 1531 | 1207 | 4700 | 4738 | 4703 | 4896 | 5078 | 5033 |
| 11.5 | 1207 | 1642 | 1944 | 2324 | 2464 | 2614 | 2993 | 2981 | 2630 | 2281 | 1935 | 1593 | 1253 | 4595 | 4644 | 4612 | 4818 | 5011 | 4971 |
| 12 | 1067 | 1664 | 1973 | 2366 | 2509 | 2664 | 3055 | 3109 | 2741 | 2376 | 2014 | 1655 | 1299 | 4483 | 4542 | 4514 | 4733 | 4937 | 4902 |
| 12.5 | 944 | 1687 | 2002 | 2408 | 2555 | 2715 | 3116 | 3237 | 2853 | 2471 | 2092 | 1717 | 1345 | 4364 | 4434 | 4409 | 4641 | 4857 | 4827 |
| 13 | 837 | 1710 | 2031 | 2450 | 2601 | 2766 | 3178 | 3365 | 2964 | 2566 | 2171 | 1779 | 1391 | 4240 | 4319 | 4299 | 4544 | 4771 | 4746 |
| 13.5 | 743 | 1733 | 2061 | 2492 | 2646 | 2816 | 3239 | 3494 | 3076 | 2661 | 2250 | 1841 | 1438 | 4110 | 4200 | 4183 | 4441 | 4679 | 4660 |
| 14 | 661 | 1756 | 2090 | 2534 | 2692 | 2867 | 3301 | 3623 | 3188 | 2757 | 2328 | 1904 | 1484 | 3974 | 4075 | 4062 | 4333 | 4582 | 4568 |
| 14.5 | 588 | 1778 | 2119 | 2576 | 2738 | 2918 | 3362 | 3752 | 3301 | 2852 | 2408 | 1967 | 1530 | 3834 | 3945 | 3936 | 4219 | 4480 | 4472 |
| 15 | 524 | 1801 | 2148 | 2618 | 2783 | 2968 | 3424 | 3881 | 3413 | 2948 | 2487 | 2029 | 1577 | 3689 | 3810 | 3805 | 4102 | 4374 | 4371 |
| −30% | −20% | −10% | 0% | +10% | +20% | +30% | −30% | −20% | −10% | 0% | +10% | +20% | +30% | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4540 | 4503 | 4469 | 4436 | 4405 | 4375 | 4346 | 4432 | 4433 | 4435 | 4436 | 4438 | 4439 | 4441 |
| 2.5 | 4724 | 4682 | 4644 | 4607 | 4571 | 4537 | 4505 | 4601 | 4603 | 4605 | 4607 | 4608 | 4610 | 4612 |
| 3 | 4886 | 4840 | 4797 | 4755 | 4716 | 4678 | 4642 | 4749 | 4751 | 4753 | 4755 | 4757 | 4759 | 4761 |
| 3.5 | 5029 | 4977 | 4929 | 4884 | 4840 | 4798 | 4758 | 4877 | 4879 | 4881 | 4884 | 4886 | 4888 | 4890 |
| 4 | 5152 | 5096 | 5043 | 4993 | 4945 | 4899 | 4855 | 4986 | 4988 | 4991 | 4993 | 4995 | 4998 | 5000 |
| 4.5 | 5257 | 5196 | 5139 | 5084 | 5033 | 4983 | 4935 | 5077 | 5079 | 5082 | 5084 | 5087 | 5089 | 5092 |
| 5 | 5346 | 5280 | 5218 | 5159 | 5103 | 5049 | 4997 | 5151 | 5154 | 5157 | 5159 | 5162 | 5165 | 5167 |
| 5.5 | 5419 | 5348 | 5282 | 5218 | 5158 | 5100 | 5044 | 5210 | 5213 | 5215 | 5218 | 5221 | 5224 | 5227 |
| 6 | 5478 | 5402 | 5331 | 5263 | 5198 | 5136 | 5077 | 5253 | 5257 | 5260 | 5263 | 5266 | 5269 | 5272 |
| 6.5 | 5523 | 5442 | 5366 | 5294 | 5225 | 5159 | 5095 | 5284 | 5287 | 5290 | 5294 | 5297 | 5300 | 5304 |
| 7 | 5555 | 5469 | 5388 | 5312 | 5238 | 5168 | 5101 | 5301 | 5304 | 5308 | 5312 | 5315 | 5319 | 5322 |
| 7.5 | 5575 | 5484 | 5398 | 5317 | 5240 | 5166 | 5094 | 5306 | 5310 | 5314 | 5317 | 5321 | 5325 | 5328 |
| 8 | 5583 | 5487 | 5397 | 5312 | 5230 | 5152 | 5076 | 5300 | 5304 | 5308 | 5312 | 5316 | 5320 | 5323 |
| 8.5 | 5581 | 5480 | 5386 | 5296 | 5210 | 5127 | 5048 | 5283 | 5287 | 5292 | 5296 | 5300 | 5304 | 5308 |
| 9 | 5570 | 5464 | 5364 | 5270 | 5179 | 5093 | 5009 | 5256 | 5261 | 5265 | 5270 | 5274 | 5278 | 5283 |
| 9.5 | 5549 | 5438 | 5333 | 5234 | 5140 | 5049 | 4962 | 5220 | 5225 | 5230 | 5234 | 5239 | 5243 | 5248 |
| 10 | 5519 | 5403 | 5294 | 5190 | 5091 | 4996 | 4905 | 5176 | 5180 | 5185 | 5190 | 5195 | 5200 | 5204 |
| 10.5 | 5481 | 5360 | 5246 | 5138 | 5035 | 4936 | 4840 | 5123 | 5128 | 5133 | 5138 | 5143 | 5148 | 5153 |
| 11 | 5436 | 5309 | 5190 | 5078 | 4970 | 4867 | 4768 | 5062 | 5067 | 5073 | 5078 | 5083 | 5088 | 5093 |
| 11.5 | 5383 | 5251 | 5128 | 5011 | 4899 | 4791 | 4688 | 4994 | 5000 | 5005 | 5011 | 5016 | 5021 | 5027 |
| 12 | 5323 | 5187 | 5059 | 4937 | 4821 | 4709 | 4601 | 4920 | 4925 | 4931 | 4937 | 4942 | 4948 | 4953 |
| 12.5 | 5258 | 5116 | 4983 | 4857 | 4736 | 4620 | 4509 | 4839 | 4845 | 4851 | 4857 | 4862 | 4868 | 4874 |
| 13 | 5186 | 5039 | 4901 | 4771 | 4646 | 4526 | 4410 | 4752 | 4758 | 4764 | 4771 | 4777 | 4783 | 4788 |
| 13.5 | 5109 | 4957 | 4814 | 4679 | 4550 | 4425 | 4306 | 4660 | 4666 | 4673 | 4679 | 4685 | 4691 | 4697 |
| 14 | 5027 | 4870 | 4722 | 4582 | 4448 | 4320 | 4196 | 4562 | 4569 | 4576 | 4582 | 4589 | 4595 | 4601 |
| 14.5 | 4940 | 4778 | 4625 | 4480 | 4342 | 4210 | 4082 | 4460 | 4467 | 4474 | 4480 | 4487 | 4494 | 4500 |
| 15 | 4849 | 4681 | 4524 | 4374 | 4232 | 4095 | 3963 | 4353 | 4360 | 4367 | 4374 | 4381 | 4388 | 4395 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, C.-C.; Hsu, C.-C.; Liu, J.-H. The Decision-Making for the Optimization of Finance Lease with Facilities’ Two-Dimensional Deterioration. Systems 2022, 10, 210. https://doi.org/10.3390/systems10060210
Fang C-C, Hsu C-C, Liu J-H. The Decision-Making for the Optimization of Finance Lease with Facilities’ Two-Dimensional Deterioration. Systems. 2022; 10(6):210. https://doi.org/10.3390/systems10060210
Chicago/Turabian StyleFang, Chih-Chiang, Chin-Chia Hsu, and Je-Hung Liu. 2022. "The Decision-Making for the Optimization of Finance Lease with Facilities’ Two-Dimensional Deterioration" Systems 10, no. 6: 210. https://doi.org/10.3390/systems10060210
APA StyleFang, C.-C., Hsu, C.-C., & Liu, J.-H. (2022). The Decision-Making for the Optimization of Finance Lease with Facilities’ Two-Dimensional Deterioration. Systems, 10(6), 210. https://doi.org/10.3390/systems10060210






