Model Signatures for the Integration of Simulation Models into System Models
Abstract
1. Introduction
- A clear and automated assignment of domain models to system elements is possible;
- The compatibility of domain models can be automatically evaluated;
- The most appropriate combination of domain models given a certain requirements-driven goal can be identified.
2. State of the Art
2.1. Function-Oriented Model-Based Systems Engineering
2.2. Integration and Coupling of Simulation Models
3. Research Question
- How can the parameters in the system element be structured for testing and design with domain models?
- How can model signatures for domain models be defined unambiguously and machine-readable?
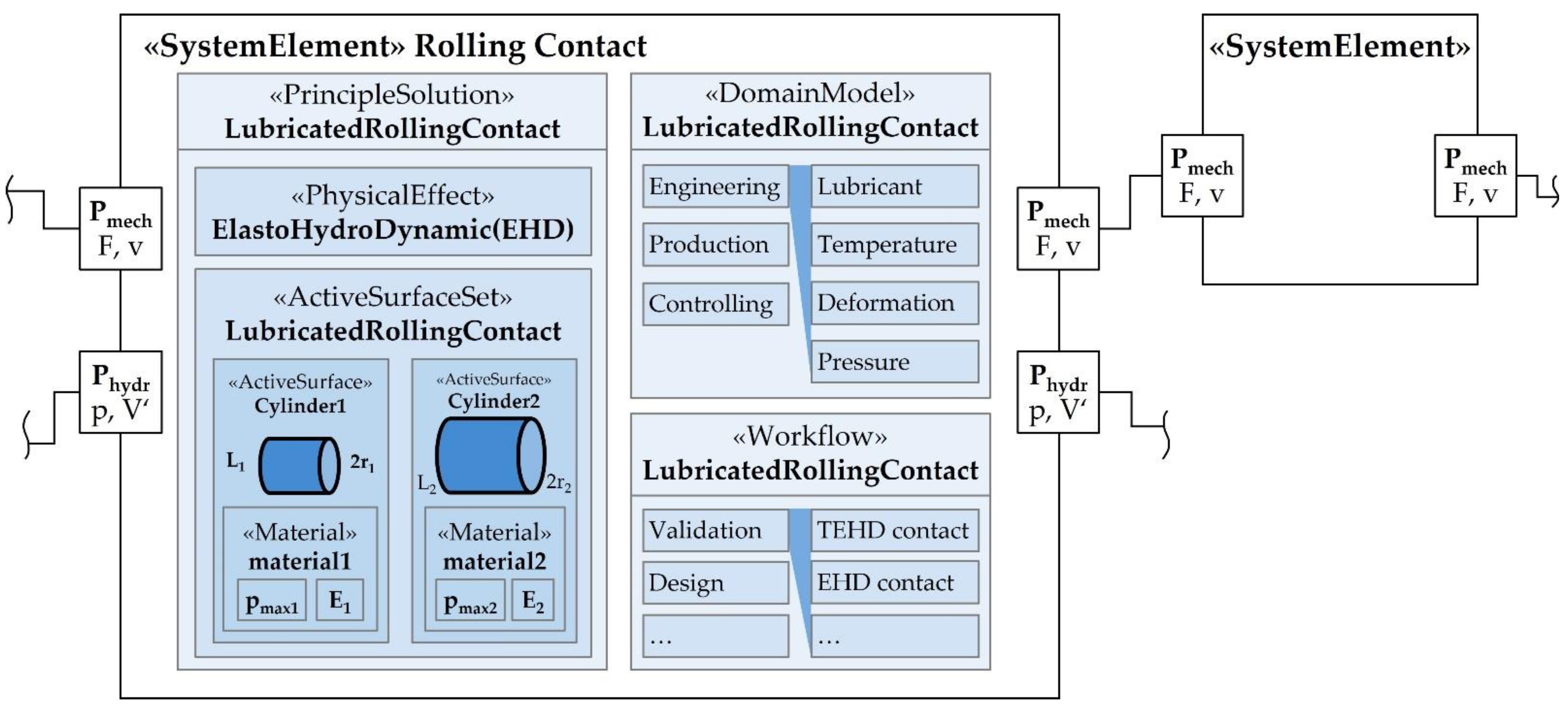
4. System Element Parameter Concept
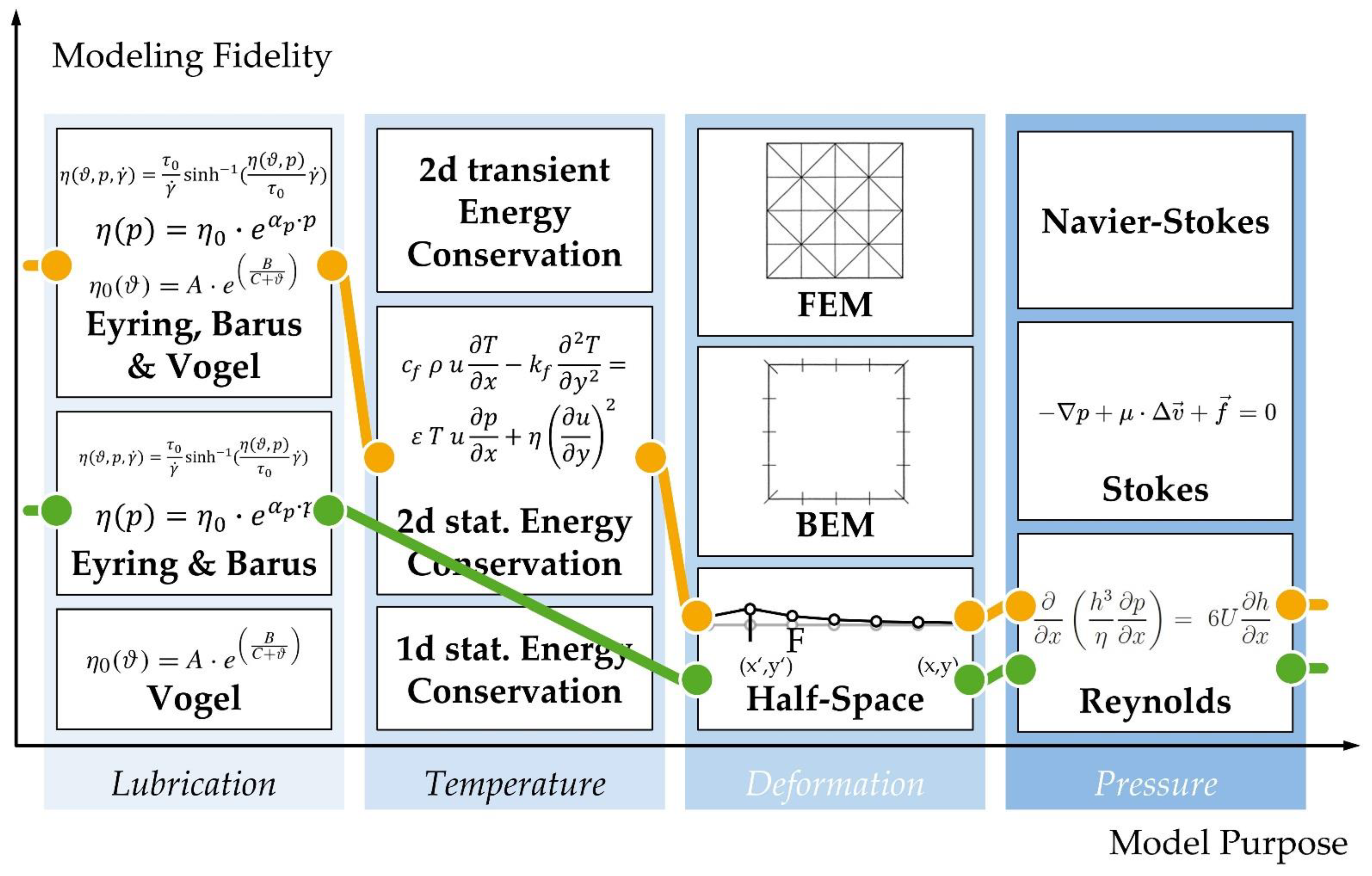
5. Model Signature for Domain Models
5.1. Domain Model Requirements for the Model Signature
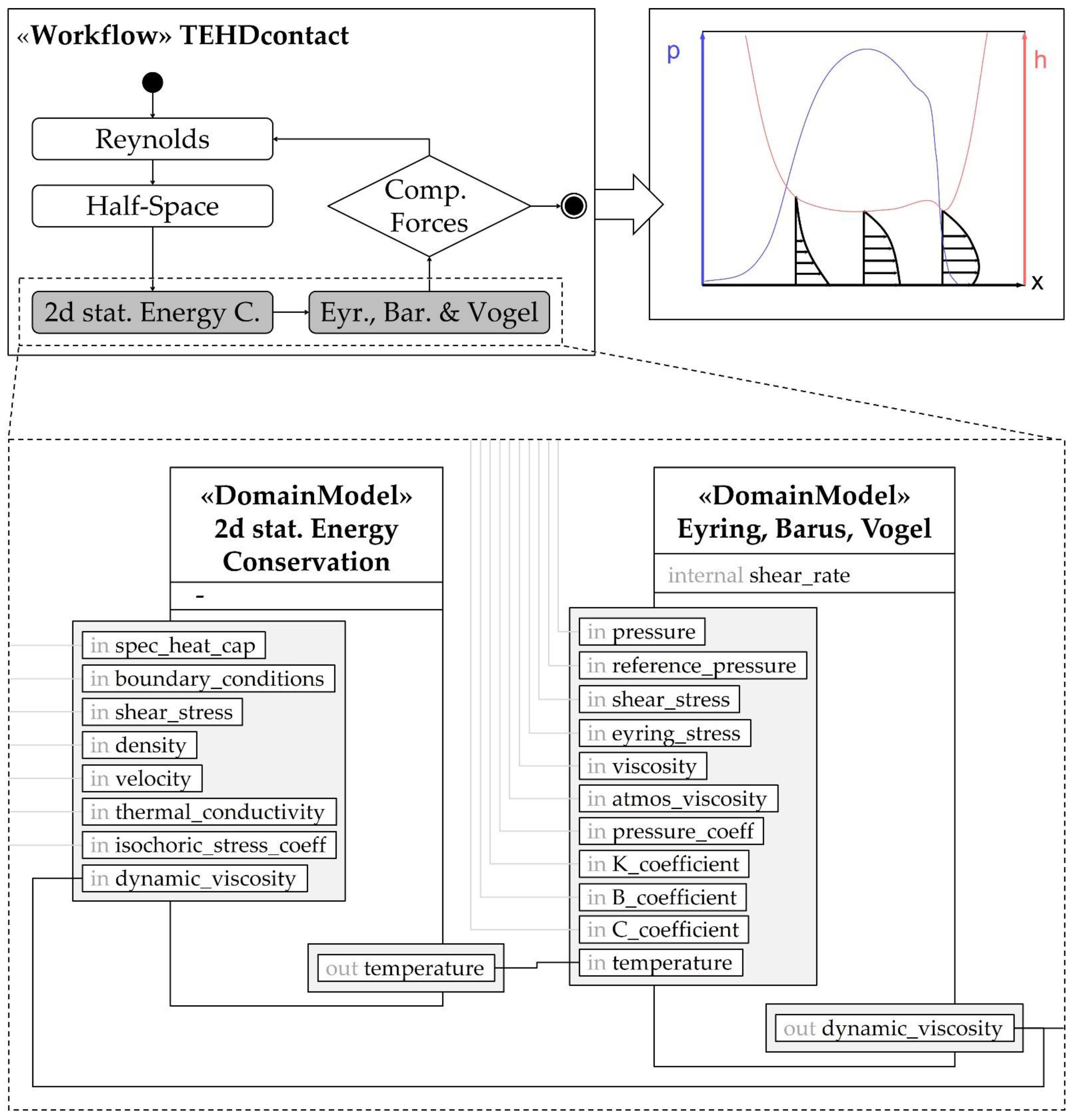
5.2. Proposal of a Model Signature for Domain Models
6. Discussion, Conclusion and Outlook
6.1. Discussion
6.2. Conclusions
6.3. Outlook
Author Contributions
Funding
Conflicts of Interest
References
- INCOSE. Systems Engineering Vision. 2020. Available online: https://sdincose.org/wp-content/uploads/2011/12/SEVision2020_20071003_v2_03.pdf (accessed on 4 October 2022).
- Ropohl, G. Allgemeine Technologie: Eine Systemtheorie der Technik; KIT Scientific Publishing: Karlsruhe, Germany, 2009. [Google Scholar]
- Jacobs, G.; Konrad, C.; Berroth, J.; Zerwas, T.; Höpfner, G.; Spütz, K. Function-Oriented Model-Based Product Development. In Design Methodology for Future Products: Data Driven, Agile and Flexible, 1st ed.; Krause, D., Heyden, E., Eds.; Springer eBook Collection; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Spütz, K.; Berges, J.; Jacobs, G.; Berroth, J.; Konrad, C. Classification of Simulation Models for the Model-based Design of Plastic-Metal Hybrid Joints. Procedia CIRP 2022, 109, 37–42. [Google Scholar] [CrossRef]
- Husung, S.; Weber, C.; Mahboob, A. Model-Based Systems Engineering: A New Way for Function-Driven Product Development. In Design Methodology for Future Products; Springer: Cham, Switzerland, 2022; pp. 221–241. [Google Scholar] [CrossRef]
- Chabibi, B.; Anwar, A.; Nassar, M. Towards an alignment of SysML and simulation tools. In Proceedings of the 2015 IEEE/ACS 12th International Conference of Computer Systems and Applications (AICCSA), Marrakech, Morocco, 17–20 November 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Object Management Group. OMG System Modeling Language Specification: Version 1.5. Available online: https://www.omg.org/spec/SysML/1.5 (accessed on 14 July 2022).
- Stachowiak, H. Allgemeine Modelltheorie; Springer: Wien, Austria, 1973. [Google Scholar]
- Nigischer, C.; Bougain, S.; Riegler, R.; Stanek, H.P.; Grafinger, M. Multi-domain simulation utilizing SysML: State of the art and future perspectives. Procedia CIRP 2021, 100, 319–324. [Google Scholar] [CrossRef]
- Kim, H.; Fried, D.; Menegay, P.; Soremekun, G.; Oster, C. Application of Integrated Modeling and Analysis to Development of Complex Systems. Procedia Comput. Sci. 2013, 16, 98–107. [Google Scholar] [CrossRef][Green Version]
- Wilking, F.; Sauer, C.; Schleich, B.; Wartzack, S. Integrating Machine Learning in Digital Twins by utilizing SysML System Models. In Proceedings of the 2022 17th Annual System of Systems Engineering Conference (SOSE), Rochester, NY, USA, 7–11 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 297–302. [Google Scholar] [CrossRef]
- Husung, S.; Weber, C.; Mahboob, A. Integrating Model-Based Design of Mechatronic Systems with Domain-Specific Design Approaches. Proc. Des. Soc. 2022, 2, 1895–1904. [Google Scholar] [CrossRef]
- Husung, S.; Gerhard, D.; Jacobs, G.; Kowalski, J.; Rumpe, B.; Zeman, K.; Zerwas, T. Model signatures for design and usage of simulation-capable model networks in MBSE. In Proceedings of the IFIP 19th International Conference on Product Lifecycle Management, Grenoble, France, 7–13 July 2022. [Google Scholar]
- Hoepfner, G.; Kowalski, J.; Faustmann, C.; Zerwas, T.; Kranabitl, P.; Vafaei, S.; Jacobs, G.; Hick, H. A Classification Method for the Systematic Identification of Models and Workflows in MBSE. In DS 119: Proceedings of the 33rd Symposium Design for X (DFX2022), Hamburg, Germany, 22–23 September 2022; The Design Society: Glasgow, UK, 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Torres, W.; Brand, M.V.D.; Serebrenik, A. Model Management Tools for Models of Different Domains: A Systematic Literature Review. In Proceedings of the 13th Annual IEEE International Systems Conference, Hyatt Grand Cypress Hotel, Orlando, FL, USA, 8–11 April 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Torres, W.; Brand, M.G.J.V.D.; Serebrenik, A. A systematic literature review of cross-domain model consistency checking by model management tools. Softw. Syst. Model. 2021, 20, 897–916. [Google Scholar] [CrossRef]
- Haberhauer, H.; Bodenstein, F. Maschinenelemente; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Broy, M. Challenges in automotive software engineering. In Proceedings of the 28th International Conference on Software Engineering, Shanghai China, 20–28 May 2006; Osterweil, L.J., Ed.; Association for Computing Machinery: New York, NY, USA, 2006; pp. 33–42. [Google Scholar]
- France, R.; Rumpe, B. Model-driven Development of Complex Software: A Research Roadmap. In Proceedings of the Future of Software Engineering, Minneapolis, MN, USA, 23–25 May 2007; Briand, L.C., Ed.; IEEE: Los Alamitos, CA, USA, 2007; pp. 37–54. [Google Scholar] [CrossRef]
- Drave, I.; Rumpe, B.; Wortmann, A.; Berroth, J.; Hoepfner, G.; Jacobs, G.; Spuetz, K.; Zerwas, T.; Guist, C.; Kohl, J. Modeling mechanical functional architectures in SysML. In Proceedings of the 23rd ACM/IEEE International Conference on Model Driven Engineering Languages and Systems, Virtual Event, Canada, 16–23 October 2020; Syriani, E., Ed.; Association for Computing Machinery: New York, NY, USA, 2020; pp. 79–89. [Google Scholar]
- Zerwas, T.; Jacobs, G.; Spütz, K.; Höpfner, G.; Drave, I.; Berroth, J.; Guist, C.; Konrad, C.; Rumpe, B.; Kohl, J. Mechanical concept development using principle solution models. IOP Conf. Series: Mater. Sci. Eng. 2021, 1097, 012001. [Google Scholar] [CrossRef]
- Menninger, B.; Wiechel, D.; Rackow, S.; Höpfner, G.; Oleff, C.; Berroth, J.; Gräßler, I.; Jacobs, G. Modellierung und Analyse funktionaler Varianz komplexer technischer Systeme. In Proceedings of the 33nd Symposium Design for X, Hamburg, Germany, 22–23 September 2022. [Google Scholar]
- Börner, M.F.; Frieges, M.H.; Späth, B.; Spütz, K.; Heimes, H.H.; Sauer, D.U.; Li, W. Challenges of second-life concepts for retired electric vehicle batteries. Cell Rep. Phys. Sci. 2022, 3, 19. [Google Scholar] [CrossRef]
- Zhang, Y.; Roeder, J.; Jacobs, G.; Berroth, J.; Hoepfner, G. Virtual Testing Workflows Based on the Function-Oriented System Architecture in SysML: A Case Study in Wind Turbine Systems. Wind 2022, 2, 599–616. [Google Scholar] [CrossRef]
- Koller, R. Konstruktionslehre für den Maschinenbau. Grundlagen zur Neu- und Weiterentwicklung Technischer Produkte mit Beispielen, 4th ed.; Springer eBook Collection Computer Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Pahl, G.; Beitz, W.; Feldhusen, J.; Grote, K.-H. Engineering design. In A Systematic Approach, 3rd ed.; Springer: London, UK, 2007. [Google Scholar]
- Koller, R.; Kastrup, N. Prinziplösungen zur Konstruktion Technischer Produkte, 2., Neubearb. Aufl.; Springer: Berlin, Germany, 1998. [Google Scholar]
- Zhang, Y.; Hoepfner, G.; Berroth, J.; Pasch, G.; Jacobs, G. Towards Holistic System Models Including Domain-Specific Simulation Models Based on SysML. Systems 2021, 9, 76. [Google Scholar] [CrossRef]
- Habermehl, C.; Höpfner, G.; Berroth, J.; Neumann, S.; Jacobs, G. Optimization Workflows for Linking Model-Based Systems Engineering (MBSE) and Multidisciplinary Analysis and Optimization (MDAO). Appl. Sci. 2022, 12, 5316. [Google Scholar] [CrossRef]
- Höpfner, G.; Jacobs, G.; Zerwas, T.; Drave, I.; Berroth, J.; Guist, C.; Rumpe, B.; Kohl, J. Model-Based Design Workflows for Cyber-Physical Systems Applied to an Electric-Mechanical Coolant Pump. IOP Conf. Series: Mater. Sci. Eng. 2021, 1097, 012004. [Google Scholar] [CrossRef]
- Fischer, D.; von Goeldel, S.; Jacobs, G.; Stratmann, A.; König, F. Investigation of lubricant supply in rolling point contacts under starved conditions using CFD simulations. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1097, 012007. [Google Scholar] [CrossRef]
- Feldermann, A.; Neumann, S.; Jacobs, G. CFD simulation of elastohydrodynamic lubrication problems with reduced order models for fluid–structure interaction. Tribol.-Mater. Surf. Interfaces 2017, 11, 30–38. [Google Scholar] [CrossRef]
- Paskaleva, G.; Mazak-Huemer, A.; Wimmer, M.; Bednar, T. Leveraging integration facades for model-based tool interoperability. Autom. Constr. 2021, 128, 103689. [Google Scholar] [CrossRef]
- Reilley, K.A.; Edwards, S.; Peak, R.; Mavris, D. Methodologies for Modeling and Simulation in Model-Based Systems Engineering Tools. In Proceedings of the AIAA SPACE 2016, Long Beach, California, 13–16 September 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Nikolaidou, M.; Kapos, G.-D.; Tsadimas, A.; Dalakas, V.; Anagnostopoulos, D. Challenges in SysML Model Simulation. Adv. Comput. Sci. 2016, 5, 49–56. Available online: http://www.acsij.org/acsij/article/view/544 (accessed on 13 July 2022).
- Cao, Y.; Liu, Y.; Fan, H.; Fan, B. SysML-based uniform behavior modeling and automated mapping of design and simulation model for complex mechatronics. Comput.-Aided Des. 2013, 45, 764–776. [Google Scholar] [CrossRef]
- Modelica Association. Functional Mock-up Interface Specification. Available online: https://fmi-standard.org/docs/3.0/ (accessed on 12 July 2022).
- Blochwitz, T.; Otter, M.; Arnold, M.; Bausch, C.; Clauss, C.; Elmqvist, H.; Junghanns, A.; Mauss, J.; Monteiro, M.; Neidhold, T.; et al. The Functional Mockup Interface for Tool independent Exchange of Simulation Models. In Proceedings of the 8th International Modelica Conference, Technical Univeristy, Dresden, Germany, 20–22 March 2011; Linköping University Electronic Press: Linköping, Sweden, 2011; pp. 105–114. [Google Scholar]
- Kaslow, D.; Soremekun, G.; Kim, H.; Spangelo, S. Integrated model-based systems engineering (MBSE) applied to the Simulation of a CubeSat mission. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–14. [Google Scholar] [CrossRef]
- Cawasji, K.A.; Baras, J.S. SysML Executable Model of an Energy-Efficient House and Trade-Off Analysis. In Proceedings of the 4th IEEE International Symposium on Systems Engineering, Rome Marriott Park Hotel, Roma, Italy, 1–3 October 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Otter, M.; Reiner, M.; Tobolář, J.; Gall, L.; Schäfer, M. Towards Modelica Models with Credibility Information. Electronics 2022, 11, 2728. [Google Scholar] [CrossRef]
- Bender, M.; Laurin, K.; Lawford, M.; Pantelic, V.; Korobkine, A.; Ong, J.; Mackenzie, B.; Bialy, M.; Postma, S. Signature required: Making Simulink data flow and interfaces explicit. Sci. Comput. Program. 2015, 113, 29–50. [Google Scholar] [CrossRef]
- Sirin, G.; Paredis, C.J.J.; Yannou, B.; Coatanea, E.; Landel, E. A Model Identity Card to Support Simulation Model Development Process in a Collaborative Multidisciplinary Design Environment. IEEE Syst. J. 2015, 9, 1151–1162. [Google Scholar] [CrossRef]
- Zeigler, B.P. Theory of modeling and simulation. In Discrete Event and Iterative System Computational Foundations, 3rd ed.; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Van Acker, B.; De Meulenaere, P.; Denil, J.; Durodie, Y.; Van Bellinghen, A.; Vanstechelman, K. Valid (Re-)Use of Models-of-the-Physics in Cyber-Physical Systems Using Validity Frames. In Proceedings of the 2019 Spring Simulation Conference (SpringSim), Tucson, AZ, USA, 9 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–12. [Google Scholar]
- Benveniste, A.; Caillaud, B.; Nickovic, D.; Passerone, R.; Raclet, J.-B.; Reinkemeier, P.; Sangiovanni-Vincentelli, A.; Damm, W.; Henzinger, T.; Larsen, K.G. Contracts for Systems Design: Theory. Res. Rep. 2015, 1, 1–86. [Google Scholar]
- Ribeiro dos Santos, C.A.; Hany Saleh, A.; Schrijvers, T.; Nicolai, M. CONDEnSe: Contract Based Design Synthesis. In Proceedings of the 2019 ACM IEEE 22nd International Conference on Model Driven Engineering Languages and Systems (MODELS), Munich, Germany, 15–20 September 2019; Staff, I., Ed.; IEEE: Piscataway, NJ, USA, 2019; pp. 250–260. [Google Scholar]
- Feldmann, S.; Kernschmidt, K.; Vogel-Heuser, B. Combining a SysML-based Modeling Approach and Semantic Technologies for Analyzing Change Influences in Manufacturing Plant Models. Procedia CIRP 2014, 17, 451–456. [Google Scholar] [CrossRef]
- Houpert, L. New Results of Traction Force Calculations in Elastohydrodynamic Contacts. J. Tribol. 1985, 107, 241–245. [Google Scholar] [CrossRef]
- Bader, N.F. Traction in EHL-Contacts: The influence of local fluid rheology and temperatures. 2018. Available online: https://www.repo.uni-hannover.de/handle/123456789/4499?locale-attribute=en (accessed on 28 October 2022).
- DIN EN ISO 80000-1. Größen und Einheiten. Teil 1: Allgemeines. 2013. Available online: https://dx.doi.org/10.31030/2007309 (accessed on 25 August 2022).
- No Magic. Cameo Systems Modeler Documentation. Available online: https://docs.nomagic.com/display/CSM190SP4/Cameo+Systems+Modeler+Documentation (accessed on 14 July 2022).
- Kowalski, J.; Torrilhon, M. Moment Approximations and Model Cascades for Shallow Flow. Commun. Comput. Phys. 2019, 25, 669–702. [Google Scholar] [CrossRef]
- Zimmerman, A.G.; Kowalski, J. Monolithic Simulation of Convection-Coupled Phase-Change: Verification and Reproducibility. In Recent Advances in Computational Engineering: Proceedings of the 4th International Conference on Computational Engineering (ICCE 2017) in Darmstadt, Darmstadt, Germany, 28–29 September 2017; Schäfer, M., Behr, M., Mehl, M., Wohlmuth, B., Eds.; Lecture Notes in Computational Science and Engineering; Springer Nature: Cham, Switzerland, 2018; pp. 177–197. [Google Scholar]
- Turnitsa, C.; Padilla, J.J.; Tolk, A. Ontology for Modeling and Simulation. In Proceedings of the Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; IEEE Press: Orlando, FL, USA, 2010; pp. 643–651. [Google Scholar]
- Staab, S.; Studer, R. (Eds.) Handbook on Ontologies; International Handbooks on Information Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zerwas, T.; Jacobs, G.; Kowalski, J.; Husung, S.; Gerhard, D.; Rumpe, B.; Zeman, K.; Vafaei, S.; König, F.; Höpfner, G. Model Signatures for the Integration of Simulation Models into System Models. Systems 2022, 10, 199. https://doi.org/10.3390/systems10060199
Zerwas T, Jacobs G, Kowalski J, Husung S, Gerhard D, Rumpe B, Zeman K, Vafaei S, König F, Höpfner G. Model Signatures for the Integration of Simulation Models into System Models. Systems. 2022; 10(6):199. https://doi.org/10.3390/systems10060199
Chicago/Turabian StyleZerwas, Thilo, Georg Jacobs, Julia Kowalski, Stephan Husung, Detlef Gerhard, Bernhard Rumpe, Klaus Zeman, Seyedmohammad Vafaei, Florian König, and Gregor Höpfner. 2022. "Model Signatures for the Integration of Simulation Models into System Models" Systems 10, no. 6: 199. https://doi.org/10.3390/systems10060199
APA StyleZerwas, T., Jacobs, G., Kowalski, J., Husung, S., Gerhard, D., Rumpe, B., Zeman, K., Vafaei, S., König, F., & Höpfner, G. (2022). Model Signatures for the Integration of Simulation Models into System Models. Systems, 10(6), 199. https://doi.org/10.3390/systems10060199








