1. Introduction
1.1. Background of The Work
With the development of information technology and the network economy, a new waste product recycling mode, such as eBay, eRecyclingCorp and so on, has spread rapidly around the world. The typical characteristic is that consumers complete the entire recycling process through e-commerce platforms and logistics mail service. In particular, many countries have proposed that the extensive use of next-generation information technologies, such as the Internet and artificial intelligence, should be made to build an intelligent, efficient, traceable and integrated online and offline (O2O) recycling and processing system [
1,
2,
3]. The participation of e-commerce platforms in waste product recycling is conducive to the stable development of a closed-loop supply chain (CLSC) [
4,
5], while it poses new problems to operation and management. The focus of this paper is on recycling cooperation problems, which have received more attention in recent years.
Guide and Wassenhove (2011) first proposed the concept of product recovery management [
6]. On this basis, the relationship between enterprise recovery strategy selection and recovery cost in different recovery channels was further studied [
7,
8]. In the early recycling stage, door-to-door recovery was the main way for enterprises to recycle waste products [
9]. Later, retailers also gradually joined in the recycling process. The “Internet + Recycling” model applies modern information technologies such as the Internet to traditional renewable resources’ recycling and urban solid waste classification [
10], which improves the recycling rate of waste and reduces garbage emissions [
11]. In this sense, this paper focuses on consumers providing information about waste products through online platforms and mail, and the cooperation of manufacturers and e-commerce platforms to share recycling and profits in cooperative alliances. Meanwhile, the government participated in the “Internet + Recycling” process to support and supervise enterprises in the cooperation alliance. In this context, the goal of this paper is to discuss appropriate strategies for the recycling alliance to achieve a stable O2O recycling system.
1.2. Motivation of The Work
In recent years, although many scholars have paid more attention to the problem of waste product recycling, it still has limitations on the work. Firstly, most of the existing literature assumes that enterprises are completely rational in the cooperation alliance [
12]. That is, they choose their own strategies for the purpose of maximizing profits [
13]. Nevertheless, in reality, it is impossible for enterprises to remain completely rational, and there will be other factors that affect their strategic decisions. Secondly, most of the researchers only concentrate on the strategic decision of enterprises in finite-order games. The evolution process of enterprises’ corporate behavior in the long-term cooperation is rarely considered. In reality, the cooperation and competition between enterprises is a continuous long-term process. Thirdly, the existing literature indicates that researchers pay more attention to the enterprises’ game mechanism and regard government’s behavior as an exogenous variable in the game model. How to investigate three-player evolutionary game problems related to the cooperation alliance of waste production recycling is an interesting and promising topic that needs to be further studied.
In summary, according to an overview of the waste product recycling problem, although researchers have made significant progress in this field, the following questions and challenges still exist: (1) How can manufacturers and e-commerce platforms (online and offline, such as O2O) build a cooperation alliance in the waste product recycling process? (2) How should the evolutionary game between enterprises (manufacturers and e-commerce platforms) and government be formulated and solved? (3) What are the optimal strategies for enterprises and government in the three-player game? (4) What is the effect of cooperation costs and government subsidies on enterprises decision making?
1.3. Contributions of the Work
To address the above-mentioned issues, this paper focuses on the waste products multi-channel recycling system, which includes manufacturers, e-commerce platforms and government. Particularly, all players in this game are assumed to be bounded rational participants. Since the emergence of the network platform recycling channel has changed the traditional recycling mode, evolutionary game theory is better suited to analyze the stability of the multi-channel recycling system. The purpose of this paper is to analyze the O2O recycling model for waste products consisting of government, manufacturing enterprises and e-commerce platforms. In addition, from the perspective of practice, this paper discusses the evolution stability strategy in three-player evolution game with different situations. Additionally, through numerical analysis, this research examines the factors that affect players’ stability strategy choices.
The contributions of this paper include three points. Firstly, both the government intervention and bounded rationality participants are integrated into the waste products multi-channel recycling problem. In addition, the discussion of the evolutionary stable strategy is the main focus of this paper. Secondly, the responsibilities and tasks of government participation are fully considered in the recycling process. The government not only provides subsidies and publicity support (cost subsidies and advertising), but also carries out its supervision and punishment duties (tax revenue). Thirdly, the influence and function of different factors on the evolution of participants’ behavior are analyzed. In particular, under certain circumstances, the players’ behavior could change from no-cooperative to cooperative under the influence of parameters. This paper establishes the model and analyzes the results and also indicates the management significance of establishing the O2O recycling cooperation system.
The remainder of this paper is organized as follows: The next section describes and analyzes the existing literature.
Section 3 shows the problem description, parameters and assumptions. Asymptotic stability of the equilibrium points and evolutionary stability strategies are introduced in
Section 4. Numerical experiments are executed, and their findings are reported in
Section 5. Ultimately,
Section 6 summarizes the conclusions and future research opportunities.
2. Literature Review
In recent years, online and offline cooperation recycling, as one of the critical problems in CLSC, has garnered increasing attention. This paper contributes to the literature on recycling channels, government intervention strategies in CLSC and the evolutionary game in supply chain.
Channel management, especially the selection of recycling channels for waste products, is an important issue in reverse supply chain management [
7,
14,
15]. Numerous scholars have studied the recycling channels of waste products and pointed out the impact of recycling channels’ selection on product pricing and enterprise earnings in the CLSC [
6,
8,
16,
17,
18]. Recently, Internet platforms have played important roles in waste recycling [
19]. Internet technology makes online recycling increasingly popular, and a growing number of companies are gradually adopting O2O recycling channels [
20,
21]. Among the above research streams, research on the effects of government intervention in CLSC is relatively limited.
Waste product recycling management and CLSC operation involve many stakeholders, including governments [
22]. China, Japan, Germany and other countries have provided government subsidies for the recycling process of waste electronic products to incentivize enterprises and individuals [
23,
24,
25,
26]. Modeling of government regulation and its impact on operation has emerged as a vital direction for scholars to study the CLSC [
27]. In CLSC, government subsidies are provided to different participators, and the impact of transfer prices in the recycling process will also be different [
28], which in turn will affect the efficiency of CLSC recovery and overall profit [
29]. Webster (2008) analyzes the impact of government subsidies on re-manufacturing, considering that subsidies are paid only to the re-manufacturer, only to the manufacturer or both [
30]. Sheu (2011) further enriches the research on government subsidies and discusses the waste product recycling problem when suppliers can also enjoy government subsidies in reverse logistics [
31]. With the development of the Internet, diversified product sales and recycling channels have appeared in the supply chain. Ma et al. (2013) study the subject of the government consumption-subsidy program and dual-channel CLSC [
32]. They show that both the manufacturer and the retailer are beneficiaries of the consumption-subsidy, while whether the e-tailer benefits or not is uncertain. The government’s intervention mechanism in CLSC includes not only reward mechanisms, but also punishment mechanisms [
33]. Hafezalkotob (2017) develops a price-energy-saving competition and cooperation model for two green supply chains (GSCs) under government financial intervention [
34]. It shows that the government can coordinate green supply chains to achieve financial, social and environmental goals through an appropriate tariff mechanism. Hu et al. (2014) investigate market competition and total societal welfare in the presence of tax and subsidy policy intervention, proving the effectiveness of tax and subsidy policies in promoting green products [
35]. The above research helps us understand the impact of government intervention mechanisms on the operation of CLSC. However, there are few studies on the impact of diversified government intervention strategies, such as subsidies, taxes and advertising on waste product recycling operations, etc. Therefore, a comprehensive study of the impact of government intervention strategies on waste recycling operations will help expand the existing research scope.
Using classical game theory to solve supply chain problems is very common [
36], and most of the supply chain participants in these studies are completely rational [
20,
37]. However, in reality, the game participants are often bounded rational [
38]. Some scholars try to use evolutionary games to describe problems in the supply chain, including reverse logistics operations [
39], green finance [
40,
41,
42], low-carbon production [
43] and other aspects. [
44] develop an evolutionary game model to analyze the tendency of the coordinated decisions and explore the coordination mechanism regarding whether to coordinate in the sustainable humanitarian supply chain [
44]. Lin et al. (2021) establish an evolutionary game theory framework embedded in the pricing model to study the long-term green strategic behavior of shipping lines [
45]. From a long-term perspective, the evolutionary game can better show the stable strategy of the participants in the supply chain [
46]. In supply chain systems, channel coordination can be achieved by incentivizing aligned contracts. It is a great method to use the evolutionary game to analyze the relationship between the evolutionary strategies of supply chain members for channel coordination and the profit surplus distribution [
47,
48]. In summary, the above studies illustrate that evolutionary games have become a widely used approach to study supply chain issues. Especially, CLSC contains a greater number of collaborative fields, namely the recycling process, the location of suppliers and the selection of suitable partners [
49]. According to the above literature, evolutionary game theory is used to manage the complex relationship among the players, which is more conducive to solve practical problems in CLSCs. The summary is shown in
Table 1.
To sum up, this paper builds a multi-party evolutionary game model of waste production recycling considering government intervention. Through analyzing the stability of the system, it provides meaningful insights for the dynamic strategic evolution process of the cooperation recycling system.
3. Model and Assumption
3.1. Problem Definition
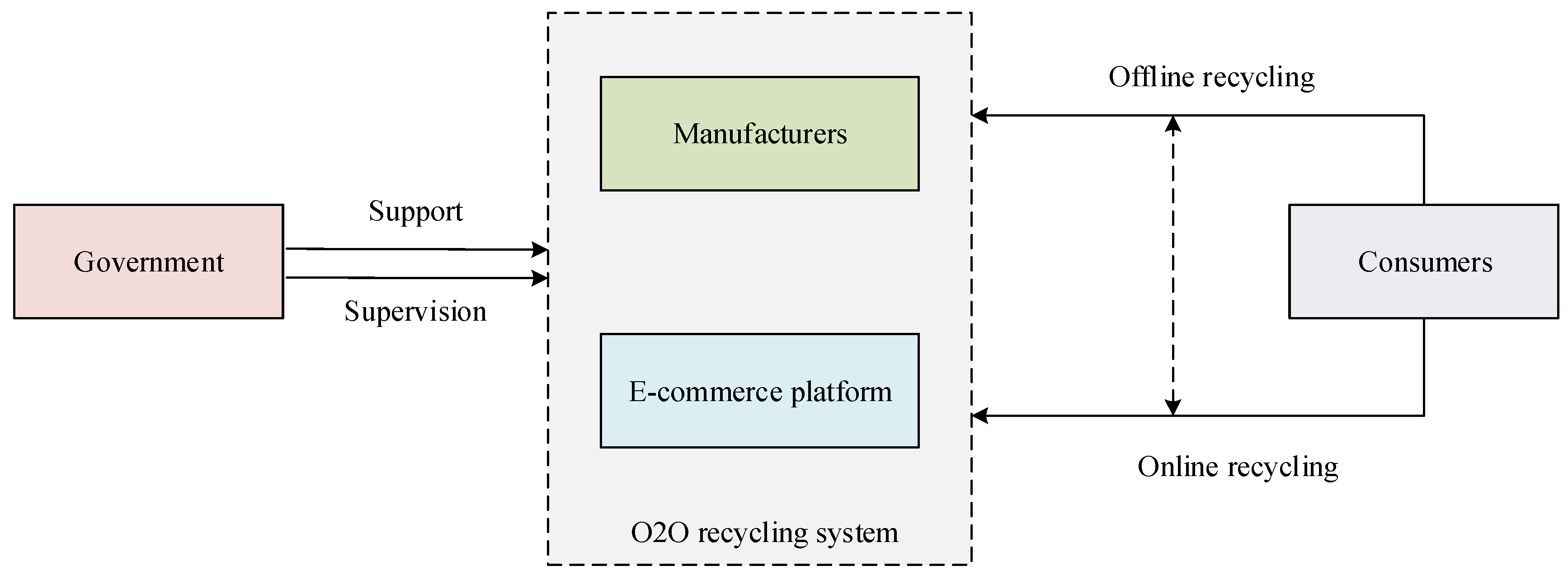
The online to offline (O2O) recycling system is an organic combination of manufacturers and e-commerce platforms that is characterized by the smooth connection between the manufacturers’ offline business and the e-commerce platform’s online business. In this sense, the system is very complex, being multi-participant and multi-element. Meanwhile, the government also plays an important role as a participant in the system. In a real closed-loop supply chain, because it contains a large number of manufacturers and e-commerce platforms, this cannot guarantee that individuals in any group can pursue the optimal strategy completely rationally. In this context, we establish a tripartite game evolution model of government, manufacturers and e-commerce platforms to explore the behavioral strategy selection and system evolution path. Among them, manufacturers and e-commerce platforms respectively carry out the waste product recycling business. With the development of information technology, the asymmetric information and the fragmented logistics restrict the waste product recycling in the consumer market. Building an O2O recycling system composed of manufacturers and e-commerce platforms can ensure the smooth circulation of waste product information and logistics, explore more potential environmental protection consumers and recover more waste products to increase enterprise profits. For example, Apple and Huawei both have their own electronics recycling business. Meanwhile, in 2014, Apple partnered with eBay to recycle and sell manufactured iPhones. On 6 September 2022, JD and Huawei jointly launched a sustainable plan to promote the development of circular economy by encouraging users to consume rationally, recycle old goods and trade in old goods for new ones.
However, in the process of building the O2O recycling system, enterprises (manufacturers and e-commerce platforms) should invest a certain amount of human, material and financial resources. The government hopes that manufacturers and e-commerce platforms can reach cooperation in the waste product recycling process, so it will take some measures to promote cooperation between enterprises and platforms. For example, in 1970, the Japanese government promulgated the Waste Disposal Law, which imposed penalties, such as fines and taxes, on illegally discarded waste. Later, in the Basic Law for Promoting the Formation of a Recycling Society promulgated by the Japanese government, detailed incentives were formulated for the recycling of waste. In 2009, the U.S. government also required remanufactured parts and related materials to be prioritized in government procurement projects in the Remanufactured Materials Advisory Notice. The O2O recycling system has formed a new recycling mode, named “Internet + Recycling”. In this context, the relationship between enterprises and government is depicted in
Figure 1.
The government fulfills its intervention responsibilities by supporting and supervising enterprises. In terms of support, the government provides certain subsidies to encourage enterprises to build a cooperative system and actively promotes the recycling cooperative enterprises to improve their reputation. As for the supervision, the government introduces the mechanism of collecting environmental pollution fees for enterprises and levies environmental pollution taxes on enterprises that do not actively join the recycling cooperation.
3.2. Decision Framework
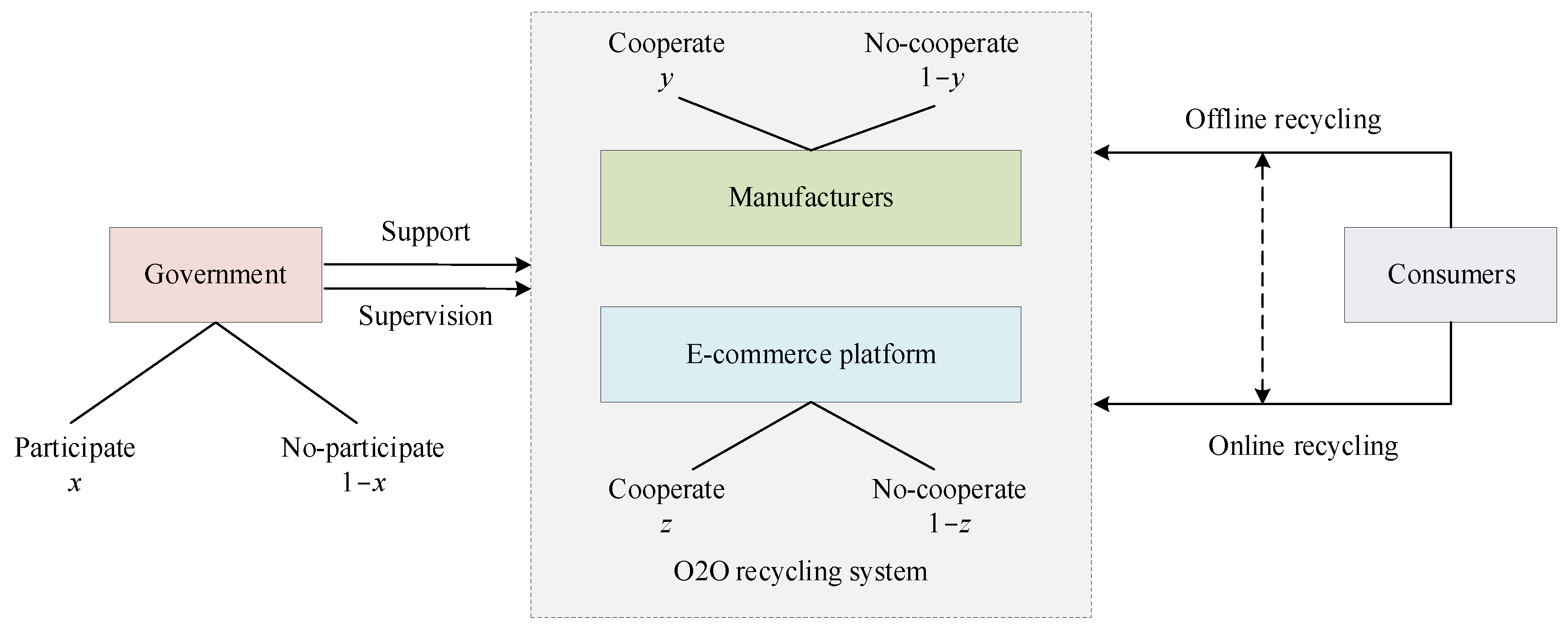
In the process of establishing O2O recycling system, enterprises have to pay additional costs on system construction. Therefore, enterprises have two strategic choices, “Cooperate” or “No-cooperate”. The government may actively participate in the construction of the recycling system and exert its support and supervision responsibilities, or it may not participate and allow the enterprise to develop freely. It also has two strategic choices, “Participate” or “No-participate”. According to the above analysis, a three-player evolutionary game decision-making framework regarding the O2O recycling system was constructed. It is depicted in
Figure 2.
In this paper, manufacturers, e-commerce platforms and government are all participants in the evolutionary game. The government participates in the recycling system with probability and not with the probability . Manufacturers and e-commerce platforms consider whether to cooperate to establish an O2O recycling system. In terms of manufacturers and e-commerce platforms, the probability of the strategy “Cooperate” for the initial state is and , respectively. The probability of the strategy “No-cooperate” for the initial state is and , respectively, where .
3.3. Assumptions
In order to construct the three-player game model and analyze the stability of the strategies and equilibrium points, we set the following assumptions in this paper:
Assumption 1. Manufacturers are responsible for product manufacturing, re-manufacturing and waste product recycling; e-commerce platformsare responsible for product sale and waste product recycling; and governmentsupports and supervises manufacturers and e-commerce platforms in the cooperation recycling process. All three participants are bounded rational economists, and the strategy choice gradually evolves to the optimal strategy over time.
Assumption 2. The set of strategies of the government is {Participate, No-participate}. When the government participates in O2O recycling system, it will be affirmed and praised for its work, and gain profit. When the government does not participate, it gets benefits, where. When the government participates, it investsin advertising and supplies recycling subsidyfor the enterprise in O2O recycling system. When the enterprise exits the recycling system, the government will collect environmental taxes from the no-cooperation enterprise, such that the taxes for manufacturersand e-commerce platformsareand, respectively, where.
Assumption 3. When manufacturers and e-commerce platformschoose not to cooperate in recycling process, they just obtain the initial income through recycling waste products separately. The initial income for them isand, respectively.
Assumption 4. When manufacturers and e-commerce platformschoose cooperation recovery, a total investment costis required to establish cooperation, and the cost sharing ratio coefficients between manufacturersand e-commerce platformsareand, respectively. Meanwhile, the additional income from cooperation recovery is, and the income distribution ratio coefficients areand. When the government participates in the cooperation recovery, the actual cost of cooperation is, and the actual increase of manufacturers and platform is.
Assumption 5. When one party actively cooperates and one party breaches the contract, the cooperative party shall bear a certain cooperation cost, and the defaulting party shall pay certain liquidated damages. Among them, when manufacturerschoose to cooperate and e-commerce platformschoose not to cooperate, e-commerce platformsshall pay liquidated damagesto manufacturers. Conversely, manufacturersshall pay liquidated damagesto e-commerce platforms.
According to the above five assumptions, the return matrix of three-player game in the recycling system can be obtained, as shown in
Table 2 and
Table 3 below:
According to the return matrix in
Table 1 and
Table 2, the expected return (
) and the average return (
) of government participation and no-participation are respectively:
The expected return (
) and the average return (
) of manufacturers cooperation and no-cooperation are respectively:
The expected return (
) and the average return(
) of e-commerce platform cooperation and no-cooperation are respectively:
3.4. Using the Evolutionary Stability Strategy of Replication Dynamic Equations to Solve
Through the above analysis, the replication dynamic equation of the government’s strategic choice is,
The replication dynamic equation of the manufacturer’s strategic choice is,
The replication dynamic equation of the e-commerce platform’s strategic choice is,
By combining the above three equations, the replication dynamics of governments, enterprises and platforms are as follows:
According to the stability theory discriminate method proposed by Lyapunov (1992) [
50], the evolutionary stability strategy (ESS) of the differential equation system can be obtained from the local stability analysis of the Jacobian matrix of the system [
51,
52,
53,
54]. From above equations, the Jacobian matrix of the system is as follows:
In an asymmetric game, if the evolutionary game equilibrium
is an evolutionary stable equilibrium, then
must be a strict Nash equilibrium, and the strict Nash equilibrium is a pure strategy equilibrium [
55]. That is, in an asymmetric game, the mixed strategy equilibrium must not be an evolutionary stable equilibrium. Therefore, we only need to discuss the asymptotic stability of the pure strategy equilibrium. That is, in this paper, according to above dynamical system, if
, it can be obtained that the local equilibrium points are
,
,
,
,
,
,
,
. It is sufficient to analyze the asymptotic stability of these eight pure strategy Nash equilibria. According to evolutionary game theory, the equilibrium point that satisfies all eigenvalues of the Jacobian matrix that are non-positive is the evolutionary stability point (ESS) of the system [
56].
According to the research by Selten (1980, 1983), we solve and analyze the evolutionary stability strategies in next section [
55,
57].
4. Asymptotic Stability of the Equilibrium Points and Evolutionary Stability Strategies
First, analyze the case that the equilibrium point is
. At this time, the Jacobian matrix is,
It can be seen that the eigenvalues of Jacobian matrix
are
,
and
at this time. By analogy, the eigenvalues of the Jacobian matrix corresponding to the eight equilibrium points can be obtained by substituting them into the Jacobian matrix, as shown in
Table 4.
For a linear time invariant system
, the necessary and sufficient condition is that all eigenvalues of the system matrix
lie in the left half of the complex plane (excluding the imaginary axis). When the eigenvalues fall on the imaginary axis, the system is stable in the sense of Lyapunov. When there is one on the right half plane, the system is unstable, i.e., Lyapunov’s first method. It is also known as the indirect method, which judges the stability of the system by solving the solution of the system state equation or by calculating the characteristic polynomial and eigenvalue of the system matrix. According to the criterion of Jacobian matrix, when all eigenvalues of the determinant at the equilibrium point are less than 0, the point is an ESS point; if all the eigenvalues are positive, it is the saddle point; if the eigenvalue has a positive and negative cross, it is a stable point. According to this criterion, the sign of eigenvalue at each equilibrium point under different conditions can be calculated to determine whether it is a stable point of system evolution. Based on the Lyapunov stability theorem, we can get the following theorems with
Table 3.
Theorem 1. When or, the equilibrium point is asymptotically stable.
To clearly describe the results, the corresponding phase diagrams are shown in
Figure 3.
According to
Figure 3, when
or
, the three eigenvalues of the equilibrium point
are all less than zero. It means that when the government does not participate, the liquidated damages paid by manufacturers to e-commerce platforms is greater than the cooperation recovery cost paid by e-commerce platforms; on the other hand, if the liquidated damages paid by e-commerce platforms to manufacturers is greater than the cooperative recovery cost paid by manufacturers, the equilibrium point is
, and the corresponding evolutionary stability strategy combination is {Participate, Cooperate, Cooperate}. According to the assumptions in the paper, when the government participates, the enterprise will get the corresponding subsidy in cooperation recycling process, so that the actual cost paid by enterprises in the cooperation process will be reduced. When the cost of cooperation decreases, enterprises will have a greater incentive to reach cooperation. In reality, when the government does not participate in the cooperation, if the liquidated damages paid to the cooperative enterprise are greater than the cost for cooperation, with its loss of income, the enterprise behavior will eventually tend to cooperate in the evolution process.
Theorem 2. When and , the equilibrium pointand are asymptotically stable.
To clearly describe the results, the corresponding phase diagrams are shown in
Figure 4.
According to
Figure 4, when
and
, the three eigenvalues of the equilibrium point
and
are all less than zero. It means that when government participates in the cooperation recycling process, the sum of the liquidated damages, publicity income sharing and the exemption environment protection tax is less than the actual cooperation cost of the manufacturers and e-commerce platforms, respectively, The equilibrium points are
and
, and the corresponding evolutionary stability strategy combination is {Participate, Cooperate, Cooperate} and {Participate, No-cooperate, No-cooperate}. In practice, when enterprises choose to cooperate, their additional benefit may be less than the actual cost, resulting in loss of enterprises’ profit. Under these circumstances, enterprises have no incentive to create a cooperation system, and eventually enterprises’ behavior will tend to be no-cooperative in the evolution process. Therefore, the evolution stability strategy combination of the government, manufacturers and e-commerce platforms is {Participate, No-cooperate, No-cooperate}. On the contrary, when enterprises actively build a cooperative relationship and establish the O2O recycling system, the additional net income will be greater than zero. Under the circumstances, with the government participation, the evolution stability strategy combination of three players is {Participate, Cooperate, Cooperate}.
Theorem 3. When and ; or and , the equilibrium point is asymptotically stable.
To clearly describe the results, the corresponding phase diagrams are shown in
Figure 5.
According to
Figure 5, when
and
; or
and
, the three eigenvalues of the equilibrium point
are all less than zero. It means that, we can get the equilibrium point
and the corresponding evolutionary stability strategy (Participate, Cooperate, Cooperate) in the following case. That is, when government participates in the cooperation recycling process, the sum of the liquidated damages, publicity income sharing and the exemption environment protection tax is greater than the actual cooperation cost of manufacturers and e-commerce platforms; when government does not participate, the liquidated damages paid by no-cooperation enterprises to cooperation enterprises is less than the cooperation recovery cost paid by enterprises, respectively. In practice, with the participation of the government, when the additional income of an enterprise unilaterally creating the cooperation may be greater than its cost, the enterprise cooperation recovery is still profitable. When the government does not participate, the liquidated damages for the unilateral creation of the cooperation enterprise may not be enough to pay the cost of the cooperation. Therefore, in the long-term evolution game process for three players, the government should actively participate in the O2O recycling system, and enterprises should establish a cooperative recycling relationship to form the O2O recycling system; thus, the evolution stability strategy combination would be {Participate, Cooperate, Cooperate}.
According to the above theorems, the corresponding results are depicted in
Table 5.
5. Numerical Simulation
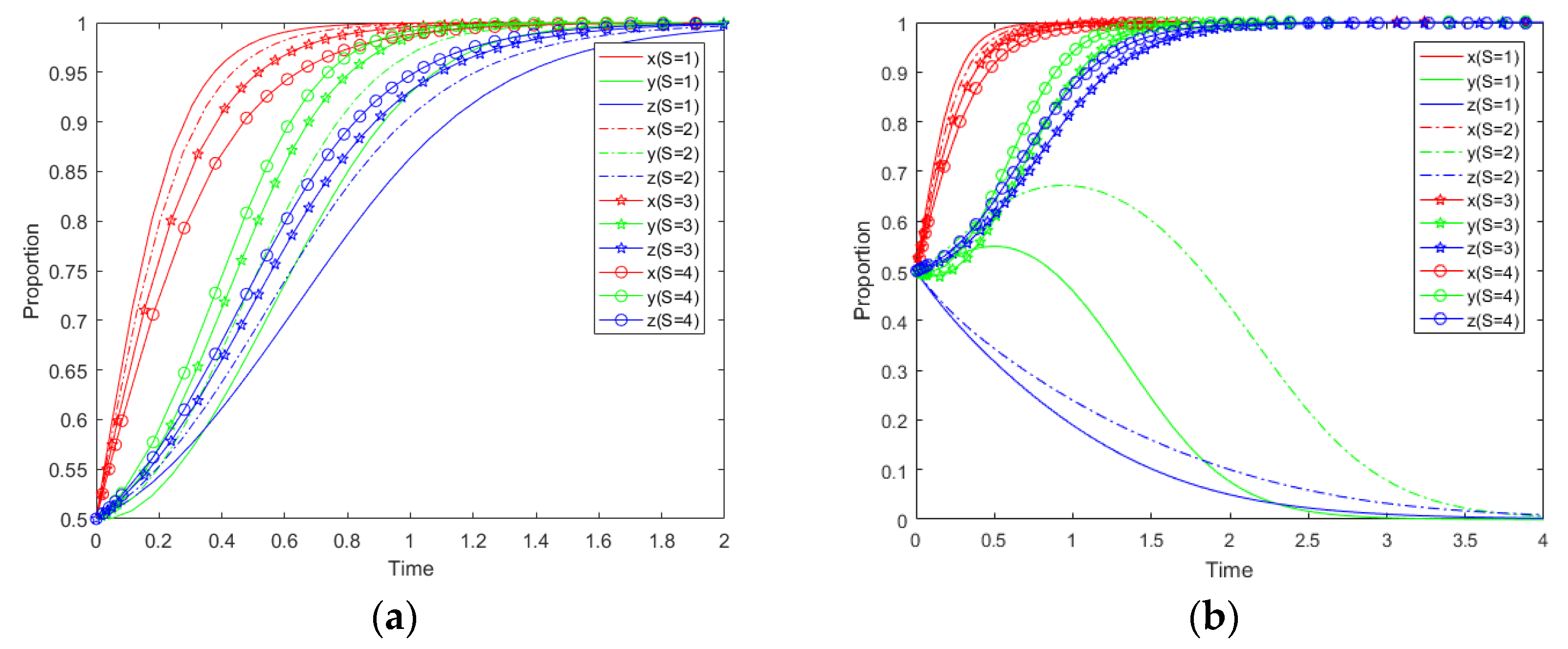
In order to analyze the evolutionary path and stable trajectory of the game among the government, manufactures and platforms in the cooperative recycling supply chain system under government intervention, this paper uses MATLAB2016b to simulate and analyze the above evolutionary game model. Because the real data set is huge and difficult to obtain and process, the data adopted in the numerical example are simulated and estimated. It does not have real significance to some extent but has certain economic significance. These data were manipulated before being employed to closely comply with certain assumptions of this study. We obtained the scale coefficients from 0 to 1. For constant parameters, such as rewards and punishments, we set three groups of different values according to the relationship that satisfies the three eigenvalues to meet the three cases of the above assumptions and carried out simulation verification. In combination with the actual situation, the parameters are set as follows;
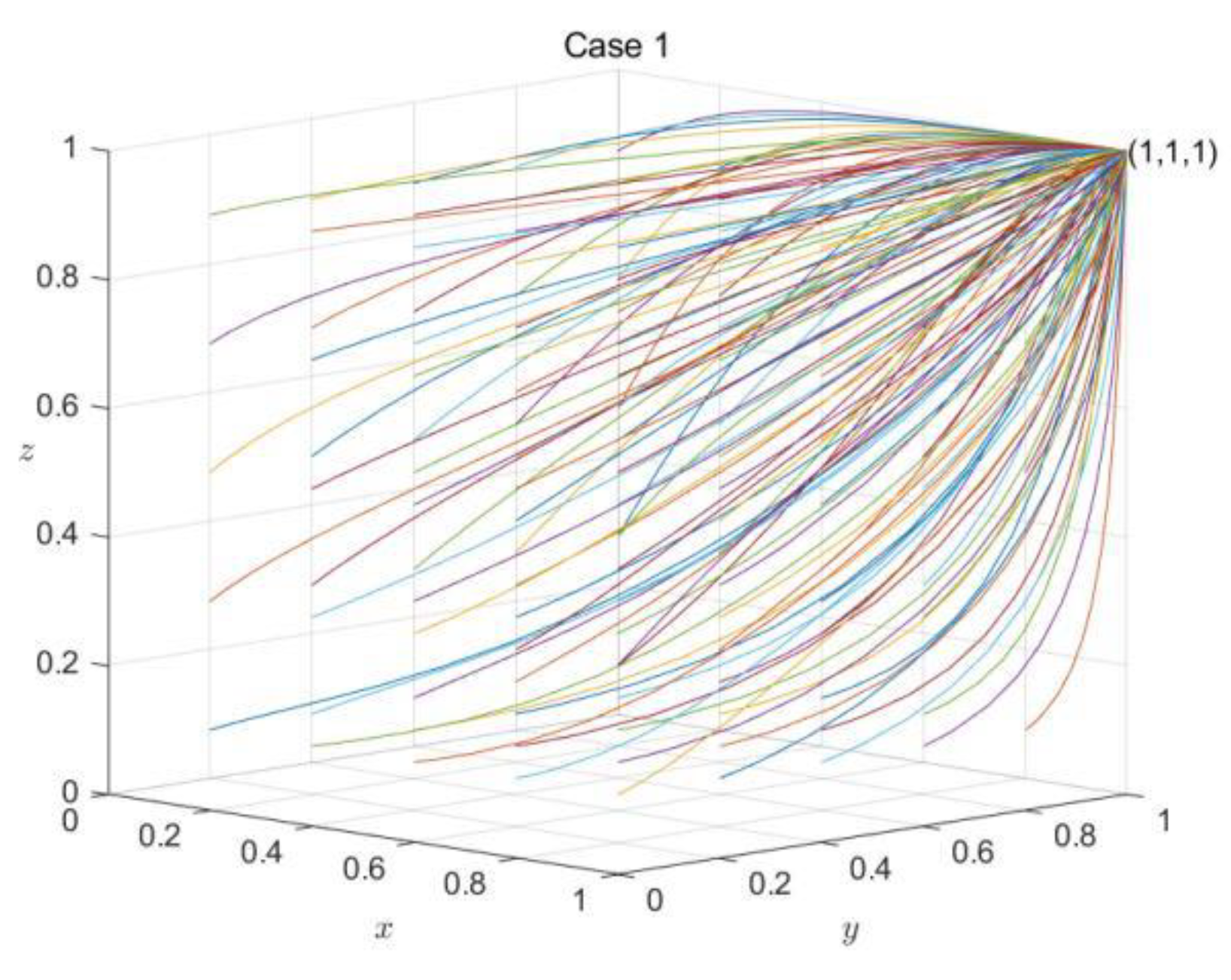
Case 1: When or, the equilibrium point is asymptotically stable. So, we set .
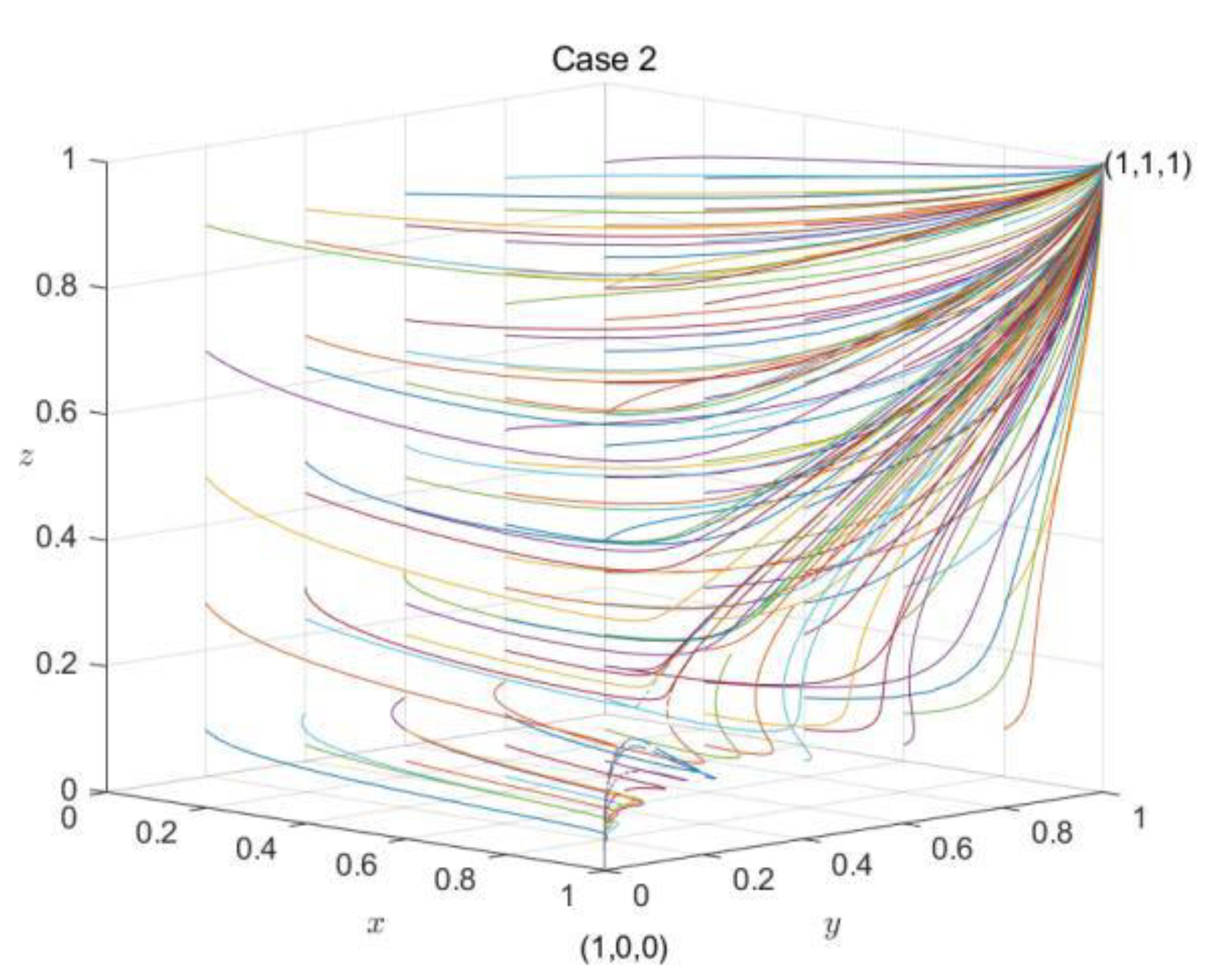
Case 2: When and , the equilibrium point and are asymptotically stable. So, we set .
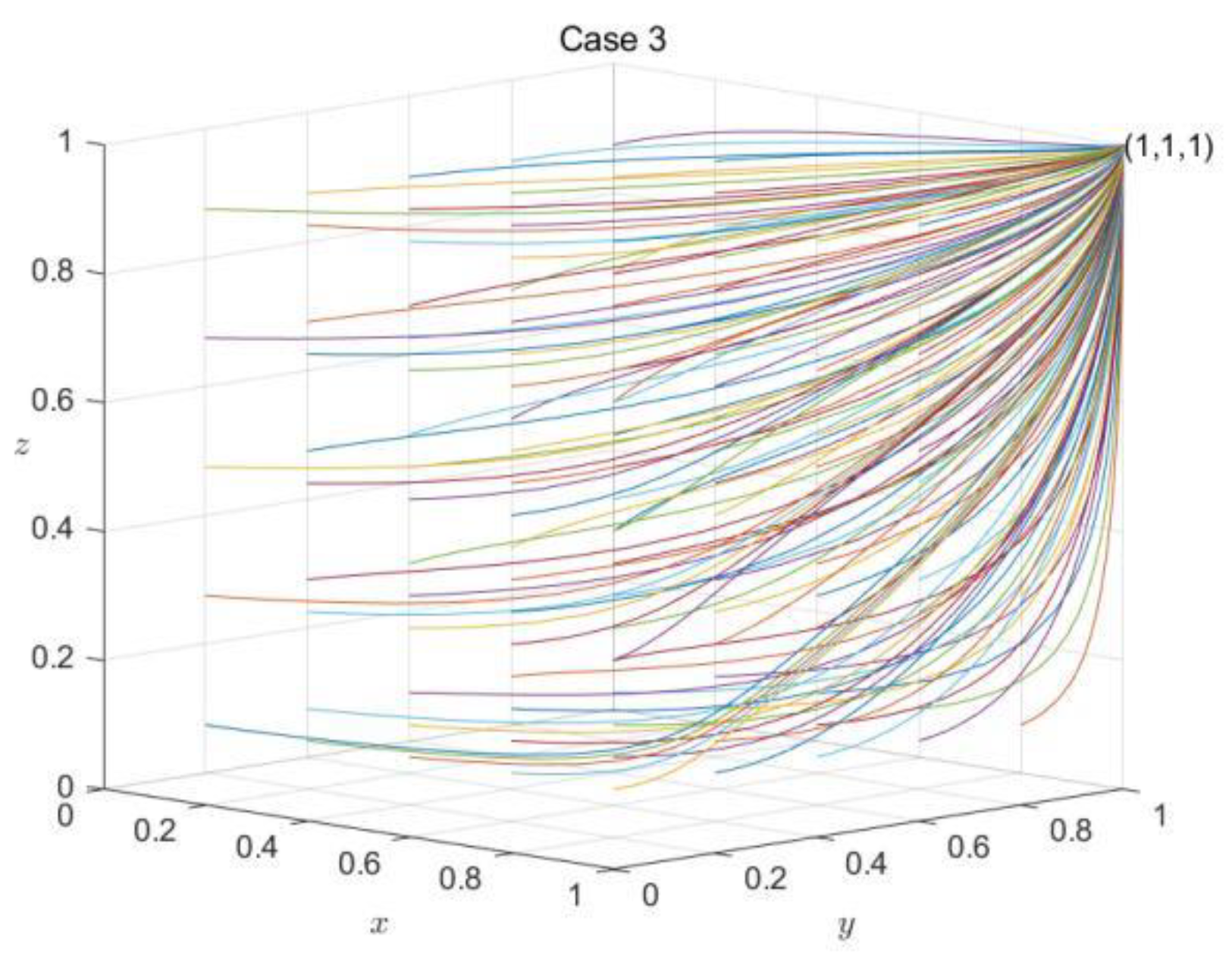
Case 3: When and ; or and , the equilibrium point is asymptotically stable. So, we set .
5.1. The Stability Simulation of Equilibrium Point
We make the value of the parameters of the income matrix equal and input the dynamic system into Matlab. The strategy of the three players starts from 0.1 to 1, simulates with a spacing of 0.2 and finally draws 125 lines; the output result is shown in the corresponding lines in
Figure 6,
Figure 7 and
Figure 8.
The parameter settings of Cases 1, 2 and 3 satisfy the conditions in Theorems 1, 2 and 3, respectively. The three groups of values are evolved 50 times over time from different initial strategy combinations, and the results are shown in
Figure 6,
Figure 7 and
Figure 8.
It can be seen from
Figure 6,
Figure 7 and
Figure 8 that the final evolution of the system is stable as follows: Case 1 at
, Case 2 at
and
and Case 3 at
. It means that these points are the evolutionary stable strategy (ESS) for different conditions. Similarly, like the results in
Section 4, when the actual cost of enterprises participating in cooperation recycling is small or medium, with the participation of the government, enterprise behavior will tend to be cooperative in the evolution process (stable at
). However, when the actual cost of enterprise participating in cooperation recycling is large, there are two situations that enterprise behavior tends to be cooperation and no-cooperation in the evolution process (stable at
and
). In reality, when the actual cost of establishing cooperation recycling for enterprises is too large, even if the government provides mutual support and supervision, there is still the possibility that the cooperation between enterprises cannot be achieved. The government should actively create a conducive environment for enterprises to reduce the cost of building cooperation. Under this condition, the enterprise behavior is more generalized to cooperation in the process of long-term evolution.
5.2. Impacts of Changes in Government Subsidies and Advertising on Evolutionary Paths
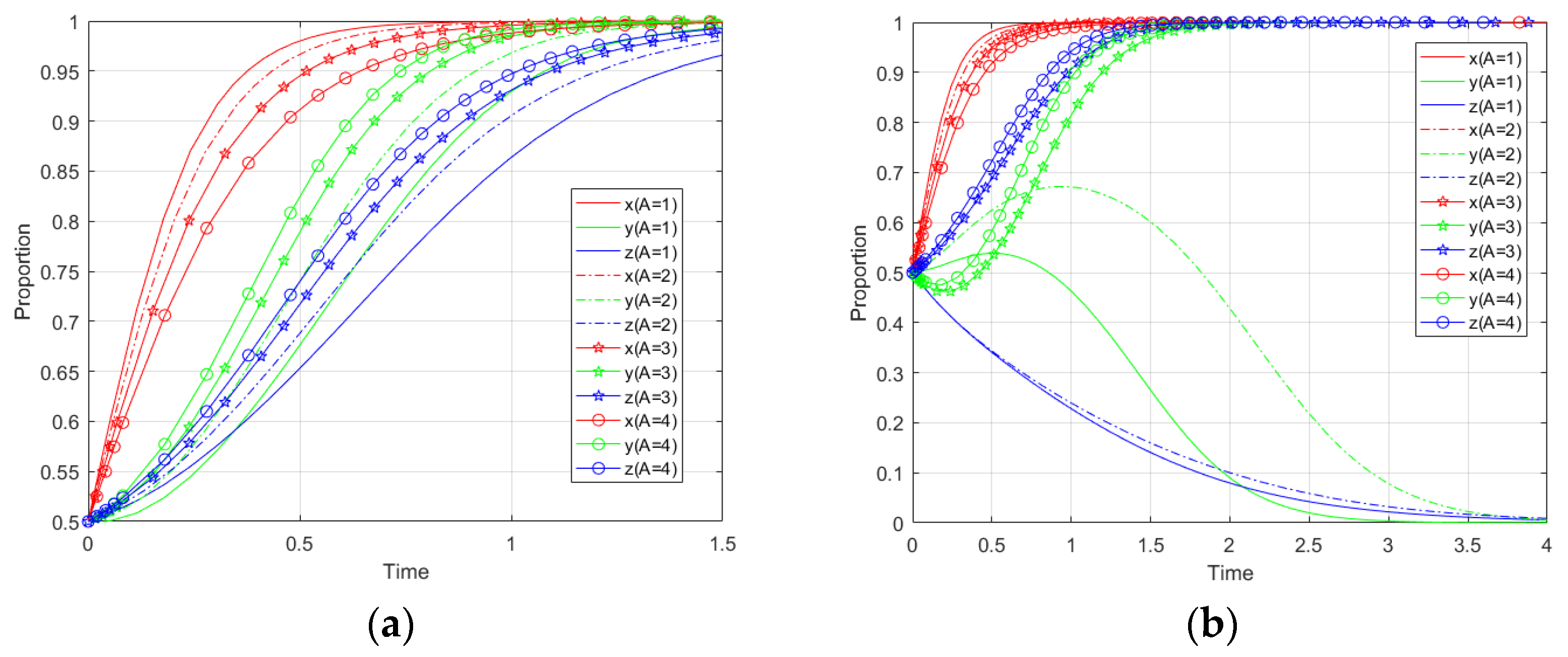
With Case 1, we analyzed impacts of changes in government subsidies and advertising on evolutionary paths, and the simulation results are shown in
Figure 9a and
Figure 10a. In
Figure 9a and
Figure 10a, the solid line is used as a benchmark for comparison. Increasing government subsidies and advertising to enterprises can enable enterprises to reach a stable equilibrium point earlier than the initial state. Meanwhile, increasing government subsidies and advertising to enterprises can enable government to reach a stable equilibrium point later than the initial state. In Case 3, we achieved the same result as described above, and the related analysis is omitted in paper.
Similarly, we analyzed the influence of government subsidies and advertising on the game players’ behavior evolution in Case 2, and the simulation results are shown in
Figure 9b and
Figure 10b. We still use the solid line as a benchmark for comparison. Increasing government subsidies and advertising to enterprises can enable enterprises to reach the no-cooperation stable equilibrium point later than the initial state. Moreover, as government subsidies and advertising increase, enterprises’ behavior will evolve into being stable for cooperative strategies.
In practice, government has effectively helped enterprises to accelerate the pace of cooperation recycling by taking measures such as incentive subsidies and advertising publicity campaigns. However, when government needs to spend too much money in the participation process, it reaches equilibrium points at a slower rate. When it provides too little money, there will be enterprises that do not actively cooperate. Therefore, the government should choose an appropriate financial expenditure to promote enterprise cooperation, so as to achieve a win-win result for economic and environment improvement.
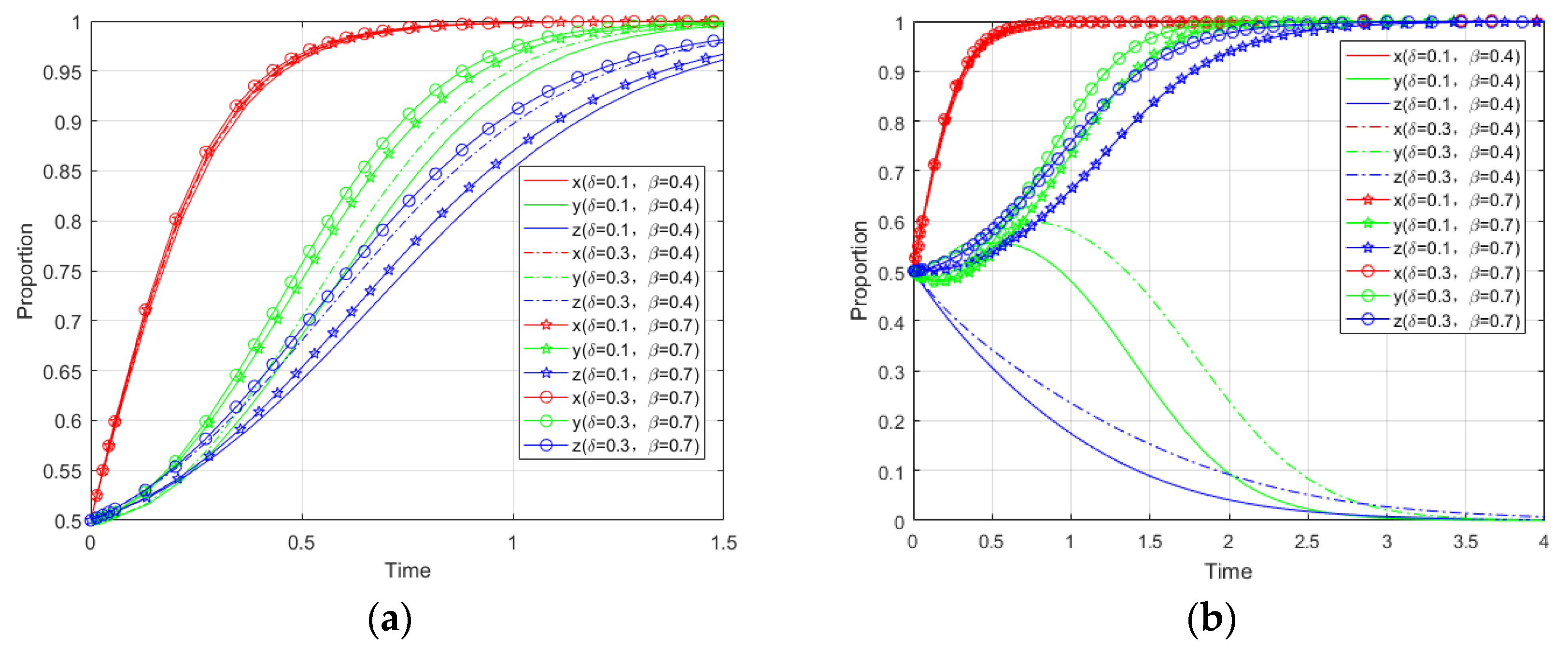
5.3. Impacts of Changes in Tax Coefficient on Evolutionary Paths
In Case 1, when government increases the environmental tax rate for no-cooperation enterprises, the rate that the behavior of both parties tends to cooperate will increase at the same time, and the impact on the no-cooperation party will be significantly greater than that on the cooperation party, as shown in
Figure 11a. In Case 3, we achieved the same result as described above, and the related analysis is omitted in paper.
Meanwhile, we analyzed the influence of changing the environmental tax rate on the game players’ behavior evolution in Case 2, and the simulation results are shown in
Figure 11b. When the environmental tax rate of one party remains unchanged, changing the environmental tax rate of the other party will simultaneously affect the rate at which the evolutionary behavior of both parties tends to stabilize. With the increasing of environmental tax rate, if the two parties stabilize in a no-cooperate strategy, the rate of stabilization will decrease; otherwise, it will become faster.
In fact, the government can appropriately raise the environmental protection tax of enterprises in the legal and reasonable circumstances, which can improve the environmental awareness of enterprises and increase the motivation of enterprises to invest in environmental protection. Meanwhile, it also has a positive effect on enterprises in other industries for environmental protection.
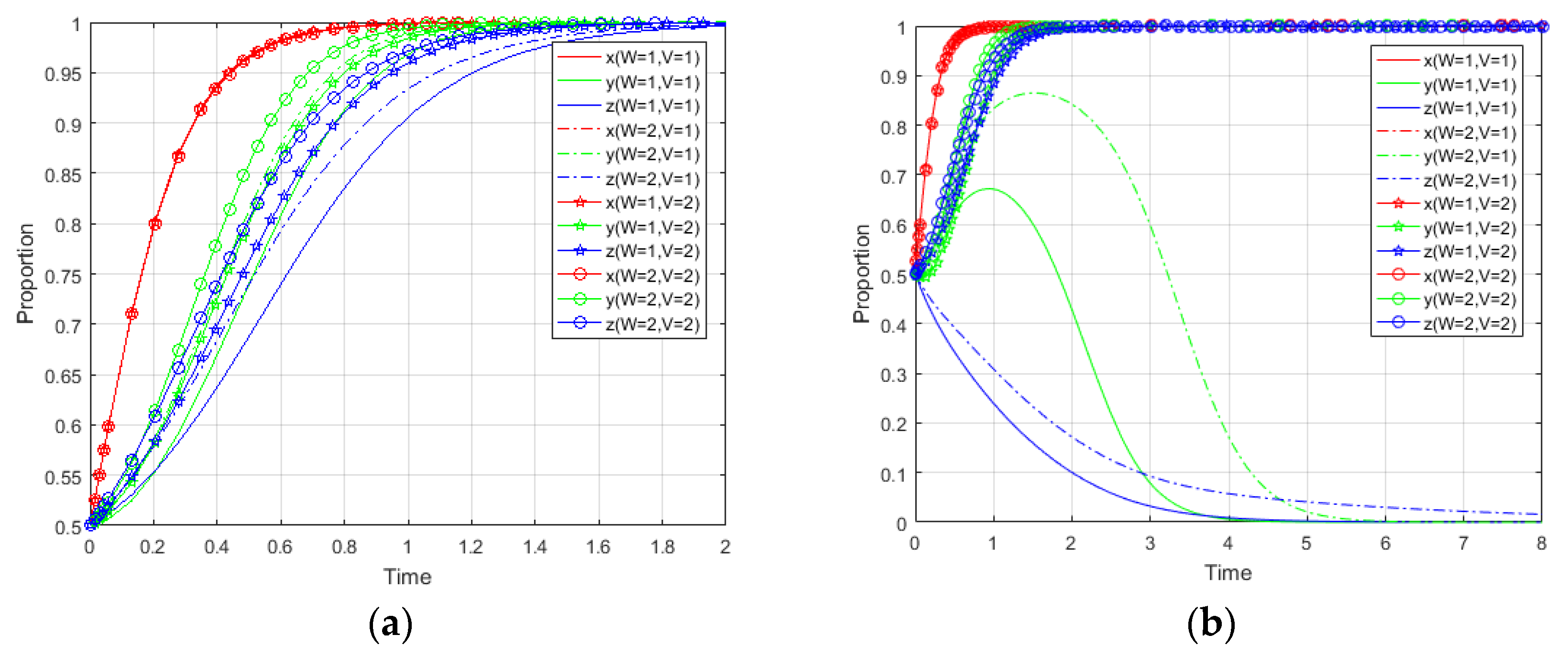
5.4. Impacts of Changes in Liquidated Damages on Evolutionary Paths
In Case 1, when the liquidated damages paid by the no-cooperation enterprises become larger, the rate that the behavior of both enterprises tends to cooperate will increase at the same time. The impact on the no-cooperation enterprises themselves is significantly greater than that on the cooperative enterprises, as shown in
Figure 12a.
Similarly, we analyzed the influence of the liquidated damages on the game players’ behavior evolution in Case 2, and the simulation results are shown in
Figure 12b. When the liquidated damages of one enterprise remain unchanged, changing the liquidated damages of the other enterprise will simultaneously affect the rate at which both parties tend to stabilize. With the increasing of liquidated damages, if the two enterprises stabilize in {No-cooperate, No-cooperate}, the stabilization rate will decrease; otherwise, it will become faster. This result is very similar to the conclusions found in
Figure 11b.
In practice, when the enterprise needs to pay a higher liquidated damages rate for no-cooperation, the enterprise may actively cooperate because he cannot bear the penalty for no-cooperation. The cooperative enterprise will also choose to actively cooperate because it gets more penalty to make up for the cost of establishing the cooperation. Therefore, the liquidated damages mechanism in the cooperation contract can be used to promote the successful establishment of the cooperative recycling system of enterprises.
6. Conclusions
The focus of this paper is to explore the construction of the O2O recycling system with government participation. Among them, government’s behavior is divided into “Participate” and “No-participate”; the behavior of manufacturers and e-commerce platforms is divided into “Cooperate” and “No-cooperate”. Thus, a three-player evolutionary game model is constructed in this context. Then, the stability of the system and the participants’ evolutionary stable strategy are discussed through analytical solutions and numerical simulations. Finally, this paper studies the influence of government intervention intensity and institutional construction cost on the evolution of participation strategy.
The research results of this study show the following: (a) As important members of the closed-loop supply chain, whether enterprises actively participate in the cooperative recycling or not depends on the actual cost of establishing the cooperative recycling system. The government support and supervision will affect the actual cost of enterprises. (b) When the actual cost of establishing the cooperative recycling system is small or medium, under the influence of government support and supervision measures, all enterprises’ behavior will eventually evolve into the cooperative recycling of waste products. (c) When the actual cost of establishing the cooperative recycling system is large, under the influence of government support and supervision measures, there will be two kinds of evolutionary results for enterprises, both cooperation or both no-cooperation. (d) It is the best strategy choice for government to participate in cooperation recycling system.
The conclusions obtained in this paper provide interesting theoretical and practical insights into the development of waste product recycling supply chain in the context of Internet. First of all, an O2O waste product recycling system cooperated between manufacturers and e-commerce platforms is designed in this research. It has realized the organic combination of online and offline channels in the waste product recycling process. Second, it considers the theoretical link between the role of the government and the establishment of a stable O2O waste recycling system. Additionally, it highlights the guiding role of the government in the green supply chain. Third, the multiplayer evolutionary game model is introduced into the waste product recycling supply chain, which solves the problem of cooperation under the incomplete project approval of participants and is conducive to solving practical problems.
In practice, most of the motivation for cooperation comes from the increase of enterprise income brought by cooperation. Firstly, government can provide corresponding support and supervision services to facilitate the realization of cooperation between enterprises. In the recycling process of waste products, the government can promote enterprises’ cooperation through the reward strategy and the punishment strategy. The government should have a comprehensive understanding of the process of enterprises’ cooperation when formulating rewards and penalties. The cost paid and benefits obtained in the process of cooperation will directly affect the cooperation intention of enterprises. Relying solely on the pressure of government policies, it is impossible to successfully complete the recycling cooperation between enterprises. Secondly, with the maturity of the “Internet + Recycling” mode, manufacturers want to expand their recycling channels, so cooperating with e-commerce platforms is a good choice. Meanwhile, e-commerce platforms hope to enhance their visibility and credibility, so cooperating with manufacturers is also a nice strategy. The establishment of the multi-channel model of waste products helps to get the full recycling of waste products in the market. It is a win-win result for manufacturers and e-commerce platforms. Enterprises should actively break down the original channel barriers, and actively explore and innovate recycling channels. Thirdly, the recovery process of enterprise cooperation is a long-term process. The evolutionary game model can better present the behavior of enterprises and government and uncover the changes in participants’ behaviors and strategies in time. Enterprises should use evolutionary thinking and long-term vision to treat every decision in the operation process. Business management is a dynamic process of evolution, rather than a short-term static process. Enterprises seek their own optimal strategic choice in the process of long-term evolutionary game. Finally, various factors that affect the behavior of participants will be taken into account, which is more conducive to the study of the enterprise recycling process in real society, so as to ultimately realize the sustainable development of the closed-loop supply chain.
More complex situations will be presented in future studies. For example, a waste recycling system becomes a multiplayer game when consumers’ recycling intentions and recycling decisions are taken into account. Issues such as the intensity of government participation are also needed further consideration. These are interesting questions that will be investigated in the future.
Author Contributions
B.X.: Conceptualization, Methodology, Data Curation, Validation, Writing—original draft. K.A.: Supervision, Writing—review and editing, Overall revision of the article, Validation. Y.C.: Mathematics Analysis, Software, Visualization, Investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (grant No.: 72031009); the National Social Foundation of China (grant No.: 20BJL135). Key soft science project of science and Technology Department of Henan Province (grant No.: 222400410021). Henan Province Philosophy and Social Science Planning Project (grant No.: 2022CZH015).General research project of Humanities and Social Sciences in Colleges and Universities of Henan Province (Project name is research on game behavior evolution and risk decision making of cross-border e-commerce enterprises in gray market); Henan Province New Liberal Arts Research and Reform Practice Project (Reform and Practice of the Reform and Improvement of Liberal Arts Majors in Local Ordinary Undergraduate Colleges—Taking the National First-Class Undergraduate Majors in E-commerce as an Example).
Data Availability Statement
Data sharing not applicable to this article as no data sets were generated or analyzed during the current study.
Conflicts of Interest
No conflict of interest exists in the submission of this manuscript, and all authors have read and agreed to the published version of the manuscript.
References
- Wang, H.; Han, H.; Liu, T.; Tian, X.; Xu, M.; Wu, Y.; Gu, Y.; Liu, Y.; Zuo, T. “Internet+” recyclable resources: A new recycling mode in China. Resour. Conserv. Recycl. 2018, 134, 44–47. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Lu, H.; Yang, H.; Wang, C. Integrating offline logistics and online system to recycle e-bicycle battery in China. J. Clean. Prod. 2020, 247, 119095. [Google Scholar] [CrossRef]
- Miao, S.; Liu, D.; Ma, J.; Tian, F. System dynamics modelling of mixed recycling mode based on contract: A case study of online and offline recycling of E-waste in China. Math. Comput. Model. Dyn. Syst. 2020, 26, 234–252. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, R.; Shen, L.; Jin, M. Decisions and coordination of green e-commerce supply chain considering green manufacturer’s fairness concerns. Int. J. Prod. Res. 2020, 58, 7471–7489. [Google Scholar] [CrossRef]
- Liu, M.; Li, Z.; Anwar, S.; Zhang, Y. Supply chain carbon emission reductions and coordination when consumers have a strong preference for low-carbon products. Environ. Sci. Pollut. Res. 2021, 28, 19969–19983. [Google Scholar] [CrossRef]
- Guide, V.D.R., Jr.; Van Wassenhove, L.N. Managing product returns for remanufacturing. Prod. Oper. Manag. 2011, 10, 142–155. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Bhattacharya, S.; Van Wassenhove, L.N. Closed-loop supply chain models with product remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Van Wassenhove, L.N. Reverse channel design: The case of competing retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, K.; Zhang, S.; Wang, R.; Wang, H. The door-to-door recycling scheme of household solid wastes in urban areas: A case study from Nagoya, Japan. J. Clean. Prod. 2017, 163, 366–373. [Google Scholar] [CrossRef]
- Chiang, W.K.; Chhajed, D.; Hess, J.D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Shen, L.; Jin, M. Operational modes of E-closed loop supply chain considering platforms’ services. Int. J. Prod. Econ. 2022, 251, 108551. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, L.; Cao, B.; Fan, X. Benefit distribution and stability analysis of enterprises’ technological innovation cooperation alliance. Comput. Ind. Eng. 2021, 161, 107637. [Google Scholar] [CrossRef]
- Petersen, J.A.; McAlister, L.; Reibstein, D.J.; Winer, R.S.; Kumar, V.; Atkinson, G. Choosing the right metrics to maximize profitability and shareholder value. J. Retail. 2009, 85, 95–111. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- Chen, J.H.; Mei, J.X.; Cao, J.J. Decision making of hybrid recycling channels selection for closed-loop supply chain with dominant retailer. Comput. Integr. Manuf. Syst. 2021, 27, 954–964. [Google Scholar]
- Zheng, B.R.; Yang, C.; Yang, J.; Huang, H.J. Product remanufacturing, channel competition and manufacturer encroachment. J. Manag. Sci. 2018, 21, 98–111. [Google Scholar]
- Zheng, B.R.; Yang, C.; Yang, J. Impact of Collection Type on Manufacturer’s Channel Encroachment Strategy. J. Manag. Sci. 2019, 32, 92–105. [Google Scholar]
- Li, Z.; Zhao, J.; Meng, Q. Dual-channel recycling e-waste pricing decision under the impact of recyclers’ loss aversion and consumers’ bargaining power. Environ. Dev. Sustain. 2021, 8, 11697–11720. [Google Scholar] [CrossRef]
- Dhanorkar, S. Environmental benefits of internet-enabled C2C closed-loop supply chains: A quasi-experimental study of Craigslist. Manag. Sci. 2019, 65, 660–680. [Google Scholar] [CrossRef]
- Li, C.; Feng, L.; Luo, S. Strategic introduction of an online recycling channel in the reverse supply chain with a random demand. J. Clean. Prod. 2019, 236, 117683. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, Y. Exploring the strategies of online and offline recycling channels in closed-loop supply chain under government subsidy. Environ. Sci. Pollut. Res. 2022, 29, 21591–21602. [Google Scholar] [CrossRef]
- Song, L.; Yan, Y.; Yao, F. Closed-loop supply chain models considering government subsidy and corporate social responsibility investment. Sustainability 2020, 12, 2045. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, X.; Chen, Z.; Zhong, Y.; Fan, T. Impact of subsidy policies on recycling and remanufacturing using system dynamics methodology: A case of auto parts in China. J. Clean. Prod. 2014, 74, 161–171. [Google Scholar] [CrossRef]
- Sun, M.; Yang, X.; Huisingh, D.; Wang, R.; Wang, Y. Consumer behavior and perspectives concerning spent household battery collection and recycling in China: A case study. J. Clean. Prod. 2015, 107, 775–785. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, J.; Li, B.Y.; Wang, Z. Trade-off between remanufacturing and recycling of WEEE and the environmental implication under the Chinese Fund Policy. J. Clean. Prod. 2017, 167, 97–109. [Google Scholar] [CrossRef]
- Wang, Z.; Huo, J.; Duan, Y. Impact of government subsidies on pricing strategies in reverse supply chains of waste electrical and electronic equipment. Waste Manag. 2019, 95, 440–449. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Zhang, K.; Bai, T.; Shang, J. Reward–penalty mechanism for closed-loop supply chains under responsibility-sharing and different power structures. Int. J. Prod. Econ. 2015, 170, 178–190. [Google Scholar] [CrossRef]
- Wan, N.; Hong, D. The impacts of subsidy policies and transfer pricing policies on the closed-loop supply chain with dual collection channels. J. Clean. Prod. 2019, 224, 881–891. [Google Scholar] [CrossRef]
- Jena, S.K.; Sarmah, S.P.; Padhi, S.S. Impact of government incentive on price competition of closed-loop supply chain systems. Inf. Syst. Oper. Res. 2018, 56, 192–224. [Google Scholar] [CrossRef]
- Mitra, S.; Webster, S. Competition in remanufacturing and the effects of government subsidies. Int. J. Prod. Econ. 2008, 111, 287–298. [Google Scholar] [CrossRef]
- Sheu, J.B. Bargaining framework for competitive green supply chains under governmental financial intervention. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 573–592. [Google Scholar] [CrossRef]
- Ma, W.M.; Zhao, Z.; Ke, H. Dual-channel closed-loop supply chain with government consumption-subsidy. Eur. J. Oper. Res. 2013, 226, 221–227. [Google Scholar] [CrossRef]
- Chen, C.K.; Akmalul’Ulya, M. Analyses of the reward-penalty mechanism in green closed-loop supply chains with product remanufacturing. Int. J. Prod. Econ. 2019, 210, 211–223. [Google Scholar] [CrossRef]
- Hafezalkotob, A. Competition, cooperation, and coopetition of green supply chains under regulations on energy saving levels. Transp. Res. Part E Logist. Transp. Rev. 2017, 97, 228–250. [Google Scholar] [CrossRef]
- Hu, G.; Wang, L.; Chen, Y.; Bidanda, B. An oligopoly model to analyze the market and social welfare for green manufacturing industry. J. Clean. Prod. 2014, 85, 94–103. [Google Scholar] [CrossRef]
- Xie, B.; Li, W.; Zhao, D.; Jiang, P. Effects of network externalities and recycling channels on closed-loop supply chain operation incorporating consumers’ dual preferences. Math. Probl. Eng. 2022, 3, 3347303. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, L.; Chen, Z. Game analysis of access control based on user behavior trust. Information 2019, 10, 132. [Google Scholar] [CrossRef]
- Smith, J.M. Evolution and the Theory of Games. Am. Sci. 1976, 64, 41–45. [Google Scholar]
- Gu, W.; Wei, L.; Zhang, W.; Yan, X. Evolutionary game analysis of cooperation between natural resource-and energy-intensive companies in reverse logistics operations. Int. J. Prod. Econ. 2019, 218, 159–169. [Google Scholar] [CrossRef]
- Han, F.X.; Xiao, H.J.; Peng, D.H.; Huo, S.Y. Development motive investigation of green finance under the new normal economy—Based on a three-party game among the government, bank and enterprises. Rev. Econ. Manag. 2017, 33, 88–94. [Google Scholar]
- Liu, M.; Hao, L. Research on evolutionary game strategies of participants from the perspective of green development. Mod. Manag. 2018, 5, 95–98. [Google Scholar]
- Cui, H.; Wang, R.; Wang, H. An evolutionary analysis of green finance sustainability based on multi-agent game. J. Clean. Prod. 2020, 269, 121799. [Google Scholar] [CrossRef]
- Zhao, D.; Hao, J.; Cao, C.; Han, H. Evolutionary game analysis of three-player for low-carbon production capacity sharing. Sustainability 2019, 11, 2996. [Google Scholar] [CrossRef]
- Li, C.; Zhang, F.; Cao, C.; Liu, Y.; Qu, T. Organizational coordination in sustainable humanitarian supply chain: An evolutionary game approach. J. Clean. Prod. 2019, 219, 291–303. [Google Scholar] [CrossRef]
- Lin, D.Y.; Juan, C.J.; Ng, M. Evaluation of green strategies in maritime liner shipping using evolutionary game theory. J. Clean. Prod. 2021, 279, 32–68. [Google Scholar] [CrossRef]
- Shu, Y.; Dai, Y.; Ma, Z. Evolutionary game theory analysis of supply chain with fairness concerns of retailers. J. Ind. Manag. Optim. 2022, 18, 1–29. [Google Scholar] [CrossRef]
- Hosseini-Motlagh, S.M.; Choi, T.M.; Johari, M.; Nouri-Harzvili, M. A profit surplus distribution mechanism for supply chain coordination: An evolutionary game-theoretic analysis. Eur. J. Oper. Res. 2022, 301, 561–575. [Google Scholar] [CrossRef]
- Hu, H.; Li, Y.; Tian, M.; Cai, X. Evolutionary game of small and medium-sized enterprises’ accounts-receivable pledge financing in the supply chain. Systems 2022, 10, 21. [Google Scholar] [CrossRef]
- Zhi, B.; Liu, X.; Chen, J.; Jia, F. Collaborative carbon emission reduction in supply chains: An evolutionary game-theoretic study. Manag. Decis. 2019, 57, 1087–1107. [Google Scholar] [CrossRef]
- Lyapunov, A.M. The general problem of the stability of motion. Int. J. Control 1992, 55, 531–534. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bertram, J.E. Control system analysis and design via the second method of lyapunov: (I) continuous-time systems (II) discrete time systems. IRE Trans. Autom. Control 1960, 4, 112. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Wake, G.C. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl. Math. Lett. 2002, 15, 955–960. [Google Scholar] [CrossRef]
- Araujo, R.A.; Moreira, H.N. Lyapunov stability in an evolutionary game theory model of the labour market. EconomiA 2014, 15, 41–53. [Google Scholar] [CrossRef]
- Selten, R. A note on evolutionarily stable strategies in asymmetric animal conflicts. J. Theor. Biol. 1980, 84, 93–101. [Google Scholar] [CrossRef]
- Li, F.; Qian, X.; Kong, J.; Luo, Z. Evolutionary Game Analysis of Information Sharing Among Closed-loop Supply Chain Members in Cloud Environment. Arab. J. Sci. Eng. 2022, 47, 3945–3961. [Google Scholar] [CrossRef]
- Selten, R. Evolutionary stability in extensive two-person games. Math. Soc. Sci. 1983, 5, 269–363. [Google Scholar] [CrossRef]
Figure 1.
O2O recycling system.
Figure 1.
O2O recycling system.
Figure 2.
Decision framework for players in game.
Figure 2.
Decision framework for players in game.
Figure 3.
Phase diagram of Theorem 1. (Note: The direction of the arrow in the figure represents the evolution path of the strategies, and the intersection of all lines indicates the evolution stability strategy (ESS)).
Figure 3.
Phase diagram of Theorem 1. (Note: The direction of the arrow in the figure represents the evolution path of the strategies, and the intersection of all lines indicates the evolution stability strategy (ESS)).
Figure 4.
Phase diagram of Theorem 2. (Note: The direction of the arrow in the figure represents the evolution path of the strategies, and the intersection of all lines indicates the evolution stability strategy (ESS)).
Figure 4.
Phase diagram of Theorem 2. (Note: The direction of the arrow in the figure represents the evolution path of the strategies, and the intersection of all lines indicates the evolution stability strategy (ESS)).
Figure 5.
Phase diagram of Theorem 3. (Note: The direction of the arrow in the figure represents the evolution path of the strategies, and the intersection of all lines indicates the evolution stability strategy (ESS)).
Figure 5.
Phase diagram of Theorem 3. (Note: The direction of the arrow in the figure represents the evolution path of the strategies, and the intersection of all lines indicates the evolution stability strategy (ESS)).
Figure 6.
Equilibrium Point of Case 1.
Figure 6.
Equilibrium Point of Case 1.
Figure 7.
Equilibrium Point of Case 2.
Figure 7.
Equilibrium Point of Case 2.
Figure 8.
Equilibrium Point of Case 3.
Figure 8.
Equilibrium Point of Case 3.
Figure 9.
Impacts of changes in government subsidies: (a) Case 1 and (b) Case 2.
Figure 9.
Impacts of changes in government subsidies: (a) Case 1 and (b) Case 2.
Figure 10.
Impacts of changes in advertising: (a) Case 1 and (b) Case 2.
Figure 10.
Impacts of changes in advertising: (a) Case 1 and (b) Case 2.
Figure 11.
Impacts of changes in tax coefficient: (a) Case 1 and (b) Case 2.
Figure 11.
Impacts of changes in tax coefficient: (a) Case 1 and (b) Case 2.
Figure 12.
Impacts of changes in liquidated damages: (a) Case 1 and (b) Case 2.
Figure 12.
Impacts of changes in liquidated damages: (a) Case 1 and (b) Case 2.
Table 1.
The summary of literature and factors addressed by our study.
Table 1.
The summary of literature and factors addressed by our study.
| Literatures | Closed-Loop Supply Chain | Cooperation for Online and Offline | Waste Products Recovery | Evolutionary Game | Government Participation |
|---|
| [40] | | | | √ | √ |
| [41] | √ | | | √ | |
| [37] | √ | | √ | | √ |
| [39] | √ | | √ | √ | |
| [43] | | | | √ | |
| [44] | √ | √ | √ | | |
| [49] | √ | | | √ | √ |
| [42] | | | | √ | √ |
| [45] | | | | √ | |
| [46] | | | | √ | |
| [36] | √ | √ | √ | | |
| [48] | | | | √ | |
| [47] | | | | √ | |
| Our study | √ | √ | √ | √ | √ |
Table 2.
Government “participate” in recycling system.
Table 2.
Government “participate” in recycling system.
| | P |
|---|
| Cooperate | No-Cooperate |
|---|
| M | Cooperate | | |
| + V |
| |
| No-cooperate | | + |
| |
| |
Table 3.
Government “no-participate” in recycling system.
Table 3.
Government “no-participate” in recycling system.
| | P |
|---|
| Cooperate | No-Cooperate |
|---|
| M | Cooperate | | |
| |
| |
| No-cooperate | | |
| |
| |
Table 4.
The eigenvalues of Jacobian matrix at different equilibrium points.
Table 4.
The eigenvalues of Jacobian matrix at different equilibrium points.
| Equilibrium | | | |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Table 5.
The stability of the equilibrium point.
Table 5.
The stability of the equilibrium point.
| Equilibrium | Case 1 | Case 2 | Case 3 |
|---|
| Stability | | Stability | | Stability |
|---|
| | Saddle point | | Unstable point | | Unstable point |
| | Unstable point | | Saddle point | | Saddle point |
| | Unstable point | | Saddle point | | Saddle point |
| | Unstable point | | Unstable point | | Unstable point |
| | Unstable point | | ESS | | Unstable point |
| | Unstable point | | Unstable point | | Unstable point |
| | Unstable point | | Unstable point | | Unstable point |
| | ESS | | ESS | | ESS |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).