Abstract
Multi-criteria decision-making (MCDM) issues related to hydrogen energy usually involve weight consideration of evaluation criteria, ambiguous evaluation information provided by experts, and lacking or incomplete evaluation information. Conventionally, the MCDM calculation method cannot effectively and simultaneously process evaluation information. To effectively address this issue, this study proposed a novel general data envelopment analysis (DEA)-based approach for MCDM issues of hydrogen energy under a fuzzy environment. The proposed general DEA-based approach integrates the typical DEA method, analytic hierarchy process (AHP) method, hesitant fuzzy linguistic term set (HFLTS), and the soft set to process the MCDM problems under a fuzzy environment. For the numerical verification, this study used the case of hydrogen energy key technologies ranking, as an important development reference for carbon reduction to further verify the correctness and reasonableness of the proposed approach. The calculation results were also compared with those from the typical DEA method, typical AHP/DEA method, and the fuzzy AHP/DEA method. The numerical verification results show that the proposed method can effectively process the MCDM problems under a fuzzy environment than listing different calculation methods.
1. Introduction
Different evaluation criteria may be of conflicting nature; thus, multi-criteria decision-making (MCDM) is a complex and difficult process. The MCDM is an important technique and a branch of operations research used for finding optimal outcomes in complex scenarios with various metrics and conflicting goals and criteria [1]. MCDM can help the decision maker based on their preferences in situations of multiple conflicting criteria. Therefore, many scholars continue to develop new methods to solve problems in different application fields, such as supply chain management [2], civil engineering and infrastructure [3], transport and logistics [4], energy [5], high-dose-rate brachytherapy treatments [6], naval aircraft selection [7], and so on. The computational logic of operations research assists decision-makers in the subjective assessment of alternatives under multiple criteria by designing mathematical models and computational tools [8,9]. With the evolution of the times and the advancement of science and technology, MCDM involves a variety of methodological studies. For example, the data envelopment analysis (DEA) approach is one of the frequently used nonparametric MCDM evaluation approaches. It was initially proposed by Charnes et al. [10] by measuring the similar relative efficiency performance of decision-making units (DMUs) by simultaneously integrating multi-output and -input. The DEA method can effectively measure the relative efficiency of DMUs and solve many decision-making problems. Since its first use in 1979, this approach has received more research attention increasingly and has been widely used in many fields. For the problem handling of the hierarchical structure, the analytic hierarchy process (AHP) method that can effectively handle the weight consideration of evaluation criteria was first presented by Saaty [11], who used the pairwise comparisons among criteria and alternatives to deal with the qualitative and quantitative information in the decision-making procedure. AHP method, modeled as a hierarchical structure, divides a large problem into small and easy-to-resolve problems. Relevant development of the MCDM calculus method is still in the growth stage, such as the preference ranking organization method for enrichment evaluation (PROMETHEE) [12,13], the visekriterijumska optimizacija i kompromisno resenje, the technique for order preference by similarity to ideal solution (TOPSIS), and the elimination and choice translating reality (ELECTRE), and so on. However, the MCDM issues for obtaining hydrogen energy usually involve the evaluation of weight criteria. The evaluation information provided by experts for ambiguous or incomplete information situations cause difficulties in decision evaluation.
In a real-world situation, because uncertainty and fuzziness usually exist in human judgment, a decision has to be made in situations when pertinent data are not precisely known. Therefore, people or decision makers are more inclined to evaluate language through natural language expressions rather than using precise numerical values. Zadeh [14] introduced the concept of a fuzzy set to deal with ambiguous situations. The advantage of a fuzzy set is that it uses fuzzy numbers instead of crisp numbers to express the relative importance of alternatives and criteria. Many research methods are integrated with the fuzzy set to deal with practical issues for various fields, such as group decision-making [15], risk assessment [16,17], supplier evaluation [18], location selection [19], and supplier selection [20,21,22], and so on. To deal with the MCDM problem, many levels and factors need to be considered and require the participation of relevant experts from different backgrounds and fields, such as chemistry, engineering, energy, and environmental protection. Experts in different fields may be unable to make correct judgments or provide advice under unfamiliar situations, which simultaneously includes complete, incomplete, or hesitant information. Rodriguez et al. [23] first proposed the hesitant fuzzy linguistic term set (HFLTS) to deal with hesitant information for MCDM problems. The HFLTS combines the concept of the fuzzy linguistic approach and the hesitant fuzzy set to represent the hesitant information of the experts and uses different linguistic terms to estimate a linguistic variable instead of using single terms. Since then, many studies in various fields have explored related issues of HFLTS information. In the questionnaire survey and collection process, an incomplete questionnaire is regarded as an invalid questionnaire; it may lead to the loss of some valuable information provided by professional experts, resulting in biased solution results. Molodtsov [24] proposed the soft set theory, which uses the concept of supplementary information to deal with incomplete questionnaires, making invalid questionnaires into usable ones. Under this method, all key information in the questionnaire can be considered, and no valuable information is lost.
In recent years, many major developing countries have proposed to formulate carbon reduction policies and technologies. Hydrogen only produces water after the reaction and does not emit carbon dioxide, and the technology to manufacture low (zero) carbon has gradually matured, therefore hydrogen is considered as an important energy storage carrier that can take full advantage of renewable and sustainable energy sources [25]. Under the global trend of green energy and environmental protection, hydrogen energy is regarded as an important key to achieve the goal of net zero carbon emissions, which also becomes a new project developed by major countries. However, a wide range of aspects needs to be considered in the development of new energy and renewable energy technologies, such as the country’s economic aspects, commercial potential, the internal research and development (R&D) capabilities, development costs, etc. Moreover, hydrogen energy research and development require a huge resource investment. When resource is limited, it is critical to find a potential approach to make the best profits out of investing in hydrogen energy technology (HET) development and long-term hydrogen economy development.
Obtaining hydrogen energy via MCDM usually involves the evaluation of weight criteria. The evaluation information provided by experts is sometimes ambiguous or incomplete, which causes difficulties in decision evaluation. Therefore, the evaluation of HET is considered a complex MCDM problem. Recently, Lee et al. [26] proposed a two-phase MCDM method, which includes the DEA approach and fuzzy AHP method, to evaluate the relative efficiency of HET. Although Lee et al.’s method can handle complicated HET evaluation problems under a complete information environment, their method could not consider hesitant and non-existent information and will thus lose some important information during the solution process, incur subjective conditions, and bias of solution result. To overcome these situations under a fuzzy environment, this study proposed a novel fuzzy AHP/DEA method that integrates soft set and HFLTS. The proposed method can fully consider available information, improve the performance of energy technology, increase the output of hydrogen energy, effectively reduce the input of costs, and scientifically implement the hydrogen energy economy.
This study is arranged in sections as follows. Section 2 presents some concepts and fundamental definitions related to the DEA method, fuzzy AHP method, soft set, and HFLTS. Section 3 proposes the novel, soft DEA-based approach for solving the efficiency of HET. Section 4 presents the numerical examples of HET and discusses the comparison of solutions obtained with other related methods. Finally, Section 5 presents the conclusion and suggestions.
2. Preliminary Knowledge
2.1. The Data Envelopment Analysis (DEA) Method
The DEA method was initially proposed by Charnes [10] to evaluate the relative efficiency of a group of DMUs, including single-input-single-output, single-input-multiple-output, or multiple-input-and-output. Because the DEA method can effectively measure the relative efficiency of DMUs as well as solve many decision-making problems, this approach has received more research attention increasingly and has been widely used in many fields. For example, Okur and Ercan [27] built a comprehensive efficiency evaluation approach that combined the DEA method and the AHP method to measure efficiency in the apparel retail industry. The named approach can determine the priority areas that need focus and alert managers to adopt new strategic actions for increasing the performance of apparel retailers. Peng et al. [28] combined the DEA and TOPSIS methods to establish a green material index system; poorer-performing materials can be screened and excluded for classifying suitable suppliers. Halkos and Argyropoulou [29] proposed a two-stage DEA method, the first stage input variables include energy consumption, capital, and labor, and the second stage input variables include sulfur dioxide and GDP, considering respiratory deaths as the final output, estimated the highest overall efficiency in terms of energy and air pollution damage to the health of the population of 23 countries over the period of 1990-2017. The DEA method has been applied in many fields, such as tourism [30], dredging productivity assessment [31], portfolio selection [32], chemical enterprises safety assessment [33], and so on.
The Charnes-Cooper-Rhodes (CCR) model is the standard model of the DEA method and is described below [10,34]:
where and are number of inputs i and output r for the jth observed DMU; m is the number of inputs, and s is the number of outputs; and are the weight to be determined by the jth input and output; n is the number of DMUs.
2.2. The Fuzzy AHP Method
The fuzzy AHP method combines the concept of a fuzzy set and the AHP approach to perform the MCDM evaluation. The AHP method was initially introduced by Saaty [11] to handle complex decision-making problems with a hierarchical structure while considering and processing both factual (objective or quantitative) as well as judgmental (subjective or qualitative) information. It uses judgment comparison of the score of each criterion from expert knowledge, determines the relative importance between criteria, and finds the best alternative for efficiently handling the decision-making issues. Since then, the AHP method has been widely applied in many fields; for instance, Huang et al. [35] combined the cloud model with the AHP method and considered the quantitative and qualitative influencing factors from the search, rescue, and medical treatment after an earthquake, to construct the performance evaluation index system, which can effectively optimize the rescue process. Cheemakurthy and Garme [36] combined the fuzzy AHP method and particle swarm optimization to develop a structure for evaluating the ferries’ operational requirements and use it as a ferry to assess the basis of the approach. Related research using the AHP method has been used in many fields, such as human resource management [37], tourism factory contractor selection [38], code recommendation system [39], training simulation systems [40], and so on. While typical AHP methods can solve problems systematically, they cannot handle the fuzzy information provided by experts. Thus, to remove such drawbacks of AHP, the fuzzy set is employed with the AHP method. Zadeh [14] proposed fuzzy sets to handle fuzzy and uncertain information, using fuzzy logic to process the uncertainty of decision-making factors. Among the existing techniques, the geometric mean approach presented by Buckley [41] and the extent analysis approach presented by Chang [42] are widely used by researchers. In this study, we applied the extent analysis approach and the triangular fuzzy numbers (TFNs) to calculate the fuzzy weight. The calculation and definition related to the TFNs are shown as follows:
Definition 1 [14].
Consider and are two TFN, the operational laws of addition, subtraction, and reciprocal as follows:
Definition 2 [26,43].
Assume be a fuzzy pairwise comparison matrix, and let be a TFN value, the value of the fuzzy composition range with respect to the ith object is defined as
Definition 3 [26,43].
The values of were compared, and the possibility degree was calculated as, .
where d is the ordinate of the highest point of intersection between and , and compare and via the values of and . The minimum possibility degree of , and the possibility degree of fuzzy number can be defined by:
Definition 4 [26,43].
Assume that , for i = 1, 2, 3, …, n. The weight is defined in Equation (9), where are the n elements, and the weight vectors W (non-fuzzy number) were normalized as follows:
The fuzzy AHP method procedure is as follows.
Step 1: Make a pairwise comparison based on a fuzzy scale.
Let be a fuzzy pairwise comparison judgments matrix, let be a TFN, and the fuzzy scale (Table 1) is used to perform pairwise comparisons between the assessment factors [44].

Table 1.
The triangular fuzzy scale of pairwise comparison.
Step 2: Defuzzify the TFN value.
To compare the respective TFNs, the center of area (COA) defuzzification method [45] is applied. According to Equation (12) to defuzzify the TFN value, shown as .
Step 3: Calculate the consistency ratio (CR)
To check the consistency of expert assessment opinions, the CR and consistency index (CI) were calculated according to the aggregated value of TFN in step 2, as shown in Equations (13)–(15).
where is the largest eigenvector of the fuzzy pairwise comparison matrix A, and n is the size of the pairwise matrix. The random index (RI) value is based on the different matrix sizes, as shown in Table 2 [11].

Table 2.
RI value for different matrix sizes.
Step 4: Rank alternatives based on their optimal weight calculation
After multiplying the weight of each evaluation criterion obtained in step 3 by each alternative, they are ranked from high to low according to the alternative weighted score result.
2.3. The Hesitant Fuzzy Linguistic Term Set (HFLTS)
Rodriguez et al. [23] developed a concept that uses a set of possible linguistic terms to represent the hesitation of the experts to deal with hesitant information in group decision-making issues. Since then, many studies in various fields have explored related issues of HFLTS information. For example, Chang [46] proposed a method that integrated soft set and HFLTS to select suitable liquid crystal display (LCD) module suppliers in the supply chain. Guo et al. [12] proposed a two-stage approach to select the proper location of floating photovoltaic power plants. They used relative entropy to compute the weight of the decision-makers in the first phase and adopted an improved hesitant fuzzy linguistic DEMATEL-PROMETHEE method to rank alternatives in the second phase. The research result can contribute to site selection and sustainable development of floating photovoltaic power plants. Wang et al. [47] presented a group decision-making approach to assessing instructional performance in a hesitant fuzzy linguistic environment, applying proportional HFLTS to express decision-maker preferences. The Chinese Foreign Cooperative Education Project proved that the teaching performance evaluation is more scientific, objective, and accurate, and the teaching quality is improved. The HFLTS has also been used to deal with decision-making issues in many fields, such as judicial execution [48], occupational safety risk assessment [49], new service development analysis [50], water pollution treatment technology [51], enterprises decision [52], reliability engineering [53,54], and hotel selection of travelers [55], and so on.
Some basic properties and operations of HFLTS are described below.
Definition 5 [56].
Let be a linguistic term set (LTS). For example, if . A HFLTS , is an ordered finite subset of continuous linguistic terms of S.
Definition 6 [23,53].
Let be an LTS. is an arbitrary hesitant LTS of S. The lower and upper bounds of the hesitant LTS are defined as follows:
Definition 7 [23,54].
The envelope of HFLTS , named as , is the linguistic interval between the lower and upper bounds :
Definition 8 [46].
Assume l is the left limit value of the interval and u is the right limit value of the interval. Defuzzification of the hesitant fuzzy information (HFI) () by arithmetic mean are defined as follows:
2.4. The Soft Set
Molodtsov [24] introduced a novel mathematical method called the soft set method, which can deal with the related problems of uncertain data and ambiguous data, fully consider all key information in the questionnaire, not lose valuable information, and make invalid questionnaires usable ones. The soft set-related studies include Bind and Isaac [57] proposed a decision-making framework that used two single-valued neutrosophic soft sets and introduced a weighted similarity measure; they applied this framework to the clinical application of evaluating certain medical parameters, identified the best type of radiotherapy treatment for tumors in moving organs (such as lungs or chest walls) and demonstrated the feasibility of this decision-making framework. Chang [13] proposed a selection technique for dealing with incomplete information, which combines the concept of the PROMETHEE II method and the soft sets to select suitable contractors among non-existent or missing data during the evaluation process. In addition to the above applications, the soft set is also widely used in many fields, such as decision-making problems [58], network communication [59], supply chain management [60], and so on. The soft set method is defined as follows: let U refer to a universe of discourse, E be a set of parameters related to the objects in U, the set P(U) be the power set of U and O ⊆ E, and M, N are non-empty subsets of E.
Definition 9 [24,61].
Assume that a pair (F, M) is called a soft set U, where F is a mapping given by F: M → P(U). A soft set over U is a series of parameterized subsets of universe U.
Definition 10 [24,62].
Let two soft sets (F, M) and (G, N) be on a common universal set U, and (F, M) be the intersection of (G, N), represented by (H, O), if
Definition 11 [40,62].
Let two soft sets (F, M) and (G, N) be on a common universal set U, the union of (F, M) and (G, N) is represented by (H, O), then the following conditions are satisfied:
3. Methodology
3.1. The Planning of the Research Method
As the world gradually pays attention to the trend of green energy and environmental protection, many major developing countries have successively put forward long-term plans for zero carbon emissions and proposed the development of carbon emission reduction policies and technologies. Under the global trend of green energy and environmental protection, hydrogen energy is regarded as an important key to achieve the goal of net zero carbon emissions; it is becoming a new project developed by major countries. However, hydrogen energy research and development require a huge resource investment. Finding the approach to make the best profit out of investing in HET development under limited resources is a critical issue in the long-term development of the hydrogen economy. However, because the experts have different experiences and backgrounds, they may give ambiguous information, partially hesitant information, or partially uncertain information about the factors to be assessed. The traditional research methods for solving MCDM problems cannot simultaneously deal with ambiguous information, hesitant information, or uncertain information provided by experts at the same time. Usually, the above information is eliminated, which often results in the loss of important information. In addition, the weight consideration of the evaluation criteria affects the main results of the energy technology evaluation. To solve the above issues, this paper proposed a general DEA-based method that integrates the fuzzy AHP method, HFLTS, and soft set to solve the relative efficiency issues of energy technology evaluation. The DEA method used the best practice production frontier to evaluate the relative efficiency of a DMU by multiple inputs and outputs; besides, the fuzzy AHP method can not only adopt a hierarchical structure, considering both qualitative and quantitative information but also deal with ambiguous situations, then use the TFN calculation to obtain the objectively reasonable weights of criteria. Besides, both HFLTS and soft set can fully consider hesitant information and handle incomplete information provided by experts, without losing any valuable information.
3.2. The Research Procedure
In this study, the general DEA-based approach addressed and evaluated the relative efficiency of DMUs for the MCDM problem, consisting of seven steps, and the flow chart is shown in Figure 1.
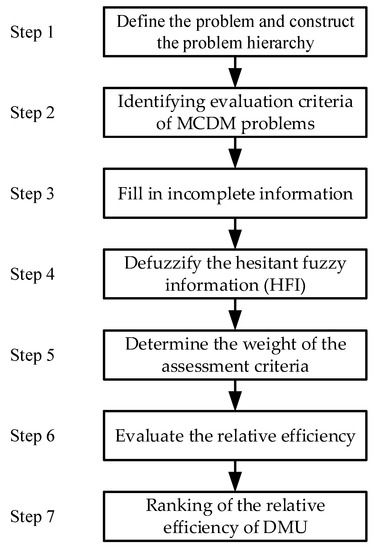
Figure 1.
The flow chart of the proposed general DEA-based approach.
- Step 1.
- Define the problem and construct the problem hierarchy.
This involves analysis of the decision-making environment, organizing a committee to define the problem for the MCDM problem, conducting hierarchical analysis to facilitate understanding of the evaluation criteria, and looking for an alternative to be used to achieve the goal.
- Step 2.
- Identifying evaluation criteria of MCDM problems.
This involves constructing and determining the evaluation criteria for the MCDM problem, listing these criteria under a hierarchical structure, and conducting a questionnaire with experts. It is helpful for subsequent analysis of the efficiency of the DMU for the MCDM problem.
- Step 3.
- Fill in incomplete information.
To overcome the condition that incomplete information must be deleted directly during the traditional data collection approach, the soft set concept from Section 2.4 was used to handle evaluation criteria scores containing incomplete or nonexistent information, and other known information was averaged, and then the incomplete information is filled.
- Step 4.
- Defuzzify the HFI.
Focusing on the part containing HFI provided by experts during the questionnaire procedure, used the Equation (19) to defuzzify the HFI.
- Step 5.
- Determine the weight of the assessment criteria.
Equation (19) is used to defuzzify the TFN value convert into the exact value in the comparison matrix of criteria; then the AHP method is applied to assess the relative priorities of criteria through Equations (13)–(15) to calculate the CR value. Confirming that the information provided by the experts meets the consistency standard (CR < 0.1), and the weight value of criteria according to the weight calculation is determined.
- Step 6.
- Evaluate the relative efficiency.
The weight value of each criterion obtained in step 5 is multiplied by the score value of each DMU; then, the DEA-based approach is applied to measure the relative efficiency of DMU in the MCDM problem through the output to input ratio.
- Step 7.
- Ranking of the relative efficiency of DMU.
According to the solution results in step 6, the efficiency of DMU is sorted from large to small, and the relative efficiency of DMU is analyzed to provide the best suggestion for decision makers.
4. Numerical Analysis
4.1. Overview
Green energy is the most critical issue for environmental protection, renewable energy, and the effective use of limited energy. Hydrogen has the characteristic of producing only water after the reaction and does not release carbon dioxide. It has also become an important development technology for carbon reduction. The related issues of energy technology include several assessment criteria and involve qualitative and quantitative information, belonging to the complex group MCDM problems to evaluate energy performance, it is necessary to invite experts from related fields such as academic, management, or industrial, to discuss and ensure that the assessment results are correct and reasonable. However, for developing the technology, many factors need to be considered; it can thus be regarded as a complex group MCDM problem.
To verify the correctness and applicability of the method proposed in this paper, this section gives an illustrative case of the HET [26]. The case of HET for a hydrogen economy comprised of four criteria, including economic impact (EI), business potential (BP), inner ability (IA), and technology derivatives (TD). Thirteen technologies included natural gas hydrogen production technology (T1), thermochemical hydrogen production technology (T2), water electrolysis hydrogen production technology (T3), solid chemical storage technology (T4), high purity hydrogen separation technology (T5), portable fuel cell technology (T6), fuel cell vehicle technology (T7), home/industry system technology (T8), micro fuel cell technology (T9), fuel cell technology for laptops (T10), portable power fuel cell technology (T11), power generation fuel cell technology (T12), and home/APU fuel cell technology (T13). The consultant committee of HET development comprised five experts (Expert 1, Expert 2, Expert 3, Expert 4, and Expert 5) who provided scores of fuzzy evaluations of the goal for a hydrogen economy, as shown in Table 3. The evaluation scores of thirteen outputs (energy technology), the data of single input (development cost, DC), and the currency exchange rate unit (mil.KRW) are presented in Table 4.

Table 3.
Fuzzy evaluation scores of the criteria for a hydrogen economy.

Table 4.
Evaluation score of output and the development cost of input.
4.2. Application of DEA Approach
In the typical DEA method [63], the weight of DMU is usually determined by the subjective consciousness of experts. In this section, equal weights are adopted so that the weights of EI, BP, IA, and TD are all 0.25. Then, multiplied by the average mean of output evaluation score of Table 4, since the typical DEA method only can handle the exact data during the solution procedure, the information provided by Experts 4 and 5, including hesitant and non-existent information, is deleted, only the complete information from Experts 1–3 can be used to calculate as an average value. The obtained data about 4 outputs and 1 input as shown in Table 5, the calculation of DEA is continued, and the efficiency score and ranking are also shown in Table 5.

Table 5.
Relative efficiency score and rank of HET by the typical DEA method.
4.3. Application of Typical Analytic Hierarchy Process/Data Envelopment Analysis (AHP/DEA) Method
The typical AHP method can systematically solve problems with a multi-level and hierarchical structure that contain both qualitative and quantitative elements, making it an effective tool for handling complex decisions. Extending the concept of the AHP method, the typical AHP/DEA method [64] used the AHP method for the weight calculation and utilized the DEA method to determine the efficiency of DMU. However, the typical AHP/DEA method cannot deal with the hesitant and incomplete information issues. During information processing (Table 3 and Table 4), because Experts 4 and 5 provided partially incomplete information and hesitant information, these decisions cannot be handled by the typical AHP/DEA method. Thus, the information from Experts 4 and 5 should be eliminated, and complete information provided by Experts 1–3 should be used to calculate the criteria weight by the typical AHP/DEA method; the solution procedure was as follows:
According to the Table 3 and Equations (13)–(15) to calculate the CR values, the solution process of the consistency test is shown below:
After checking that the CR value < 0.1 in the consistency test, the judgments were determined to be acceptable. Then, based on information provided by Experts 1–3 in Table 3 to perform the weight calculation, the results indicated that EI, BP, and IA had the most important weight value at 0.262, followed by the weights of TD at 0.224.
The typical DEA method has the limitation that it cannot deal with incomplete data. In Table 4, only the complete information of Experts 1–3 was used for calculation. Then, the weight value obtained above was multiplied by the mean value from Experts 1–3 to obtain data of four outputs and one input; as shown in Table 6, the calculation of DEA is continued, then the efficiency of DMU and the efficiency score and rank were determined, as shown in Table 6.

Table 6.
Relative efficiency score and rank of HET by the typical AHP/DEA method.
4.4. Application of the Fuzzy Analytic Hierarchy Process/Data Envelopment Analysis Method
The advantages of the typical AHP/DEA approach are that it can acquire expert knowledge by preference, analyze qualitative criteria to measure alternatives, and effectively evaluate the relative efficiency of DMUs (alternatives). However, during the data collection process, hesitant information may occur due to inconsistent attitudes or different preferences among experts regarding measurement scales. A typical AHP method would delete the partially hesitant information during the calculation procedure, causing some important information to be ignored. To handle the HFI, Kumar et al. [43] proposed the fuzzy AHP/DEA method to effectively solve the limits of the typical AHP/DEA method. The fuzzy AHP method reflects the ambiguity of human thinking with interval values, and TFNs are often used to estimate the ambiguity of parameters related to options. TFNs are represented by boundaries rather than clear numbers to reflect the ambiguity of decision makers when choosing alternatives or comparison of criteria. The definition of fuzzy AHP/DEA and its solution process are described herein.
According to the fuzzy evaluation matrix of Table 3, Equations (4)–(7) from Definition 2 were used to calculate the TFNs value of the four criteria , and the results are shown in Table 7.

Table 7.
The fuzzy pairwise comparison matrix of assessment criteria.
Table 7 and Equation (8) of Definition 3 were used to calculate the possibility degree. Then, Equation (9) was used to calculate the minimum possibility degree, the result of the calculation is shown in Table 8.

Table 8.
The values of .
According to Table 8 and Definition 4, the weight vector was determined by using Equations (10) and (11). After determining the weight of the four criteria, the calculation results indicated that EI, BP, and IA had the most important weight value at 0.257, followed by the weights of TD at 0.229.
The DEA method cannot handle information, including partially hesitant and nonexistent information. Therefore, referring to Section 4.3, average scores are provided by Experts 1–3 and the weight value calculated from the fuzzy AHP method is multiplied, and the result is shown in Table 9. Then, the efficiency of DMU is calculated by the DEA method; the DMU numerical results and ranking are shown in Table 9.

Table 9.
Relative efficiency score and rank of HET by the fuzzy AHP/DEA method.
4.5. Application of the Proposed Method
In recent years, HET has become an important development technology for carbon reduction. However, because several factors need to be considered for technology research and development, this requires the input of relevant experts from different backgrounds and various fields, such as chemistry, engineering, energy, environmental protection, etc. Moreover, experts in different fields may not be able to make correct judgments or provide advice under unfamiliar situations, which usually results in hesitant or nonexistent information. Traditional data collection procedures remove any ambiguous or incomplete information, which may cause the bias assessments. To overcome these issues, this paper presents the extended AHP/DEA method combined with the soft set and HFLTS to deal with the issue of HET, using the following steps:
- Step 1 and Step 2.
- Organize a committee to construct and determine the evaluation criteria for HET
First, the organizing committee determines the criteria for achieving the goals of the hydrogen economy and implements a questionnaire.
- Step 3.
- Fill in incomplete information
As shown in Table 3, in the case when Expert 4 does not understand the criteria relationship between EI and BP, Expert 4 may not be able to give a clear score. The incomplete information will be deleted directly in the traditional data collection method and lead to the loss of some important information. To overcome these conditions, this study used the concept of a soft set from Section 2.4 to average the other known information and fill in the incomplete information.
- Step 4.
- Defuzzify the hesitant fuzzy information
As shown in Table 3, Expert 5 gave a hesitant score because of his different preferences or inconsistent attitudes regarding the scale of the evaluation. Typically, solving such an approach will remove some hesitant information provided by Expert 5 during the calculation process, causing some important information to be ignored. To deal with the HFI, this study used Equation (19) to defuzzify the HFI, the calculation results as shown in Table 10.

Table 10.
Relative efficiency score and rank by the proposed DEA-based method.
- Step 5.
- Determine the weight of the evaluation criteria
According to Table 3, Equation (12) was used to defuzzy TFNs and convert them to exact values. For example, if Expert 2 gives TFNs a score of (2/3, 1, 3/2) at BP for EI, then after the defuzzification calculation by the COA approach, the value is 1.056.
A pairwise comparison matrix of a single value was converted through the process of defuzzification. Based on Table 3, Equations (13)–(15) were to calculate , then the calculation of the CI value was obtained. The calculation results showed that the CR value was 0.081, which met the consistency standard (CR < 0.1), confirming the consistency of the information provided by the experts.
The calculated results showed that EI had the most important weight value at 0.299, followed by the weights of BP, IA, and TD at 0.288, 0.236, and 0.177, respectively.
- Step 6 and Step 7.
- Evaluation and ranking of the relative efficiency of DMUs
4.6. Comparison and Discussion
This study summarizes the results of numerical analysis among various methods to demonstrate the efficiency and correct the proposed novel DEA-based method, as shown in Table 11. From Table 11, we find that the typical DEA method, AHP/DEA method, and fuzzy AHP/DEA method ignored the information provided by Experts 4 and 5; hence, their solution results and ranking are not much different. The proposed DEA-based method can fully consider all of the information provided by experts; it can efficiently distinguish the efficiency and ranking of various HET. The main differences between the four calculation methods, as shown in Table 11 and Table 12, are as follows.

Table 11.
Comparison of solutions among various methods.

Table 12.
Differences in solution characteristics between the three calculation methods.
- (1)
- Consider the relative weight of the criteria. Since typical DEA methods assume equal weights of criteria, it is difficult to distinguish the importance of each criterion efficiently. On the other hand, the AHP/DEA method, fuzzy AHP/DEA method, and the proposed novel DEA-based method used the AHP method to full consideration the relative weight of HET criteria.
- (2)
- Consistency test of information provided by experts. The typical DEA method and the fuzzy AHP/DEA method cannot handle the consistency test of information provided by experts. The AHP/DEA method and the proposed novel DEA-based method can handle consistency tests of information provided by experts.
- (3)
- Handling of incomplete information. The typical DEA method, the AHP/DEA method, and the fuzzy AHP/DEA method cannot handle incomplete information provided by experts. When processing questionnaire information, as long as there is incomplete information in the questionnaire, it is usually regarded as invalid and discarded. Since the information provided by Experts 4 and 5 includes hesitant or nonexistent information, it is deleted during the solution process and will possibly ignore important information provided by some experts, resulting in biased and unobjective calculation results. The proposed novel, DEA-based method integrates the typical DEA method, AHP method, HFLTS, and the soft set to process the MCDM problems under a fuzzy environment. The proposed method can deal with hesitant and nonexistent information and can help decision makers to consider all available information fully to obtain a more reasonable and correct solution result.
- (4)
- The critical technologies ranking of HET. According to the typical DEA method [63], the critical technologies ranking of the HET was . Based on the typical AHP/DEA method [64], the critical technologies ranking of the HET was . According to the fuzzy AHP/DEA method [43], the critical technologies ranking of the HET was . Based on the proposed method, the critical technologies ranking of the HET was .
5. Conclusions
Energy is the most basic need for people’s livelihood. Since hydrogen is the most abundant element in the universe, it has high energy density and will not produce carbon dioxide after combustion. Thus, hydrogen energy is clean and has multiple uses. At present, hydrogen development in various countries takes power generation, industry, and transportation vehicles as the three major application directions. However, due to cost constraints, the immaturity of hydrogen production technology, and many factors that need to be considered in technology development, the vision of the hydrogen economy has not yet been realized. Thus, finding the most suitable R&D and production technology for hydrogen under the existing approaches and insufficient resources can be regarded as a complex MCDM problem.
The evaluation criteria for the MCDM problem usually need to consider the number of attributes, which also includes the ambiguity, hesitation, and incomplete information provided by experts due to personal and professional preferences. The conventional MCDM calculation method cannot effectively simultaneously process the ambiguous, hesitant, or incomplete information provided by experts (such as [26,43,63,64]). This study proposed a novel general DEA-based approach for MCDM problems under a fuzzy environment. It integrates the typical DEA method, AHP method, the soft set, and HFLTS to evaluate the efficiency of HET. Empirical analysis proved that the proposed method could consider the weight of evaluation criteria, can fully consider the available information, measure the relative efficiency of HET in the hydrogen economy through the output to input ratio under a hesitant and incomplete information environment, and rank the HET effectively. According to the results of the proposed method, natural gas hydrogen technology, fuel cell vehicle technology, and home/industrial system technology are the most efficient among the 13 hydrogen energy technologies. The results can also provide energy policymakers with a reference for optimal alternatives or R&D for resource allocations. The advantages of the proposed general DEA-based approach are summarized as follows. The proposed general DEA-based approach:
- (1)
- Considers the weight of evaluation criteria of MCDM problems.
- (2)
- Processes ambiguous information provided by experts.
- (3)
- Processes hesitant information provided by experts.
- (4)
- Processes incomplete information provided by experts.
- (5)
- Fully considers the available information provided by experts.
- (6)
- Performs consistency tests to check whether the evaluation information is consistent.
- (7)
- The fuzzy AHP/DEA method [43] is a special case of the proposed general DEA-based approach.
Taking HET as an example, this study demonstrates the effectiveness and correctness of the proposed method through numerical analysis. In the future, the proposed method can be applied and extended to handle group MCDM issues in different fields, such as performance evaluation, supplier selection, risk estimate and rank, and so on.
Author Contributions
Conceptualization, H.-Y.C. and K.-H.C.; methodology, H.-Y.C. and K.-H.C.; H.-Y.C.; validation, H.-Y.C.; data curation, H.-Y.C.; writing—original draft preparation, H.-Y.C. and K.-H.C.; writing—review and editing, H.-Y.C. and K.-H.C.; funding acquisition, H.-Y.C. and K.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the National Science and Technology Council, Taiwan, for financially supporting this research under Contract No. MOST 110-2410-H-145-001, MOST 111-2221-E-145 -003 and MOST 111-2221-E-145 -004.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MCDM | Multi-criteria decision-making |
| DEA | Data envelopment analysis |
| AHP | Analytic hierarchy process |
| HFLTS | Hesitant fuzzy linguistic term set |
| DMUs | Decision-making units |
| PROMETHEE | Preference ranking organization method for enrichment evaluation |
| TOPSIS | Technique for order preference by similarity to ideal solution |
| ELECTRE | Elimination and choice translating reality |
| HET | Hydrogen energy technology |
| CCR | Charnes-Cooper-Rhodes |
| TFNs | Triangular fuzzy numbers |
| COA | Center of area |
| CR | Consistency ratio |
| CI | Consistency index |
| RI | Random index |
| LCD | Liquid crystal display |
| HFI | Hesitant fuzzy information |
| EI | Economic impact |
| BP | Business potential |
| IA | Inner ability |
| TD | Technology derivatives |
| DC | Development cost |
| R&D | Research and development |
References
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.N.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sust. Energ. Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Kusi-Sarpong, S.; Gupta, H.; Sarkis, J. A supply chain sustainability innovation framework and evaluation methodology. Int. J. Prod. Res. 2019, 57, 1990–2008. [Google Scholar] [CrossRef]
- Rashidi, M.; Ghodrat, M.; Samali, B.; Kendall, B.; Zhang, C.W. Remedial modelling of steel bridges through application of analytical hierarchy process (AHP). Appl. Sci. 2017, 7, 168. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, Z.G.; Zhang, H.; Wang, Y.; Yang, Y.H.; Li, Y. An integrated MCDM approach considering demands-matching for reverse logistics. J. Clean. Prod. 2019, 208, 199–210. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Gonzalez-Pachon, J.; Romero, C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res. 2017, 258, 607–616. [Google Scholar] [CrossRef]
- Chang, K.H. A novel risk ranking method based on the single valued neutrosophic set. J. Ind. Manag. Optim. 2022, 18, 2237–2253. [Google Scholar] [CrossRef]
- Meada, S.M.N.; Costa, I.P.A.; Castro, M.A.P.; Favero, L.P.; Costa, A.P.A.; Corrica, J.V.P.; Gomes, C.F.S.; Santos, M. Multi-criteria analysis applied to aircraft selection by Brazilian Navy. Production 2021, 31, e20210011. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildiene, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1979, 3, 339. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Guo, F.J.; Gao, J.W.; Liu, H.H.; He, P.L. Locations appraisal framework for floating photovoltaic power plants based on relative-entropy measure and improved hesitant fuzzy linguistic DEMATEL-PROMETHEE method. Ocean Coast. Manag. 2021, 215, 105948. [Google Scholar] [CrossRef]
- Chang, K.H. A novel contractor selection technique using the extended PROMETHEE II method. Math. Probl. Eng. 2021, 2021, 3664709. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, F.; Dong, J.Y. A preference degree for intuitionistic fuzzy values and application to multi-attribute group decision making. Inform. Sci. 2016, 370, 127–146. [Google Scholar] [CrossRef]
- Wen, T.C.; Chung, H.Y.; Chang, K.H.; Li, Z.S. A flexible risk assessment approach integrating subjective and objective weights under uncertainty. Eng. Appl. Artif. Intell. 2021, 103, 104310. [Google Scholar] [CrossRef]
- Ishizaka, A.; Tasiou, M.; Martinez, L. Analytic hierarchy process-fuzzy sorting: An analytic hierarchy process-based method for fuzzy classification in sorting problems. J. Oper. Res. Soc. 2020, 71, 928–947. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Pedrycz, W.; Kuang, Y.X.; Zhang, Z. Type-2 fuzzy multi-objective DEA model: An application to sustainable supplier evaluation. Appl. Soft Comput. 2016, 46, 424–440. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Grover, N. Intuitionistic fuzzy multi-attribute group decision-making with an application to plant location selection based on a new extended VIKOR method. Inform. Sci. 2016, 370, 184–203. [Google Scholar] [CrossRef]
- Chang, K.H. A novel enhanced supplier selection method used for handling hesitant fuzzy linguistic information. Math. Probl. Eng. 2022, 2022, 6621236. [Google Scholar] [CrossRef]
- Xu, Z.; Qin, J.D.; Liu, J.; Martinez, L. Sustainable supplier selection based on AHPSort II in interval type-2 fuzzy environment. Inform. Sci. 2019, 483, 273–293. [Google Scholar] [CrossRef]
- Chang, K.H. A novel supplier selection method that integrates the intuitionistic fuzzy weighted averaging method and a soft set with imprecise data. Ann. Oper. Res. 2019, 272, 139–157. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory-first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, P.C.; Niu, M.; Maddy, J. The survey of key technologies in hydrogen energy storage. Int. J. Hydrogen Energy 2016, 41, 14535–14552. [Google Scholar] [CrossRef]
- Lee, S.K.; Mogi, G.; Li, Z.L.; Hui, K.S.; Lee, S.K.; Hui, K.N.; Park, S.Y.; Ha, Y.J.; Kim, J.W. Measuring the relative efficiency of hydrogen energy technologies for implementing the hydrogen economy: An integrated fuzzy AHP/DEA approach. Int. J. Hydrogen Energy 2011, 36, 12655–12663. [Google Scholar] [CrossRef]
- Okur, N.; Ercan, T. Evaluating retail efficiency using DEA and AHP: A case in the Turkish apparel retail industry. J. Fash. Market. Manag. 2022. (Early Access). [Google Scholar] [CrossRef]
- Peng, C.; Feng, D.Z.; Guo, S.D. Material selection in green design: A method combining DEA and TOPSIS. Sustainability 2021, 13, 5497. [Google Scholar] [CrossRef]
- Halkos, G.; Argyropoulou, G. Modeling energy and air pollution health damaging: A two-stage DEA approach. Air Qual. Atmos. Health 2021, 14, 1221–1231. [Google Scholar] [CrossRef]
- Nurmatov, R.; Lopez, X.L.F.; Millan, P.P.C. Tourism, hospitality, and DEA: Where do we come from and where do we go? Int. J. Hosp. Manag. 2021, 95, 102883. [Google Scholar] [CrossRef]
- Lai, H.H.; Chang, K.H.; Lin, C.L. A novel method for evaluating dredging productivity using a data envelopment analysis-based technique. Math. Probl. Eng. 2019, 2019, 5130835. [Google Scholar] [CrossRef]
- Amin, G.R.; Hajjami, M. Improving DEA cross-efficiency optimization in portfolio selection. Expert Syst. Appl. 2021, 168, 114280. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, S.L.; Liu, Y.Y.; Zhang, L.Z.P.; Li, Y.P. A safety vulnerability assessment for chemical enterprises: A hybrid of a data envelopment analysis and fuzzy decision-making. J. Loss Prevent. Proc. 2018, 56, 95–103. [Google Scholar] [CrossRef]
- Soheilirad, S.; Govindan, K.; Mardani, A.; Zavadskas, E.K.; Nilashi, M.; Zakuan, N. Application of data envelopment analysis models in supply chain management: A systematic review and meta-analysis. Ann. Oper. Res. 2018, 271, 915–969. [Google Scholar] [CrossRef]
- Huang, S.N.; Chen, Y.P.; Feng, X.S.; Qiao, T.T.; Yu, D.D.; Yang, Y.Q. Research on dynamic assessment method of earthquake scene rescue performance based on AHP and cloud model. Mathematics 2022, 10, 207. [Google Scholar] [CrossRef]
- Cheemakurthy, H.; Garme, K. Fuzzy AHP-based design performance index for evaluation of ferries. Sustainability 2022, 14, 3680. [Google Scholar] [CrossRef]
- Khatoon, A.; Khan, N.A.; Parvin, F.; Wahid, M.S.; Jamal, M.T.; Azhar, S. Green HRM: Pathway towards environmental sustainability using AHP and FAHP in a nascent parsimony. Int. J. Manpow. 2022, 43, 805–826. [Google Scholar] [CrossRef]
- Chang, K.H.; Chain, K.; Wen, T.C.; Yang, G.K. A novel general approach for solving a supplier selection problem. J. Test. Eval. 2016, 44, 1911–1924. [Google Scholar] [CrossRef]
- Akbar, M.A.; Khan, A.A.; Huang, Z.Q. Multicriteria decision making taxonomy of code recommendation system challenges: A fuzzy-AHP analysis. Inform. Technol. Manag. 2022. (Early Access). [Google Scholar] [CrossRef]
- Chang, K.H.; Chang, Y.C.; Chain, K.; Chung, H.Y. Integrating soft set theory and fuzzy linguistic model to evaluate the performance of training simulation systems. PLoS ONE 2016, 11, e0162092. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Set Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Kumar, A.; Shankar, R.; Debnath, R.M. Analyzing customer preference and measuring relative efficiency in telecom sector: A hybrid fuzzy AHP/DEA study. Telemat. Inform. 2015, 32, 447–462. [Google Scholar] [CrossRef]
- Mirhedayatian, M.; Jelodar, M.J.; Adnani, S.; Akbarnejad, M.; Saen, R.F. A new approach for prioritization in fuzzy AHP with an application for selecting the best tunnel ventilation system. Int. J. Adv. Manuf. Tech. 2013, 68, 2589–2599. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Roodposhti, M.S.; Jankowski, P.; Blaschke, T. A GIS-based extended fuzzy multi-criteria evaluation for landslide susceptibility mapping. Comput. Geosci. 2014, 73, 208–221. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.H. Enhanced assessment of a supplier selection problem by integration of soft sets and hesitant fuzzy linguistic term set. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1635–1644. [Google Scholar] [CrossRef]
- Wang, L.; Rong, L.L.; Teng, F.; Liu, P.D. Teaching performance evaluation based on the proportional hesitant fuzzy linguistic prioritized choquet aggregation operator. Int. J. Comput. Int. Sys. 2021, 14, 635–650. [Google Scholar] [CrossRef]
- Wu, S.S.; Lin, J.; Zhang, Z.Y.; Yang, Y.S. Hesitant fuzzy linguistic agglomerative hierarchical clustering algorithm and its application in judicial practice. Mathematics 2021, 9, 370. [Google Scholar]
- Boyaci, A.C.; Solmaz, M.B.; Kabak, M. A model proposal for occupational health and safety risk assessment based on multi-criteria hesitant fuzzy linguistic term sets: An application in plastics industry. J. Fac. Eng. Archit. Gaz. 2021, 36, 1041–1053. [Google Scholar]
- Dincer, H.; Yuksel, S.; Martinez, L. House of quality-based analysis of new service development using context free grammar evaluation-enhanced fuzzy hybrid modelling. IEEE Access 2021, 9, 138415–138431. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Liu, Y.; Lin, Z.J.; Chen, J.W.; Chen, Y. Research on emergency treatment technology for water pollution accidents where the pollutants are not included in the emergency database. Water Sci. Technol. 2021, 84, 2318–2334. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Xu, Z.S. Work resumption after epidemic using three-way decisions. Int. J. Fuzzy Syst. 2021, 23, 630–641. [Google Scholar] [CrossRef]
- Chang, K.H. A more general reliability allocation method using the hesitant fuzzy linguistic term set and minimal variance OWGA weights. Appl. Soft Comput. 2017, 56, 589–596. [Google Scholar] [CrossRef]
- Chang, K.H.; Wen, T.C.; Chung, H.Y. Soft failure mode and effects analysis using the OWG operator and hesitant fuzzy linguistic term sets. J. Intell. Fuzzy Syst. 2018, 34, 2625–2639. [Google Scholar] [CrossRef]
- Wang, X.K.; Wang, S.H.; Zhang, H.Y.; Wang, J.Q.; Li, L. The recommendation method for hotel selection under traveller preference characteristics: A cloud-based multi-criteria group decision support model. Group Decis. Negot. 2021, 30, 1433–1469. [Google Scholar] [CrossRef]
- Lado-Sestayo, R.; Fernandez-Castro, A.S. The impact of tourist destination on hotel efficiency: A data envelopment analysis approach. Eur. J. Oper. Res. 2019, 272, 674–686. [Google Scholar] [CrossRef]
- Bind, R.; Isaac, P. Neutrosophic soft set and clinical application. J. Inform. Sci. Eng. 2021, 37, 381–393. [Google Scholar]
- Akcetin, E.; Kamaci, H. Three-valued soft set and its multi-criteria group decision making via TOPSIS and ELECTRE. Sci. Iran. 2021, 28, 3719–3742. [Google Scholar]
- Ulucay, V. Q-neutrosophic soft graphs in operations management and communication network. Soft Comput. 2021, 25, 8441–8459. [Google Scholar] [CrossRef]
- Wen, T.C.; Chang, K.H.; Lai, H.H. Integrating the 2-tuple linguistic representation and soft set to solve supplier selection problems with incomplete information. Eng. Appl. Artif. Intell. 2020, 87, 103248. [Google Scholar] [CrossRef]
- Ali, M.I.; Shabir, M.; Feng, F. Representation of graphs based on neighborhoods and soft sets. Int. J. Mach. Learn. Cybern. 2017, 8, 1525–1535. [Google Scholar] [CrossRef]
- Maji, P.K.; Biswas, R.; Roy, A.R. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef]
- Kocisova, K.; Hass-Symotiuk, M.; Kludacz-Alessandri, M. Use of the DEA method to verify the performance model for hospitals. E M Ekon. Manag. 2018, 21, 125–140. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Aggarwal, U.; Charles, V. An integrated AHP-DEA multi-objective optimization model for sustainable transportation in mining industry. Resour. Policy 2021, 74, 101180. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).