Risk Evaluation of Water Environmental Treatment PPP Projects Based on the Intuitionistic Fuzzy MULTIMOORA Improved FMEA Method

Abstract

The water environment treatment public-private partnership (PPP) project has a long cooperation period, large investment scale, high technical requirements, and more complex risks, which are very important to identifying and preventing risks. This paper establishes a risk evaluation model for water environmental treatment PPP projects based on the intuitionistic fuzzy Multi-Objective Optimization on the basis of a Ratio Analysis plus the full Multiplicative form (MULTIMOORA) improved Failure Mode and Effects Analysis (FMEA) method. Firstly, the risk indicators system of the water environmental treatment PPP project was constructed through the literature frequency statistics method and semi-structured interviews. Subsequently, the intuitionistic fuzzy FMEA method was used to assess the risk factors in terms of three aspects—occurrence(O), severity(S), and non-detectability(D)—and gather expert information, and the expert assessment method and deviation maximization model method were applied to assign the risk factors. Finally, Intuitionistic fuzzy Multi-Objective Optimization on the basis of a Ratio Analysis plus the full Multiplicative form (IF-MULTIMOORA) was applied to determine the risk indicator ranking and was combined with the water environmental treatment PPP project in Pingyu for example verification. The results show that the top five risk levels of PPP projects in Pingyu water environmental treatment are financing risk (changing financing conditions/high costs), market changes, government intervention and credit problems, imperfect legal and regulatory systems, and inflation. The risk assessment model proposed in this paper enables: (1) the evaluation of risk indicators from three perspectives, which is more accurate and comprehensive; (2) the introduction of intuitionistic fuzzy risk factor language variables to reasonably represent expert views; (3) the use of IF-MULTIMOORA for risk ranking to avoid the problem that RNP is the same and difficult to rank. This paper has important practical significance in promoting risk prevention and achieving the sustainable development of water environment treatment PPP projects.

1. Introduction

PPP mode refers to the establishment of a cooperative relationship between government departments and private sectors to jointly provide public goods and services [1]. While improving the supply efficiency of public goods and services, it forms a new investment and financing mode of sharing interests and risks between government and social capital. With the development of China’s society, the water pollution problem has become one of the crucial factors restricting China’s economic and social development [2]. Water environment treatment PPP projects are gaining more and more attention due to their advantages such as relieving the financial pressure on the government and effectively improving the efficiency of the treatment. Most water environment treatment PPP projects are characterized by a long cooperation period, large investment scale, high technical requirements, large number of stakeholders, and complex transaction structure [3,4]. In the long investment period and operation period of PPP projects, there will be many uncertain factors [5] whose complexity will lead to low interest of social capital, unclear risk allocation, and complex risk factors. Appropriate risk management is important to ensure that desired objectives are achieved [6]. However, many PPP projects fail to achieve their project objectives due to improper risk management [7]. Identifying the risks that may exist in water environmental treatment PPP projects and identifying the key risk points is particularly important to achieve the objectives of water environmental treatment PPP projects.

The difficulty in water environment treatment PPP projects is how to achieve reasonable and effective risk management. However, in the process of project implementation, there are still problems such as unclear responsibilities for multi-departmental “separate management” [8] and emphasis on construction rather than operation [9]; especially in risk management, the government often does not know the risks faced by the project and simply focuses on reducing project inputs [9], project managers lack effective solutions and control measures for common problems and risks and do not combine the project itself to carry out targeted risk management and prevention [10]. The identification of project risks, the identification of risks prone to occur according to project characteristics, and the targeted development of appropriate management plans and preventive measures are issues that need to be addressed urgently. At present, most of the research on the PPP project risk of water environmental treatment focuses on a single risk index or a stage of the project but does not pay attention to all aspects of the whole project risk. For example, Santandrea et al. [11] addresses the financing risks of healthcare PPP projects; Xiong et al. [12] focuses on ex-post risk management of PPP projects, starting with risk impact assessment and proposing measures such as renegotiation and early termination, focusing only on the post-management phase.

As a very important safety and reliability analysis tool, FMEA has been widely used to make risk management decisions, such as aerospace, automotive, nuclear, and healthcare industries [13,14,15,16]. It has also been widely used in risk management [17,18]. Unlike other critical analysis tools, the purpose of FMEA is to find out all possible failure modes and effects within the system, determine the cause of the failure mode, and then eliminate or reduce the specific failure, rather than finding a solution after the failure occurs [19]. In FMEA, risk assessment can be carried out by the O, S, and D of risk indicators. In FMEA, risk assessment is carried out by developing risk priorities, which are determined by multiplication of risk factor scores. Although there are many attractions, in practice, FMEA risk assessment is often affected by uncertainty, and it is easy to appear that the same priority of risk is difficult to rank the problem. Fuzzy set theory is a suitable tool to solve such problems.

Multi-objective optimization method of proportional analysis (MOORA) is a multi-objective optimization method. By constructing the alternative objective decision matrix, the ratio system and the reference point method are combined to determine the most suitable objective [20]. In 2010, Brauers and Zavadskas [21] improved MOORA to MULTIMOORA by adding Full Multiplicative Form and employing Dominance Theory to obtain a final integrative ranking based on the results of these triple subordinate methods. It is more perfect and accurate than the traditional decision-making method. As a multi-objective decision method, MULTIMOORA has been widely used in various multi-scheme decision problems due to its advantages such as short operation time, low decision complexity and strong robustness [22]. For example, Zavadskas et al. (2017) [23] applied MULTIMOORA to the selection of building materials; Geetha et al. (2019) [24] applied the MULTIMOORA decision-making method based on intuitionistic hesitant fuzzy sets to the selection of medical waste treatment methods. MULTIMOORA is also widely used in risk assessment [25,26]. However, multi-objective problems often involve uncertainty, while the ordinary MULTIMOORA method uses clear numbers, which cannot express the uncertainty of information well. In order to enable it to solve more complex decision problems, scholars have improved MULTIMOORA [27]. Zhang et al. [28] used a single triangular fuzzy number to represent expert opinions, and then used MULTIMOORA for evaluation. Liang et al. [29] used Hesitant Fuzzy Linguistic Term Set (HFLTS) to study the evaluation information in MULTIMOORA, which could well reflect the hesitating-decision makers. This paper also follows the fuzzy idea and uses the IF-MULTIMOORA method to rank risk indicators. It solves the problem that it is difficult for experts to use accurate data to evaluate indicators and can deal with the uncertainty of information better.

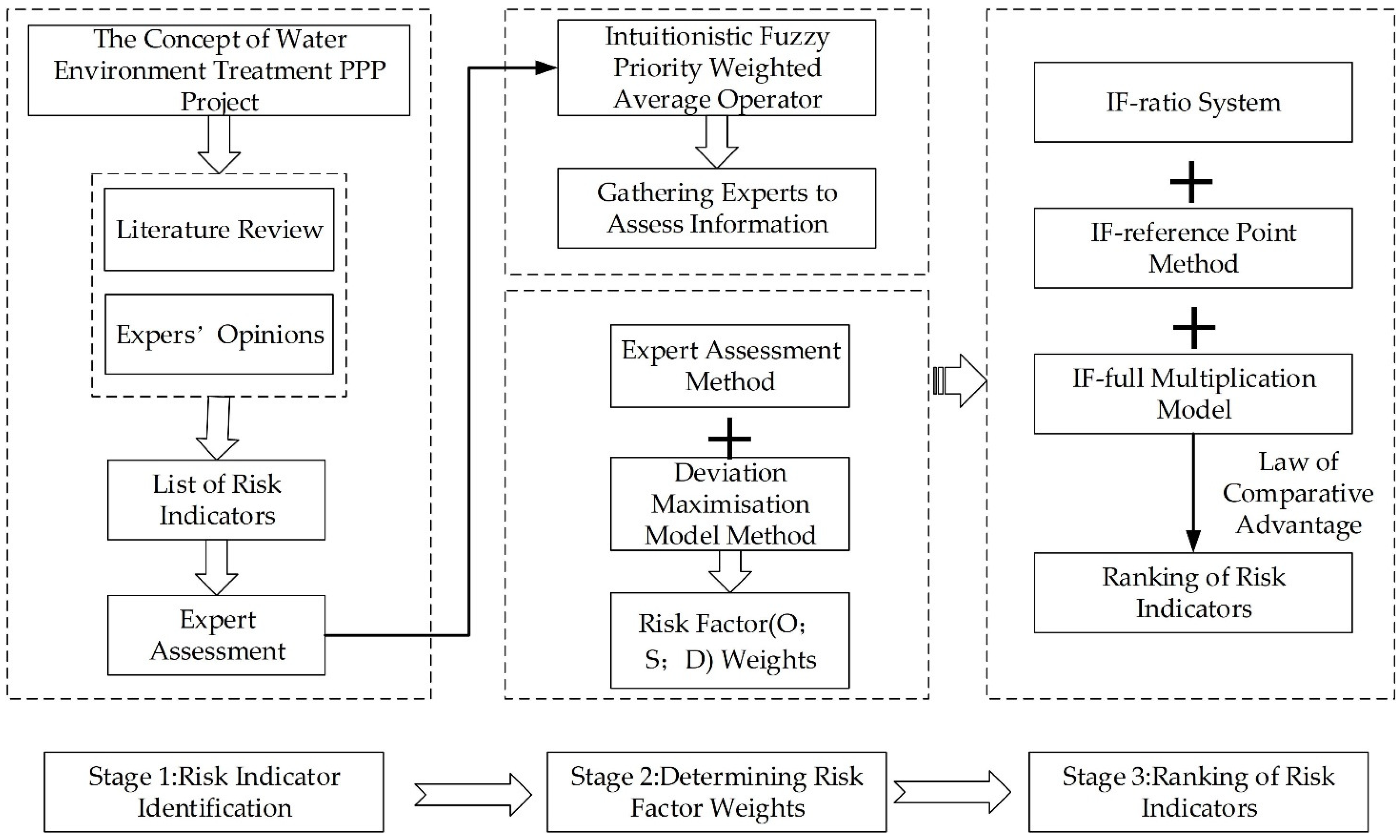
In this paper, a risk assessment model of water environmental treatment PPP project based on IF-MULTIMOORA improved FMEA method is established. The whole life cycle risk assessment indicator system of water environmental treatment PPP projects is established, which covers a variety of risk types and is more comprehensive. Intuitionistic fuzzy FMEA method was used to determine the O, S, and D of risk three risk factors and determine the weights, starting from these three aspects, using fuzzy ideas to assess the risk indicators, the different characteristics of risk indicators into consideration, improving the accuracy of the assessment; at the same time, the IF-MULTIMOORA method is used to avoid the determination of risk indicator weights and directly rank the risk indicators to determine the key risk indicators and focus the risk management on the risk issues that are prone to the project and carry out targeted risk management.

The second part of the paper is a literature review; the third part is the research methodology, which constructs a risk evaluation model for water environmental treatment PPP projects; the fourth part is an example study, which applies the developed model to practice; and the fifth part is the conclusion, which summarizes the theoretical contributions and limitations of the paper.

2. Literature Review

Establishing an objective and reliable risk indicator system is essential for the risk evaluation of water environmental treatment PPP projects [30]. Jin and Cui [31] combined with the characteristics of current water environment treatment PPP projects, based on literature reading method, collated, and summarized four first-level indicators of financing risk, project technology and management risk, government regulation risk, and environmental risk. Commonly used risk identification methods are the literature review method [32], brain storming method [33], etc. The risk identification of water environment treatment PPP projects cannot simply rely on a risk identification method but need to use a combination of several of these risk identification methods, play the advantages of multiple identification methods, make up for the disadvantages of a single identification method, comprehensive and systematic identification of risk factors.

There are also different approaches to risk assessment by domestic and international scholars. Song et al. [34] proposed a risk evaluation model based on the group analytic hierarchy process (GAHP), rough set theory, and cloud model theory. Zhai et al. [35] used a project scoring tool to design and score questions on 23 evaluation indicators in their study of investment risk in PPP projects, applied analytic hierarchy process (AHP) to determine the weights of each risk indicator, and finally used mixed center-point triangular winterization weight function to determine the investment risk evaluation level.

Most of the current research on PPP project risk assessment starts from a single project phase or a single risk indicator such as investment and financial risk, and the evaluation indicators used are often very similar to those of general PPP projects; and most of the studies on risk evaluation focus on the probability of risk occurrence, project risk level, etc., and do not consider the differences in different aspects of risk such as frequency and severity. The FMEA method assesses the risk level of an indicator by calculating the risk priority number (RPN = O × S × D) from three risk factors: O, S, and D. However, the traditional FMEA method has many shortcomings; expert assessment information is difficult to quantify accurately in practical applications [36,37]; it also does not consider the relative weights of risk factors, which is unreasonable; and it is easy to have the same RPN and difficult to sort [19]. At the same time, the RPN calculated by the traditional FMEA method cannot reflect the real situation when the scores of the two risk factors are at opposite ends [38]. How to establish a whole life cycle risk indicator system with the characteristics of water environmental treatment PPP projects, starting from the various characteristics of the risk, more effective identification, prevention of risk, and improve the efficiency of water environmental treatment PPP project governance needs to be studied in depth.

3. Research Methodology

This paper firstly uses the literature frequency statistics method and semi-structured interviews to construct a whole-life risk indicator system for PPP projects; then adopts the intuitionistic fuzzy FMEA method, treats the expert assessment information of risk indicator as fuzzy variables, adopts the intuitionistic fuzzy weighted average operator was utilized to aggregate the experts’ evaluation information of different priority level; the comprehensive weighting method, which combines the expert assessment method and the deviation maximization model method, determines the comprehensive weighting of the risk factors from both subjective and objective aspects; finally, MULTIMOORA was used to determine the risk ranking of the project. The research framework is shown in Figure 1.

3.1. Risk Indicator Identification Based on Literature Frequency Statistics and Semi-Structured Interviews

This section examines the relevant literature and uses literature frequency statistics to conduct a preliminary screening of the risks throughout the life cycle of PPP projects. The risk indicators of 15 PPP project risk identification-related literature were sorted out. From these, risk indicators with a frequency of less than five times and risks that are significantly different from those of water environment treatment PPP projects were excluded. The preliminary screening indicator system is shown in

Table 1. Frequency statistics of risk indicators literature for water environmental treatment PPP projects.

Serial Number	Risk Indicator	Literature Related to Risk Identification of PPP Projects in China *															Frequency
		A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
1	Expropriation/Communalization	√	√				√		√		√		√	√		√	8
2	Government intervention and credit issues	√	√	√		√	√	√	√	√	√	√	√	√	√	√	14
3	Third party delays/defaults	√	√	√		√	√			√			√			√	8
4	Inflation	√	√	√	√	√	√	√	√	√	√	√	√	√		√	14
5	Project approval delays	√	√	√		√			√	√	√	√	√		√	√	11
6	Conflicting/incomplete/changed contract documents	√	√	√	√	√		√	√	√	√		√	√		√	12
7	Financing risks (financing terms/costs)	√	√	√	√	√		√	√	√	√		√		√	√	12
8	Completion risk	√		√			√			√	√	√				√	7
9	Supply risk	√	√	√	√			√		√	√	√	√			√	10
10	Design and technical risks (planning, defects, changes)	√				√		√		√	√		√			√	7
11	Hydrological/climatic/address conditions risk	√		√		√	√		√				√	√	√	√	9
12	Insufficient revenue from main business			√			√		√	√				√			5
13	Market changes	√	√	√	√	√	√		√	√	√		√			√	11
14	Construction cost risk			√		√	√		√	√			√	√		√	8
15	Inadequate capacity of the Franchisee	√	√										√		√	√	5
16	Force majeure risks (political, natural conditions)	√	√	√	√	√	√	√	√	√		√	√	√	√	√	14
17	Organizational coordination risk	√		√	√	√		√		√			√	√		√	9
18	Quality and construction safety risks		√	√		√	√		√	√		√		√		√	9
19	Operating cost overruns			√	√	√			√	√	√	√	√		√	√	10
20	All kinds of disputes and infringements			√		√	√		√			√					5
21	Project transfer risk	√		√				√				√	√				5
22	Public satisfaction			√			√			√				√		√	5
23	Change of social capital	√		√				√				√	√				5
24	Changes in laws and regulations and inadequate regulatory system	√		√	√		√	√	√	√	√		√	√	√		11

* References: A-[39], B-[40], C-[41], D-[42], E-[43], F-[44], G-[10], H-[45], I-[46], J-[47], K-[48], L-[49], M-[50], N-[51], O-[52].

.

There are 24 risk indicators for water environmental treatment PPP projects sorted out in Table 1. In order to avoid the lack of risk indicators specific to water environmental treatment PPP projects, this study combines the method of relevant expert interviews with semi-structured interviews with experts who have participated in water environmental treatment PPP projects. Based on the results of the interviews, the risk indicators were screened and supplemented to improve their completeness. In summary, this study identifies the list of risks and interpretation of the meaning of water environmental treatment PPP projects as shown in

Table 2. Table explaining the meaning of risk indicators.

Risk Indicators	Meaning
Expropriation/communalization FM01	Public ownership of projects imposed by the government;
Government intervention and credit issues FM02	The government intervenes in the construction, operation and other activities of the project, which affects the decision-making power of the social capital; the government’s failure to perform the responsibilities and obligations stipulated in the contract will cause harm to the project;
Changes in laws and regulations and inadequate regulatory system FM03	The harm caused by the poor effectiveness, partial conflict and poor operability of existing legislation on PPP projects; the consequences of increased costs and reduced benefits due to changes in relevant laws, regulations and other government macroeconomic policies.
Environmental protection FM04	Higher costs, delays or other losses to the project as a result of increased environmental requirements from government or community groups.
Tax adjustments FM05	Including changes in tax policy by central or local government.
Force majeure risks (political, natural conditions) FM06	Events or circumstances occur when a party to the contract cannot avoid or overcome the situation; damage caused by natural disasters such as fire, flood, earthquake, typhoon, etc.
Hydrological/climatic/geological condition risk FM07	Objective adverse natural conditions at the project site are causing disruption to the progress of the project, such as climatic conditions, special geographical circumstances, and poor site conditions.
Third party delays/defaults FM08	Failure by project participants other than the government and the social capital party to fulfil their contractual responsibilities and obligations.
Inflation FM09	Refers to consequences such as an increase in the overall price level and a decrease in the purchasing power of money leading to an increase in the cost of the project.
Market changes FM10	Changes in market demand due to macroeconomic, social environment, demographic changes, adjustment of laws and regulations, etc.
Financing risks (changes in financing terms/high costs) FM11	Including risks arising from poorly structured financing, inadequate financial markets and accessibility of finance, the most significant form of which is difficulty in raising capital.
Public satisfaction FM12	Some members of the public have a more negative attitude towards water environment treatment and reject the construction of the project, which affects the progress of the project.
Completion risk FM13	This is manifested by delays in construction schedules, cost overruns, failure to meet the targets set at the time of design when the project is commissioned, resulting in insufficient cash inflows and failure to repay debts on time.
Supply risk FM14	Refers to losses to the project caused by the untimely supply of raw materials, resources, machinery and equipment or energy.
Inadequate earnings from main operations FM15	The hidden risks resulting from a single revenue model for project operations, over-reliance on government payments, and no or insufficient revenue from other operations.
Conflicting/incomplete/changed contract documents FM16	The risk of errors in contractual documents, inflexible design, inconsistencies between documents, including unreasonable allocation of risks and unclear scope of responsibilities and obligations; the risk that the project contract itself will be imperfect and need to be amended in accordance with the actual situation and incur certain costs, and the risk that contractual changes may also affect the public-private partnership and even cause the breakdown of the public-private partnership leading to project failure.
Design and technical risks (planning, defects, changes) FM17	The design is not adapted to the needs of the project due to poor planning and survey and design, resulting in increased design costs, delayed works or even renovation or reconstruction of works in progress or already built; the technology used is not mature, does not meet the intended standards and requirements, or has poor applicability, forcing the private sector to make additional investments in technical renovation.
Construction cost risk FM18	Risk of higher-than-expected construction costs due to inadequate cost management by the contractor.
Project approval delays FM19	Projects are subject to a complex approval process, and it is very difficult to make the necessary commercial adjustments to the nature and scale of the project after approval
Inadequate capacity of the Franchisee FM20	Losses arising from the slow progress of the project due to low construction and operational productivity caused by the concessionaire’s lack of capacity, etc.
Organizational coordination risk FM21	The lack of organizational and coordination capacity of the project company, resulting in increased communication costs and conflicts between the parties involved in the project.
Quality and construction safety risks FM22	The risk of quality failing to meet project requirements; the risk of safety incidents occurring during the construction of the project due to inadequate safety measures.
Operating cost overruns FM23	Operating cost overruns due to government mandated product and service standards, non-operator factors such as force majeure on interest rates and exchange rates, poor operational management, etc.
All types of disputes and infringements FM24	The risk of incidents such as infringements and labor disputes occurring during the construction of the project.
Change of social capital FM25	The risk of uncertainty in the implementation of the project arising from the withdrawal or entry of one or more investors due to disputes between social capitals or for other reasons.
Project transfer risk FM26	Inadequate maintenance of the project implementation by the social capital, which affects the use of the project after handover or due to delays in handover by government departments.

, containing 26 risk elements.

3.2. Risk Indicator Assessment and Information Aggregation

3.2.1. Risk Indicator Assessment Based on Intuitionistic Fuzzy FMEA

In this paper, we use the three risk factors of O, S, and D from the traditional FMEA method [53]. Due to the great uncertainty and incompleteness of the information related to risk in practice, it is difficult for experts to make a precise evaluation from the form of real numbers from 1 to 10, and they prefer to use linguistic variables to evaluate the actual performance of risk indicators from various aspects of risk factors. Therefore, in this section, risk indicators are considered as fuzzy variables, and experts evaluate the actual performance of risk indicator $F{M}_i\left(i=1,2,\cdots ,m\right)$ under risk factor $R{F}_j\left(j=1,2,\cdots ,n\right)$ by linguistic variables. The evaluation results can be converted into the corresponding intuitive fuzzy numbers according to the rules in

Table 3. Risk assessment language variable levels [54].

Language Variables	Intuitionistic Fuzzy Number
Extremely low (EL)	(0.025, 0.900)
Very low (VL)	(0.075, 0.850)
Low(L)	(0.150, 0.750)
Medium Low (ML)	(0.350, 0.550)
Medium (M)	(0.500, 0.500)
Medium High (MH)	(0.550, 0.350)
High (H)	(0.750, 0.150)
Very High (VH)	(0.850, 0.075)
Extremely high (EH)	(0.900, 0.025)

.

3.2.2. Information Aggregation for Risk Indicator Assessment Based on Intuitionistic Fuzzy Weighted Average Operators

If there are s experts, they are classified into s priority levels according to their knowledge structure and domain experience, denoted as $D{M}_k\left(k=0,1,\cdots ,s\right)$, i.e., $D{M}_1$ has the highest priority level as its knowledge structure is closer to the FMEA evaluation object and it has more experience in this domain, and its assessment information is given priority in the risk evaluation. In this section, the intuitionistic fuzzy weighted average operator was utilized to aggregate the experts’ evaluation information of different priority level.

${\tilde{\alpha }}_{ij}^k=\left({\mu }_{ij}^{\left(k\right)},{\nu }_{ij}^{\left(k\right)}\right)$ is the number of intuitionistic fuzzy numbers transformed by the experts of the $k$th rank for the linguistic evaluation information of the risk indicator ${FM}_i$ regarding the risk factor $R{F}_j$; ${\tilde{R}}_k={({\tilde{\alpha }}_{ij}^k)}_{m\times n}$ denotes the intuitionistic fuzzy evaluation matrix of the risk factor given by the experts of the $k$th rank.

Step 1: Since the later IF-MULTIMOORA ranking method requires subtraction and division of the assessment information according to the type of risk factor, and the corresponding operation rules for intuitionistic fuzzy numbers are yet to be improved, ${\tilde{\alpha }}_{ij}^k=\left({\mu }_{ij}^{\left(k\right)},{\nu }_{ij}^{\left(k\right)}\right)$ is transformed as follows in order to enhance the universality of the method.

$${\tilde{\alpha }}_{ij}^{*}{}^{\left(k\right)}=\{\begin{array}{l}{\tilde{\alpha }}_{ij}^{\left(k\right)}=\left({\mu }_{ij}^{\left(k\right)},{\upsilon }_{ij}^{\left(k\right)}\right),j\in B;\\ Neg\left({\tilde{\alpha }}_{ij}^{\left(k\right)}\right)=\left({\upsilon }_{ij}^{\left(k\right)},{\mu }_{ij}^{\left(k\right)}\right),j\in C.\end{array},$$

(1)

It is possible to obtain ${\tilde{\alpha }}^{*}{}_{ij}^{\left(k\right)}=\left({\mu }^{*}{}_{ij}^{\left(k\right)},{\upsilon }^{*}{}_{ij}^{\left(k\right)}\right)$, where B is the set of benefit-based risk factors and C is the set of cost-based risk factors, this paper uses the traditional FMEA method of 3 risk factors of O, S, and D, all of which are cost-based risk factors.

Step 2: The intuitionistic fuzzy weighted average operator is used to assemble the expert information as shown in Equation (2) [55].

$$IFPWA\left({\tilde{\alpha }}_{ij}^{*}{}^{\left(1\right)},{\tilde{\alpha }}_{ij}^{*}{}^{\left(2\right)},\cdots ,{\tilde{\alpha }}_{ij}^{*}{}^{\left(s\right)}\right)={\tilde{\alpha }}_{ij}=\left(1-{\displaystyle \prod }_{k=1}^s{\left(1-{\mu }_{ij}^{*}{}^{\left(k\right)}\right)}^{\frac{T_k}{{{\displaystyle \sum }}_{k=1}^s{T}_k}},{\displaystyle \prod }_{k=1}^s{\upsilon }_{ij}^{*}{{}^{\left(k\right)}}^{\frac{T_k}{{{\displaystyle \sum }}_{k=1}^s{T}_k}}\right)$$

(2)

where $T_k={\displaystyle \prod }_{t=1}^{k-1}s\left({\tilde{\alpha }}_{ij}^{*}{}^{\left(t\right)}\right)\left(k=2,3,\cdots ,s\right),T_1=1$; where $s\left(\tilde{\alpha }\right)$ is the fuzzy vector score function, calculated as in Equation (3).

$$s\left(\tilde{\alpha }\right)=\mu +\frac{1}{2}\left(1-\mu -\upsilon \right)$$

(3)

This results in an intuitive fuzzy composite evaluation matrix $\tilde{R}={\left({\tilde{\alpha }}_{ij}\right)}_{m\times n}$ of risk indicators.

3.3. Determination of Risk Factor Weights

The traditional FMEA risk assessment process does not take into account risk factor weighting information and treats O, S and D as equally important, which is clearly not the case and results in a less accurate risk sequence for the final failure mode. However, it is difficult to determine the risk factor weights directly, so many weight calculation methods have been applied to determine the risk factor weights in FMEA, mainly the subjective weighting method [26], the objective weighting method [56] and the comprehensive weighting method [57], among which the comprehensive assignment method has been adopted by many scholars because it can consider both subjective and objective reasons.

In this paper, a combination of expert assessment method and deviation maximization model method is used to determine the comprehensive weighting of risk factors from both subjective and objective aspects.

3.3.1. Risk Factor Assessment and Information Aggregation

Organize assessment experts to score the importance of the 3 risk factors of O, S and D, in the final risk ranking of failure modes combined with Table 1, prioritize experts on a scale of 1-S, and obtain the risk factor weighting intuitionistic fuzzy evaluation matrix ${\tilde{W}}_k={\left({\tilde{\alpha }}^k{}_j\right)}_{1\times n},\left(k=1,\cdots ,s\right)$, using Equation (2), gather information from experts to obtain the risk factor weighting intuitionistic fuzzy comprehensive evaluation matrix $\tilde{W}={\left({\tilde{\alpha }}_j\right)}_{1\times n}$.

3.3.2. Determination of Subjective Weights Based on Expert Assessment Method

The greater the value of the risk factor weight information score function, the greater the weight. The subjective weight of the risk factor is determined based on the score function value, as shown in Equation (4).

$${\omega }_j^s=\frac{s\left({\tilde{\alpha }}_j\right)}{{{\displaystyle \sum }}_{j=1}^{n}s\left({\tilde{\alpha }}_j\right)}$$

(4)

where ${\omega }_j^s$ denotes the subjective weight value of the intuitive fuzzy number of priority $s$ expert scoring of risk factor $j$.

3.3.3. Objective Weighting Based on Deviation Maximization

When the weight of an attribute in a multi-attribute decision problem is completely unknown, the greater the similarity of the evaluation information under a particular attribute, the less useful that attribute is in differentiating the alternatives and the less weight it has. This section uses the Hamming distance to measure the similarity of the evaluation information.

Let ${\tilde{\alpha }}_1=\left({\mu }_1,{\upsilon }_1\right)$ and ${\tilde{\alpha }}_2=\left({\mu }_2,{\upsilon }_2\right)$ be two intuitionistic fuzzy numbers, then the Hamming distance between ${\tilde{\alpha }}_1$ and ${\tilde{\alpha }}_2$ is:

$$d\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2\right)=\frac{1}{2}\left(\left|{\mu }_1-{\mu }_2\right|+\left|{\upsilon }_1-{\upsilon }_2\right|+\left|{\pi }_1-{\pi }_2\right|\right)$$

Based on the Hamming distance, the deviation maximization model is constructed:

$$\max {\displaystyle \sum }_{j=1}^n{\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{i\ne l}d\left({\tilde{\alpha }}_{ij},{\tilde{\alpha }}_{lj}\right){\omega }_j^O,$$

(5)

where ${\displaystyle \sum }_{j=1}^n{\left({\omega }_j^O\right)}^2=1,{\omega }_j^O\ge 0,j=1,2,\cdots ,n$ is the objective weighting of the risk factor.

Construct the Lagrange function to solve the model as shown in Equation (6).

$$L\left(\omega ,\lambda \right)=d\left(\omega \right)+\frac{\lambda }{2}\left({\displaystyle \sum }_{j=1}^n{\left({\omega }_j^O\right)}^2-1\right),$$

(6)

Find the partial derivative of the equation such that the following equation holds.

$$\{\begin{array}{l}\frac{\partial L\left(\omega ,\lambda \right)}{\partial {\omega }_j^O}={\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{i\ne l}d\left({\tilde{\alpha }}_{ij},{\tilde{\alpha }}_{lj}\right){\omega }_j^O+\lambda {\omega }_j^O=0;\\ \frac{\partial L\left(\omega ,\lambda \right)}{\partial \lambda }={\displaystyle \sum }_{j=1}^n{\omega }_j^O-1=0\end{array},$$

(7)

The optimal solution for the objective weights of the risk factors is derived and normalized, as in Equation (8).

$${\omega }_j^O=\frac{{{\displaystyle \sum }}_{i=1}^m{{\displaystyle \sum }}_{l\ne i}d\left({\tilde{\alpha }}_{ij},{\tilde{\alpha }}_{lj}\right)}{{{\displaystyle \sum }}_{j=1}^n{{\displaystyle \sum }}_{i=1}^m{{\displaystyle \sum }}_{l\ne i}d\left({\tilde{\alpha }}_{ij},{\tilde{\alpha }}_{lj}\right)},j=1,2,\cdots ,n,$$

(8)

3.3.4. Determination of Combined Risk Factor Weights

Finally, the vectors of subjective and objective risk factor weights are aggregated to determine the combined weights of the risk factors, as in Equation (9).

$${\omega }_j={\phi }_1{\omega }_j^S+{\phi }_2{\omega }_j^O,$$

(9)

where ${\phi }_1$ and ${\phi }_2$ are the relative importance of the subjective and objective weights, respectively, $0\le {\phi }_1,{\phi }_2\le 1,{\phi }_1+{\phi }_2=1,j=1,2,\cdots ,n$.

3.4. Risk Ranking Based on the IF-MULTIMOORA Method

The IF-MULTIMOORA risk ranking method is based on the MUTIMOORA method and is formed by introducing the IF-ratio system, the IF-reference point method, the IF-full multiplication model and the advantage theory [58]. The IF-ratio system, the IF-reference point method, and the IF-full multiplication model are, respectively, represented by the combined utility value, the Tchebycheff distance, and the multiplicative utility value of the risk indicator under all risk factors.

Theorem 1.

The rules for comparing fuzzy numbers are: let ${\tilde{\alpha }}_1=\left({\mu }_1,{\upsilon }_1\right)$ and ${\tilde{\alpha }}_2=\left({\mu }_2,{\upsilon }_2\right)$ be two intuitionistic fuzzy numbers, and their comparison methods are:① if $s_1\left({\tilde{\alpha }}_1\right)>s_2\left({\tilde{\alpha }}_2\right)$, then ${\tilde{\alpha }}_1>{\tilde{\alpha }}_2$; ② if $s_1\left({\tilde{\alpha }}_1\right)=s_2\left({\tilde{\alpha }}_2\right)$, then ${\tilde{\alpha }}_1={\tilde{\alpha }}_2$holds when $h_1\left({\tilde{\alpha }}_1\right)=h_2\left({\tilde{\alpha }}_2\right)$ holds; ${\tilde{\alpha }}_1>{\tilde{\alpha }}_2$ holds when $h_1\left({\tilde{\alpha }}_1\right)>h_2\left({\tilde{\alpha }}_2\right)$ holds; ${\tilde{\alpha }}_1<{\tilde{\alpha }}_2$ holds when $h_1\left({\tilde{\alpha }}_1\right)<h_2\left({\tilde{\alpha }}_2\right)$holds.

Theorem 2.

Let ${\tilde{\alpha }}_j=\left({\mu }_j, {\upsilon }_j\right)\left(j=1,2,\cdots ,n\right)$ be a set of intuitionistic fuzzy numbers and let $IFWA:V^n\to V$, then

$$IFWA\left({\tilde{\alpha }}_1, {\tilde{\alpha }}_2, \cdots , {\tilde{\alpha }}_n\right)={\omega }_1{\tilde{\alpha }}_1\oplus {\omega }_2{\tilde{\alpha }}_2\oplus \cdots \oplus {\omega }_n{\tilde{\alpha }}_n={\oplus }_{j=1}^n{\omega }_j{\tilde{\alpha }}_j$$

is said to be the intuitionistic fuzzy weighted average operator, where $V$ is the intuitionistic fuzzy set, $w={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$ is the weight vector of ${\tilde{\alpha }}_j\left(j=1,2,\cdots ,n\right)$, and ${\omega }_j\in \left[0, 1\right]\left(j=1,2,\cdots ,n\right), {\displaystyle \sum }_{j=1}^n{\omega }_j=1$.

Theorem 3.

Let ${\tilde{\alpha }}_j=\left({\mu }_j, {\upsilon }_j\right)\left(j=1,2,\cdots ,n\right)$ be a set of intuitionistic fuzzy numbers and let $IFWG, V^n\to V$, then

$$IFWG\left({\tilde{\alpha }}_1, {\tilde{\alpha }}_2, \cdots , {\tilde{\alpha }}_n\right)={\tilde{\alpha }}_1{}^{{\omega }_1}\otimes {\tilde{\alpha }}_2{}^{{\omega }_2}\otimes \cdots \otimes {\tilde{\alpha }}_n{}^{{\omega }_n}={\oplus }_{j=1}^n{\tilde{\alpha }}_j{}^{{\omega }_j}$$

is an intuitionistic fuzzy weighted geometric operator, where $V$is the intuitionistic fuzzy set, $w={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$is the weight vector of ${\tilde{\alpha }}_j\left(j=1,2,\cdots ,n\right)$, and ${\omega }_j\in \left[0, 1\right]\left(j=1,2,\cdots ,n\right), {\displaystyle \sum }_{j=1}^n{\omega }_j=1$.

Step 1: IF-ratio system

According to Theorem 2, the total utility value of $F{M}_i$ is calculated by the intuitive fuzzy comprehensive evaluation matrix of risk indicators and the weight vector of risk factors, as shown in Equation (10). Ranking of the total utility values of risk indicators according to Theorem 1. The smaller the total utility value, the higher the risk ranking.

$${\tilde{y}}_i^{*}=IFWA\left({\tilde{\alpha }}_{i1},{\tilde{\alpha }}_{i2},\cdots ,{\tilde{\alpha }}_{in}\right)={\oplus }_{j=1}^n{\omega }_j{\tilde{\alpha }}_{ij}=\left(1-{\displaystyle \prod }_{j=1}^n{\left(1-{\mu }_{ij}\right)}^{{\omega }_j},{\displaystyle \prod }_{j=1}^n{\upsilon }_{ij}{}^{{\omega }_j}\right),$$

(10)

Step 2: IF-Reference Point Method

Using the positive ideal reference point method, the Tchebycheff distance of the risk factors is calculated as shown in Equation (11). The greater the distance, the higher the risk ranking.

$$d\left({\tilde{\beta }}_j,F{M}_i\right)={\left\{{\displaystyle \sum }_{j=1}^n{\left[d\left({\tilde{\beta }}_j,{\tilde{\alpha }}_{ij}\right)\right]}^{\gamma }\right\}}^{\frac{1}{\gamma }},\gamma \in N^{+}$$

Robustness is greatest when $\gamma \to \infty$, so that:

$$d\left({\tilde{\beta }}_j,F{M}_i\right)=\underset{1\le j\le n}{max}d\left({\tilde{\beta }}_j,{\tilde{\alpha }}_{ij}\right)=\underset{1\le j\le n}{max}\frac{{\omega }_j}{2}\left(\left|{\mu }_{ij}-1\right|+\left|{\upsilon }_{ij}\right|+\left|{\pi }_{ij}\right|\right),$$

(11)

Step 3: IF-Full Multiplier Model

According to Theorem 3, the multiplicative utility value of each risk indicator is calculated using the risk factor intuitionistic fuzzy comprehensive evaluation matrix and the risk factor weight vector, as in Equation (12), where the smaller the multiplicative utility value, the higher the risk ranking.

$${\tilde{U}}_i^{*}=IFWG\left({\tilde{\alpha }}_{i1},{\tilde{\alpha }}_{i2},\cdots ,{\tilde{\alpha }}_{in}\right)={\oplus }_{j=1}^n{\tilde{\alpha }}_{ij}{}^{{\omega }_j}=\left({\displaystyle \prod }_{j=1}^n{\mu }_{ij}{}^{{\omega }_j}, 1-{\displaystyle \prod }_{j=1}^n{\left(1-{\upsilon }_{ij}\right)}^{{\omega }_j}\right)$$

(12)

Step 4: Advantage theory

The IF-MUTIMOORA method consists of the above three steps. The risks are ranked according to Theorem 1 and each of the three risk rankings has the same degree of importance. The model incorporates advantage theory and compares the generalized dominance relationship of the ternary array of three rankings of risk indicators derived from each step to determine the final risk ranking of the failure mode.

4. Case Study

4.1. Project Overview

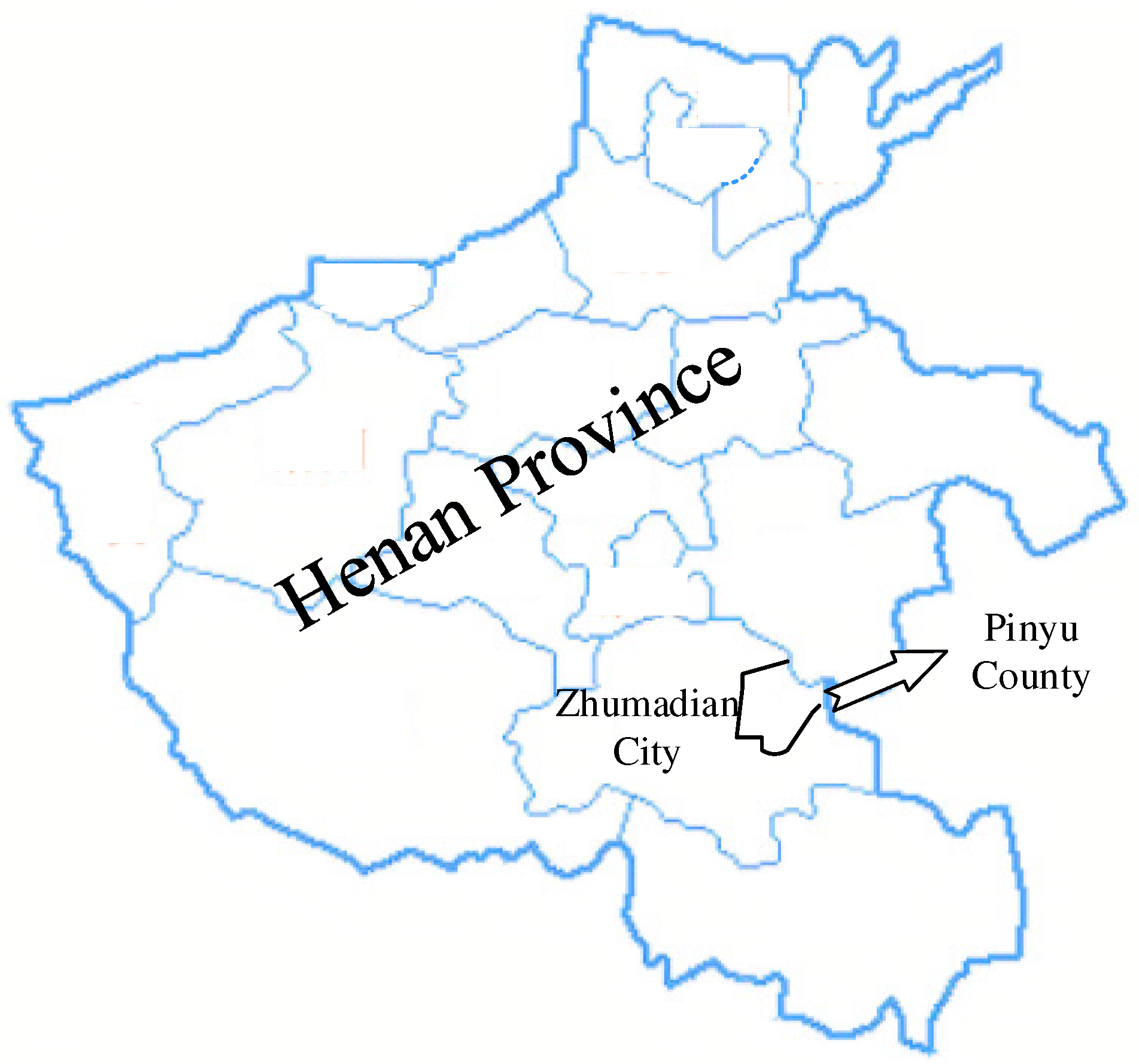
Pingyu County is located in the east of Zhumadian City, Henan Province, China (as shown in Figure 2). It is located in the Huaihe River system, with more than 3400 large and small channels, a total length of 4140 km. Xiaohong River and Ruhe River, tributaries of Huaihe River, flow through the county. The length of Xiaohonghe County is 50.2 km, with a watershed area of 939 square kilometers, accounting for 73% of Pingyu County. The length of Ruhe County is 20.54 km, with a watershed area of 290 square kilometers, accounting for 22% of Pingyu County. With the economic development in Pingyu County, the water quality has deteriorated, and the ecological environment has been degraded. In 2017, Henan Water Conservancy Investment Group Limited won the tender to undertake the PPP project’s design, construction, and operation for the water environment treatment and ecological restoration project in Pingyu County. This section takes the water environment treatment PPP project in Pingyu County as an example for risk evaluation.

4.2. Risk Indicator Assessment and Information Aggregation

4.2.1. Risk Indicator Assessment Based on Intuitive Fuzzy FMEA

Three experts familiar with the Pingyu project were selected to assess the project risk factors and risk indicators. The detailed information of experts is shown in

Table 4. Profiles of experts.

Expert	Type of Organization	Working Experience in PPP Projects	Detailed Introduction
1	Pingyu water environment treatment PPP project operation department	4 years	Responsible for ensuring the long-term and effective operation of the project, with a clear understanding of the risks faced by the project.
2	Research institution	8 years	Mainly engaged in PPP project research, with rich theoretical experience. Field research and in-depth analysis of several PPP projects (including Pingyu water environmental treatment PPP project).
3	Construction company in Pingyu water environmental treatment PPP project	6 years	Participated in the whole construction process of Pingyu water environment treatment PPP project, have a detailed understanding of the project, familiar with the construction process risks.

. The information table for the assessment of linguistic variables is shown in

Table 5. Information sheet on the assessment of expert linguistic variables.

Risk Factor	O			S			D			Risk Factor	O			S			D
Expert	DM1	DM2	DM3	DM1	DM2	DM3	DM1	DM2	DM3	Expert	DM1	DM2	DM3	DM1	DM2	DM3	DM1	DM2	DM3
Risk factor weight	VH	H	VH	EH	EH	VH	H	H	VH	Risk factor weight	VH	H	VH	EH	EH	VH	H	H	VH
FM01	L	ML	L	H	M	H	L	ML	L	FM14	ML	ML	ML	M	M	MH	VL	L	L
FM02	L	L	L	H	H	VH	ML	M	ML	FM15	H	H	H	H	MH	H	M	M	M
FM03	ML	L	ML	MH	MH	H	M	ML	M	FM16	M	MH	MH	H	H	H	MH	H	H
FM04	L	L	ML	MH	H	H	H	MH	MH	FM17	ML	M	ML	H	MH	H	M	MH	M
FM05	M	M	M	MH	M	MH	ML	M	M	FM18	MH	H	MH	H	H	H	M	M	M
FM06	L	L	VL	EH	VH	VH	L	VL	L	FM19	ML	M	M	MH	H	H	ML	M	M
FM07	M	ML	M	M	MH	M	ML	L	ML	FM20	M	MH	MH	H	H	VH	M	MH	M
FM08	H	H	MH	MH	MH	MH	MH	H	H	FM21	M	ML	L	M	M	M	M	M	MH
FM09	MH	MH	MH	M	M	MH	H	H	H	FM22	M	M	M	VH	H	VH	MH	MH	M
FM10	MH	MH	MH	H	MH	H	MH	H	H	FM23	M	M	M	MH	H	H	H	MH	H
FM11	MH	H	MH	H	VH	H	MH	H	H	FM24	M	ML	M	ML	ML	L	MH	M	MH
FM12	M	H	M	MH	H	H	M	MH	MH	FM25	MH	MH	M	H	H	H	M	M	M
FM13	ML	ML	M	H	H	H	M	M	MH	FM26	MH	H	H	MH	H	MH	M	ML	M

.

4.2.2. Information Aggregation for Risk Factor Assessment Based on Intuitionistic Fuzzy Weighted Average Operators

Based on the above table of expert linguistic variable assessment information (Table 4), combined with the risk indicator linguistic variable rating table (Table 3), the IFPWA operator was used to assemble expert assessment information.

Take the occurrence of risk for risk indicator FM01 as an example, ${\tilde{\alpha }}_{F{M}_{01},1}^1=\left({0.150}^{\left(1\right)},{0.750}^{\left(1\right)}\right)$,${\tilde{\alpha }}_{F{M}_{01},1}^2=\left({0.350}^{\left(2\right)},{0.550}^{\left(2\right)}\right),{\tilde{\alpha }}_{F{M}_{01},1}^3=\left({0.150}^{\left(3\right)},{0.750}^{\left(3\right)}\right)$, Transforming ${\tilde{\alpha }}_{ij}^k=\left({\mu }_{ij}^{\left(k\right)},{\nu }_{ij}^{\left(k\right)}\right)$ using Equation (1) yields ${\tilde{\alpha }}^{*}{}_{F{M}_{01},1}^1=\left({0.750}^{\left(1\right)},{0.150}^{\left(1\right)}\right)$, ${\tilde{\alpha }}^{*}{}_{F{M}_{01},1}^2=\left({0.350}^{\left(2\right)},{0.550}^{\left(2\right)}\right)$, ${\tilde{\alpha }}^{*}{}_{F{M}_{01},1}^2=\left({0.750}^{\left(2\right)},{0.150}^{\left(2\right)}\right)$.

Use Equation (3) to calculate their modified score functions, substituting into Equation (2), and we get:

$$IFPWA\left({\tilde{\alpha }}_{F{M}_{01}1}^{*}{}^{\left(1\right)},{\tilde{\alpha }}_{F{M}_{01}1}^{*}{}^{\left(2\right)},{\tilde{\alpha }}_{F{M}_{01}1}^{*}{}^{\left(3\right)}\right)={\tilde{\alpha }}_{F{M}_{01}1}=\left(0.709,0.187\right)$$

Similarly, an intuitive fuzzy composite evaluation matrix of risk indicators can be obtained, as shown in

Table 6. Intuitionistic fuzzy integrated evaluation matrix.

Risk Factor	O	S	D	Risk Factor	O	S	D
FM01	(0.709, 0.187)	(0.189, 0.723)	(0.709, 0.187)	FM14	(0.550, 0.350)	(0.490, 0.504)	(0.800, 0.111)
FM02	(0.150, 0.750)	(0.150, 0.750)	(0.148, 0.752)	FM15	(0.150, 0.750)	(0.166, 0.733)	(0.500, 0.500)
FM03	(0.500, 0.500)	(0.166, 0.733)	(0.153, 0.746)	FM16	(0.470, 0.511)	(0.150, 0.750)	(0.335, 0.565)
FM04	(0.721, 0.176)	(0.335, 0.565)	(0.173, 0.727)	FM17	(0.540, 0.376)	(0.166, 0.733)	(0.479, 0.507)
FM05	(0.166, 0.733)	(0.337, 0.562)	(0.335, 0.565)	FM18	(0.337, 0.562)	(0.150, 0.750)	(0.500, 0.500)
FM06	(0.781, 0.126)	(0.025, 0.900)	(0.787, 0.121)	FM19	(0.535, 0.391)	(0.335, 0.565)	(0.535, 0.391)
FM07	(0.511, 0.464)	(0.479, 0.507)	(0.616, 0.278)	FM20	(0.470, 0.511)	(0.150, 0.750)	(0.479, 0.507)
FM08	(0.490, 0.504)	(0.470, 0.511)	(0.376, 0.542)	FM21	(0.560, 0.387)	(0.500, 0.500)	(0.490, 0.504)
FM09	(0.350, 0.550)	(0.490, 0.504)	(0.150, 0.750)	FM22	(0.500, 0.500)	(0.077, 0.848)	(0.361, 0.547)
FM10	(0.150, 0.750)	(0.150, 0.750)	(0.077, 0.847)	FM23	(0.500, 0.500)	(0.335, 0.565)	(0.166, 0.733)
FM11	(0.150, 0.750)	(0.075, 0.850)	(0.075, 0.850)	FM24	(0.511, 0.464)	(0.594, 0.302)	(0.376, 0.542)
FM12	(0.476, 0.518)	(0.335, 0.565)	(0.470, 0.511)	FM25	(0.361, 0.547)	(0.150, 0.750)	(0.500, 0.500)
FM13	(0.544, 0.365)	(0.150, 0.750)	(0.490, 0.504)	FM26	(0.335, 0.565)	(0.337, 0.562)	(0.511, 0.464)

.

4.3. Risk Factor Weighting

4.3.1. Determination of Subjective Weights Based on the Expert Assessment Method

The expert evaluation information for the three risk factors O, S, and D are shown in Table 4. Firstly, the expert information is assembled using Equation (2). The steps are the same as 4.2.2 to obtain the intuitive fuzzy comprehensive evaluation matrix of risk factor weights. The results are shown in Table 6. Using the corresponding score function values, the subjective weight values of the risk factors are obtained according to Equation (4) as ${\omega }_j^S=\{0.330,0.352,0.318\}$.

4.3.2. Objective Weighting Based on Deviation Maximization

Based on the intuitionistic fuzzy comprehensive evaluation matrix of risk factors in Table 6, the deviation maximization optimization model is constructed according to Equations (5) to (9), and the objective weight vector of risk factors is obtained as ${\omega }_j^O=\{0.314,0.298,0.443\}$; the objective and subjective weights are taken to be the same, i.e., ${\alpha }_1={\alpha }_2=0.5$; the total weight of risk factors is determined as ${\omega }_j=\{0.322,0.298,0.380\}$.

The weights for the three risk factors O, S, and D are calculated in the table shown in

Table 7. Calculation of risk factor weights.

Risk Factor	${\tilde{\mathit{\alpha }}}_{\mathit{j}}{}^{\left(1\right)}$	${\tilde{\mathit{\alpha }}}_{\mathit{j}}{}^{\left(2\right)}$	${\tilde{\mathit{\alpha }}}_{\mathit{j}}{}^{\left(3\right)}$	${\tilde{\mathit{\alpha }}}_{\mathit{j}}$	$\mathit{s}\left({\tilde{\mathit{\alpha }}}_{\mathit{j}}\right)$	${\mathit{\omega }}_{\mathit{j}}$
O	(0.850, 0.075)	(0.750, 0.150)	(0.850, 0.075)	(0.825, 0.092)	0.867	0.322
S	(0.900, 0.025)	(0.900, 0.025)	(0.850, 0.075)	(0.886, 0.035)	0.926	0.298
D	(0.750, 0.150)	(0.750, 0.150)	(0.850, 0.075)	(0.789, 0.119)	0.835	0.380

.

4.4. Ranking of Risk Indicators

According to the risk indicator ranking steps of IF-MULTIMOORA, the combined utility value, Tchebycheff distance and multiplicative utility value of the risk factors were obtained using Equations (10)–(12), respectively, as shown in

Table 8. Parameters related to the IF-MULTIMOORA method.

Risk Indicator	${\mathit{y}}_{\mathit{i}}$	${\mathit{d}}_{\mathit{m}\mathit{a}\mathit{x}}$	${\mathit{U}}_{\mathit{j}}$	Risk Indicator	${\mathit{y}}_{\mathit{i}}$	${\mathit{d}}_{\mathit{m}\mathit{a}\mathit{x}}$	${\mathit{U}}_{\mathit{j}}$
FM01	(0.635, 0.251)	0.242	(0.468, 0.435)	FM14	(0.690, 0.219)	0.152	(0.604, 0.340)
FM02	(0.158, 0.738)	0.377	(0.132, 0.779)	FM15	(0.339, 0.611)	0.274	(0.234, 0.692)
FM03	(0.296, 0.641)	0.375	(0.204, 0.715)	FM16	(0.352, 0.574)	0.295	(0.274, 0.648)
FM04	(0.460, 0.419)	0.367	(0.298, 0.596)	FM17	(0.448, 0.493)	0.248	(0.347, 0.590)
FM05	(0.303, 0.592)	0.295	(0.250, 0.654)	FM18	(0.386, 0.561)	0.253	(0.295, 0.639)
FM06	(0.693, 0.195)	0.290	(0.278, 0.568)	FM19	(0.507, 0.411)	0.206	(0.447, 0.477)
FM07	(0.572, 0.362)	0.170	(0.522, 0.436)	FM20	(0.419, 0.547)	0.253	(0.322, 0.629)
FM08	(0.460, 0.500)	0.276	(0.412, 0.551)	FM21	(0.537, 0.442)	0.226	(0.492, 0.499)
FM09	(0.337, 0.592)	0.377	(0.249, 0.666)	FM22	(0.359, 0.583)	0.283	(0.237, 0.693)
FM10	(0.127, 0.777)	0.409	(0.099, 0.822)	FM23	(0.346, 0.588)	0.369	(0.261, 0.659)
FM11	(0.104, 0.808)	0.410	(0.080, 0.850)	FM24	(0.507, 0.417)	0.276	(0.447, 0.484)
FM12	(0.457, 0.507)	0.235	(0.407, 0.559)	FM25	(0.393, 0.556)	0.253	(0.301, 0.635)
FM13	(0.451, 0.490)	0.253	(0.341, 0.595)	FM26	(0.435, 0.499)	0.217	(0.378, 0.556)

, which resulted in the ranking of the risk indicators under the IF-ratio system, IF-reference point method, and IF-full multiplicative model.

The final ranking of risk indicators based on the IF-MULTIMOORA method is shown in

Table 9. IF-MULTIMOORA method risk indicator ranking table.

Risk Indicator	IF-Ratio System	IF-Reference Point Method	IF-Full Multiplication Model	IF-MULTIMOORA	Risk Indicator	IF-Ratio System	IF-Reference Point Method	IF-Full Multiplication Model	IF-MULTIMOORA
FM01	24	20	24	23	FM01	25	26	26	26
FM02	3	3	3	3	FM02	6	14	5	9
FM03	4	5	4	4	FM03	10	9	10	10
FM04	19	7	14	11	FM04	16	19	17	18
FM05	5	8	8	6	FM05	11	17	11	12
FM06	26	10	15	16	FM06	22	24	22	24
FM07	23	25	25	25	FM07	13	15	13	14
FM08	17	12	20	15	FM08	21	22	23	22
FM09	7	4	7	5	FM09	9	11	6	8
FM10	2	2	2	2	FM10	8	6	9	7
FM11	1	1	1	1	FM11	20	13	21	20
FM12	15	21	19	19	FM12	12	18	12	13
FM13	18	16	16	17	FM13	14	23	18	21

, which gives the following ranking of risk indicators for the PingYu project.

4.5. Discussion

Using the improved FMEA method based on intuitionistic fuzzy MULTIMOORA proposed in this paper, the top five risk levels of the water environment treatment PPP project in Pingyu are financing risk (changing financing conditions/high costs), market changes, government intervention and credit problems, imperfect legal and regulatory systems, and inflation. Combined with the research results, in-depth interviews were conducted with project experts and the following insights were summarized:

Combined with the research results, in-depth interviews were conducted with project experts and the following insights were summarized:

Financing risk is the most common risk problem in PPP water environment treatment projects. Due to the public welfare nature of water environment treatment PPP projects, the project income is unstable, and the government is prone to financing risk if it simply seeks to reduce the project cost. Managers need to improve their ability to identify risks, understand the development prospects of the industry in the field of PPP projects, collect the data of similar projects, analyze the characteristics of their own projects, and formulate targeted preventive measures. Constantly broadening the financing channels, and thus changing the single financing method, through multi-channel financing can reduce the risks caused by the single financing method, and it can especially reduce some high-risk financing channels.

Market changes and inflation are market risks. Water environment treatment PPP projects are of strong public welfare nature, and their benefits are difficult to guarantee. Market changes can easily affect the projects. Project managers should always be familiar with the market situation, conduct scientific and sufficient market investigation, and do a good job of market risk emergency filing. A corresponding compensation mechanism may be specified in the relevant contract or agreement to ensure that the project has sufficient funds to ensure a reasonable return and the corresponding debt service capacity.

Government intervention and credit problems, and imperfect legal and regulatory systems are political risks. Since the government plays a dominant role in public welfare projects, and the government is less sensitive to changes in the market environment than social capital parties, the risk of government intervention will also have a significant impact on the implementation of projects. The government’s functions and powers at each stage of a PPP project should be clarified. The government must do what the law authorizes it to do. The establishment of a common governance system with project participants as the main body can promote the healthy development of PPP model. At the same time, since water environment treatment projects generally use feasibility gap subsidy and other ways to ensure the income of social capital, the government credit risk has an important impact on the operation of the project. To solve the trust-breaking problem, all the participants should help the spirit of the contract and cooperate sincerely to form a virtuous circle. Within the organization, managers should improve management systems and eliminate opportunism. In view of the risk of imperfect legal and regulatory systems, it is necessary to sort out the laws and regulations faced by the development, construction, and specific operation of the project, and strengthen the reasonable prevention of legal risks. When necessary, professional legal personnel should be used to ensure that the project construction and other activities are carried out legally and in compliance. Managers should improve the PPP supervision system, clarify the regulatory agencies, and distinguish the ownership of regulatory power, so as to solve the problem of social capital’s inappropriateness caused by excessive and insufficient supervision in PPP practice. Improving the PPP supervision system should also increase the transparency of PPP project information, reduce the information asymmetry, reduce the cost of supervision, and ensure the efficiency of supervision.

These measures are of great help to the risk management of Pingyu water environmental treatment PPP project and contribute to the sustainable development of the project. The risk assessment model proposed in this paper is suitable for most water environment treatment PPP project. Through the project risk assessment, the risk ranking can be clarified, so that the project manager can focus on the possible risks and allocate resources reasonably. Furthermore, they can make reasonable use of limited resources for the risks that are easy to occur and improve the utilization rate of resources. It helps project managers make correct decisions when facing risks and improve their ability to cope with risks.

This paper uses literature frequency statistics to synthesize risk indicators from fifteen papers. It combines semi-structured interviews to screen and supplement the indicator system. It also establishes a risk assessment system that covers the whole project life cycle and the possible occurrence of multiple types of risk indicators, which is more comprehensive. The improved FMEA method with the intuitive fuzzy concept still relies on expert judgment. However, it is reasonable to use this method to identify risk indicators from various aspects of the risk such as its O, S, and D. The results turn out to be more accurate than the previous way of risk assessment. The IF-MULTIMOORA method adopted in this paper solves the problem that the traditional MULTIMOORA method is only applicable to the real number background, and introduces the intuitionistic fuzzy priority weighted average operator (IFWA) and intuitionistic fuzzy weighted geometric operator (IFWG) into the ratio system and the whole model to avoid information loss, simple operation and robustness. It is possible to identify those risks that are prone to occur in a project so that targeted measures can be taken in advance and develop risk prevention strategies.

5. Conclusions

It is challenging to control pollution sources with water environment treatment PPP projects. The division of governance responsibilities between the government and governance units is unclear and technically complex. Identifying and preventing risks is even more critical. Taking the general theory of the PPP model as the cornerstone, this paper analyzes and studies the implementation of water environmental treatment PPP projects, and comprehensively identifies the risk indicators of the whole life cycle of water environmental treatment PPP projects by means of literature review and semi-structured interviews. Subsequently, the information on the assessment of risk indicators was intuitively fuzzy processed, and a comprehensive weighting method combining the expert assessment method and the deviation maximization model method is used to determine the total weighting of the risk factors from both subjective and objective aspects, and finally, MULTIMOORA is used to determine the ranking of the project risk indicators.

The theoretical contributions of this paper are mainly:

• The improved FMEA method is used to evaluate the risk indicators from the three aspects of O, S and D, which is more specific and comprehensive and improves the accuracy of evaluation.
• The introduced intuitive fuzzy risk assessment linguistic variables and the determination of subjective and objective weights based on the expert assessment method and the deviation maximization method, overcome the shortcomings of the previous risk indicator evaluation in which it is difficult to evaluate accurately and the risk factor weights are unreasonable.
• The IF-ratio system, IF-reference point method, IF-full multiplication model, and advantage theory are used to obtain the risk degree ranking of risk indicators, avoiding the situation where RPN is the same and difficult to sort.

There are still improvements that can be made to this paper:

• There are deficiencies in identifying risk indicators for water environmental treatment PPP projects. This paper identifies risk indicators through a literature review and semi-structured interviews. Although the risk indicators were identified under various methodological theories regarding the literature screening process, the list of risk indicators was determined without particular revision in conjunction with the various stages of the water environmental treatment PPP project. Improvements can continue to be made.
• Although the risk indicator assessment provided the ranking for the risk degree, it did not refine the results nor determine the corresponding degree index of risk indicators. The original decision matrix of this paper was obtained mostly in the way of Delphi research, over-relying on the experts’ own experience and knowledge structure. However, more data is needed to support the conclusion.