A Federated Mixed Logit Model for Personal Mobility Service in Autonomous Transportation Systems
Abstract
:1. Introduction
- How to preserve user data privacy while creating a shareable and customized intelligent core to support and optimize the operation of the service [19];
- How to coordinate the idle resources allocated at the edge to ease the burden of the central server and improve the robustness of the service in the meantime [20];
- How to serve mass heterogeneous users by addressing their diversified mobility demands with user-oriented solutions for a high quality of service (QoS) [21].
- An MXL-oriented federated learning problem with local and global learning steps is first defined to harness the travel choice heterogeneity of individuals by building their local models synergistically and privately.
- FMXL is designed with two species, i.e., FMXL-SPL (FMXL based on sampling) and FMXL-AGG (FMXL based on aggregation). In particular, in global learning, FMXL-SPL can estimate a distribution equivalent to the posterior distribution of conventional MXL, and FMXL-AGG can simplify the distribution estimation by the average aggregation operation for better performance.
- FMXL is evaluated based on a public dataset (Swissmetro) with static and dynamic recommendation scenarios. As a result, it can improve model predicted rates by about 10% compared to a flat logit model and reduce estimation time by about compared to a centralized MXL model.
2. Literature Review
2.1. Emerging Challenges
- Data security and privacy: It is defined as preventing direct access to users’ private data, which has become a widespread concern. For instance, cooperative ITS (C-ITS) in the EU must acquire an explicit consent agreement before processing the user data [29]. Therefore, data silos as represented by smart objects associated with individuals tend to be more restricted to prevent the actual application of PMS.
- Service scalability and latency: It represents the ability to serve a large number of users while guaranteeing quick responses. With the continuous growth of user volumes, the central cloud may become the performance bottleneck for an immediate response, as it undertakes the majority of functionalities to support PMS [17,20]. In such a case, the reliability and availability of PMS may be downgraded when maintaining high QoS (e.g., less latent and intrusive in providing service responses).
- User heterogeneity and personalization: It reflects the behavioral diversity among users, which can be similar or discrepant with a dynamic nature related to time, space, and people. Accordingly, to better support user demands in various manners, PMS needs to handle user heterogeneity and provide personalized recommendations efficiently and effectively [30].
2.2. Related Solutions
3. Methodology
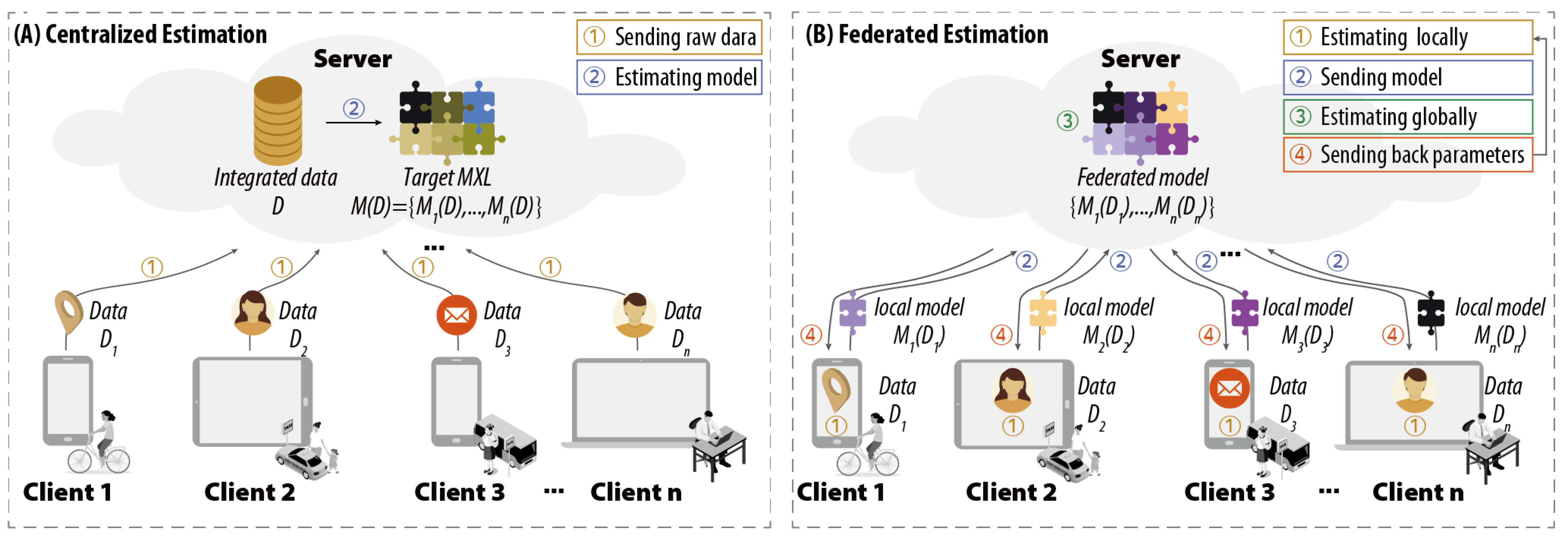
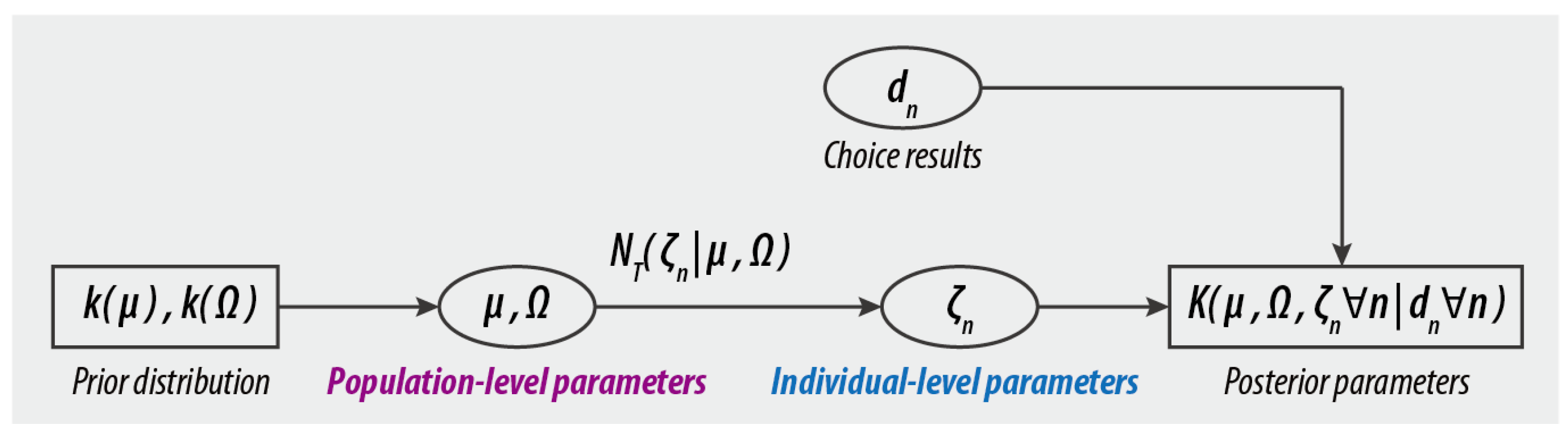
3.1. Problem Definition
- Privacy: As an essential precondition, each client does not share data , but only communicates with the server to exchange learning parameters, such as local model .
- Synergetic: The estimation process operates simultaneously and collaboratively both at server and clients, which can improve the utilization of resources at the edge and reduce the workload of the server in the cloud.
- Heterogeneous: The estimated model can be heterogeneous across clients to represent individual-level preferences.
3.2. Mixed Logit Model (MXL)
3.3. The Proposed Federated Mixed Logit Model (FMXL)
- Local Estimation, in which each client estimates its individual-level parameters based on local data;
- Global Estimation, in which the server updates the population-level parameters based on non-intrusive and sensitive information (including but not limited to individual-level parameters) from the clients;
- Interaction Mechanism, which specifies how the server and clients interact with each other to achieve a valid estimation required by the model.
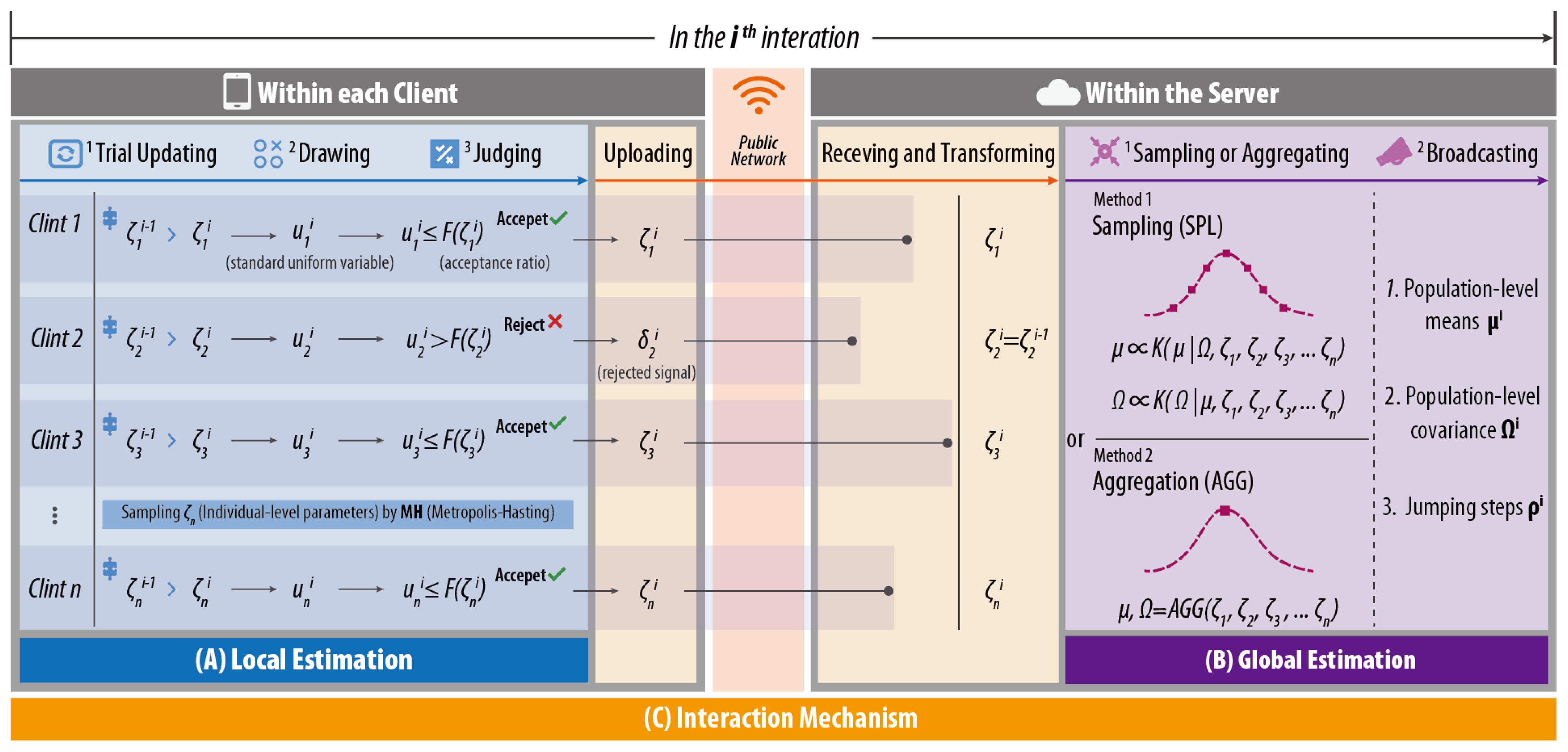
3.3.1. Local Estimation in the Client
- Step I: For client n, a trial value of is created according to Equation (11).where is the Cholesky factor of , v are M independent variables from , and is a parameter of the jumping distribution specified by the server in every iteration;
- Step II: Accordingly, a standard uniform variable u is drawn, according to Equation (12).where represents standard uniform distribution;
- Step III: An acceptance ratio is calculated according to Equation (13):
- Step IV: If , is accepted, and then, let ; otherwise, let .
3.3.2. Global Estimation in the Server
- Sampling-based method (FMXL-SPL): It follows the standard Gibbs approach to sample the conditional posterior of global parameters;
- Aggregation-based method (FMXL-AGG): It adopts the widely-used federated average algorithm FedAvg [22] to calculate the global parameters.
Sampling (SPL)-Based Method—FMXL-SPL
- Step I: First, by drawing M-dimensional multivariate standard normal , and then calculating the Choleski factor of , can be estimated according to Equation (19):
- Step II: Based on the M-dimensional standard normal distribution for , noted as , the Choleski factor of can be calculated, and finally, can be obtained according to Equation (20) directly:
Aggregation (AGG) Method—FMXL-AGG
3.3.3. Synchronous Client–Server Interaction
| Algorithm 1 Pseudocode for FMXL model. |
|
4. Performance Evaluation
4.1. Evaluation Preparation
4.1.1. Data and Model Structure
4.1.2. Simulation Settings and Scenarios
- Static estimation: We assume that all data have already been generated. The model is estimated under 30,000 iterations, 15,000 of which are used as burn-in draws, while the remaining are used to update posterior distributions.
- Dynamic estimation: We assume that the number of clients and their local data will increase gradually and dynamically in each estimation round (which consists of 2000 iterations). Specifically, the initial number of clients to activate the estimation is 300, which will increase at a random rate between 8% to 10% of the total clients until the total number of 840 is reached. Moreover, the local dataset of the client contains 1∼2 initial menus and grows with 1∼2 menus per estimation round.
4.1.3. Evaluation Metrics and Baselines
- Log-Likelihood (LL): It is calculated according to Equation (26), where Y represents the number of samples in the test set and represents the logit probability of sample y;
- Predicted Rate (PR): According to Equation (27), is a binary variable, which is one if the model predicts the mode correctly, and otherwise zero;
- Estimation Time (ET): In each iteration, ET can be split into two parts, i.e., computation time and communication time. Accordingly, of centralized and federated approaches are defined by Equations (28) and (29), respectively, in which, represents the number of participated clients; and represent computation time of client n and the server at the iteration, respectively; represents communication time of client n at the iteration. Note that the communication time in the downlink, as well as the computation time in each local client, is ignored, since the time consumed in the uplink is negligible compared to the one of downlink [45], and in this study, clients are utilized to measure how the workload can be reduced for the central server by using the idle resources at the edge.
- Flat logit model (FAL): It represents the willingness-to-pay form (explained in Section 4.1.1), which assumes that the preference parameters do not vary across individuals. Moreover, it is estimated by centralized MH sampling.
- Mixed logit model (MXL): It is the foundation model of our proposed FMXL. In addition, it is estimated by the centralized three-layered Gibbs sampling process.
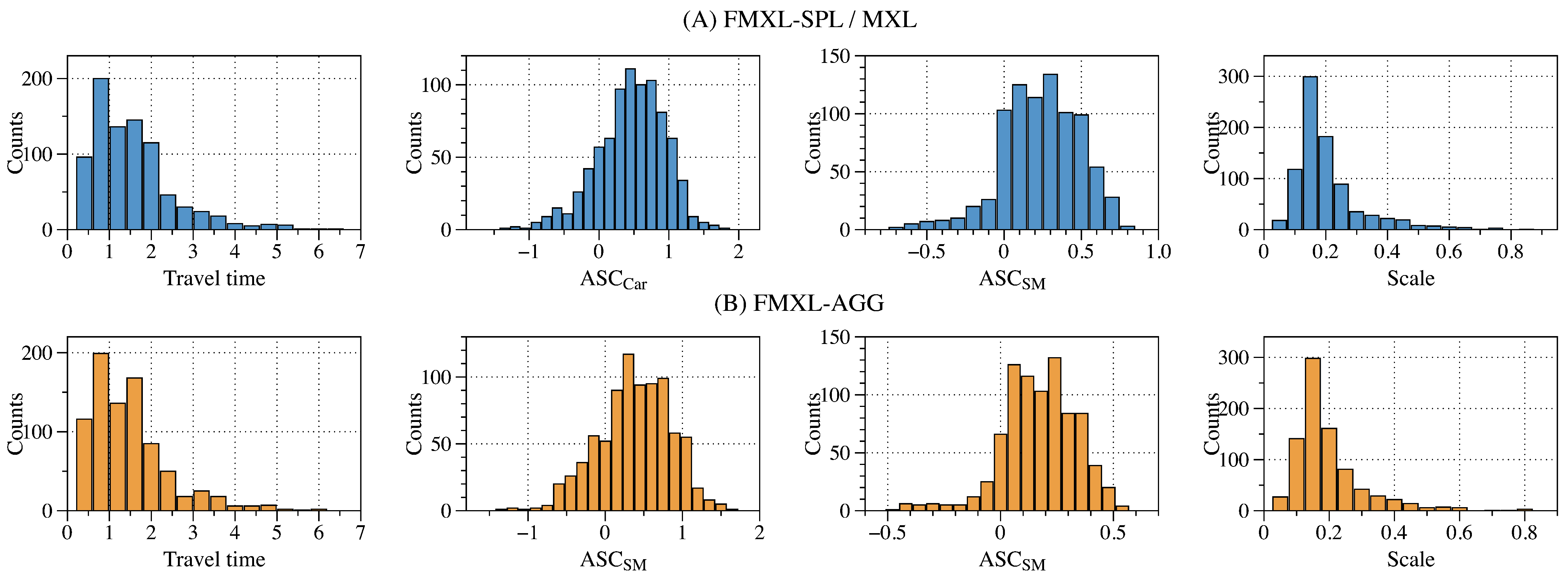
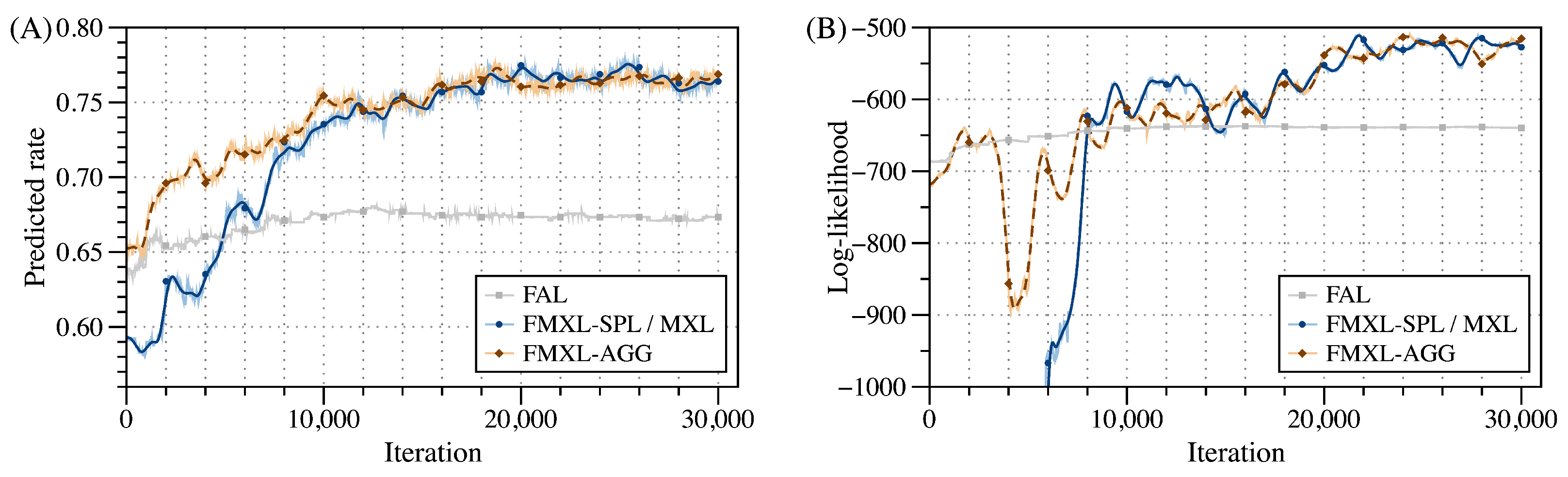
4.2. Evaluation Results
4.2.1. Evaluation Results of Static Estimation
4.2.2. Evaluation Results of Dynamic Estimation
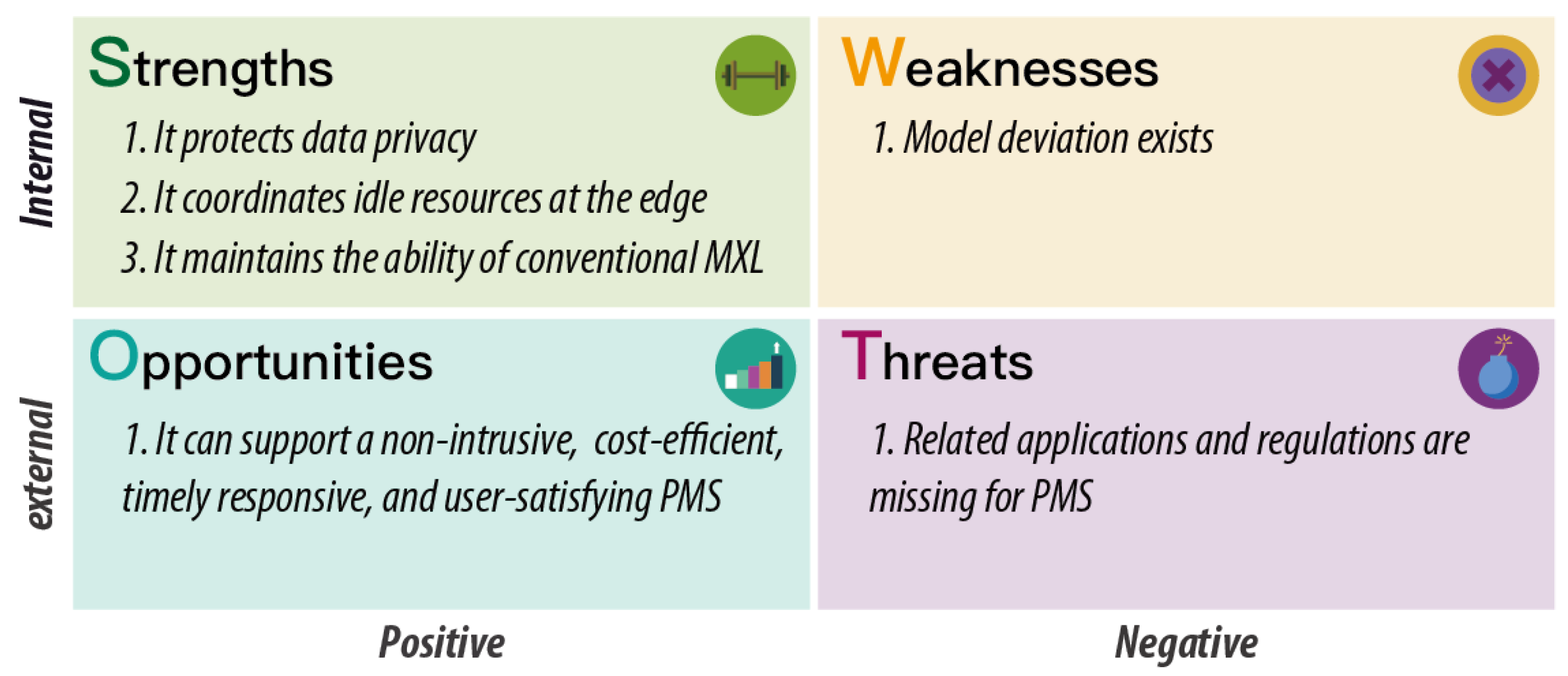
- It inherits the advantages of both FL and MXL that can better harness the heterogeneity among users in a collaborative and privacy-preserving manner.
- It can reduce ET by about 40% compared to the centralized baselines, and can better support the dynamic scenarios with a stable performance growth and also the highest PR and LL, improved by about 13% and 19%, respectively.
4.3. Discussions
4.3.1. Application for Individual Travelers
4.3.2. Application for System Modelers
4.3.3. Application for Service Managers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TS | Transportation Systems |
| ITS | Intelligent Transportation Systems |
| ATS | Autonomous Transportation Systems |
| MS | Mobility Service |
| PMS | Personal Mobility Service |
| QoS | Quality of Service |
| AI | Artificial Intelligence |
| FL | Federated Learning |
| DCM | Discrete Choice Model |
| MXL | Mixed Logit Model |
| FMXL | Federated Mixed Logit model |
| FMXL-SPL | FMXL based on Sampling |
| FMXL-AGG | FMXL based on Aggregation |
| LL | Log-Likelihood |
| PR | Predicted Rate |
| ET | Estimation Time |
| FAL | Flat Logit |
References
- You, L.; Tunçer, B.; Zhu, R.; Xing, H.; Yuen, C. A Synergetic Orchestration of Objects, Data, and Services to Enable Smart Cities. IEEE Internet Things J. 2019, 6, 10496–10507. [Google Scholar] [CrossRef]
- Czech, P. Autonomous Vehicles: Basic Issues. Sci. J. Silesian Univ. Technol. Ser. Transp. 2018, 100, 15–22. [Google Scholar] [CrossRef]
- Hamadneh, J.; Esztergár-Kiss, D. The Influence of Introducing Autonomous Vehicles on Conventional Transport Modes and Travel Time. Energies 2021, 14, 4163. [Google Scholar] [CrossRef]
- Singh, S.; Saini, B.S. Autonomous Cars: Recent Developments, Challenges, and Possible Solutions. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1022, 012028. [Google Scholar] [CrossRef]
- Turoń, K.; Czech, P. The Concept of Rules and Recommendations for Riding Shared and Private E-Scooters in the Road Network in the Light of Global Problems. In Modern Traffic Engineering in the System Approach to the Development of Traffic Networks; Macioszek, E., Sierpiński, G., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1083, pp. 275–284. [Google Scholar]
- You, L.; Zhao, F.; Cheah, L.; Jeong, K.; Zegras, P.C.; Ben-Akiva, M. A Generic Future Mobility Sensing System for Travel Data Collection, Management, Fusion, and Visualization. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4149–4160. [Google Scholar] [CrossRef]
- You, L.; He, J.; Wang, W.; Cai, M. Autonomous Transportation Systems and Services Enabled by the Next-Generation Netw. IEEE Netw. 2022, 36, 66–72. [Google Scholar] [CrossRef]
- Lewicki, W.; Stankiewicz, B.; Olejarz-Wahba, A.A. The Role of Intelligent Transport Systems in the Development of the Idea of Smart City. In Smart and Green Solutions for Transport Systems; Sierpiński, G., Ed.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1091, pp. 26–36. [Google Scholar]
- Schéele, S. A Supply Model for Public Transit Services. Transp. Res. Part B Methodol. 1980, 14, 133–146. [Google Scholar] [CrossRef]
- Spieser, K.; Treleaven, K.; Zhang, R.; Frazzoli, E.; Morton, D.; Pavone, M. Toward a Systematic Approach to the Design and Evaluation of Automated Mobility-on-Demand Systems: A Case Study in Singapore. In Road Vehicle Automation; Meyer, G., Beiker, S., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 229–245. [Google Scholar]
- Nikitas, A.; Kougias, I.; Alyavina, E.; Njoya Tchouamou, E. How Can Autonomous and Connected Vehicles, Electromobility, BRT, Hyperloop, Shared Use Mobility and Mobility-As-A-Service Shape Transport Futures for the Context of Smart Cities? Urban Sci. 2017, 1, 36. [Google Scholar] [CrossRef] [Green Version]
- You, L.; Motta, G.; Liu, K.; Ma, T. CITY FEED: A Pilot System of Citizen-Sourcing for City Issue Management. ACM Trans. Intell. Syst. Technol. 2016, 7, 1–25. [Google Scholar] [CrossRef]
- Sarasini, S.; Linder, M. Integrating a Business Model Perspective into Transition Theory: The Example of New Mobility Services. Environ. Innov. Soc. Transit. 2018, 27, 16–31. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Yang, C.S.; Yu, L.C.; Lin, C.F.; Yao, H.H.; Chen, D.Y.; Lai, K.R.; Chang, P.C. Development of a Cloud-Based Service Framework for Energy Conservation in a Sustainable Intelligent Transportation System. Int. J. Prod. Econ. 2015, 164, 454–461. [Google Scholar] [CrossRef]
- Bitam, S.; Mellouk, A. Its-Cloud: Cloud Computing for Intelligent Transportation System. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 2054–2059. [Google Scholar]
- Din, S.; Paul, A.; Rehman, A. 5G-enabled Hierarchical Architecture for Software-Defined Intelligent Transportation System. Comput. Netw. 2019, 150, 81–89. [Google Scholar] [CrossRef]
- Manogaran, G.; Alazab, M. Ant-Inspired Recurrent Deep Learning Model for Improving the Service Flow of Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3654–3663. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, J.J.Q.; Kang, J.; Niyato, D.; Zhang, S. Privacy-Preserving Traffic Flow Prediction: A Federated Learning Approach. IEEE Internet Things J. 2020, 7, 7751–7763. [Google Scholar] [CrossRef]
- Hahn, D.; Munir, A.; Behzadan, V. Security and Privacy Issues in Intelligent Transportation Systems: Classification and Challenges. IEEE Intell. Transp. Syst. Mag. 2019, 13, 181–196. [Google Scholar] [CrossRef] [Green Version]
- Yu, R.; Huang, X.; Kang, J.; Ding, J.; Maharjan, S.; Gjessing, S.; Zhang, Y. Cooperative Resource Management in Cloud-Enabled Vehicular Networks. IEEE Trans. Ind. Electron. 2015, 62, 7938–7951. [Google Scholar] [CrossRef]
- Sodhro, A.H.; Obaidat, M.S.; Abbasi, Q.H.; Pace, P.; Pirbhulal, S.; Yasar, A.; Fortino, G.; Imran, M.A.; Qaraqe, M. Quality of Service Optimization in an IoT-driven Intelligent Transportation System. IEEE Wirel. Commun. 2019, 26, 10–17. [Google Scholar] [CrossRef] [Green Version]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Artificial Intelligence and Statistics; PMLR: Fort Lauderdale, FL, USA, 2017; pp. 1273–1282. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated Machine Learning: Concept and Applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and Open Problems in Federated Learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- You, L.; Liu, S.; Chang, Y.; Yuen, C. A Triple-Step Asynchronous Federated Learning Mechanism for Client Activation, Interaction Optimization, and Aggregation Enhancement. IEEE Internet Things J. 2022. [Google Scholar] [CrossRef]
- McFadden, D.; Train, K. Mixed MNL Models for Discrete Response. J. Appl. Econom. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Danaf, M.; Becker, F.; Song, X.; Atasoy, B.; Ben-Akiva, M. Online Discrete Choice Models: Applications in Personalized Recommendations. Decis. Support Syst. 2019, 119, 35–45. [Google Scholar] [CrossRef]
- Song, X.; Danaf, M.; Atasoy, B.; Ben-Akiva, M. Personalized Menu Optimization with Preference Updater: A Boston Case Study. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 599–607. [Google Scholar] [CrossRef] [Green Version]
- Vinel, A.; Lyamin, N.; Isachenkov, P. Modeling of V2V Communications for C-ITS Safety Applications: A CPS Perspective. IEEE Commun. Lett. 2018, 22, 1600–1603. [Google Scholar] [CrossRef]
- Nabizadeh, A.H.; Leal, J.P.; Rafsanjani, H.N.; Shah, R.R. Learning Path Personalization and Recommendation Methods: A Survey of the State-of-the-Art. Expert Syst. Appl. 2020, 159, 113596. [Google Scholar] [CrossRef]
- Crivellari, A.; Beinat, E. LSTM-Based Deep Learning Model for Predicting Individual Mobility Traces of Short-Term Foreign Tourists. Sustainability 2020, 12, 349. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Li, T.; Hu, R.; Fu, Y.; Gu, J.; Xiong, H. Joint Representation Learning for Multi-Modal Transportation Recommendation. Proc. AAAI Conf. Artif. Intell. 2019, 33, 1036–1043. [Google Scholar] [CrossRef]
- Liu, H.; Tong, Y.; Zhang, P.; Lu, X.; Duan, J.; Xiong, H. Hydra: A Personalized and Context-Aware Multi-Modal Transportation Recommendation System. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA; pp. 2314–2324. [Google Scholar]
- Zhu, X.; Wang, F.; Chen, C.; Reed, D.D. Personalized Incentives for Promoting Sustainable Travel Behaviors. Transp. Res. Part C Emerg. Technol. 2020, 113, 314–331. [Google Scholar] [CrossRef]
- Azevedo, C.L.; Seshadri, R.; Gao, S.; Atasoy, B.; Akkinepally, A.P.; Christofa, E.; Zhao, F.; Trancik, J.; Ben-Akiva, M. Tripod: Sustainable Travel Incentives with Prediction, Optimization, and Personalization. In Proceedings of the Transportation Research Record 97th Annual Meeting, Washington, DC, USA, 7–11 January 2018. [Google Scholar]
- Zhu, X.; Feng, J.; Huang, S.; Chen, C. An Online Updating Method for Time-Varying Preference Learning. Transp. Res. Part C Emerg. Technol. 2020, 121, 102849. [Google Scholar] [CrossRef]
- Liu, H.; Tong, Y.; Han, J.; Zhang, P.; Lu, X.; Xiong, H. Incorporating Multi-Source Urban Data for Personalized and Context-Aware Multi-Modal Transportation Recommendation. IEEE Trans. Knowl. Data Eng. 2022, 34, 723–735. [Google Scholar] [CrossRef]
- Lin, G.; Liang, F.; Pan, W.; Ming, Z. Fedrec: Federated Recommendation with Explicit Feedback. IEEE Intell. Syst. 2020, 36, 21–30. [Google Scholar] [CrossRef]
- Yu, C.; Qi, S.; Liu, Y. FedDeepFM: Ad CTR Prediction Based on Federated Factorization Machine. In Proceedings of the 2021 IEEE Sixth International Conference on Data Science in Cyberspace (DSC), Shenzhen, China, 9–11 October 2021; pp. 195–202. [Google Scholar]
- Scarpa, R.; Alberini, A.; Bateman, I.J. (Eds.) Applications of Simulation Methods in Environmental and Resource Economics; The Economics of Non-Market Goods and Resources; Springer: Dordrecht, The Netherlands, 2005; Volume 6. [Google Scholar]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Chib, S.; Greenberg, E. Understanding the Metropolis-Hastings Algorithm. Am. Stat. 1995, 49, 327–335. [Google Scholar]
- Bierlaire, M.; Axhausen, K.; Abay, G. The Acceptance of Modal Innovation: The Case of Swissmetro. In Proceedings of the Swiss Transport Research Conference, Ascona, Switzerland, 1–3 March 2001. [Google Scholar]
- Ben-Akiva, M.; McFadden, D.; Train, K. Foundations of Stated Preference Elicitation: Consumer Behavior and Choice-Based Conjoint Analysis. Found. Trends® Econom. 2019, 10, 1–144. [Google Scholar] [CrossRef] [Green Version]
- Dinh, C.T.; Tran, N.H.; Nguyen, M.N.; Hong, C.S.; Bao, W.; Zomaya, A.Y.; Gramoli, V. Federated Learning over Wireless Networks: Convergence Analysis and Resource Allocation. IEEE/ACM Trans. Netw. 2020, 29, 398–409. [Google Scholar] [CrossRef]
- Schein, A.I.; Popescul, A.; Ungar, L.H.; Pennock, D.M. Methods and Metrics for Cold-Start Recommendations. In Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Tampere, Finland, 11–15 August 2002; pp. 253–260. [Google Scholar]
- Cottrill, C.D.; Pereira, F.C.; Zhao, F.; Dias, I.F.; Lim, H.B.; Ben-Akiva, M.E.; Zegras, P.C. Future Mobility Survey: Experience in Developing a Smartphone-Based Travel Survey in Singapore. Transp. Res. Rec. J. Transp. Res. Board 2013, 2354, 59–67. [Google Scholar] [CrossRef] [Green Version]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially Private Federated Learning: A Client Level Perspective. arXiv 2017, arXiv:1712.07557. [Google Scholar]
- Phong, L.T.; Aono, Y.; Hayashi, T.; Wang, L.; Moriai, S. Privacy-Preserving Deep Learning via Additively Homomorphic Encryption. IEEE Trans. Inf. Forensics Secur. 2017, 13, 1333–1345. [Google Scholar] [CrossRef]

| Related Solutions | Data Security and Privacy | Service Scalability and Latency | User Heterogeneity and Personalization | |
|---|---|---|---|---|
| ML-based model | Trans2vec [32] | ○ | ○ | ◐ |
| Hydra-L [33] | ○ | ○ | ◐ | |
| Hydra-H [37] | ○ | ● | ◐ | |
| FedDeepFM [39] | ● | ● | ○ | |
| FedRec [38] | ● | ● | ○ | |
| DCM-based model | LCM-T [36] | ○ | ◐ | ◐ |
| MXL [26] | ○ | ○ | ● | |
| Online-MXL [27] | ○ | ◐ | ● | |
| FL+DCM | FMXL (Proposed) | ● | ● | ● |
| Predicted Rate | Log-Likelihood | Estimation Time (s) | |||
|---|---|---|---|---|---|
| Communication | Computation | Total | |||
| FAL | 67.342% | −638.859 | 3.790 | 58.622 | 62.412 |
| MXL | 77.254% | −542.542 | 3.790 | 75.987 | 79.777 |
| FMXL-SPL | 77.254% | −542.542 | 5.427 | 41.465 | 46.892 |
| FMXL-AGG | 77.100% | −548.169 | 5.427 | 28.186 | 33.613 |
| FAL | FMXL-SPL / MXL | FMXL-AGG | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Fixed | |||||||||
| Posterior Mean | Std. Dev. | Posterior Mean | Std. Dev. | Posterior Mean | Std. Dev. | Posterior Mean | Std. Dev. | Posterior Mean | Std. Dev. | |
| 0.071 | 0.037 | −0.014 | 0.059 | 0.892 | 0.131 | −0.033 | 0.036 | 0.839 | 0.073 | |
| 0.627 | 0.047 | 0.479 | 0.064 | 0.546 | 0.086 | 0.429 | 0.042 | 0.498 | 0.058 | |
| 0.606 | 0.048 | 0.248 | 0.058 | 0.263 | 0.055 | 0.246 | 0.030 | 0.135 | 0.020 | |
| −0.625 | 0.039 | −2.020 | 0.096 | 0.939 | 0.127 | −1.915 | 0.072 | 0.857 | 0.060 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, L.; He, J.; Zhao, J.; Xie, J. A Federated Mixed Logit Model for Personal Mobility Service in Autonomous Transportation Systems. Systems 2022, 10, 117. https://doi.org/10.3390/systems10040117
You L, He J, Zhao J, Xie J. A Federated Mixed Logit Model for Personal Mobility Service in Autonomous Transportation Systems. Systems. 2022; 10(4):117. https://doi.org/10.3390/systems10040117
Chicago/Turabian StyleYou, Linlin, Junshu He, Juanjuan Zhao, and Jiemin Xie. 2022. "A Federated Mixed Logit Model for Personal Mobility Service in Autonomous Transportation Systems" Systems 10, no. 4: 117. https://doi.org/10.3390/systems10040117
APA StyleYou, L., He, J., Zhao, J., & Xie, J. (2022). A Federated Mixed Logit Model for Personal Mobility Service in Autonomous Transportation Systems. Systems, 10(4), 117. https://doi.org/10.3390/systems10040117






