Exploring the Effect of Misinformation on Infectious Disease Transmission
Abstract
1. Introduction
- Karafillakis and Larson [11] identified the most common reasons for vaccine hesitancy, namely, perceptions that: (1) new vaccines are developed too quickly resulting in insufficient testing; (2) a pandemic is not a life-threatening illness, and is comparable to mild flu; and (3) a vaccine could cause disease and long-term adverse reactions;
- Lorini et al. [7] summarised the ‘3C’ model of factors for vaccine hesitancy. The factors that influence the vaccination decision are: (1) complacency, as people do not value the vaccine as a need, (2) convenience, in that the vaccine is difficult to access, and (3) confidence, as the vaccine or provider is not trusted;
- Wiyeh et al. [12] described the spread of vaccine hesitancy as an “outbreak”. The researchers make a distinction between vaccine hesitancy behaviours: baseline vaccine hesitancy, which refers to the level of refusal or delay in vaccine acceptance that is constantly present in the population and, while it may vary, changes are unlikely to be sudden; reactive vaccine hesitancy, where the delay in acceptance due to vaccine-related events shows a rapid spike in hesitancy levels, usually subsiding at a slow rate.
2. Literature Review
2.1. Related Information, Fear and Rumour Spreading Dynamic Models
2.2. Related Infectious Disease and Vaccination Dynamic Models
3. Material and Methods
3.1. System Dynamics Sensitivity Analysis Combined with Loop Impact Analysis
- Positive feedback loop (reinforcing), a feedback loop is positive if a change in the source variable will cause the target to change in the same direction;
- Negative feedback loop (balancing), a feedback loop is negative if a change in the source variable will cause the target to change in the opposite direction.
- Dominant loop: A loop that is primarily responsible for model behaviour over some time interval is known as a dominant loop [40];
- Dominant structure: A model’s dominant structure is a subset of the model’s feedback structure, which is responsible for the model’s particular behaviour;
- Point of inflection (POI): A point of inflection is a time of notable change in a model’s behaviour. It is a point on the logistic curve where the loop reaches half of its maximum value.
3.2. LTM Method
- The link score is computed for stocks, connectors, and flows. It measures the contribution and polarity of a link between an independent variable and a dependent variable;
- The loop score is computed as a product of link scores. It measures the contribution of a feedback loop to the behaviour of the model and is indicative of the feedback polarity;
- The relative loop score is a normalised loop score measure taking on a value between −1 and 1. It reports the polarity and fractional contribution of a feedback loop to the change in the value of all stocks at a point in time [47].
3.3. The Misinformation/Disease Model Structure
Fraction × Vaccine Confidence(t)
3.4. The Misinformation/Disease Model Interaction
3.5. The Misinformation/Disease Model Feedback Loops
4. Experimental Results
4.1. Exploring a Range of R0 Values
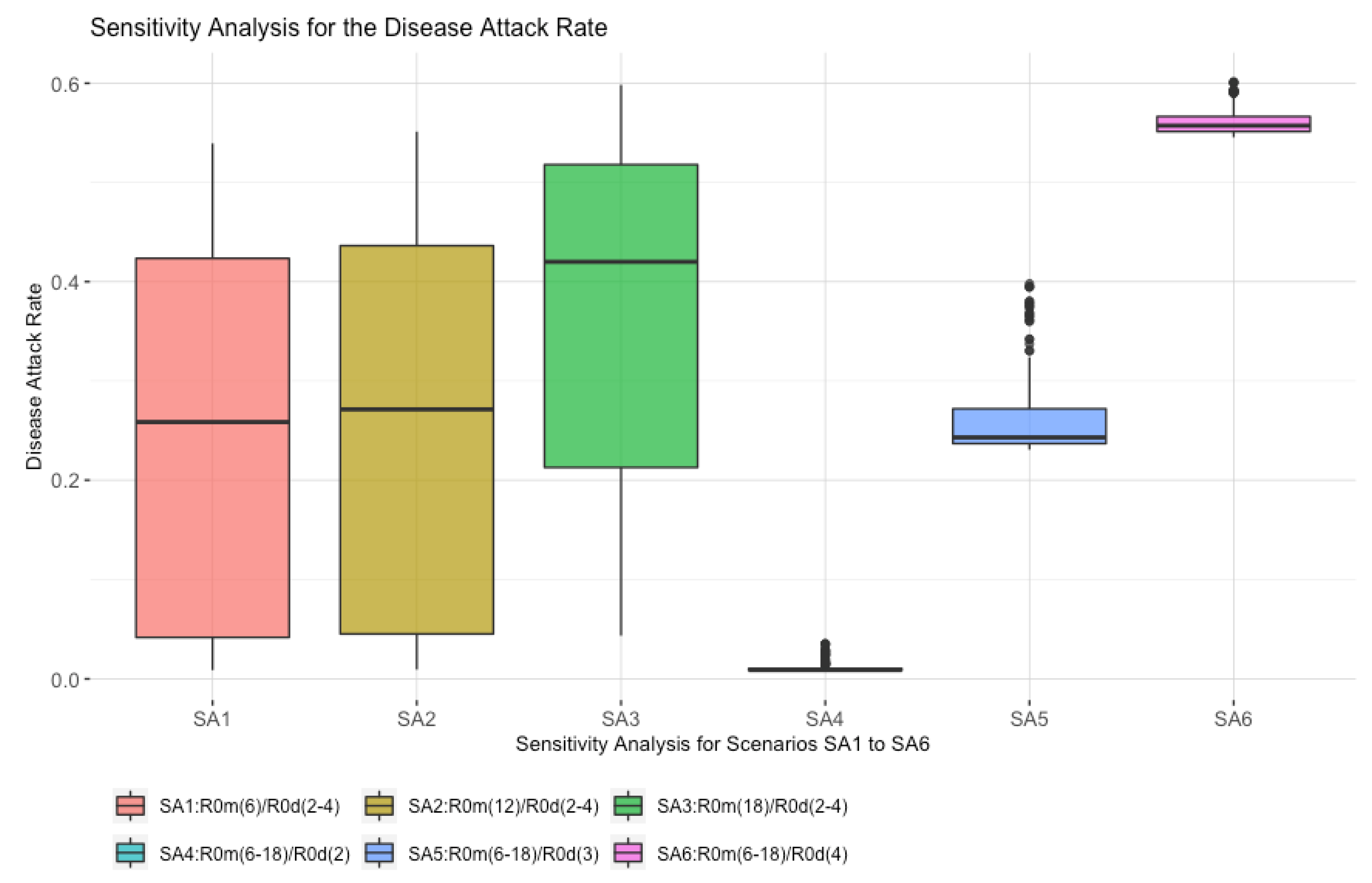
4.2. Sensitivity Analysis for Scenarios SA1 to SA6
- The highest median value for the disease attack rate is scenario SA6, where R0d is fixed at four, and R0m varies between six and eighteen. This shows the potential impact that a strong misinformation contagion process has on the outcome;
- Scenario SA1 has the R0m at six, although, even with this low value, the maximum disease attack rate is high at over 40%. This shows reduced vaccine confidence results in lower vaccine uptake;
- Scenario SA3 shows a significant increase in the disease attack rate as compared to SA1 and SA2, where R0d varies between two and four, and R0m is fixed at 18. This shows the impact of high misinformation, which leads to lower vaccine uptake, thereby providing the disease with more opportunities to spread.
- There is an overall pattern whereby varying R0m (SA4, SA5, and SA6) has a higher impact on the disease attack rate than varying R0d (SA1, SA2, and SA3).
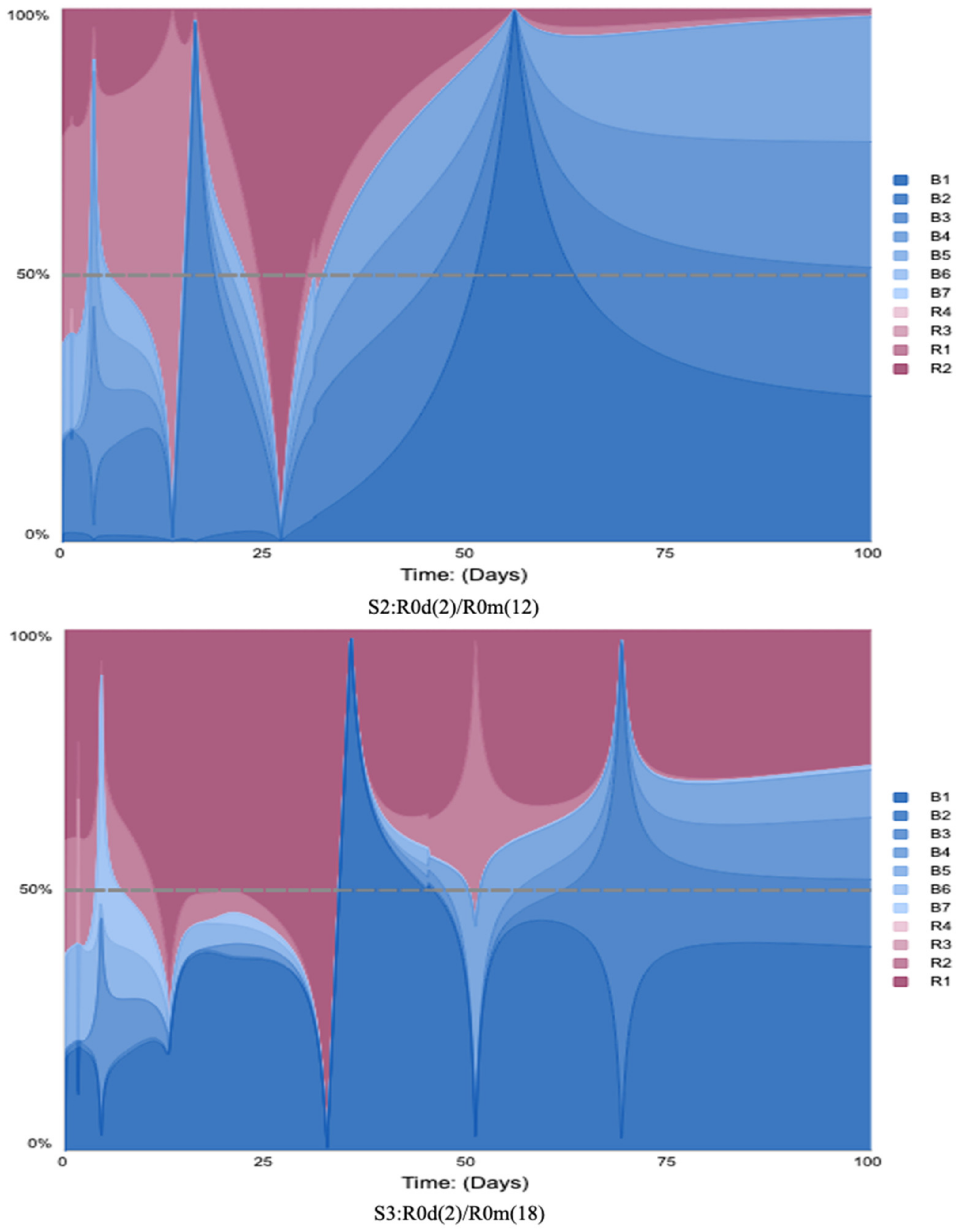
4.3. The Scenarios S1 to S9 with LTM Analysis
- When R0d is fixed at two, and R0m varies between 12 and 18, scenarios S1, S2, and S3 show a notable change in the reinforcing loops’ average relative scores, from 17% to 41%. However, with R0m fixed at six, when R0d varies, (S1, S4, and S7) the reinforcing loops’ average relative scores do not increase. This suggests that the variation in R0m has a bigger impact on the reinforcing loops’ dominance;
- When R0d equals three and R0m varies between six and eighteen (S4, S5, and S6), the reinforcing loops’ average relative scores change from 18% to 29%. With R0m fixed at 12 (S2, S5, and S8), the reinforcing contribution increases from 24% to 42%;
- When R0d equals four, and R0m varies between 12 and 18 (S7, S8, and S9), the reinforcing loops’ average relative scores change from 16% to 23%. With R0m fixed at 18 (S3, S6, and S9), the reinforcing contribution decreases from 41% to 23%. The decline in the reinforcing contribution is caused by vaccine confidence stock, which is a goal-seeking structure. The result shows that high disease and misinformation impact model feedback loops scores and the vaccine confidence stock’s goal-seeking structure adjust the vaccine confidence level.
| R0m | Low Value (L) = 6 | Feedback Loop’s Score | Medium Value (M) = 12 | Feedback Loop’s Score | High Value (H) = 18 | Feedback Loop’s Score | |
|---|---|---|---|---|---|---|---|
| R0d | |||||||
| Low Value (L) = 2 | S1 | R = 17.69% B = 82.31% | S2 | R = 24.19% B = 75.81% | S3 | R = 41.21% B = 58.79% | |
| Medium Value (M) = 3 | S4 | R = 18.1% B = 81.9% | S5 | R = 24.06% B = 75.94% | S6 | R = 29.57% B = 70.43% | |
| High Value (H) = 4 | S7 | R = 16.26% B = 83.74% | S8 | R = 42.03% B = 57.97% | S9 | R = 23.16% B = 76.84% | |

4.4. Sensitivity Analysis SA1 to SA6 Combined with LTM
- Scenario SA6 shows the highest impact for the B5 (vaccine confidence adjustment) feedback loop, where R0d is fixed at four, and R0m varies between six and eighteen. The B5 (vaccine confidence adjustment) feedback loop’s relative score increases by more than −25%. This shows the potential impact of the misinformation contagion process;
- Scenario SA1 shows the least impact for the B5 (vaccine confidence adjustment) feedback loop, where R0m is fixed at six, and R0d varies between two and four, although even with this low value, the B5 (vaccine confidence adjustment) feedback loop’s relative score increases by almost −22%. This shows the impact of reduced vaccine confidence, leading to a change in the vaccine confidence rate;
- Scenario SA3 also shows an impact on the B5 (vaccine confidence adjustment) feedback loop, where R0d varies between two and four, and R0m is fixed at 18. The B5 (vaccine confidence adjustment) feedback loop’s relative score is almost −25%. This shows the effect of high misinformation, leading to lower vaccine uptake;
- Scenario SA4 shows an increase for the B5 (vaccine confidence adjustment) feedback loop score, where R0d is fixed at two, and R0m varies between six and eighteen, although, even with this low value of R0d, the B5 (vaccine confidence adjustment) feedback loop’s relative score increases by almost −19%. This shows the impact of R0m and R0d, leading to change in the vaccine confidence and disease attack rate;
- The analysis shows a pattern whereby varying R0m (SA4, SA5, and SA6) has a higher impact on the loop score for B5 (vaccine confidence adjustment) and disease attack rate, as well than varying R0d (SA1, SA2, and SA3).
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bloom, B.R.; Marcuse, E.; Mnookin, S. Addressing Vaccine Hesitancy. Science 2014, 344, 339. [Google Scholar] [CrossRef] [PubMed]
- Morens, D.M.; Fauci, A.S. Emerging Infectious Diseases: Threats to Human Health and Global Stability. PLoS Pathog. 2013, 9, e1003467. [Google Scholar] [CrossRef] [PubMed]
- CDC. List of Vaccines Used in United States. Available online: https://www.cdc.gov/vaccines/vpd/vaccines-list.html (accessed on 6 April 2022).
- Wolfe, R.; Sharp, L. Anti-vaccinationists Past and Present. BMJ 2002, 325, 430–432. [Google Scholar] [CrossRef] [PubMed]
- Rosselli, R.; Martini, M.; Bragazzi, N.L. The old and the new: Vaccine hesitancy in the era of the Web 2.0. Challenges and opportunities. J. Prev. Med. Hyg. 2016, 57, E47–E50. [Google Scholar]
- MacDonald, N.E.; Eskola, J.; Liang, X.; Chaudhuri, M.; Dube, E.; Gellin, B.; Goldstein, S.; Larson, H.; Manzo, M.L.; Reingold, A.; et al. Vaccine Hesitancy: Definition, Scope and Determinants. Vaccine 2015, 33, 4161–4164. [Google Scholar] [CrossRef]
- Lorini, C.; Santomauro, F.; Donzellini, M.; Capecchi, L.; Bechini, A.; Boccalini, S.; Bonanni, P.; Bonaccorsi, G. Health literacy and vaccination: A systematic review. Hum. Vaccines Immunother. 2018, 14, 478–488. [Google Scholar] [CrossRef]
- Larson, H. Prof Heidi Larson (LSHTM) on Her Book Stuck: How Vaccine Rumors Start—And Why They Don’t Go Away. Online Interview. 2020. Available online: https://www.youtube.com/watch?v=MM-JiQhYDbw (accessed on 15 October 2020).
- Larson, H.J.; Jarrett, C.; Eckersberger, E.; Smith, D.M.D.; Paterson, P. Understanding Vaccine Hesitancy around Vaccines and Vaccination from a Global Perspective: A Systematic Review of Published Literature, 2007–2012. Vaccine 2014, 32, 2150–2159. [Google Scholar] [CrossRef]
- Who.Int. Addressing Vaccine Hesitancy. Available online: https://www.who.int/immunization/sage/meetings/2014/october/3_SAGE_WG_Strategies_addressing_vaccine_hesitancy_2014.pdf (accessed on 15 February 2020).
- Karafillakis, E.; Larson, H.J. The benefit of the doubt or doubts over benefits? A systematic literature review of perceived risks of vaccines in European populations. Vaccine 2017, 35, 4840–4850. [Google Scholar] [CrossRef]
- Wiyeh, A.B.; Cooper, S.; Nnaji, C.A.; Wiysonge, C.S. Vaccine hesitancy ‘outbreaks’: Using epidemiological modeling of the spread of ideas to understand the effects of vaccine related events on vaccine hesitancy. Expert Rev. Vaccines 2018, 17, 1063–1070. [Google Scholar] [CrossRef]
- Tafuri, S.; Gallone, M.S.; Cappelli, M.G.; Martinelli, D.; Prato, R.; Germinario, C. Addressing the anti-vaccination movement and the role of HCWs. Vaccine 2014, 32, 4860–4865. [Google Scholar] [CrossRef]
- Davies, P.; Chapman, S.; Leask, J. Antivaccination Activists on the World Wide Web. Arch. Dis. Child. 2002, 87, 22–25. [Google Scholar] [CrossRef]
- Celentano, D.D.; Thomas, W.V. Social Networks and Health: Models, Methods, and Applications. Am. J. Epidemiol. 2010, 172, 488. [Google Scholar] [CrossRef]
- Larson, H.J.; De Figueiredo, A.; Xiahong, Z.; Schulz, W.S.; Verger, P.; Johnston, I.G.; Cook, A.R.; Jones, N.S. The State of Vaccine Confidence 2016: Global Insights Through a 67-Country Survey. eBioMedicine 2016, 12, 295–301. [Google Scholar] [CrossRef]
- Lahouati, M.; De Coucy, A.; Sarlangue, J.; Cazanave, C. Spread of vaccine hesitancy in France: What about YouTube™? Vaccine 2020, 38, 5779–5782. [Google Scholar] [CrossRef]
- The Guardian. I’m Not an Anti-Vaxxer, but US Health Workers’ Vaccine Hesitancy Raises Alarm. Available online: https://www.theguardian.com/world/2021/jan/10/coronavirus-covid-19-vaccine-hesitancy-us-health-workers (accessed on 10 January 2021).
- Thaker, J.; Subramanian, A. Exposure to COVID-19 Vaccine Hesitancy Is as Impactful as Vaccine Misinformation in Inducing a Decline in Vaccination Intentions in New Zealand: Results from Pre-Post Between-Groups Randomized Block Experiment. Front. Commun. 2021, 6, 159. [Google Scholar] [CrossRef]
- Law, T. Israel’s COVID-19 Vaccination Rollout Is Slowing at a Critical Moment. That’s a Warning for the Rest of Us. Time. Available online: https://time.com/5947967/israel-covid-vaccine-rollout/ (accessed on 8 June 2021).
- Sontag, A.; Rogers, T.; Yates, C.A. Misinformation can prevent the suppression of epidemics. J. R. Soc. Interface 2022, 19, 20210668. [Google Scholar] [CrossRef]
- Gabriel, C.; Carter, T. Information Transmission Through Human Informants: Simulation. CASOS 1996. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, J. Dynamical Model about Rumor Spreading with Medium. Discret. Dyn. Nat. Soc. 2013, 2013, 586867. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Cintrón-Arias, A.; Kaiser, D.; Castillo-Chavez, C. The power of a good idea: Quantitative modeling of the spread of ideas from epidemiological models. Phys. A Stat. Mech. Its Appl. 2006, 364, 513–536. [Google Scholar] [CrossRef]
- Epstein, J.M.; Parker, J.; Cummings, D.; Hammond, R.A. Coupled Contagion Dynamics of Fear and Disease: Mathematical and Computational Explorations. PLoS ONE 2008, 3, e3955. [Google Scholar] [CrossRef]
- Li, C. A study on time-delay rumor propagation model with saturated control function. Adv. Differ. Equ. 2017, 2017, 255. [Google Scholar] [CrossRef]
- Liu, X.; Li, T.; Tian, M. Rumor spreading of a SEIR model in complex social networks with hesitating mechanism. Adv. Differ. Equ. 2018, 2018, 391. [Google Scholar] [CrossRef]
- Larson, H. Stuck: Vaccine Rumors Start and Why They Don’t Go Away; Oxford University Press: New York, NY, USA, 2020. [Google Scholar]
- Ehrhardt, M.; Gašper, J.; Kilianová, S. SIR-based mathematical modeling of infectious diseases with vaccination and waning immunity. J. Comput. Sci. 2019, 37, 101027. [Google Scholar] [CrossRef]
- Raimundo, S.M.; Yang, H.M.; Engel, A.B. Modelling the effects of temporary immune protection and vaccination against infectious diseases. Appl. Math. Comput. 2007, 189, 1723–1736. [Google Scholar] [CrossRef]
- Hamami, D.; Cameron, R.; Pollock, K.G.; Shankland, C. Waning Immunity Is Associated with Periodic Large Outbreaks of Mumps: A Mathematical Modeling Study of Scottish Data. Front. Physiol. 2017, 8, 233. [Google Scholar] [CrossRef]
- Leung, T.; Campbell, P.; Hughes, B.D.; Frascoli, F.; McCaw, J.M. Infection-acquired versus vaccine-acquired immunity in an SIRWS model. Infect. Dis. Model. 2018, 3, 118–135. [Google Scholar] [CrossRef]
- Nkamba, L.N.; Manga, T.T.; Agouanet, F.; Manyombe, M.L.M. Mathematical model to assess vaccination and effective contact rate impact in the spread of tuberculosis. J. Biol. Dyn. 2019, 13, 26–42. [Google Scholar] [CrossRef]
- Rabiu, M.; Willie, R.; Parumasur, N. Mathematical analysis of a disease-resistant model with imperfect vaccine, quarantine and treatment. Ric. Mat. 2020, 69, 603–627. [Google Scholar] [CrossRef]
- Ghaffarzadegan, N.; Lyneis, J.; Richardson, G.P. How small system dynamics models can help the public policy process. Syst. Dyn. Rev. 2010, 27, 22–44. [Google Scholar] [CrossRef]
- Darabi, N.; Hosseinichimeh, N. System dynamics modeling in health and medicine: A systematic literature review. Syst. Dyn. Rev. 2020, 36, 29–73. [Google Scholar] [CrossRef]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modeling for a Complex World; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Duggan, J.; Oliva, R. Methods for Identifying Structural Dominance. Syst. Dyn. Rev. 2013, 29. (Virtual Special Issue). Available online: https://www.researchgate.net/publication/272823783_Methods_of_identifying_structural_dominance (accessed on 9 June 2021).
- Ford, D. A behavioral approach to feedback loop dominance analysis. Syst. Dyn. Rev. 1999, 15, 3–36. [Google Scholar] [CrossRef]
- Peterson, D.W.; Eberlein, R.L. Reality check: A bridge between systems thinking and system dynamics. Syst. Dyn. Rev. 1994, 10, 159–174. [Google Scholar] [CrossRef]
- Ford, A.; Flynn, H. Statistical screening of system dynamics models. Syst. Dyn. Rev. 2005, 21, 273–303. [Google Scholar] [CrossRef]
- Kampmann, C.E.; Oliva, R. Loop eigenvalue elasticity analysis: Three case studies. Syst. Dyn. Rev. 2006, 22, 141–162. [Google Scholar] [CrossRef]
- Güneralp, B. Towards coherent loop dominance analysis: Progress in eigenvalue elasticity analysis. Syst. Dyn. Rev. 2006, 22, 263–289. [Google Scholar] [CrossRef]
- Mojtahedzadeh, M.; Andersen, D.; Richardson, G.P. Using Digest to implement the pathway participation method for detecting influential system structure. Syst. Dyn. Rev. 2004, 20, 1–20. [Google Scholar] [CrossRef]
- Loops That MatterTM Overview. Available online: https://www.iseesystems.com/resources/help/v2/Content/05b%20-LoopsThatMatter/LTMOverview.htm (accessed on 12 September 2021).
- Schoenberg, W.; Davidsen, P.; Eberlein, R. Understanding model behavior using the Loops that Matter method. Syst. Dyn. Rev. 2020, 36, 158–190. [Google Scholar] [CrossRef]
- Schoenberg, W.; Hayward, J.; Eberlein, R. Improving Loops that Matter. Proceedings Systemdynamics.org. 2021. Available online: https://proceedings.systemdynamics.org/2021/papers/P1036.pdf (accessed on 18 October 2021).
- Biggerstaff, M.; Cauchemez, S.; Reed, C.; Gambhir, M.; Finelli, L. Estimates of the reproduction number for seasonal, pandemic, and zoonotic influenza: A systematic review of the literature. BMC Infect. Dis. 2014, 14, 480. [Google Scholar] [CrossRef]
- Vivion, M.; Sidi, E.A.L.; Betsch, C.; Dionne, M.; Dubé, E.; Driedger, S.M.; Gagnon, D.; Graham, J.; Greyson, D.; Hamel, D.; et al. Prebunking messaging to inoculate against COVID-19 vaccine misinformation: An effective strategy for public health. J. Commun. Health 2022, 15, 1–11. [Google Scholar] [CrossRef]
- Salathé, M.; Khandelwal, S. Assessing Vaccination Sentiments with Online Social Media: Implications for Infectious Disease Dynamics and Control. PLoS Comput. Biol. 2011, 7, e1002199. [Google Scholar] [CrossRef] [PubMed]
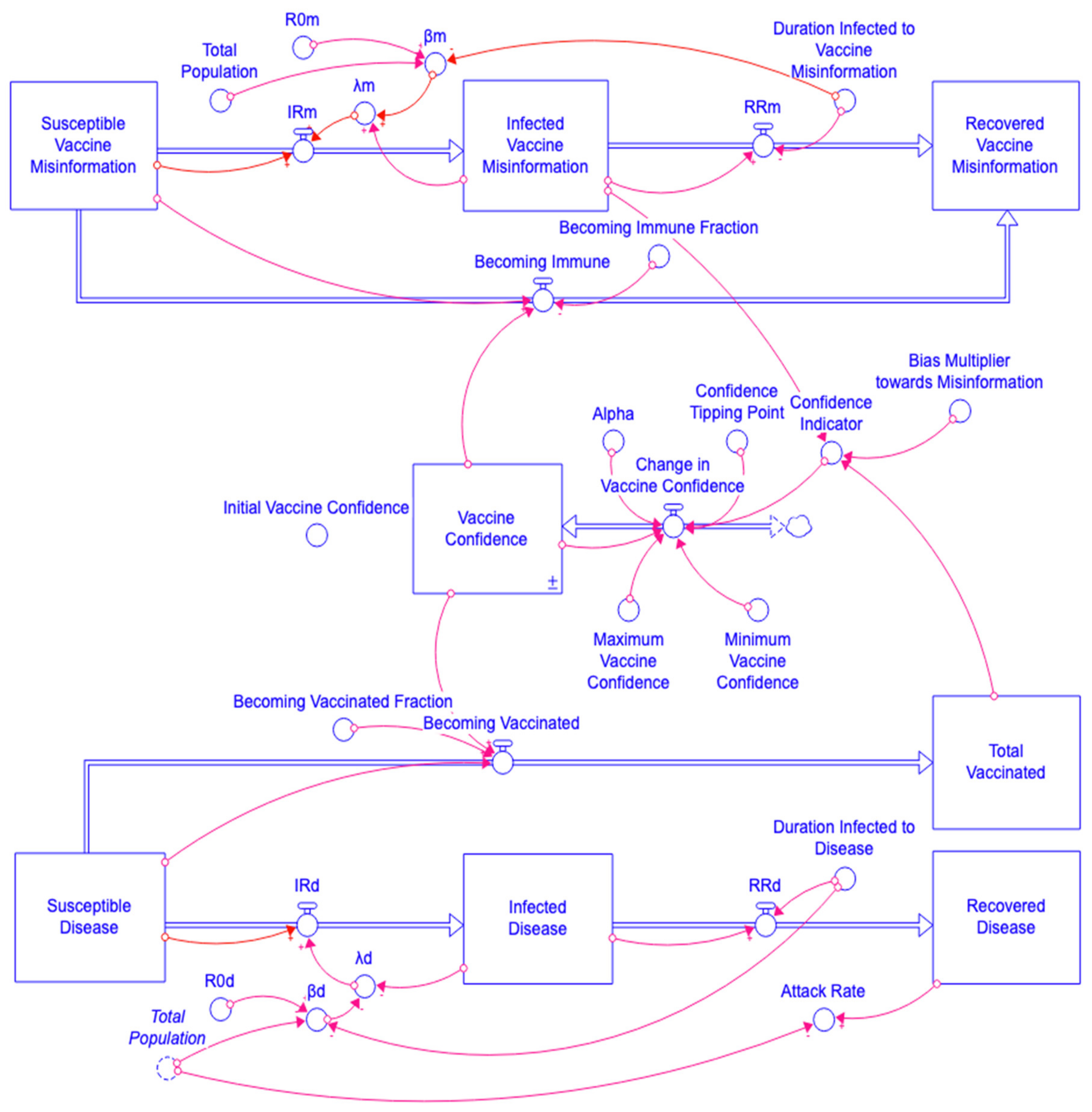




| Loop ID | Loop Description | Loop Variables |
|---|---|---|
| R1 | Misinformation contagion process | Infected Vaccine Misinformation → λm → IRm → Infected Vaccine Misinformation |
| R2 | Disease contagion process | Infected Disease → λd → IRd → Infected Disease |
| R3 | Vaccine Confidence leads to more vaccinations, which in turn increase Vaccine Confidence | Vaccine Confidence → Becoming Vaccinated → Total Vaccinated → Confidence Indicator → Change in Vaccine Confidence → Vaccine Confidence |
| R4 | Vaccine Confidence reduces the spread of misinformation, which increases Vaccine Confidence | Vaccine Confidence → Becoming Immune → Susceptible Vaccine Misinformation → IRm → Infected Vaccine Misinformation → Confidence Indicator → Change in Vaccine Confidence → Vaccine Confidence |
| B1 | Misinformation recovery | Infected Vaccine Misinformation → RRm → Infected Vaccine Misinformation |
| B2 | Disease recovery | Infected Disease → RRd → Infected Disease |
| B3 | Immune to misinformation reduces misinformation vulnerability | Susceptible Vaccine Misinformation → Becoming Immune → Susceptible Vaccine Misinformation |
| B4 | Vaccination reduces disease vulnerability | Susceptible Disease → Becoming Vaccinated → Susceptible Disease |
| B5 | Vaccine confidence adjustment | Vaccine Confidence → Change in Vaccine Confidence → Vaccine Confidence |
| B6 | Depletion disease | Susceptible Disease → IRd → Susceptible Disease |
| B7 | Depletion misinformation | Susceptible Vaccine Misinformation → IRm → Susceptible Vaccine Misinformation |
| R0m | Low Value (L) = 6 | Medium Value (M) = 12 | High Value (H) = 18 | |
|---|---|---|---|---|
| R0d | ||||
| Low Value (L) = 2 | S1 | S2 | S3 | |
| Medium Value (M) = 3 | S4 | S5 | S6 | |
| High Value (H) = 4 | S7 | S8 | S9 | |
| No | R0m | R0d |
|---|---|---|
| SA1 | R0m = 6 (Low) | R0d = Uniform (2,4) |
| SA2 | R0m = 12 (Medium) | R0d = Uniform (2,4) |
| SA3 | R0m = 18 (High) | R0d = Uniform (2,4) |
| SA4 | R0m = Uniform (6,18) | R0d = 2 (Low) |
| SA5 | R0m = Uniform (6,18) | R0d = 3 (Medium) |
| SA6 | R0m = Uniform (6,18) | R0d = 4 (High) |
| R0m | Low Value (L) = 6 | Disease Attack Rate | Medium Value (M) = 12 | Disease Attack Rate | High Value (H) = 18 | Disease Attack Rate | |
|---|---|---|---|---|---|---|---|
| R0d | |||||||
| Low Value (L) = 2 | S1 | 0.01 | S2 | 0.012 | S3 | 0.057 | |
| Medium Value (M) = 3 | S4 | 0.23 | S5 | 0.243 | S6 | 0.404 | |
| High Value (H) = 4 | S7 | 0.545 | S8 | 0.557 | S9 | 0.602 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mumtaz, N.; Green, C.; Duggan, J. Exploring the Effect of Misinformation on Infectious Disease Transmission. Systems 2022, 10, 50. https://doi.org/10.3390/systems10020050
Mumtaz N, Green C, Duggan J. Exploring the Effect of Misinformation on Infectious Disease Transmission. Systems. 2022; 10(2):50. https://doi.org/10.3390/systems10020050
Chicago/Turabian StyleMumtaz, Nabeela, Caroline Green, and Jim Duggan. 2022. "Exploring the Effect of Misinformation on Infectious Disease Transmission" Systems 10, no. 2: 50. https://doi.org/10.3390/systems10020050
APA StyleMumtaz, N., Green, C., & Duggan, J. (2022). Exploring the Effect of Misinformation on Infectious Disease Transmission. Systems, 10(2), 50. https://doi.org/10.3390/systems10020050






