An Epidemiological Analysis for Assessing and Evaluating COVID-19 Based on Data Analytics in Latin American Countries
Abstract
Simple Summary
Abstract
1. Introduction
- (i)
- Investigation of COVID-19 behavior in Latin America based on confirmed cases and deaths reported up until 31 December 2021.
- (ii)
- Mapping of the incidence rate by country to assess COVID-19 in Latin America.
- (iii)
- Forecasting of COVID-19 cases in Latin American countries until January 2022.
- (iv)
- Comparison of the trend changes in COVID-19 by country, observing and describing the number of infection waves each country experienced.
- (v)
- Formulation of the basic (instantaneous or effective) reproduction number () with values across different countries and the analysis of the effects of quarantine measures on transmission rates [35].
- (vi)
- Proposal of an epidemic model to predict future disease spread, which can serve as a tool for developing predictive scenarios.
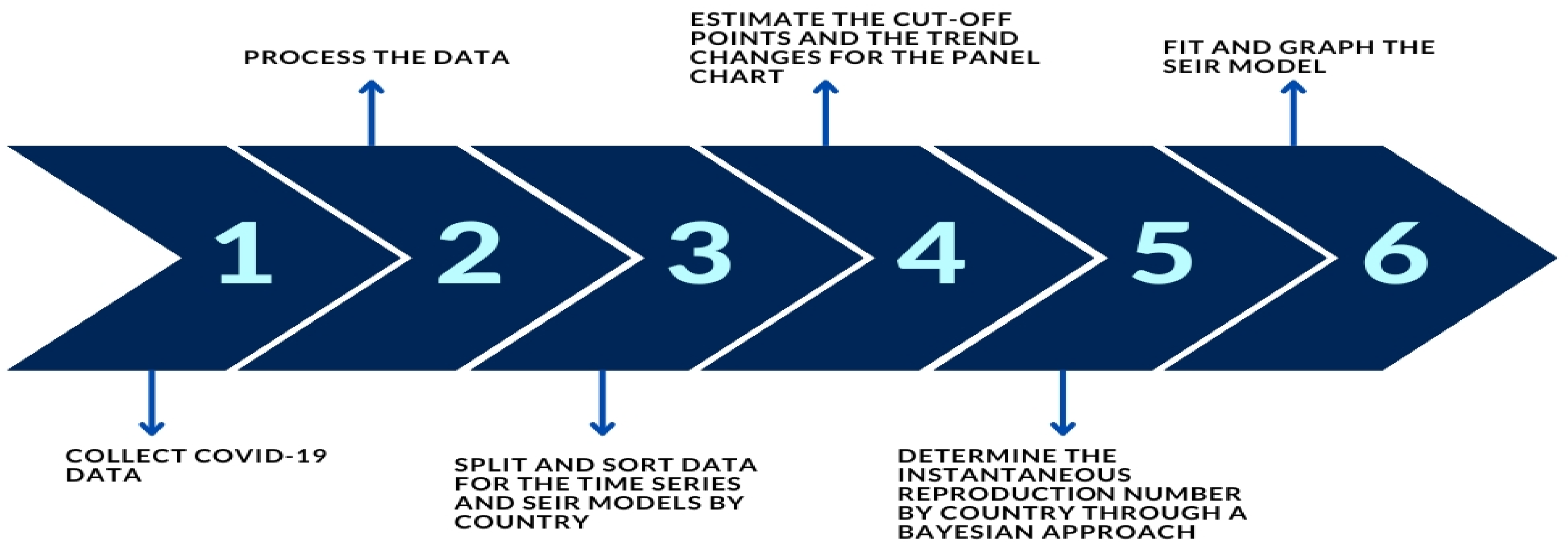
2. Methodology
2.1. Estimation of the Instantaneous Reproduction Number
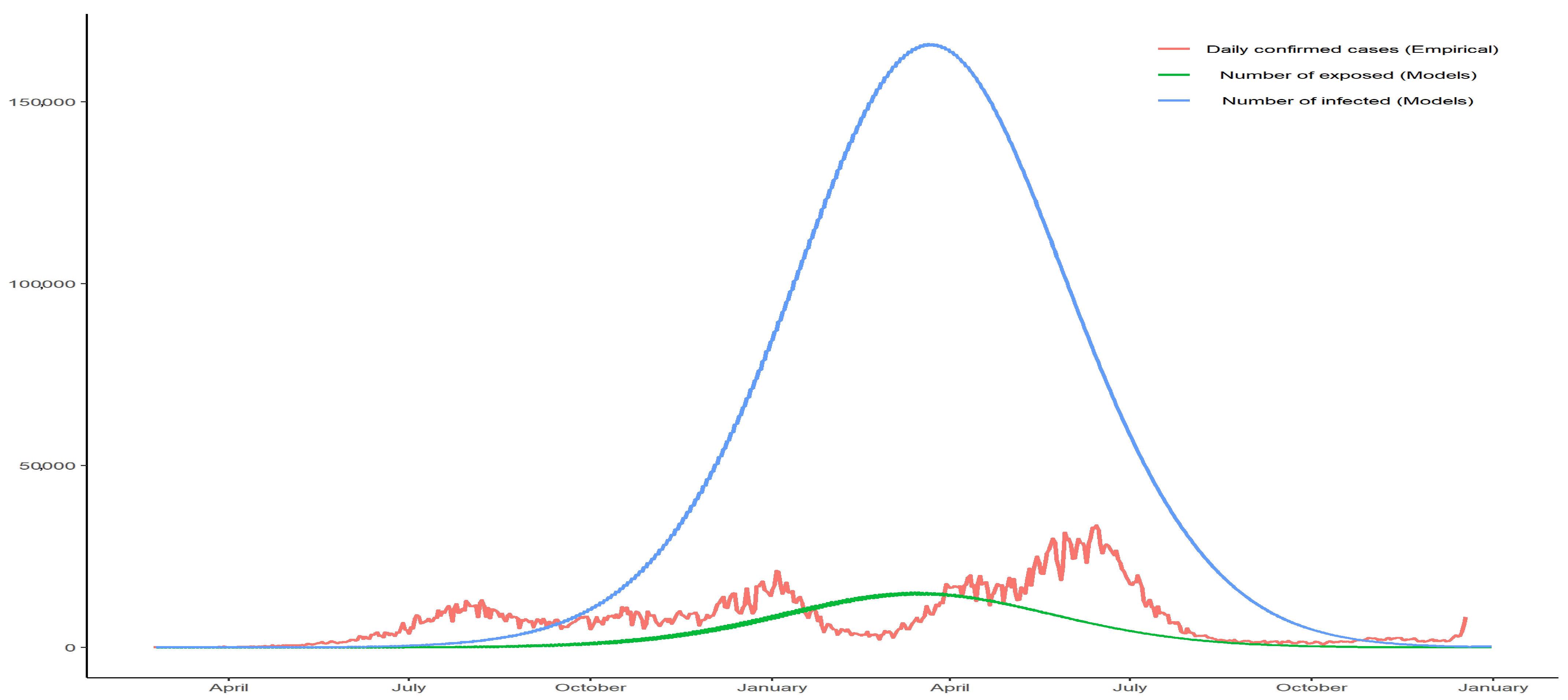
2.2. SEIR Model
2.3. Time-Series Models and Forecasting
| Algorithm 1 Automatic ARIMA modeling procedure |
|
2.4. Trend Estimation
2.5. Detection of Trend Shifts
3. Case Study
3.1. Data, Methodology, and Software
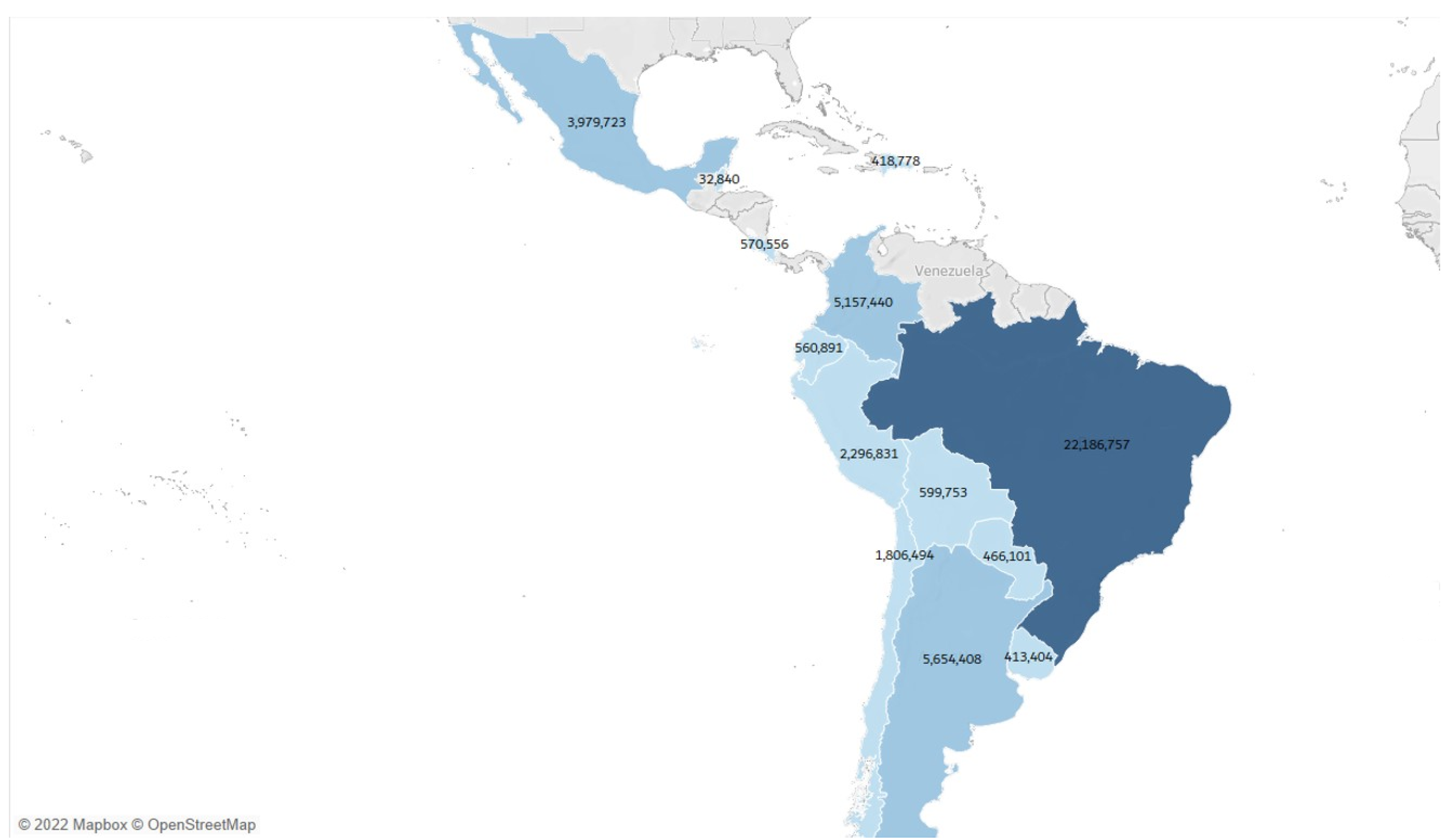
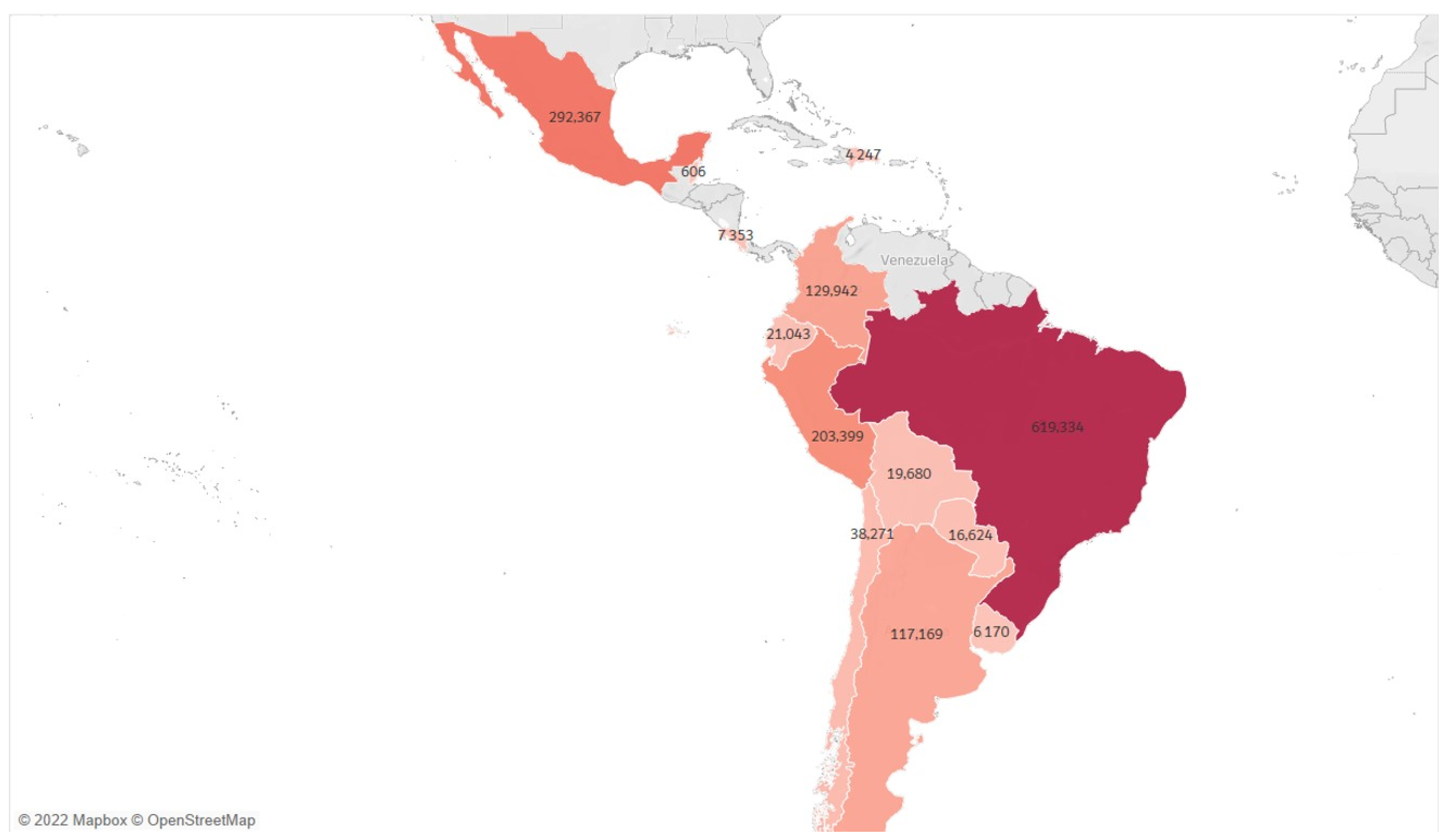
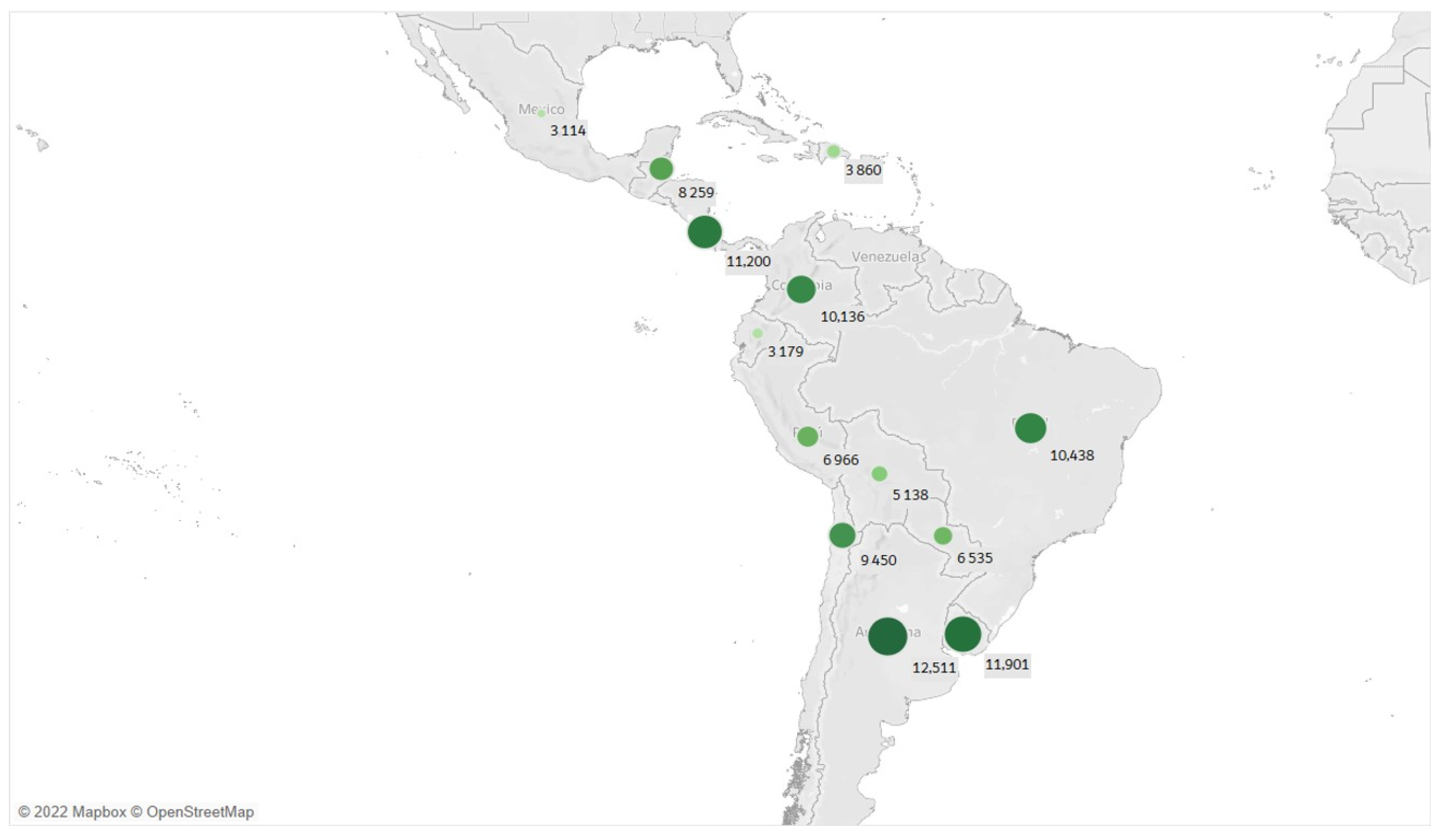
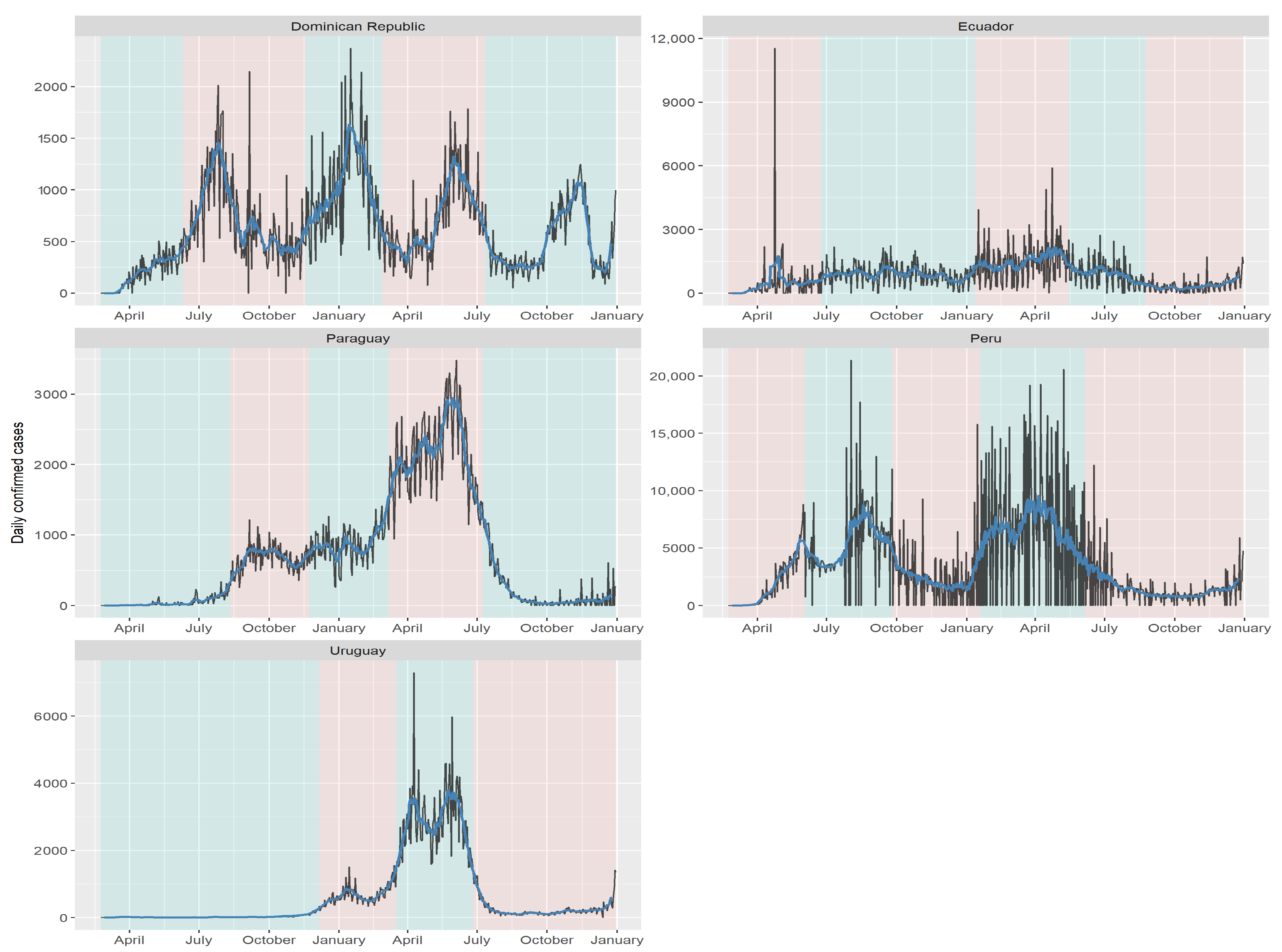
3.2. Exploratory Data Analysis
3.3. Epidemic Model
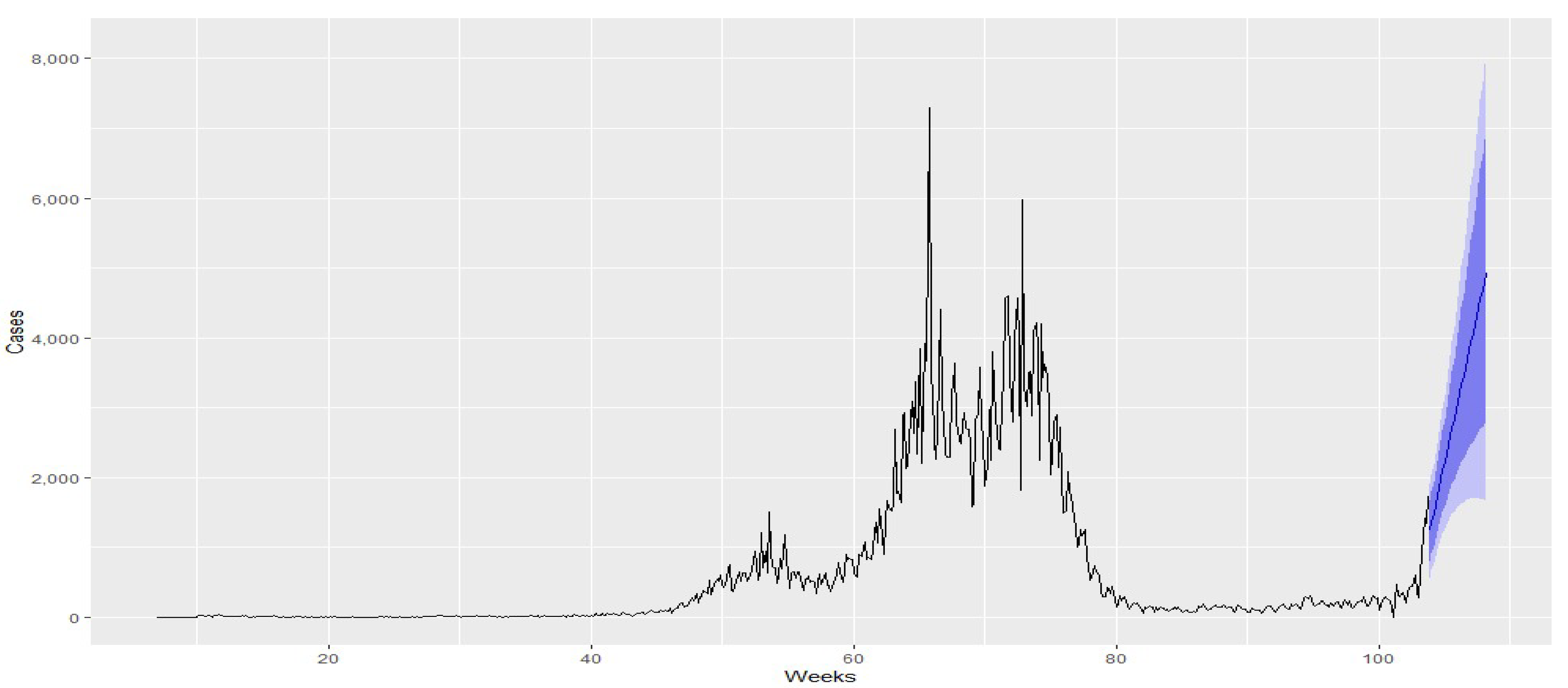
3.4. Main Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Chakraborty, T.; Ghosh, I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Solitons Fractals 2020, 135, 109850. [Google Scholar] [CrossRef]
- Fraser, C.; Cummings, D.A.; Klinkenberg, D.; Burke, D.S.; Ferguson, N.M. Influenza transmission in households during the 1918 pandemic. Am. J. Epidemiol. 2011, 174, 505–514. [Google Scholar] [CrossRef]
- WH Organization. Coronavirus Disease (COVID-19) Pandemic. 2020. Available online: www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 19 May 2023).
- De la Fuente-Mella, H.; Rubilar, R.; Chahuán-Jiménez, K.; Leiva, V. Modeling COVID-19 cases statistically and evaluating their effect on the economy of countries. Mathematics 2021, 9, 1558. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: New York, NY, USA, 2002. [Google Scholar]
- Box, G.; Jenkins, G. Time Series Analysis Forecasting and Control; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Ospina, R.; Leite, A.; Ferraz, C.; Magalhaes, A.; Leiva, V. Data-driven tools for assessing and combating COVID-19 out-breaks based on analytics and statistical methods in Brazil. Signa Vitae 2022, 18, 18–32. [Google Scholar]
- Jerez-Lillo, N.; Alvarez, B.L.; Gutierrez, J.M.; Figueroa-Zuniga, J.; Leiva, V. A statistical analysis for the epidemiological surveillance of COVID-19 in Chile. Signa Vitae 2022, 18, 19–30. [Google Scholar]
- Fierro, R.; Leiva, V.; Balakrishnan, N. Statistical inference on a stochastic epidemic model. Commun. Stat. Simul. Comput. 2015, 44, 2297–2314. [Google Scholar] [CrossRef]
- Intissar, A. A mathematical study of a generalized SEIR model of COVID-19. SciMed. J. 2020, 2, 30–67. [Google Scholar] [CrossRef]
- Boselli, P.M.; Soriano, J.M. COVID-19 in Italy: Is the mortality analysis a way to estimate how the epidemic lasts? Biology 2023, 12, 584. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Gondim, J.A.M.; Machado, L. Optimal quarantine strategies for the COVID-19 pandemic in a population with a discrete age structure. Chaos Solitons Fractals 2020, 140, 110166. [Google Scholar] [CrossRef]
- Stojkoski, V.; Sandev, T.; Kocarev, L.; Pal, A. Geometric Brownian motion under stochastic resetting: A stationary yet nonergodic process. Phys. Rev. E 2021, 104, 014121. [Google Scholar] [CrossRef]
- Vinod, D.; Cherstvy, A.G.; Wang, W.; Metzler, R.; Sokolov, I.M. Nonergodicity of reset geometric Brownian motion. Phys. Rev. E 2022, 105, L012106. [Google Scholar] [CrossRef]
- Vinod, D.; Cherstvy, A.G.; Metzler, R.; Sokolov, I.M. Time-averaging and nonergodicity of reset geometric Brownian motion with drift. Phys. Rev. E 2022, 106, 034137. [Google Scholar] [CrossRef]
- Eikenberry, S.E.; Mancuso, M.; Iboi, E.; Phan, T.; Eikenberry, K.; Kuang, Y.; Kostelich, E.; Gumel, A.B. To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 2020, 5, 293–308. [Google Scholar] [CrossRef]
- Gondim, J.A.M. Preventing epidemics by wearing masks: An application to COVID-19. Chaos Solitons Fractals 2021, 143, 110599. [Google Scholar] [CrossRef]
- Stutt, R.O.J.H.; Retkute, R.; Bradley, M.; Gilligan, C.A.; Colvin, J. A modelling framework to assess the likely effectiveness of facemasks in combination with ’lock-down’ in managing the COVID-19 pandemic. Proc. R. Soc. A 2020, 476, 20200376. [Google Scholar] [CrossRef]
- Vasconcelos, G.L.; Brum, A.A.; Almeida, F.A.G.; Macêdo, A.M.S.; Duarte-Filho, G.C.; Ospina, R. Standard and anomalous waves of COVID-19: A multiple-wave growth model for epidemics. Braz. J. Phys. 2021, 51, 1867–1883. [Google Scholar] [CrossRef]
- Vasconcelos, G.L.; Macedo, A.M.S.; Duarte-Filho, G.C.; Brum, A.A.; Ospina, R.; Almeida, F.A.G. Power law behaviour in the saturation regime of fatality curves of the COVID-19 pandemic. Sci. Rep. 2021, 11, 4619. [Google Scholar] [CrossRef]
- Wu, K.; Darcet, D.; Wang, Q.; Sornette, D. Generalized logistic growth modeling of the COVID-19 outbreak: Comparing the dynamics in provinces in China and in the rest of the world. Nonlinear Dyn. 2020, 101, 1561–1581. [Google Scholar] [CrossRef]
- Pérez-Ortega, J.; Almanza-Ortega, N.N.; Torres-Poveda, K.; Martínez-González, G.; Zavala-Díaz, J.C.; Pazos-Rangel, R. Application of data science for cluster analysis of COVID-19 mortality according to sociodemographic factors at municipal level in Mexico. Mathematics 2022, 10, 2167. [Google Scholar] [CrossRef]
- Cavalcante, T.; Ospina, R.; Leiva, V.; Cabezas, X.; Martin-Barreiro, C. Weibull regression and machine learning survival models: Methodology, comparison, and application to biomedical data related to cardiac surgery. Biology 2023, 12, 442. [Google Scholar] [CrossRef]
- Sokhansanj, B.A.; Zhao, Z.; Rosen, G.L. Interpretable and predictive deep neural network modeling of the SARS-Cov-2 spike protein sequence to predict COVID-19 disease severity. Biology 2022, 11, 1786. [Google Scholar] [CrossRef]
- Sardar, I.; Akbar, M.A.; Leiva, V.; Alsanad, A.; Mishra, P. Machine learning and automatic ARIMA/Prophet models-based forecasting of COVID-19: Methodology, evaluation, and case study in SAARC countries. Stoch. Environ. Res. Risk Assess. 2022, 37, 345–359. [Google Scholar] [CrossRef]
- Cacha, I.H.; Díaz, J.S.; Castrillo, M.; García, A.L. Forecasting COVID-19 spreading through an ensemble of classical and machine learning models: Spain’s case study. Sci. Rep. 2023, 13, 6750. [Google Scholar] [CrossRef]
- Marzouk, M.; Elshaboury, N.; Abdel-Latif, A.; Azab, S. Deep learning model for forecasting COVID-19 outbreak in Egypt. Process. Saf. Environ. Prot. 2021, 153, 363–375. [Google Scholar] [CrossRef]
- Alkady, W.; ElBahnasy, K.; Leiva, V.; Gad, W. Classifying COVID-19 based on amino acids encoding with machine learning algorithms. Chemom. Intell. Lab. Syst. 2022, 224, 104535. [Google Scholar] [CrossRef]
- Ullah, A.; Malik, K.M.; Saudagar, A.K.; Khan, M.B.; Hasanat, M.H.; AlTameem, A.; AlKhathami, M.; Sajjad, M. COVID-19 genome sequence analysis for new variant prediction and generation. Mathematics 2022, 10, 4267. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Tsai, J.F.; Lin, M.H.; Hu, Y.C. A hybrid model with spherical fuzzy-AHP, PLS-SEM and ANN to predict vaccination intention against COVID-19. Mathematics 2021, 9, 3075. [Google Scholar] [CrossRef]
- Delgado, E.J.; Cabezas, X.; Martin-Barreiro, C.; Leiva, V.; Rojas, F. An equity-based optimization model to solve the location problem for healthcare centers applied to hospital beds and COVID-19 vaccination. Mathematics 2022, 10, 1825. [Google Scholar] [CrossRef]
- Ito, K.; Piantham, C.; Nishiura, H. Relative instantaneous reproduction number of Omicron SARS-CoV-2 variant with respect to the Delta variant in Denmark. J. Med. Virol. 2022, 94, 2265–2268. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, J.K. Statistical Analysis of Stochastic Processes in Time; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Senel, K.; Özdinc, M.; Ozturkcan, S.; Akgul, A. Instantaneous R for COVID-19 in Turkey: Estimation by Bayesian statistical inference. Turk. Klin. J. Med. Sci. 2020, 40, 127–131. [Google Scholar]
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef]
- Kong, L.; Duan, M.; Shi, J.; Hong, J.; Chang, Z.; Zhang, Z. Compartmental structures used in modeling COVID-19: A scoping review. Infect. Dis. Poverty 2022, 11, 72. [Google Scholar] [CrossRef]
- Chumachenko, D.; Meniailov, I.; Bazilevych, K.; Chumachenko, T.; Yakovlev, S. Investigation of statistical machine learning models for COVID-19 epidemic process simulation: Random forest, K-nearest neighbors, gradient boosting. Computation 2022, 10, 86. [Google Scholar] [CrossRef]
- Al-Rashedi, A.; Al-Hagery, M.A. Deep learning algorithms for forecasting COVID-19 cases in Saudi Arabia. Appl. Sci. 2023, 13, 1816. [Google Scholar] [CrossRef]
- Chowell, G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infect. Dis. Model. 2017, 2, 379–398. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- He, S.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020, 101, 1667–1680. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Cryer, J.D.; Chan, K.S. Time Series Analysis with Applications in R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kirchgässner, G.; Wolters, J.; Hassler, U. Introduction to Modern Time Series Analysis; Springer: New York, NY, USA, 2012. [Google Scholar]
- Papastefanopoulos, V.; Linardatos, P.; Kotsiantis, S. COVID-19: A comparison of time series methods to forecast percentage of active cases per population. Appl. Sci. 2020, 10, 3880. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: New York, NY, USA, 2000. [Google Scholar]
- Burns, P. Robustness of the Ljung-Box Test and Its Rank Equivalent. SSRN 443560. 2002. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=443560 (accessed on 16 June 2023).
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Winters, P.R. Forecasting sales by exponentially weighted moving averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Estimating and testing linear models with multiple structural changes. Econometrica 1988, 66, 47–78. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Krispin, R. Hands-On Time Series Analysis with R: Perform Time Series Analysis and Forecasting Using R; Packt Publishing, Limited: Birmingham, UK, 2019. [Google Scholar]
- Tableau (Version 2023.1) [Computer Software]. Tableau Software. Available online: www.tableau.com (accessed on 16 June 2023).
- Martin-Barreiro, C.; Ramirez-Figueroa, J.A.; Cabezas, X.; Leiva, V.; Galindo-Villardón, M.P. Disjoint and functional principal component analysis for infected cases and deaths due to COVID-19 in South American countries with sensor-related data. Sensors 2021, 21, 4094. [Google Scholar] [CrossRef]
- Nishiura, H.; Chowell, G. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Dordrecht, Germany, 2009; pp. 103–121. [Google Scholar]
- Cortés-Carvajal, P.D.; Cubilla-Montilla, M.; González-Cortés, D.R. Estimation of the instantaneous reproduction number and its confidence interval for modeling the COVID-19 pandemic. Mathematics 2022, 10, 287. [Google Scholar] [CrossRef]
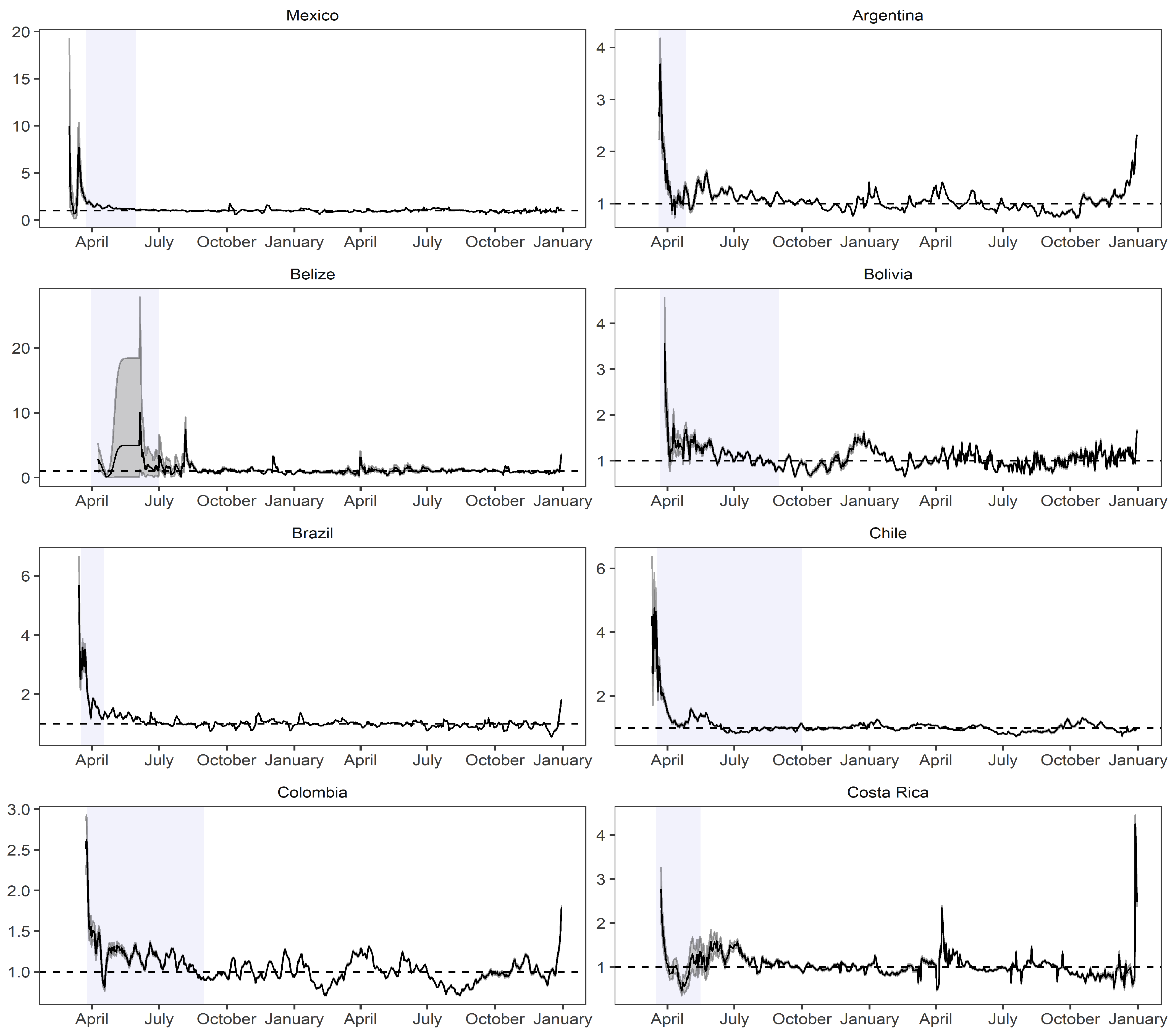
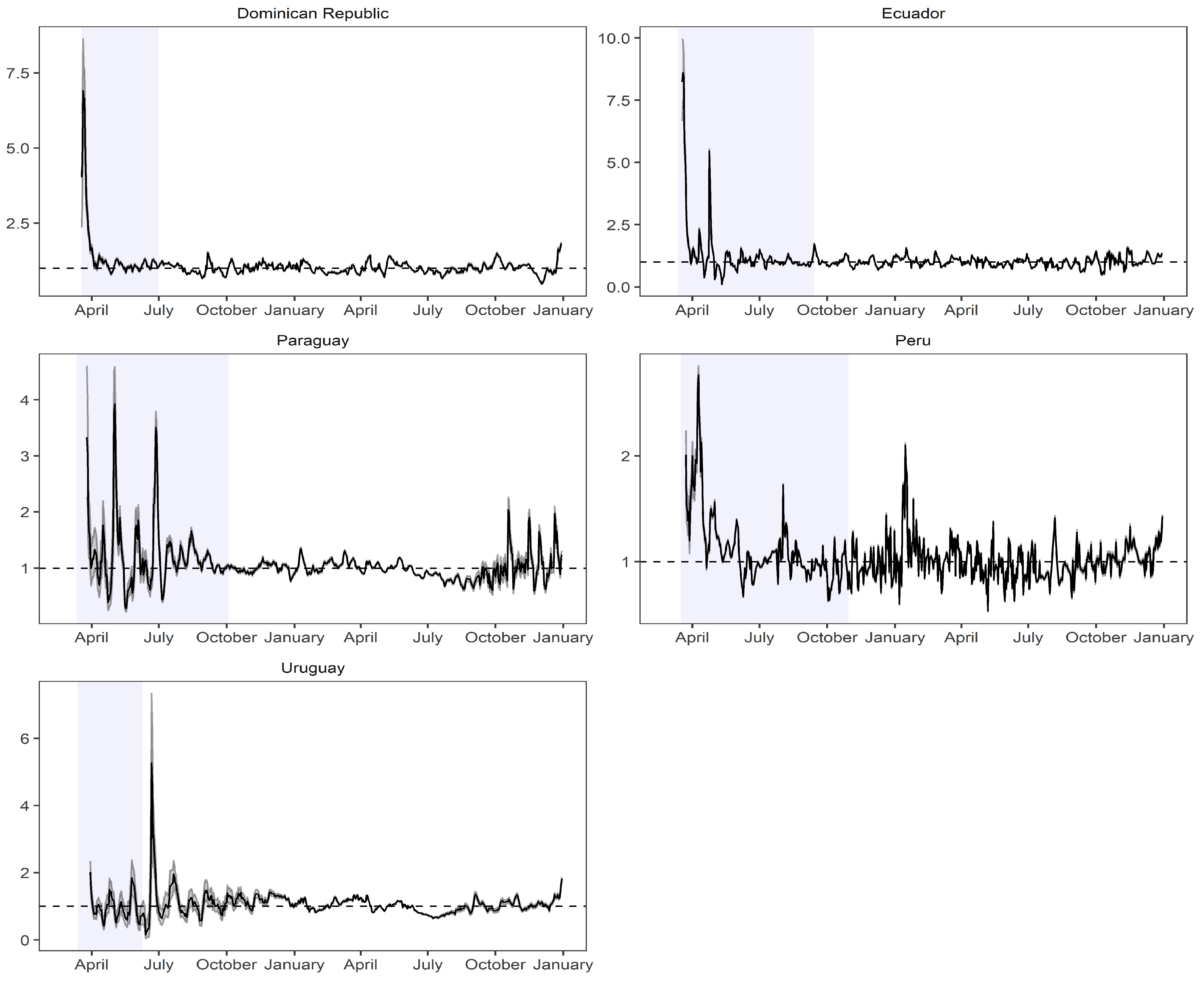
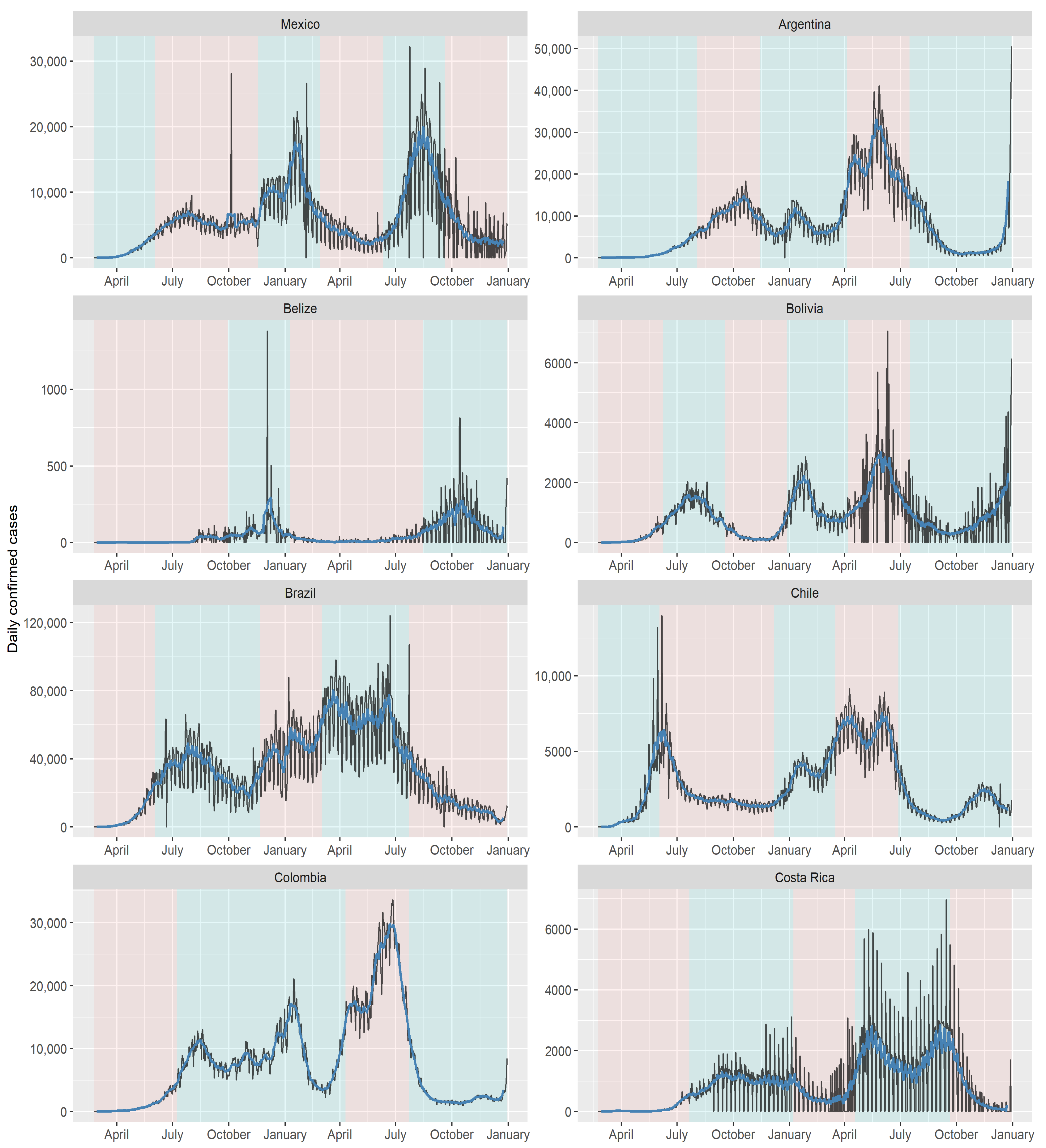
| Country | Cut-Off Point | ||||
|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | |
| Argentina | 3 August 2020 | 13 November 2020 | 5 April 2021 | 16 September 2021 | N/A |
| Belize | 29 September 2020 | 9 November 2020 | 15 August 2021 | N/A | N/A |
| Bolivia | 8 June 2020 | 17 September 2020 | 27 December 2020 | 7 April 2021 | 17 June 2021 |
| Brazil | 2 June 2020 | 21 November 2020 | 2 March 2021 | 23 September 2021 | N/A |
| Chile | 2 June 2020 | 6 December 2020 | 17 March 2021 | 28 June 2021 | N/A |
| Colombia | 8 July 2020 | 10 April 2021 | 23 June 2021 | N/A | N/A |
| Costa Rica | 21 June 2020 | 7 January 2021 | 18 April 2021 | 20 September 2021 | N/A |
| Dominican Republic | 10 June 2020 | 18 November 2020 | 27 February 2021 | 12 July 2021 | N/A |
| Ecuador | 24 June 2020 | 12 January 2021 | 15 May 2021 | 24 August 2021 | N/A |
| Mexico | 2 June 2020 | 18 November 2020 | 27 February 2021 | 11 June 2021 | 20 September 2021 |
| Paraguay | 11 August 2020 | 23 November 2020 | 7 March 2021 | 9 July 2021 | N/A |
| Peru | 3 June 2020 | 25 September 2020 | 19 January 2021 | 5 June 2021 | N/A |
| Uruguay | 6 December 2020 | 17 March 2021 | 26 June 2021 | N/A | N/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leiva, V.; Alcudia, E.; Montano, J.; Castro, C. An Epidemiological Analysis for Assessing and Evaluating COVID-19 Based on Data Analytics in Latin American Countries. Biology 2023, 12, 887. https://doi.org/10.3390/biology12060887
Leiva V, Alcudia E, Montano J, Castro C. An Epidemiological Analysis for Assessing and Evaluating COVID-19 Based on Data Analytics in Latin American Countries. Biology. 2023; 12(6):887. https://doi.org/10.3390/biology12060887
Chicago/Turabian StyleLeiva, Víctor, Esdras Alcudia, Julia Montano, and Cecilia Castro. 2023. "An Epidemiological Analysis for Assessing and Evaluating COVID-19 Based on Data Analytics in Latin American Countries" Biology 12, no. 6: 887. https://doi.org/10.3390/biology12060887
APA StyleLeiva, V., Alcudia, E., Montano, J., & Castro, C. (2023). An Epidemiological Analysis for Assessing and Evaluating COVID-19 Based on Data Analytics in Latin American Countries. Biology, 12(6), 887. https://doi.org/10.3390/biology12060887








