Uncertainty Modeling of a Modified SEIR Epidemic Model for COVID-19
Abstract
:Simple Summary
Abstract
1. Introduction
2. Mathematical Epidemic Model for COVID-19 in Wuhan
3. Model Calibration
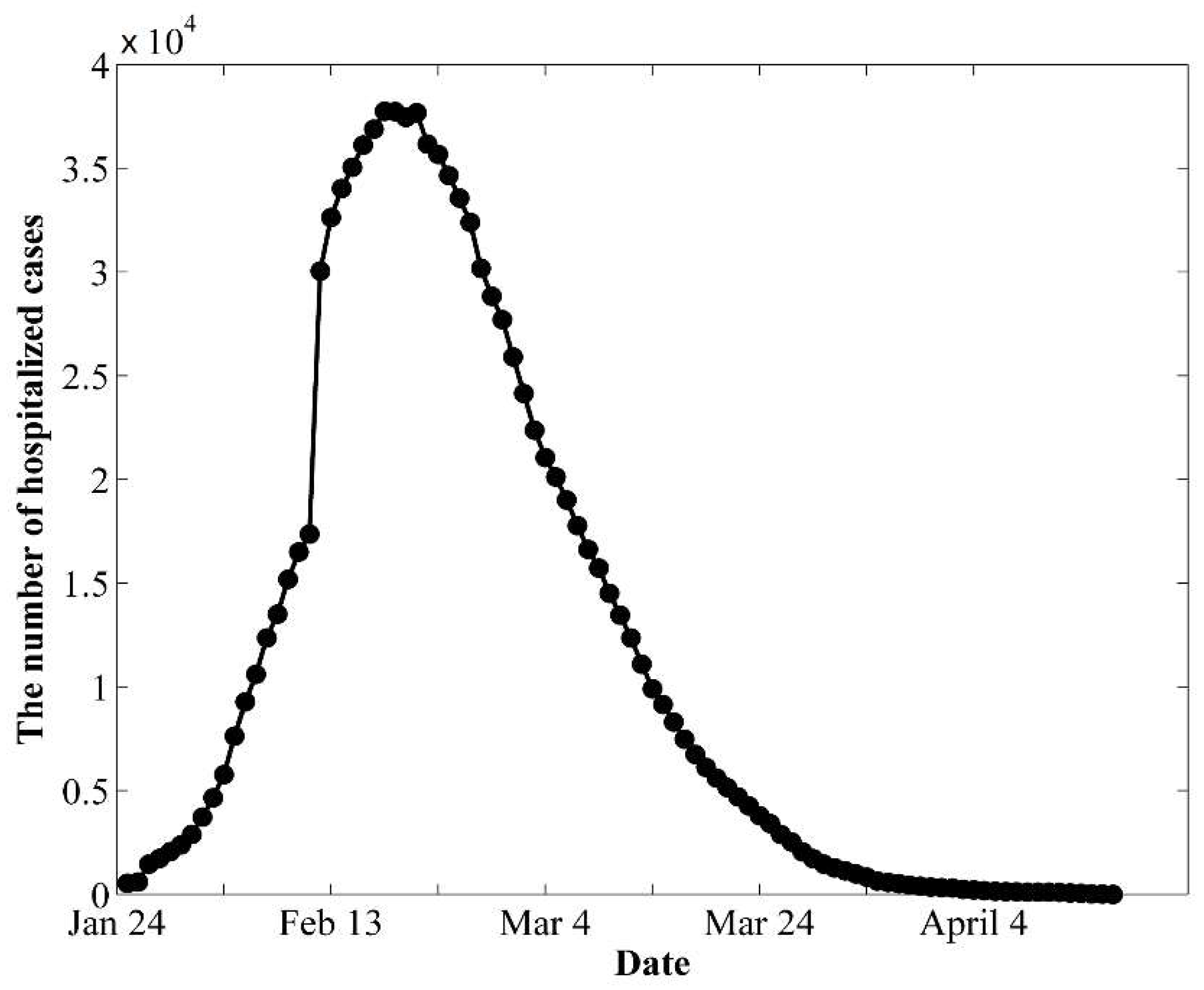
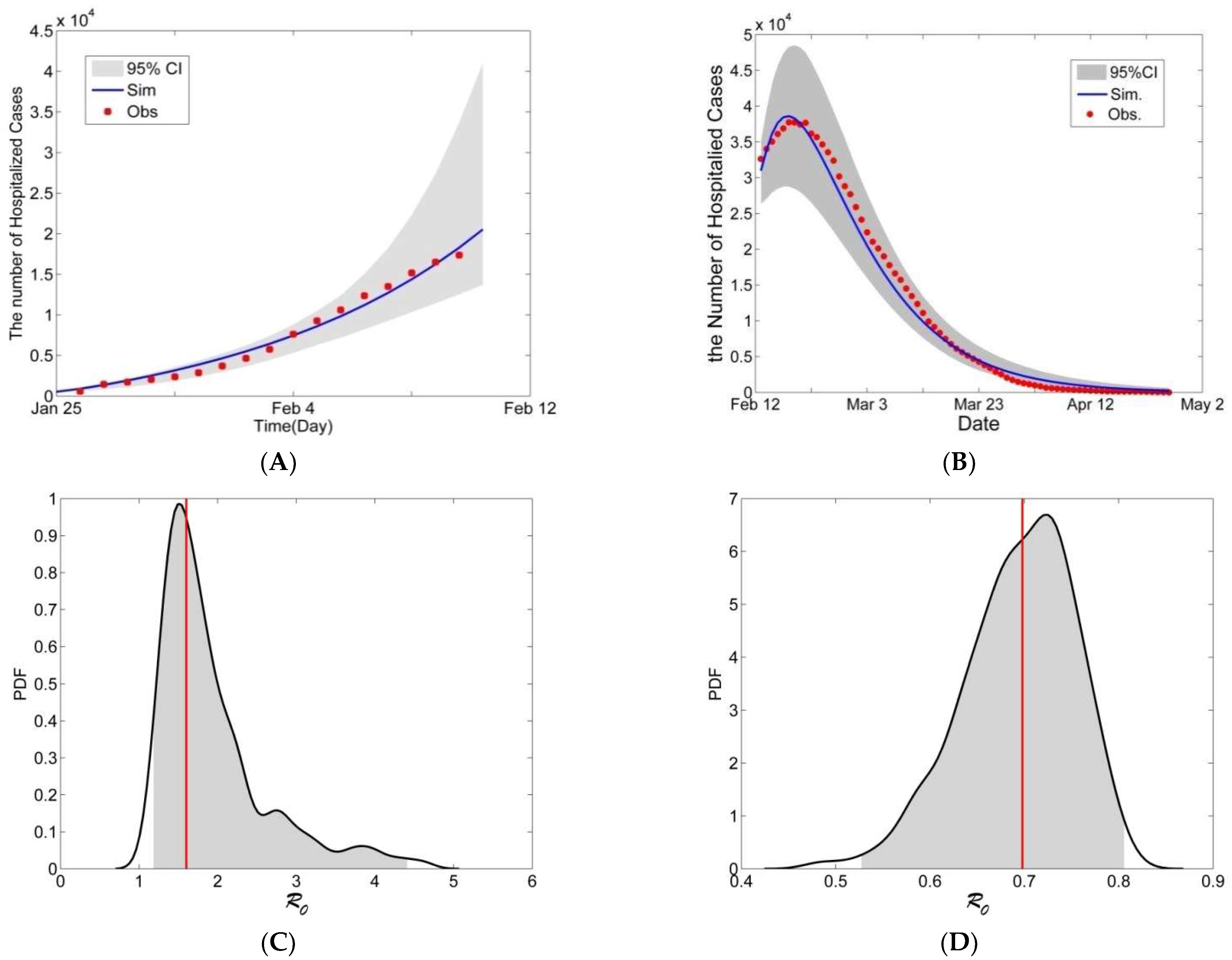
3.1. Data
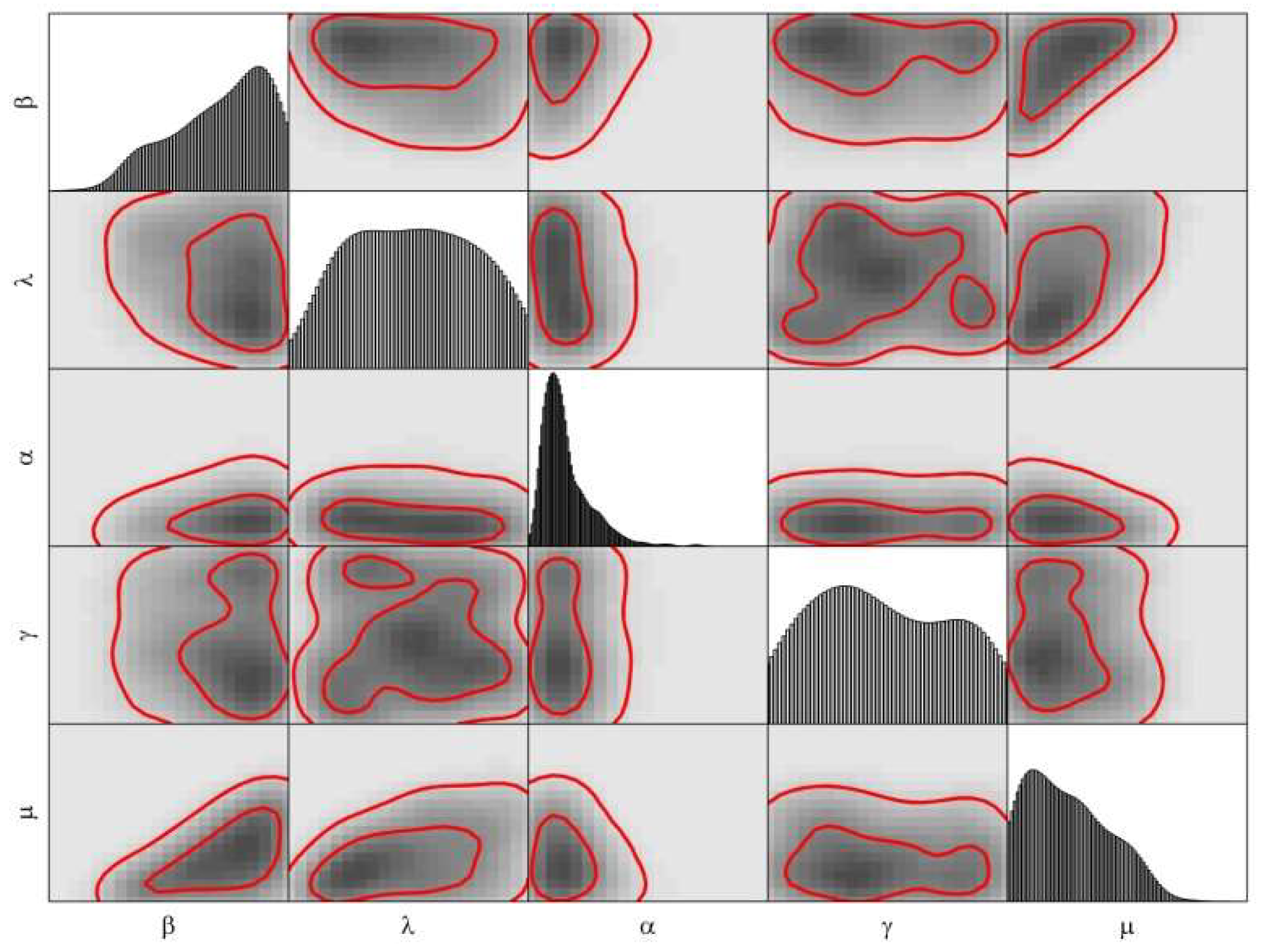
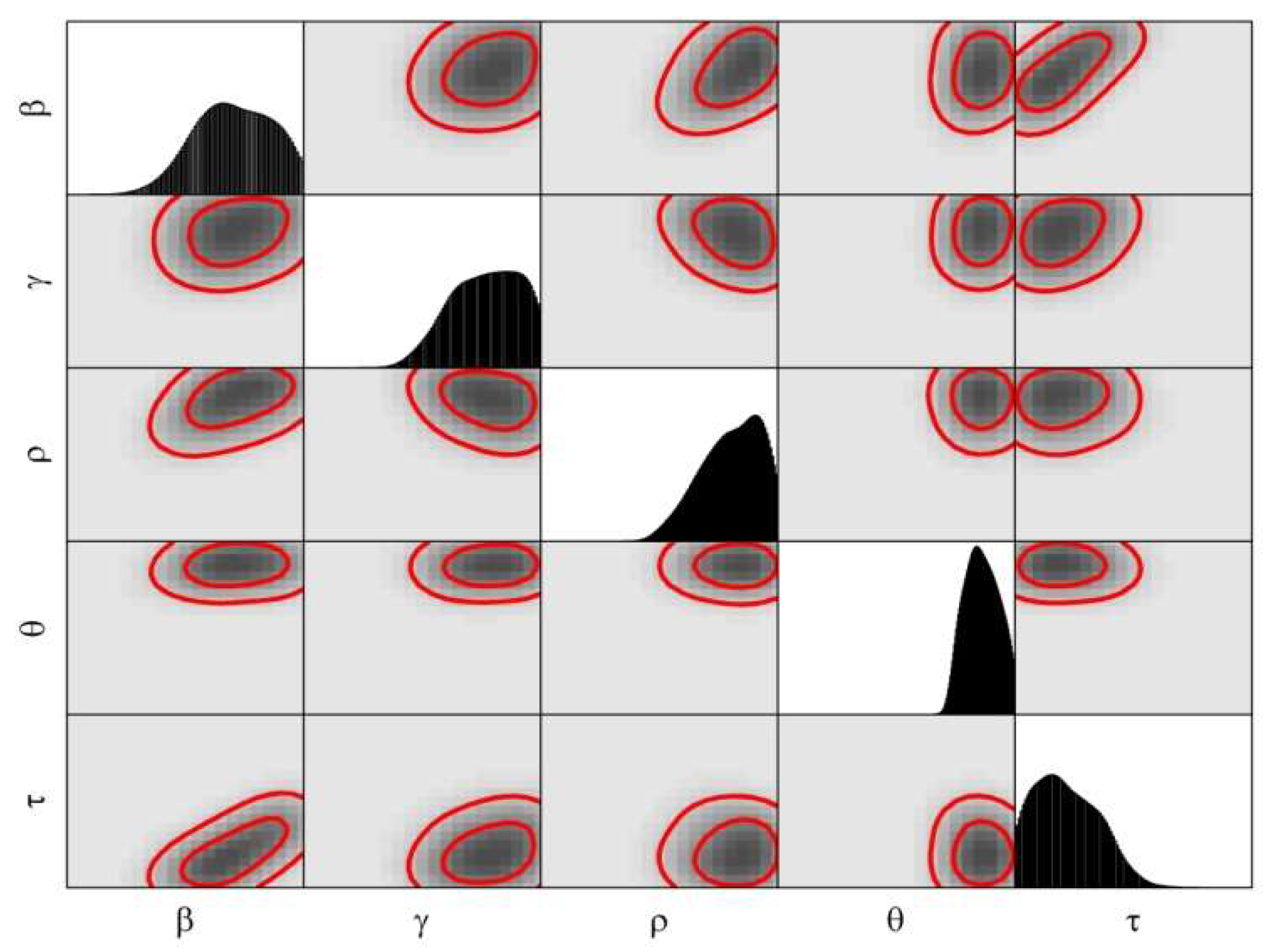
3.2. Calibration
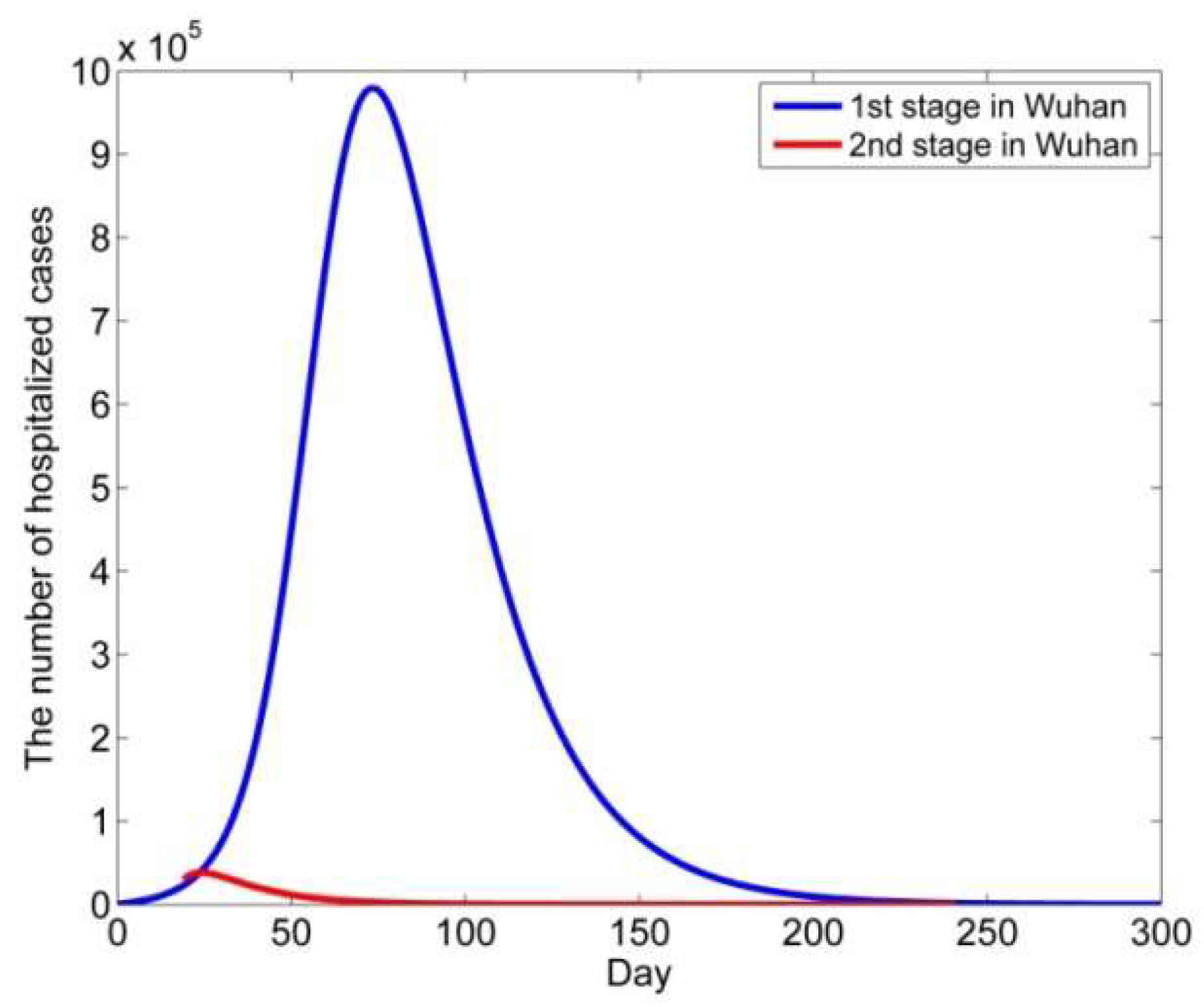
4. Modeling the COVID-19 Epidemic in Wuhan
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. MATLAB Codes
References
- Li, Q.; Guan, X.H.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Wang, Y.; Tian, C.; Chen, Y.; Mao, J. The experimences of Community-dwelling older adults during the COVID-19 Lockdown in Wuhan: A qualitative study. J. Adv. Nurs. 2021, 77, 4805–4814. [Google Scholar] [CrossRef] [PubMed]
- Vurlaila, I.; Hidayat, A.A.; Pardamean, B. Locakdown strategy worth lives: The SEIRD modeling in COVID-19 outbreak in Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2021, 729, 012002. [Google Scholar] [CrossRef]
- National Health Commission of the People’s Republic of China. Diagnosis and Treatment Guideline for New Coronavirus Pneumonia, 5th ed.; National Health Commission of the People’s Republic of China: Beijing, China, 2020; Available online: https://www.chinacdc.cn/jkzt/crb/xcrxjb/202002/W020200205535799210271.pdf (accessed on 1 May 2020).
- Kupferschmidt, K.; Cohen, J. Can China’s COVID-19 strategy work elsewhere. Science 2020, 367, 1061–1062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riley, S.; Fraser, C.; Donnelly, C.A.; Ghani, A.C.; Abu-Raddad, L.J.; Hedley, A.J.; Leung, G.M.; Ho, L.-M.; Lam, T.-H.; Thach, T.Q.; et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: Impact of Public Health Interventions. Science 2003, 300, 1961–1966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, R.M.; May, R.M. Infectious Disease of Humans; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Heesterbeek, H.; Anderson, R.M.; Anderson, V.; Bansal, S.; De Angelis, D.; Dye, C.; Eames, K.T.D.; Edmunds, W.J.; Frost, S.D.W.; Funk, S.; et al. Modeling infectious disease dynamics in the complex landscape of global health. Science 2015, 347, aaa4339. [Google Scholar] [CrossRef] [Green Version]
- Ross, R. The Prevention of Malaria; John Muarry: London, UK, 1911. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics, IV: Analysis of experimental epidemics of the virus disease mouse ectromelia. Epidemiol. Infect. 1939, 37, 172–187. [Google Scholar] [CrossRef] [Green Version]
- Dantas, E.; Tosin, M.; Cunha, A., Jr. Calibration of a SEIR-SEI epidemic model to describe the Zika virus ourbreak in Brazil. Appl. Math. Comput. 2018, 338, 249–259. [Google Scholar]
- Ghowell, G.; Fenimore, P.W.; Castillo-Garsow, M.A.; Castillo-Chavez, C. SARS outbreaks n Ontario, Hong Kong and Singapore: The role of diagnosis and isolation as a control mechanism. J. Theor. Biol. 2003, 224, 1–8. [Google Scholar]
- Dye, C.; Gay, N. Modeling the SARS epidemic. Science 2003, 300, 1884–1885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lipsitch, M.; Cohen, T.; Cooper, B.; Robins, J.M.; Ma, S.; James, L. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003, 300, 1966–1970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chowell, G.; Blumberg, S.; Sirmonsent, L.; Miller, M.A.; Viboud, C. Synthesizing data and models for the spread of MERS-Cov, 2013: Key role of index cases and hospital transmission. Epidemics 2014, 9, 40–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCOV outbreak originating in Wuhan, China: A modeling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.-S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and prediction af the epidemics tren of COVID-19 in China under public health interventions. J. Theorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Pastore y Piontti, A.; Mu, K.; Rossi, L.; Sun, K. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreaks. Science 2020, 368, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.; Yuan, C. Simple model to assess Wuhan lock-down effect and region efforts during COVID-19 epidemic in China mainland. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Zhou, H.; Zhou, F. Study on SARS-CoV-2 transmission and the effects of control measures in China. PLoS ONE 2020, 15, e0242649. [Google Scholar] [CrossRef]
- Ewald, J.; Sieber, P.; Garde, R.; Lang, S.N.; Schuster, S.; Ibrahim, B. Trends in mathematical modeling of host-pathogen interactions. Cell. Mol. Life Sci. 2020, 77, 467–480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peter, S.; Dittrich, P.; Ibrahim, B. Structure and hierarchy of SARS-CoV-2 infection dynamics models revealed by reaction network analysis. Viruses 2021, 13, 14. [Google Scholar] [CrossRef]
- Hufsky, F.; Lamkiewicz, K.; Almeida, A.; Aouacheria, A.; Arighi, C.; Bateman, A.; Baumbach, J.; Beerenwinkel, N.; Brandt, C.; Cacciabue, M.; et al. Computational strategies to combat COVID-19: Useful tolls to accelerate SARS-CoV_2 and coronavirus research. Brief. Bioinform. 2021, 22, 642–663. [Google Scholar] [CrossRef]
- Guzzi, P.H.; Petrizzelli, F.; Mazza, T. Disease spreading modeling and analysis: A survey. Brief. Bioinform. 2022, 23, bbac230. [Google Scholar] [CrossRef] [PubMed]
- Ai, J.; Zhang, H.; Xu, T.; Wu, J.; Zhu, M.; Yu, Y.Q.; Zhang, H.-Y.; Li, Y.; Zhou, X.; Shen, Z.; et al. Optimizing diagnostic strategy for novel coronavirus pneumonia, a multi-center study in eastern China. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Hao, X.; Cheng, S.; Wu, D.; Wu, T.; Lin, X.; Wang, C. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 2020, 584, 420–424. [Google Scholar] [CrossRef]
- Pekar, J.; Worobey, M.; Moshiri, N.; Scheffler, K.; Wertheim, J.O. Timing the SARS-CoV-2 index case in Hubei province. Science 2021, 372, 412–417. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Towers, S.; Geisse, K.V.; Zheng, Y. Assessing potential repercussions using a seasonally forced SIR model. J. Theor. Biol. 2011, 289, 259–268. [Google Scholar] [CrossRef]
- Wuhan Municipal Health Commission, Hubei Province. Available online: http://wjw.wuhan.gov.cn (accessed on 1 May 2020).
- Baidu. Real Time Data of Novel Pneumonia Epidemic Situation. Available online: http://voice.baidu.com/act/newpneumonia (accessed on 1 May 2020).
- National Health Commission of The Peoples’ Republic of China. Up to 24:00 February 12th Novel Coronavirus Pneumonia Epidemic Situation; National Health Commission of the Peoples’ Republic of China: Beijing, China, 2020.
- Vrugt, J.A.; Sadegh, M. Toward diagnostic model calibration and evaluation: Approximate Bayesian computation. Water Resour. Res. 2013, 49, 4335–4345. [Google Scholar] [CrossRef] [Green Version]
- Beaumont, M.A.; Cornuet, J.M.; Marin, J.M.; Robert, C.P. Adaptive approximate Bayesian computation. Biometrika 2009, 96, 983–990. [Google Scholar] [CrossRef] [Green Version]
- Fearnhead, P.; Prangle, D. Constructing summary statistic for approximate Bayesian computation: Semi-automatic approximate Bayesian computation. J. R. Stat. Soc. Ser. B Stat. Methodol. 2012, 74, 419–474. [Google Scholar] [CrossRef] [Green Version]
- Vo Brenda, N.; Drovandi Christopher, C.; Pettitt Anthony, N.; Simpson Matthew, J. Quantifying uncertainty in parameter estimates for stochastic models of collective cell spreading using approximate Bayesian computation. Math. Biosci. 2015, 263, 133–142. [Google Scholar]
- Datta, G.S.; Ghosh, M. On the invariance of noninformative priors. Ann. Stat. 1996, 24, 141–159. [Google Scholar] [CrossRef]
- Tang, B. Orthogonal array-based Latin hypercubes. J. Am. Stat. Assoc. 1993, 88, 1392–1397. [Google Scholar] [CrossRef]
- Owen, A.B. Controlling correlations in Latin hypercube samples. J. Am. Stat. Assoc. 1994, 89, 1517–1522. [Google Scholar] [CrossRef]
- Linkletter, C.; Bingham, D.; Sitter, R.; Ye, K.; Hengartner, N.; Higdon, D. ComparingDesigns of Experiments for Screening and Prediction in Computer Experiments; Technical Report LA-UR-03-8524; Los Alamos National Laboratory: Walnut Creek, CA, USA, 2003. [Google Scholar]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef] [Green Version]
- Cohn, J. Wuhan seafood market may not be source of novel virus spreading globally. Science 2020, 10, 1126. [Google Scholar] [CrossRef]
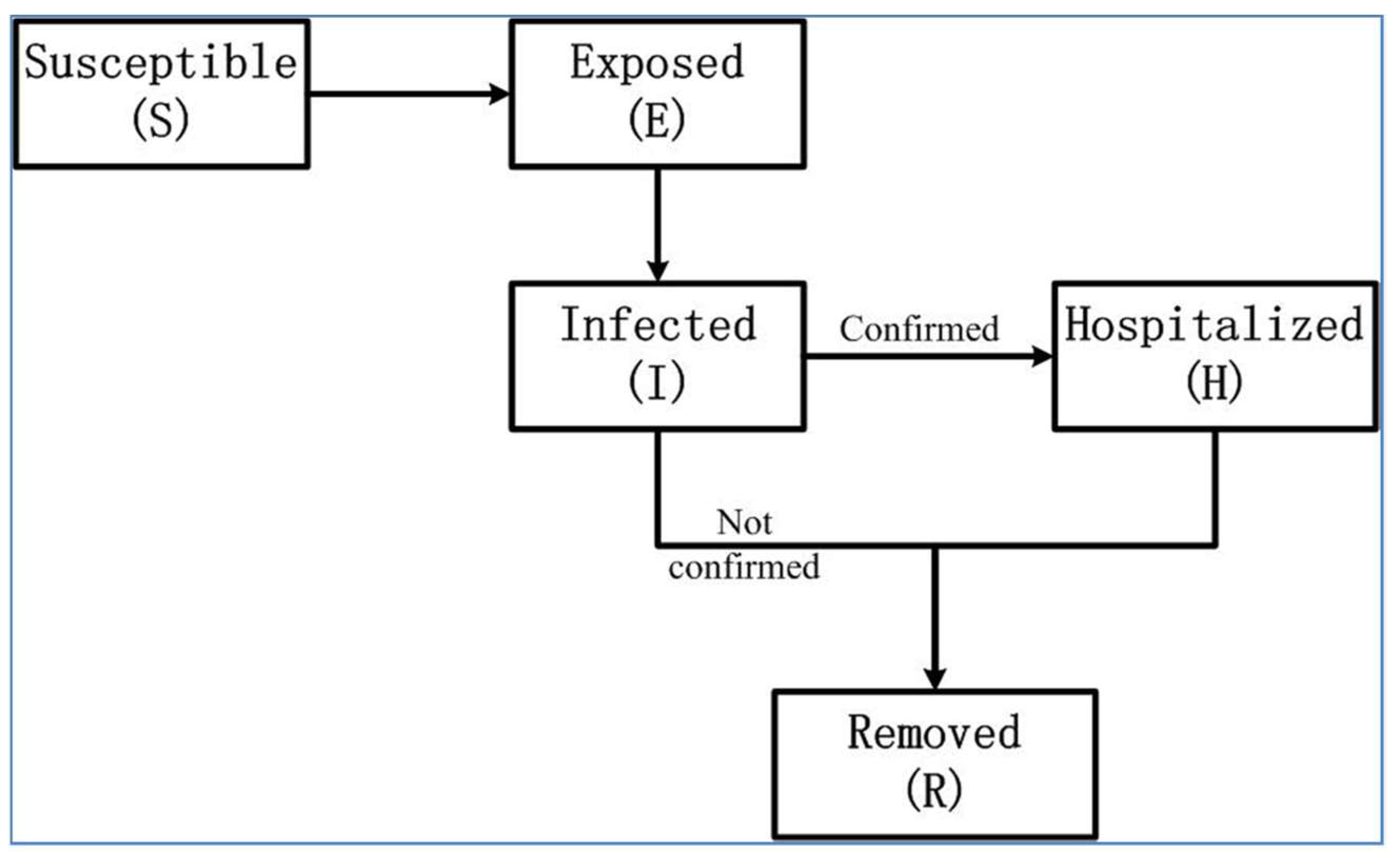

| Parameter | Definition |
|---|---|
| β(1-I/N) | Transmission rate per day |
| λ | Rate of progression to infectious state per day |
| α | Rate of progression from the infectious to the hospitalized state per day |
| γ | Rate of progression from the infectious state to the removed state per day |
| μ | Rate of progression from the hospitalized state to the removed state per day |
| Start Date | Evidence | Source |
|---|---|---|
| 8 December 2019 | Clinical cases | N Engl Med J [1] |
| 1 December 2019 | Clinical cases | Lancet [41] |
| November 2019 | Inferred from the above result | Science [42] |
| Mid-October and mid- November 2019 | Simulation | Science [27] |
| 15 November 2019 to 30 November 2019 | This study | |
| 2 November 2019 to 20 November 2019 | This study |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, P.; Zhang, S.; Pan, H. Uncertainty Modeling of a Modified SEIR Epidemic Model for COVID-19. Biology 2022, 11, 1157. https://doi.org/10.3390/biology11081157
Wang Y, Wang P, Zhang S, Pan H. Uncertainty Modeling of a Modified SEIR Epidemic Model for COVID-19. Biology. 2022; 11(8):1157. https://doi.org/10.3390/biology11081157
Chicago/Turabian StyleWang, Yanjin, Pei Wang, Shudao Zhang, and Hao Pan. 2022. "Uncertainty Modeling of a Modified SEIR Epidemic Model for COVID-19" Biology 11, no. 8: 1157. https://doi.org/10.3390/biology11081157
APA StyleWang, Y., Wang, P., Zhang, S., & Pan, H. (2022). Uncertainty Modeling of a Modified SEIR Epidemic Model for COVID-19. Biology, 11(8), 1157. https://doi.org/10.3390/biology11081157





