Study of Low-Velocity Impact Damage in Composite Laminates Based on Crack Energy
Abstract
1. Introduction
2. Materials and Methods
2.1. Failure Initiation Criterion
2.2. Cohesive Zone Model
2.3. Finite Element Simulation
2.3.1. Geometrical Parameters and Boundary Conditions
2.3.2. Contact Definition and Material Properties
2.4. Low-Velocity Impact Test
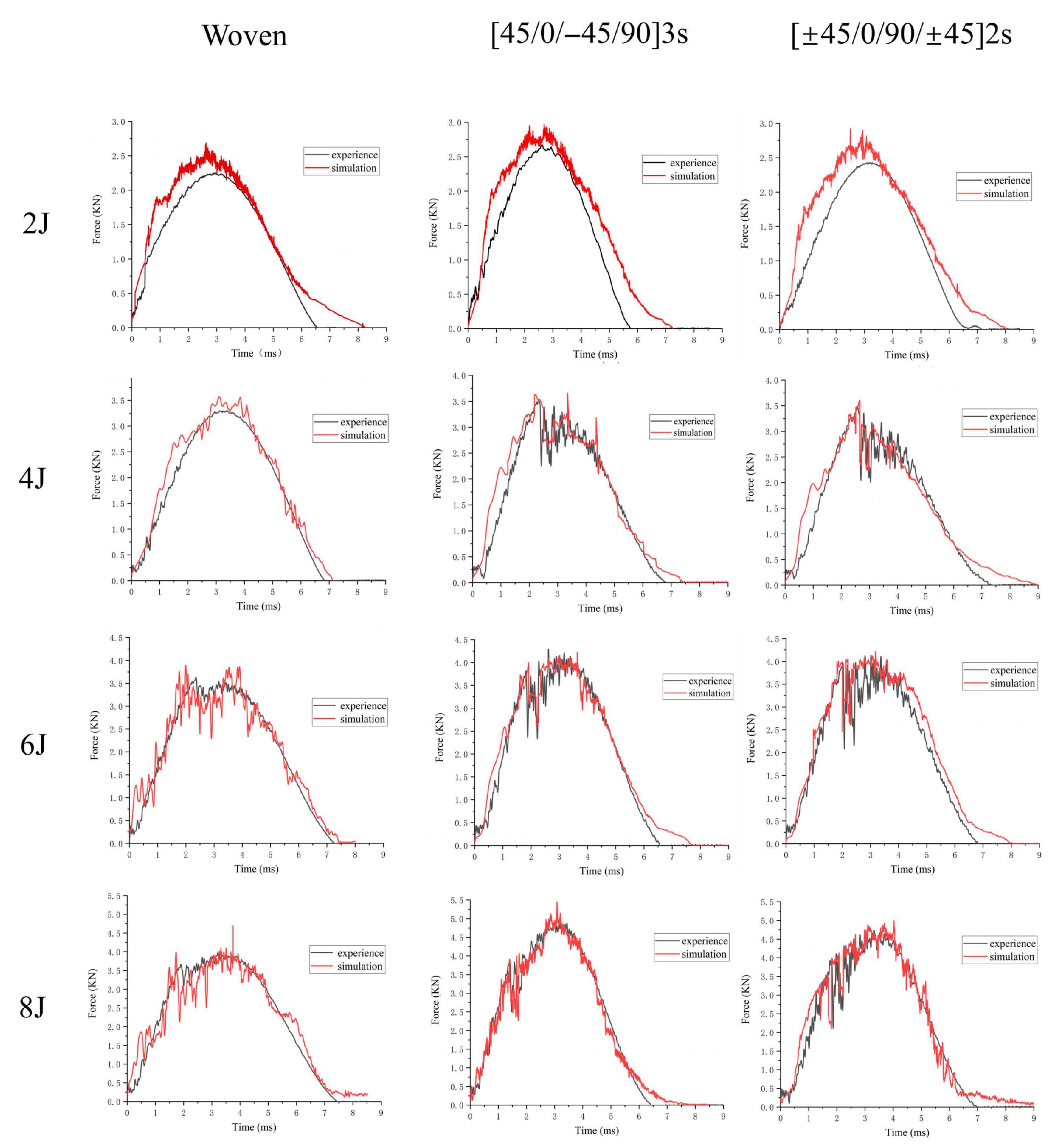
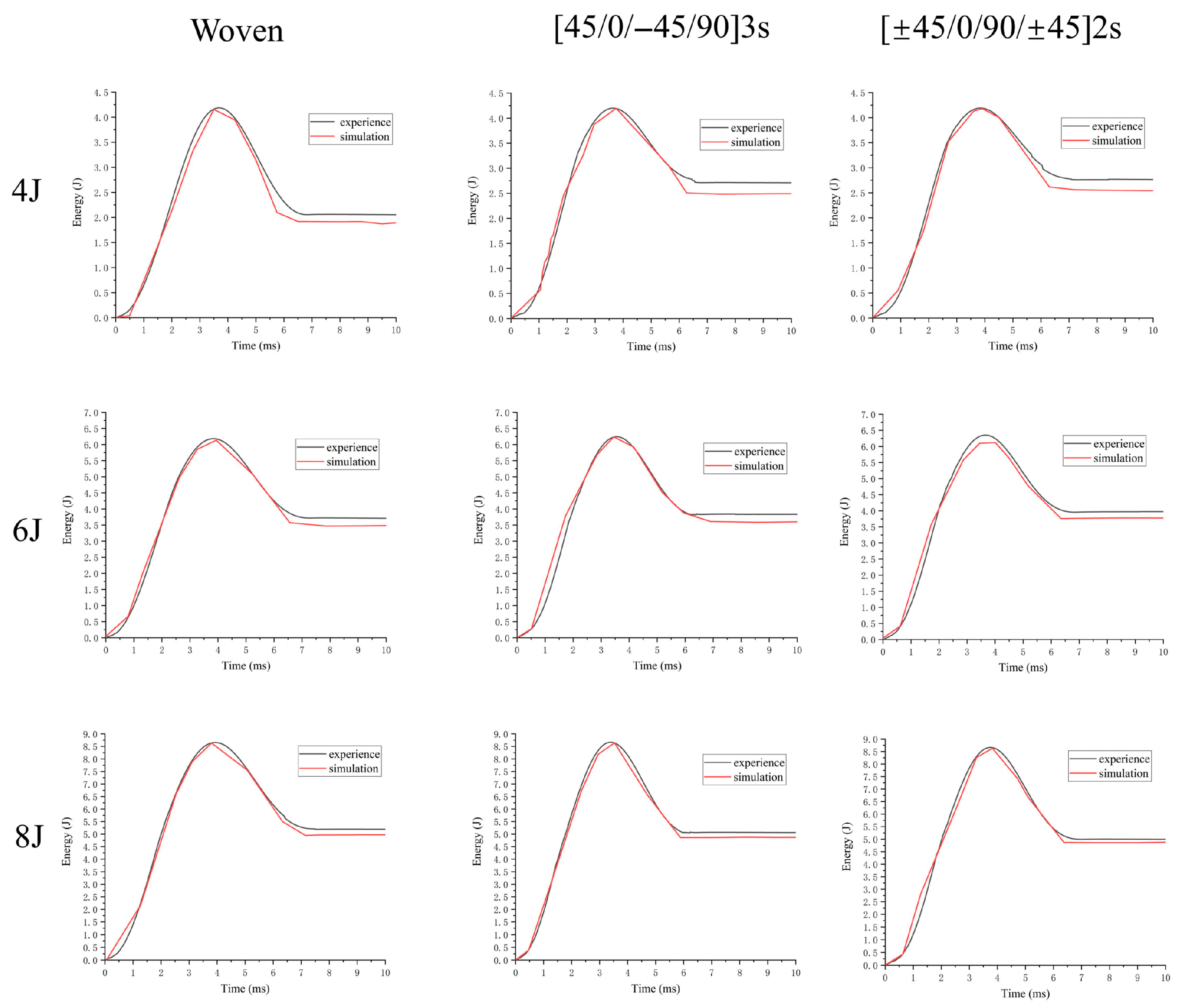
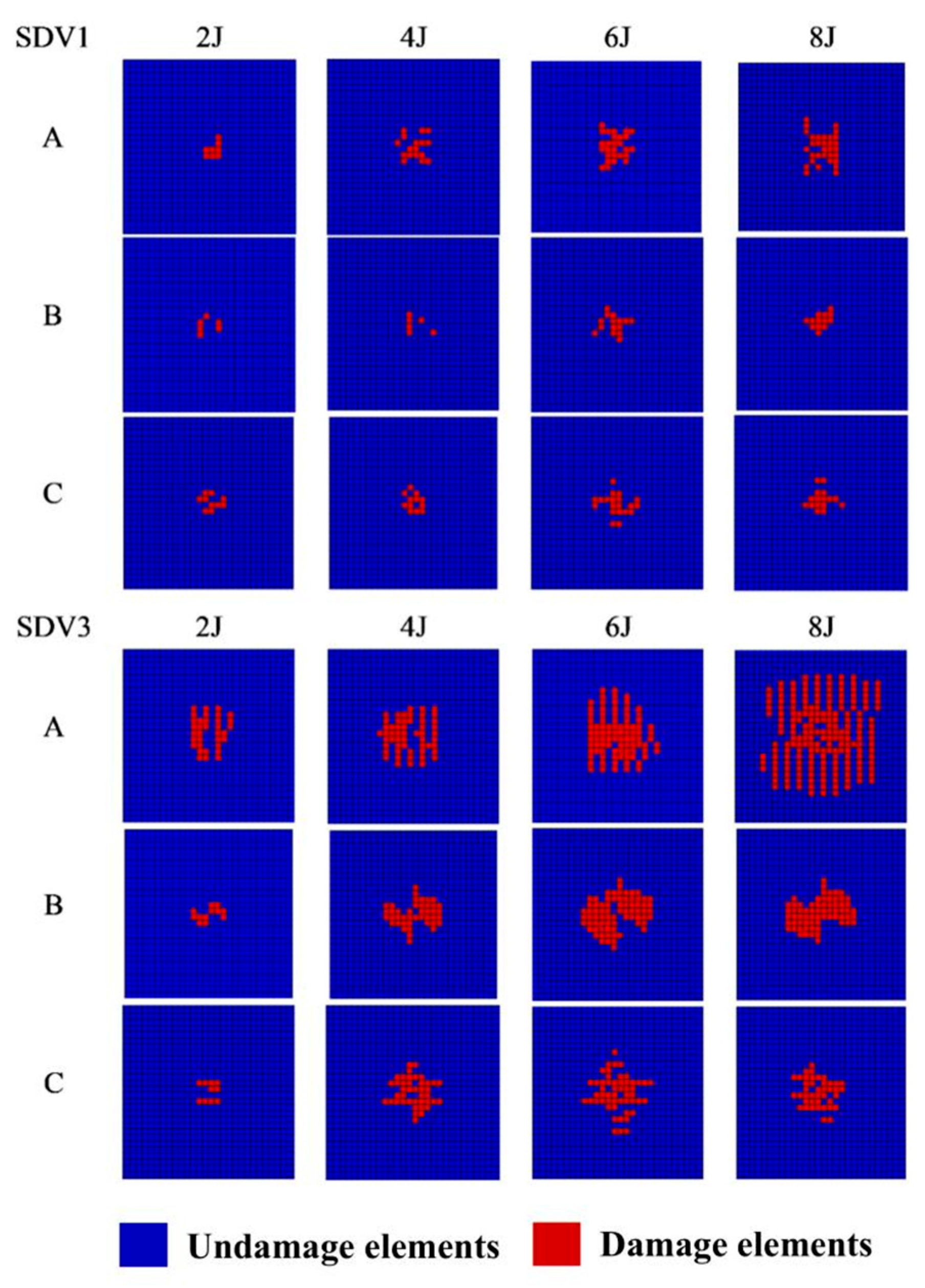
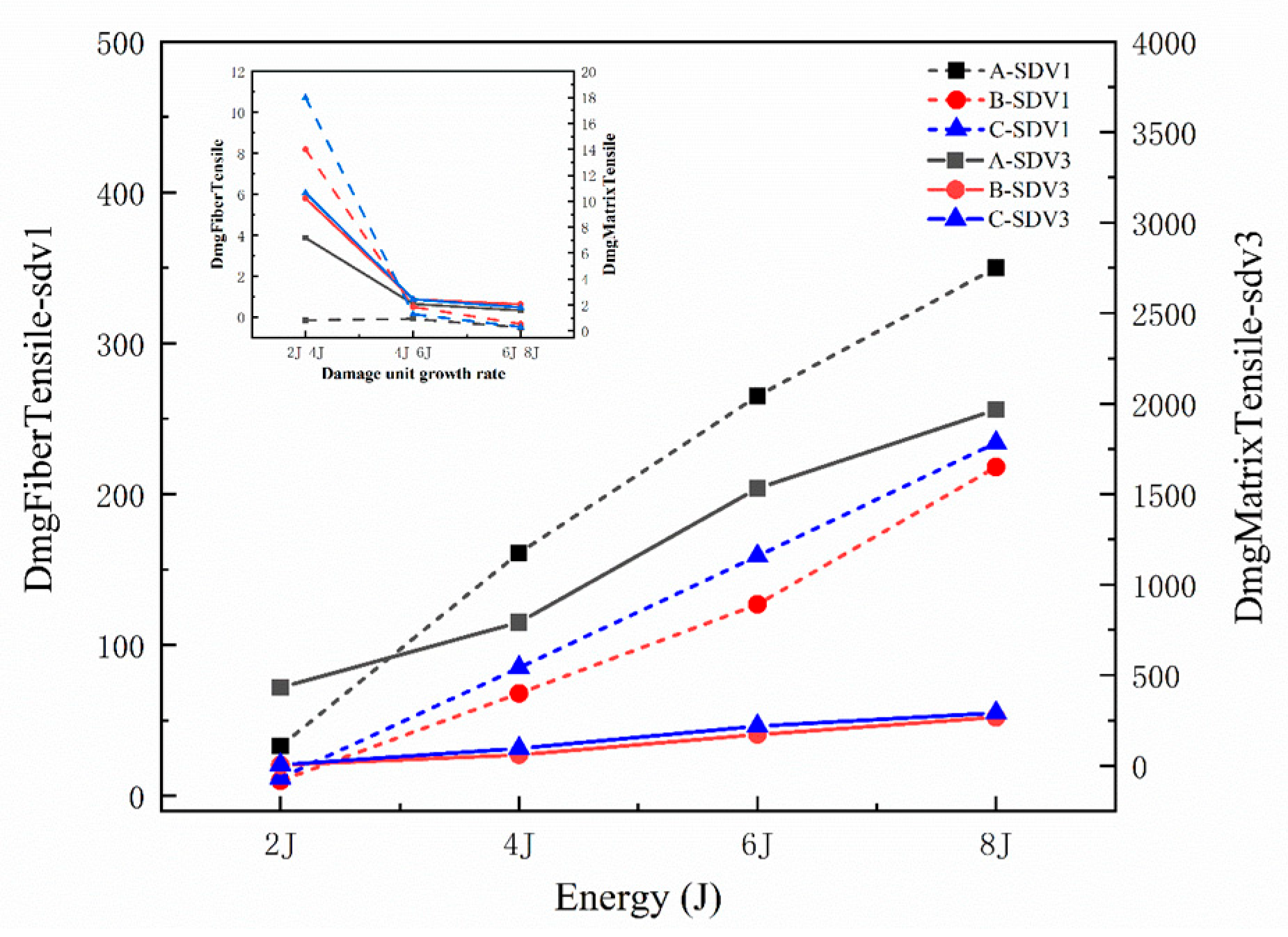
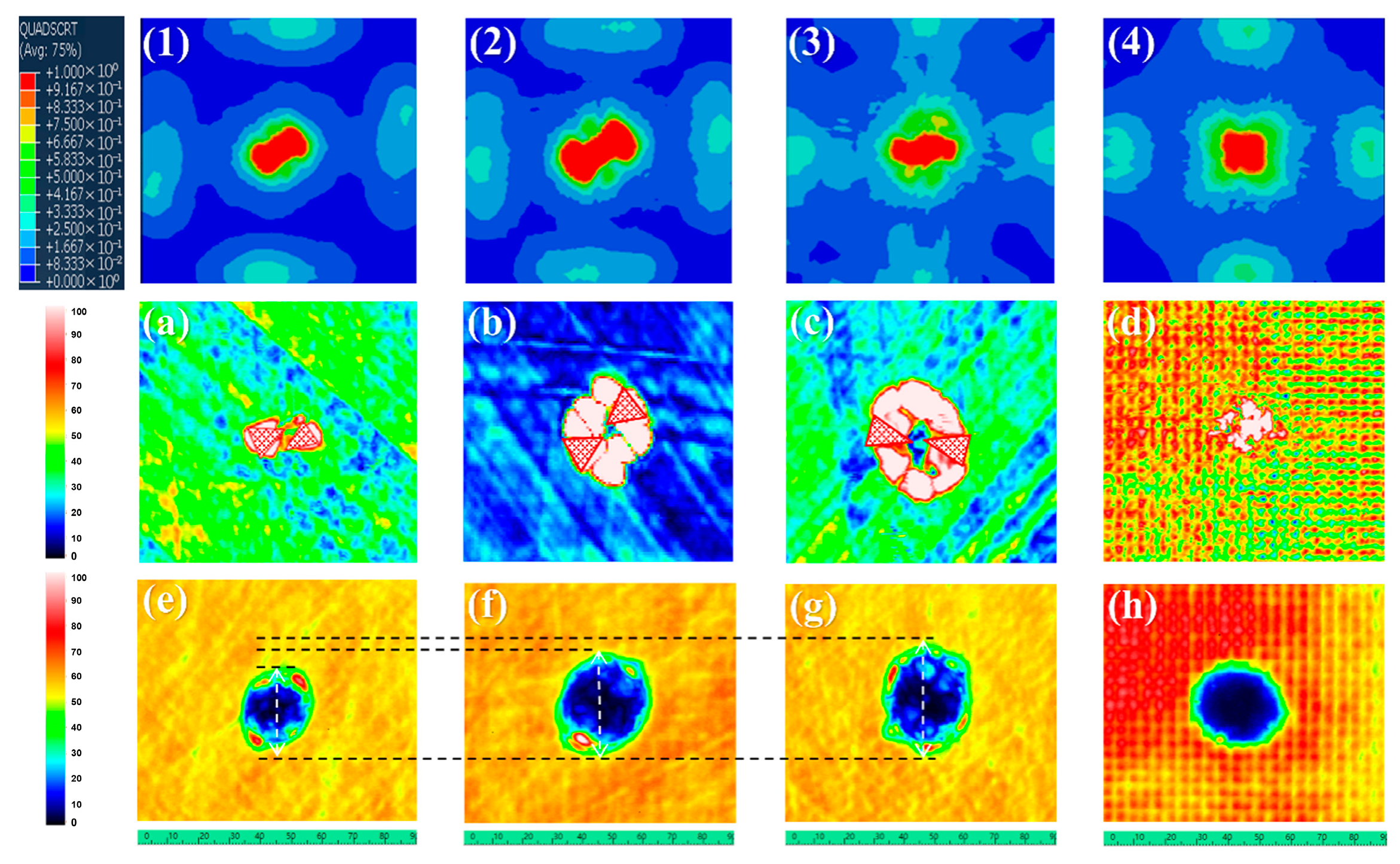
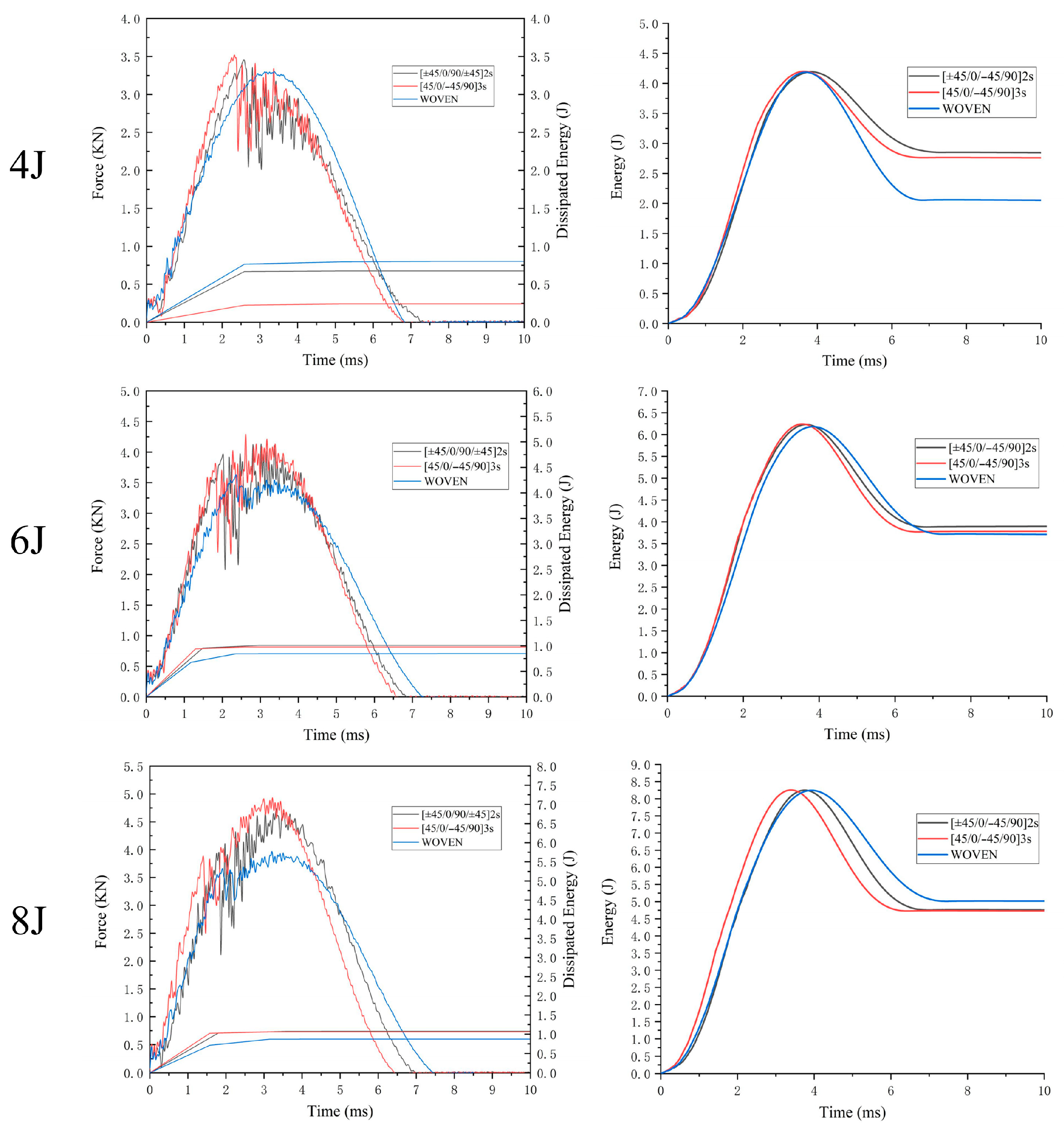
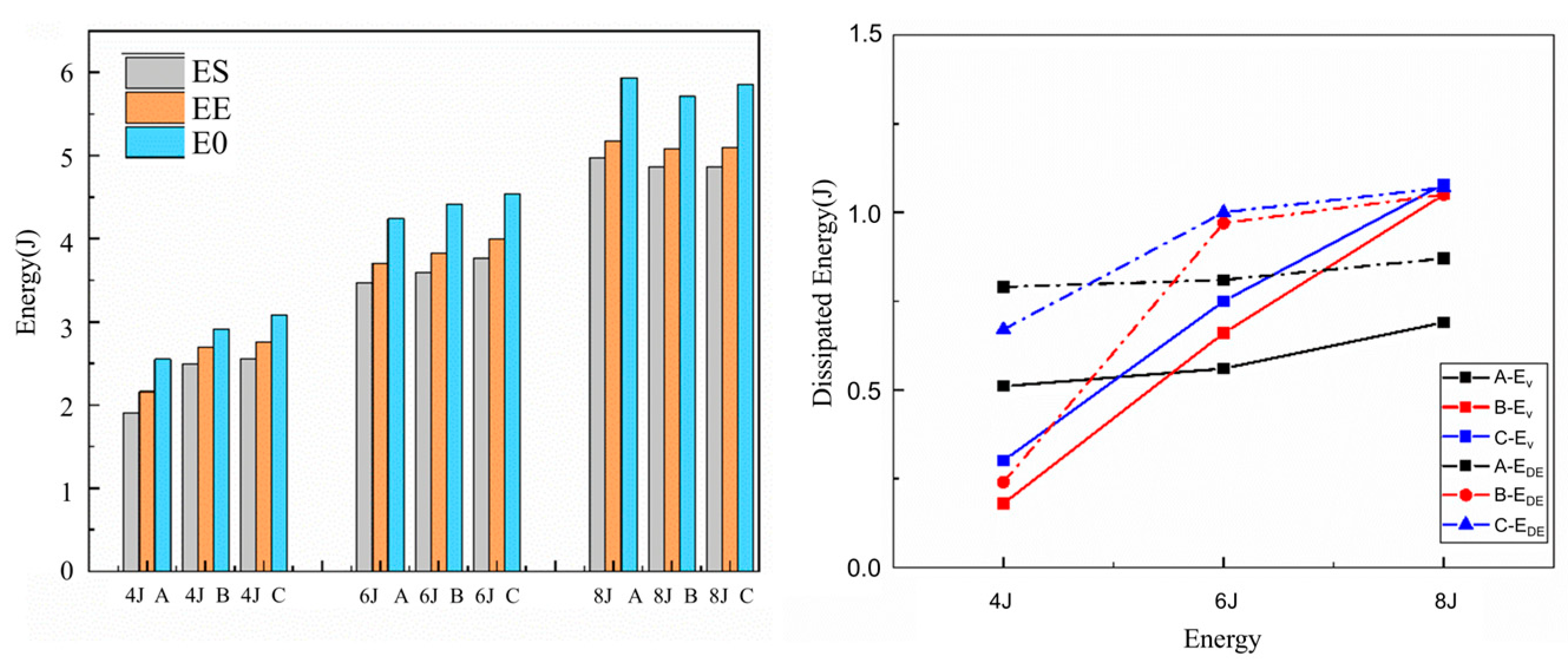
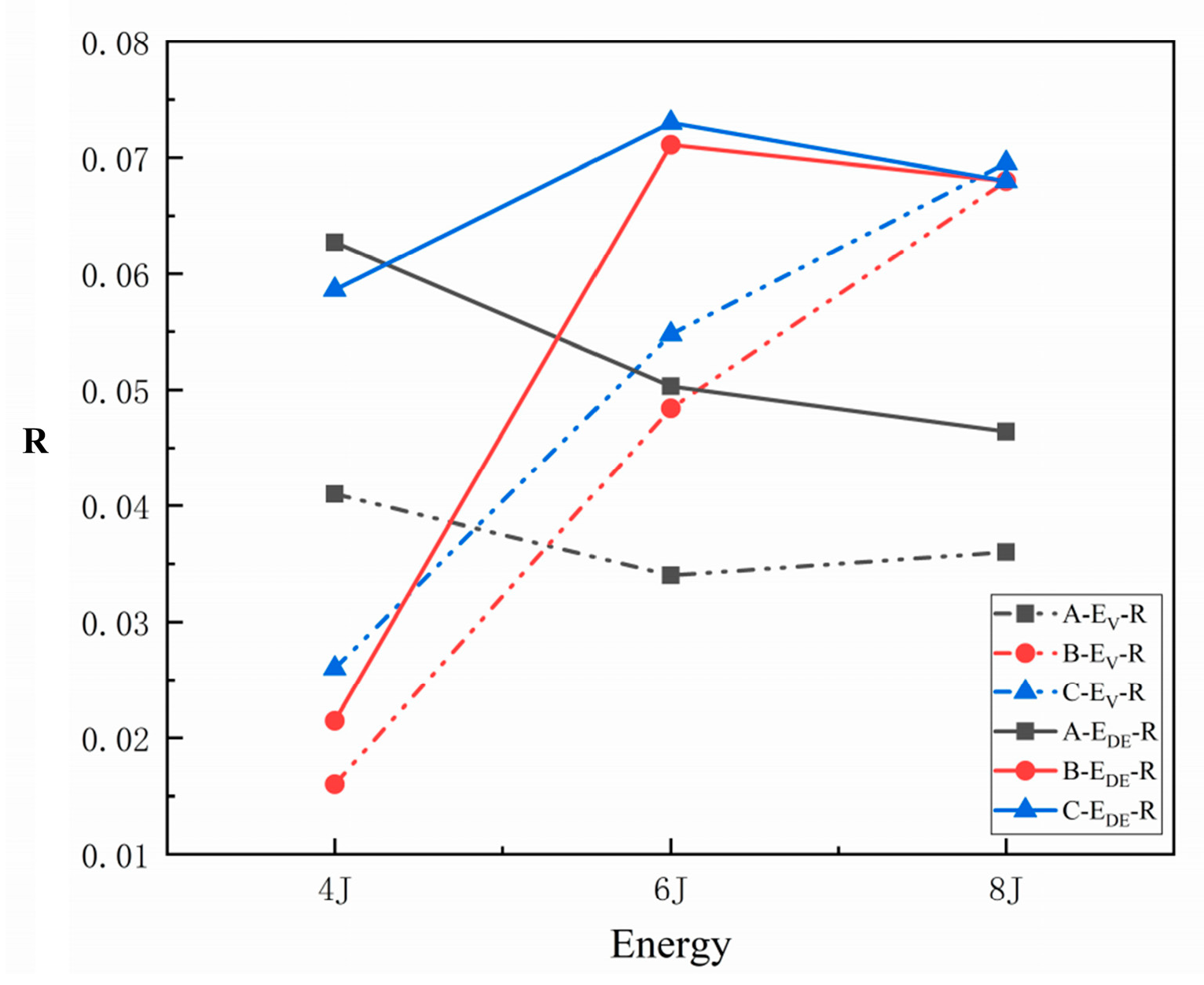
3. Results and Discussion
4. Conclusions
- 1.
- The impact of obtaining carbon fiber laminates with three different structures is as follows:
- 2.
- The following representation methods are proposed:
| Index | Characterization |
|---|---|
| The increase in cracks based on the crack dissipation energy | The performance of cracks in the overall damage. The damage state of the plate can be predicted to some extent. |
| The change in failure energy | A reference to describe the impact of damage deformation on the unidirectional ply and woven structured panels. |
| R-value combined with crack energy | Predict the impact damage resistance of each structural laminate (more accurately). |
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Falzon, B.G.; Tan, W. Experimental and numerical studies on the impact response of damage-tolerant hybrid unidirectional/woven carbon-fibre reinforced composite laminates. Compos. Prart. B Eng. 2018, 136, 101–118. [Google Scholar] [CrossRef]
- Marsh, G. Aero engines lose weight thanks to composites. Reinf. Plast. 2012, 56, 32–35. [Google Scholar] [CrossRef]
- Yan, L.; Xu, H. Lightweight composite materials in automotive engineering: State-of-the-art and future trends. Alex. Eng. J. 2025, 118, 1–10. [Google Scholar] [CrossRef]
- Islami, D.P.; Muzaqih, A.F.; Adiputra, R.; Prabowo, A.R.; Firdaus, N.; Ehlers, S.; Braun, M.; Jurkovič, M.; Smaradhana, D.F.; Carvalho, H. Structural design parameters of laminated composites for marine applications: Milestone study and extended review on current technology and engineering. Results Eng. 2024, 24, 103195. [Google Scholar] [CrossRef]
- Alam, M.J.; Abedin, M.J.; Rahman, M.Z. Nanoparticles, nanocomposites, green/eco-composites, and hybrid composites and their applications in energy sectors. In Comprehensive Materials Processing, 2nd ed.; Hashmi, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 321–339. [Google Scholar]
- Yang, F.; Cantwell, W. Impact damage initiation in composite materials. Compos. Sci. Technol. 2010, 70, 336–342. [Google Scholar] [CrossRef]
- Wang, M.; Shi, L.; Pan, Z.; Wu, Z. Mechanical response and damage mechanism of carbon/Kevlar hybrid braiding composite laminates under quasi-static indentation and low-velocity impact loading. Thin-Walled Struct. 2025, 213, 113291. [Google Scholar] [CrossRef]
- Zheng, K.; Cao, D.; Hu, H.; Chen, H.; Cai, W.; Li, S. Comprehensive investigation on modelling of low-velocity impact damage response of composite laminates—Experimental correlation and assessment. Compos. Struct. 2024, 345, 118412. [Google Scholar] [CrossRef]
- Faggiani, A.; Falzon, B. Predicting low-velocity impact damage on a stiffened composite panel. Compos. Part A Appl. Sci. Manuf. 2010, 41, 737–749. [Google Scholar] [CrossRef]
- Gliszczynski, A.; Kubiak, T.; Wawer, K. Barely visible impact damages of GFRP laminate profiles—An experimental study. Compos. Part B Eng. 2019, 158, 10–17. [Google Scholar] [CrossRef]
- Ellis, T.S.; Karasz, F.E. Interaction of epoxy resins with water: The depression of glass transition temperature. Polymer 1984, 25, 664–669. [Google Scholar] [CrossRef]
- Guha, R.D.; Rahmani, F.; Berkowitz, K.; Pasquinelli, M.; Grace, L.R. Temporal evolution of the behavior of absorbed moisture in a damaged polymer-quartz composite: A molecular dynamics study. Comput. Mater. Sci. 2022, 214, 111690. [Google Scholar] [CrossRef]
- Ibekwe, S.; Li, G. Low Velocity Impact Damage on Laminated Polymer Composites. In Encyclopedia of Materials: Plastics and Polymers; Hashmi, M.S.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 241–266. [Google Scholar]
- Zheng, X.; Wu, Y.; Zheng, C.; Bai, H.; Liu, R. Quasistatic and low-velocity impact properties of entangled metallic wire material–silicone rubber composites. J. Mater. Res. Technol. 2023, 23, 3856–3868. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, H.; Ng, C.-T.; Fu, J.; Zhang, Z.; Wang, C. On the low-velocity impact properties of CFRP/HAFRP interlayer hybrid fibre composite laminates. Eng. Struct. 2024, 315, 118387. [Google Scholar] [CrossRef]
- Chen, X.; Peng, Y.; Wang, K.; Wang, X.; Liu, Z.; Huang, Z.; Zhang, H. Experimental and simulation study on bonded repaired low-velocity impact of carbon fiber reinforced plastic laminates for rail vehicles. J. Mater. Res. Technol. 2023, 28, 446–458. [Google Scholar] [CrossRef]
- Lyu, Q.; Wang, B.; Guo, Z. Predicting post-impact compression strength of composite laminates under multiple low-velocity impacts. Compos. Part A Appl. Sci. Manuf. 2023, 164, 107322. [Google Scholar] [CrossRef]
- Jing, K.; Zhou, H.; Wang, H.; Yan, H.; Xie, S. Multiscale damage and low-velocity impact study of three-dimensional woven composites. Thin-Walled Struct. 2024, 202, 112132. [Google Scholar] [CrossRef]
- Li, N.; Du, J.; Lee, H.M.; Liu, W.; Zheng, Y.; Lee, H.P. Damage characterization and modelling of FRP laminated composites subjected to external edge-on impact. Compos. Part B Eng. 2024, 287, 111819. [Google Scholar] [CrossRef]
- Li, X.; Liu, P.; Cheng, H.; Liu, C.; Zhu, Y.; Zhang, K. Experimental and numerical analysis of low-velocity impact damage of CFRP laminates with negative Poisson ratio (NPR) rubber protective layer. Thin-Walled Struct. 2023, 191, 111066. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, X. Numerical analysis of unidirectional carbon-fibre/epoxy composite laminates under low velocity impacts of different forms. Comput. Mater. 2024, 231, 112611. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, L.; Xuan, S.; Fan, X.; Fu, B.; Xue, X.; Yao, X. An efficient surrogate model for damage forecasting of composite laminates based on deep learning. Compos. Struct. 2024, 331, 117863. [Google Scholar] [CrossRef]
- David-West, O.; Nash, D.; Banks, W. An experimental study of damage accumulation in balanced CFRP laminates due to repeated impact. Compos. Struct. 2008, 83, 247–258. [Google Scholar] [CrossRef]
- Yao, T.; Li, D.; Jiang, L. Parametric theoretical prediction of elastic properties and strength of fine weave pierced C/C composites. Compos. Struct. 2023, 325, 117614. [Google Scholar] [CrossRef]
- Russo, A.; Palumbo, C.; Riccio, A. The role of intralaminar damages on the delamination evolution in laminated composite structures. Heliyon 2023, 9, e15060. [Google Scholar] [CrossRef]
- Shao, M.; Cai, D.A.; Yu, Q.; Xing, D.; Hu, F.; Kuang, N.; Zhou, G. On mechanical properties of double-sided-loop 2D woven laminated composites. Compos. Struct. 2023, 312, 116874. [Google Scholar] [CrossRef]
- Kim, H.B.; Naito, K.; Oguma, H. Mode II fracture toughness of two-part acrylic-based adhesive in an adhesively bonded joint: End-notched flexure tests under static loadinG. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1795–1808. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Gambino, B.; Mellone, A.; Spagnolo, M. Mode-I Fracture Behavior of CFRPs: Numerical Model of the Experimental Results. Materials 2019, 12, 513. [Google Scholar] [CrossRef]
- Han, J.; Lei, L.; Liu, S.; Zhang, J. Fatigue damage analysis and life prediction of 3D braided SiC/SiC composites with multi-scale approach. Compos. Struct. 2024, 349–350, 118447. [Google Scholar] [CrossRef]
- SIMULIA ABAQUS, Version 6.14-5; Dassault Systèmes: Providence, RI, USA, 2014.
- Zhang, T. Research on Repair Performance of T300/7901 Carbon Fiber Composite Laminate. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2023. [Google Scholar] [CrossRef]
- Zhao, Q.L.; Hou, Y.L.; Liu, Z.; Li, C. Multi-scale modeling of the low-velocity impact and compression after impact behaviors of plain woven carbon-fiber-reinforced composites. China Mech. Eng. 2021, 32, 1732–1742. [Google Scholar]
- ASTM D7136/D7136M-20; Standard test method for measuring the damage resistance of a fiber-reinforced polymer matrix composite to a drop-weight impact event. ASTM International: West Conshohocken, PA, USA, 2020.
- Hongkarnjanakul, N.; Bouvet, C.; Rivallant, S. Validation of low velocity impact modelling on different stacking sequences of CFRP laminates and influence of fibre failure. Compos. Struct. 2013, 106, 549–559. [Google Scholar] [CrossRef]
- Cao, Y.; Cai, Y.; Zhao, Z.; Liu, P.; Han, L.; Zhang, C. Predicting the tensile and compressive failure behavior of angle-ply spread tow woven composites. Compos. Struct. 2020, 234, 111701. [Google Scholar] [CrossRef]
- Khashaba, U.A. A comprehensive study of low-velocity impact behavior and damage evaluation of angle-ply thin woven GFRP composites under elevated temperatures. Compos. Sci. Technol. 2024, 252, 110608. [Google Scholar] [CrossRef]
- Xiao, J.; Bathias, C. Fatigue behaviour of unnotched and notched woven glass/epoxy laminates. Compos. Sci. Technol. 1994, 50, 141–148. [Google Scholar] [CrossRef]
- Curtis, P.T.; Bishop, S.M. An assessment of the potential of woven carbon fibre-reinforced plastics for high performance applications. Composites 1984, 15, 259–265. [Google Scholar] [CrossRef]
- GB/T 18694-2002; Chinese Standard. Non-destructive testing--Ultrasonic inspection--Characterization of search unit and sound field. State General Administration of the People’s Republic of China for Quality Supervision and Inspection and Quarantine: Beijing, China, 2002.
- Liu, M.; Pan, Q.; Gao, M.; Luo, C.; Tang, Z.; Sun, Z. Experimental study of the impact damage pattern of carbon fiber reinforced resin matrix composite laminates. Failure Anal. Prev. 2016, 11, 283–288+299. [Google Scholar] [CrossRef]
- Hongbo, H. Investigation of Constituents Damage and Interface Strength of Laminate Made of Carbon Fiber Woven Fabrics. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2019. [Google Scholar]
- Yuan, K.; Shen, L.; Xiong, W.; Yao, S.; He, J.; Wang, Z. The impact and post-impact flexural behaviors of CFRP/aluminum-honeycomb sandwich. Int. J. Impact Eng. 2023, 174, 104507. [Google Scholar] [CrossRef]
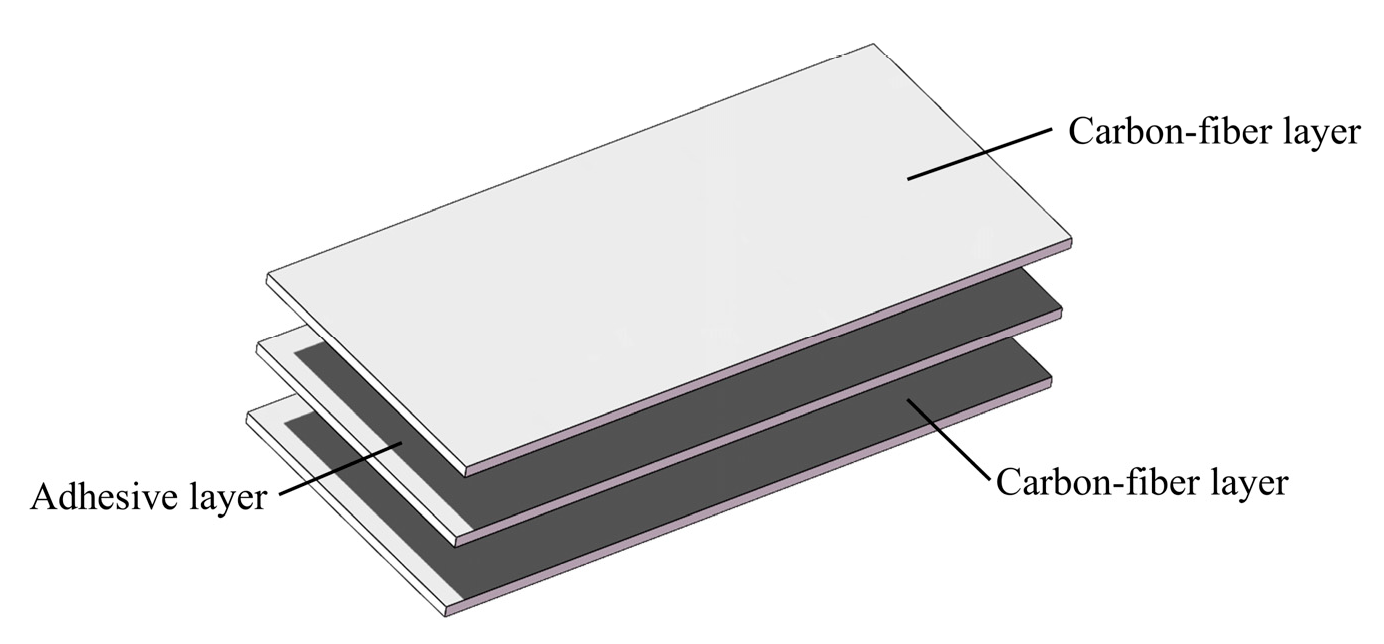
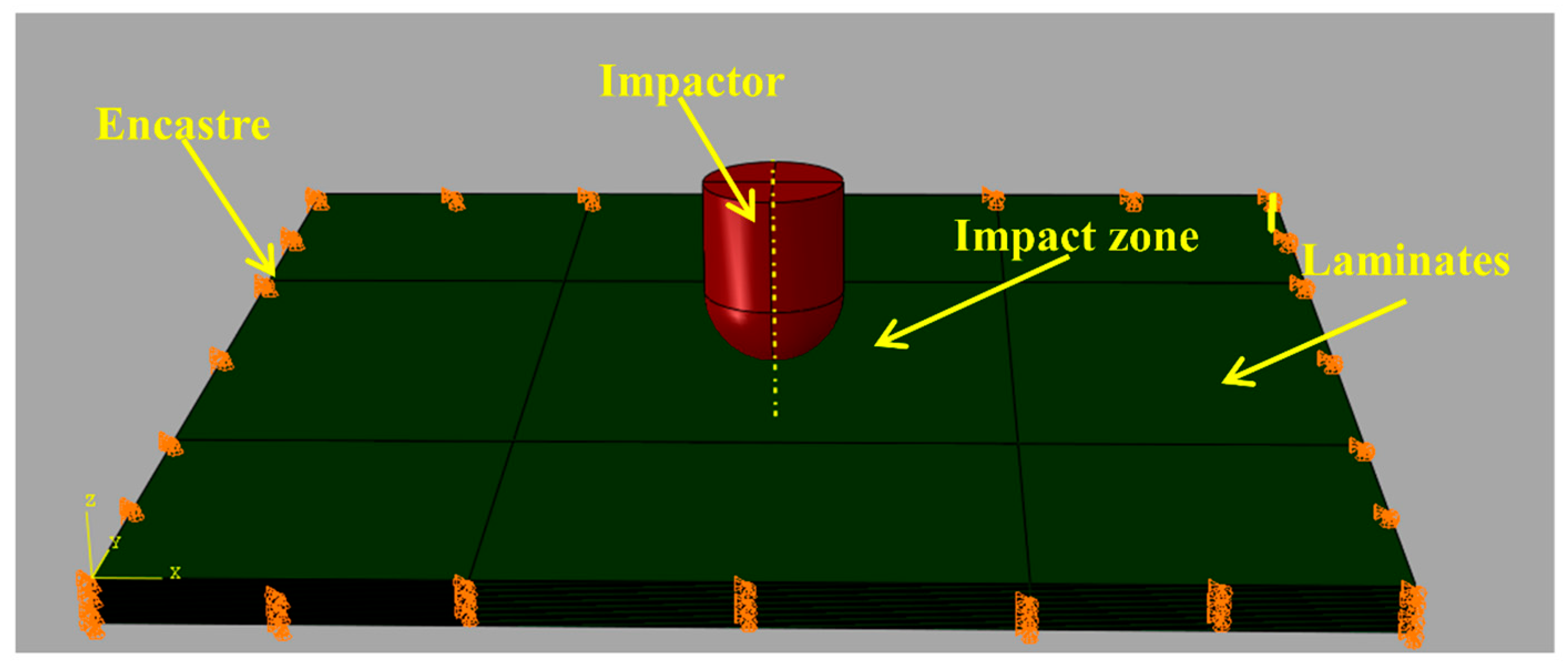

| Carbon Fiber Layer | Cohesive | |
|---|---|---|
| E1/GPa | 138 | E11 = 100,000 |
| E2/GPa | 9.31 | |
| E3/GPa | 9.31 | |
| G12/GPa | 4.81 | E22 = 100,000 |
| G13/GPa | 4.81 | |
| G23/GPa | 5 | |
| υ12 | 0.32 | E33 = 100,000 |
| υ13 | 0.32 | |
| υ23 | 0.45 | |
| Elastic Constants | Strength Parameters | ||
|---|---|---|---|
| Ey11/G Pa | 184.771 | tensile strength XyT/MPa | 2890 |
| Ey22 = Ey33/GPa | 19.172 | Compression strength XyC/MPa | 2065 |
| Gy12 = Gy13/GPa | 8.462 | tensile strength YyT/MPa | 92 |
| Gy23/GPa | 6.760 | Compression strength YyC/MPa | 187 |
| υ12 = υ13 | 0.28 | Shear strength Sy12 = Sy13/MPa | 107 |
| υ23 | 0.42 | Shear strength Sy23/MPa | 61 |
| Plain Woven | [45/0/−45/90]3s | [±45/0/90/±45]2s | |
|---|---|---|---|
| The number of failed cells | max | min | mid |
| The growth rate of damage cells | lower | higher | |
| Delamination damage | smaller and more concentrated. | diamond-shaped or cross-shaped | |
| Impact damage | smaller area and more concentrated. | a smaller impact damage a larger internal damage area | |
| Macroscopic damage | a few small cracks around the crater and no obvious damage to the back | more damage | |
| Crack dissipation energy | 4 J: The woven structure was greater. 6 J 8 J: The woven structure is slightly smaller. | ||
| Resistance to impact damage | max | mid | min |
| Major reasons | 1. The interwoven mesh structure of each layer impeding the downward movement of the punch. 2. The ±45° angle of unidirectional lay-up causes the uniformity of stress transfer to affect delamination damage. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y.; Ma, X.; Feng, C.; Ding, Y.; Ma, K. Study of Low-Velocity Impact Damage in Composite Laminates Based on Crack Energy. Fibers 2025, 13, 115. https://doi.org/10.3390/fib13090115
Shang Y, Ma X, Feng C, Ding Y, Ma K. Study of Low-Velocity Impact Damage in Composite Laminates Based on Crack Energy. Fibers. 2025; 13(9):115. https://doi.org/10.3390/fib13090115
Chicago/Turabian StyleShang, Yingming, Xu Ma, Chencheng Feng, Yanhong Ding, and Ke Ma. 2025. "Study of Low-Velocity Impact Damage in Composite Laminates Based on Crack Energy" Fibers 13, no. 9: 115. https://doi.org/10.3390/fib13090115
APA StyleShang, Y., Ma, X., Feng, C., Ding, Y., & Ma, K. (2025). Study of Low-Velocity Impact Damage in Composite Laminates Based on Crack Energy. Fibers, 13(9), 115. https://doi.org/10.3390/fib13090115






