Performance Prediction of GFRP-Reinforced Concrete Deep Beams Containing a Web Opening in the Shear Span
Abstract
1. Introduction
2. Model Development
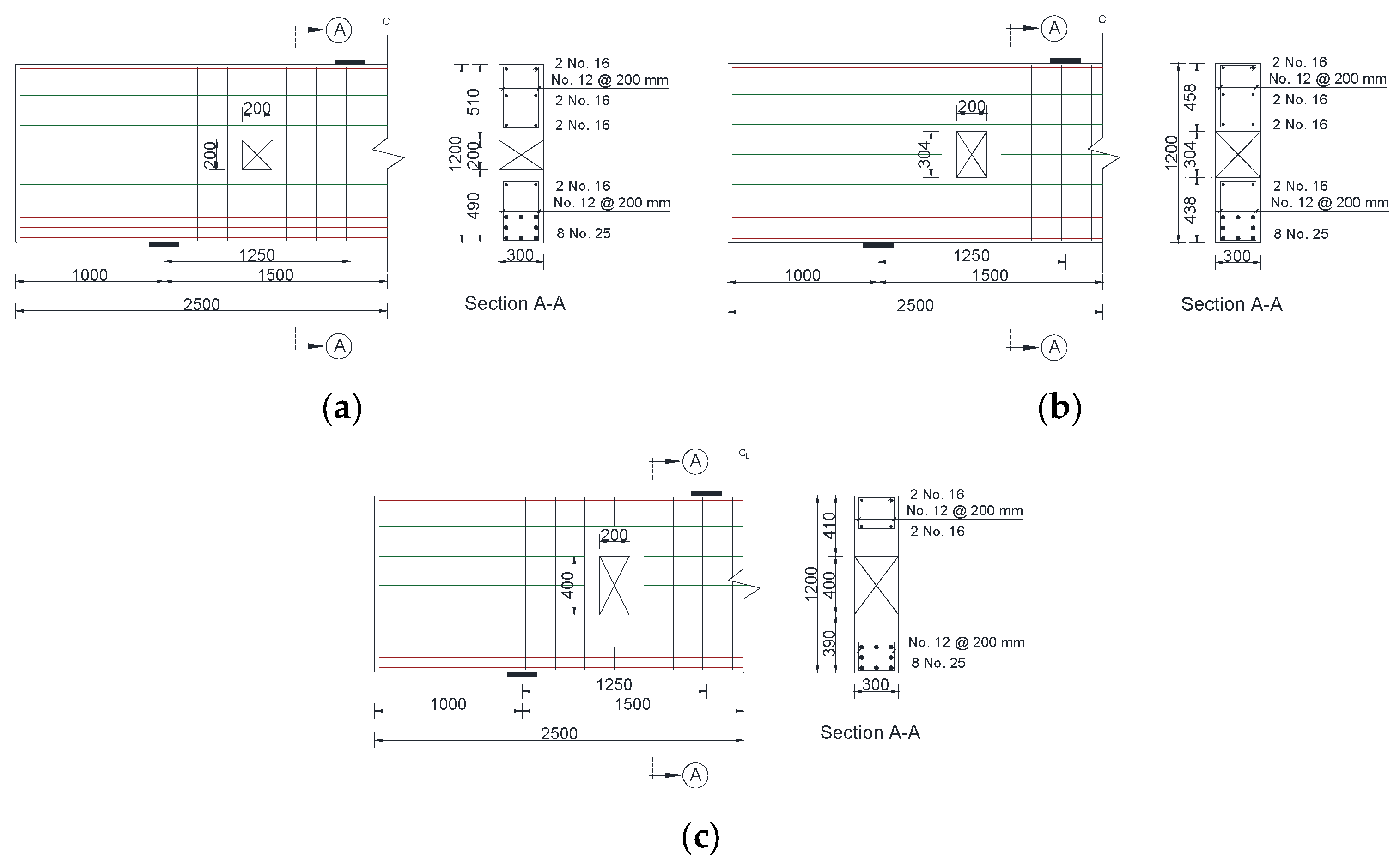
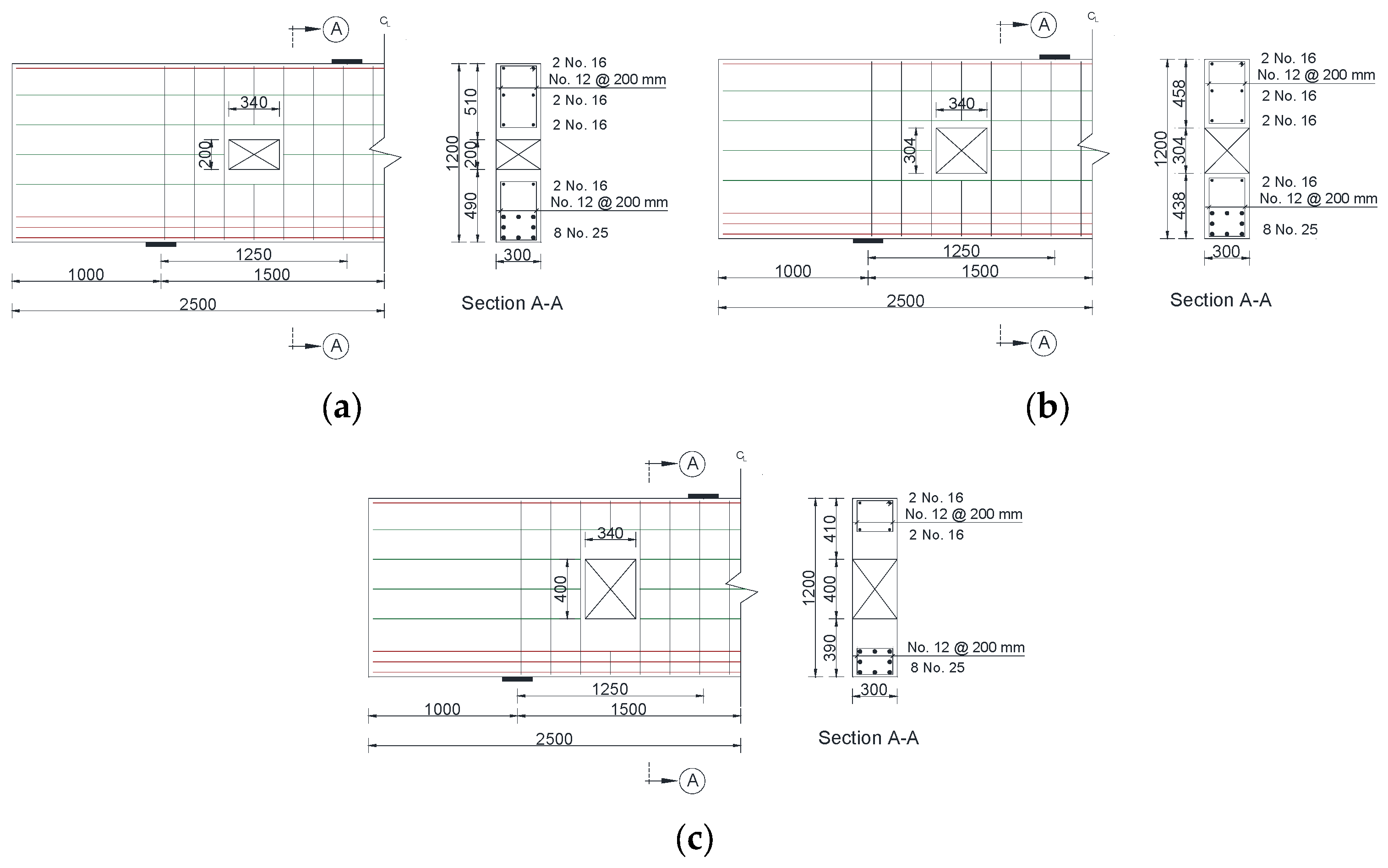
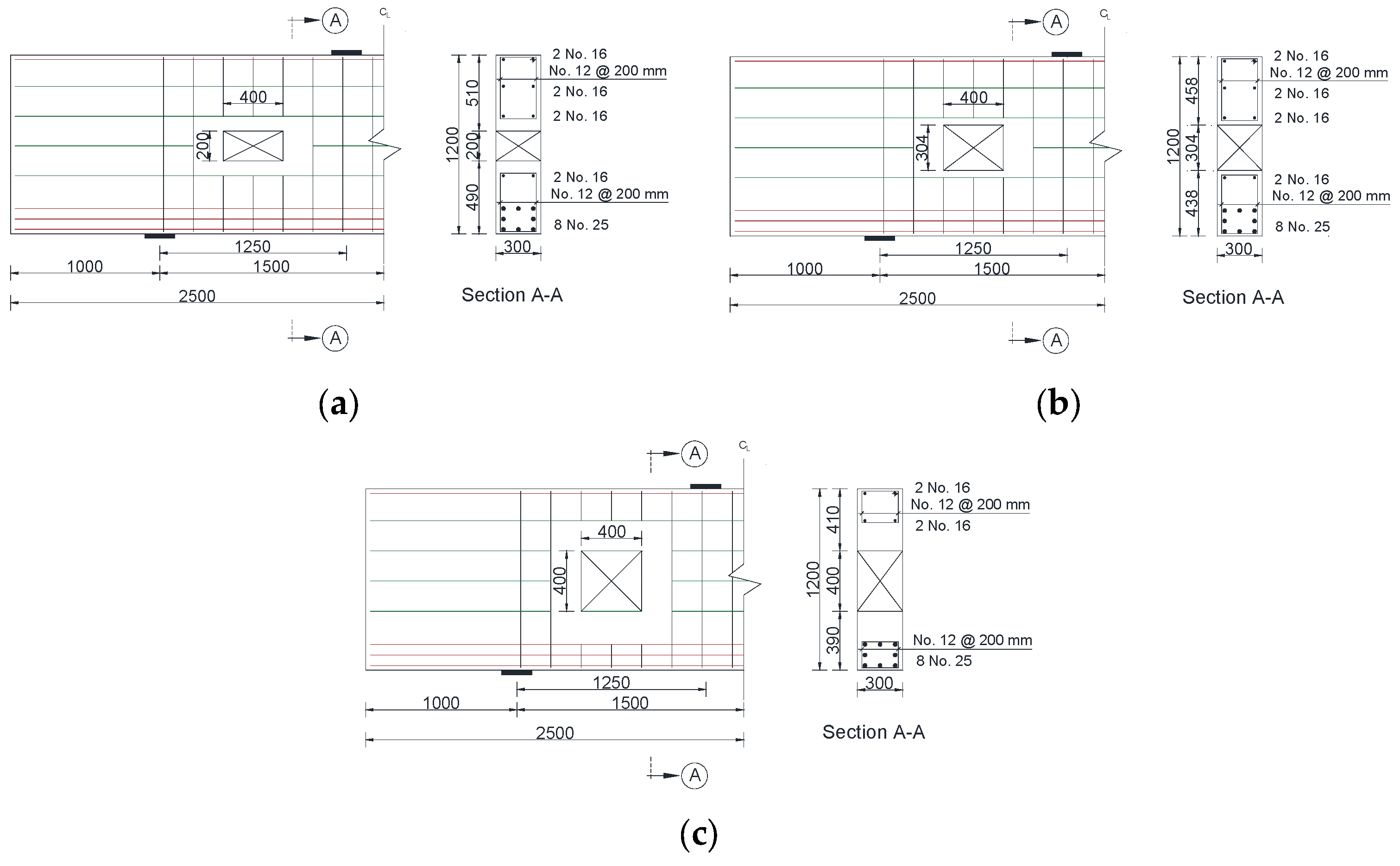
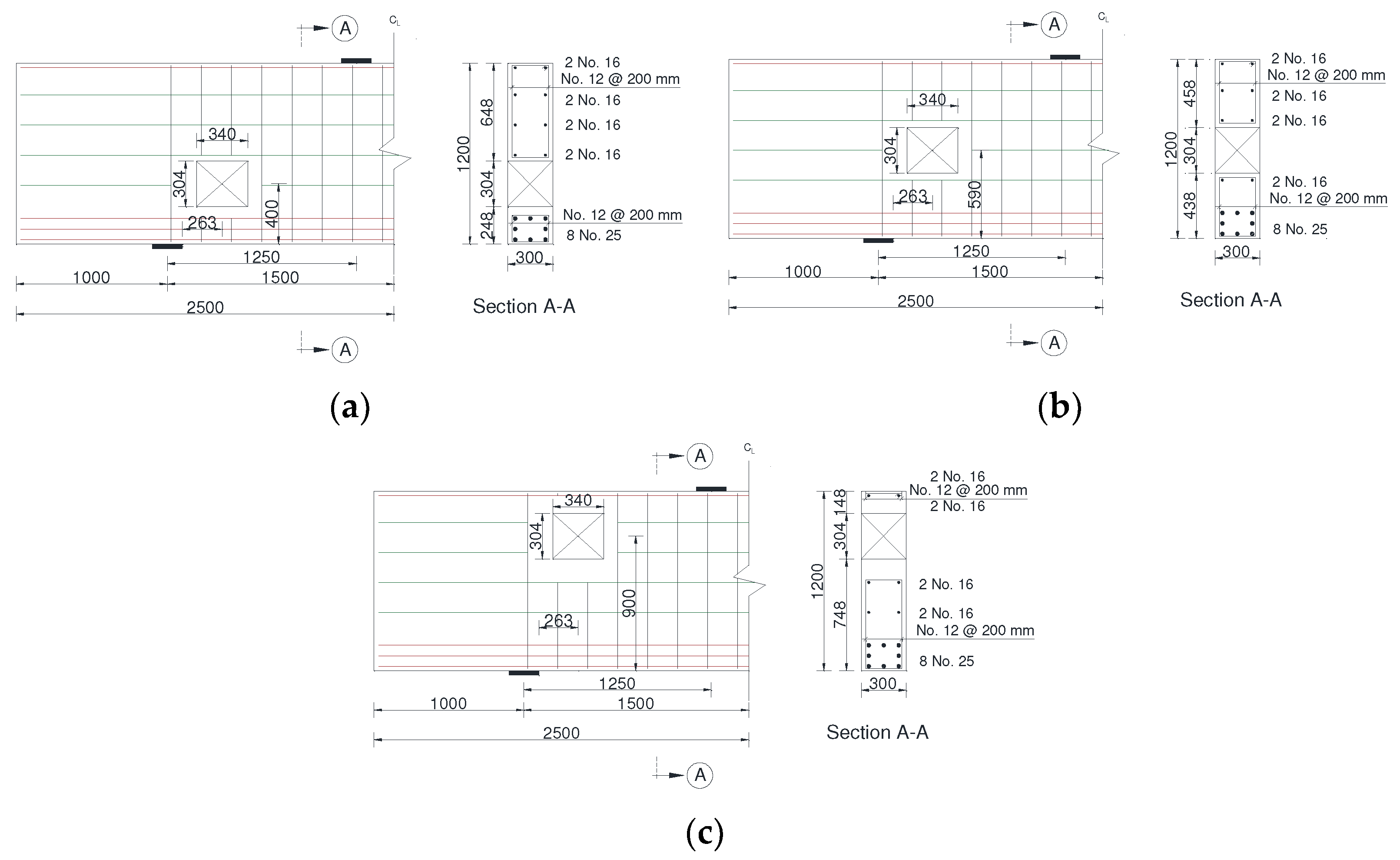
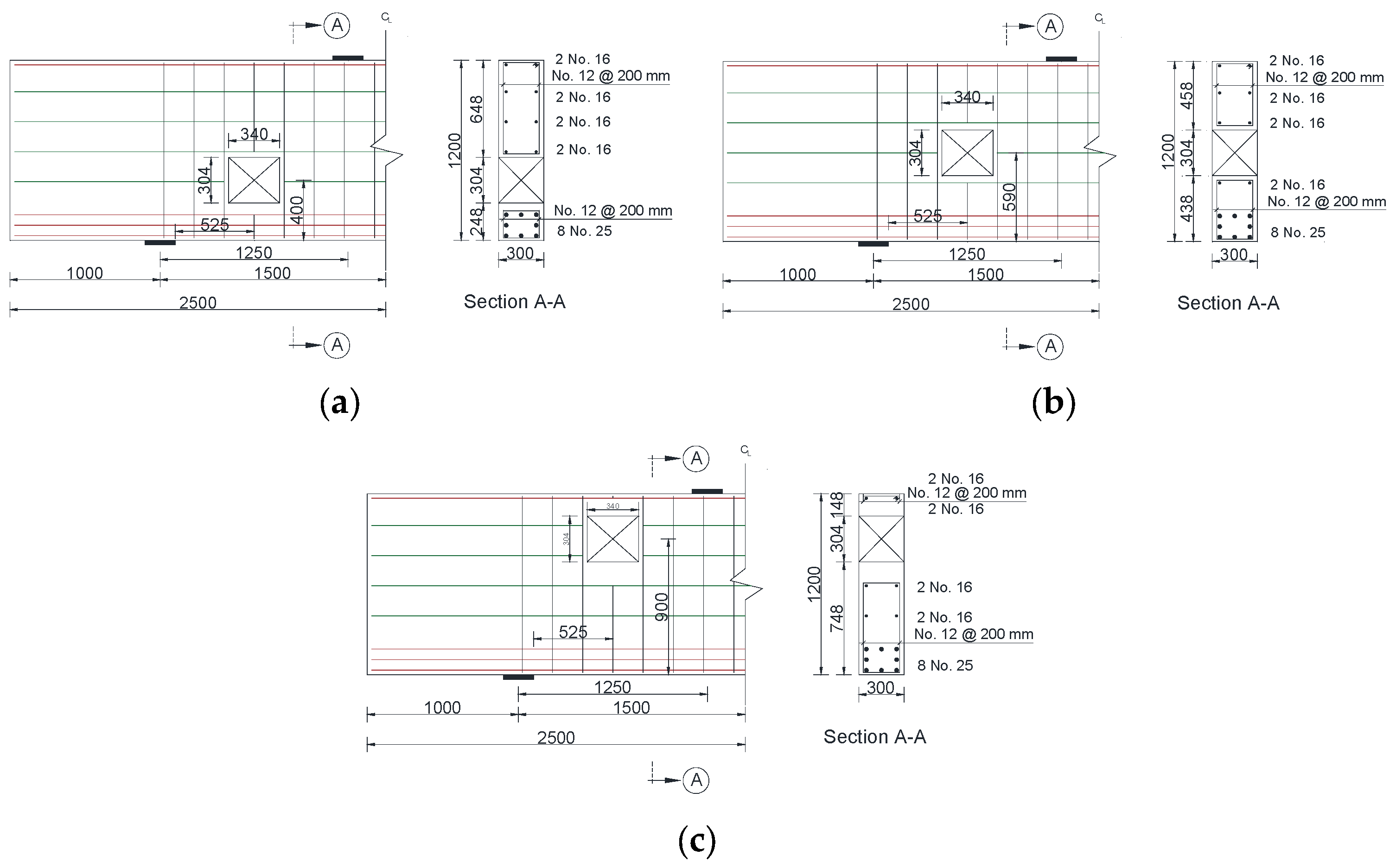
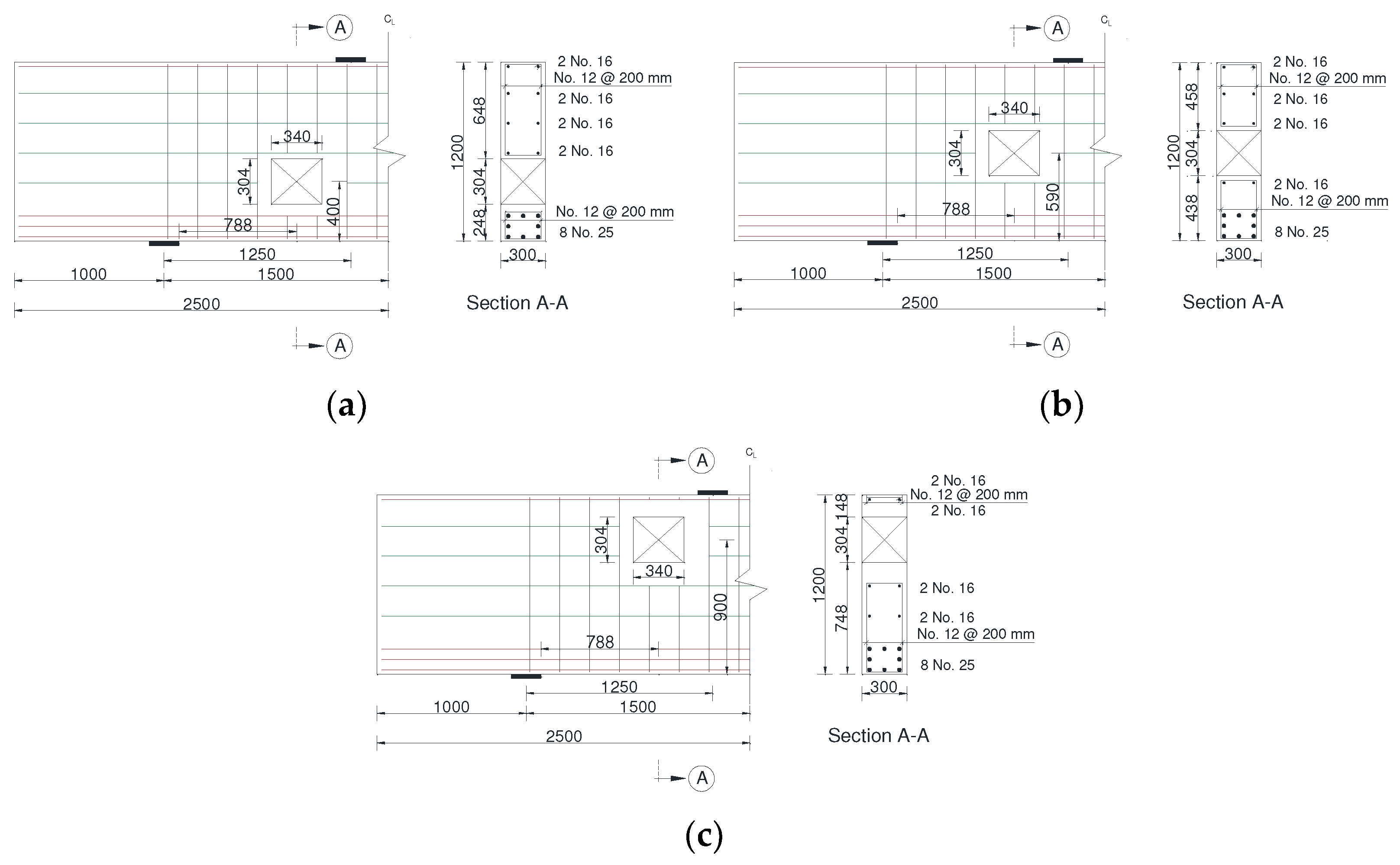
2.1. Geometry of the Beam Models
2.2. Constitutive Laws of Materials
2.3. Types of Element and Boundary Conditions
3. Model Verification
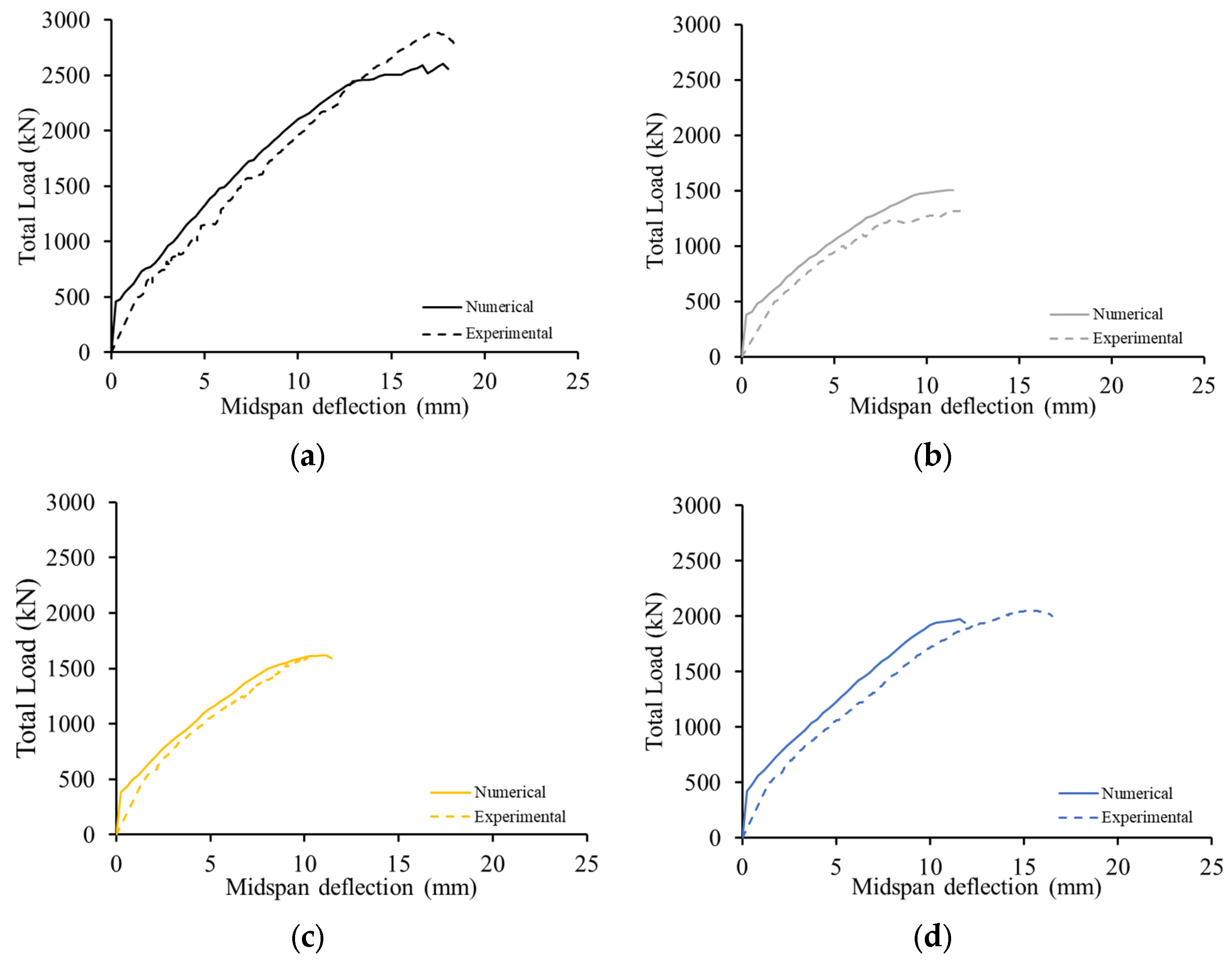
3.1. Load-Deflection Response
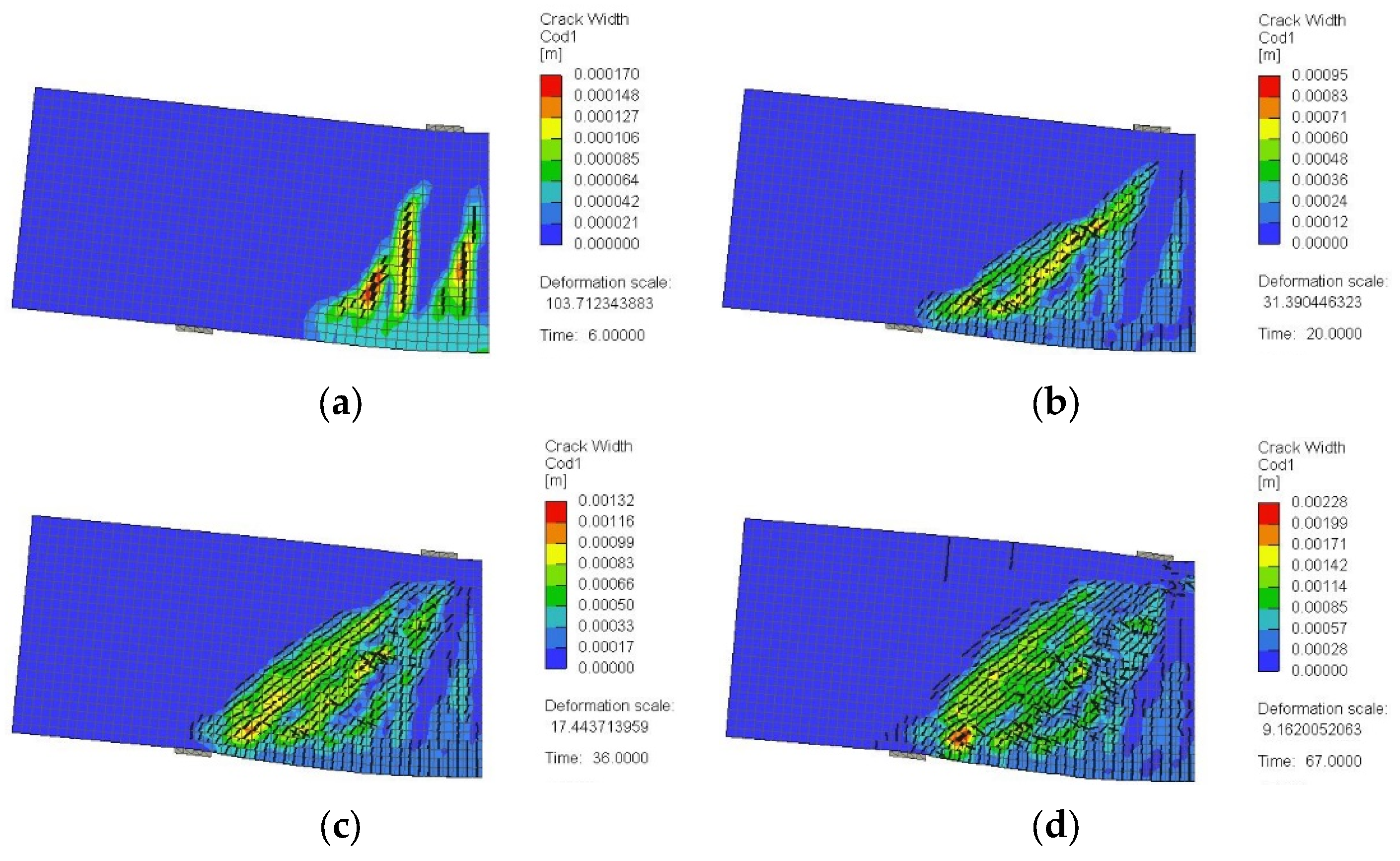
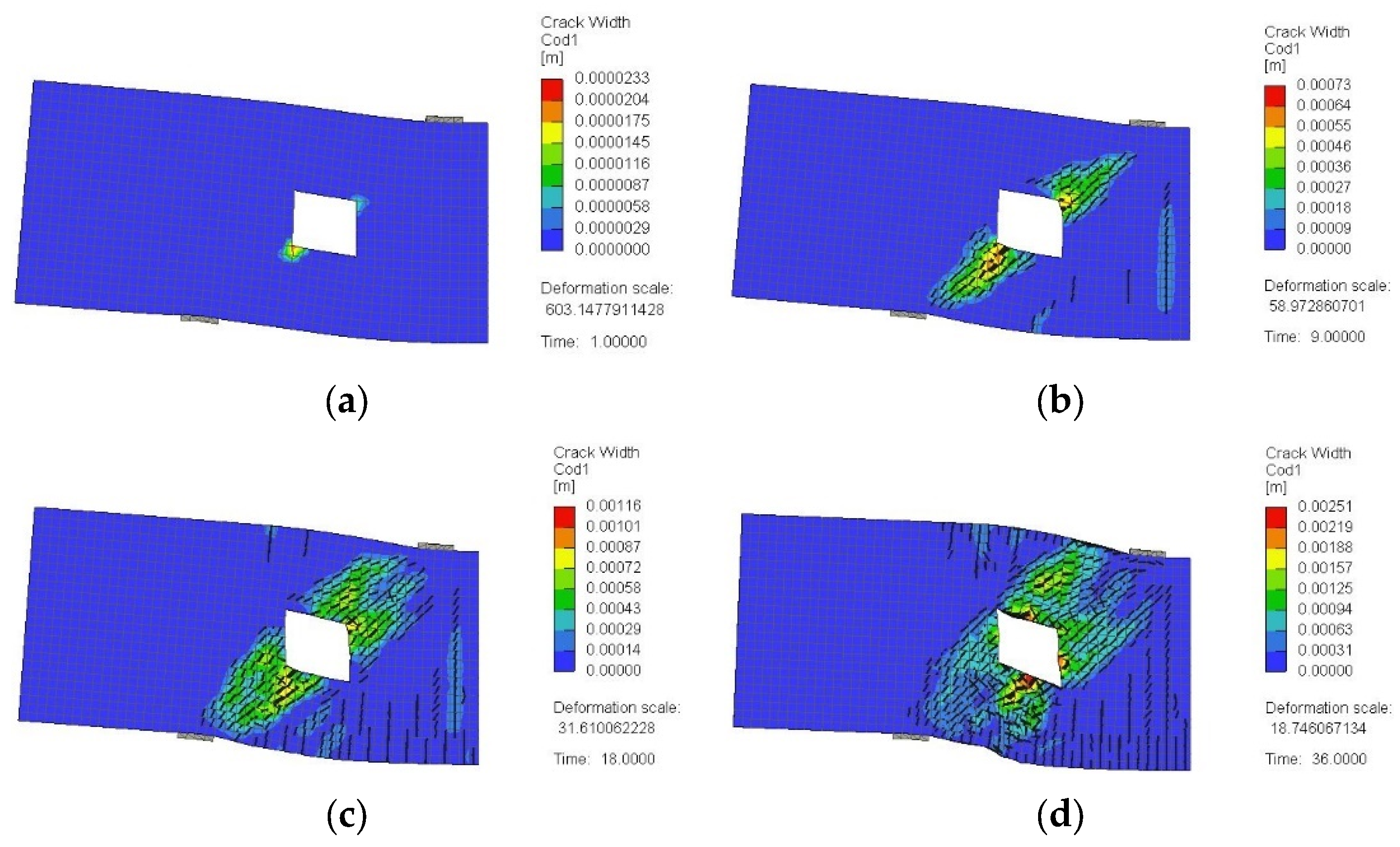
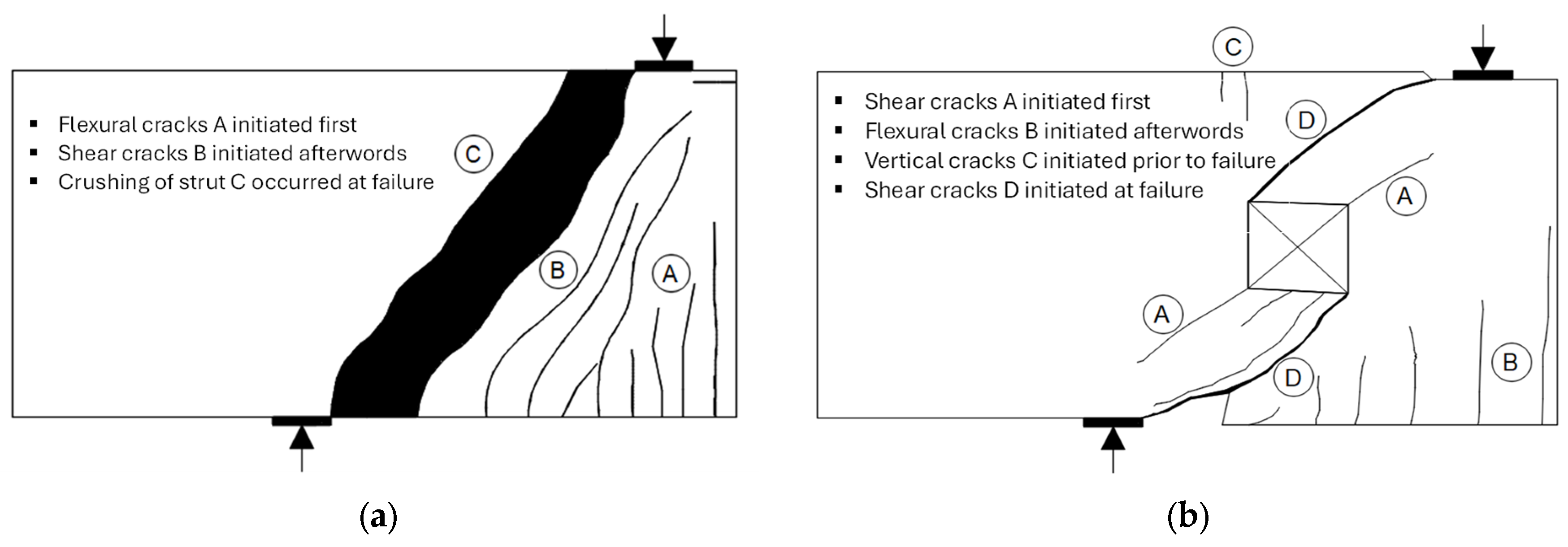
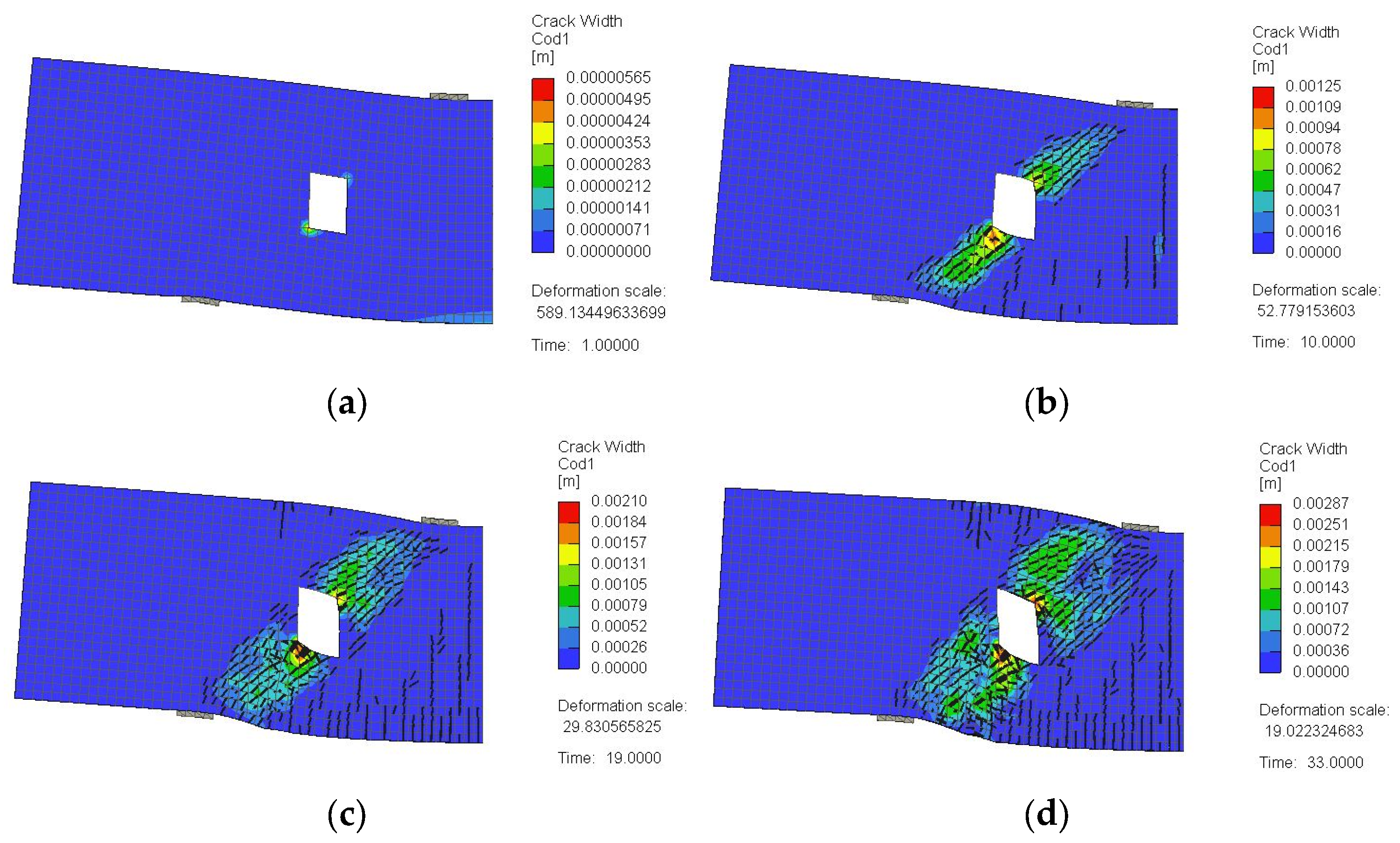
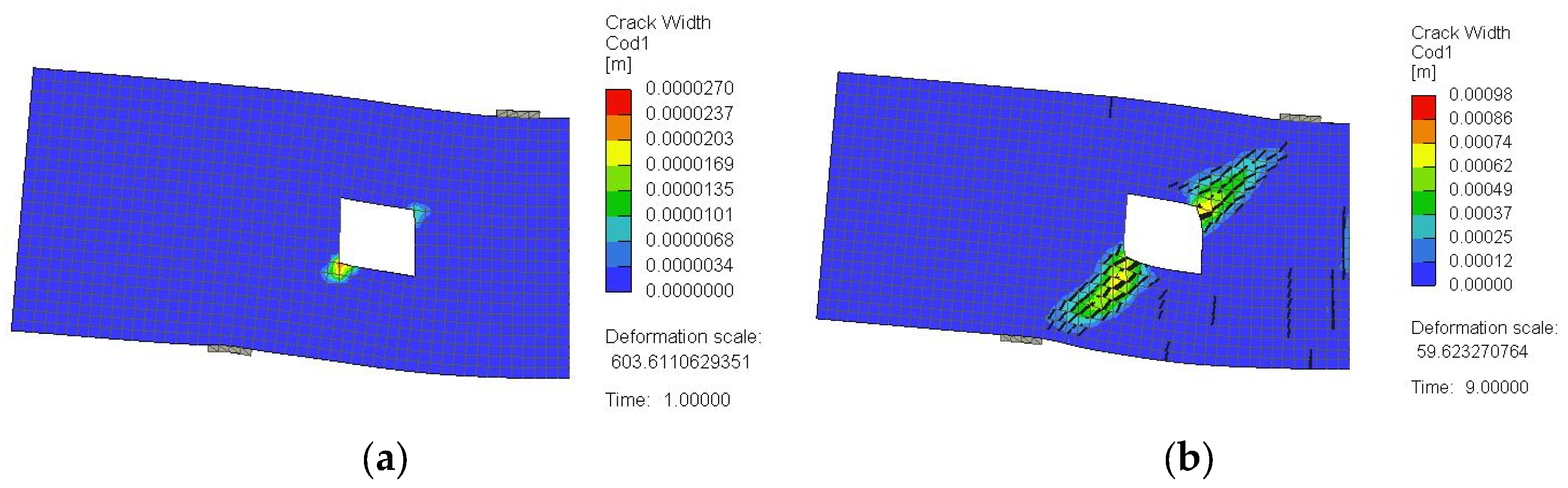
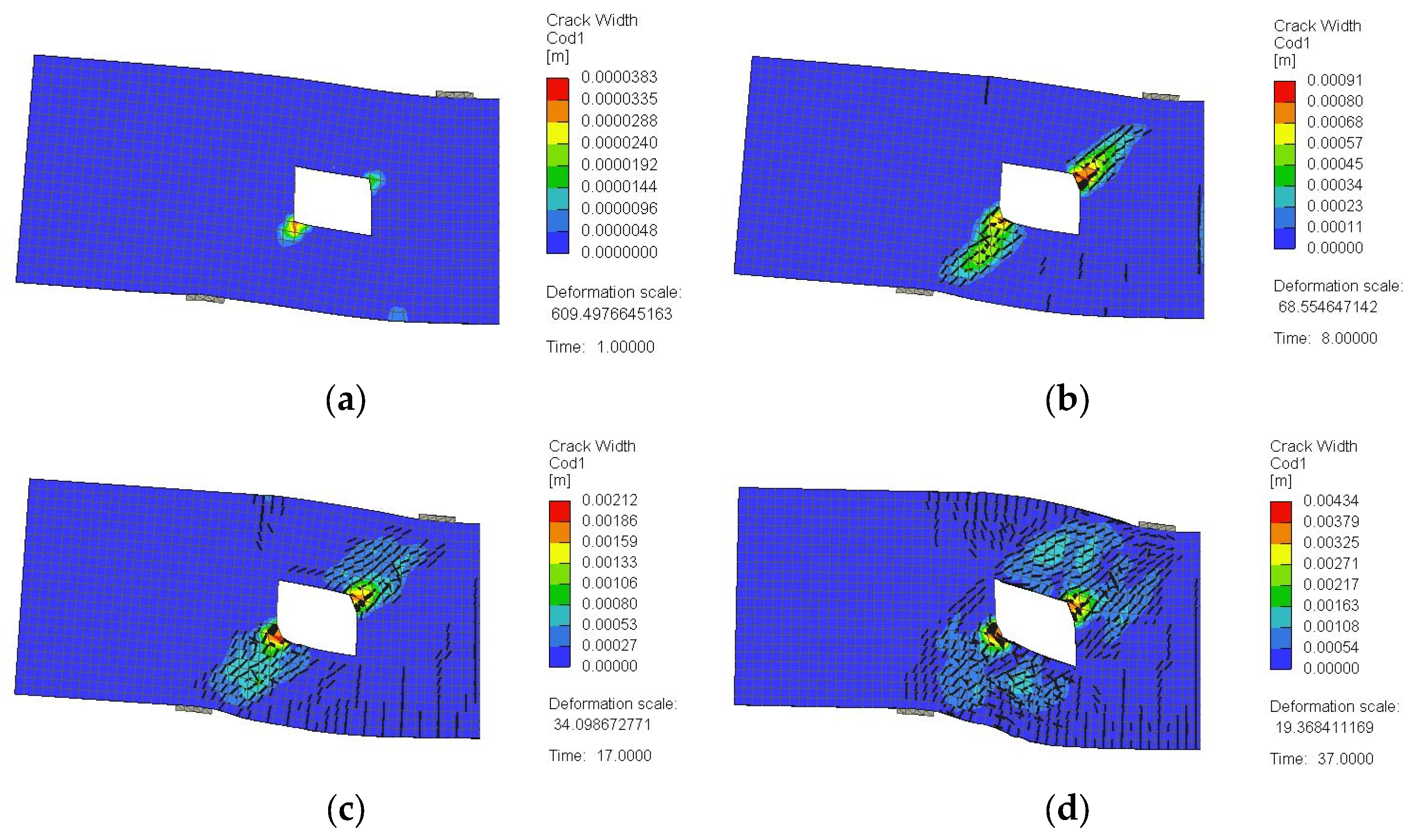
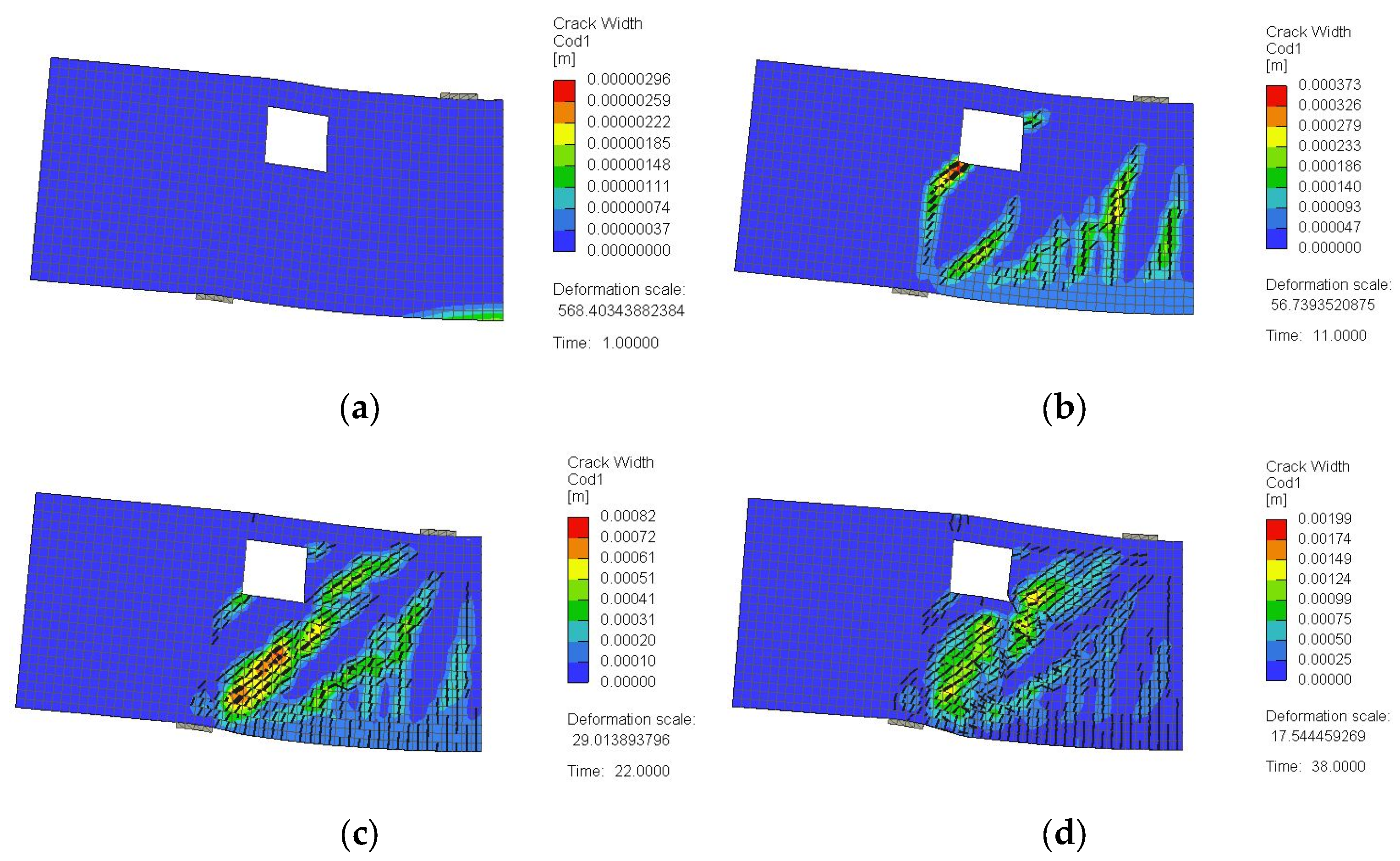
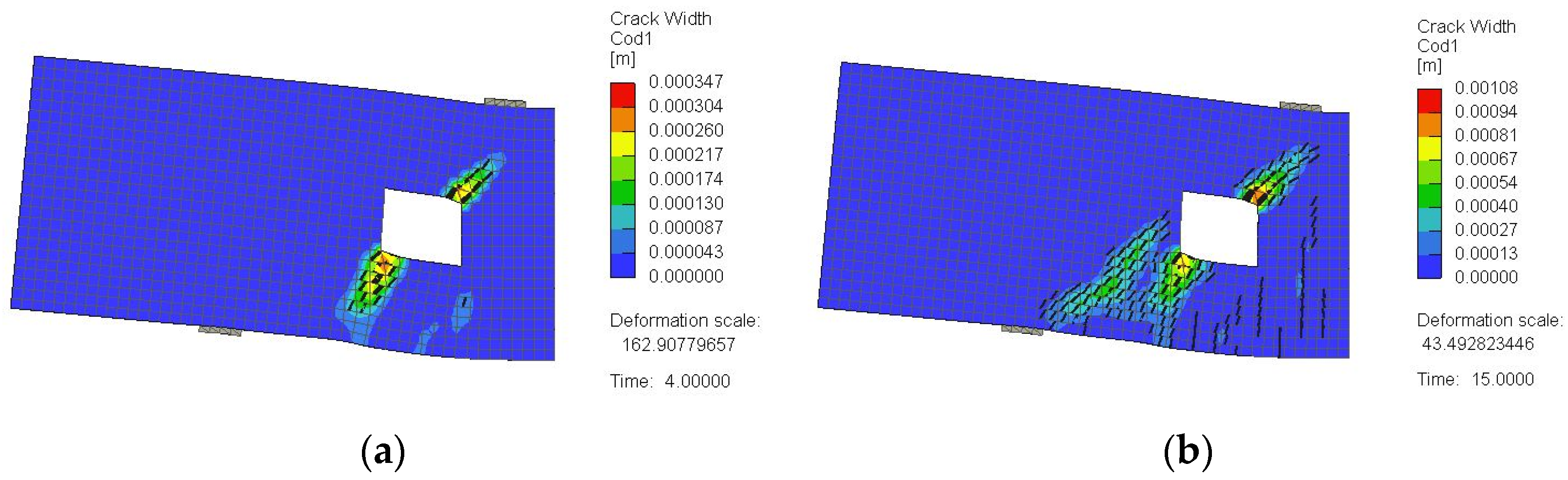
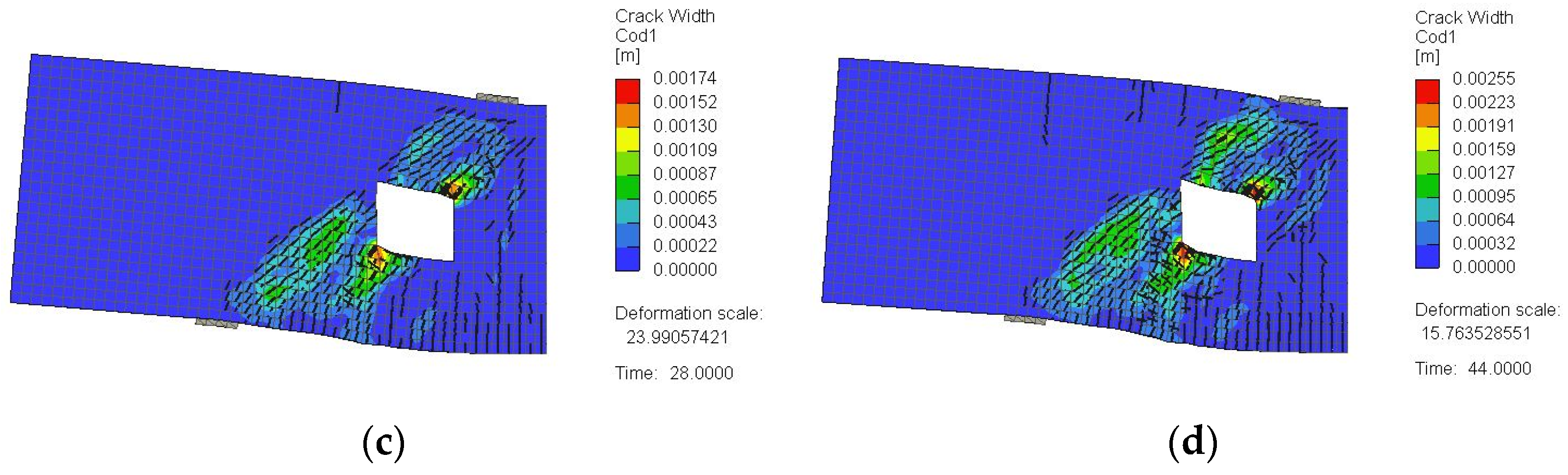
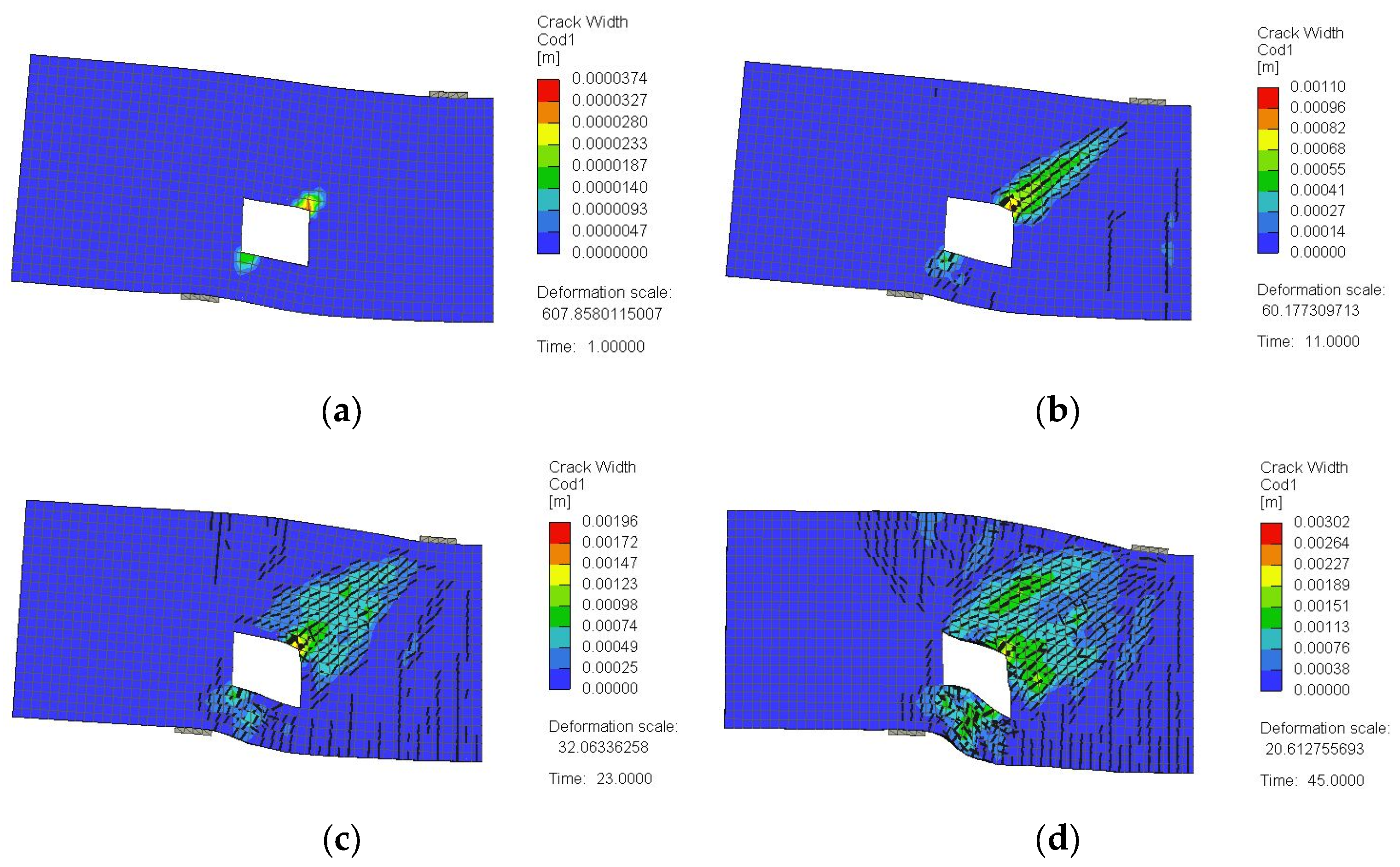
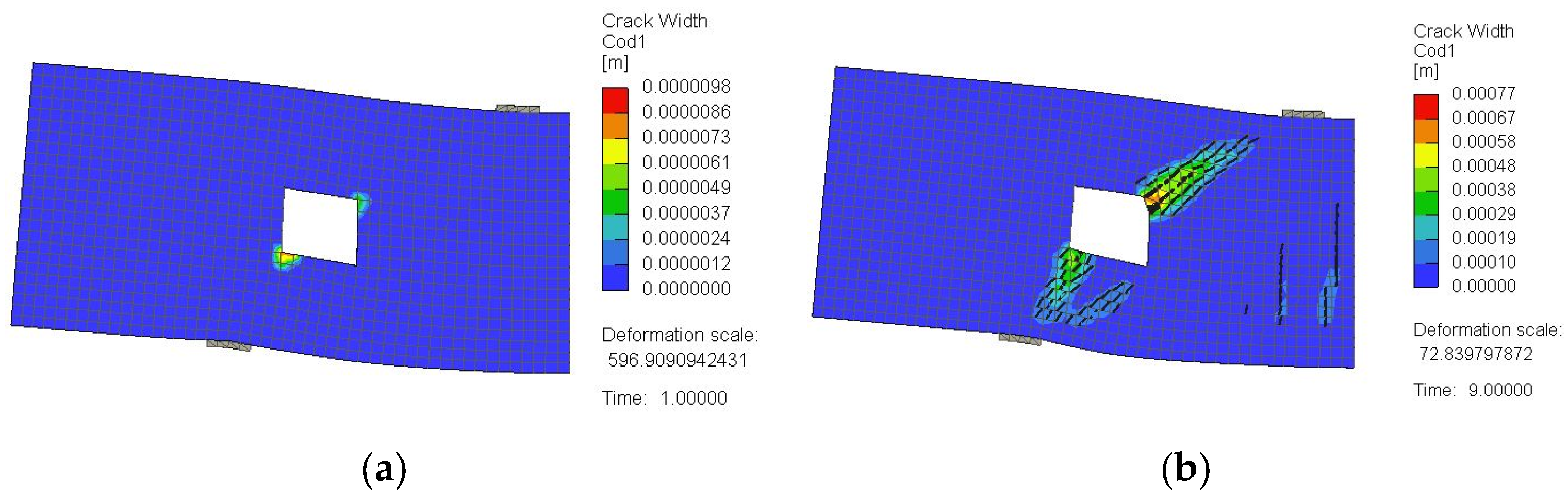
3.2. Crack Pattern and Failure Mode
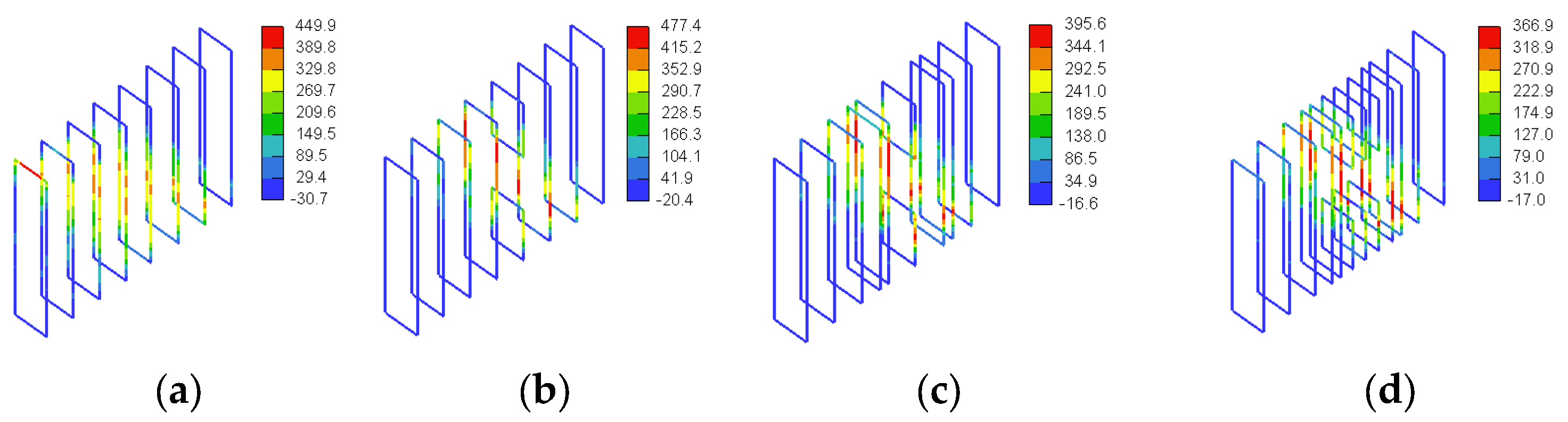
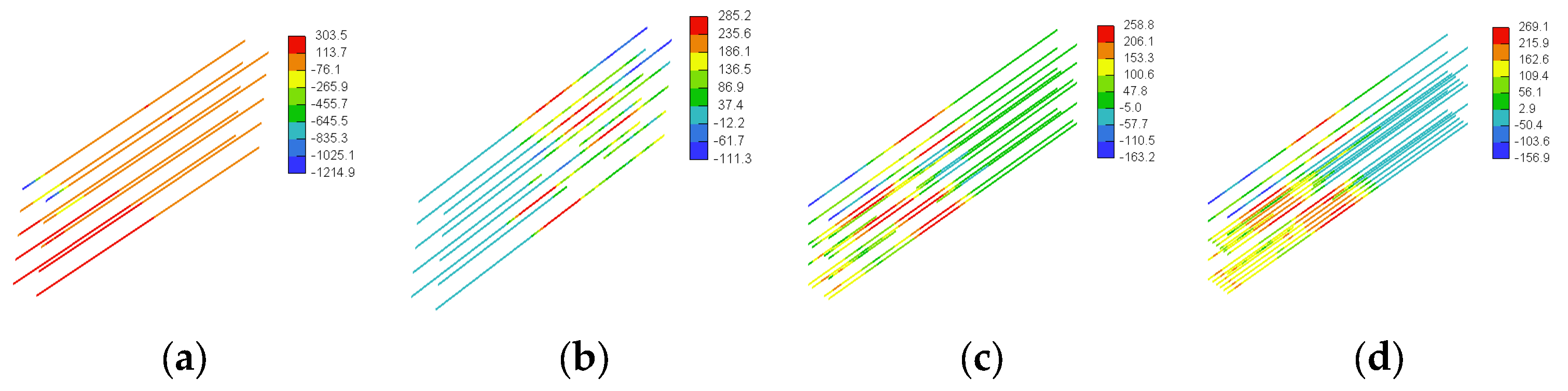
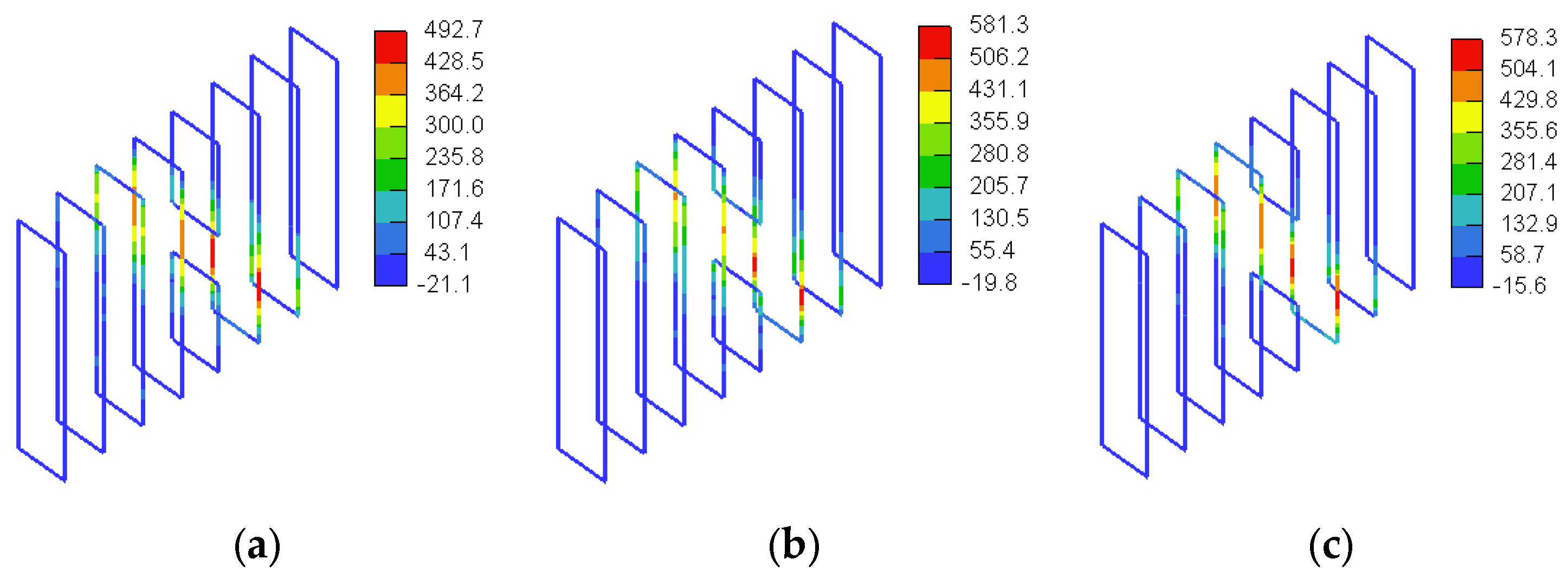
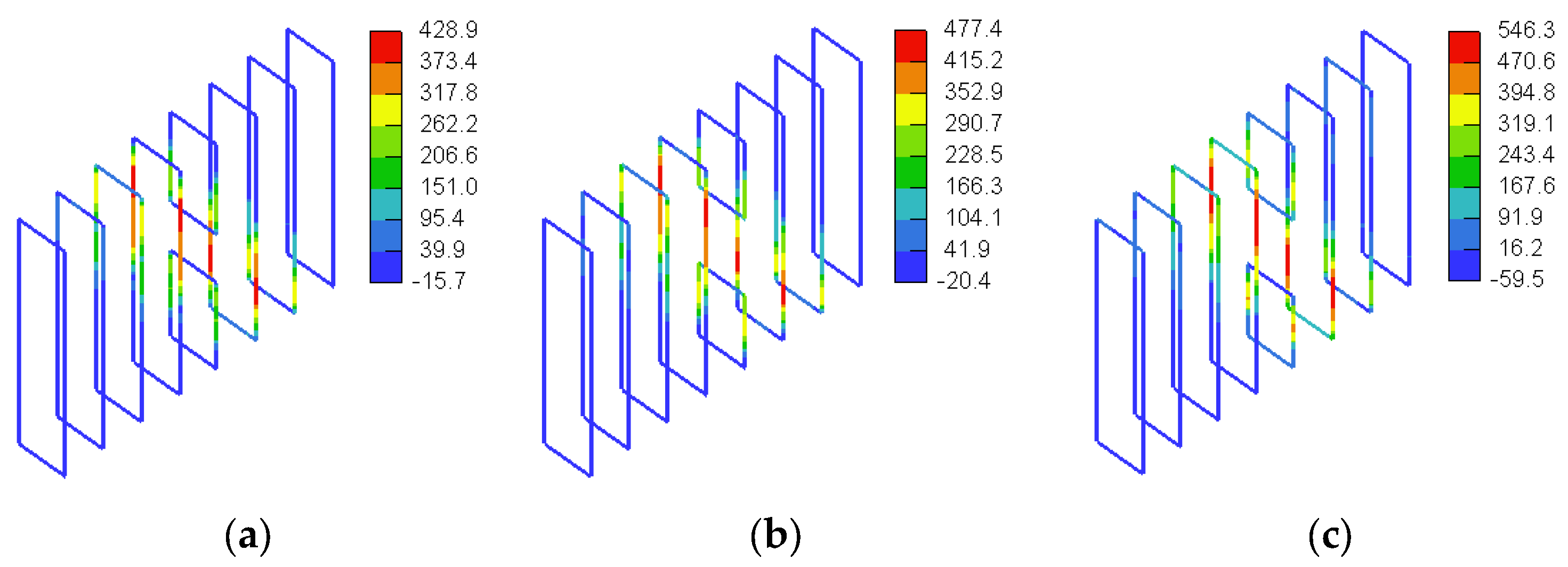
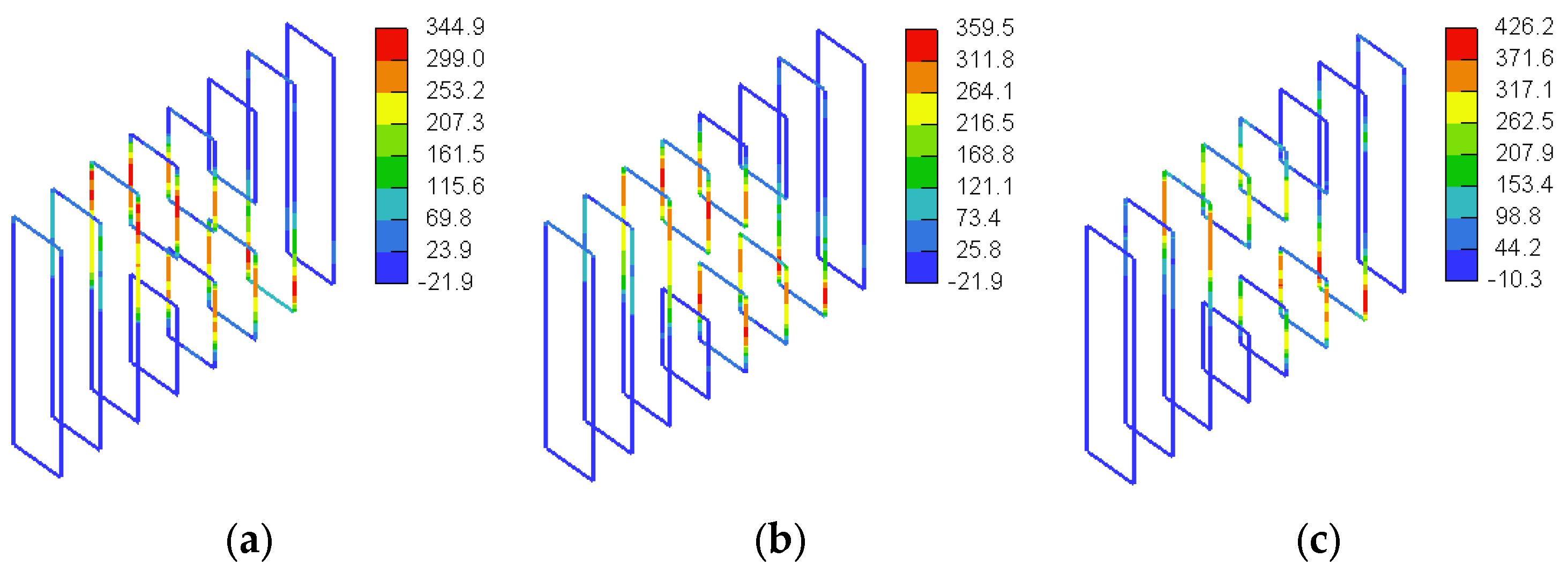
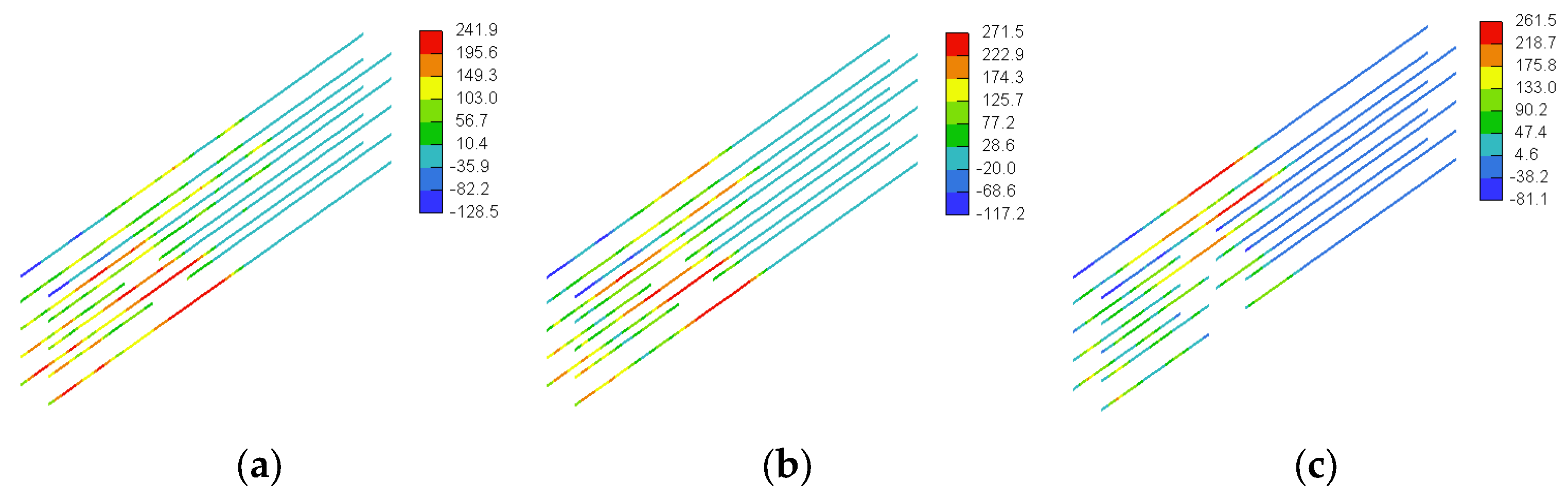
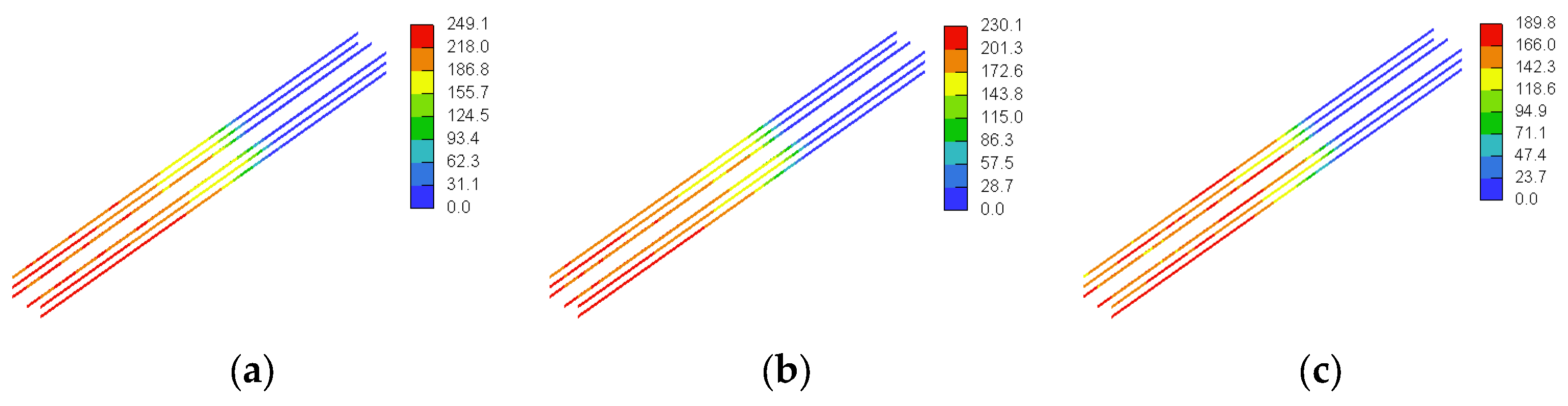
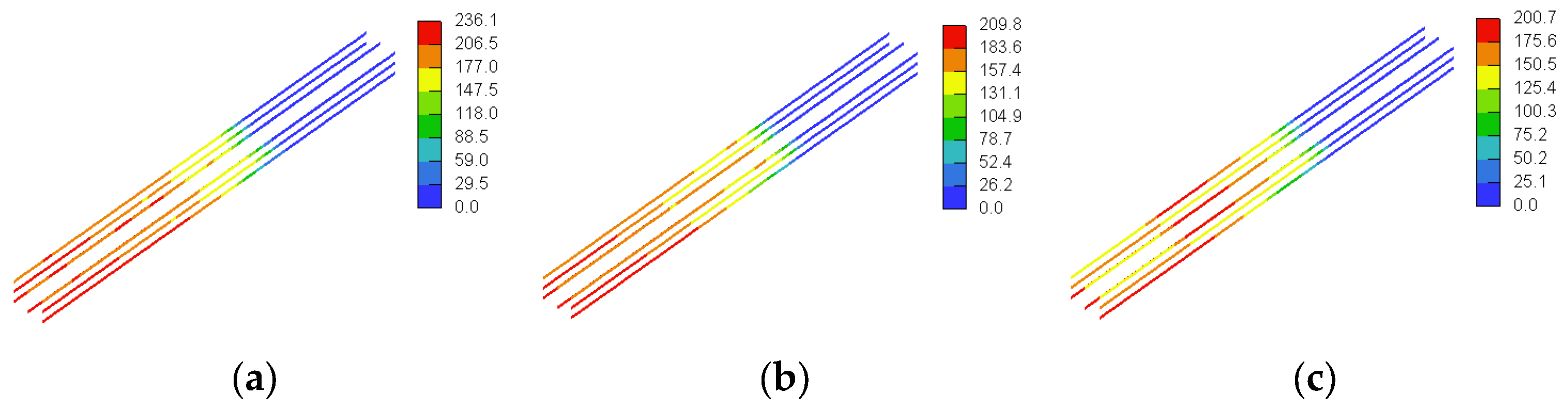
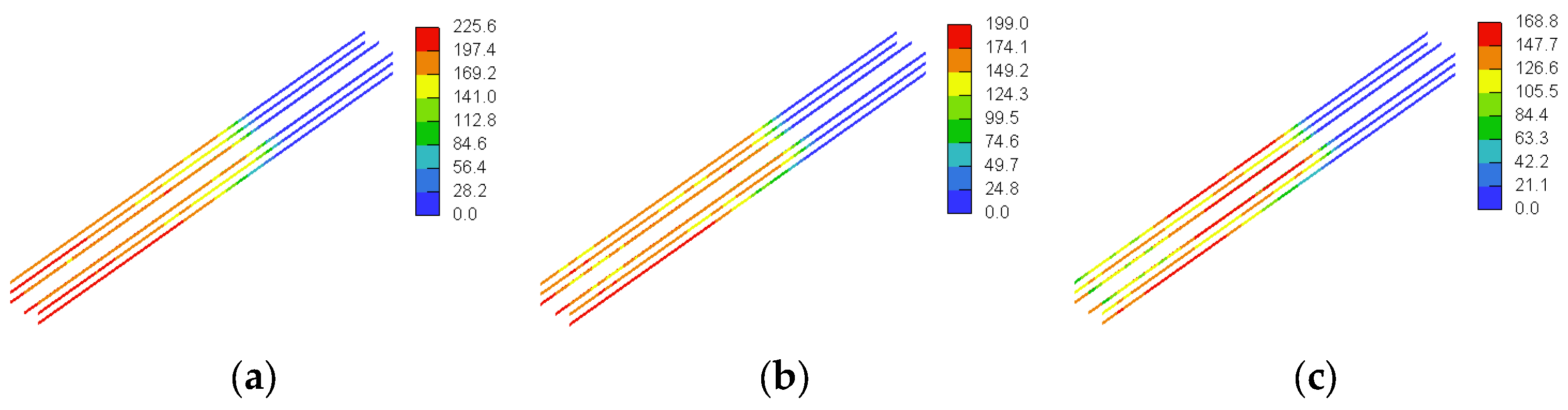
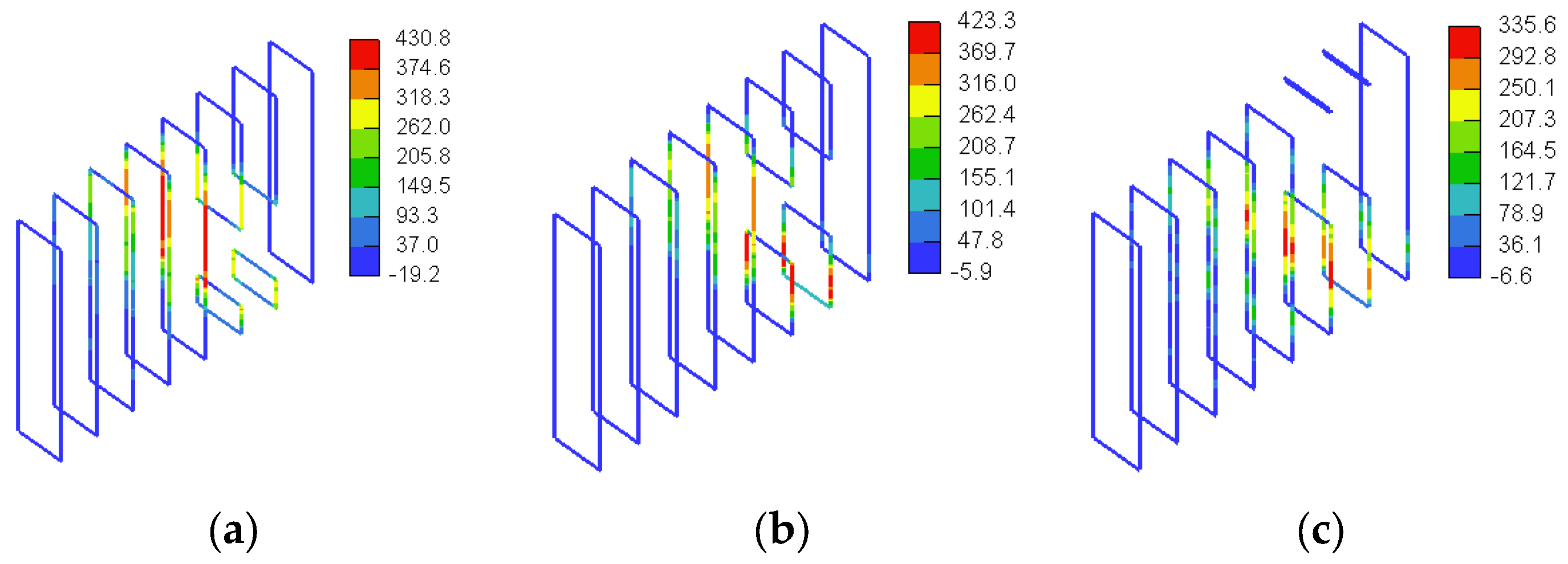
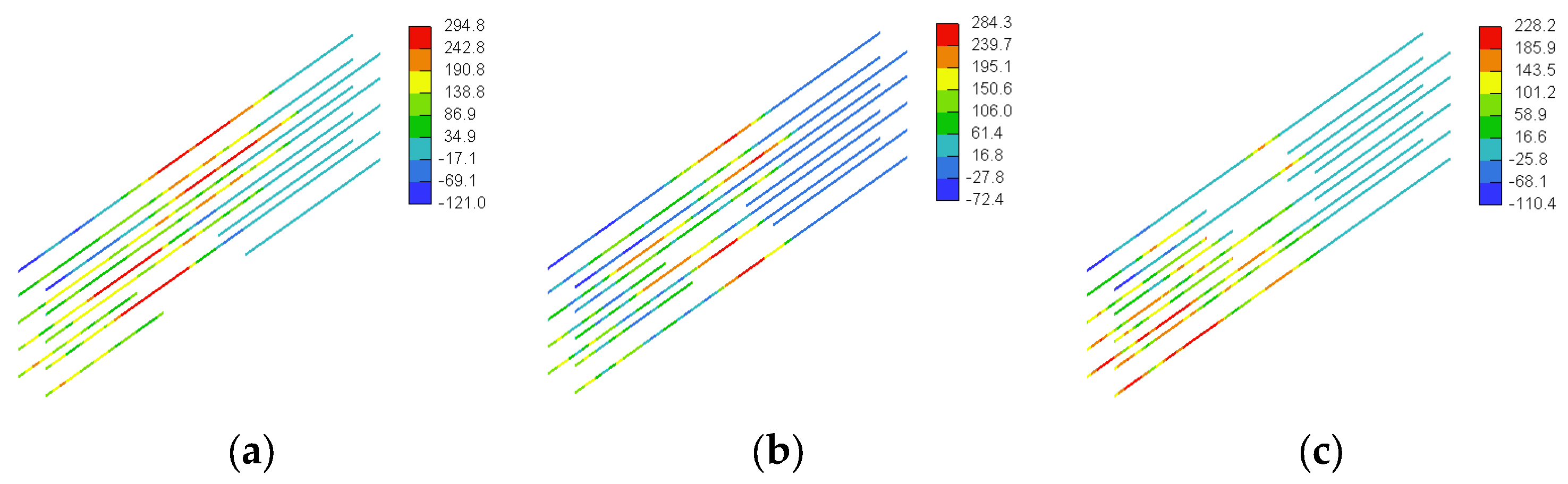
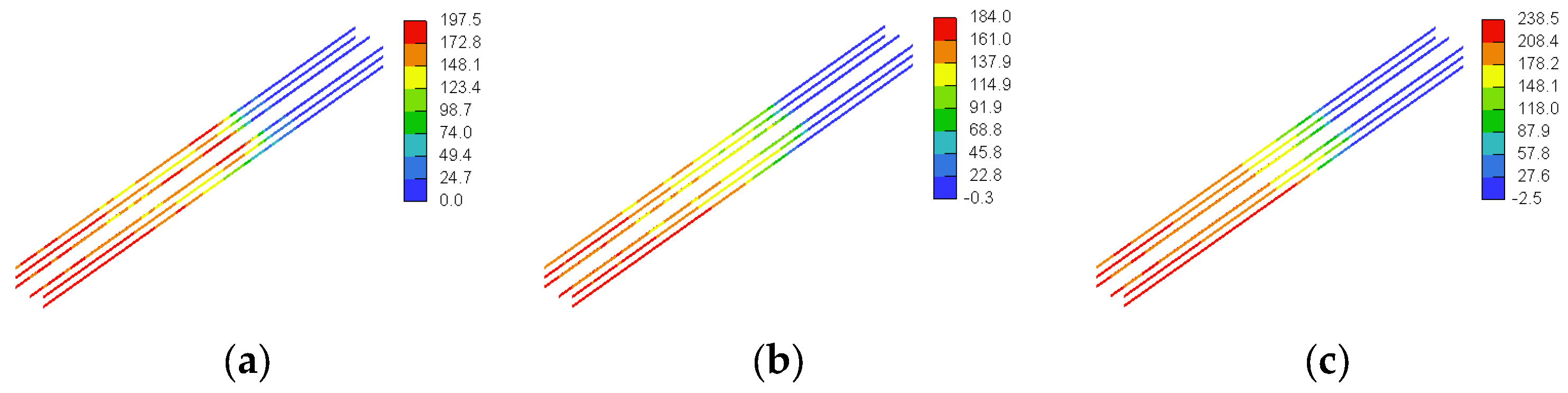
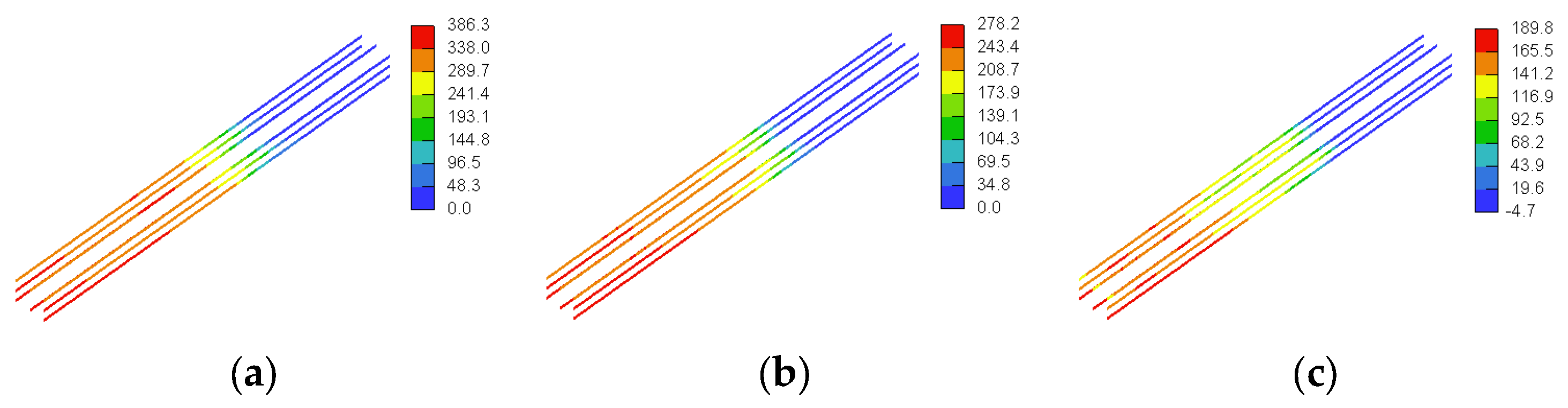
3.3. GFRP Stresses
4. Parametric Study
4.1. Deep Beam Models with Different Opening Sizes
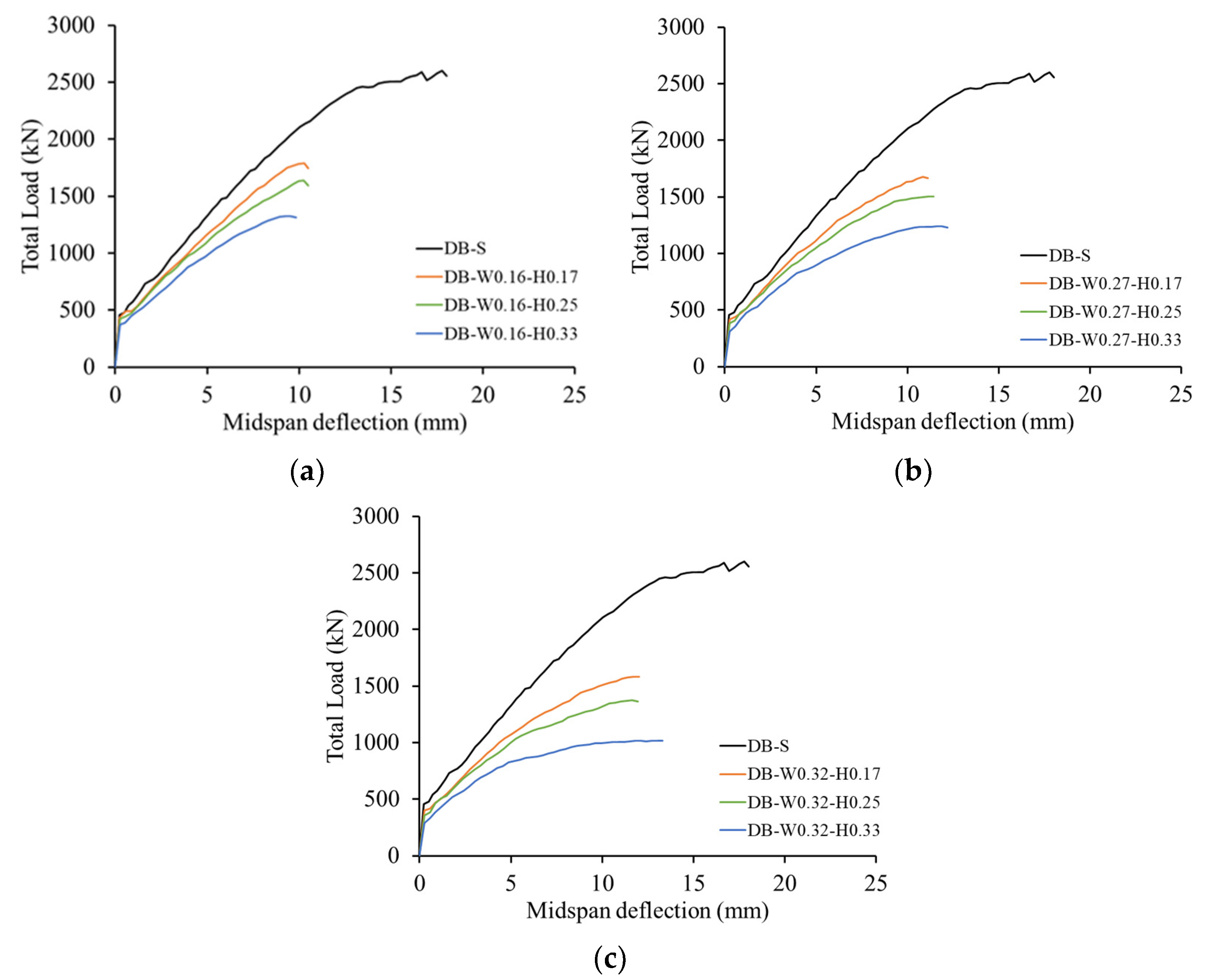
4.1.1. Load-Deflection Response
4.1.2. Crack Pattern and Failure Mechanism
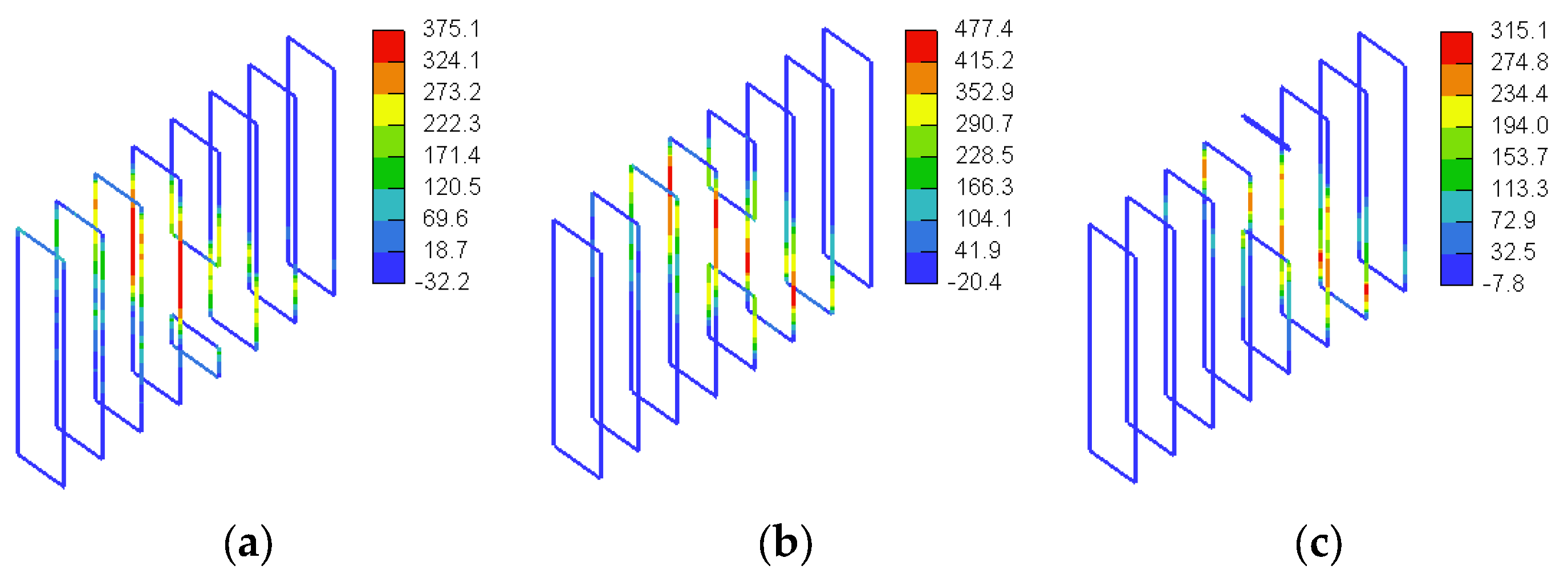
4.1.3. GFRP Stresses
4.2. Deep Beam Models with Different Opening Locations
4.2.1. Load-Deflection Response
4.2.2. Crack Pattern and Failure Mechanism
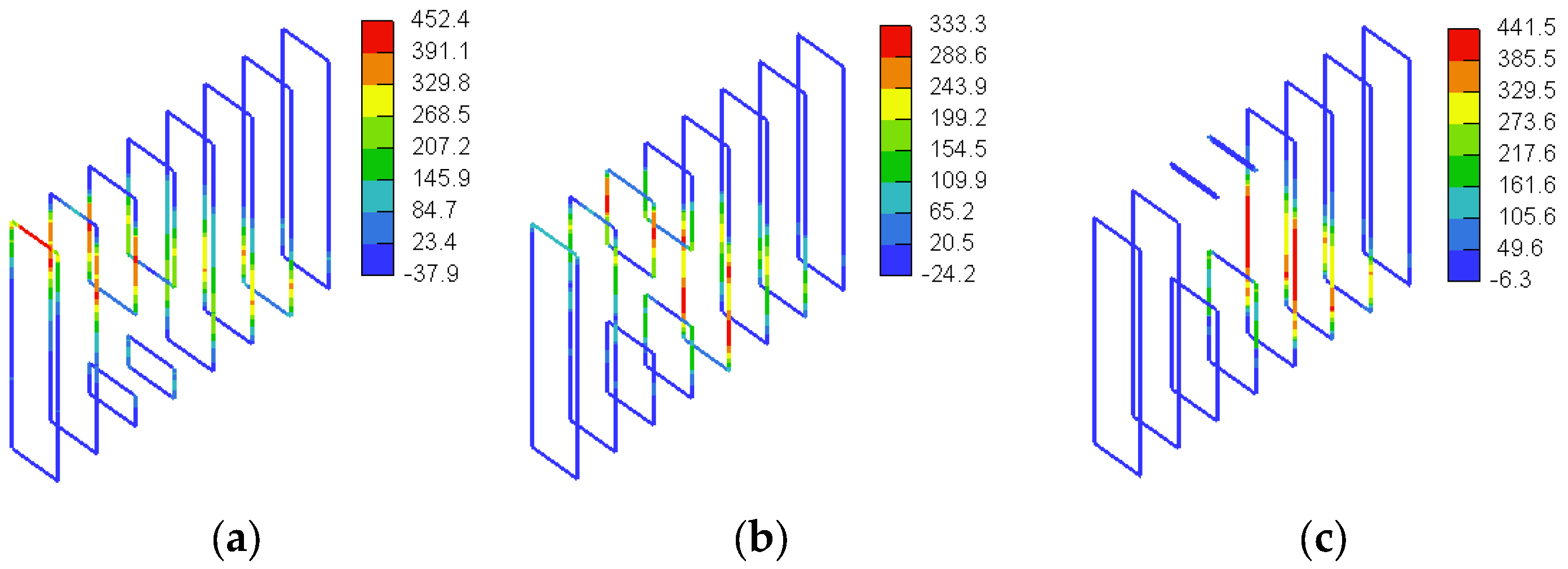
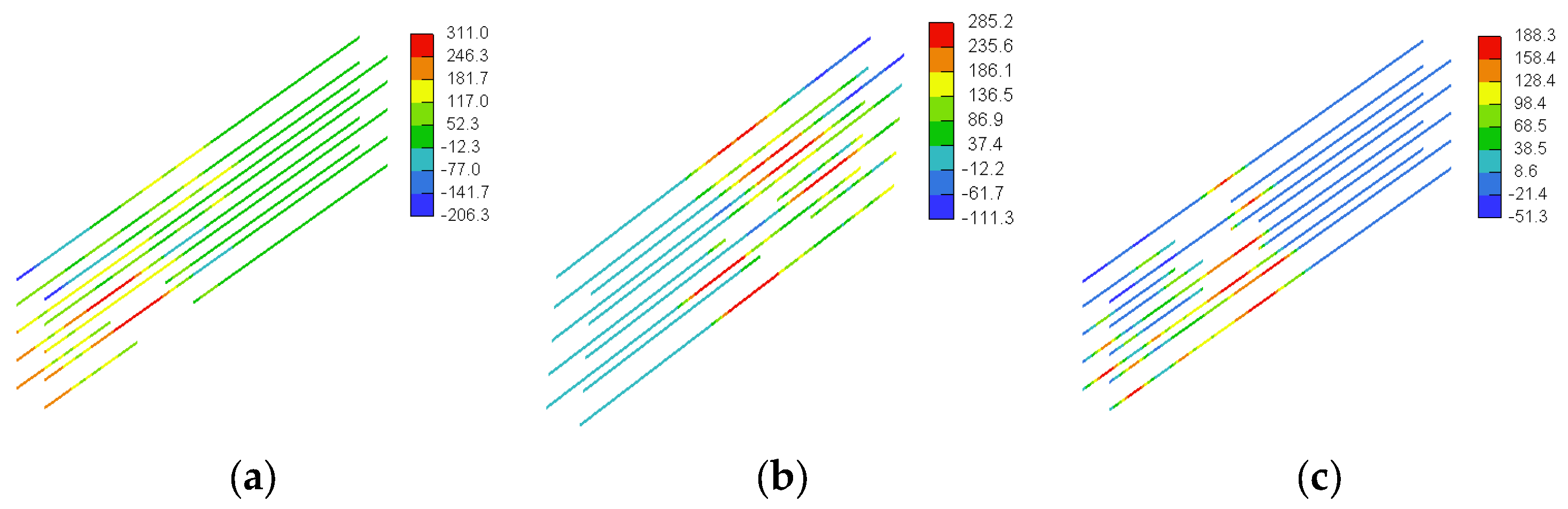
4.2.3. GFRP Stresses
5. Simplified Analytical Formulas
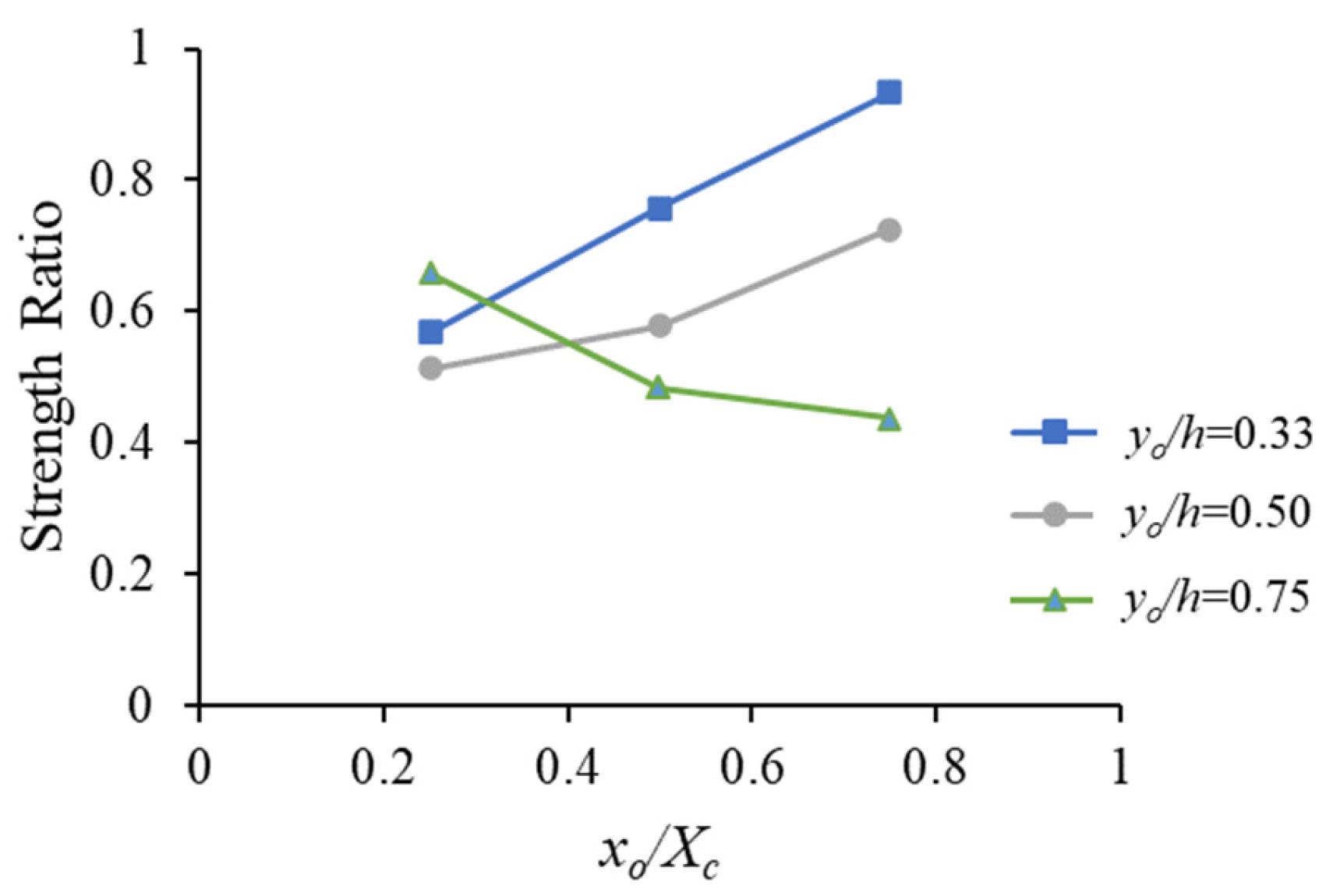
5.1. Deep Beam Models with Different Opening Locations
5.2. Deep Beams with a Web Opening Shifted from the Midpoint of the Shear Span
6. Conclusions
- For the beam models with yo/h values of 0.33 and 0.50, the strength increased with an increase in the distance measured from the face of the support within the shear span. The strength of the beam models with a yo/h of 0.33 tended to be higher than that of their counterparts with a yo/h of 0.50, and this behavior was more evident with an increase in the distance from the face of the support plate. The beam models with a yo/h of 0.75 exhibited an opposite trend, where the strength decreased with an increase in the distance measured from the face of the support within the shear span because such a movement resulted in an opening closer the load plate.
- For the beam models having a web opening closer to the support plate (xo/Xc = 0.25), strength reductions of 43 and 49% were recorded at yo/h values of 0.33 and 0.50, respectively. When the opening was pushed upward away from the natural load path (xo/Xc = 0.25 and yo/h = 0.75), a lower strength reduction of 34% was recorded.
- For the beam models having a web opening with an xo/Xc of 0.50, strength reductions of 24, 42, and 52% were recorded at yo/h values of 0.33, 0.50, and 0.75, respectively.
- The beam model with xo/Xc = 0.75 and yo/h = 0.33 exhibited a negligible strength reduction of 7% because the web opening was in the tension side and did not interrupt the natural load path. In contrast, the beam model with a web opening closer to the load plate (xo/Xc = 0.75 and yo/h = 0.75) exhibited a significant strength reduction of 56% because the web opening was in the compression zone close to the load plate and fully interrupted the natural load path.
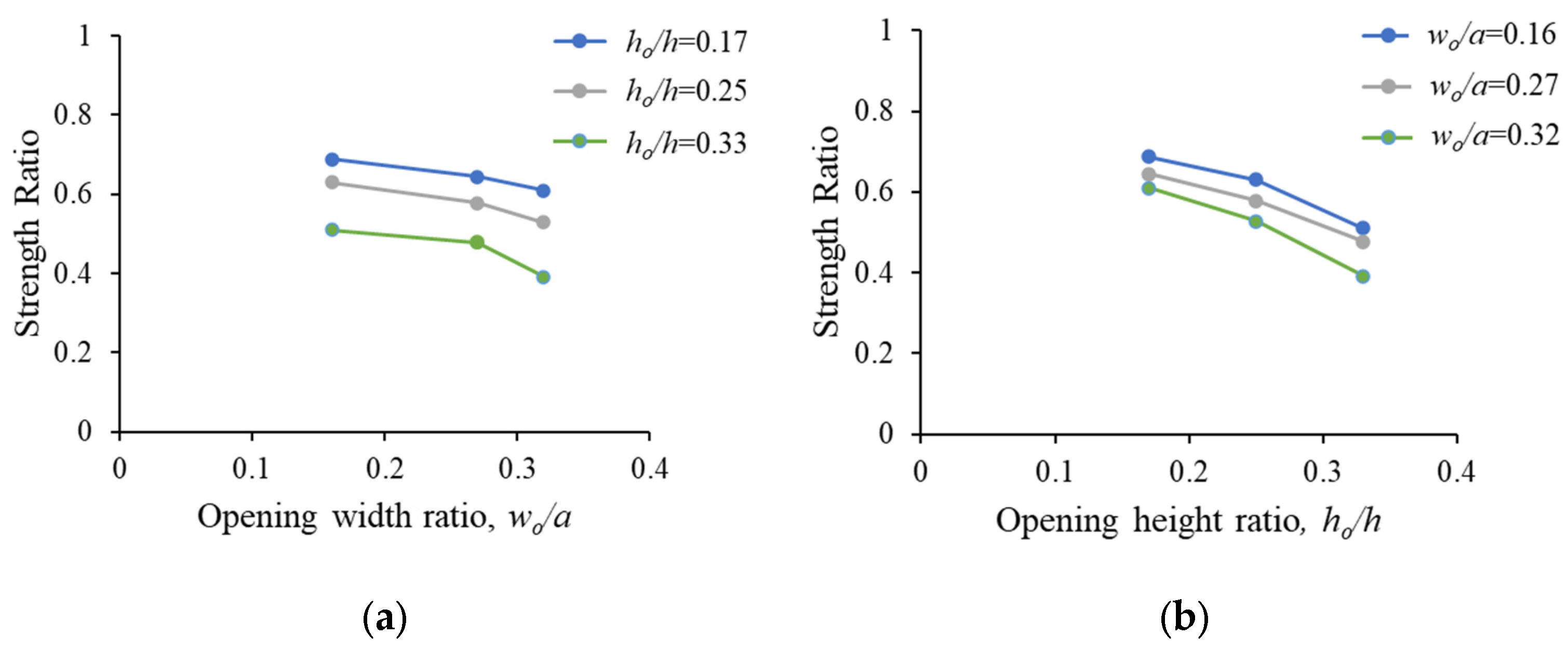
- For the beam models with a web opening in the middle of the shear span, the strength decreased with an increase in either the opening width or height. The rate of the strength reduction caused by increasing the opening height was, however, more significant than that produced by increasing the opening width. At the same wo/a of 0.16, strength reductions of 31–49% were recorded for the deep beam models having an opening in the midpoint of the shear span with ho/h values of 0.17–0.33. More pronounced respective strength reductions of 39–61% were recorded for the deep beam models with the greater wo/a of 0.32.
- The existing empirical equation for concrete deep beams reinforced with conventional steel bars with a web opening provided unconservative and/or inconsistent predictions for the ultimate load of the beam models reinforced with GFRP bars.
- Refined empirical equations were introduced for shear strength prediction of GFRP-reinforced concrete deep beams with a web opening of different sizes and locations within the shear span. The refined analytical formulas tended to provide conservative/reasonable predictions for the shear capacity of the GFRP-reinforced concrete deep beams considered in the present study.
- The simulation models developed and verified in the present study can be used as a numerical platform in future research to study the effect of using different types of reinforcing bars (e.g., carbon, glass, steel with different yield strengths) on the behavior of concrete deep beams with and without a web opening in the shear span. Future research should further investigate the effect of the anchorage length and bond condition of GFRP reinforcing bars on the response of the GFRP-reinforced deep beams.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- American Concrete Institute ACI. Building Code Requirements for Structural Concrete and Commentary on Building Code Requirements for Structural Concrete (ACI 318R-19); American Concrete Institute (ACI): Farmington Hills, MI, USA, 2014. [Google Scholar]
- MacGregor, J.; Wight, J. Reinforced Concrete Mechanics and Design, 4th ed.; SI Units; Prentice Hall: Singapore, 2005. [Google Scholar]
- Kong, F. Reinforced Concrete Deep Beams; Blackie and Son Ltd.: London, UK, 1999. [Google Scholar]
- Mansour, M.; Tan, K.-H. Concrete Beams with Openings Analysis and Design; CRC Press: New York, NY, USA, 1999. [Google Scholar]
- CSA S806-12; Design and Construction of Building Structures with Fiber-Reinforced Polymers. Canadian Standards Association CSA: Mississauga, ON, Canada, 2012.
- ACI 440.1R-15; ACI Committee 440. Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2019.
- Bakis, C.; Bank, L.; Brown, V.; Cosenza, E.; Davalos, J.; Lesko, J.; Machida, A.; Rizkalla, S.; Triantafillou, T. Fiber-reinforced polymer composites for construction-state-of-the-art review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef]
- Bank, L. Composites for Construction: Structural Design with FRP Materials; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gangarao, H.; Taly, N.; Vijay, P. Reinforced Concrete Design with FRP Composites; CRC Press: New York, NY, USA, 2006. [Google Scholar]
- Nanni, A.; De Luca, A.; Zadeh, H. Reinforced Concrete with FRP Bars: Mechanics and Design; CRC Press: New York, NY, USA, 2014. [Google Scholar]
- Omeman, Z.; Nehdi, M.; El-Chabib, H. Experimental study on shear behavior of carbon fiber-reinforced polymer reinforced concrete short beams without web reinforcement. Can. J. Civ. Eng. 2008, 35, 1–10. [Google Scholar] [CrossRef]
- Abed, F.; El-Chabib, H.; Alhamaydeh, M. Shear characteristics of GFRP reinforced polymer reinforced concrete deep beams without web reinforcement. J. Reinf. Plast. Compos. 2012, 31, 1063–1073. [Google Scholar] [CrossRef]
- Farghaly, A.S.; Benmokrane, B. Shear behavior of FRP-reinforced concrete deep beams without web reinforcement. J. Compos. Constr. 2013, 17, 04013015. [Google Scholar] [CrossRef]
- Andermatt, M.; Lubell, A. Behavior of concrete deep beams reinforced with internal fiber-reinforced polymer—Experimental study. ACI Struct. J. 2013, 110, 585–594. [Google Scholar]
- Kim, D.; Lee, j.; Lee, Y. Effectiveness factor of strut-and-tie model for concrete deep beams reinforced with FRP rebars. Compos. Part B 2014, 56, 117–125. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Wang, X.; Han, D. Experimental study on shear behavior of BFRP-reinforced recycled aggregate concrete deep beams without stirrups. KSCE. J. Civ. Eng. 2016, 21, 2289–2299. [Google Scholar]
- Alhamad, S.; Al-Banna, Y.; Al-Osman, A.; Mouthassseeb, J.; Abdalla, S.; Abed, F. Effect of shear span-to-depth ratio on the shear behavior of BFRP-RC deep beams. MATEC 2017, 120, 01012. [Google Scholar] [CrossRef]
- Abed, F.; El-Refai, A.; Abdalla, S. Experimental and finite element investigation of the shear performance of BFRP-RC short beams. Structures 2019, 20, 689–701. [Google Scholar] [CrossRef]
- Abu-Obaida, A.; El-Ariss, B.; El-Maaddawy, T. Behavior of short-span concrete members internally reinforced with glass fiber–reinforced polymer bars. J. Compos. Constr. 2018, 22, 04018038. [Google Scholar] [CrossRef]
- Syroka-Korol, E.; Tejchman, J.; Mroz, Z. Experimental and numerical assessment of size effect in geometrically similar slender concrete beams with basalt reinforcement. Eng. Struct. 2017, 141, 272–291. [Google Scholar] [CrossRef]
- Mohamed, K.; Farghaly, A.S.; Benmokrane, B. Effect of vertical and horizontal web reinforcement on the strength and deformation of concrete deep beams reinforced with GFRP bars. J. Struct. Eng. 2017, 143, 04017079. [Google Scholar] [CrossRef]
- Song, B.; Jin, L.; Zhang, J.; Du, X. Size effect tests on shear strength of Basalt FRP-RC deep beams with different shear-span ratios. Eng. Struct. 2023, 294, 116740. [Google Scholar] [CrossRef]
- Frappier, J.; Mohamed, K.; Farghaly, A.; Benmokrane, B. Behavior and strength of glass fiber-reinforced polymer reinforced concrete deep beams with web openings. ACI Struct. J. 2019, 116, 275–285. [Google Scholar] [CrossRef]
- Arabasi, S.; El-Maaddawy, T. Reinforcing of discontinuity regions in concrete deep beams with GFRP composite bars. Compos. Part C Open Access 2020, 3, 100064. [Google Scholar] [CrossRef]
- Ge, W.; Zhang, J.; Cao, D.; Tu, Y. Flexural behaviors of hybrid concrete beams reinforced with BFRP bars and steel bars. Constr. Build. Mater. 2015, 87, 28–37. [Google Scholar] [CrossRef]
- Kazemi, M.; Daneshfar, M.; Zandi, Y.; Agdas, A.S.; Yousefieh, N.; Mohammadifar, L.; Rahmani, A.; Saberian, M.; Mamdouh, A.; Khadimallah, M.A.; et al. Effects of the Concrete Strength and FRP Reinforcement Type on the Non-Linear Behavior of Concrete Deep Beams. Sustainability 2022, 14, 4136. [Google Scholar] [CrossRef]
- Brown, M.; Bayrak, O. Investigation of deep beams with various load configurations. ACI Struct. J. 2007, 104, 611–620. [Google Scholar]
- Tan, K.; Lu, H. Shear behavior of large reinforced concrete deep beams and code comparison. ACI Struct. J. 1999, 96, 836–845. [Google Scholar]
- Mihaylov, B.; Bentz, E.; Collins, M. Behavior of large deep beams subjected to monotonic and reversed cyclic shear. ACI Struct. J. 2010, 107, 726–734. [Google Scholar]
- Sheikh-Sobeh, A. Numerical Simulation of Concrete Beams with Discontinuity Regions Reinforced with Nonmetallic Reinforcing Bars. Master’s Thesis, United Arab Emirates University, Abu Dhabi, United Arab Emirates, June 2023. [Google Scholar]
- ATENA Computer Software, Cervenka Consulting s.r.o.: Prague, Czech Republic. Available online: https://www.cervenka.cz/ (accessed on 25 March 2022).
- Imjai, T.; Guadagnini, M.; Pilakoutas, K. Bend strength of FRP bars: Experimental investigation and bond modeling. J. Mater. Civ. Eng. 2017, 29, 04017024. [Google Scholar] [CrossRef]
- Imjai, T.; Garcia, R.; Guadagnini, M.; Pilakoutas, K. Strength degradation in curved fiber-reinforced polymer (FRP) bars used as concrete reinforcement. Polymers 2020, 12, 1653. [Google Scholar] [CrossRef] [PubMed]
- Gooranorimi, O.; Claure, G.; Suaris, W.; Nanni, A. Bond-slip effect in flexural behavior of GFRP RC slabs. Compos. Struct. 2018, 193, 80–86. [Google Scholar] [CrossRef]
- Sheikh-Sobeh, A.; Kachouh, N.; El-Maaddawy, T. Numerical analysis of concrete deep beams reinforced with glass fiber-reinforced polymer bars. Buildings 2023, 13, 2767. [Google Scholar] [CrossRef]
- Yang, K.; Eun, H.; Chung, H. The influence of web openings on the structural behavior of reinforced high-strength concrete deep beams. Eng. Struct. 2006, 28, 1825–1834. [Google Scholar] [CrossRef]
- El-Maaddawy, T.; El-Ariss, B. Behavior of concrete beams with short shear span and web opening strengthened in shear with CFRP composites. J. Compos. Constr. 2012, 16, 47–59. [Google Scholar] [CrossRef]
- Kong, F.; Sharp, G. Structural idealisation for deep beams with web openings. Mag. Concr. Res. 1977, 29, 81–91. [Google Scholar] [CrossRef]
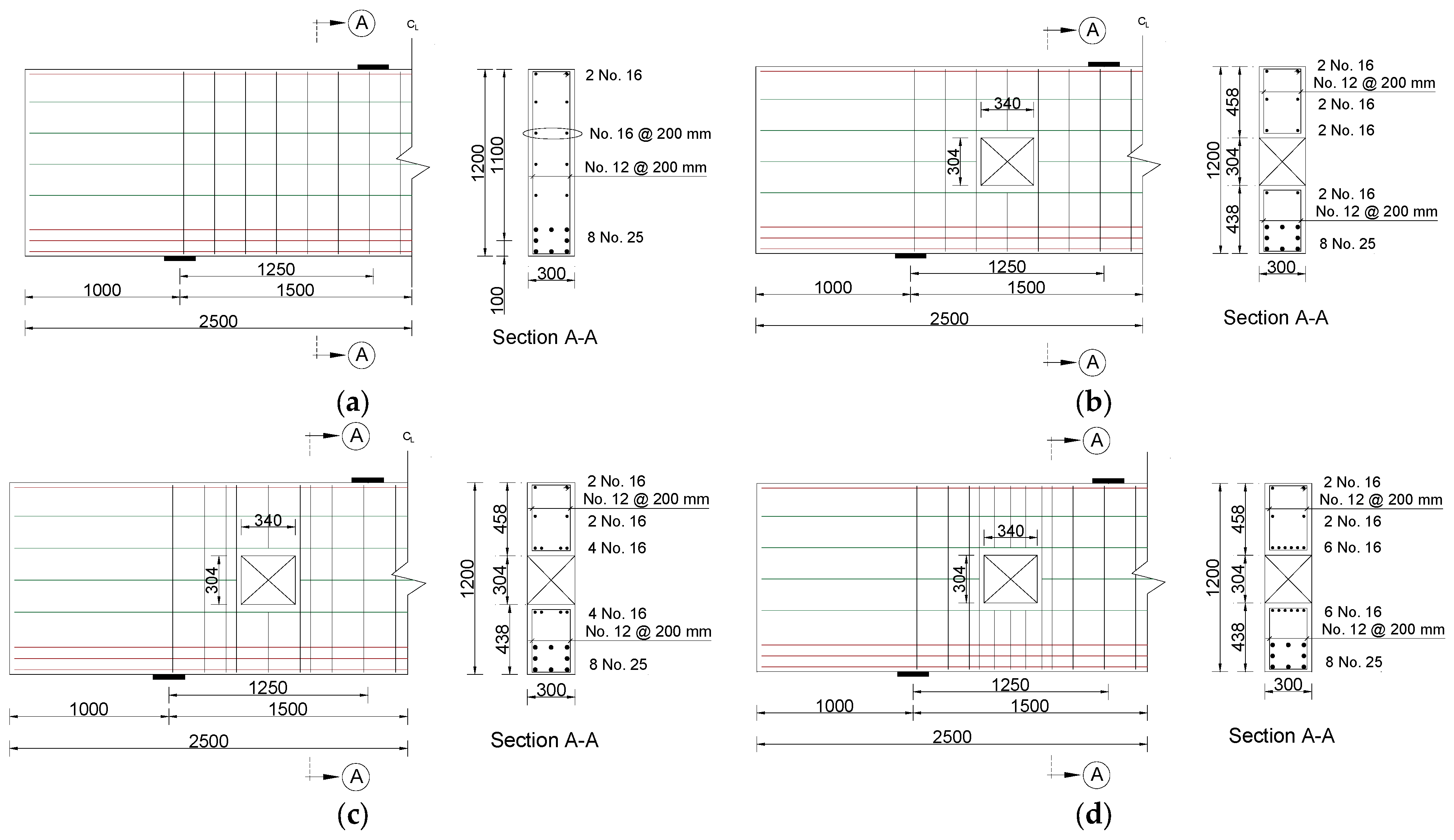
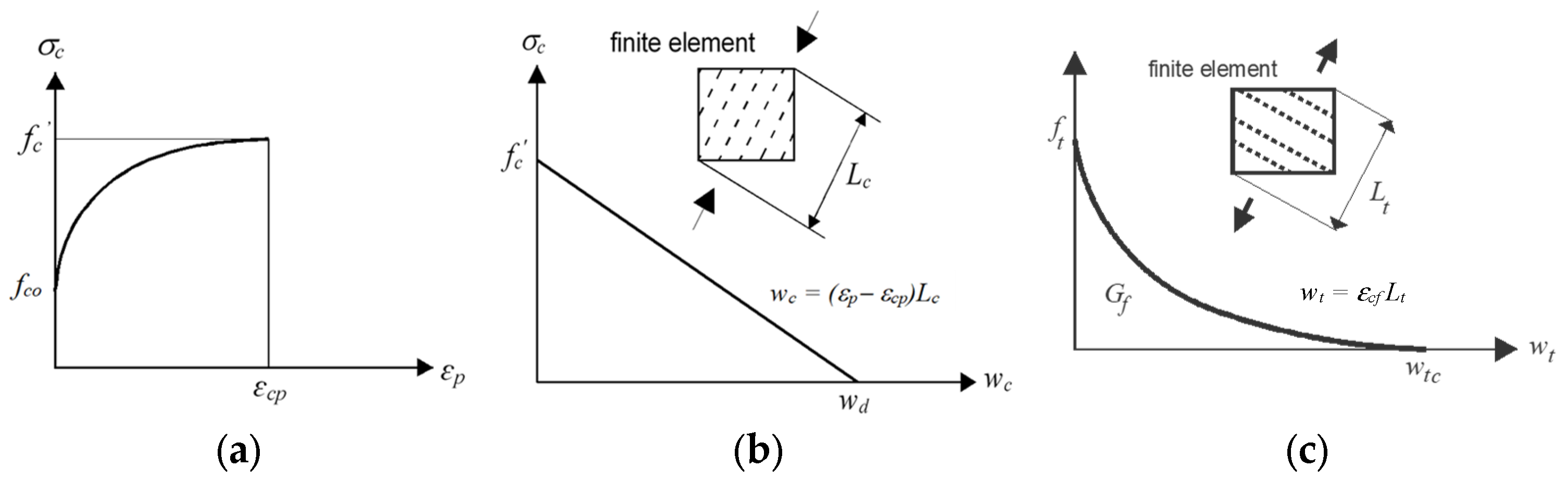










| Parameter | Description | Value * | Unit |
|---|---|---|---|
| f’c | Compressive strength | 37.00 (45.00) | MPa |
| Ec | Elastic modulus | 33,254.00 (35,496.00) | MPa |
| μ | Poisson’s ratio | 0.2 | N/A |
| ft | Tensile strength | 2.83 (3.33) | MPa |
| Gf | Specific fracture energy | 70.75 (83.25) | N/m |
| εcp | Plastic concrete strain at compressive strength | 0.0011 (0.0012) | N/A |
| wd | Critical compressive displacement | 0.50 | mm |
| Models | Ultimate Load (kN) | Deflection Capacity (mm) | ||||
|---|---|---|---|---|---|---|
| Experimental 1 | Numerical | Error (%) 2 | Experimental 1 | Numerical | Error (%) 2 | |
| DB-S | 2904 | 2601 | −10% | 17.3 | 17.8 | +3% |
| DB-O1 | 1328 | 1489 | +12% | 12.7 | 10.8 | +15% |
| DB-O2 | 1619 | 1619 | 0% | 11.3 | 11.2 | −0.9% |
| DB-O3 | 2067 | 1978 | −4% | 16.2 | 11.6 | −28% |
| Model Designation | Opening Size (mm) | |
|---|---|---|
| wo * | ho ** | |
| DB-W0.16-H0.17 | 200 | 200 |
| DB-W0.16-H0.25 | 304 | |
| DB-W0.16-H0.33 | 400 | |
| DB-W0.27-H0.17 | 340 | 200 |
| DB-W0.27-H0.25 | 304 | |
| DB-W0.27-H0.33 | 400 | |
| DB-W0.32-H0.17 | 400 | 200 |
| DB-W0.32-H0.25 | 304 | |
| DB-W0.32-H0.33 | 400 | |
| Model Designation | Opening Size (mm) | Ultimate Load (kN) | Deflection at Ultimate (mm) | |
|---|---|---|---|---|
| wo | ho | |||
| DB-S | - | - | 2601 | 17.8 |
| DB-W0.16-H0.17 | 200 | 200 | 1789 | 10.3 |
| DB-W0.16-H0.25 | 304 | 1637 | 10.3 | |
| DB-W0.16-H0.33 | 400 | 1327 | 9.5 | |
| DB-W0.27-H0.17 | 340 | 200 | 1678 | 10.8 |
| DB-W0.27-H0.25 | 304 | 1504 | 11.2 | |
| DB-W0.27-H0.33 | 400 | 1239 | 11.9 | |
| DB-W0.32-H0.17 | 400 | 200 | 1585 | 11.7 |
| DB-W0.32-H0.25 | 304 | 1374 | 11.7 | |
| DB-W0.32-H0.33 | 400 | 1019 | 13.0 | |
| Model Designation | Opening Location (mm) | |
|---|---|---|
| xo * | yo ** | |
| DB-X0.25-Y0.33 | 262.5 | 400 |
| DB-X0.25-Y0.50 | 590 | |
| DB-X0.25-Y0.75 | 900 | |
| DB-X0.50-Y0.33 | 525 | 400 |
| DB-X0.50-Y0.50 | 590 | |
| DB-X0.50-Y0.75 | 900 | |
| DB-X0.75-Y0.33 | 787.5 | 400 |
| DB-X0.75-Y0.50 | 590 | |
| DB-X0.75-Y0.75 | 900 | |
| Model Designation | Opening Location (mm) | Ultimate Load (kN) | Deflection at Ultimate (mm) | |
|---|---|---|---|---|
| xo * | yo ** | |||
| DB-S | - | - | 2601 | 17.8 |
| DB-X0.25-Y0.33 | 262.5 | 400 | 1478 | 11.6 |
| DB-X0.25-Y0.50 | 590 | 1337 | 9.2 | |
| DB-X0.25-Y0.75 | 900 | 1714 | 9.6 | |
| DB-X0.50-Y0.33 | 525 | 400 | 1971 | 11.5 |
| DB-X0.50-Y0.50 | 590 | 1504 | 11.2 | |
| DB-X0.50-Y0.75 | 900 | 1259 | 6.9 | |
| DB-X0.75-Y0.33 | 787.5 | 400 | 2429 | 18.4 |
| DB-X0.75-Y0.50 | 590 | 1881 | 11.4 | |
| DB-X0.75-Y0.75 | 900 | 1139 | 9.7 | |
| Model | Ultimate Load (kN) | ||||
|---|---|---|---|---|---|
| Numerical | Kong’s Formula [38] Equation (1) | Refined Formula Equation (2) | |||
| Prediction | Error (%) 1 | Prediction | Error (%) 1 | ||
| DB-W0.16-H0.17 | 1789 | 1942 | +9 | 1378 | −23 |
| DB-W0.16-H0.25 | 1637 | 1863 | +14 | 1373 | −16 |
| DB-W0.16-H0.33 | 1327 | 1385 | +4 | 966 | −27 |
| DB-W0.27-H0.17 | 1678 | 1928 | +15 | 1438 | −14 |
| DB-W0.27-H0.25 | 1504 | 1709 | +14 | 1291 | −14 |
| DB-W0.27-H0.33 | 1239 | 1242 | +1 | 892 | −28 |
| DB-W0.32-H0.17 | 1585 | 1871 | +18 | 1405 | −11 |
| DB-W0.32-H0.25 | 1374 | 1653 | +20 | 1258 | −8 |
| DB-W0.32-H0.33 | 1019 | 1038 | +2 | 709 | −30 |
| Model | Ultimate Load (kN) | ||||
|---|---|---|---|---|---|
| Numerical | Kong’s Formula [38] Equation (1) | Refined Formula Equation (3) | |||
| Prediction | Error (%) 1 | Prediction | Error (%) 1 | ||
| DB-X0.25-Y0.33 | 1478 | 1216 | −18 | 1436 | −3 |
| DB-X0.25-Y0.50 | 1337 | 2264 | +69 | 1188 | −11 |
| DB-X0.25-Y0.75 | 1714 | 3513 | +105 | 1848 | 8 |
| DB-X0.50-Y0.33 | 1971 | 916 | −54 | 1825 | −7 |
| DB-X0.50-Y0.50 | 1504 | 1709 | +14 | 1683 | 12 |
| DB-X0.50-Y0.75 | 1259 | 2863 | +127 | 1349 | 7 |
| DB-X0.75-Y0.33 | 2429 | 1042 | −57 | 2055 | −15 |
| DB-X0.75-Y0.50 | 1884 | 1461 | −22 | 1877 | 0 |
| DB-X0.75-Y0.75 | 1139 | 2399 | +111 | 910 | −20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheikh-Sobeh, A.; Kachouh, N.; El-Maaddawy, T. Performance Prediction of GFRP-Reinforced Concrete Deep Beams Containing a Web Opening in the Shear Span. Fibers 2024, 12, 66. https://doi.org/10.3390/fib12080066
Sheikh-Sobeh A, Kachouh N, El-Maaddawy T. Performance Prediction of GFRP-Reinforced Concrete Deep Beams Containing a Web Opening in the Shear Span. Fibers. 2024; 12(8):66. https://doi.org/10.3390/fib12080066
Chicago/Turabian StyleSheikh-Sobeh, Amena, Nancy Kachouh, and Tamer El-Maaddawy. 2024. "Performance Prediction of GFRP-Reinforced Concrete Deep Beams Containing a Web Opening in the Shear Span" Fibers 12, no. 8: 66. https://doi.org/10.3390/fib12080066
APA StyleSheikh-Sobeh, A., Kachouh, N., & El-Maaddawy, T. (2024). Performance Prediction of GFRP-Reinforced Concrete Deep Beams Containing a Web Opening in the Shear Span. Fibers, 12(8), 66. https://doi.org/10.3390/fib12080066







