Numerical Modeling of Mid-IR Lasers Based on Tb-Doped Chalcogenide Multicore Fibers
Abstract
1. Introduction
2. Materials and Methods
2.1. Model of Active Tb-Doped Chalcogenide Glass
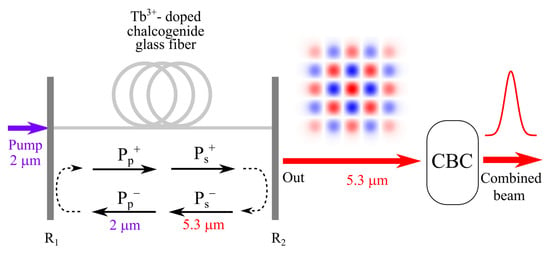
2.2. Model of Multicore Fiber: Features and Advantages of Out-of-Phase Supermode
2.3. Modeling Laser Action in Tb-Doped Chalcogenide Multicore Fibers
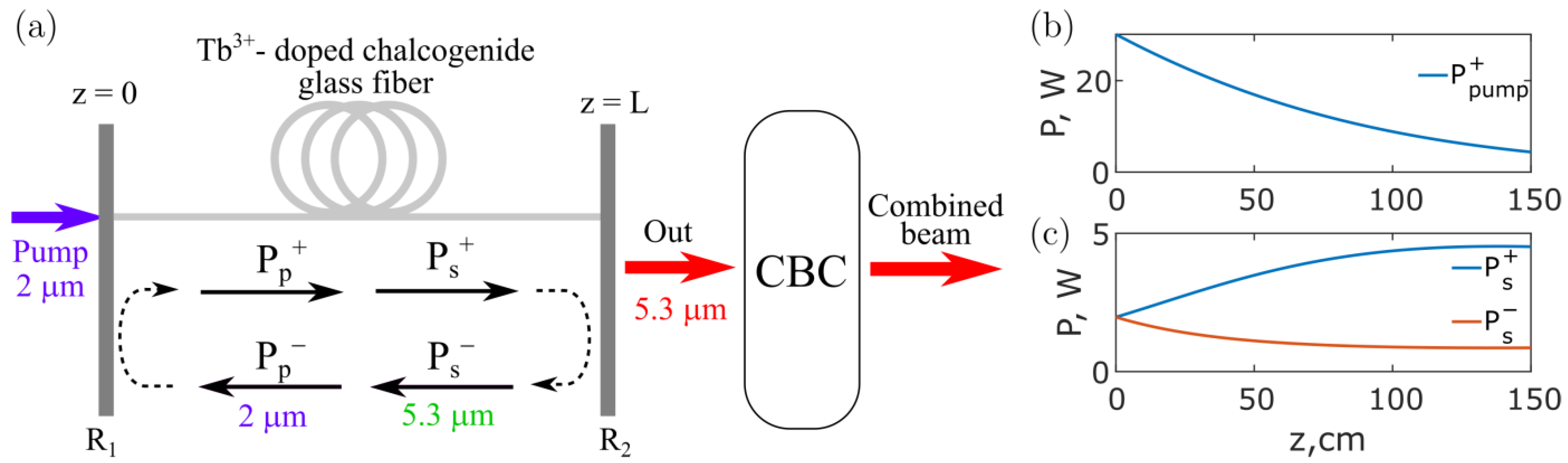
3. Results
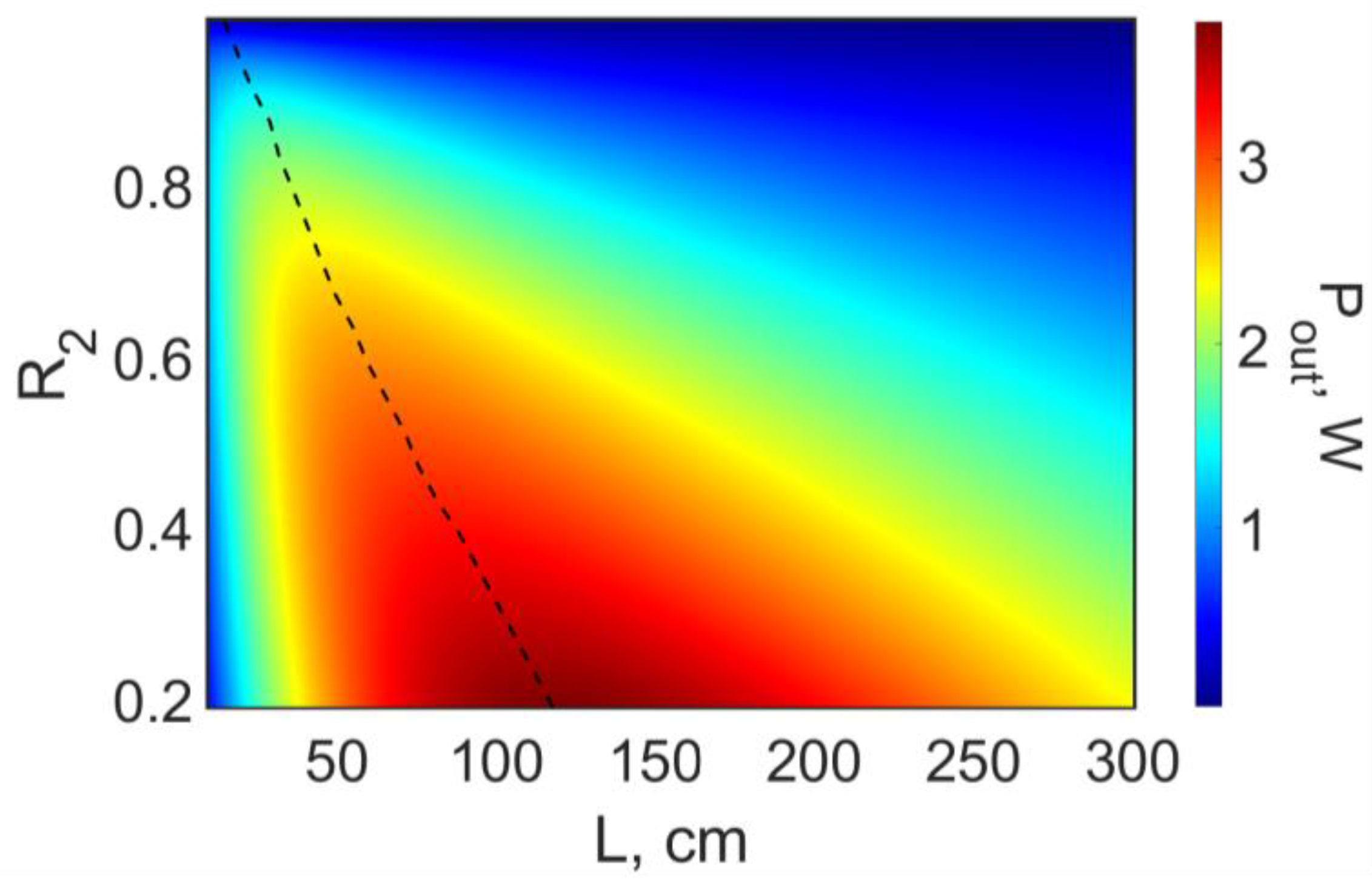
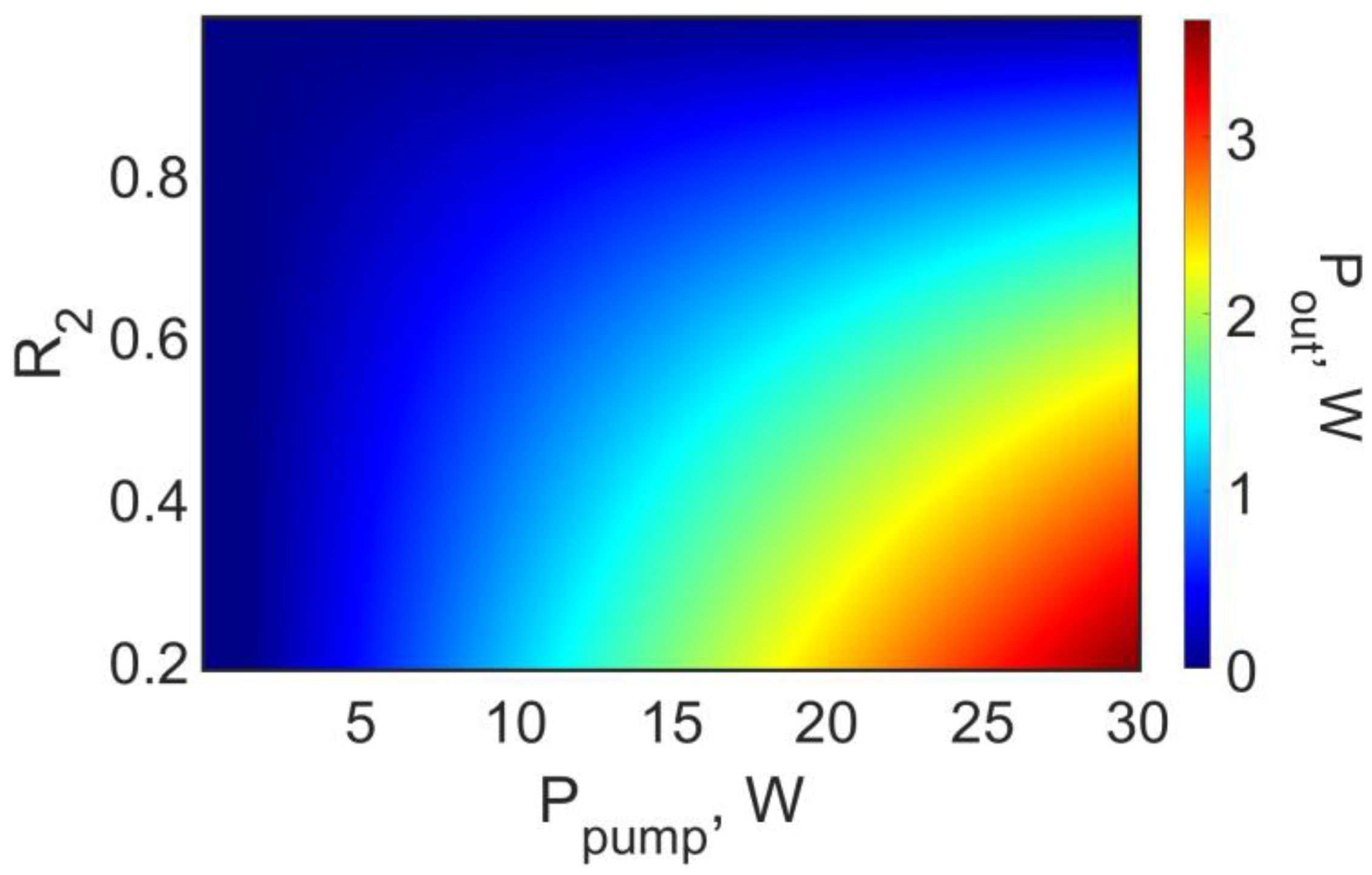
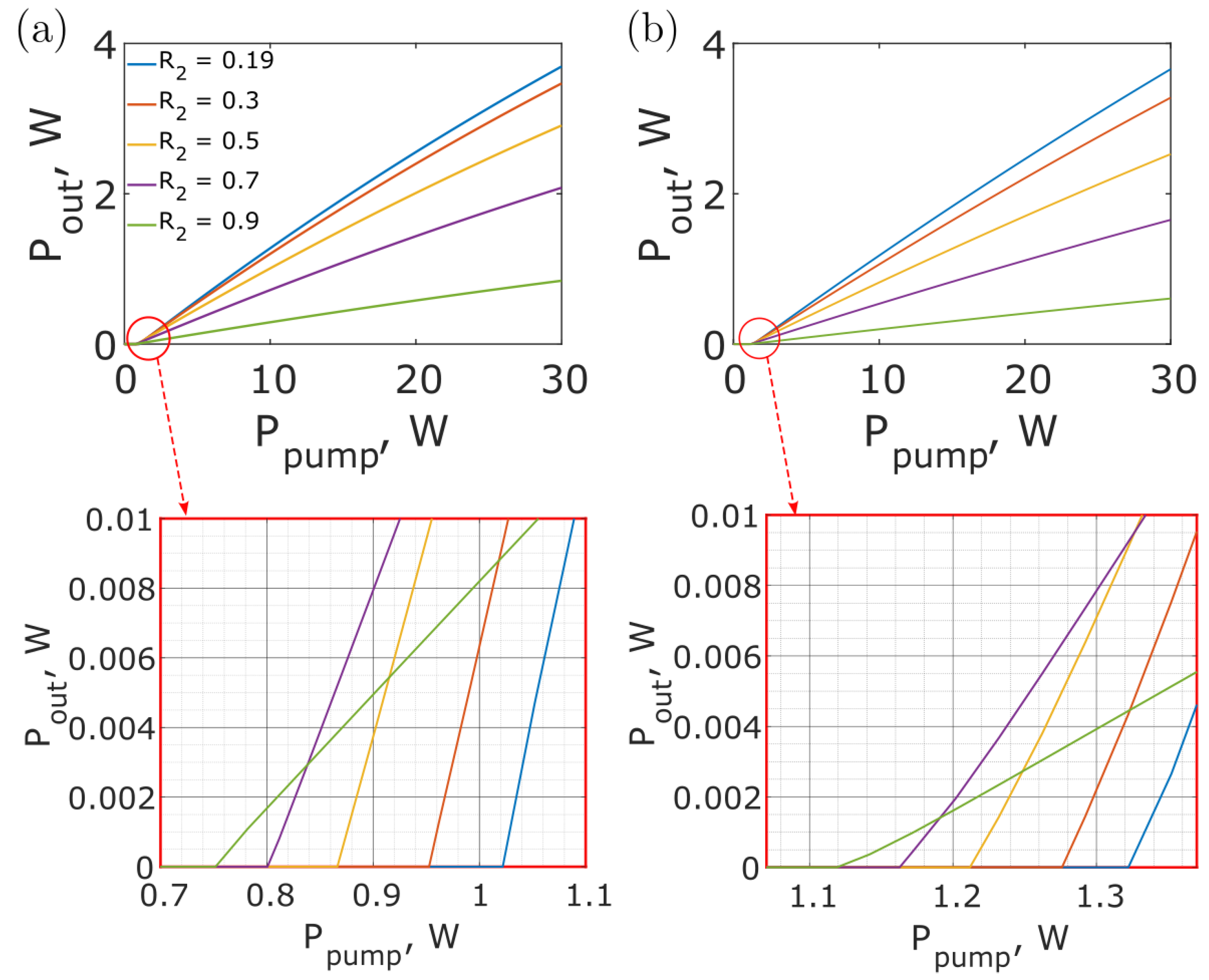
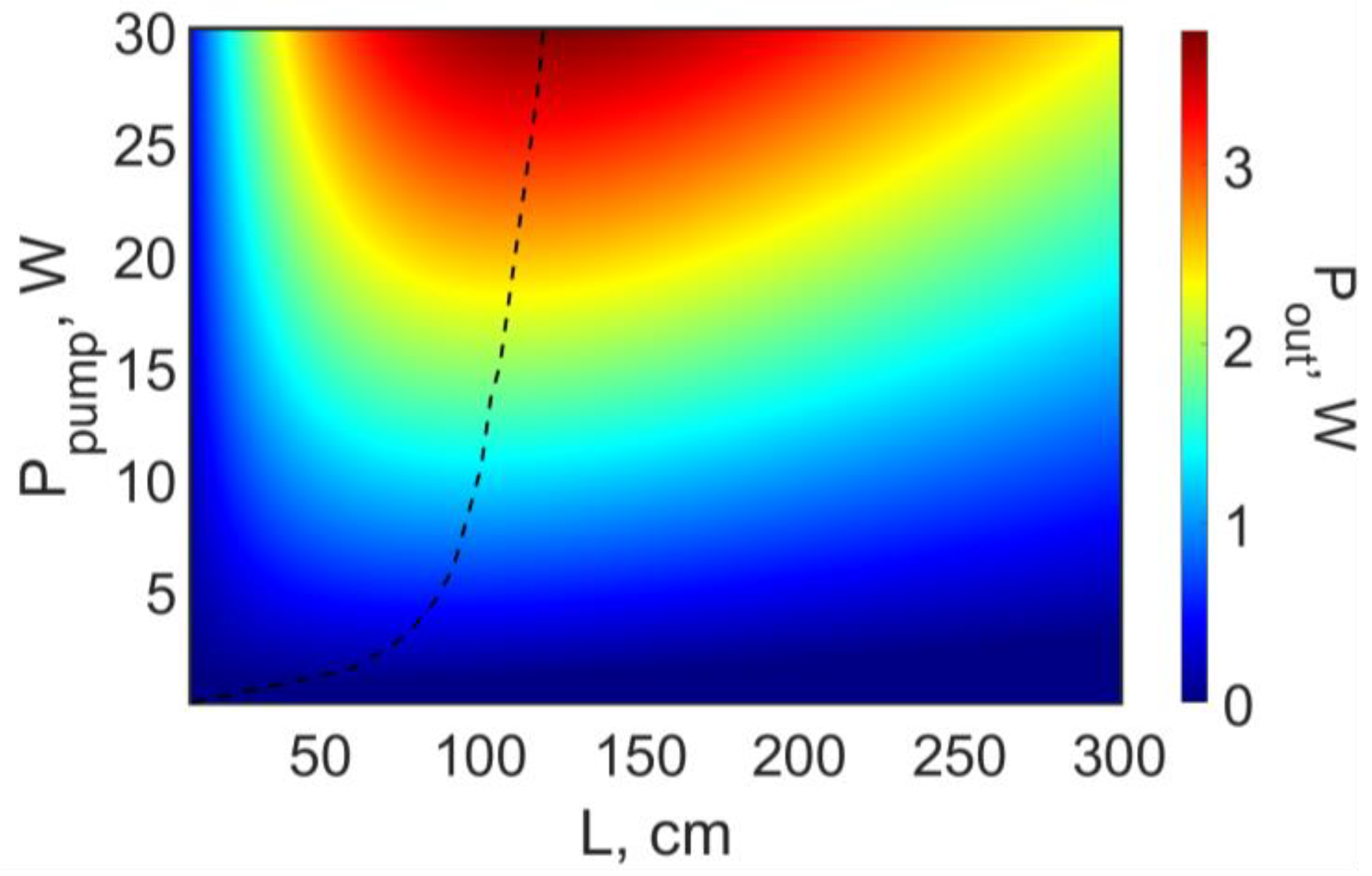
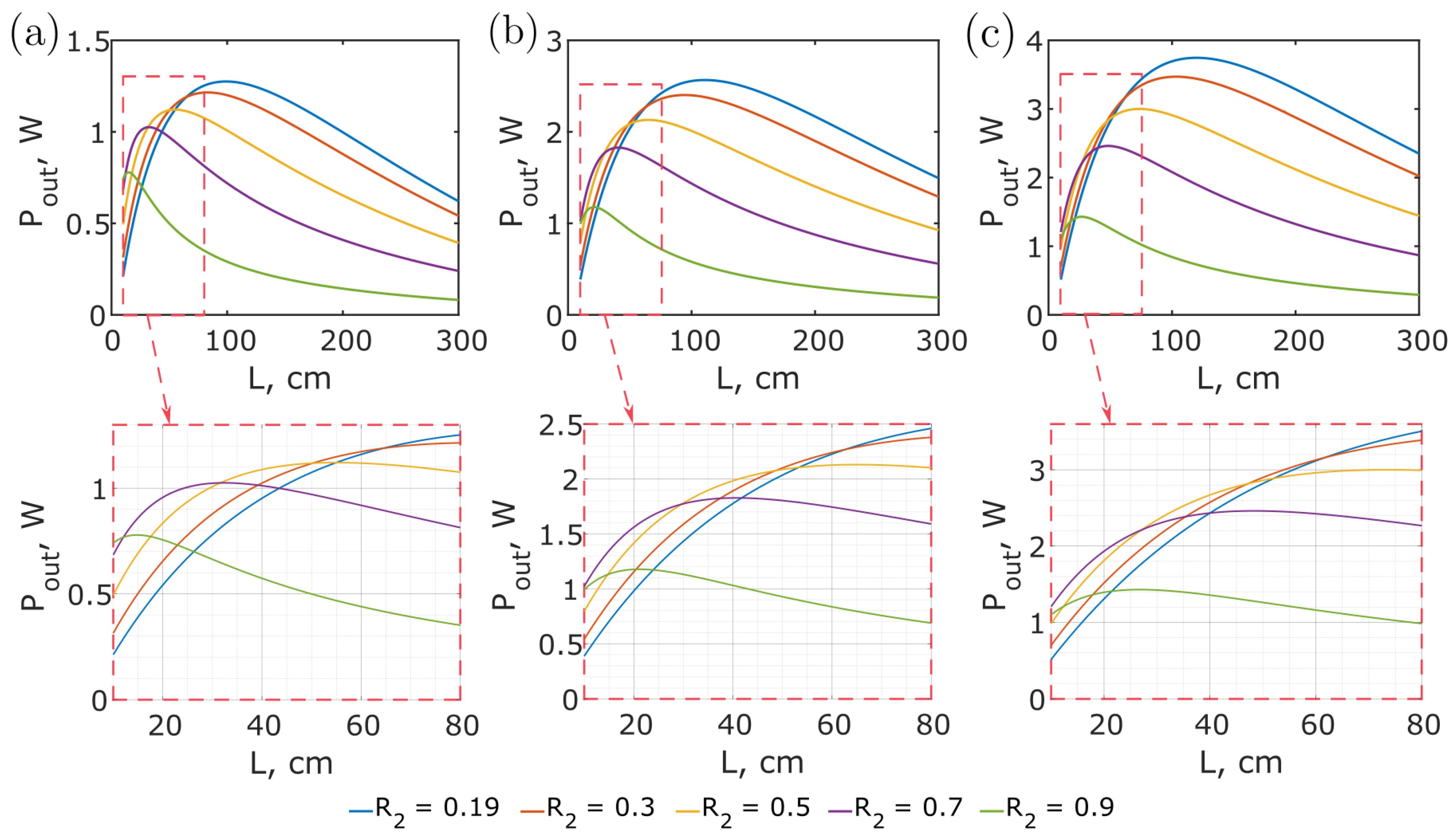
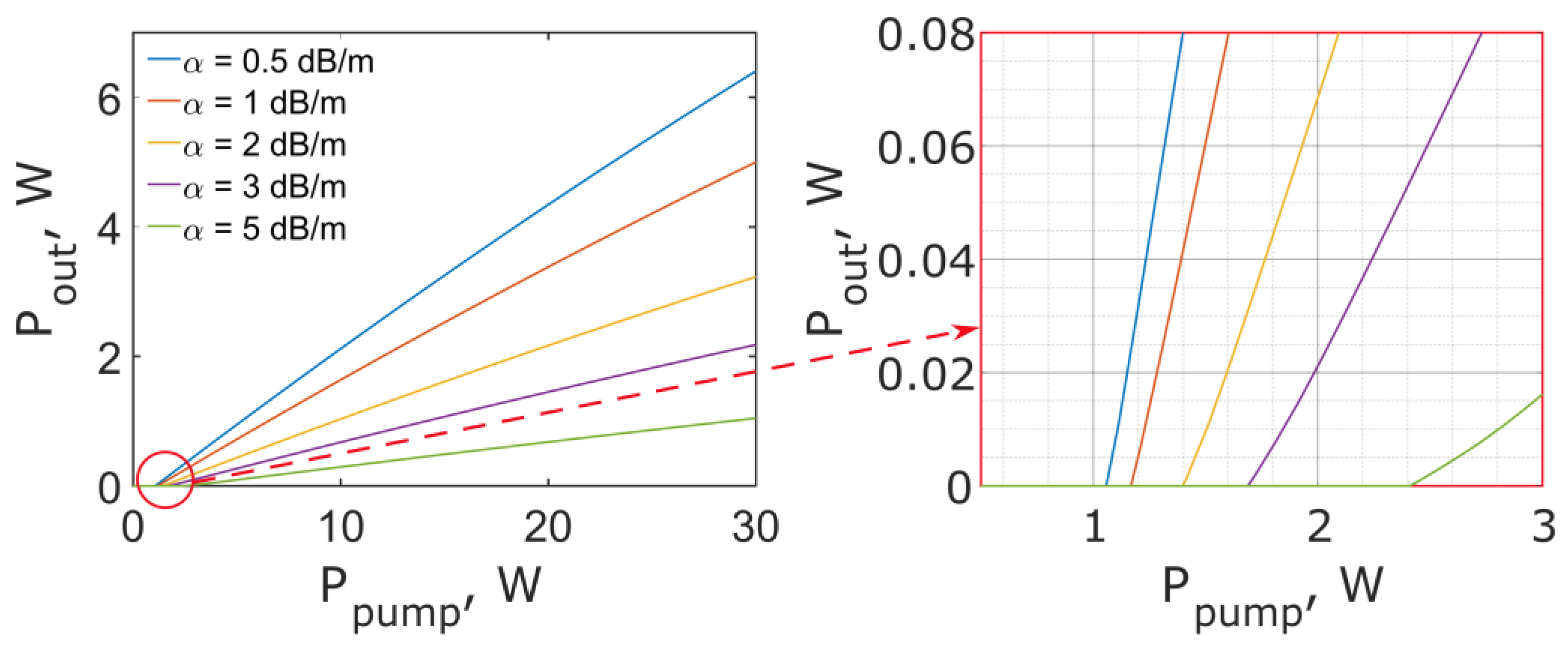
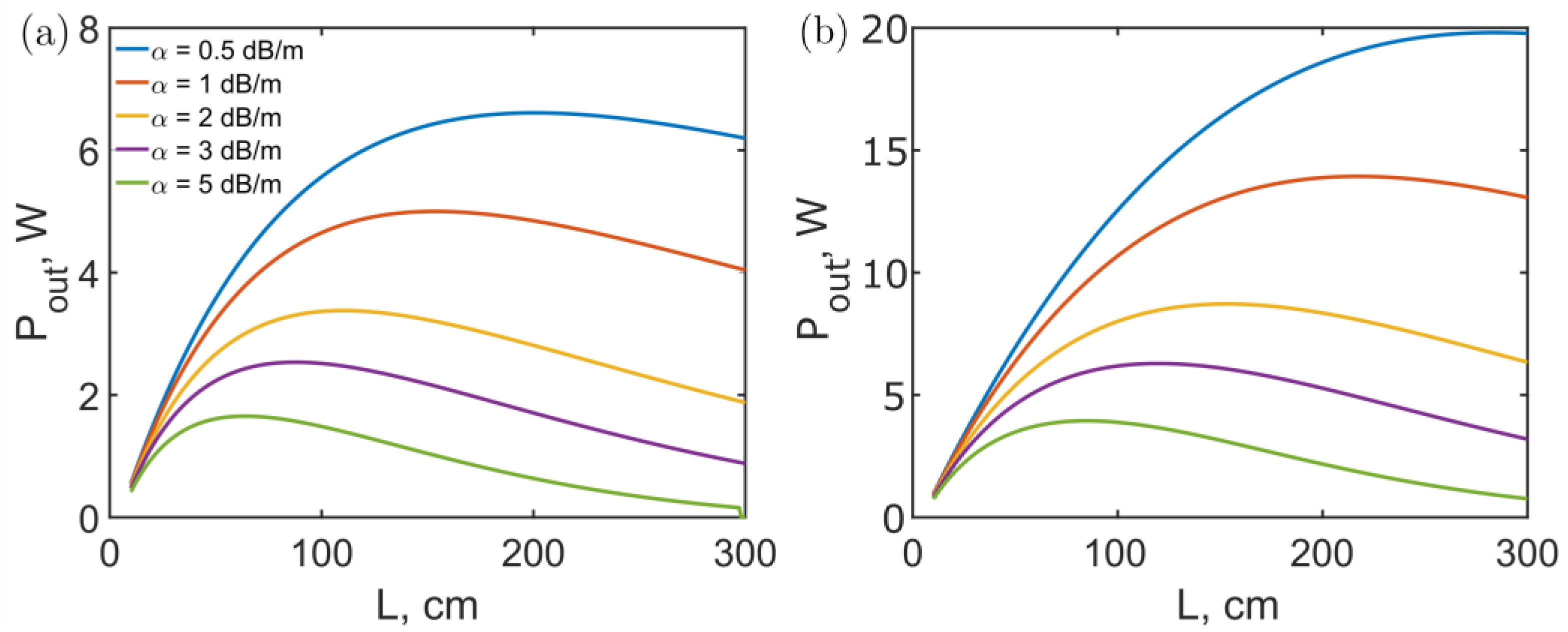
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jackson, S. Towards high-power mid-infrared emission from a fibre laser. Nat. Photonics 2012, 6, 423–431. [Google Scholar] [CrossRef]
- Ebrahim-Zadeh, M.; Sorokina, I.T. Mid-Infrared Coherent Sources and Applications; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef]
- Hugi, A.; Villares, G.; Blaser, S.; Liu, H.C.; Faist, J. Mid-Infrared Frequency Comb Based on a Quantum Cascade Laser. Nature 2012, 492, 229–233. [Google Scholar] [CrossRef]
- Silvestri, C.; Qi, X.; Taimre, T.; Bertling, K.; Rakić, A.D. Frequency Combs in Quantum Cascade Lasers: An Overview of Modeling and Experiments. APL Photonics 2023, 8, 020902. [Google Scholar] [CrossRef]
- Gladyshev, A.V.; Kosolapov, A.F.; Khudyakov, M.M.; Yatsenko, Y.P.; Kolyadin, A.N.; Krylov, A.A.; Pryamikov, A.D.; Biriukov, A.S.; Likhachev, M.E.; Bufetov, I.A.; et al. 4.4-μm Raman Laser Based on Hollow-Core Silica Fibre. Quantum Electron. 2017, 47, 491–494. [Google Scholar] [CrossRef]
- Bufetov, I.A.; Kosolapov, A.F.; Pryamikov, A.D.; Gladyshev, A.V.; Kolyadin, A.N.; Krylov, A.A.; Yatsenko, Y.P.; Biriukov, A.S. Revolver Hollow Core Optical Fibers. Fibers 2018, 6, 39. [Google Scholar] [CrossRef]
- Aghbolagh, F.B.A.; Nampoothiri, V.; Debord, B.; Gerome, F.; Vincetti, L.; Benabid, F.; Rudolph, W. Mid IR Hollow Core Fiber Gas Laser Emitting at 4.6 μm. Opt. Lett. 2019, 44, 383–386. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, W.; Cui, Y.; Li, H.; Pei, W.; Li, X.; Li, Z.; Wang, M.; Wang, Z. 3.1 W Mid-Infrared Fiber Laser at 4.16 μm Based on HBr-Filled Hollow-Core Silica Fibers. Opt. Lett. 2022, 47, 5785–5788. [Google Scholar] [CrossRef]
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Roberts, P.J.; Allan, D.C. Single-Mode Photonic Band Gap Guidance of Light in Air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed]
- Falconi, M.C.; Laneve, D.; Prudenzano, F. Advances in Mid-IR Fiber Lasers: Tellurite, Fluoride and Chalcogenide. Fibers 2017, 5, 23. [Google Scholar] [CrossRef]
- Fortin, V.; Bernier, M.; Bah, S.T.; Vallée, R. 30 W Fluoride Glass All-Fiber Laser at 2.94 μm. Opt. Lett. 2015, 40, 2882–2885. [Google Scholar] [CrossRef] [PubMed]
- Fortin, V.; Jobin, F.; Larose, M.; Bernier, M.; Vallée, R. 10-W-Level Monolithic Dysprosium-Doped Fiber Laser at 3.24 μm. Opt. Lett. 2019, 44, 491–494. [Google Scholar] [CrossRef] [PubMed]
- Maes, F.; Fortin, V.; Poulain, S.; Poulain, M.; Carrée, J.-Y.; Bernier, M.; Vallée, R. Room-Temperature Fiber Laser at 3.92 μm. Optica 2018, 5, 761–764. [Google Scholar] [CrossRef]
- Shaw, L.B.; Cole, B.; Thielen, P.A.; Sanghera, J.S.; Aggarwal, I.D. Mid-Wave IR and Long-Wave IR Laser Potential of Rare-Earth Doped Chalcogenide Glass Fiber. IEEE J. Quantum Electron. 2001, 37, 1127–1137. [Google Scholar] [CrossRef]
- Sójka, Ł.; Tang, Z.; Zhu, H.; Bereś-Pawlik, E.; Furniss, D.; Seddon, A.B.; Benson, T.M.; Sujecki, S. Study of Mid-Infrared Laser Action in Chalcogenide Rare Earth Doped Glass with Dy3+, Pr3+ and Tb3+. Opt. Mater. Express 2012, 2, 1632–1640. [Google Scholar] [CrossRef]
- Tang, Z.; Furniss, D.; Fay, M.; Sakr, H.; Sójka, L.; Neate, N.; Weston, N.; Sujecki, S.; Benson, T.M.; Seddon, A.B. Mid-Infrared Photoluminescence in Small-Core Fiber of Praseodymium-Ion Doped Selenide-Based Chalcogenide Glass. Opt. Mater. Express 2015, 5, 870. [Google Scholar] [CrossRef]
- Sojka, L.; Tang, Z.; Furniss, D.; Sakr, H.; Fang, Y.; Beres-Pawlik, E.; Benson, T.M.; Seddon, A.B.; Sujecki, S. Mid-Infrared Emission in Tb3+-Doped Selenide Glass Fiber. J. Opt. Soc. Am. B 2017, 34, A70–A79. [Google Scholar] [CrossRef]
- Karaksina, E.V.; Shiryaev, V.S.; Churbanov, M.F.; Anashkina, E.A.; Kotereva, T.V.; Snopatin, G.E. Core-Clad Pr(3+)-Doped Ga(In)-Ge-As-Se-(I) Glass Fibers: Preparation, Investigation, Simulation of Laser Characteristics. Opt. Mater. 2017, 72, 654–660. [Google Scholar] [CrossRef]
- Sojka, L.; Benson, T.M.; Furniss, D.; Tang, Z.; Sakr, H.; Seddon, A.B.; Sujecki, S. The Modelling of Fibre Lasers for Mid-Infrared Wavelengths. Recent Trends Comput. Photonics 2017, 204, 39–75. [Google Scholar] [CrossRef]
- Quimby, R.S.; Shaw, L.B.; Sanghera, J.S.; Aggarwal, I.D. Modeling of Cascade Lasing in Dy: Chalcogenide Glass Fiber Laser with Efficient Output at 4.5 μm. IEEE Photon. Technol. Lett. 2008, 20, 123–125. [Google Scholar] [CrossRef]
- Falconi, M.C.; Palma, G.; Starecki, F.; Nazabal, V.; Troles, J.; Adam, J.-L.; Taccheo, S.; Ferrari, M.; Prudenzano, F. Dysprosium-Doped Chalcogenide Master Oscillator Power Amplifier (MOPA) for Mid-IR Emission. J. Light. Technol. 2017, 35, 265–273. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Kim, A.V. Numerical Simulation of Ultrashort Mid-IR Pulse Amplification in Praseodymium-Doped Chalcogenide Fibers. J. Light. Technol. 2017, 35, 5397–5403. [Google Scholar] [CrossRef]
- Xiao, X.; Xu, Y.; Guo, H.; Wang, P.; Cui, X.; Lu, M.; Wang, Y.; Peng, B. Theoretical Modeling of 4.3 μm Mid-Infrared Lasing in Dy3+-Doped Chalcogenide Fiber Lasers. IEEE Photonics J. 2018, 10, 1501011. [Google Scholar] [CrossRef]
- Shiryaev, V.S.; Sukhanov, M.V.; Velmuzhov, A.P.; Karaksina, E.V.; Kotereva, T.V.; Snopatin, G.E.; Denker, B.I.; Galagan, B.I.; Sverchkov, S.E.; Koltashev, V.V.; et al. Core-Clad Terbium Doped Chalcogenide Glass Fiber with Laser Action at 5.38 μm. J. Non-Cryst. Solids 2021, 567, 120939. [Google Scholar] [CrossRef]
- Denker, B.; Fjodorow, P.; Frolov, M.; Galagan, B.; Koltashev, V.; Plotnichenko, V.; Sukhanov, M.; Sverchkov, S.; Velmuzhov, A. Rare earth doped selenide glasses as laser materials for the 5-6 μm spectral range. Photonics 2023, 10, 1323. [Google Scholar] [CrossRef]
- Koltashev, V.V.; Frolov, M.P.; Leonov, S.O.; Sverchkov, S.E.; Galagan, B.I.; Korostelin, Y.V.; Skasyrsky, Y.K.; Snopatin, G.E.; Sukhanov, M.V.; Velmuzhov, A.P.; et al. Characteristics of a CW ∼5 μm Ce3+-Doped Chalcogenide Glass Fiber Laser. Laser Phys. Lett. 2023, 20, 095801. [Google Scholar] [CrossRef]
- Koltashev, V.V.; Denker, B.I.; Galagan, B.I.; Snopatin, G.E.; Sukhanov, M.V.; Sverchkov, S.E.; Velmuzhov, A.P.; Plotnichenko, V.G. 150 mW Tb3+ Doped Chalcogenide Glass Fiber Laser Emitting at λ > 5 μm. Opt. Laser Technol. 2023, 161, 109233. [Google Scholar] [CrossRef]
- Klenke, A.; Müller, M.; Stark, H.; Stutzki, F.; Hupel, C.; Schreiber, T.; Tünnermann, A.; Limpert, J. Coherently Combined 16-Channel Multicore Fiber Laser System. Opt. Lett. 2018, 43, 1519–1522. [Google Scholar] [CrossRef]
- Fsaifes, I.; Ranély-Vergé-Dépré, C.-A.; Veinhard, M.; Bellanger, S.; Chanteloup, J.-C. Far Field Energy Distribution Control Using a Coherent Beam Combining Femtosecond Digital Laser. Opt. Express 2023, 31, 8217–8225. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Andrianov, A.V.; Anashkina, E.A.; Litvak, A.G. Coherent Amplification of High-Power Laser Radiation in Multicore Fibers from a Rectangular Array of Cores. Opt. Lett. 2021, 46, 246–249. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Kalinin, N.A.; Anashkina, E.A.; Egorova, O.N.; Lipatov, D.S.; Kim, A.V.; Semjonov, S.L.; Litvak, A.G. Selective Excitation and Amplification of Peak-Power-Scalable Out-of-Phase Supermode in Yb-Doped Multicore Fiber. J. Light. Technol. 2020, 38, 2464–2470. [Google Scholar] [CrossRef]
- Andrianov, A.; Kalinin, N.; Anashkina, E.; Leuchs, G. Highly Efficient Coherent Beam Combining of Tiled Aperture Arrays Using Out-of-Phase Pattern. Opt. Lett. 2020, 45, 4774–4777. [Google Scholar] [CrossRef] [PubMed]
- Kalinin, N.A.; Anashkina, E.A.; Leuchs, G.; Andrianov, A.V. Lenslet Array-Free Efficient Coherent Combining of Broadband Pulses at the Output of a Multicore Fiber with a Square Core Grid. Opt. Express 2022, 30, 1013–1020. [Google Scholar] [CrossRef] [PubMed]
- Svelto, O.; Hanna, D.C. Principles of Lasers; Springer: New York, NY, USA, 2010. [Google Scholar]
- Brown, D.C.; Hoffman, H.J. Thermal, Stress, and Thermo-Optic Effects in High Average Power Double-Clad Silica Fiber Lasers. IEEE J. Quantum Electron. 2001, 37, 207–217. [Google Scholar] [CrossRef]
- Antipov, O.; Dobrynin, A.; Getmanovskiy, Y.; Karaksina, E.; Shiryaev, V.; Sukhanov, M.; Kotereva, T. Thermal Lensing and Laser-Induced Damage in Special Pure Chalcogenide Ge35As10S55 and Ge20As22Se58 Glasses under Quasi-CW Fiber Laser Irradiation at 1908 nm. Photonics 2023, 10, 252. [Google Scholar] [CrossRef]
- Kuznetsov, I.; Chizhov, S.; Palashov, O. High-Energy and High-Average-Power Two-Channel Yb:YAG Amplifier with Passive Coherent Combining. J. Opt. Soc. Am. B 2022, 39, 2692–2696. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value |
|---|---|---|
| Pump wavelength at 1 → 4 (7F6 → 7F2) transition | λp | 2 μm |
| Laser wavelength at 2 → 1 (7F5 → 7F6) transition | λs | 5.3 μm |
| Total lifetime of level 2 (7F5) | τ2 | 7.5 ms |
| Total (non-radiative) lifetime of level 3 (7F4) | τ3 | 10 μs |
| Total lifetime of level 4 (7F2) | τ4 | 0.1 ms |
| Absorption cross-section at 1 → 4 (7F6 → 7F2) transition | σ14 | 0.7 × 10−20 cm2 |
| Emission cross-section at 4 → 1 (7F2 → 7F6) transition | σ41 | 0.7 × 10−20 cm2 |
| Absorption cross-section at 1 → 2 (7F6 → 7F5) transition | σ12 | 0.35 × 10−20 cm2 |
| Emission cross-section at 2 → 1 (7F5 → 7F6) transition | σ21 | 1.09 × 10−20 cm2 |
| Parameter | Symbol | Value |
|---|---|---|
| Cavity multicore fiber length | L | 30–300 cm |
| Diameter of Tb-doped core | d | 20 µm |
| Distance between core centers | Δ | 25 µm |
| Tb concentration in the core | NTb | 2 × 10−19 cm−3 |
| Numerical aperture (cores/cladding) | NA | 0.189 |
| Cladding diameter | D | 300 µm |
| Effective mode field area at λs = 5.3 μm | Aeff | 4892 µm2 |
| Overlap integral (pump with Tb-doped cores) | Γp | 0.11 |
| Overlap integral (laser wave with Tb-doped cores) | Γs | 0.91 |
| Background fiber loss | α | 1.7 dB/m (for Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8) |
| 0.5–5 dB/m (for Figure 9 and Figure 10) | ||
| Reflection coefficient at z = 0 | R1 | 0.999 |
| Reflection coefficient at z = L for laser wave | R2 | 0.19–0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salnikov, N.I.; Andrianov, A.V.; Anashkina, E.A. Numerical Modeling of Mid-IR Lasers Based on Tb-Doped Chalcogenide Multicore Fibers. Fibers 2024, 12, 25. https://doi.org/10.3390/fib12030025
Salnikov NI, Andrianov AV, Anashkina EA. Numerical Modeling of Mid-IR Lasers Based on Tb-Doped Chalcogenide Multicore Fibers. Fibers. 2024; 12(3):25. https://doi.org/10.3390/fib12030025
Chicago/Turabian StyleSalnikov, Nikolay I., Alexey V. Andrianov, and Elena A. Anashkina. 2024. "Numerical Modeling of Mid-IR Lasers Based on Tb-Doped Chalcogenide Multicore Fibers" Fibers 12, no. 3: 25. https://doi.org/10.3390/fib12030025
APA StyleSalnikov, N. I., Andrianov, A. V., & Anashkina, E. A. (2024). Numerical Modeling of Mid-IR Lasers Based on Tb-Doped Chalcogenide Multicore Fibers. Fibers, 12(3), 25. https://doi.org/10.3390/fib12030025